Variable-fidelity hypervolume-based expected improvement criteria for multi-objective efficient global optimization of expensive functions

Abstract

Variable-fidelity surrogate-based efficient global optimization (EGO) method with the ability to adaptively select low-fidelity (LF) and high-fidelity (HF) infill point has emerged as an alternative to further save the computational cost of the single-fidelity EGO method. However, in terms of the variable-fidelity surrogate-assisted multi-objective optimization methods, existing methods rely on empirical parameters or are unable to adaptively select LF/HF sample in the optimal search process. In this paper, two variable-fidelity hypervolume-based expected improvement criteria with analytic expressions for variable-fidelity multi-objective EGO method are proposed. The first criterion relies on the concept of variable-fidelity expected improvement matrix (VFEIM) and is obtained by aggregating the VFEIM using a simplified hypervolume-based aggregation scheme. The second criterion termed as VFEMHVI is derived analytically based on a modified hypervolume definition. Both criteria can adaptively select new LF/HF samples in the iterative optimal search process to update the variable-fidelity models towards the HF Pareto front, distinguishing the proposed methods to the rests in the open literature. The constrained versions of the two criteria are also derived for problems with constraints. The effectiveness and efficiency of the proposed methods are verified and validated over analytic problems and demonstrated by two engineering problems including aerodynamic shape optimizations of the NACA0012 and RAE2822 airfoils. The results show that the VFEMHVI combined with the normalization-based strategy to define the reference point is the most efficient one over the compared methods.

1 Introduction

Surrogate-based optimization (SBO) method is a promising approach to reduce the computational cost in expensive simulation-based engineering design optimization problems, as the surrogate model can be used to replace the expensive simulations during the optimization and the cost of building a surrogate model is almost negligible compared with an expensive simulation. Among the available surrogate models, Kriging [1] or Gaussian process regression [2] has gained popularity due to its capability of providing the prediction of a function and the uncertainty of the prediction. In the field of engineering optimization design, the Kriging-based efficient global optimization (EGO) [3] method utilizing the expected improvement (EI) criterion has gotten popularity after its birth, for it enables the searching of global optimum with much less number of expensive function evaluations than the methods such as evolutionary algorithms. For example, EGO has been applied to improve the performance of the axial flow compressor rotor [4] or cascades [5], cryogenic liquid turbine stage [6] and turbine blade [7], etc. The advent of the EGO method greatly inspired the research and development of the SBO [8, 9], including utilizing the variable-fidelity (VF) surrogate to save the computational cost of the optimization task further [10, 11] or extending the EGO for single-objective optimization to solve multi-objective problems [12, 13], etc.

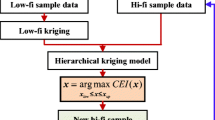
VF surrogate uses a set of numerical methods with varying degrees of fidelity and computational expense (e.g., potential theory, Euler equations, and Navier–Stokes equations) to approximate the unknown function of interest as a function of the independent variables while reducing the more expensive high-fidelity simulations [14]. Among the different types of VF surrogate, the Co-Kriging and its variants [15, 16], have gained much attention and been adapted to develop VF surrogate-assisted EGO-like method (VFEGO). The augmented expected improvement and the statistic lower bounding criterion were proposed to guide the selection of the location and fidelity level of the next infill sample in [17, 18], respectively. More recently, the extended expected improvement-based on an enhanced Co-Kriging, VF expected improvement (VF-EI) based on Hierarchical Kriging (HK), VF lower confidence bound based on additive scaling VF surrogate, and the expected improvement-based criterion for gradient-enhanced VF surrogate were developed in [19,20,21,22], respectively. Those methods can be viewed as a generalized EGO method using different types of VF surrogate models and infill sampling criteria (ISC). Compared with the EI criterion for the single-fidelity EGO method, the distinct feature of the ISCs used in the various VFEGO methods is the ability to adaptively determine the fidelity level of the infill sampling point to be evaluated at.

On extending the EGO to treat multi-objective problems, the multi-objective efficient global optimization (MOEGO) is one of the most frequently studied surrogate model-based optimization algorithms as it enforces a more careful search since it integrates both the prediction and error estimates [23,24,25,26,27,28,29,30,31]. The MOEGO method shares the same framework of EGO method, consisting of the initialization phase and the iterative search phase. In the initialization phase, the initial samples are generated by the design of experiments (DOE) method and then evaluated using the computational expensive simulation tools. Based on those initial samples, the Kriging models for each objective function are constructed. Then MOEGO proceeds to the iterative phase. At each iteration, the multi-objective EI function is maximized to obtain one infill point which is evaluated with the expensive function. Such a procedure will iterate until the stopping rule is met. It can be noted that the MOEGO approach differs from the EGO method at two aspects: multiple Kriging models are built for each objective and multi-objective EI-based criterion is adopted to guide the selection of the next infill point. The efficiency of the MOEGO method mainly depends on the multi-objective EI infill criterion used [31]. There are different kinds of criteria to be used in MOEGO, the expected angle-penalized length improvement criterion [13], the hypervolume-based EI criterion [24], probability of hypervolume improvement criterion [25], the Euclidean distance-based EI criterion [26], the maximin distance-based EI criterion [27], the expected inverted penalty boundary intersection improvement [28], the expected improvement matrix-based infill criterion [29], the modified hypervolume-based EI criterion [32], etc. Among those criteria, the last two criteria are of the distinct feature being cheap-to-evaluate and yet efficient to obtain well-distributed solutions compared to other aforementioned criteria, but the performance comparison between those two criteria has never been conducted. Nevertheless, the MOEGO method has been demonstrated to be effective and efficient in engineering applications, such as the airfoil shape optimization [31], bump inlet shape optimization to minimize the total pressure distortions [33], S-shape supersonic axial flow compressor cascade optimization [5], etc.

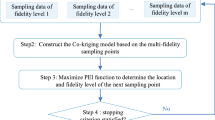
In terms of using the VF surrogate-based optimization method to solve the expensive multi-objective engineering problems, the existing method can be classified into three categories. The first group of VF surrogate-based algorithms [34,35,36,37,38] finds the Pareto Front (PF) on the LF surrogate first, followed by choosing promising solutions on the PF to be evaluated by HF simulations. With HF samples, the iterative optimization process starts with tuning VF surrogate and followed by determining the PF on the VF surrogate. The third step of the iterative phase is choosing solutions on the obtained PF to be evaluated at the HF level. The termination condition is checked and if not met, the VF surrogate is updated with the newly obtained HF samples. This kind of method has been applied to optimize the antenna [34] and airfoil [37]. It should be noted that how to select a limited number of promising solutions from a large amount of PF solutions is still a challenging task. Moreover, for methods belonging to the first group, the number of LF samples is fixed during the design, while HF samples are repetitively added in the iterative optimization stage. It is, of course, not the most efficient way, since it is always questionable how many LF samples would be sufficient. The other way, and a potentially better way, is that both LF and HF samples are adaptively added. The second group of methods incorporates the VF surrogate into the population-based evolutionary algorithms [39,40,41,42,43,44,45,46]. Such algorithms usually start from the population initialization and then evaluate the individuals using LF and HF simulators, respectively. With the available LF and HF samples, the VF surrogates for each objective are then constructed. The population is evolved iteratively with the fitness of each individual calculated by using the VF surrogate model. After certain evolutionary iterations, individuals in the current population are chosen by sophisticated model manage strategies and to be evaluated by LF/HF simulators. Effectiveness of such VF surrogate-based evolutionary algorithms have been demonstrated by optimizing a torque arm [42] and a stiffened cylindrical shell [43]. Disappointedly, the population-based methods still need thousands of function evaluations which might be unacceptable in some scenarios and the sophisticated model manage strategy usually relies on empirical parameters. For example, a threshold of the minimum of minimum distance is required for the online variable-fidelity surrogate-assisted multi-objective genetic algorithm [42]. The VF surrogate-based method following the MOEGO framework (VFMOEGO) is classified into the third group, including an output space entropy search method [47] in the Bayesian optimization field. With the initialization stage to prepare the initial data set and build the VF surrogates for each objective, the iterative optimization process starts. In each iteration, an output space entropy-based ISC is utilized to determine the spatial position and fidelity level of the next sample point to be evaluated at. In other words, the LF and HF samples will be adaptively added. It can be noted that such VF surrogate-based method follows the MOEGO framework and is free of the empirical parameter. Like MOEGO, the efficiency of this kind of method heavily relies on the adopted ISC. Unfortunately, the ISC proposed in the output space entropy search method stands on the assumption that the value of lower fidelity of an objective must be smaller than that of the corresponding higher fidelity [47]. This indicates the output space entropy search method is applicable to solve problems with such features, limiting its usefulness in engineering applications. Therefore, proposing a general ISC for VFMOEGO method is required to solve engineering problems.

To fill in this gap, two general cheap-to-evaluate ISCs for VFMOEGO method are proposed, by extending the HK model-based VF-EI criterion for single-objective optimization to the multi-objective scenario. The performance of the VFMOEGO methods utilizing the proposed ISCs is illustrated using analytic examples and two real-world engineering examples. The comparisons between the proposed approaches and existing approaches considering the computational efficiency and robustness are made. The merits of the proposed approach are analyzed and summarized.

The remainder of this paper is organized as follows. Sect. 2 recalls the theoretical background. Then, in Sect. 3, the proposed ISCs are introduced in detail with the implementation and illustration. The compared methods, analytic, and real-world test problems for the comparative study, and the results of the comparative study are given in Sect. 4. Conclusions and future works are summarized in Sect. 5.

2 Background and terminology

This study aims to solve the following multi-objective optimization (MOO) problem based on HF expensive numerical simulation with the assistance of LF but cheaper numerical analysis:

$$ \begin{gathered} \mathop {\min }\limits_{{{\mathbf{x}} \in \Omega }} F({\mathbf{x}}) = \left\{ {f_{1} ({\mathbf{x}}),f_{2} ({\mathbf{x}}), \ldots ,f_{i} ({\mathbf{x}}), \ldots ,f_{M} ({\mathbf{x}})} \right\} \hfill \\ {\text{with assistance of }}F_{lf} ({\mathbf{x}}) = \left\{ {f_{1,lf} ({\mathbf{x}}),f_{2,lf} ({\mathbf{x}}), \ldots ,f_{i,lf} ({\mathbf{x}}), \ldots ,f_{M,lf} ({\mathbf{x}})} \right\}, \hfill \\ \end{gathered} $$

(1)

where $F({\mathbf{x}})$ and $F_{lf} ({\mathbf{x}})$ denote the objective functions evaluated by HF and LF numerical simulators, respectively, ${\mathbf{x}}$ is the vector of design parameters with length being $d$, $M$ represents the number of objectives, $\Omega \in {\mathbb{R}}^{d}$ is the design space. A point ${\mathbf{x}}$ is said to Pareto-dominate another point ${\mathbf{x^{\prime}}}$ if $f_{i} ({\mathbf{x}}) \le f_{i} \left( {{\mathbf{x}}^{\prime } } \right)\forall i$ and there exists some $j \in \{ 1,2, \ldots ,M\}$ such that $f_{j} ({\mathbf{x}}) < f_{j} \left( {{\mathbf{x}}^{\prime } } \right)$. The optimal solutions of a MOO problem is a set of points ${\mathcal{X}}^{*} \subset \Omega$ such that no point ${\mathbf{x}}^{\prime } \in \Omega \backslash {\mathcal{X}}^{*}$ Pareto-dominates a point ${\mathbf{x}} \in {\mathcal{X}}^{*}$. The solution set ${\mathcal{X}}^{*}$ is called the optimal Pareto set and the corresponding set of function values $F^{*}$ is called the optimal Pareto front (PF). The PF with $k$ solutions is denoted as:

$$ {\text{PF}} = \left\{ {f_{1}^{j} ,f_{2}^{j} , \ldots f_{M}^{j} } \right\},j = 1,2, \ldots ,k. $$

(2)

Our goal is to approximate PF by minimizing the computational cost through the VFMOEGO method or obtain a better approximation of PF with a budgeted cost. In the proposed VFMOEGO methods, each objective is to be approximated by an HK model. Meanwhile, the HK model is built based on Kriging. And the ISCs used in the VFMOEGO methods are developed by extending the VF-EI function for single-objective VFEGO method to VFMOEGO. Thus, the basics of the Kriging, HK, and VF-EI are briefed as follows.

2.1 Kriging

Kriging is an interpolation technique that originated from the geostatistical community and then applied to approximate expensive black-box functions [1]. It hypothesizes that a random process exits in each sampling site, and consists of two parts: the trend function and the random process:

$$ Y\left( {\mathbf{x}} \right) = \beta_{0} + Z\left( {\mathbf{x}} \right). $$

(3)

For ordinary Kriging, the trend function $\beta_{0}$ is an unknown constant and $Z\left( {\mathbf{x}} \right)$ is a stationary random process with zero mean and process variance $\sigma^{{2}}$. The covariance of $Z\left( {\mathbf{x}} \right)$ can be expressed as:

$$ {\text{CoV}}\left( {Z\left( {\mathbf{x}} \right),Z\left( {{\mathbf{x^{\prime}}}} \right)} \right) = \sigma^{2} R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right), $$

(4)

where $R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)$ is the spatial correlation function depending on the Euclidean distance between two sites ${\mathbf{x}}$ and ${\mathbf{x^{\prime}}}$. The common-used correlation functions are the squared exponential function, the Matérn function, and the exponential function. In the field of design and analysis of computer experiment (DACE), the widely used squared exponential function (aka Gaussian correlation) is expressed as:

$$ R\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = \exp \left( { - \sum\limits_{i = 1}^{d} {\theta_{i} } \left| {x_{i} - x^{\prime}_{i} } \right|^{{2}} } \right), $$

(5)

where $\theta_{i} ,i = 1,2, \ldots d$ are parameters measuring the activity of the variable and being determined in the model fitting process.

By minimizing the mean square error (MSE) of the random process subject to the unbiasedness constraint, the Kriging prediction $\hat{y}\left( {\mathbf{x}} \right)$ along with the MSE $s^{2} \left( {\mathbf{x}} \right)$ of the prediction at any unvisited point ${\mathbf{x}}$ can be derived as:

$$ \begin{aligned} \hat{y}\left( {\mathbf{x}} \right) & = \beta_{0} + {\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} \left( {{\mathbf{y}}_{s} - \beta_{0} {\mathbf{1}}} \right) \\ s^{2} \left( {\mathbf{x}} \right) & = \sigma^{2} \left\{ {1.0 - {\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{r}} + {{\left[ {{\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{1}} - 1} \right]^{2} } \mathord{\left/ {\vphantom {{\left[ {{\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{1}} - 1} \right]^{2} } {\left( {{\mathbf{1}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{1}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{\mathbf{1}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{1}}} \right)}}} \right\}, \\ \end{aligned} $$

(6)

where ${\mathbf{r}}$ is a correlation vector between the unobserved point and the sample points, ${\mathbf{R}}$ is the correlation matrix whose elements are correlation functions between sample points, ${\mathbf{y}}_{s}$ is the column vector that contains the responses at the sample points, ${\mathbf{1}}$ is a column vector filled with ones. For more details about Kriging refer to [1].

2.2 Hierarchical Kriging for variable-fidelity surrogate modeling

HK [48] is distinct from other VF model by taking the low-fidelity (LF) function as the model trend for the HF model to avoid calculating the covariance matrix between LF and HF samples. HK has been proved to be more computational efficient without losing accuracy compared with Co-Kriging [49,50,51]. To begin with, the Kriging model of LF function is built based on the LF samples. The prediction and MSE of the LF Kriging are denoted as $\hat{y}_{{{\text{lf}}}} \left( {\mathbf{x}} \right)$ and $s_{{{\text{l}}f}}^{2} \left( {\mathbf{x}} \right)$ respectively. Then the LF Kriging is used as the model trend of the Kriging for the HF function of the form:

$$ Y\left( {\mathbf{x}} \right) = \beta_{lf} \hat{y}_{lf} \left( {\mathbf{x}} \right) + Z\left( {\mathbf{x}} \right), $$

(7)

where $\beta_{lf}$ is a scaling factor representing how the LF Kriging $\hat{y}_{lf} \left( {\mathbf{x}} \right)$ correlates the HF function, $Z\left( {\mathbf{x}} \right)$ represents the random process having zero mean and variance with the same form shown in (4). Via minimizing the MSE of the random process subject to the unbiasedness constraint, the HK predictor $\hat{y}\left( {\mathbf{x}} \right)$ and its MSE $s^{2} \left( {\mathbf{x}} \right)$ are formulated as:

$$ \begin{gathered} \hat{y}\left( {\mathbf{x}} \right) = \beta_{lf} \hat{y}_{lf} \left( {\mathbf{x}} \right) + {\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} \left( {{\mathbf{y}}_{s} - \beta_{{{\text{lf}}}} {\mathbf{F}}} \right) \\ s^{2} \left( {\mathbf{x}} \right) = \sigma^{2} \left\{ {1 - {\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{r}} + {{\left[ {{\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{F}} - \hat{y}_{lf} \left( {\mathbf{x}} \right)} \right]^{2} } \mathord{\left/ {\vphantom {{\left[ {{\mathbf{r}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{F}} - \hat{y}_{lf} \left( {\mathbf{x}} \right)} \right]^{2} } {\left( {{\mathbf{F}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{F}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{\mathbf{F}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{F}}} \right)}}} \right\}, \\ \end{gathered} $$

(8)

where $\beta_{lf} { = }\left( {{\mathbf{F}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{F}}} \right)^{ - 1} {\mathbf{F}}^{{\text{T}}} {\mathbf{R}}^{ - 1} {\mathbf{y}}_{s}$, ${\mathbf{r}}$ is a correlation vector between the unobserved point and the HF sample points, ${\mathbf{R}}$ is the correlation matrix whose elements are correlation functions between HF sample points, ${\mathbf{y}}_{s}$ is the column vector that contains the true responses at the HF sample points, ${\mathbf{F}} = \left[ {\hat{y}_{{{\text{lf}}}} \left( {{\mathbf{x}}^{\left( 1 \right)} } \right), \ldots ,\hat{y}_{{l{\text{f}}}} \left( {{\mathbf{x}}^{\left( n \right)} } \right)} \right]^{{\text{T}}}$ represents the $n$ predictions from the LF Kriging at the HF sample sites $\left[ {{\mathbf{x}}^{\left( 1 \right)} , \ldots ,{\mathbf{x}}^{\left( n \right)} } \right]^{{\text{T}}}$. Details about the HK model can be found in [48].

2.3 HK-based variable-fidelity EI

In the VFEGO method proposed in [19], a new infill sample point is obtained by the VF-EI criterion at each iteration of the iterative optimization phase to update the HK model to reach the global optimum of the HF function efficiently. The VF-EI is derived based on the assumption that the prediction from the HK model for the objective function at any unvisited point ${\mathbf{x}}$ obeys the following normal distribution:

$$ \begin{array}{*{20}c} {\hat{Y}({\mathbf{x}},l)\sim N\left[ {\hat{y}({\mathbf{x}}),s^{2} ({\mathbf{x}},l)} \right],} & {l = 1,2} \\ \end{array} , $$

(9)

with

$$ s^{2} \left( {{\mathbf{x}},l} \right) = \left\{ {\begin{array}{*{20}c} {\beta_{lf}^{2} s_{lf}^{2} \left( {\mathbf{x}} \right),} & {l = 1{\text{ for LF level}}} \\ {s^{2} \left( {\mathbf{x}} \right),} & {l = 2{\text{ for HF level}}} \\ \end{array} } \right.. $$

(10)

With this, the improvement w.r.t. the best-observed HF objective value so far $f_{\min }$ is formulated as:

$$ I_{{{\text{vf}}}} ({\mathbf{x}},l) = \max \left( {f_{\min } - \hat{Y}({\mathbf{x}},l),0} \right), $$

(11)

which is a function of both the spatial location ${\mathbf{x}}$ and fidelity level $l$. Then the VF-EI relating to the above improvement function can be derived as:

$$ {\text{EI}}_{vf} \left( {{\mathbf{x}},l} \right) = \left( {f_{\min } - \hat{y}\left( {\mathbf{x}} \right)} \right)\Phi \left( {\frac{{f_{\min } - \hat{y}\left( {\mathbf{x}} \right)}}{{s\left( {{\mathbf{x}},l} \right)}}} \right) + s\left( {{\mathbf{x}},l} \right)\phi \left( {\frac{{f_{\min } - \hat{y}\left( {\mathbf{x}} \right)}}{{s\left( {{\mathbf{x}},l} \right)}}} \right), $$

(12)

where $\Phi \left( \cdot \right)$ and $\phi \left( \cdot \right)$ are the cumulative distribution function and probability density function of the standard normal distribution. It can be noted that the above VF-EI only relates to the improvement of the HF function, which means the infilling of both LF and HF samples are HF-optimum oriented. It should be noted that, in the above VF-EI function, the cost ratio between LF and HF simulations are not taken into consideration. The disadvantage of such a feature is it might not be as efficient as other methods including a cost-control strategy in some applications [21]. But for problems with varying cost over the design space or the cost ratio between LF and HF simulations are not know beforehand, its performance will be more robust [52]. The new sample point ${\mathbf{x}}$ and its fidelity $l$ at each iteration are determined by maximizing the VF-EI, that is:

$$ {\mathbf{x}},l = \mathop {\arg \max }\limits_{{{\mathbf{x}} \in \Omega ,l = 1,2}} {\text{EI}}_{vf} \left( {{\mathbf{x}},l} \right). $$

(13)

If the new sample is found to be an LF one ($l = 1$), which means that adding an LF sample will improve the HF objective function most, it will be evaluated by the cheaper analysis; otherwise, the new sample will be evaluated by the expensive analysis ($l = 2$).

3 Proposed criteria for VFMOEGO

This work aims to develop the ISCs for the VFMOEGO method. The overall steps of the VFMOEGO are described first. VFMOEGO follows the framework of EGO/MOEGO and consists of the initialization and iterative optimization phases. The initialization phase includes the generation of the LF and HF initial samples by the DOE method individually and the evaluation of the LF and HF samples using the simulation tool at the corresponding fidelity level. The iterative optimization stage proceeds with the construction of the HK models for each objective function based on the initial data set. Then the spatial position and fidelity level to be evaluated at the next sample point are obtained by maximizing the ISC. Third, the simulator is invoked to get the LF/HF response of the sample point. The data set is augmented before the check of the termination condition. The iterative optimization phase will continue iteratively until the stopping rule is met.

In VFMOEGO, each objective is approximated by an HK model. The objective vector of the studying point ${\mathbf{x}}$ then can be considered as the following M-dimensional independent Gaussian random variables:

$$ \begin{array}{*{20}c} {\hat{Y}_{i} ({\mathbf{x}},l)\sim N\left[ {\hat{y}_{i} ({\mathbf{x}}),s_{i}^{2} ({\mathbf{x}},l)} \right],} & {l = 1,2} \\ \end{array} ,i = 1, \ldots ,M, $$

(14)

where $\hat{y}_{i} ({\mathbf{x}})$ is the prediction of the studying point ${\mathbf{x}}$ offered by the ith HK model, $s_{i} \left( {{\mathbf{x}},l} \right)$ with $l = 1$ or $l = 2$ represents the variance at LF or HF level offered by the ith HK model. With this, the proposed two criteria are derived as follows.

3.1 Variable-fidelity expected improvement matrix-based criterion

When dealing with the MOO problem, the current best-observed HF objective value $f_{\min }$ in single-objective VFEGO expands in two directions: (1) the number of points in the current best solution increases from one to $k$ and (2) the dimension of each point changes from one to $M$. Hence the current best solution for MOO is a 2-D matrix:

$$ \left[ {\begin{array}{*{20}c} {f_{1}^{1} } & {f_{1}^{2} } & \cdots & {f_{1}^{M} } \\ {f_{2}^{1} } & {f_{2}^{2} } & \cdots & {f_{2}^{M} } \\ \vdots & \vdots & \ddots & \vdots \\ {f_{k}^{1} } & {f_{k}^{2} } & \cdots & {f_{k}^{M} } \\ \end{array} } \right]. $$

(15)

Inspired by this, the scalar function VF-EI for single objective VFEGO can also be expanded into a 2-D matrix for MOO. Correspondingly, the variable-fidelity expected improvement matrix (VFEIM) is formulated as:

$$ \left[ {\begin{array}{*{20}c} {{\text{EI}}_{vf}^{1,1} \left( {{\mathbf{x}},l} \right)} & {{\text{EI}}_{vf}^{2,1} \left( {{\mathbf{x}},l} \right)} & \cdots & {{\text{EI}}_{vf}^{M,1} \left( {{\mathbf{x}},l} \right)} \\ {{\text{EI}}_{vf}^{1,2} \left( {{\mathbf{x}},l} \right)} & {{\text{EI}}_{vf}^{2,2} \left( {{\mathbf{x}},l} \right)} & \cdots & {{\text{EI}}_{vf}^{M,2} \left( {{\mathbf{x}},l} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {{\text{EI}}_{vf}^{1,k} \left( {{\mathbf{x}},l} \right)} & {{\text{EI}}_{vf}^{2,k} \left( {{\mathbf{x}},l} \right)} & \cdots & {{\text{EI}}_{vf}^{M,k} \left( {{\mathbf{x}},l} \right)} \\ \end{array} } \right], $$

(16)

with

$$ EI_{{{\text{vf}}}}^{i,j} \left( {{\mathbf{x}},l} \right) = \left( {f_{j}^{i} - \hat{y}_{i} ({\mathbf{x}})} \right)\Phi \left( {\frac{{f_{j}^{i} - \hat{y}_{i} ({\mathbf{x}})}}{{s_{i} ({\mathbf{x}},l)}}} \right) + s_{i} ({\mathbf{x}},l)\phi \left( {\frac{{f_{j}^{i} - \hat{y}_{i} ({\mathbf{x}})}}{{s_{i} ({\mathbf{x}},l)}}} \right), $$

(17)

$$ s_{i} \left( {{\mathbf{x}},l} \right) = \left\{ {\begin{array}{*{20}c} {\beta_{0}^{2} s_{lf,i}^{2} \left( {\mathbf{x}} \right),} & {l = 1{\text{ for LF level}}} \\ {s_{i}^{2} \left( {\mathbf{x}} \right),} & {l = 2{\text{ for HF level}}} \\ \end{array} } \right., $$

(18)

where $F_{j} = \left\{ {f_{j}^{i} } \right\},i = 1,2, \ldots ,M,j = 1,2, \ldots ,k$ are the $k$ non-dominated front points in the current HF sample set. Figure 1a, b illustrate the VFEIM with $l = 1$ (LF level) and $l = 2$ (HF level), respectively. It can be noted that the ith row in the matrix represents the VF-EIs beyond the ith non-dominated point in all objectives and the jth column in the matrix represents the VF-EI in jth objective beyond all the non-dominated points. To sum up, the VFEIM contains all the information about the VF-EIs of the studying point ${\mathbf{x}}$ beyond all the non-dominated front points in each direction.

Fig. 1

2-D illustrations of the VF-EIM

It can be noted that the VFEIM is a simple and natural extension. However, the VFEIM gives no comprehensive measurement of how much the studying point can improve the PF approximation. Thus, a strategy to aggregate VFEIM into a scalar value to judge the overall improvement of the studying point compared against the current PF approximation should be utilized. The aggregation scheme based on hypervolume measurement in [29] is adopted.

Hypervolume is an indicator measuring the volume (or hypervolume in high dimensional space) of the region dominated by the PF approximation ${\mathbf{P}}$ and bounded by a reference point ${\mathbf{r}} \in {\mathbb{R}}^{M}$:

$$ H({\mathbf{P}}) = \, V\left( {{\mathbf{y}} \in {\mathbb{R}}^{M} |{\mathbf{P}} \prec {\mathbf{y}} \prec {\mathbf{r}}} \right), $$

(19)

where ${\mathbf{P}} \prec {\mathbf{y}}$ means ${\mathbf{y}}$ Pareto-dominates ${\mathbf{P}}$, $V\left( \cdot \right)$ denotes the hypervolume of a bounded space. Figure 2 presents the hypervolume in 2-D space. The reference point ${\mathbf{r}}$ is specified by the user with a relatively large value to ensure that it is dominated by any point in the PF. A higher value of the hypervolume indicator means a better distribution of a PF approximation. However, the hypervolume indicator is expensive to compute when the number of objectives is larger than two.

Fig. 2

2-D illustration of the hypervolume

For a given point ${\mathbf{y}} \in {\mathbb{R}}^{M}$, the hypervolume improvement related to add it into the current PF approximation is defined as the growth of $H({\mathbf{P}})$. It is illustrated in Fig. 3 and formulated as:

$$ I_{{{\text{hv}}}} ({\mathbf{y}}) = H({\mathbf{P}} \cup {\mathbf{y}}) - H({\mathbf{P}}). $$

(20)

As the $I_{{{\text{hv}}}} ({\mathbf{y}})$ being the difference between two hypervolumes, it inherits the computational burden of hypervolume when the number of objectives is larger than two. Therefore, a simplified hypervolume improvement function is proposed in [29] and defined to be the minimum of the $k$ hypervolume improvements of ${\mathbf{y}}$ with respect to each point on the PF approximation, which is expressed as:

$$ I_{{{\text{hvs}}}} ({\mathbf{x}}) = \mathop {\min }\limits_{j = 1}^{k} \left[ {H\left( {{\mathbf{P}}_{j} \cup {\mathbf{y}}} \right) - H\left( {{\mathbf{P}}_{j} } \right)} \right], $$

(21)

where ${\mathbf{P}}_{j} = \left( {f_{1}^{j} ,f_{2}^{j} , \ldots ,f_{i}^{j} , \ldots ,f_{M}^{j} } \right)$. The above formula is cheap-to-evaluate as the hypervolume improvement of a point over the other single point can be calculated analytically and formula (21) can be expressed as:

$$ I_{{{\text{hvs}}}} ({\mathbf{x}}) = \mathop {\min }\limits_{j = 1}^{k} \left[ {\prod\limits_{i = 1}^{M} {\left( {r_{i} - y_{i} ({\mathbf{x}})} \right)} - \prod\limits_{i = 1}^{M} {\left( {r_{i} - f_{i}^{j} } \right)} } \right]. $$

(22)

Fig. 3

The 2-D illustration of the hypervolume improvement

Notably, in Eq. (22), $y_{i} ({\mathbf{x}}) = f_{i}^{j} - \left( {f_{i}^{j} - y_{i} ({\mathbf{x}})} \right)$. Then taking the form of the simplified hypervolume improvement and replacing the improvement $f_{i}^{j} - y_{i} ({\mathbf{x}})$ by the corresponding expected improvement, i.e. the $\left( {i,j} \right)$ element of the VFEIM ${\text{EI}}_{{{\text{vf}}}}^{i,j} \left( {{\mathbf{x}},l} \right)$, the VFEIM can be aggregated as:

$$ {\rm VFEIM}_{\rm h} ({\mathbf{x}},l) = \mathop {\min }\limits_{j = 1}^{k} \left[ {\prod\limits_{i = 1}^{M} {\left[ {r_{i} - \left( {f_{i}^{j} - {\text{EI}}_{{{\text{vf}}}}^{i,j} \left( {{\mathbf{x}},l} \right)} \right)} \right]} - \prod\limits_{i = 1}^{M} {\left( {r_{i} - f_{i}^{j} } \right)} } \right]. $$

(23)

It is clear to note that the ${\rm VFEIM}_{\rm h} ({\mathbf{x}},l)$ is cheap-to-evaluate as it is expressed in the closed-form. Though the ${\rm VFEIM}_{\rm h} ({\mathbf{x}},l)$ is obtained by simply taking the form of the simplified hypervolume improvement function, it is still interpretable. The following example with two objectives is adopted to illustrate this. Assuming an arbitrary point ${\mathbf{P}}_{j}$ on the current PF approximation set as shown in Fig. 4, then the expected improvements over ${\mathbf{P}}_{j}$ with respect to a studying point ${\mathbf{y}}\left( {\mathbf{x}} \right) \in {\mathbb{R}}^{2}$ are $\left( {{\text{EI}}_{{{\text{vf}}}}^{1,j} \left( {{\mathbf{x}},l} \right),EI_{{{\text{vf}}}}^{2,j} \left( {{\mathbf{x}},l} \right)} \right)$ and illustrated as the dashed arrows in the figure. With this, the term $\left( {f_{1}^{j} - {\text{EI}}_{{{\text{vf}}}}^{1,j} \left( {{\mathbf{x}},l} \right),f_{2}^{j} - {\text{EI}}_{{{\text{vf}}}}^{2,j} \left( {{\mathbf{x}},l} \right)} \right)$ can be interpreted as the expected position of the concerned non-dominated front point ${\mathbf{P}}_{j}$, denoted as ${\mathbf{P^{\prime}}}_{j}$ in the figure. The hypervolume improvement of ${\mathbf{P^{\prime}}}_{j}$ over ${\mathbf{P}}_{j}$ will be calculated exactly as $\prod\limits_{i = 1}^{2} {\left[ {r_{i} - \left( {f_{i}^{j} - EI_{{{\text{vf}}}}^{i,j} \left( {{\mathbf{x}},l} \right)} \right)} \right]} - \prod\limits_{i = 1}^{2} {\left( {r_{i} - f_{i}^{j} } \right)}$, which is termed as the simplified expected hypervolume improvement and indicated by the region filled with the darker color.

Fig. 4

2-D illustration of the simplified hypervolume improvement

It is worth to note that aggregated VFEIM function ${\rm VFEIM}_{\rm h} ({\mathbf{x}},l)$ only relates to the improvement of the HF approximation of PF. The aggregated VFEIM function for the HF level, ${\rm VFEIM}_{\rm h} ({\mathbf{x}},l = 2)$, indicates the expected improvement of the HF approximation of PF if an HF sample point is added. But aggregated VFEIM function for the LF level, ${\rm VFEIM}_{\rm h} ({\mathbf{x}},l = 1)$, is the expected improvement of the HF approximation of PF when an LF sample is added. In a word, the infillings of both LF and HF samples are toward to improve the HF approximation of PF, which is a unique property of the VFEIM-based criteria.

As the ${\rm VFEIM}_{\rm h} ({\mathbf{x}},l)$ function takes the minimal of the $k$ simplified expected hypervolume improvements, then the PF approximation will get the integral improvement if ${\rm VFEIM}_{\rm h} ({\mathbf{x}},l)$ is maximized. In other words, in VFMOEGO with the VFEIM-based criterion, the new sample point ${\mathbf{x}}$ and its fidelity level l can be determined by solving the following maximization problem:

$$ {\mathbf{x}},l = \mathop {\arg \max }\limits_{{_{{{\mathbf{x}} \in \Omega ,l = 1,2}} }} \, {\rm VFEIM}_{\rm h} ({\mathbf{x}},l). $$

(24)

If the fidelity level $l = 1$, which means that adding an LF sample will improve the PF approximation most, the true responses of the sample point ${\mathbf{x}}$ will be obtained by calling the cheaper analysis tool; otherwise, the new sample will be evaluated at the HF level (i.e. $l = 2$). It should be mentioned that the responses of the sample point ${\mathbf{x}}$ for each objective can also be evaluated at different fidelity levels by solving the following sub-optimization problem:

$$ {\mathbf{x}},{\mathbf{l}} = \mathop {\arg \max }\limits_{{_{{{\mathbf{x}} \in \Omega ,{\mathbf{l}} \in \Omega_{l} }} }} \, VFEIM_{{\text{h}}} ({\mathbf{x}},{\mathbf{l}}), $$

(25)

where ${\mathbf{l}}$ is now a vector containing the fidelity levels for each objective to be evaluated at; $\Omega_{l}$ represents the design space of the fidelity level. For a 2-objective problem with two fidelity levels, the possible value for ${\mathbf{l}}$ includes $\left[ {\left( {1,1} \right),\left( {1,2} \right),\left( {2,1} \right),\left( {2,2} \right)} \right]$. The criterion (25) will lead to a more flexible VFMOEGO method and it is possible to utilizing such setting in the above ISC. Empirically to say, it depends on the problem to be solved in choosing (24) or (25). If the objectives are all obtained by using a single simulator or the evaluation costs for the different objectives are identical, the criterion (24) should be adopted as it will reduce the implementation effort and the difficulty in solving the mixed-integer maximization problem. Otherwise, the criterion (25) is recommended. For example, for an aircraft wing optimization problem, the drag coefficient $C_{{\text{D}}}$ is to be minimized and the lift coefficient $C_{{\text{L}}}$ is to be maximized. As both the drag and lift coefficient are calculated through the computational fluid dynamic (CFD) simulator, it would be more convenient to use criterion (24) as the CFD simulator will be invoked once in evaluating the sample point ${\mathbf{x}}$ at the identical fidelity level. While, if the drag coefficient and the structural stress of the wing are to be minimized, two simulators are involved to obtain the responses no matter what the fidelity level vector is. Hence, the more flexible criterion (25) is recommended. As the two real-world problems to be solved later are both based on CFD simulations, the criterion (24) is to be used hereafter.

3.2 Variable-fidelity expected modified hypervolume improvement-based criterion

The second criterion is developed based on a modified hypervolume improvement function proposed in [32]. First, the hypervolume improvement function in (20) is reorganized into the following form by introducing the local upper bounds ${\mathbf{U}}$ (LUBs) [53]:

$$ I_{{{\text{hv}}}} ({\mathbf{x}}){ = }\sum\limits_{j = 1}^{m} V \left( {\left[ {{\mathbf{y}},{\mathbf{U}}_{j} } \right]} \right) - V_{{{\text{overlap}}}} ({\mathbf{y}}), $$

(26)

where $m$ indicates the number of LUBs, ${\mathbf{U}}_{j} \in {\mathbb{R}}^{M} ,j = 1,2, \ldots m$ represents the LUBs related to the current PF approximation. The LUBs denote a set of points that cannot be dominated by one another that $\forall {\mathbf{U}}_{i} \in {\mathbf{U}},\forall {\mathbf{U}}_{j} \in {\mathbf{U}} \Rightarrow {\mathbf{U}}_{i} \not \prec {\mathbf{U}}_{j}$ (The procedure and code to generate LUBs with a reference point and an initial PF approximation can be found in [32]). With LUBs, the non-dominated region can be defined as $\Theta = \left\{ {{\mathbf{a}} \in {\mathbb{R}}^{M} |\exists {\mathbf{U}}_{i} \in {\mathbf{U}}:{\mathbf{a}} \prec \prec {\mathbf{U}}_{i} } \right\}$, ($\prec \prec$ means strong Pareto-dominance, i.e. ${\mathbf{a}} \prec \prec {\mathbf{b}} \Leftrightarrow \forall 1 \le i \le M:{\text{a}}_{i} {\text{ < b}}_{i}$). The relationship between the LUBs ${\mathbf{U}}$ and current PF approximation is exemplified in Fig. 5. Detail properties of the LUBs can be found in [53]. In (26), $V\left( {\left[ {{\mathbf{y}},{\mathbf{U}}_{i} } \right]} \right)$ represents the hypervolume of the hyper-rectangle with the two points ${\mathbf{y}}$ and ${\mathbf{U}}_{j}$ as the diagonal points, the first term $\sum\limits_{j = 1}^{m} V \left( {\left[ {{\mathbf{y}},{\mathbf{U}}_{j} } \right]} \right)$ denotes the volume sum of those regions dominated by ${\mathbf{y}}$, $V_{{{\text{overlap}}}} ({\mathbf{y}})$ is the volume of the overlapped part in the first term. As shown in Fig. 5, the areas with different shaded lines represent the regions for different $\left[ {{\mathbf{y}},{\mathbf{U}}_{j} } \right]$ and the colored area relates to the value of $V_{{{\text{overlap}}}}$.

Fig. 5

LUBs and the modified hypervolume improvement

As the $V_{{{\text{overlap}}}} ({\mathbf{y}})$ cannot be calculated analytically when the number of objectives is larger than two. Hence a modified hypervolume improvement function is defined by neglecting the second term of (26) and expressed in detail as:

$$ I_{{{\text{hvm}}}} ({\mathbf{x}}){ = }\sum\limits_{j = 1}^{m} V \left( {\left[ {{\mathbf{y}},{\mathbf{U}}_{j} } \right]} \right) = \sum\limits_{j = 1}^{m} {\left[ {\prod\limits_{i = 1}^{M} {\left( {U_{j}^{i} - y_{i} ({\mathbf{x}})} \right)} } \right]} . $$

(27)

It has been proved that $I_{{{\text{hvm}}}} ({\mathbf{x}}) \ge 0$ and $I_{{{\text{hvm}}}} ({\mathbf{x}}) > 0$ when and only when ${\mathbf{y}} \in \Theta$[32]. Moreover, it has been demonstrated that the above modified hypervolume improvement shares the identical properties with the original hypervolume improvement function in MOO, e.g. the improvement function is monotonically decreasing with increasing $y_{i} (i = 1,2, \cdots M)$. While the modified hypervolume improvement can be calculated analytically compared with the original one. Recall that, in VFMOEGO, the objective vector $y_{i} ({\mathbf{x}}),i = 1,2, \ldots ,M$ of the studying point ${\mathbf{x}}$ follows M-dimensional independent Gaussian distribution as shown in (14), the expectation of the modified hypervolume improvement (VFEMHVI) function can be derived as:

$$ \begin{gathered} {\text{VFEMHVI}}({\mathbf{x}},l) = E\left[ {I_{{{\text{hvm}}}} ({\mathbf{x}})} \right] = E\left[ {\sum\limits_{j = 1}^{m} {\left[ {\prod\limits_{i = 1}^{M} {\left( {U_{j}^{i} - y_{i} ({\mathbf{x}})} \right)} } \right]} } \right], \\ = \sum\limits_{j = 1}^{m} {\left[ {\prod\limits_{i = 1}^{M} {E\left( {U_{j}^{i} - y_{i} ({\mathbf{x}})} \right)} } \right]} = \sum\limits_{j = 1}^{m} {\left[ {\prod\limits_{i = 1}^{M} {EI_{{{\text{vf}}}}^{i,j} ({\mathbf{x}},l,U_{j}^{i} )} } \right]} \\ \end{gathered} $$

(28)

where

$$ {\text{EI}}_{vf}^{i,j} ({\mathbf{x}},l,U_{j}^{i} ) = \left( {U_{j}^{i} - \hat{y}_{i} ({\mathbf{x}})} \right)\Phi \left( {\frac{{U_{j}^{i} - \hat{y}_{i} ({\mathbf{x}})}}{{s_{i} ({\mathbf{x}},l)}}} \right) + s_{i} ({\mathbf{x}},l)\phi \left( {\frac{{U_{j}^{i} - \hat{y}_{i} ({\mathbf{x}})}}{{s_{i} ({\mathbf{x}},l)}}} \right). $$

(29)

It can be also noted that the infillings of both LF and HF samples based on VFEMHVI are toward improving the HF approximation of PF. Moreover, Eq. (29) takes the identical form of Eq. (17) but the values of LUBs are used in (29) as the reference value instead of the current PF approximation. Thus Eq. (28) can be regarded as the aggregation result of the variable-fidelity LUBs-based expected improvement matrix which is expressed as:

$$ \left[ {\begin{array}{*{20}c} {{\text{EI}}_{vf}^{1,1} ({\mathbf{x}},l,U_{1}^{1} )} & {EI_{vf}^{2,1} ({\mathbf{x}},l,U_{1}^{2} )} & \cdots & {{\text{EI}}_{vf}^{M,1} ({\mathbf{x}},l,U_{1}^{M} )} \\ {{\text{EI}}_{vf}^{1,2} ({\mathbf{x}},l,U_{2}^{1} )} & {EI_{vf}^{2,2} ({\mathbf{x}},l,U_{2}^{2} )} & \cdots & {{\text{EI}}_{vf}^{M,2} ({\mathbf{x}},l,U_{2}^{M} )} \\ \vdots & \vdots & \ddots & \vdots \\ {{\text{EI}}_{vf}^{1,m} ({\mathbf{x}},l,U_{m}^{1} )} & {EI_{vf}^{2,m} ({\mathbf{x}},l,U_{m}^{2} )} & \cdots & {{\text{EI}}_{vf}^{M,m} ({\mathbf{x}},l,U_{m}^{M} )} \\ \end{array} } \right]. $$

(30)

In other words, the VFEMHVI function can also be regarded as based on the VFEIM concept. But the reference values used in each element of the VFEIM and the aggregation scheme are different from that of the VFEIM_h. For VFMOEGO with the VFEMHVI-based criterion, the new sample point ${\mathbf{x}}$ and its fidelity level l can be determined by solving the following maximization problem:

$$ {\mathbf{x}},l = \mathop {\arg \max }\limits_{{_{{{\mathbf{x}} \in \Omega ,l = 1,2}} }} {\text{ VFEMHVI}}({\mathbf{x}},l). $$

(31)

The VFEMHVI criterion is derived analytically hence to be computational efficient when solving (31). It should be mentioned that, in criterion (31), treating $l$ as a vector as that of the VFEIM-based criterion in (25) is also possible. The reason for proposing a criterion with $l$ as a scalar is identical to that explained in the last subsection.

3.3 Constraints handling

For a problem with $M_{{\text{C}}}$ computationally expensive inequality constraints $g_{i} ({\mathbf{x}}) \le 0,i = 1, \ldots ,M_{{\text{C}}}$, the constraints are also modeled by HK. The prediction of the HK model for the constraints at a point can be considered as the following normal distribution,

$$ \begin{array}{*{20}c} {\hat{G}_{i} ({\mathbf{x}},l)\sim N\left[ {\hat{g}_{i} ({\mathbf{x}}),s_{g,i}^{2} ({\mathbf{x}},l)} \right],} & {l = 1,2} \\ \end{array} ,i = 1, \ldots ,M_{{\text{C}}} , $$

(32)

where $\hat{g}_{i} ({\mathbf{x}})$ is the prediction of the ith HK model for constraint, $s_{g,i}^{2} ({\mathbf{x}},l),l = 1,2$ represents the uncertainty of the ith model due to the lack of LF and HF samples. Then, the probability of satisfying the ith constraint is

$$ P[G_{i} ({\mathbf{x}},l) \le 0] = \Phi \left( {\frac{{0 - \hat{g}_{i} ({\mathbf{x}})}}{{s_{{{\text{g,}}i}} ({\mathbf{x}},l)}}} \right). $$

(33)

Eventually, the criteria for the constrained problem can be formulated as:

$$ {\text{C}}{\rm VFEIM}_{\rm h} ({\mathbf{x}},l) = {\rm VFEIM}_{\rm h} ({\mathbf{x}},l) \cdot \prod\limits_{i = 1}^{{M_{{\text{C}}} }} P \left[ {G_{i} ({\mathbf{x}},l) \le 0} \right], $$

(34)

$$ {\text{CVFEMHVI}}({\mathbf{x}},l) = {\text{VFEMHVI}}({\mathbf{x}},l) \cdot \prod\limits_{i = 1}^{{M_{{\text{C}}} }} P \left[ {G_{i} ({\mathbf{x}},l) \le 0} \right]. $$

(35)

By maximizing the above criteria, the spatial location of a new sample point and its fidelity level to be evaluated at can then be determined.

3.4 Implementation of the VFMOEGO method

The algorithm 1 is given as the implementation of the VFMOEGO with the VFEMHVI criterion and the corresponding framework is sketched in Fig. 6a. It is noted that a reference point is required from the user for both criteria. In this work, except for imputing the reference point from the user, introducing a normalization procedure to release such a burden for the user is also available. In detail, all the LF and HF objective responses are scaled using the minima and maxima of the HF objective responses of the current HF samples, then the reference point is set to $r_{j} = 1.1$ for $j = 1,2, \ldots ,M$. Figure 6b shows the VFMOEGO method using such a normalization procedure. The influence of the two strategies to specify the reference point will be discussed within the section of numerical experiments. For VFMOEGO with VFEIM_h criterion, the procedure is identical thus not repeated.

Fig. 6

Flowchart of the VFMOEGO method with a reference point provided by user and b introducing normalization procedure

3.5 Illustration of the proposed criteria and method

In this subsection, a two-objective ZDT2 test problem [42] is employed to illustrate the proposed criteria and methods. The formulation of the ZDT2 problem is given as:

$$ \begin{gathered} \mathop {\min }\limits_{{{\mathbf{x}} \in \Omega }} F({\mathbf{x}}) = \left\{ {f_{1} ({\mathbf{x}}),f_{2} ({\mathbf{x}})} \right\} \hfill \\ {\text{with assistance of }}F_{lf} ({\mathbf{x}}) = \left\{ {f_{1,lf} ({\mathbf{x}}),f_{2,lf} ({\mathbf{x}})} \right\} \hfill \\ f_{1} ({\mathbf{x}}) = f_{1,lf} ({\mathbf{x}}) = x_{1} \hfill \\ f_{2} ({\mathbf{x}}) = g({\mathbf{x}}) \times h({\mathbf{x}}) \hfill \\ f_{2,lf} ({\mathbf{x}}) = (0.9 \times g({\mathbf{x}}) + 1.1) \times (1.1 \times h({\mathbf{x}}) - 0.1) \hfill \\ {\text{where }}g({\mathbf{x}}) = 1 + \frac{9}{n - 1}\sum\limits_{i = 2}^{n} {x_{i} } \hfill \\ h({\mathbf{x}}) = 1 - \sqrt {f_{1} ({\mathbf{x}})/g({\mathbf{x}})} \hfill \\ 0 \le x_{i} \le 1,i = 1, \ldots ,n. \hfill \\ \end{gathered} $$

(36)

First, the VFEIM_h criterion employing the normalization procedure, the VFEMHVI criterion with the user specifying the reference point, and the VFEMHVI utilizing the normalization procedure (denoted as VFEMHVIN for short) are compared. For the reference point of the ZDT2 problem, ${\mathbf{r}} = \left[ {11,11} \right]$ is adopted here. Identical initial LF/HF samples are used to calculate the 2-objective criteria and the contours in the 2-D design space are shown in Fig. 7, respectively. In these figures, the dots present the sampled points, the color of the contours indicates the value of the criteria. The darker the color the higher the value. First, it can be noted that, by comparing Fig. 7a, b, the contours of the VFEIM_h criteria at LF level (i.e. $l = 2$) have very similar trends to its corresponding HF criteria (i.e. $l = 2$) but differ in magnitude. This observation holds for VFEMHVI criteria as shown in Fig. 7c–f. Through comparing the VFEIM_h and VFEMHVIN criterion at HF level by observing the Fig. 7b, f, it is expected to see that the trend and magnitude of the contours of those two criteria are different as the two criteria differ at the reference values used and the aggregation scheme. The dissimilarity of the criteria at the LF level can also be noticed through Fig. 7a, e. Though the trend and magnitude of the VFEIM_h and VFEMHVIN criterion are different, they suggest the identical next sample point shown as the pentagrams in those figures. The third observation that can be noticed is the influence of the strategy on specifying the reference point. With Fig. 7d, f shown the VFEMHVI and VFEMHVIN criterion at the HF level, not only the trend but also the next sample point suggested are disparate. This indicates the performance of the method utilizing the normalization procedure might deviate from that by receiving the reference point from the user.

Fig. 7

Plots of the criteria in the design space of ZDT2 problem. a VFEIM_h with $l = 1$. b VFEIM_h with $l = 2$. c VFEMHVI with $l = 1$. d VFEMHVI with $l = 2$. e VFEMHVIN with $l = 1$. f VFEMHVIN with $l = 2$

Second, the first five refine steps of the VFMOEGO method with different criteria in solving the ZDT2 problem of six design variables using identical initial LF and HF samples are sketched in Fig. 8 and Tables 1, 2, and 3. The initial HF non-dominated solutions (HFNDS), representing the initial HF approximation of PF, are represented by the filled squares. The added LF/HF samples in the iterative optimization procedure are shown by filled triangles/circles. The true PF of the ZDT2 problem is also presented in those figures. It can be noted that all methods select LF/HF samples adaptively in the iterative optimization process, which is the unique property of the proposed criteria. For example, the five sample points selected by VFEIM_h are evaluated at the LF–HF–LF–HF–LF level. While the VFEMHVI determined the first five points to be evaluated at LF–HF–HF–HF–HF level. In terms of the spatial position the samples added in the first five iterations (see Tables 1, 2, and 3), the three criteria have diverse favors. For instance, the first point chosen by the three criteria is all evaluated at the LF level but with different spatial locations, i.e. [6.2e−5, 2.0165], [0.8969, 0.2339], and [3.7e−5, 2.0077] respectively. Even though, the performance metric, i.e. the normalized hypervolume (NHV), is increased continuously indicating that the HF approximation of PF is improved remarkably by all methods (The NHV will be detailed in the section of the numerical experiment). The above illustrations demonstrate the effectiveness of the proposed criteria on improving the HF approximation of PF and the ability to adaptively select LF and HF samples in the iterative phase of the VFMOEGO method. More numerical examples are included in the next section to support this observation.

Fig. 8

Refinement process of the VFMOEGO method on the ZDT2 problem with different criterion: a VFEIM_h, b VFEMHVI, c VFEMHVIN

Table 1 Refinement process of the VFEIM_h-based optimization of the ZDT2 problem

Table 2 Refinement process of the VFEMHVI-based optimization of the ZDT2 problem

Table 3 Refinement process of the VFEMHVIN-based optimization of the ZDT2 problem

4 Examples and results

4.1 Analytic test cases

In this subsection, analytic numerical examples are adopted to demonstrate the applicability and efficiency of the proposed criteria. These examples are also solved by the corresponding single-fidelity methods employing the criteria of HF level only, i.e. setting $l = 2$ in (24) or (31). The three single-fidelity methods utilizing HF simulations are denoted as EIM_h, EMHVI, EMHVIN, and the three variable-fidelity approaches are termed as VFEIM_h, VFEMHVI, VFEMHVIN, respectively.

For clarity, the procedure of single-fidelity MOEGO employing the EIM_h criteria is introduced briefly. In the initialization phase, HF initial samples are generated by DOE method and then HF simulator is invoked to obtain the responses of those HF samples. The iterative optimization stage proceeds with the construction of the Kriging models for each objective function based on the initial data set. Then the spatial position of the next sample point is obtained by maximizing the EIM_h function (i.e. $EIM_{{\text{h}}} ({\mathbf{x}}){ = }VFEIM_{{\text{h}}} ({\mathbf{x}},l{ = 2})$). Third, the simulator is called to get the HF response of the sample point. The HF data set is augmented before the check of the termination condition. The iterative optimization phase will continue iteratively until the stopping rule is met.

The formulations of analytic numerical examples from [41, 42] are summarized in Table 4. The computational cost ratio (CR) between an HF evaluation and an LF one for all the test cases is set to be 4. On 6-D ZDT problems, the initial HF sample size for single-fidelity MOEGO method is set as 11d-1 following [29], where d represents the dimension of the design variable; for variable-fidelity methods, the initial HF and LF sample sizes are set as 5d and (6d-1)*CR to ensure the cost on the evaluation of the initial samples are identical to that of the single-fidelity methods. On the 2-D POL problem, 21 HF initial samples are used in single-fidelity method, 16 HF and 20 LF samples are adopted for the variable-fidelity methods. For the maximization of the VFEIM or VFEMHVI-based criterion, which is a mix-integer problem of one integer variable with two levels, it is maximized at LF (i.e. $l = 1$) and HF (i.e. $l = 2$) level respectively by the genetic algorithm (GA) as depicted in Algorithm 1. The GA is used with the following settings: the maximum generation being 100, population size being 100, probability of mutation and crossover being 0.2 and 0.8, respectively. Such settings are also employed to maximize single-fidelity criteria. A maximal equivalent iteration number for the iterative phase is adopted as the termination condition of each algorithm. For the equivalent iteration number is expressed as:

$$ {\text{EquivIter}} = \frac{1}{{{\text{CR}}}}{\text{iter}}_{{{\text{LF}}}} + {\text{iter}}_{{{\text{HF}}}} , $$

(37)

Table 4 Formulations and true PF for numerical examples

where ${\text{iter}}_{{{\text{LF}}}}$ and ${\text{iter}}_{{{\text{HF}}}}$ represent the number of iterations choosing an LF and HF simulation calls. Notably, the number of equivalent iterations reduces to the iteration number for the single-fidelity method. The maximal allowed equivalent iteration for all methods on the 6-D ZDT problems and the 2-D POL problem is set as 100 and 70, respectively. Considering the randomness of the LHS method and GA, all problems are solved by each method with 11 times. The reference point needed for EMHVI and VFEMHVI is set as (11, 11) for three ZDT problems and (80, 80) for the POL problem.

The numerical experiments over those analytic problems are conducted with the aid of PlatEMO, an open-source platform for comparison of multi-objective optimization method [54]. In the platform, several metrics are available to measure the quality of solutions obtained. In this work, two metrics are employed to compare the performance of different methods on solving analytic problems, that is, normalized hypervolume (NHV) [55] and inverted generational distance (IGD) [56] that measure the proximity to the true PF and the diversity of solutions simultaneously. NHV and IGD have widely been adopted for fair assessing the performance of multi-objective algorithms [57, 58]. A larger value of NHV or a smaller value of IGD indicates better quality of the HF approximation of the PF. The definition of reference points for NHV calculation and true PF for IGD calculation of those analytic problems can be found in [54]. The number of HF solutions to approximate the PF is also counted to show the differences among all compared methods. The Wilcoxon rank-sum test with significance level 0.05 is applied to identify whether the means of the results obtained by one criterion is significantly different from the results obtained by the VFEMHVIN criterion. The result is labeled by the signs ‘ + ’, ‘–’ and ‘≈’, which indicate that the result is significantly better, significantly worst, and comparable statistically.

Tables 5 and 6 present the statistic results of NHV and IGD over the analytic test instances. The Wilcoxon rank-sum test results between one method and VFEMHVIN are presented in the parentheses in those tables. Moreover, the number of one method performs significantly better, worst, and comparable statistically to VFEMHVIN is counted and listed in Tables 5 and 6. From the statistic results of NHV metric shown in Table 5, it can be noted that the VFEMHVIN performs better or comparative to all the rest five methods over all test problems. In detail, compared with the three single-fidelity methods, VFEMHVIN is better on 3, 2, and 1 of the four problems and comparable on 1, 2, and 3 of the four problems. This demonstrates the optimization gains can be improved by utilizing VF surrogate-based method. The VFEIM_h performs statistically worse than VFEMHVIN on ZDT2 and POL problems, and comparable to VFEMHVIN on ZDT1 and ZDT3 problems. Recall the two differences between VFEIM_h and VFEMHVIN, it can be concluded that the reference values and the adopted aggregation scheme for the variable-fidelity expected improvement matrix affects the performance of the corresponding criterion. The VFEMHVI is statistically comparable to VFEMHVIN over all analytic test cases. As VFEMHVI and VFEMHVIN only differ at the way to generate the reference point, this indicates that the normalization-based strategy to generate the reference point preserves the ability of the VFEMHVI criterion in finding solutions with a high level of convergence and diversity, while is superior on without the need to specify the reference point by the user/designer. Though the effects of reference point specification strategy are not obvious in above test results, it should be admitted that the strategy does affect the performance of the method relying on the hypervolume concept based on our preliminary studies. Such a phenomenon has been pointed out before and more suggestions on specifying the reference point can be found in [59,60,61]. Inspired by this, a dynamic reference point specification strategy will be investigated the future work. With the IGD statistic results shown in Table 6, the comparison conclusion is identical, i.e. VFEMHVIN performs better or comparative to all the rest five methods over all test problems. While the VFEMHVIN is now superior to EIM_h, EMHVI, EMHVIN, and VFEIM_h over 4, 3, 3, and 2 problems.

Table 5 Statistics of the NHV values of the final PF approximation obtained by the compared methods

Table 6 Statistics of the IGD values of the final PF approximation obtained by the compared methods

The number of HF solutions to approximate the PF of each method is counted in Table 7. Generally, the single- and variable-fidelity expected improvement matrix-based methods, i.e. EIM_h and VFEIM_h can obtain more solutions to approximate the PF on one or two problems. While the EMHVI, EMHVIN performs worst in terms of the number of solutions on the approximated PF. The ability of VFEMHVI and VFEMHVIN in this aspect is still comparable. Figure 9 shows the final PF approximation by each algorithm with the median IGD value on the 11 runs on all the analytic test problems. The differences of the number of HF solutions approximating the PF can be observed in Fig. 9 institutively. Moreover, it can be also seen that all methods can obtain promising PF approximations on the ZDT1 and ZDT2 problems with continuous PF. While, on the two problems with discrete PF (ZDT3 and POL), the VF surrogate-based methods approximate the PF better as the single-fidelity method generally missed part of the discrete PF. Especially in the ZDT3 problem, it can be noted that the rightmost part of the discrete PF is missed by the three single-fidelity methods.

Table 7 Statistics of the number of HF solutions for the final PF approximation obtained by the compared methods

Fig. 9

Plots of the final PF approximation obtained by each algorithm with the median IGD value in the 11 runs on different problems: a ZDT1, b ZDT2, c ZDT3, d POL

Table 8 compares the number of LF/HF samples added during the iterative optimization process of each method. From Table 8, the ability of the VF surrogate-based method in adaptively selecting LF/HF samples during the iterative optimization process can be observed. In terms of the portion of LF or HF samples on the whole sample set added, it depends on the problem. For example, the LF samples chosen by the three variable-fidelity methods took up nearly half of the total added samples on the three ZDT problems. While, on the POL problem, the three variable-fidelity methods spent most computational cost on HF samples. Generally, this is determined by the correlation between LF and HF functions. If the LF function correlates well to the HF function, added more LF samples is beneficial to improve the accuracy of the HK model and hence the optimization performance.

Table 8 Added LF and HF samples of each method

The Wilcoxon rank-sum tests among the three single-fidelity methods are also conducted to reveal the best one as the comparison among the three single-fidelity methods has never been reported in the open literature. Table 9 shows the test results using the IGD values. It can be noted that the EIM_h is significantly worse than EMHVIN on three cases over the four test problems and performs comparably to EMHVIN on the ZDT3 problem. Again, normalization-based reference point specification strategy still maintains the ability of EMHVI-based method as the comparable performance between EMHVI and EMHVIN can be observed in Table 9.

Table 9 Wilcoxon rank sum test results of IGD metric among three single-fidelity methods

Finally, the effect of cost ratio on the three variable-fidelity methods is investigated. Though no cost-control strategy is incorporated in the proposed criteria, the cost ratio affects the number of initial LF samples hence the initial surrogates and optimization process. Before presenting the experiment results, it is expected that the variable-fidelity method will perform better if the cost ratio increases. This is due to more LF samples can be used with a larger cost ratio within the setting context. Providing the LF and HF functions correlate well, more LF samples will generally improve the accuracy of the VF surrogate models which will benefit the optimization task. In detail, additional experiments with CR = 3 and CR = 8 are conducted on the ZDT2 and ZDT3 problems with the obtained results shown in Table 10. The results of CR = 4 are taken from Table 5 and 6. Indeed, the statistic results of NHV and IGD values follows the above expectation. For instance, the mean IGD values of VFEIM_h on ZDT3 problem with CR = 3, 4, and 8 are 2.6102e-2, 2.6038e-2, and 2.3487e-2, respectively, indicating the method performs better with the increase of CR.

Table 10 Statistic results of variable-fidelity methods with different cost ratios

Table 11 Statistic results of compared methods on NACA0012 airfoil optimization

5 Engineering optimization design cases

5.1 NACA0012 airfoil optimization in transonic inviscid flow

The first engineering design case is the drag minimization and lift maximization of the NACA0012 airfoil. The 2-objective minimization problem is formulated as:

$$ \mathop {\min }\limits_{{{\mathbf{x}} \in \Omega }} F({\mathbf{x}}) = \left\{ {C_{{\text{D}}} , - C_{{\text{L}}} } \right\}, $$

(38)

where $C_{{\text{D}}} ,C_{{\text{L}}}$ is the drag and lift coefficient respectively at the angle of attack 1.25 and free-stream Mach number 0.8. The HF and LF analysis are defined as CFD simulations solving the Euler equations with different convergence criteria. The transonic inviscid flow simulation is conducted by the open-source CFD simulator SU2 [62]. The grid corresponding to the simulation for the baseline airfoil is presented in Fig. 10. The LF CFD simulation terminates after 120 iteration and the HF simulation stops until the density residual is lower than 10^–8. The histories of residual, drag, and lift coefficients for the baseline airfoil is shown in Fig. 11. The lift and drag coefficients for the baseline NACA0012 airfoil from the inviscid simulation are 0.3269 and 0.0214, respectively. It should be mentioned that this problem is not a much expensive problem to allow multiple runs to obtain statistical performance of each method on this problem. From Fig. 11, it can also be observed that the computational cost ratio of the HF simulation to the LF simulation for the baseline airfoil is approximately 2.6. However, it is found the number of iteration for an HF simulation to reach the specified residual is dependent on the spatial position of a sample point in the optimization process, resulting in cost ratio varying between 2 and 60 over the design space. Varying cost for expensive engineering design problems has been observed before and a specified strategy to treat the varying cost in design space exploration for a single-fidelity method is proposed in [52]. While the inclusion of a scheme to deal with varying cost over the design space is out of the scope of this work and will be conducted in the future. To this end, the cost ratio is specified to be 3 for the NACA0012 airfoil optimization problem.

Fig. 10

Sketch of grid for CFD simulation for baseline NACA0012 airfoil

Fig. 11

Convergence histories for the baseline NACA0012 airfoil

Hicks–Henne bump functions [63] with a total of 18 design variables are used in the geometry parameterization of the NACA0012 airfoil. The new airfoil is obtained by adding disturbation (the summation of bump functions) on the lower and upper surfaces of the baseline shape. The lower and upper profile disturbation $\Delta_{l}$ and $\Delta_{u}$ are expressed as:

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {\Delta_{l} = - \sum\limits_{i = 1}^{9} {\delta_{li} } f_{i} (x), \, \delta_{li} \in [ - 0.01,0.01]} \\ {\Delta_{u} = \sum\limits_{i = 1}^{9} {\delta_{ui} } f_{i} (x), \, \delta_{ui} \in [ - 0.01,0.01]} \\ \end{array} } \right., \hfill \\ f_{i} (x) = \sin^{3} \left( {\pi x^{e(i)} } \right),\quad e(i) = \log (0.5)/\log \left( {x_{i} } \right), \, i = 1, \ldots ,9 \hfill \\ x = \left[ {0.05,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.95} \right] \hfill \\ \end{gathered} $$

(39)

The amplitudes of bumps $\delta_{li}$ and $\delta_{ui} ,\left( {i = 1, \cdots ,9} \right)$ are the 18 design variables of the optimization. The initial sample size for single-fidelity methods is set as 5d. For variable-fidelity methods, the number of initial HF and LF samples is set as 2d and $3{\text{d}} \times {\text{CR}}$, respectively. All methods stop once the 90 allowed equivalent iteration is used out. Only NHV is adopted in the performance assessment, as no true PF is available for the calculation of IGD of the practical problem. The reference point used for NHV estimation is [0.1, 0]. To demonstrate the effectiveness of the variable-fidelity methods as well as release the computational burden of the experiments, the EMHVI method is chosen among the three single-fidelity methods to solve the practical engineering design problem. The EMHVI is chosen as it performs better than EIM_h and comparative to EMHVIN in the experiments over the analytic problems.

The NACA0012 airfoil optimization problem is solved by each method with 11 times and Table 11 presents the statistic results of the compared methods over this problem. As observed, the VFEMHVIN performs statistically better than EMHVI and VFEMHVI, and is comparable to the VFEIM_h method. The slightly worse performance of VFEMHVI compared with the VFEMHVIN indicates that an inappropriate reference point for the hypervolume calculation in the VFEMHVI criterion will deteriorate its performance and the normalization-based strategy to define the reference point is still applicable in practical problem. From the number of LF/HF samples for each method shown in Table 11, the ability to adaptively determining LF/HF sample in the iterative optimization phase is well demonstrated in the practical engineering design problem. PF approximations with median NHV value among the 11 runs by each method are shown in Fig. 12. Recall the objective values of the baseline airfoil (0.0214, − 0.3269), it can be noted that all methods can obtain improved solutions. Representative optimal solutions are selected to show the details. The objective values for the three optimal solutions (denoted as the Min. drag, Balance, Max. lift) are (0.001612, − 0.2909), (0.0163, -0.7506), (0.05986, − 0.9263), respectively. Figures 13 and 14 compare the shapes and the Mach number contours of the baseline NACA0012 and optimal airfoils. It can be seen the optimal airfoils are all asymmetrical and generally thinner especially at the backward parts.

Fig. 12

PF approximations with median NHV value by each method on NACA0012 airfoil optimization problem

Fig. 13

Comparison of baseline NACA0012 and optimal airfoils

Fig. 14

Mach number contour comparison of baseline NACA0012 and optimal airfoils

5.2 RAE2822 airfoil optimization in viscous turbulent flow

The second engineering design case is the drag minimization and lift maximization of the RAE2822 airfoil. The 2-objective minimization problem is formulated as:

$$ \mathop {\min }\limits_{{{\mathbf{x}} \in \Omega }} F({\mathbf{x}}) = \left\{ {C_{{\text{D}}} , - C_{{\text{L}}} } \right\}, $$

(40)

where $C_{{\text{D}}} ,C_{{\text{L}}}$ are the drag and lift coefficient respectively at the angle of attack 2.9 and free-stream Mach number 0.734. The HF and LF analysis are defined as CFD simulations solving the Reynolds-averaged Naiver–Stokes equations with different convergence criteria in SU2. The grid corresponding to the simulation for the baseline airfoil is presented in Fig. 15. The LF CFD simulation terminates after 800 iterations and the HF simulation stops until the density residual is lower than 10^–7, resulting in the CR $\approx$ 6. The histories of residual, drag, and lift coefficients for the baseline airfoil is shown in Fig. 16. The lift and drag coefficients for the baseline RAE2822 airfoil from the viscous turbulent flow simulation are 0.8210 and 0.0206, respectively. Airfoil parameterization strategy in the NACA0012 case is employed. The amplitudes of bumps $\delta_{li}$ and $\delta_{ui} ,\left( {i = 1, \ldots ,9} \right)$ are the 18 design variables of the optimization but with a reduced range for each variable as [− 0.0001, 0.0001] to ensure the possibility of encountering simulation failures as low as possible. It should be mentioned that such treatment will limit the optimization gain, but it is necessary to conduct the comparative study smoothly. Strategy to deal with the simulation failures in our previous work [64] can be incorporated to potentially improve the robustness and efficiency of the proposed methods in solving practical engineering problems in presence of simulation failures and is left for future work. The settings of the initial sample size and termination criterion hold identical to that in the NACA0012 case. The reference point used for NHV estimation is [0.05, − 0.4] (See Fig. 16).

Fig. 15

Sketch of grid for CFD simulation for baseline RAE2822 airfoil

Fig. 16

Convergence histories for the baseline RAE2822 airfoil

The RAE airfoil optimization problem is solved by each method with 11 times and Table 11 presents the statistic results of the compared methods over this problem. As observed, the VFEMHVIN performs statistically better than EMHVI and VFEMHVI, and is comparable to the VFEIM_h method. Again, the slightly worse performance of VFEMHVI compared with the VFEMHVIN indicates that an inappropriate reference point for the hypervolume calculation in the VFEMHVI criterion will deteriorate its performance and the normalization-based strategy to define the reference point is still applicable in this more expensive practical problem. The ability to adaptively choosing LF/HF sample in the iterative optimization phase is demonstrated from the number of LF/HF samples for each method shown in Table 12. PF approximations with median NHV value among the 11 runs by each method are shown in Fig. 17. It can be noted that all methods can improve the baseline design in at least one of the objectives. Representative optimal solutions are selected to show the details. The objective values for the three optimal solutions (denoted as the Min. drag, Balance, Max. lift) are (0.0105, − 0.6315), (0.01649, − 0.9918), (0.05298, − 1.197), respectively. Figures 18 and 19 compare the shapes and the Mach number contours of the baseline RAE2822 and optimal airfoils. It can be seen the optimal airfoils are all asymmetrical and generally thinner especially at the backward parts. The shock intensity is decreased significantly for the Min. drag optimal solution and increased sharply for the Max. lift design.

Table 12 Statistic results of compared methods on RAE2822 airfoil optimization

Fig. 17

PF approximations with median NHV value by each method on RAE2822 airfoil optimization problem

Fig. 18

Comparison of baseline RAE2822 and optimal airfoils

Fig. 19

Mach number contour comparison of baseline RAE2822 and optimal airfoils

6 Discussion

This section presents a discussion on the merits, limitations, and avenues of improvements of the proposed approaches. The discussion is based on the introduction in Sect. 3 and above experimental results but also extends to broader comments.

Comparison between the two criteria Both criteria are formulated explicitly and cheap-to-evaluate. The VFEIM_h criterion is obtained heuristically via replacing the improvement in the simplified hypervolume improvement function by the corresponding expected improvement. The idea is simple and straightforward. While the VFEMHVI is derived analytically based on the modified hypervolume improvement. The modified hypervolume improvement shares the identical properties with the original hypervolume improvement function in MOO but the properties of the simplified hypervolume improvement function behind VFEIM_h is not clear. From the test results, it can be concluded that the VFEMHVI incorporating the normalization-based strategy to define the reference point is the more efficient one. Though the VFEIM_h performs slightly worse in obtaining solutions with high quality, it still has an advantage of being able to obtain more solutions to approximate the PF.

Limitations As presented in Sect. 3, the current criteria are developed for application with two levels of fidelity. We believe that extending the two-level HK model to multi-fidelity one and developing dedicated criteria can be a remedy to tackle this problem.

Avenues for improvement Beside the development of criterion for multi-fidelity applications, several other avenues for improvements can be envisioned. For problems with varying cost over the design space, incorporation of a cost-control strategy might be helpful to potentially enhance the efficiency of the proposed method in such application. The simulation failures in practical engineer problems, especially for CFD-based applications, is critical to the proposed sequential method since it will lead to the premature halt of the iterative optimization process. Integration of an efficient strategy to attack the simulation failures might improve the robustness and optimization efficiency of the approaches. Parallelizing the proposed criteria can be an alternative to deal with simulation failures and accelerate the optimization process with the aid of parallel computation.

7 Summary and future works

In this paper, two variable-fidelity hypervolume-based expected improvement criteria for multi-objective efficient global optimization of expensive-to-evaluate functions with the assistance of cheaper-to-evaluate functions were proposed. Both criteria can be regarded as a multi-objective extension of the variable-fidelity expected improvement for the single-objective variable-fidelity EGO method. The first criterion, VFEIM_h, was obtained by aggregating the variable-fidelity expected improvement matrix using a simplified hypervolume-based aggregation scheme. The second criterion, VFEMHVI, was derived analytically based on a modified hypervolume definition. It was found the second criterion can also be obtained by using the variable-fidelity expected improvement matrix via replacing the reference values and utilizing the other aggregation scheme. Both criteria can adaptively select new LF/HF samples in the iterative optimal search process to update the variable-fidelity models towards the HF Pareto front, distinguishing the proposed methods to the rests in the open literature. The constrained versions of the two criteria were also derived. As both criteria are based on the hypervolume measure, a reference point for hypervolume calculation is necessary. Except for specifying it by the user/designer, a strategy based on normalization was also proposed and implemented. The effectiveness and efficiency of the proposed methods were then verified and validated over analytic multi-objective problems and demonstrated for aerodynamic shape optimizations of the NACA0012 airfoil in transonic inviscid flow and RAE2822 in a viscous turbulent flow. It was shown that the VFEMHVI combined with the normalization-based strategy to define the reference point is the most efficient method over the compared single-fidelity and variable-fidelity ones. Except for applying the proposed method to more complex test problems and real-world engineering problems from the application view, the performance of the general criterion (25), which allows the objectives of the newly selected sample to be evaluated as different fidelities, will be explored.

Appendix

Gaussian_CDF and Gaussian_PDF are the Gaussian cumulative distribution function and probability density function respectively, and are defined as follows.