Sequential optimization using multi-level cokriging and extended expected improvement criterion

Abstract

To reduce the computational cost of metamodel based design optimization that directly relies on the computationally expensive simulation, the multi-fidelity cokriging method has gained increasing attention by fusing data from two or more models with different levels of fidelity. In this paper, an enhanced cokriging based sequential optimization method is proposed. Firstly, the impact of considering full correlation of data among all models on the hyper-parameter estimation during cokriging modeling is investigated by setting up a unified maximum likelihood function. Then, to reduce the computational cost, an extended expected improvement function is established to more reasonably identify the location and fidelity level of the next response evaluation based on the original expected improvement criterion. The results from comparative studies and one airfoil aerodynamic optimization application show that the proposed cokriging based sequential optimization method is more accurate in modeling and efficient in model evaluation than some existing popular approaches, demonstrating its effectiveness and relative merits.

1 Introduction

The application of surrogate models or metamodels to predicting the response of a computationally expensive simulation function has grown in popularity for engineering design optimization over the past 15 years (Jin et al. 2001; Simpson et al. 2001; Yang et al. 2005; Shi et al. 2013). Sometimes, the evaluation on the complex system of interest is so expensive that straightforward application of the metamodel-based optimization might be too costly. Generally, a complicated physical process can be modeled using several methods with different levels of fidelity, or a computer code for a complex problem can be run at different levels of fidelity. For example, the aerodynamic analysis in aerospace engineering can be implemented using the high-fidelity computational fluid dynamics (CFD) simulation or low-fidelity engineering handbook equations; further CFD can also be solved with fine (high-fidelity) or coarse (low-fidelity) mesh. Therefore, the multi-fidelity modeling approach that combines the data from two or more models/codes (uniformly referred to as models hereafter in this paper) with different levels of fidelity to efficiently construct a metamodel has gained increasing attention in optimization design (Qian and Wu 2008; Zheng et al. 2013; Park et al. 2016; Ng and Eldred 2012; Tuo et al. 2013; Chen et al. 2015; El-Beltagy and Wright 2001). The differences between various MFS frameworks have been investigated in detail with the aid of examples including algebraic functions and a borehole example by Park et al. (2017). As a well-known multi-fidelity modeling technique with good computational characteristics, the cokriging method combining two data sets respectively from high- and low-fidelity responses based on the Gaussian process theory has been widely studied and applied to aerodynamic analysis (Han et al. 2012; Laurenceau and Sagaut 2008) and aerodynamic optimization (Toal and Keane 2011; Huang et al. 2013), robust optimization of gas-turbine compressor blade (Keane 2015), and prediction of soil bulk density (Yang et al. 2016). To handle multi-level computer models with a hierarchy of fidelity that often exist in engineering problems, the original two-level cokriging method has been extended to multi-level (s-level) cokriging using a hierarchical updating treatment (Kennedy and O’Hagan 2000). However, it is often difficult to know beforehand how many samples are needed to construct a sufficiently accurate metamodel, and thus sequential optimization based on the bi- and multi- level cokriging methods have been introduced to further reduce the computational cost (Xiong et al. 2008; Huang et al. 2006; Gratiet and Cannamela 2015) by employing the sequential sampling strategies (Jin et al. 2002; Xiong et al. 2009; Zhu et al. 2015).

For the multi-level cokriging based sequential optimization, one key procedure is to estimate the unknown hyper-parameters during cokriging modeling, which evidently has impact on the accuracy of metamodel as well as optimization. In the well-known Bayesian discrepancy-based autoregressive multi-fidelity model using GP proposed by Kennedy and O′ Hagan, the assumption of a Markov property for the covariance structure of the observed data is made, and these hyper-parameters are divided into s groups and then estimated group by group using the maximum likelihood estimation method considering the correlation of the observed data from two models with adjacent fidelities (Kennedy and O'Hagan 2000). Later, based on the autoregressive model proposed by Kennedy and O′ Hagan, Forrester et al. went into more detail about the hyper-parameter estimation of cokriging from the sampling point of view (Forrester et al. 2007). To reduce the numerical complexity and computational expense in estimating the model hyper-parameters of the method proposed by Kennedy and O’ Hagan, Le Gratiet adopted the “Jeffreys priors” and Bayesian method to obtain the closed-form estimations of more model hyper-parameters firstly and estimate the rest using the maximum likelihood estimation method group by group at the sacrifice of the prediction accuracy, in which only the correlation among the observed data from the same model was exploited (Le Gratiet 2013). Overall, although the existing multi-fidelity cokriging modeling approaches utilize the data from all models for response prediction, most of those methods only consider the correlation of the data from two models with adjacent fidelities or from the same model in estimating the unknown hyper-parameters using the maximum likelihood estimation method. Since the lower-fidelity models generally yield a similar trend of the highest-fidelity response, all models with different fidelities actually are correlated to each other to some extent. If the correlation can be fully utilized for hyper-parameter estimation, the accuracy of cokriging metamodel may be improved. Therefore, a unified maximum likelihood function is established accordingly for hyper-parameter estimation in an all-in-one manner during cokriging modeling by utilizing the full correlation of data among all models in this work.

The other important issue associated with the cokriging based sequential optimization is the sequential sampling strategy. As a more efficient one, the objective-oriented approach that brings the design objective into account has been widely studied. The most popular objective-oriented sequential sampling criterion was developed by Jones et al. in their efficient global optimization (EGO) algorithm (Jones et al. 1998), which employs an expected improvement (EI) function to balance the trade-off between the global exploration for reducing the metamodel uncertainty and the local exploitation for searching the optimum. Further, Sasena investigated and compared different objective-oriented sequential sampling criteria to shown their relative merits (Sasena 2002). Xiong et al. (2008) developed a bi-fidelity optimization approach, in which the statistical lower bounding criterion is employed for sequential sampling. However, these methods merely adopt the high-fidelity simulations to construct or update the metamodels. In some region of design space, if the accuracy improvement of the updated metamodel using samples respectively from higher- and lower-fidelity models is relatively close, the lower-fidelity samples are preferred since it is computationally cheaper. Thus, Huang et al. (2006) developed a kriging based sequential optimization scheme using multiple-fidelity responses, in which an integrated objective-oriented sequential sampling criterion was proposed to determine both the location and fidelity level of the subsequent new evaluation to reduce the computational cost. However, during our study, it is found that the samples generated by this criterion may cluster within a certain region, which clearly will cause a waste of samples and thus reduce the efficiency of optimization. Therefore, an extended sequential sampling strategy is established by introducing a sample density function into the one proposed by Huang et al., which can further reduce the computational cost through more reasonably identifying the location and the fidelity level of the new evaluation.

The contributions of this work mainly lie in: 1) based on the autoregressive model proposed by Kennedy and O′ Hagan, establishing a unified maximum likelihood function for hyper-parameter estimation to investigate the impact of utilizing full correlation of all observed data on the accuracy of cokriging metamodel during modeling; 2) developing an extended objective-oriented sequential sampling strategy with the consideration of the sample cluster issue to reduce the computational cost of the cokriging based sequential optimization. The remainder of the paper is organized as follows. In Section 2, the basic ideas of the cokriging technique for hierarchical multi-fidelity modeling is briefly reviewed. In Section 3, the proposed cokriging based sequential optimization method is presented in detail along with the hyper-parameter estimation method and the objective-oriented sampling strategy. In Section 4, comparative studies are conducted to verify the effectiveness of the proposed method. In Section 5, an airfoil shape multi-fidelity optimization problem is solved to further demonstrate the effectiveness of the proposed method. Conclusions are drawn in Section 6.

2 Review on hierarchical multi-level cokriging modeling

The classic mathematical formula of hierarchical multi-level cokriging metamodel proposed by Kennedy and O’Hagan (2000) based on Gaussian process (GP) considering s levels of models y¹(x), …, y^s(x) is represented as

$$ {y}^t\left(\mathbf{x}\right)={\rho}_{t-1}{y}^{t-1}\left(\mathbf{x}\right)+{\delta}^t\left(\mathbf{x}\right),t=2,\dots, s $$

(1)

where x = [x₁, x₂, …, x_p] ∈ ℝ^p is a p-dimensional set of input variables, and y^t(x): ℝ^p → ℝ  (t = 1, …, s) denotes the model response at the t^th level of fidelity.

A larger t corresponds to a higher level of fidelity, and thus y¹(x) is the lowest-fidelity model and y^s(x) is the highest one. The parameter ρ_t − 1 represents the scaling factor, capturing the strength of the relationship between y^t(x) and y^t − 1(x); δ^t(x) represents the discrepancy between y^t(x) and ρ_t − 1y^t − 1(x), and it is considered to be independent of y^t − 1(x), …, y¹(x). The dependence assumed in our work refers to the dependence of the priori of δ and y^t − 1(x), …, y¹(x) before the collection of data. The additivity of GPs should be utilized during the modeling of the proposed cokriging method, of which the premise is that the two GPs added together should be independent to each other.

It is assumed that the model output response is observed without random measurement error. For the t^th level (t = 1,...,s) model, it is supposed that a set of response observations ${\mathbf{d}}_t={\left[{y}^t\left({\mathbf{x}}_1^t\right),\dots, {y}^t\left({\mathbf{x}}_{n_t}^t\right)\right]}^T$ at input sites ${\mathbf{D}}_t={\left[{\left({\mathbf{x}}_1^t\right)}^T,{\left({\mathbf{x}}_2^t\right)}^T,\dots, {\left({\mathbf{x}}_{n_t}^t\right)}^T\right]}^T$ have been collected. Let $\mathbf{d}={\left[{\mathbf{d}}_1^T,\dots, {\mathbf{d}}_s^T\right]}^T$ denotes all of the collected response data from all models at the input space Γ = [D₁; D₂; …; D_s]. Furthermore, the correlation matrix between response observations taken at points in D_k and D_l (D_k ⊆ Γ,D_l ⊆ Γ) is denoted by R_t(D_k, D_l); if k = l, R_t(D_k, D_k) is denoted as R_t(D_k)   (D_k ⊆ Γ). One popular choice for R_t(x, x^′) in the computer experiment literature is the Gaussian correlation function

$$ {R}_t\left(\mathbf{x},{\mathbf{x}}^{\prime}\right)={r}_t\left(\mathbf{x}-{\mathbf{x}}^{\prime },{\boldsymbol{\theta}}^t\right)=\exp \left\{-{\sum}_{k=1}^p{\theta}_k^t{\left({x}_k-{x}_k^{\prime}\right)}^2\right\} $$

(2)

where ${\boldsymbol{\theta}}^t={\left[{\theta}_1^t,{\theta}_2^t,\dots, {\theta}_p^t\right]}^T$ is a vector of spatial correlation parameters (aka scale or roughness parameters) with respect to each dimension of the input variable x. It is used to represent the rate at which the correlation between y^t(x) and y^t(x^′) decays to zero as x and x’ diverge.

In the cokriging modeling, the GP theory is applied to build metamodels for the functional response of interest. Based on various assumptions, a GP model in a classical form can be built to represent the highest-fidelity output responsey^s(x).

$$ {y}^s\left(\mathbf{x}\right)\sim \mathcal{GP}\left(m\left(\mathbf{x}\right),V\left(\mathbf{x},{\mathbf{x}}^{\prime}\right)\right) $$

(3)

where m(x) is the mean function usually expressed as h(x)^Tβ, with h(x)^T denoting a column vector of pre-specified polynomial functions (i.e., constant, linear, quadratic, etc.), and β a column vector of the to-be-determined regression coefficients; V(x, x^′) = σ²R(x, x^′) = σ²r(x − x^′, θ) is the covariance function, representing the spatial covariance between any two inputs x and x’ of the process.

The unknown parameters ϕ = {β, σ², θ, ρ}, referred to as hyper-parameters, characterizes the GP model, where the regression coefficients are β = (β₁, …, β_s)^T,the scaling factors $\boldsymbol{\uprho} ={\left({\rho}_1,\dots, {\rho}_{s-1}\right)}^T$, ${\boldsymbol{\upsigma}}^{\boldsymbol{2}}={\left({\sigma}_1^2,\dots, {\sigma}_s^2\right)}^T$ and the spatial correlation parameters $\boldsymbol{\uptheta} ={\left({\boldsymbol{\theta}}_1,\dots, {\boldsymbol{\theta}}_s\right)}^T$. Once ϕ are estimated, the s-level cokriging model is established, of which the response prediction and the corresponding mean square error (MSE) at any new input sites x_p (x_p $={\left[{\mathbf{x}}_1^T,{\mathbf{x}}_2^T,\dots, {\mathbf{x}}_{n_p}^T\right]}^T$) can be predicted. Since the same structure of cokriging model is employed for the proposed FC method as that of the one proposed by Kennedy and O’Hagan, the formulations of the involved matrixes and vectors (such as h(x)^T and V(x, x^′)) as well as the response prediction and MSE above are the same as that of FC. To introduce the proposed method more smoothly and clearly, these formulations are presented in Subsection 3.1.

3 The proposed cokriging-based sequential optimization procedure

Although the existing multi-fidelity cokriging modeling approaches utilize the data from all models for response prediction, most of those methods only consider the correlation of the data from two models with adjacent fidelities or from the same model in estimating the unknown hyper-parameters. Therefore, a method for hyper-parameters estimation is proposed by utilizing full covariance of all the data, which is denoted as FC. Meanwhile, to more reasonably identifying the location as well as the fidelity level of the new evaluation, an extended EI (denoted as EEI) criterion is developed to further reduce the computational cost of sequential optimization.

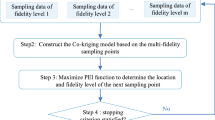
The outline of the proposed sequential optimization approach employing FC in conjunction with EEI is provided in Fig. 1 and described as below. It follows the general procedure of the existing kriging based sequential optimization proposed by Huang et al. (2006), while two improvements are made (see the two shaded boxes). The step-by-step description of the proposed cokriging based sequential optimization approach is given as follows.

Fig. 1

Flowchart of the proposed cokriging based sequential optimization approach

• Step 1: Generate certain initial input samples for each model with varying fidelity.

• Step 2: Calculate the response data of the multi-hierarchical lower-fidelity models and the single high-fidelity model.

• Step 3: Based on the current input and output data, construct the cokriging model using the FC method.

• Step 4: Obtain the global optimum based on the cokriging model.

• Step 5: Determine the input location and the model fidelity level of the next new evaluation by the EEI criterion.

• Step 6: If the convergence criterion (inequality (34)) is satisfied, go to Step 7, stop the procedure and output the current optimal solutions; if not, go to Step 2, i.e. calculate the response data of model with the selected fidelity level at the new input location in Step 5, which is then added to the old data set to update the cokriging model.

3.1 Parameter estimation considering full correlation of data

The full correlation of all the observed data is utilized in this work to obtain the hyper-parameters ϕ = {β, σ², θ, ρ} of the multilevel cokriging model, which is then compared to the methods proposed by Kennedy and O′ Hagan (denoted as KOH) (Kennedy and O'Hagan 2000) and Gratiet (denoted as BM) (Le Gratiet 2013). With KOH, the Markov property is assumed and ϕ are reckoned numerically by the maximum likelihood estimation (MLE) method in s separate steps, where only the correlation of the observed data between two models with adjacent fidelity (i.e., y^t(x) and y^t − 1(x)) is utilized. For BM, some parameters {ρ, β, σ²} are estimated based on the “Jeffreys priors” and then θ is obtained by MLE numerically in s separate steps, in which only the correlation of the observed data within the same model (i.e., y^t(x)) is explored. However, for FC, the correlation of the observed data among all the models (y¹(x), …, y^s(x)) is fully explored to estimate all hyper-parameters altogether by maximizing one unified likelihood function. For the detailed introduction of KOH and BM, readers can refer to (Kennedy and O'Hagan 2000; Le Gratiet 2013), respectively.

With FC, the high-fidelity model y^s(x) can be expressed as below based on the general formulation of cokriging model in (1).

$$ {y}^s\left(\mathbf{x}\right)=\left(\prod \limits_{i=1}^{s-1}{\rho}_i\right){y}^1\left(\mathbf{x}\right)+\left(\prod \limits_{i=2}^{s-1}{\rho}_i\right){\delta}^2\left(\mathbf{x}\right)+\dots +{\rho}_{s-1}{\delta}^{s-1}\left(\mathbf{x}\right)+{\delta}^s\left(\mathbf{x}\right) $$

(4)

It is assumed that y¹(x), δ²(x), …, δ^s(x) can be respectively modeled as a GP as below.

$$ {\displaystyle \begin{array}{l}{y}^1\left(\cdotp \right)\sim \mathcal{GP}\left({h}^1{\left(\cdotp \right)}^T{\beta}_1,{V}_d^1\right)\\ {}{\delta}^t\left(\cdotp \right)\sim \mathcal{GP}\left({h}^t{\left(\cdotp \right)}^T{\beta}_t,{V}_d^t\right),t=2,\dots, s\end{array}} $$

(5)

Then, additively the model y^s(x) can be expressed by a GP based on (4) and (5).

$$ {\displaystyle \begin{array}{c}{y}^s\left(\cdotp \right)\sim \mathcal{GP}\left({h}^1{\left(\cdotp \right)}^T{\beta}_1\left(\prod \limits_{i=1}^{s\hbox{-} 1}{\rho}_i\right)+{h}^2{\left(\cdotp \right)}^T{\beta}_2\left(\prod \limits_{i=2}^{s\hbox{-} 1}{\rho}_i\right)+\dots +{h}^s{\left(\cdotp \right)}^T{\beta}_s,\right.\\ {}\left.{\left(\prod \limits_{i=1}^{s\hbox{-} 1}{\rho}_i\right)}^2{V}_d^1+{\left(\prod \limits_{i=2}^{s\hbox{-} 1}{\rho}_i\right)}^2{V}_d^2+.\dots +{V}_d^s\right)\end{array}} $$

(6)

Based on the assumption of GP, all the collected data follow a multivariate normal distribution, i.e.

$$ \mathbf{d}\sim \mathcal{N}\left(\mathbf{H}\boldsymbol{\upbeta }, {\mathbf{V}}_d\right) $$

(7)

where the involved matrixes and vectors are formulated as below.

The matrix H of size (n₁+, …, +n_s) × s is

$$ \mathbf{H}=\left(\begin{array}{cccc}{\mathbf{H}}_1\left({\mathbf{D}}_1\right)& 0& \cdots & 0\\ {}{\rho}_1{\mathbf{H}}_1\left({\mathbf{D}}_2\right)& {\mathbf{H}}_2\left({\mathbf{D}}_2\right)& 0& 0\\ {}{\rho}_1{\rho}_2{\mathbf{H}}_1\left({\mathbf{D}}_3\right)& {\rho}_2{\mathbf{H}}_2\left({\mathbf{D}}_3\right)& {\mathbf{H}}_3\left({\mathbf{D}}_3\right)& \vdots \\ {}\vdots & \vdots & \vdots & 0\\ {}\left(\prod \limits_{i=1}^{s-1}{\rho}_i\right){\mathbf{H}}_1\left({\mathbf{D}}_s\right)& \left(\prod \limits_{i=2}^{s-1}{\rho}_i\right){\mathbf{H}}_2\left({\mathbf{D}}_s\right)& \cdots & {\mathbf{H}}_s\left({\mathbf{D}}_s\right)\end{array}\right) $$

(8)

with the vector ${\mathbf{H}}_t\left({\mathbf{D}}_{t^{\prime }}\right)={\left[{h}^t\left({\mathbf{x}}_1^{t^{\prime }}\right),{h}^t\left({\mathbf{x}}_2^{t^{\prime }}\right),\dots, {h}^t\left({\mathbf{x}}_{n_{t^{\prime}}}^{t^{\prime }}\right)\right]}^T$, where h^t(x)^T denotes a column vector of pre-specified polynomial functions (h^t(x)^T = 1 is adopted in this paper).

The vector β of size s × 1 is given as

$$ \boldsymbol{\upbeta} ={\left({\boldsymbol{\beta}}_1,\dots, {\boldsymbol{\beta}}_{\boldsymbol{s}}\right)}^{\boldsymbol{T}}. $$

(9)

The matrix V_d of size (n₁+, …, +n_s) × (n₁+, …, +n_s) is given as

$$ {\mathbf{V}}_{\mathbf{d}}=\left(\begin{array}{ccc}{V}_{1,1}& \cdots & {V}_{1,s}\\ {}\vdots & \ddots & \vdots \\ {}{V}_{s,1}& \cdots & {V}_{s,s}\end{array}\right), $$

(10)

where the t^th diagonal block (n_t × n_t) is defined as

$$ {V}_{t,t}={\sigma}_t^2{R}_t\left({\mathbf{D}}_t\right)+{\sigma}_{t-1}^2{\rho}_{t-1}^2{R}_{t-1}\left({\mathbf{D}}_t\right)+\dots +{\sigma}_1^2\left(\prod \limits_{i=1}^{t-1}{\rho}_i^2\right){R}_1\left({\mathbf{D}}_t\right), $$

(11)

and the off-diagonal block of size ${n}_t\times {n}_{t^{\prime }}$ is given by

$$ {V}_{t,{t}^{\prime }}=\left(\prod \limits_{i=t}^{t^{\prime }-1}{\rho}_i\right)\left({\sigma}_t^2{R}_t\left({\mathbf{D}}_t,{\mathbf{D}}_{t^{\prime }}\right)+\dots +{\sigma}_1^2\left(\prod \limits_{i=1}^{t-1}{\rho}_i^2\right){R}_1\left({\mathbf{D}}_t,{\mathbf{D}}_{t^{\prime }}\right)\right),\kern0.5em 1\le t<{t}^{\prime}\le s. $$

(12)

Then the MLE method is employed to estimate the hyper-parameters ϕ = {β, σ², θ, ρ}. Given the collected response data set d, the unified likelihood function of the hyper-parameters ϕ is constructed as

$$ \mathcal{L}\left(\boldsymbol{\upphi} \left|\mathbf{d}\right.\right)\propto {\left|{\mathbf{V}}_d\right|}^{-1/2}{\left|\mathbf{W}\right|}^{1/2}\exp \left\{-\frac{1}{2}{\left(\mathbf{d}-\mathbf{H}\boldsymbol{\upbeta } \right)}^T{\mathbf{V}}_d^{-1}\left(\mathbf{d}-\mathbf{H}\boldsymbol{\upbeta } \right)\right\} $$

(13)

where $\mathbf{W}={\left({\mathbf{H}}^T{\mathbf{V}}_d^{-1}\mathbf{H}\right)}^{-1}$.

Solving the maximum unified likelihood function in (13) is equivalent to maximizing its logarithm (i.e., log-likelihood function) as below.

$$ {\displaystyle \begin{array}{l}\underset{\boldsymbol{\upbeta}, {\boldsymbol{\upsigma}}^2,\boldsymbol{\uptheta}, \boldsymbol{\uprho}}{\max}\mathcal{L}\left(\boldsymbol{\upphi} \left|\mathbf{d}\right.\right)=\underset{\boldsymbol{\upbeta}, {\boldsymbol{\upsigma}}^2,\boldsymbol{\uptheta}, \boldsymbol{\uprho}}{\max}\kern0.5em \log \left[\mathcal{L}\left(\boldsymbol{\upphi} \left|\mathbf{d}\right.\right)\right]\\ {}\kern6em =\underset{\boldsymbol{\upbeta}, {\boldsymbol{\upsigma}}^2,\boldsymbol{\uptheta}, \boldsymbol{\uprho}}{\max}\kern0.5em \mathrm{\ell}\left(\boldsymbol{\upphi} \left|\mathbf{d}\right.\right)\end{array}} $$

(14)

where $\mathrm{\ell}\left(\boldsymbol{\upphi} \left|\mathbf{d}\right.\right)\propto \frac{1}{2}\log \left|\mathbf{W}\right|\hbox{-} \frac{1}{2}\log \left|{\mathbf{V}}_d\right|\hbox{-} \frac{1}{2}{\left(\mathbf{d}\hbox{-} \mathbf{H}\boldsymbol{\upbeta } \right)}^T{\mathbf{V}}_d\left(\mathbf{d}\hbox{-} \mathbf{H}\boldsymbol{\upbeta } \right)$.

According to the first order optimality condition

$$ {\displaystyle \begin{array}{c}{\left.\frac{\mathrm{\partial \ell}\left(\boldsymbol{\upphi} \left|\mathbf{d}\right.\right)}{\partial \boldsymbol{\upbeta}}\right|}_{\boldsymbol{\upbeta} =\overset{\frown }{\boldsymbol{\upbeta}}}=0\\ {}{\left(\mathbf{d}\hbox{-} \mathbf{H}\overset{\frown }{\boldsymbol{\upbeta}}\right)}^T{\mathbf{V}}_{\mathbf{d}}^{-1}\mathbf{H}={\mathbf{d}}^T{\mathbf{V}}_{\mathbf{d}}^{-1}\mathbf{H}-{\overset{\frown }{\boldsymbol{\upbeta}}}^T{\mathbf{H}}^T{\mathbf{V}}_{\mathbf{d}}^{-1}\mathbf{H}=\mathbf{0}\end{array}}, $$

(15)

the estimation in the closed-form expression $\overset{\frown }{\boldsymbol{\upbeta}}$ for β can be obtained.

$$ \overset{\frown }{\boldsymbol{\upbeta}}=\mathbf{WH}{\mathbf{V}}_{\mathbf{d}}^{-1}\mathbf{d} $$

(16)

which is expressed in a function of σ² andθ.

The rest of hyper-parameters σ², θ and ρ can be estimated by solving the maximum unifie log-likelihood function below using numerical optimization algorithm, e.g., a genetic algorithm or simulated annealing.

$$ \underset{{\boldsymbol{\upsigma}}^2,\boldsymbol{\uptheta}, \boldsymbol{\uprho}}{\max}\frac{1}{2}\log \left|\mathbf{W}\right|-\frac{1}{2}\log \left|{\mathbf{V}}_d\right|-\frac{1}{2}{\left(\mathbf{d}-\mathbf{H}\overset{\frown }{\boldsymbol{\beta}}\right)}^T{\mathbf{V}}_d\left(\mathbf{d}-\mathbf{H}\overset{\frown }{\boldsymbol{\beta}}\right) $$

(17)

β can then be estimated by using (16). It should be noticed that the hyper-parameters are estimated altogether in the proposed method by solving the unified likelihood function, while they are estimated group by group in s separate steps in KOH and BM methods. Meanwhile, the covariance among all the models is utilized. Once all the hyper-parameters are estimated, the response prediction y(x_p) and its corresponding mean square error (MSE) at any new input sites x_p (x_p $={\left[{\mathbf{x}}_1^T,{\mathbf{x}}_2^T,\dots, {\mathbf{x}}_{n_p}^T\right]}^T$) can be predicted. With the GP model, the collected data d together with the to-be-predicted responses $\boldsymbol{y}\left({\mathbf{x}}_p\right)={\left[y\left({\mathbf{x}}_1\right),\dots, y\left({\mathbf{x}}_{n_p}\right)\right]}^T$ follow a multivariate normal distribution.

$$ \left[\begin{array}{c}\mathbf{d}\\ {}\boldsymbol{y}\left({\mathbf{x}}_p\right)\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}\mathbf{H}\\ {}{\mathbf{H}}_p\end{array}\right]\boldsymbol{\upbeta}, \left[\begin{array}{cc}{\mathbf{V}}_{\mathbf{d}}& {\mathbf{T}}_p^T\\ {}{\mathbf{T}}_p& {\mathbf{V}}_p\end{array}\right]\right) $$

(18)

where H and V_d are the polynomial function and covariance matrix for the observed data d, which have been formulated in (8) and (10), respectively; H_p and V_p are the polynomial function and covariance matrix for the to-be-predicted responses y(x_p); T_p denotes the covariance matrix between y(x_p) and d. Details regarding the matrices H_p, V_p, and T_p will be given in (21)–(25) below. Then the final prediction of y(x_p) and its MSE can be computed by

$$ \overset{\frown }{\boldsymbol{y}}\left({\mathbf{x}}_p\right)={\mathbf{H}}_p\overset{\frown }{\boldsymbol{\upbeta}}+{\mathbf{T}}_p{\mathbf{V}}_{\mathbf{d}}^{-1}\left(\mathbf{d}-\mathbf{H}\overset{\frown }{\boldsymbol{\upbeta}}\right), $$

(19)

$$ \mathrm{MSE}\left[\overset{\frown }{\boldsymbol{y}}\left({\mathbf{x}}_p\right)\right]={\mathbf{V}}_p-{\mathbf{T}}_p{\mathbf{V}}_{\mathbf{d}}^{-1}{\mathbf{T}}_p^T+{\left({\mathbf{H}}_p^T-{\mathbf{H}}^T{\mathbf{V}}_{\mathbf{d}}^{-1}{\mathbf{T}}_p^T\right)}^T\mathbf{W}\left({\mathbf{H}}_p^T-{\mathbf{H}}^T{\mathbf{V}}_{\mathbf{d}}^{-1}{\mathbf{T}}_p^T\right), $$

(20)

where

$$ {\mathbf{H}}_p={\left(\left(\prod \limits_{i=1}^{s-1}{\rho}_i\right){h}^1{\left(\mathbf{x}\right)}^T,\left(\prod \limits_{i=2}^{s-1}{\rho}_i\right){h}^2{\left(\mathbf{x}\right)}^T,\dots, {\rho}_{s-1}(x){h}^{s-1}{\left(\mathbf{x}\right)}^T,{h}^s{\left(\mathbf{x}\right)}^T\right)}^T\left(\mathrm{size}\ 1\times s\right) $$

(21)

$$ {\mathbf{T}}_p=\left({t}_1{\left({\mathbf{x}}_p,{\mathbf{D}}_1\right)}^T,\dots, {t}_s{\left({\mathbf{x}}_p,{\mathbf{D}}_s\right)}^T\right)\left(\mathrm{size}\ {n}_p\times s\right) $$

(22)

$$ {t}_1{\left({\mathbf{x}}_p,{\mathbf{D}}_1\right)}^T=\left(\prod \limits_{i=1}^{s-1}{\rho}_i\right){\sigma}_1^2{R}_1\left({\mathbf{x}}_p,{\mathbf{D}}_1\right) $$

(23)

$$ {t}_t{\left({\mathbf{x}}_p,{\mathbf{D}}_t\right)}^T={\rho}_{t-1}{t}_t{\left({\mathbf{x}}_p,{\mathbf{D}}_t\right)}^T+\left(\prod \limits_{i=t}^s{\rho}_t\right){\sigma}_t^2{R}_t\left({\mathbf{x}}_p,{\mathbf{D}}_t\right),\kern1em t=2,\dots, s $$

(24)

$$ {\mathbf{V}}_p={\boldsymbol{V}}_d^s\left({\mathbf{x}}_p,{\mathbf{x}}_p\right)+{\boldsymbol{\rho}}_{\boldsymbol{s}-1}^2{\boldsymbol{V}}_d^{s-1}\left({\mathbf{x}}_p,{\mathbf{x}}_p\right)+{\boldsymbol{\rho}}_{s-1}^2{\boldsymbol{\rho}}_{s-2}^2{\boldsymbol{V}}_d^{s-2}\left({\mathbf{x}}_p,{\mathbf{x}}_p\right)+\dots +{\left(\prod \limits_{t=2}^{s-1}{\boldsymbol{\rho}}_{\boldsymbol{t}}\right)}^2{\boldsymbol{V}}_d^2\left({\mathbf{x}}_p,{\mathbf{x}}_p\right)\left(\mathrm{size}\ {n}_p\times {n}_p\right) $$

(25)

Meanwhile, it should be pointed out that in KOH and BM, the input sets are assumed to be nested, i.e., D_s ⊆ , …, ⊆ D₁, which is not necessary but allows to have a closed-form expression for the parameter posterior distribution. In KOH, it is necessary to calculate δ_t(x) = d_t + 1 ‐ ρ_ty^t(D_t + 1) to define the likelihood function in estimating the parameters $\left({\boldsymbol{\theta}}_t,{\sigma}_t^2,{\rho}_{t-1}\right)$. Meanwhile, for BM, G_t + 1 = [y^t(D_t + 1) H_t + 1(D_t + 1)] should be defined in the “Jeffreys priors” to obtain the estimations of parameters $\left({\boldsymbol{\rho}}_{t-1},{\boldsymbol{\beta}}_{\boldsymbol{t}},{\sigma}_t^2,{\boldsymbol{\theta}}_t\right)$. Clearly, y^t(D_t + 1) exists only if the sample points for y^t + 1 and y^t are nested, i.e., D_t + 1 ⊆ D_t. If not, an approximated GP model for each lower-fidelity model should be constructed firstly, based on which the multi-level cokriging model can also be constructed. However, for the FC, it is not restricted by this assumption, and thus it is more flexible.

In addition, in the FC method,the maximum likelihood function contains a matrix V_d, of which the size (n₁+, …, +n_s) × (n₁+, …, +n_s) is determined by the number of models for fusion and the number of sample points from each model. If the size of V_d is large, the computational cost in solving the maximum likelihood function will be clearly increased. Meanwhile, during the process of MLE, some garbage results may be generated. In this case, some additional repeated optimization can be conducted to help find the global optimum. For BM and KOH, since all items in their maximum likelihood function are scalars or vectors, the computational cost is clearly smaller than FC. However, compared with the computational cost of model response evaluation (in practice, it often takes a very long time to run one model evaluation), such increase in the computational time of model fusion can be negligible. The proposed FC method aims to increase the accuracy of the final cokriging model, which is still of great significance to some engineering problems.

3.2 The extended sequential sampling strategy

Several criteria have been investigated to decide a new infilling sample site for the objective-oriented sequential sampling. The statistical lower bounding (SLB) criterion and the expected improvement (EI) criterion are the two most widely used approaches in the literature. Based on the results of Jones et al.’s work (Jones et al. 1998), an extended EI (EEI) criterion is defined to determine both the location of the new input sample and the fidelity level of the new evaluation.

$$ \mathrm{EEI}\left(\mathbf{x},t\right)=\mathrm{EI}\left(\mathbf{x}\right)\times \left|\mathrm{Corr}\left(\mathbf{x},t\right)\right|\times \mathrm{CR}(t)\times \eta \left(\mathbf{x},t\right) $$

(26)

where EI(x) is the original EI function, and the other three items will be described as below.

• (1) Model correlation Corr(x, t)

Corr(x, t) represents the posterior correlation coefficient between the stochastic predicted responses ${y}_{po}^t\left(\mathbf{x}\right)$ from the t-level fidelity model and ${y}_{po}^s\left(\mathbf{x}\right)$ from the s-level (highest) fidelity one at the input site x, and can be computed by

$$ \mathrm{Corr}\left(\mathbf{x},t\right)=\mathrm{Corr}\left[{y}_{po}^t\left(\mathbf{x}\right),{y}_{po}^s\left(\mathbf{x}\right)\right]=\frac{Cov\left[{y}_{po}^t\left(\mathbf{x}\right),{y}_{po}^s\left(\mathbf{x}\right)\right]}{\sqrt{Var\left[{y}_{po}^t\left(\mathbf{x}\right)\right]\times Var\left[{y}_{po}^s\left(\mathbf{x}\right)\right]}}. $$

(27)

In (27), $Cov\left[{y}_{po}^t\left(\mathbf{x}\right),{y}_{po}^s\left(\mathbf{x}\right)\right]$ denotes the posterior covariance at the input site x between the stochastic predicted responses ${y}_{po}^t\left(\mathbf{x}\right)$ and ${y}_{po}^s\left(\mathbf{x}\right)$, and it can be obtained by

$$ {\displaystyle \begin{array}{ll} Cov\left[{y}_{po}^t\left(\mathbf{x}\right),{y}_{po}^s\left(\mathbf{x}\right)\right]& = Cov\left[{y}^t\left(\mathbf{x}\right),{y}^s\left(\mathbf{x}\right)\right]\hbox{-} {\mathbf{T}}_p^t{\mathbf{V}}_{\mathbf{d}}^{-1}{\left({\mathbf{T}}_p^s\right)}^T\\ {}& +{\left({\left({\mathbf{H}}_p^t\right)}^T-{\mathbf{H}}^T{\mathbf{V}}_{\mathbf{d}}^{-1}{\left({\mathbf{T}}_p^t\right)}^T\right)}^T\mathbf{W}\left({\left({\mathbf{H}}_p^s\right)}^T-{\mathbf{H}}^T{\mathbf{V}}_{\mathbf{d}}^{-1}{\left({\mathbf{T}}_p^s\right)}^T\right)\end{array}}, $$

(28)

where

(29)

In the above equation, ρ denotes the weight coefficient between y^t(x) and y^s(x), which is a scalar calculated as ρ = ρ_tρ_t + 1⋯ρ_s. Meanwhile, in (27), $Var\left[{y}_{po}^s\left(\mathbf{x}\right)\right]= Cov\left[{y}_{po}^s\left(\mathbf{x}\right),{y}_{po}^s\left(\mathbf{x}\right)\right]$ and $Var\left[{y}_{po}^t\left(\mathbf{x}\right)\right]= Cov\left[{y}_{po}^t\left(\mathbf{x}\right),{y}_{po}^t\left(\mathbf{x}\right)\right]$ can also be calculated by (28).

If t = s, for any x, Corr(x, t) = 1, which stands for the correlation of the stochastic predicted responses from the highest-fidelity model itself. If $t\ne ss$, for any x, |Corr(x, t)| ∈ [0, 1], which describes the ratio between the accuracy improvement for the predicted response in adding the lower-fidelity response data y^t(x) and highest-fidelity one y^s(x). It should be noticed that for the input set that already has the corresponding model response data, $Var\left[{y}_{po}^t\left(\mathbf{x}\right)\right]\times Var\left[{y}_{po}^s\left(\mathbf{x}\right)\right]$ and Cov[y^t(x), y^s(x)] are all equal to 0. In this case, Corr(x, t) is defined as 0 in our study.

• (2) Ratio of cost CR(t)

CR(t) represents the computational cost ratio of a single response evaluation between the highest-fidelity model y^s(x) and the t-level one y^t(x), i.e.

$$ \mathrm{CR}(t)=\frac{C^s}{C^t} $$

(30)

where C^s and C^t respectively represents the computational cost of a single response evaluation for the highest-fidelity model y^s(x) and the t-th level lower-fidelity modely^t(x).

If t = s, CR(t) = 1; if $t\ne ss$, CR(t) ≥1, which means that it is more efficient to employ the lower-fidelity model y^t(x) to evaluate the response. The inclusion of CR(t) in (26) aims to select the computationally cheapest model as much as possible that is then called to evaluate the response at the identified new input location, considering the trade-off from other two aspects (model correction and sample density). That is to say, if similar accuracy improvement and sample density property can be obtained, the model with the smallest cost will be selected to reduce the computational cost as much as possible.

• (3) Sample density functionη(x, t)

η(x, t) describes the density of the input samples from the same model, which is used to avoid the clustering of samples. The spatial correlation of the GP is employed to quantify the distance between the input samples, and thus η(x, t) is defined as

$$ \eta \left(\mathbf{x},t\right)={\prod}_{i=1}^{N^t}\left[1-R\left(\mathbf{x},{\mathbf{x}}^i\right)\right] $$

(31)

where N^t represents the number of samples from t-th level fidelity model, while xⁱ are the locations of input samples; R(x,xⁱ) is the spatial correlation function of GP, which is the same as that used in the cokriging modeling above.

Moreover, if higher-fidelity response data exist at a certain input location, adding new lower-fidelity response data at this input location generally contributes minimally to the improvement of the accuracy of the response prediction. Therefore, based on (31), the sample density factor function η(x, t) is redefined as below to avoid unnecessary waste of samples.

$$ \eta \left(\mathbf{x},t\right)=\prod \limits_{N^t}^{N^s}\prod \limits_{i=1}^{N^t}\left[1-R\left(\mathbf{x},{\mathbf{x}}^i\right)\right],\forall t\le s $$

(32)

Clearly, each item in (26) plays an important role. As the basis of the EEI criterion, the original EI(x) quantifies the improvement of response prediction accuracy at any input location. If Corr(x,t) is removed, the model with the lowest fidelity will always be selected for response evaluation since it has the smallest cost. If CR(t) is removed, the high-fidelity model will always be selected for response evaluation since it can obtain the maximum improvement of response prediction accuracy. If η(x, t) is removed, samples may get clustered, decreasing the optimization efficiency. In addition, if only a single model is used for response prediction, EEI will be automatically degenerated to the original EI function.

Note that apart from the EEI criterion defined in (26), other formulations certainly can be adopted to balance among the model correlation, computational cost, and the sample density property. For example, when their ratios have significantly different orders of magnitude, the small one may not be considered in the EEI criterion. In this case, the designer can analyze this influence via sensitivity studies and propose an effective formulation such as assigning different powers to the three factors based on their orders of magnitude. Different formulations used in the EEI criterion would not influence the procedure of other posterior analysis of the FC method.

Both the location of new input x_new and the corresponding model t_add called to evaluate the response at x_new are determined through maximizing the EEI function.

$$ \left({\mathbf{x}}_{new},{t}_{add}\right)=\underset{\mathbf{x},t}{\max}\mathrm{EEI}\left(\mathbf{x},t\right) $$

(33)

The optimization scheme stops when the current obtained optimal EEI objective value is smaller than a specified value γ, i.e.

$$ \underset{\mathbf{x},\mathcal{M}}{\max}\mathrm{EEI}\left(\mathbf{x},t\right)<\gamma =\alpha \%\times \left[\max \left(\mathbf{d}\right)-\min \left(\mathbf{d}\right)\right], $$

(34)

where γ is the so-called “relative stopping criterion” (Huang et al. 2006), which is defined as α% of the “active span” of the collected response data d; max(d) and min(d) respectively represent the maximum and minimum elements in the current collected response data set d; max(d) − min(d) is the “active span” of the responses; α% is selected as α %  = 0.05% in our study, corresponding to 95% confidence interval.

Clearly, x_new and t_add found by the proposed EEI criterion can make a good balance among the response accuracy improvement, the computational cost, and the sample density property, i.e. x_new and t_add try to improve the accuracy of the cokriging metamodel as much as possible with as little computational cost as possible.

4 Comparative studies

Three numerical examples and one engineering problem (shown in Table 1) are employed to test the effectiveness of the proposed hyper-parameter estimation method (FC) during cokriging metamodeling, which is compared to KOH and BM. Then, sequential optimization employing FC and EEI is then conducted to obtain the optimal solutions. For all the examples, it is assumed that s = 3 levels of fidelity y¹(x), y²(x), y³(x) exist.

Table 1 Function descriptions

4.1 Validation of FC for hyper-parameter estimation

Firstly, the FC hyper-parameter estimation method is tested. To evaluate the accuracy of the constructed cokriging metamodel, the root-mean-square mean (RSME) error is computed. A smaller RMSE corresponds to a more accurate cokriging metamodel. The RSME is calculated as

$$ \mathrm{RSME}=\sqrt{\sum {\left(\overset{\frown }{\boldsymbol{y}}\left({\mathbf{x}}_p\right)-{\boldsymbol{y}}^s\left({\mathbf{x}}_p\right)\right)}^2/{n}_p} $$

(35)

where x_p are the test sample points generated randomly and uniformly in the design region of the input x with the number as n_p = 1000; $\overset{\frown }{\boldsymbol{y}}\left({\mathbf{x}}_p\right)$ and y^s(x_p) are the response predictions at test input set x_p obtained by the cokriging model and the response model with the highest-fidelity level, respectively.

4.1.1 Numerical example 1

The input sample points for the three models y¹(x), y²(x), y³(x) are selected with n₃ = 5, n₂ = 10, and n₁ = 20, satisfying the nested property D₃ ⊆ D₂ ⊆ D₁. The non-nested input sample points are also generated uniformly with the same size. For both cases in all the examples, several different sets of input sample points are tested repeatedly with the same settings to test the robustness of the FC method, based on which the mean values of RMSE and time cost are calculated. In addition to the accuracy of cokriging, the time cost in estimating the hyper-parameters on a personal computer (Intel Corei7-4710HQ, CPU 2.50GHz) is also computed. The results are shown in Table 2, from which some noteworthy observations can be made. Firstly, for both nested and non-nested sampling strategies, the accuracy of cokriging metamodel constructed by FC is the best, followed by KOH and then BM. Specially, the RMSE of BM is almost twice that of FC. Secondly, for the time cost, FC is the most time-consuming, followed by KOH and then BM. The interpretation is that for FC, the correlation of the data from all the models is computed and fully utilized during the hyper-parameter estimation. Thus the accuracy of FC is improved compared to the other two approaches. However, in solving the MLE, a covariance matrix of large size (35 × 35 for this example) is involved for FC, resulting in an evident increase in computational cost; meanwhile, no large-scale matrix operations are involved for KOH and BM. Thirdly, compared to the results for nested sampling, the errors with the non-nested sampling for KOH and BM are slightly larger; meanwhile for FC, the two sets of results are very close to each other. The reason is that when the sample points for different fidelities are not nested, a GP model has to be constructed based on the collected data for each lower-fidelity model y^t(x) (t = 1,...,s-1) for KOH and BM, which apparently would induce certain error. Since this example is relatively simpler, the GP models constructed are generally accurate. So for KOH and BM, the difference of results between nested and non-nested sampling is very small. In addition, the variation of RSME is relatively small, indicating the robustness of FC as well as other two methods.

Table 2 Errors and time costs of FC, KOH and BM for example 1

The predicted responses from the constructed cokriging models by FC, KOH and BM with nested and non-nested sample points with one of the five sample sets are shown in Figs. 2 and 3 (see the dot dash line), where the 95% confidence interval (CI) for the prediction of each cokriging model is also plotted. Meanwhile, the true response from the highest-fidelity model (denoted by y³) and predicted response from the kriging model constructed with only the data from the highest-fidelity model y³ (denoted by HF) are also shown in Figs. 2 and 3 for comparison.

Fig. 2

Predicted responses from different models of example 1 (nested)

Fig. 3

Predicted responses from different models of example 1 (non-nested)

It is found from these figures that generally the prediction responses of the cokriging models by FC are slightly closer to the true response (y³) yielding smaller errors, compared to KOH and BM; and both KOH and FC are more accurate than BM. This exhibits great agreement to the results shown in Table 2. Meanwhile, compared to the curves (HF) produced by using only the highest-fidelity data, the cokriging models are much more accurate due to the fusion of the lower-fidelity data.

4.1.2 Numerical example 2

Similarly, nested and non-nested sample points with n₃ = 4, n₂ = 11, and n₁ = 21 are selected to test the effectiveness of the proposed FC for hyper-parameter estimation. The results of the three methods are shown in Table 3.

Table 3 Errors and time costs of the three approaches for example 2

The constructed cokriging models by FC, KOH and BM, as well as the HF model constructed with only the data from y³(x) and the true response y³ are shown in Figs. 4 and 5.

Fig. 4

Predicted responses from different models of example 2 (nested)

Fig. 5

Predicted responses from different models of example 2 (non-nested)

Similar observations can be made from Table 3 and the figures above that FC performs best with smaller errors, more accurate predicted output response curves and smaller metamodel uncertainty, compared to KOH and BM. The results of FC are the most accurate, followed by KOH and BM. For the time cost, FC is the most time-consuming, followed by KOH and then BM.

4.1.3 Numerical example 3

Since it is not easy to directly generate nested sample points as the one-dimensional examples above, only the non-nested samples are tested. For approach that can generate nested sample points, the readers can refer to Ref. (Skilling 2006). Latin Hypercube sampling (LHS) is used to select the input sample points with n₃ = 8, n₂ = 15 and n₁ = 20. The results are shown in Table 4.

Table 4 Results of the three approaches for example 3

The constructed cokriging models by FC, KOH and BM, as well as the model constructed with only the data from y³(x) (HF) and the true response y³ are shown in Fig. 6. For the two-dimensional problem, the results exhibit great agreements to what has been observed above that the accuracy of FC is clearly the best, followed by KOH and then BM; and FC is the most time-consuming, followed by KOH and then BM. As Table 4 shows, RMSE of FC is much smaller than the other two approaches. Meanwhile, the response surface produced by FC is clearly much closer to the true response surface y³, yielding smaller metamodel uncertainty.

Fig. 6

Predicted responses from different models of example 3

4.1.4 Aerodynamic modeling of wrap-around fin

In this part, the cokriging method is employed to construct the aerodynamic metamodel for a rocket with wrap-around fins (shown in Fig. 7), under the flight condition with Mach number as Ma = 4 and angle of attack as α = 6^∘. The input vector is x = [D, λ_a, t, R, Φ, L, χ₀], which is presented in Table 5.

Fig. 7

The geometric profile of the rocket

Table 5 Input vector and the bounds

CFD is employed for the aerodynamic analysis. Since this work focuses on investigating the effectiveness of FC in cokriging modeling and it is very time-consuming to run CFD here, we did not dig into setting up various CFD simulation models with different fidelities but directly utilized the CFD data provided in Ref. (Xue 2010) to create models with different fidelities. Generally, as the number of sample points increases, the accuracy of the kriging model is improved. Hence, the models with 3 levels of fidelity y¹(x), y²(x), y³(x) are replaced by different kriging models that are respectively constructed based on different numbers of CFD data (10, 20 and 32). Then the LHS method is employed to generate sample points for the three models y¹(x), y²(x), y³(x) with n₁ = 40, n₂ = 20 and n₃ = 10. The results are presented in Table 6, from which similar observations can be made that for the higher-dimensional problem, FC performs best with the smallest errors; while for the time cost, FC is the most time-consuming, followed by KOH and then BM.

Table 6 Results of three approaches for wrap-around fin aerodynamic modeling

4.2 Sequential optimization

Then, the cokriging based sequential optimization method (named as cokriging-M) employing FC for hyper-parameter estimation and EEI for sequential sampling is applied to optimization. The sequential kriging method constructed based only on the high-fidelity data that employs the original EI to sequentially generate samples (denoted as kriging), and cokriging employing FC for hyper-parameter estimation that is updated with only the high-fidelity data identified by EI (denoted as cokriging-H) are also employed for optimization, of which the results are compared to cokriging-M.

For the three approaches, the same convergence criterion in inequality (34) is employed. For the mathematical examples and the wrap-around fin example, since they are just used to test the effectiveness of the proposed sequential sampling method, the models from low to high fidelities (y¹(x), y²(x), y³(x)……) involved are all very computationally cheap, yielding almost the same computational costs. Thus, C cannot be assigned directly as the computational time of a single model evaluation. In our work, the cost C for these examples is roughly assigned based on the accuracy of the model. As the accuracy of the model improves, C assigned to this model is increased, which evidently accords with the practical situation. Although, it is a little subjective to determine the values of C (C³, C² and C¹) in our work and different values may yield different total computational cost, but similar optimal solutions. Therefore, the values of C does impact the verification process and conclusions. For brevity, only the results about the maximization of examples 2 and 3 are shown here.

For the problem of maximizing example 2, the numbers of uniformly generated initial samples for the three multi-fidelity models are n₁ = 8, n₂ = 5, n₃ = 4. It is assumed that the cost of a single model evaluation of y³, y² and y¹ is C³ = 15, C² = 2 and C¹ = 1, respectively. The cokriging model constructed by FC using the initial samples are shown in Fig. 8a and the cokriging models sequentially updated with new samples generated by the proposed EEI sampling criterion are shown in Fig. 8b–d.

Fig. 8

Initial and sequentially updated cokriging models for example 2

It is observed that with the increase of the number of samples, the predicted response of the cokriging model is getting closer to that of the high-fidelity one (y³), and the uncertainty of the cokriging model is reduced. With EEI, 2 samples from y¹ and 1 from y² are sequentially identified to update the cokriging model (see Fig. 8b). The uncertainty of the cokriging model in the latter half of the design region is slightly reduced with the maximum uncertainty value reduced from 0.0075 to 0.0049, while error exists around the optimum. Subsequently, 1 sample from y¹ and 1 from y² are identified to update the cokriging model, shown in Fig. 8c. Clearly, the accuracy in the middle design region of the updated cokriging model is increased, especially for the region around the optimum. Finally, 3 new samples from y² that are all close to the optimum are sequentially generated to further improve the accuracy of the cokriging model around the optimum (see Fig. 8d), until the convergence criterion (see inequality (34)) is satisfied. Meanwhile, as can be seen from Fig. 8d, in the front half of the design region, evident discrepancy exists between the predicted responses of the final cokriging model and the high-fidelity model y³, which however does not affect the proposed optimization procedure to find the optimal solution (x* = 2.4999, y* = 1.999).

With the same initial samples and convergence criterion, EEI in (26) without including the sample density function η(x, t) is also employed for sequential optimization, of which the cokriging models sequentially updated by 13 samples are shown in Fig. 9a–c. Clearly, it is noticed that the added samples (7 from y² and 6 from y¹) cluster around the optimum and the latter half of the design region. Although the optimal solution is accurate enough (x* = 2.4998, y* = 1.999), the total cost from the added samples is 20(7*2 + 6*1), while it is 14(5*2 + 4*1) for the proposed EEI sampling strategy. The interpretation is that adding dense and clustered samples has little effect on improving the accuracy of the metamodel, and adding too many samples far from the optimum is of little help to find the optimum. These results demonstrate the effectiveness of integration of the sample density functionη(x, t).

Fig. 9

Sequential samples without considering sample density (example 2)

The optimal solutions and the cost are listed in Table 7, from which it is found that the optimal design variable x* and objective function y* obtained by the three approaches are all very close to the real optimal solutions, while the proposed sequential optimization method is more efficient than the other two methods. From Table 7, it is also noticed that no sample from the highest-fidelity model y³(x) is selected during sequential sampling. The interpretation is that the objective-oriented sequential optimization prefers to select samples from y²(x) to improve the accuracy of metamodel near the optimum rather than y³(x), since the accuracy of y²(x) around the optimum is clearly very close to y³(x) (see Fig. 10), while its cost is cheaper (C² = 2, C¹ = 1). Therefore, the method chooses all the samples from y²(x) and y¹(x) to make the least cost.

Table 7 Optimal solution and computational cost of three approaches (example 2)

Fig. 10

Plots of 3-level fidelity models y³(x), y²(x) and y¹(x)

For the problem of maximizing example 3, it is assumed that the cost of a single model evaluation of y³, y² and y¹ is C³ = 10, C² = 2 and C¹ = 1, respectively. The initial samples are selected with n₃ = 6, n₂ = 8 and n₁ = 10, based on which the initial cokriging model is constructed, as shown in Fig. 11a. Clearly, large discrepancy exist between the predicted response of cokriging and the high-fidelity model y³. Samples sequentially identified with EEI and the updated cokrigings are shown in Fig. 11b–c. From Fig. 11b, it is observed that with the evolution of sequential optimization, the accuracy of the cokriging is clearly improved, with uncertainty clearly reduced. Meanwhile, as shown in Fig. 11c, many of the added samples are close to the optimum (indicated by star). The contour map of the final cokriging model is illustrated in Fig. 11d, from which it is also found that with the evolution of the sequential optimization, the added samples grow closer to the optimum, which is of great help to finding the optimum.

Fig. 11

Initial and updated cokriging models (example 3)

The optimal solutions and the cost are listed in Table 8, from which it is found that the optimal design variables and objective function obtained by the three approaches are all very close to the real optimal solutions, while the proposed sequential optimization method is clearly more efficient than the other two methods.

Table 8 Optimal solution and computational cost of three approaches (example 3)

5 Application to drag minimization of the NACA 0012 airfoil

The proposed sequential optimization method is applied to a benchmark aerodynamic design problem simply based on the AIAA aerodynamic design optimization discussion group (Ren et al. 2016), which is a viscous case. It aims at maximizing the lift-to-drag radio L/D of the modified NACA 0012 airfoil section at a free-stream Mach number of M_∝ = 0.8 and an angle of attack α = 2.5^∘, subject to the thickness constraint. The optimization problem is stated as

$$ {\displaystyle \begin{array}{l}\underset{\mathbf{1}\le \mathbf{x}\le \mathbf{u}}{\max }L\left(\mathbf{x}\right)/D\left(\mathbf{x}\right)\\ {}s.t.z{\left(\mathbf{x}\right)}_{\mathrm{max}}\ge {z}_{\mathrm{max}\mathrm{baseline}}\end{array}} $$

(36)

where x is the vector of design variables, depicted in detail below; z(x)_max is the airfoil maximum thickness and z_maxbaseline (z_maxbaseline = 0.12) is the maximum thickness of the original baseline airfoil.

In this work, the B-spline curve (Farin 1993) with 10 control points is employed for the shape parameterization, where the horizontal locations of the 10 control points are fixed as l = [0.1 0.3 0.5 0.7 0.9 0.9 0.7 0.5 0.3 0.1] and the vertical locations are free to move, as shown in Fig. 12. The original airfoil is considered as the baseline with the vertical locations of the 10 control points as z_baseline = [0.04698 0.06000 0.05216 0.03667 0.01450–0.01450 -0.03667 -0.05216 -0.06000 -0.04698]. The vertical locations of the 10 control points are considered as design variables x = [x₁,...,x₁₀] = [z₁,...,z₁₀].

Fig. 12

B-spine parameterization for the airfoil

CFD is employed for aerodynamic analysis and a mesh with size 512 × 512 is generated using the integrated computer engineering and manufacturing code for CFD in the Ansys software as shown in Fig. 13. The mesh density is controlled by both the numbers of cells on and normal to the airfoil surface. It should be noted that the density of the mesh significantly impacts the simulation time cost and the accuracy of CFD analysis result. As shown in Table 9, when the mesh density is increased from mesh D to mesh E, the result of L/D does not change clearly. So for this application example, CFD with mesh D is considered as the highest-fidelity model y³(x), CFD with mesh C as the intermediate-fidelity model y²(x), and CFD with mesh B as the lowest-fidelity model y¹(x).

Fig. 13

Views of the airfoil with the mesh D

Table 9 Grid density convergence study for the NACA0012 airfoil

Cokriging-M, cokriging-H and kriging are all employed to solve this optimization problem in (36). Furthermore, the optimization is also conducted directly on the CFD simulation model with mesh D (i.e. the highest-fidelity model) without employing any metamodel technique (denoted as direct), to verify the accuracy and effectiveness of the proposed cokriging-M. For cokriging-M, cokriging-H, kriging and direct, the genetic algorithm is used for searching the optima. For this drag minimization engineering problem, it is a practical problem and thus the models with different fidelities yield clearly different computational time (see Table 9). For this reason, C is directly set as the computational time of a single model evaluation for each model. Based on Table 9, it is obtained that the cost for y³, y² and y¹ is C³ = 324.5 (s), C² = 152 (s) and C¹ = 68.5 (s). For cokriging-M and cokriging-H, n₃ = 20, n₂ = 40, and n₁ = 50 sample points are respectively generated by LHS to run the three selected multi-fidelity CFD models for initial cokriging modeling; meanwhile, for kriging, n₃ = 20 high fidelity samples are generated by LHS to construct the initial model.

The results are shown in Table 10, including the optimal design variable x_opt, its objective function L/D_opt and constraint z(x_opt)_max, as well as the computational cost. From Table 10, it is found that x_opt and L/D_opt obtained by the three approaches are all very close to those generated by direct; while generally the results of proposed cokriging-M are slightly closer to that of direct yielding smaller errors, and are more efficient than the other two methods. In the optimization process, direct requires 907 highest-fidelity model evaluations, while cokriging-M just needs 46 along with 53 intermediate-fidelity model evaluations and 74 low-fidelity ones, with much less total computational cost (468) compared to that of direct (4905). L/D of the airfoil obtained by cokriging-M is clearly improved after optimization compared to the original one. These results further demonstrate the effectiveness of the cokriging based optimization method proposed in this paper.

Table 10 Comparative results of the three approaches

The airfoil curves after optimization by the proposed cokriging-M method and other approaches are shown in Fig. 14, from which it is found that compared to the baseline airfoil, the curvature and thickness of leading edge of the upper surface obtained by cokriging-M are both reduced, resulting the increase of the lift. Meanwhile, it is observed that the location of the maximum thickness of the airfoil moves backwards (baseline: l = 0.3; optimized: l = 0.37), which can make the turbulent transition delayed, and then reduce the drag. Therefore, the lift-to-drag ratio obtained by the proposed cokriging-M is increased ultimately.

Fig. 14

The airfoil curve after optimization

In addition, Fig. 15 shows the static pressure contours. It is found that the static pressure of the upper surface optimized by cokriging-M is smaller than that of the baseline airfoil (the area in blue is larger for cokriging-M); while the static pressure is smaller for the lower surface (the area in green is larger for cokriging-M), which means that the lift of the optimized airfoil by cokriging-M is increased. In Fig. 16, the pressure coefficient distributions from cokriging-M and baseline are also shown, from which it is noticed that the pressure coefficient for the upper surface is reduced after optimization; meanwhile the pressure coefficient for the lower surface is increased, resulting in increased pressure differentials, i.e. increased lift. The results in Figs. 15 and 16 show great agreements on the optimal lift coefficient obtained by the proposed method, which is increased from 0.34922 (baseline) to 0.492546 (optimized). Fig. 17 illustrates the wall shear stress of the upper and lower surfaces, where the wall shear stress optimized by cokriging-M is generally smaller than that of the baseline. Since the viscous drag force is the integration of the wall shear stress, the drag is clearly reduced after optimization with cokriging-M, exhibiting great agreement to the obtained optimal drag coefficient 0.033991 that is clearly reduced compared to the baseline 0.040307.

Fig. 15

Static pressure contours from baseline and cokriging-M

Fig. 16

Pressure coefficient distribution from baseline and cokriging-M

Fig. 17

Wall shear stress of cokriging-M and baseline

6 Conclusions

In this paper, a cokriging based sequential optimization method is proposed. With the proposed approach, the covariance among data from all the multi-fidelity models is fully utilized in estimating the hyper-parameter through establishing a unified maximum likelihood function to improve the accuracy of cokriging modeling. Moreover, an extended expected improvement sequential sampling criterion considering the sample cluster issue is developed to more reasonably identify the location and fidelity level of the next response evaluation with reduced computational cost. Through comparative studies, it is noticed that the proposed method can make more accurate cokriging response prediction than the existing popular multi-level cokriging modeling approaches due to the consideration of the full correlation of all the data, which however requires longer computational time of modeling. Meanwhile, it is more computationally efficient compared to some existing sequential optimization methods. The effectiveness and advantage of the proposed method are further demonstrated using an AIAA benchmark aerodynamic optimization problem.