1 Introduction

Bayesian optimization is a powerful global optimization method for solving expensive black-box problems (Greenhill et al. 2020; Shahriari et al. 2015), especially when the objective function is non-convex and expensive to explore. Compared with other black-box optimization algorithms, such as genetic algorithm (GA) (Holland 1975) and particle swarm optimization algorithm (PSO) (Kennedy and Eberhart 1995), Bayesian optimization is a surrogate model-based method, which enables to search the global optimum with much less number of expensive evaluation points. The surrogate model and the acquisition function are the two cores of Bayesian optimization. The surrogate model providing a basic model hypothesis of the system is constructed and updated iteratively. The most popular surrogate model by far is the Gaussian Process (GP) model(Santner et al. 2018), thus Bayesian optimization with GP model is also often referred to as sequential Kriging optimization (SKO) (Huang et al. 2006a) and efficient global optimization (EGO). The acquisition function guides the selection rule of the next sampling point. Under a GP model, the commonly used acquisition functions include expected improvement method (EI) (Jones et al. 1998), probability improvement method (PI) (Jones 2001), upper confidence bound method (UCB) (Srinivas et al. 2018), and knowledge gradient method (Frazier et al. 2008). Among them, EI is the most popular method due to its closed-form acquisition function. The core idea of EI is that if a certain point can bring the greatest expected improvement to the current best point, it will be selected as the next sample point. However, EI is very greedy, it tends to over exploit the fitted GP model, and it is very easy to fall into the local optimum (Qin et al. 2017; Bull 2011). Some recent efforts are developed to remedy the greediness of EI, including Snoek et al. (2012), Chen et al. (2017), and so on. But such methods diminish a key advantage of EI: efficient queries via a closed-form criterion. Chen et al. (2020) proposed a hierarchical EI (HEI) criterion by modifying the prior distribution and increasing the variance, the method corrects the greediness of EI while preserving a closed-form acquisition function.

Yet, in many practical instances, the evaluation of a real system of interest is too expensive, and one may consider drawing data from surrogate experiment systems with lower cost. For example, the computer simulations can be used to approximate physical experiments; the numerical simulation might involve simplifying the mathematical model of the physical reality, and it can be run at different levels of complexity. We call these systems “low-fidelity systems” (LFMs) and the real systems the “highest-fidelity systems” (HFMs).

Multi-fidelity models (MFMs) combine both HFMs and LFMs in order to achieve the desired accuracy at lower cost, and it attracted much attention from uncertainty quantification or optimization. MFMs involve generally construction of surrogate models by using variable-fidelity data. Fernández-Godino et al. (2016) reviewed a large variety of MFM implementations, and classified it as multi-fidelity surrogate models (MFSMs) and multi-fidelity hierarchical models (MFHMs). The main concept of multi-fidelity surrogate models (MFSMs) is to use an algebraic surrogate model to correct the LFMs using HFMs. Four main correction methods are space mapping, multiplicative correction, additive correction, and comprehensive correction. The key idea of space mapping is the generation of an appropriate transformation of the vector of fine model parameters \({{\textbf{x}}_{{\textrm{HF}}}}\) to the vector of coarse model parameters \({{\textbf{x}}_{{\textrm{LF}}}}\), that is \({{\textbf{x}}_{{\textrm{LF}}}} = F({{\textbf{x}}_{{\textrm{HF}}}})\), and this technique allows the vectors \({{\textbf{x}}_{{\textrm{HF}}}}\) and \({{\textbf{x}}_{{\textrm{LF}}}}\) to have different dimensions. The latter three methods can be uniformly described as \(\hat{y}_{\textrm{HF}}(\textbf{x}) = \rho ({\textbf{x}}) \cdot {y_{{\textrm{LF}}}}({\textbf{x}}) + \delta ({\textbf{x}})\), the differences among those methods are the treatment of \(\rho ({\textbf{x}})\) and \(\delta ({\textbf{x}})\). When multiple fidelity levels are involved, Loïc et al. (2020) reviewed the fusion frameworks based on Gaussian Process (GP) and classified them into four types: linear model of coregionalization (LMC), classical auto-regressive (AR1), nonlinear auto-regressive multi-fidelity Gaussian process (NARFGP), and multi-fidelity Deep Gaussian Process (MF-DGP). AR1 model is widely used in engineering design field, and the first Co-Kriging model developed by Kennedy and O’Hagan (2000) for multi-fidelity computer experiments is just based on this framework. The Co-Kriging method assumed that the covariance structure of the observed data has Markov properties and the relationship between adjacent level of fidelity has an autoregression structure. It provides a closed form of prediction uncertainty in addition to its predictive ability. Most development in the literature were within Kennedy and O’Hagan’s framework, including Higdon et al. (2004), Reese et al. (2004), Qian and Wu (2008), Le Gratiet and Garnier (2014), and Le Gratiet (2013). Besides, Han and Stefan (2012) proposed the hierarchical Kriging, in the hierarchical Kriging model, the low-fidelity Kriging model is directly used as the trend of the multi-fidelity model to avoid nested sample points. Tuo et al. (2013) proposed a class of non-stationary Gaussian Process models to link the output from different fidelity levels.

The sequential sampling strategy of multiple fidelity data has also received great interest for the purpose of constructing a sufficiently global accurate metamodel (Xiong et al. 2009; Jin et al. 2002; Le Gratiet and Cannamela 2015) or for optimization. This article focuses on the latter. Currently, the multi-fidelity Bayesian optimization still mainly focused on the expansion of EI criterion, PI criterion, and UCB criterion. In the early days, Xiong et al. (2008) applied the confidence boundary as the acquisition function of the bi-fidelity model in sequence sampling. Xf et al. (2020) proposed a variable-fidelity probability of improvement method. Among the extended methods of EI, Huang et al. (2006b) proposed an augmented EI criterion based on Co-Kriging and called it MFSKO. The method uses the correlation between different fidelities to measure the credibility, and then integrates the correlation and the evaluation cost with the EI acquisition function to determine the location and the fidelity level. As this criterion is based on EI, thus it is unavoidable from the greedy nature of EI and the samples generated may cluster within a certain area and reduce the efficiency of global optimization. He et al. (2017) proposed the EQIE criterion by dividing the EI acquisition function by a cost factor to make the cost within the consideration range of the acquisition function. Kim et al. (2018) used EI acquisition function for the hierarchical kriging model. However, those methods do not take into account the accuracy of the fidelity and the cost issue between different fidelities, thus the lower-fidelity samples are preferred since it is computationally cheaper. Liu et al. (2018) introduced a sample density function into the acquisition function proposed by Huang et al. and proposed an enhanced Co-Kriging based sequential optimization method to reduce the computational cost. Zhang et al. (2018) proposed a multi-fidelity global optimization method based on the hierarchical Kriging model to extend the MFEI. Shu et al. (2021) used the hierarchical Kriging method and proposed the expectation to further improve acquisition criteria.

The focus of this paper is on the sequential design for multi-fidelity models. Since compared with other methods, Co-Kriging can better quantify the relationship between different fidelities, and it is better at dealing with problems with random errors, so as to select new sampling points. We select the similar MFSMs of Huang et al. (2006b). The objective of this article is to develop a sequential sampling strategy such that (1) the method should be more efficient for global optimization, as most of the current multi-fidelity sequential optimization methods in literatures tend to the local optimum, the reason is that those method is based on classical EI or PI, and the surrogate model is not globally accurate. In this paper, we will firstly develop the revised expected improvement method to strike the correct balance between accurate global surrogate model and high probability of improvement. The proposed method may adaptively adjust the right tendency between exploration and exploitation during the search process; (2) the method should adaptively add sampling points from different levels of fidelity, thus, an effective criterion is required to evaluate the costs and credibility of candidate points from different levels of fidelity. In this paper, the Kullback–Leibler divergence is used to measure the credibility of a point from system with different fidelities.

The paper is organized as follows: in Sect. 2, the optimization problem and the adopted Co-Kriging method are described, after that the prediction uncertainty of the metamodel is discussed. In Sect. 3, the proposed sequential sampling strategy, especially the PEI criterion is presented and then the convergence property of PEI based method is discussed. In Sect. 4, seven analytical functions are used to compare the proposed method with MFSKO, and then the proposed method is applied to the aerodynamic shape optimization of NACA0012 airfoil. Concluding remarks are given in Sect. 5.

2 Background

2.1 The optimization problem

Suppose there are currently m systems with different fidelities (including the real system) to obtain the estimate of the same real system. We consider the systems as black boxes. Denote the input vector as \({\textbf{x}}\), and the output of those systems in increasing order of fidelity by \({f_1}({\textbf{x}}),{f_2}({\textbf{x}}), \cdots ,{f_m}({\textbf{x}})\). The goal is to optimize the response of the real system within the feasible region \(\chi \subset {R^d}\) and under some constraints, i.e.,

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{{\textbf{x}} \in \chi } {f_m}({\textbf{x}})\\ s.t.\ {g_i}({\textbf{x}}) \le 0,\ i = 1, \cdots ,{N_{\textrm{C}}} \end{array} \end{aligned}$$
(1)

where \({g_i}(\textbf{x})\) denotes the constraint function, whose closed form maybe known or unknown, \(N_{\textrm{C}}\) is the number of constraints. Each system is associated with a cost-per-evaluation denoted by \({C_1},{C_2}, \ldots ,{C_m}\) respectively. And there is an assumption that even a lower-fidelity evaluation is expensive and it is cheaper than a higher-fidelity evaluation, i.e., \({C_1}< {C_2}< \cdots < {C_m}\). Thus it is necessary to generate a surrogate model (for example a Kriging model) in order to quickly determine the next search region or for other purposes.

2.2 Co-Kriging for multiple fidelity systems

Kennedy and O’Hagan (2000) proposed a Co-Kriging model based on autoregressive assumption. In this paper, we adopt the simple version method of Huang et al. (2006b), that is

$$\begin{aligned} {f_l}({\textbf{x}}) = {f_{l - 1}}({\textbf{x}}) + {\delta _l}({\textbf{x}}), l = 2,3 \ldots m \end{aligned}$$
(2)

where \({\delta _l}({\textbf{x}}), l =1,2,3 \ldots m\) is independent of \({f_1}({\textbf{x}}),\ {f_2}({\textbf{x}}), \ldots,\ {f_m}({\textbf{x}})\), and for convenience let \({f_1}(\textbf{x}) = {\delta _1}(\textbf{x})\). \({\delta _l}(\textbf{x})\) is thought of as the “discrepancy” between a lower-fidelity system and the next higher-fidelity system. The reason is that in engineering practice, the results of equivalent experiments will be translated into condition of the real experiment firstly, and then the “discrepancy” between those systems is analyzed and quantified. Quantization of uncertain discrepancy is important and difficult, here we use GP or Kriging model to metamodel the discrepancy. As \({\delta _l}(\textbf{x})\) is usually small in scale as compared to \({f_l}(\textbf{x})\). In Kriging meta-modeling, \({\delta _l}(\textbf{x})\) is described as

$$\begin{aligned} {\delta _l}({\textbf{x}}) = {b_l}{({\textbf{x}})^T}{\beta _l} + {Z_l}({\textbf{x}}) + {\varepsilon _l},l = 2,3 \ldots m \end{aligned}$$
(3)

where \({b_l}{({\textbf{x}})^T}\) and \({\beta _l}\) are the basis function and its coefficient, \({Z_l}(x),\) is a stationary Gaussian Process and \({\varepsilon _l}\) is used to describe random error with variance \(\sigma _{\varepsilon ,l}^2\). In engineering practice, any physics system will have random error, and a computer experiment has no random error. Generally, a comprehensive test will start from computer simulation with lower fidelity and then maybe simulation with higher fidelity, and as followed as physical equivalent test and real test.

The basis functions are often selected as polynomials. In order to simplify the calculation, the constant term is generally selected. \({Z_l}(\textbf{x})\) is often assumed to be a stationary Gaussian Process with zero-mean, and generally taken a Gaussian kernel function. Then the covariance between two point \({\textbf{x}} = ({x_1},{x_2} \cdots {x_d})\) and \({\textbf{x}}' = ({x'_1},{x'_2} \cdots {x'_d})\) in system l is described as

$$\begin{aligned} {\textrm{cov}} [{\delta _l}({\textbf{x}}),{\delta _l}({\textbf{x}}')] = \sigma _{Z,l}^2\exp \left[ - \sum \limits _{j = 1}^d {{\theta _{l,j}}{{({x_j} - {{x'}_j})}^2}} \right] \end{aligned}$$
(4)

where \({\theta _{l,j}}\) is a “roughness” parameter in the kernel function when a higher value implies lower spatial correlation in dimension j, and \(\sigma _{Z,l}^2\) denotes the variance of the stochastic process. Based on equation (4), the covariance between a point \(\textbf{x}\) from system l and another point \({\textbf{x}}'\) from system \(l'\) can be derived as

$$\begin{aligned} {\textrm{cov}} [{f_l}({\textbf{x}}),{f_{l'}}({\textbf{x}}')] = \sum \limits _{i = 1}^{\min (l,l')} {{\textrm{cov}} [{\delta _i}({\textbf{x}}),{\delta _i}({\textbf{x}}')]} \end{aligned}$$
(5)

Assume we got observations \(Y_1,Y_2, \cdots ,Y_n\) from n points \({\textbf {x}}_1,{\textbf {x}}_2, \cdots ,{\textbf {x}}_n\) located in system indexes \(l_1, l_2, \cdots ,l_n,\) respectively. Let \({{\textbf {y}}}^T = [Y_1,Y_2, \cdots ,Y_n]\), and \(\hat{\varvec{\beta }}=[\hat{\beta }_{1},\hat{\beta }_{2}, \cdots ,\hat{\beta }_{m}]^T\), \({{\textbf{h}}_l}({\textbf{x}}) = [{b_1}{({\textbf{x}})^T},{b_2}{({\textbf{x}})^T}, \cdots ,{b_l}{({\textbf{x}})^T},0, \cdots, 0]^{T}\). The best linear prediction (BLP) of \({\mathbf{\beta }}\) and \({f_m}(\textbf{x})\) can be given by

$$\begin{aligned} \hat{\varvec{\beta }}= & {} {({{\textbf{H}}^T}{{\textbf{V}}^{ - 1}}{\textbf{H}})^{-1}}{{\textbf{H}}^T}{{\textbf{V}}^{ - 1}}{\textbf{y}} \end{aligned}$$
(6)
$$\begin{aligned} {\hat{f}_m}({\textbf{x}})= & {} {{\textbf{h}}_m}{({\textbf{x}})^T}\hat{\varvec{\beta }} + {{\textbf{t}}_m}{({\textbf{x}})^T}{{\textbf{V}}^{ - 1}}({\textbf{y}} - {\mathbf{H \hat{\varvec{\beta }}}}) \end{aligned}$$
(7)

where

$$\begin{aligned} {\textbf{H}}= & {} \left[ {\begin{array}{*{20}{c}} {{{\textbf{h}}_{{l_1}}}{{({\textbf{x}})}^T}}\\ {{{\textbf{h}}_{{l_2}}}{{({\textbf{x}})}^T}}\\ \vdots \\ {{{\textbf{h}}_{{l_n}}}{{({\textbf{x}})}^T}} \end{array}} \right] \\ {\textbf{V}}= & {} {[{\textrm{cov}} ({Y_i},{Y_j})]_{1 \le i,j \le n}}\\= & {} {[{\textrm{cov}} ({f_{{l_i}}}({{\textbf{x}}_i}),{f_{{l_j}}}({{\textbf{x}}_j}))]_{1 \le i,j \le n}} + {[\sigma _{\varepsilon ,l}^2{\eta _{ij}}]_{1 \le i,j \le n}}\\ {{\textbf{t}}_l}({\textbf{x}})= & {} {\left[ {{\textrm{cov}} ({f_{{l_1}}}({{\textbf{x}}_1}),{f_l}({\textbf{x}})), \cdots {\textrm{cov}} ({f_{{l_n}}}({x_n}),{f_l}({\textbf{x}}))} \right] ^T} \end{aligned}$$

Let \(f_l^p(\textbf{x})\) be the posterior distribution of the system response of input \(\textbf{x}\) from the real system, thus, the posterior mean of \(f_l^p(\textbf{x})\) is equal to the BLP predictor in (7). The posterior covariance between different points from different fidelities is

$$\begin{aligned} \begin{aligned}&{\textrm{cov}} \left[ {f_l^p({\textbf{x}}),f_{l'}^p({\textbf{x}}')} \right] = {\textrm{cov}} \left[ {{f_l}({\textbf{x}}),{f_{l'}}({\textbf{x}}')} \right] \\&\quad -\left[ {{{\textbf{h}}_l}{{({\textbf{x}})}^T},{{\textbf{t}}_l}{{({\textbf{x}})}^T}} \right] {\left[ {\begin{array}{*{20}{c}} {\textbf{0}}&{}{{{\textbf{H}}^T}}\\ {\textbf{H}}&{}{\textbf{V}} \end{array}} \right] ^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{{\textbf{h}}_{l'}}({\textbf{x}}')}\\ {{{\textbf{t}}_{l'}}({\textbf{x}}')} \end{array}} \right] \end{aligned} \end{aligned}$$
(8)

when \(l = l'\) and \(\textbf{x} = \textbf{x}'\), then (8) is an estimate of the variance of a certain estimated point.

2.3 Estimation of the hyper-parameters

As to estimate the hyper-parameters \({\theta _{l,j}}\) and \(\sigma _{Z,l}^2\), in order to reduce the amount of calculation, it is acceptable to estimate the hyper-parameters for each individual system, and once the hyper-parameters of the low-fidelity system are estimated, we assume they are fixed and the data from systems above are ignored.

For instances, when there are only two fidelities, and the basis function is a constant, then \({h_l}({\textbf{x}}) = [1,0]\) or \({h_l}({\textbf{x}}) = [1,1]\). Let \({A_t}({x_i},{x_j}) = \exp \{- {b_t}{({x_i} - {x_j})^T}({x_i} - {x_j})\}\), and \({A_1}({{\textbf{D}}_1})\) denote the covariance matrix of the lower-fidelity sampling point, then \({\theta _{l,j}}\) is referred to as \({b_1}\) and \(\sigma _{Z,l}^2\) is referred to as \(\sigma _1^2\), \({b_1}\) and \(\sigma _1^2\) can be estimated by minimizing the following negative log likelihood function

$$\begin{aligned} \begin{aligned}&\log |{{{\textbf{A}}_1}({{\textbf{D}}_1})}|+ {n_1}\log \sigma _1^2\\&\quad + {({{\textbf{y}}_1} - {{\hat{\mathbf{\beta } }}_1}{{\textbf{1}}_{n_1}})^T}{\left\{ {\sigma _1^2{{\textbf{A}}_1}({{\textbf{D}}_1})} \right\} ^{ - 1}}({{\textbf{y}}_1} - {{\hat{\mathbf{\beta }}}_1}{{\textbf{1}}_{n_1}}) \end{aligned} \end{aligned}$$
(9)

For higher-fidelity system with \({A_2}({{\textbf{D}}_2})\) as the covariance matrix, we define \({{\textbf{d}}_2} = {y_2} - {f_1}({{\textbf {D}}_2})\), where \({f_1}({{\textbf{D}}_2})\) denotes the output from \({f_1}( \cdot )\) at points in \({{\textbf{D}}_2}\). Then \({b_2},\sigma _2^2\) are estimated by minimizing the following function

$$\begin{aligned} \begin{aligned}&\log |{{{\textbf{A}}_2}({{\textbf{D}}_2})}|+ {n_2}\log \sigma _2^2 \\&\quad + {({{\textbf{d}}_2} - {{\hat{\mathbf{\beta }}}_2}{{\textbf{1}}_{n_2}})^T}{\left\{ {\sigma _2^2{{\textbf{A}}_2}({{\textbf{D}}_2})} \right\} ^{ - 1}}({{\textbf{d}}_2} - {{\hat{\mathbf{\beta }}}_2}{{\textbf{1}}_{n_2}}) \end{aligned} \end{aligned}$$
(10)

For more than two levels of fidelity, the hyper-parameters are estimated sequentially, and as the input space of the latter layer is smaller, it is much easier to solve.

2.4 Discussion about the prediction uncertainty

Let \({s_m}({\textbf{x}})\) be the standard deviation of the estimation, which can be calculated by the following formula

$$\begin{aligned} {s_m}({\textbf{x}}) = \sqrt{{\textrm{cov}}[f_l^p({\textbf{x}}),f_l^p({\textbf{x}})]} \end{aligned}$$
(11)

Based on equation (8) and (11), the posterior mean and variance of \(f_l^p({\textbf{x}})\) are obtained. As we all know, the posterior variance is also used as a measure of prediction uncertainty, the smaller the variance, the narrower the confidence interval. A domain with high certainty means less opportunity to be explored in the EI sampling criterion. However, as the hyper-parameters of the Gaussian Process are estimated from limited numbers of observations by maximum likelihood estimation, when the observations do not carry enough information about f, the estimation of hyper-parameters will lead to very disappointing results. Thus, as the variance of the \(f_l^p({\textbf{x}})\) is estimated by limited numbers of observations and we have enough reasons to make a proportional revise of the variance and make

$$\begin{aligned} s_m^P({\textbf{x}}) = {s_m}({\textbf{x}}) \cdot \lambda , \lambda >0 \end{aligned}$$
(12)

That is to say, if \(\lambda > 1\), the confidence interval of the estimated value in the actual problem should be larger than the confidence interval estimated by the surrogate model.

3 The proposed approach

In this part, we explain in detail the multi-fidelity sequential optimization method we proposed.

3.1 Multi-fidelity sequential optimization framework

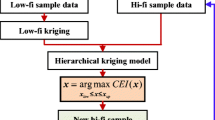
The framework of the proposed multi-fidelity sequential optimization employing Co-Kriging in conjunction with the proposed PEI criterion is illustrated in Fig. 1.

Fig. 1
figure 1

Sequential optimization framework of the proposed method

Full size image

The step-by-step description of the proposed method is as follows:

Step 1 Initial design. Compared with the traditional method, the proposed method has a greater error tolerance rate in experimental design. In this paper, Latin hypercube design(Michael 1987) is adopted in low or lower fidelity, the high-fidelity points are not needed to be the subset of low fidelity. But the optimal Latin hypercube design method is chosen in high or higher fidelity to ensure a uniformly distributed test point design combination.

Nevertheless, it is often difficult to choose a suitable initial design in practice, especially the sample size for different fidelities, the initial design of multi-fidelity is still an area worthy of further research.

Step 2 Construct the Co-Kriging model for multiple fidelity systems.

Here, we select the method illustrated in Sect. 2.2 to construct the Kriging meta-models for multiple fidelity systems.

Step 3 Sequential sampling strategy.

In the following paper, we will propose a new sequential sampling criterion called \({\textrm{PEI}}({\textbf{x}},l)\), and the location and fidelity level of the next evaluation are selected by maximizing \({\textrm{PEI}}({\textbf{x}},l)\), that is

$$\begin{aligned} \left( {{{\textbf{x}}_{n + 1}},{l_{n + 1}}} \right) = \mathop {\arg \max }\limits _{{\textbf{x}},l} {\textrm{PEI}}({\textbf{x}},l) \end{aligned}$$
(13)

Step 4 Stopping criterion.

In the setting of the stopping criterion, we believe that the stopping criterion needs to be adapted to the magnitude of the data.

$$\begin{aligned} {\Delta _s} = \max ({Y_1},{Y_2}, \cdots,{Y_n}) - \min ({Y_1},{Y_2}, \cdots,{Y_n}) \end{aligned}$$
(14)

The optimization process stops when

$$\begin{aligned} \mathop {\max }\limits _{{\textbf{x}},l} {\textrm{PEI}}({\textbf{x}},l) < \alpha \cdot {\Delta _s} \end{aligned}$$
(15)

In addition, it is required that the point that meets the stopping criterion must be on the highest fidelity. If the point that meets the stopping criterion is not the point on the highest fidelity, the highest-fidelity point closest to the stopping criterion is taken as the optimal value. Generally, we use (15) as the stop criterion. However, in Sect. 4.2, in order to compare the efficiency of the proposed method and MFSKO, we also use iteration numbers as the stopping criterion.

3.2 The proposed sequential sampling strategy

The standard EGO method employs an expected improvement (EI) function to select a new sample point in single-fidelity optimization. Huang et al. (2006b) adopted an augmented EI function to select the location and fidelity level of the next evaluation. However, both methods are based on classical EI function, and are unavoidable to the greedy drawback of EI. And in fact, we found that the samples generated by augmented EI function tend to stuck in local optima and fail to converge to a global optimum. To address this, we propose a new acquisition function called Proportional EI (PEI), which encourages exploration by increasing model uncertainty.

Proportional EI (PEI) acquisition function is defined as follows to determine the location and the fidelity level of the next sample point.

$$\begin{aligned} {\textrm{PEI}}({\textbf{x}},l) = E{I_{\textrm{P}}}({\textbf{x}}) \cdot {\alpha _1}({\textbf{x}},l) \cdot {\alpha _2}(l) \cdot {\alpha _3}({\textbf{x}},l) \cdot {\alpha _4}({\textbf{x}},l) \end{aligned}$$
(16)

As shown in equation (16), PEI is an acquisition function composed of five items: revised expected improvement, Kullback–Leibler divergence-based model difference, ratio of cost, random errors, and constraint handling item. The next five subsections will discuss these five items, respectively. Compared with Huang’s (2006b) augmented EI function, the PEI method is improved from three espects. Firstly, in order to avoid the greediness of EI, revised expected improvement function \(E{I_{\textrm{P}}}({\textbf{x}})\) is proposed, where the proportional factor is used to balance exploration and exploitation. Secondly, to measure differences in posterior distribution between system m and system l, Kullback–Leibler divergence-based model difference \({\alpha _1}({\textbf{x}},l)\) is used to replace the correlation. Besides, we add a new term \({\alpha _4}({\textbf{x}},l)\) to handle constraints, so that the PEI method can be applied to optimization problem with unknown constraint scenarios. As for \({\alpha _2}(l)\) and \({\alpha _3}({\textbf{x}},l)\), they are the same as described in augmented EI function.

3.2.1 The revised expected improvement

In (16), what we concern is the expected improvement of the highest fidelity and the expectation can be calculated as follows:

$$\begin{aligned} \begin{aligned} E{I_{\textrm{P}}}({\textbf{x}})&= \left( {{{\hat{f}}_m}({{\textbf{x}}^*}) - {{\hat{f}}_m}({\textbf{x}})} \right) \Phi \left( {\frac{{{{\hat{f}}_m}({{\textbf{x}}^*}) - {{\hat{f}}_m}({\textbf{x}})}}{{s_m^P({\textbf{x}})}}} \right) \\ {}&\quad + s_m^P({\textbf{x}}) \phi \left( {\frac{{{{\hat{f}}_m}({{\textbf{x}}^*}) - {{\hat{f}}_m}({\textbf{x}})}}{{s_m^P({\textbf{x}})}}} \right) \end{aligned} \end{aligned}$$
(17)

where \(\phi\) and \(\Phi\) are the standard normal probability density and cumulative distribution function, respectively. \({{\textbf{x}}^*}\) is the current optimal solution, and \({{\textbf{x}}^*} = \mathop {\arg }\limits _{x \in \{ {{\textbf{x}}_1},{{\textbf{x}}_2}, \cdots {{\textbf{x}}_n}\} } \max [u({\textbf{x}})]\), and \(u({\textbf{x}})\) is called utility function; in our method, we make \(u({\textbf{x}}) =- {\hat{f}_m}({\textbf{x}}) - {s_m}({\textbf{x}})\).

In (17), according to (12), the measure of uncertainty changed. In Appendix A, we will prove that for a given index \(\lambda\), there exists a corresponding \(\gamma\) called proportional factor satisfying

$$\begin{aligned} \begin{aligned} E{I_{\textrm{P}}}({\textbf{x}})&= \underbrace{\left( {{{\hat{f}}_m}({{\textbf{x}}^*}) - {{\hat{f}}_m}({\textbf{x}})} \right) \Phi \left( {\frac{{{{\hat{f}}_m}({{\textbf{x}}^*}) - {{\hat{f}}_m}({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) }_{\exp {\textrm{loi}}tation} \\ {}&\quad + \underbrace{\gamma {s_m}({\textbf{x}}) \phi \left( {\frac{{{{\hat{f}}_m}({{\textbf{x}}^*}) - {{\hat{f}}_m}({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) }_{\exp loration} \end{aligned} \end{aligned}$$
(18)

And the monotonous trend of \(\gamma\) is consistent to \(\lambda\). In the following section, we will further discuss the influence of the value of \(\gamma\) to the searching process and will adaptively adjust the value of \(\gamma\) by the sample density.

3.2.2 Kullback–Leibler divergence-based model difference

In (16), \({\alpha _1}({\textbf{x}},l)\) is the measure of the credibility or information contribution of a point from system with different fidelities, so as to control the number of low-fidelity samples. In many relevant literatures, it was computed by the correlation between the posterior estimate of point \({\textbf{x}}\) from system l to the posterior estimate of point \({\textbf{x}}\) from system m, see Huang et al. (2006b), that is

$$\begin{aligned} {\alpha _1}({\textbf{x}},l) = corr\left[ {f_l^p({\textbf{x}}),f_m^p({\textbf{x}})} \right] \end{aligned}$$

But in our test, we found that as the point is very close to the observed point, the denominator is close to 0, and the values of points far away from the samples are nearly the same. Our idea is to use the posterior distribution difference between system l and system m located at \({\textbf{x}}\) to measure the credibility or the information contribution. That is if the posterior distribution of system l is the same as system m at location \({\textbf{x}}\), then the contributions should be the same. The larger the posterior distribution difference, the lower the contribution of the point \(({\textbf{x}},l)\). There are many ways to measure differences in distribution, such as the Kullback–Leibler (KL) divergence (Gultekin and Paisley 2017), Jensen-Shannon, Wasserstein distance, and so on. Here, we use KL divergence to quantify the posterior distribution differences. Given the probability density function p and q, as the KL divergence is asymmetric, the symmetrized KL divergence is defined as

$$\begin{aligned} {D_{\textrm{KL}}}(p,q) = \frac{1}{2}{D_{\textrm{KL}}}(p|q ) + \frac{1}{2}{D_{\textrm{KL}}}(q|p) \end{aligned}$$
(19)

where \({D_{\textrm{KL}}}(p|q) = \int \limits _{ - \infty }^{ + \infty } {p({\textbf{x}}) \cdot \log } \frac{{p({\textbf{x}})}}{{q({\textbf{x}})}}d{\textbf{x}}\). Specializing to normal distribution \(p \sim N\left( {{{\hat{f}}_m}({\textbf{x}}),{s_m}({\textbf{x}})} \right)\) and \(q \sim N\left( {{{\hat{f}}_l}({\textbf{x}}),{s_l}({\textbf{x}})} \right)\), then the KL divergence is given by

$$\begin{aligned} {D_{\textrm{KL}}}(p,q) = \ln \frac{{{s_m}({\textbf{x}})}}{{{s_l}({\textbf{x}})}} + \frac{{{{({{\hat{f}}_m}({\textbf{x}}) - {{\hat{f}}_l}({\textbf{x}}))}^2} + s_l^2({\textbf{x}})}}{{2s_m^2({\textbf{x}})}} - \frac{1}{2} \end{aligned}$$
(20)

The smaller the KL divergence is, the closer the distribution is. KL divergence is equal to 0 if and only if they are identically distributed. Then we define

$$\begin{aligned} {\alpha _1}({\textbf{x}},l) = \frac{1}{{1 + \eta {{\left( {{D_{\textrm{KL}}}(p,q)} \right) }^\kappa }}} \end{aligned}$$
(21)

in which \(\eta\) and \(\kappa\) are parameters that are used to control the change rate. Obviously, as \({D_{\textrm{KL}}}(p,q) \ge 0\), \(0 < {\alpha _1}({\textbf{x}},l) \le 1\). If the distribution of system l is exactly the same as system m at location \({\textbf{x}}\), then it is regarded as equal to the real system. If \(l = m\), for any \({\textbf{x}}\), \({\alpha _1}({\textbf{x}},m) = 1\), it stands that the point from the highest-fidelity system owns the highest credibility. Generally speaking, the credibility of the surrogate system will gradually decrease with the increase of the distribution difference, which indicates that the greater the difference between the distribution of the surrogate system and the distribution of the real system, the smaller the chance the point located to that surrogate system, this is intuitive. Specially, if a point \(({\textbf{x}},l)\) or \(({\textbf{x}},m)\) has been evaluated, \({s_l}({\textbf{x}}) = 0\), or \({s_m}({\textbf{x}}) = 0\), we directly define \({\alpha _1}({\textbf{x}},l) = 0\), that is to say that the point \(({\textbf{x}},l)\) won’t be select again. That is consistent to the common sense, if observation is done at a certain location in any higher fidelity, adding new lower-fidelity observation at the same location contributes very few to the improvement of PEI. Thus, for any \({\textbf{x}}\), \({\alpha _1}({\textbf{x}},l) \in \left[ {0,1} \right]\). The values of \(\eta\) and \(\kappa\) together with \({\alpha _2}(l)\) will decide the level index of the next point, and we should decide their values according to actual situation.

3.2.3 Ratio of cost

In (16), \({\alpha _2}(l)\) is used to control the cost of evaluations. If the cost of evaluation from system l is represented by \({C_l}\), then take \({\alpha _2}(l) = \frac{{{C_m}}}{{{C_l}}}\). If \(l = m\), \({\alpha _2}(l) = 1\). If \(l \ne m\), \({\alpha _2}(l) > 1\), thus the inclusion of \({\alpha _2}(l)\) tends to select a point from the cheapest system.

If there are no random errors and do not consider the constraints, \({\alpha _1}({\textbf{x}},l)\) and \({\alpha _2}(l)\) together decide the fidelity level. If at all locations \({\textbf{x}},\) we have \({\alpha _1}({\textbf{x}},l)*{\alpha _2}(l) < 1 = {\alpha _1}({\textbf{x}},m)*{\alpha _2}(m)\), then all points are selected in the highest fidelity. If at all locations \({\textbf{x}}\), we have \({\alpha _1}({\textbf{x}},l)*{\alpha _2}(l) > 1 = {\alpha _1}({\textbf{x}},m)*{\alpha _2}(m)\), then no point will be selected from the highest fidelity. That is not what we want, as the cost factor \({\alpha _2}(l)\) is often known to us. For the case where the algorithm time is complex and unknown, we need to run the computer code with different fidelities to get an approximate estimate of the cost. In (16), we should set suitable values of \(\eta\) and \(\kappa\) to make \(\forall {\textbf{x}},l\) satisfying \({\alpha _1}({\textbf{x}},l)*{\alpha _2}(l) \in [i,1] \cup [1,j]\).

3.2.4 Consideration of random errors

In (16), the existence of \({\alpha _3}({\textbf{x}},l)\) is to adjust \(E{I_{\textrm{P}}}({\textbf{x}})\) if the output of system l contains random errors, as more replicates are added, the posterior standard deviation will reduce. Like the work of Huang et al. (2006b), the following penalization function is introduced to limit replications.

$$\begin{aligned} {\alpha _3}({\textbf{x}},l) = 1 - \frac{{{\sigma _{\varepsilon ,l}}}}{{\sqrt{s_l^2({\textbf{x}}) + \sigma _{\varepsilon ,l}^2} }} \end{aligned}$$
(22)

And if the variance of the random error is 0, then \({\alpha _3}({\textbf{x}},l) = 1\).

3.2.5 Constraint handling

The constraints in engineering optimization can be divided into two categories: known constraints and unknown constraints. The former is easy, a penalty function approach is used to handle the known constraints. The later is much more complex, and after constructing a Kriging model, the prediction of \(g({\textbf{x}})\) obeys a normal distribution \(g({\textbf{x}}) \sim N\left( {\hat{g}({\textbf{x}}),s_g^2({\textbf{x}})} \right)\), then the probability of satisfying the constraint is

$$\begin{aligned} p\left[ {g({\textbf{x}}) \le 0} \right] = \Phi \left( {\frac{{ - \hat{g}({\textbf{x}})}}{{s_g^2({\textbf{x}})}}} \right) \end{aligned}$$
(23)

Thus, in (16), \({\alpha _4}({\textbf{x}},l)\) can be defined as

$$\begin{aligned} \begin{aligned} {\alpha _4}({\textbf{x}},l)&= p\left[ {g({\textbf{x}}) \le 0} \right] \\&= \left\{ {\begin{array}{*{20}{c}} 1,\ \textrm{if}\, \textrm{known }\ g({\textbf{x}}) \le 0\\ 0,\ \textrm{if}\,\textrm{known}\, g({\textbf{x}}) > {\textrm{0}}\\ \Phi \left( {\frac{{ - \hat{g}({\textbf{x}})}}{{s_g^2({\textbf{x}})}}} \right) ,\ \textrm{if}\,\textrm{unknown}\, g({\textbf{x}}) \end{array}} \right. \end{aligned} \end{aligned}$$
(24)

3.3 Further discussion about the revised expected improvement criterion

In this part, we will further discuss the value of \(\gamma\) to the optimum and to the iterative numbers of \({\textrm{PEI}}({\textbf{x}},l)\).

3.3.1 The impact of \(\gamma\) to the optimum

In (18), we can see that EI is a tradeoff between exploitation (optimization of the predictor) and exploration (seeking areas of maximum uncertainty), while PEI introduces a coefficient \(\gamma\) to adjust the trend to exploitation or exploration. In particular, we will record \(E{I_{\textrm{P}}}({\textbf{x}})\) as \(E{I_{\textrm{P}}}({\textbf{x}},\gamma )\) in the following section. Clearly, if \(\gamma = 1\), PEI is just the standard EI.

If \(\gamma > 1\), like the work of Johns et al. (1998), one can get the partial derivative of \(E{I_{\textrm{P}}}({\textbf{x}},\gamma )\) with respect to \({s_m}\), here recorded \(I({\textbf{x}}) = {\hat{f}_m}({{\textbf{x}}^*}) - {\hat{f}_m}({\textbf{x}})\), as \(\phi\) and \(\Phi\) are the standard normal probability density and cumulative distribution function, the result is

$$\begin{aligned} \frac{{\partial E{I_{\textrm{P}}}({\textbf{x}},\gamma )}}{{\partial {s_m}({\textbf{x}})}}= & {} - {\left( {\frac{{I({\textbf{x}})}}{{{s_m}(x)}}} \right) ^2}\phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}(x)}}} \right) + \gamma \phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \nonumber \\{} & {} - \gamma \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \phi '\left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \nonumber \\= & {} - {\left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) ^2}\phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) + \gamma \phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \nonumber \\{} & {} + \gamma {\left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) ^2}\phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \nonumber \\= & {} \left[ {\gamma + \left( {\gamma - 1} \right) {{(\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}})}^2}} \right] \cdot \phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \end{aligned}$$
(25)

If \(\gamma > 1\), then \(\frac{{\partial E{I_{\textrm{P}}}({\textbf{x}},\gamma )}}{{\partial {s_m}({\textbf{x}})}} > \phi (\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}) = \frac{{\partial EI({\textbf{x}})}}{{\partial {s_m}({\textbf{x}})}}\). That is to say as \(\gamma\) increases, under the same uncertainty, the improvement of \(E{I_{\textrm{P}}}({\textbf{x}},\gamma )\) is larger, \(\gamma > 1\) will yield to explore more, and can help the multi-fidelity acquisition function jump out of the local optimum and tend to choose more “exploratory” points, which helps preventing falling into a local optimum while \(\gamma < 1\) will yield to exploit more.

3.3.2 The impact of \(\gamma\) to the numbers of iterations

Obviously, any \(\gamma > 1\) weakens the influence of \(\left[ {{{\hat{f}}_m}({{\textbf{x}}^*})-{{\hat{f}}_m}({\textbf{x}})} \right]\) on \(PEI({\textbf{x}})\), while \(I({\textbf{x}}) = {\hat{f}_m}({{\textbf{x}}^*}) - {\hat{f}_m}({\textbf{x}}) > 0\) means the improvement of the objective function, itself is positively related to the stopping rule, we prove that when \(\gamma > 1\), the iterative steps will increase. One can get several terms that cancel and then the partial derivative of \(I({\textbf{x}})\) to (18) is

$$\begin{aligned} \frac{{\partial E{I_{\textrm{P}}}({\textbf{x}},\gamma )}}{{\partial I({\textbf{x}})}}= \,& {} \Phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) + \frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}\phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) + \gamma \phi '\left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \nonumber \\=\, & {} \Phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) + (1 - \gamma )\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}\phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \nonumber \\=\, & {} \frac{{\partial EI({\textbf{x}})}}{{\partial I({\textbf{x}})}} + (1 - \gamma )\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}\phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) \end{aligned}$$
(26)

For \(I({\textbf{x}}) = {\hat{f}_m}({{\textbf{x}}^*}) - {\hat{f}_m}({\textbf{x}}) > 0\), then \(\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}\phi \left( {\frac{{I({\textbf{x}})}}{{{s_m}({\textbf{x}})}}} \right) > 0\). Thus, if \(\gamma > 1\), we have \(\frac{{\partial E{I_{\textrm{P}}}({\textbf{x}},\gamma )}}{{\partial I({\textbf{x}})}} < \frac{{\partial EI({\textbf{x}})}}{{\partial I({\textbf{x}})}}\), and as \(\gamma\) increases, \(\frac{{\partial E{I_{\textrm{P}}}({\textbf{x}},\gamma )}}{{\partial I({\textbf{x}})}}\) decreases.

As \(\frac{{\partial EI({\textbf{x}})}}{{\partial I({\textbf{x}})}} \cong \frac{{\Delta EI({\textbf{x}})}}{{\Delta I({\textbf{x}})}}\), thus, for the same \(\Delta I(x)\), \(\Delta E{I_{\textrm{P}}} ({\textbf{x}},\gamma ) < \Delta EI({\textbf{x}})\), and if \({\gamma _1} > {\gamma _2}\), we have \(\Delta E{I_{\textrm{P}}}({\textbf{x}},{\gamma _1}) < \Delta E{I_{\textrm{P}}}({\textbf{x}},{\gamma _2})\). \(E{I_{\textrm{P}}}({\textbf{x}},\gamma )\) with a lager \(\gamma\) improve less can lead to the same improve of \(I({\textbf{x}})\). Assume the real optimum is \({{\textbf{x}}^{**}}\), that is to say gap between \({\hat{f}_m}({{\textbf{x}}^*})\) and \({\hat{f}_m}({{\textbf{x}}^{**}})\) is given. Then as the iterative optimization goes on, according to the iterative stopping criteria, \(E{I_{\textrm{P}}}({\textbf{x}},\gamma )\) will be slow to stop, and the sampling points will cluster.

That is consistent to our experiments, and it was found through experiments that when \(\gamma\) is large enough, the improvement of the results will be indistinctive and the points cluster seriously, and when \(\gamma < 1\), the iterative will stop fast but easy to fall into the local optimum. We suggest select the value of \(\gamma\) between [0.1, 10].

3.3.3 Adaptive adjust of \(\gamma\) by the sample density

A larger \(\gamma\) yield to sample at the location with high uncertainty and contribute well to the modeling accuracy, thus at the initial stage of sampling, which is appropriate to choose a larger value of \(\gamma\), it will avoid early stop of iteration because of low modeling accuracy. However, at the end of the iteration, a larger \(\gamma\) may lead to the clustering of samples and large iteration numbers. As the computational cost is very expensive but the accuracy of the results improved very little, it is not cost-effective. In order to solve that problem, we suggest that the proportional factor \(\gamma\) should be adaptively adjusted during the iteration.

The adaptive criteria can be varied. This paper proposes an adaptive criterion based on the sample density, with “exploitation-exploration-exploitation” as the search mode. We select three levels \({\gamma _1}< {\gamma _2} < {\gamma _3}\). They, respectively, indicate active exploitation, balanced exploration and exploitation, and active exploration. \(\gamma\) will be valued by the following criteria:

(1) When \({\textrm{PEI}}({\textbf{x}},l)\) increase in successive iterations keeps getting smaller, it means that the current exploitation is sufficient. Then we should switch from \({\gamma _1}\) to \({\gamma _2}\) in order to increase the exploratory.

(2) When \(\max {\textrm{PEI}}({\textbf{x}},l) < k\alpha {\Delta _s}\), that means the expected improvement may be very small, we should convert from \({\gamma _2}\) to \({\gamma _3}\), and turn to active exploration. In this paper, we adopt \(k=10,\ {\gamma _1}=0.5,\ {\gamma _2} =1, \ {\gamma _3}=2\).

(3) The expected improvement in successive iterations has been increasing, which means that we have discovered new peaks through increasing exploration. At this time, in order to avoid sampling too densely, we should convert from \({\gamma _3}\) to \({\gamma _1}\) in order to hurry up the iteration process. In this paper, when the number of iterations is 1.5 times of the initial design number, we let \({\gamma _1}=0.5\).

Above all, our method can be summarized in Algorithm 1.

figure a

4 Test cases of analytical functions and application

In this section, the effectiveness of the proposed multi-fidelity sequential optimization method will be verified by test functions and an engineering application example. Obviously, the difference between the optimization result and the real optimum is an important index to measure the quality of the sequential optimization design method. On the other hand, as compared with the complex and time-consuming finite element simulation, the computational amount of sequential optimization algorithm is relatively small, so the evaluation cost (the number of high- and low-fidelity test samples) is also considered here.

4.1 An illustrative example

In this subsection, the proposed multi-fidelity sequential optimization method is illustrated with a one-dimensional method. Firstly, we use a couple of test functions created by (Sasena et al. 2002):

$$\begin{aligned} {f_h}(x)= & {} - \sin (x) - \exp (x/100) + 10, (0< x< 10)\\ {f_l}(x)= & {} - \sin (x) - \exp (x/100) + 10.3 + 0.03 \times {(x - 3)^2}\\{} & {} (0< x < 10) \end{aligned}$$

As Sasena function is also used by Huang et al. (2006b) to explain MFSKO method, here we will draw a comparison between PEI method and MFSKO method.

Fig. 2
figure 2

Search pattern for Sasena function when \(\gamma =1\)

Full size image
Fig. 3
figure 3

Search pattern for Sasena function when \(\gamma =2\)

Full size image

Here, the initial design of the test is six points located at \(x=\{0, 2, 4, 6, 8, 10\}\) in low fidelity, and two points at \(x=\{3.5, 6.5\}\) in high fidelity. Fig. 2 shows the optimization result of the proposed method by letting \(\gamma = 1\), which is similar to Huang’s MFSKO method. We can see that the search scope of MFSKO is only around the left local optimal peak and stop searching after four times iterations. The global optimum of the right peak is not found. Fig. 3 shows the searching result of the proposed method by letting \(\gamma = 2\), the method jumps out of the local optimal, and successfully finds the global optimum. A series of examples listed below will further demonstrate that the proposed PEI method with adaptive value of \(\gamma\) is indeed helpful to explore the global optimum.

The reason for this is that the EI function itself has a tendency to fall into a local optimum, that is the greediness of the EI. So a single-fidelity optimization example is given. We choose the high-fidelity Sasena function above as test function. The initial design is \(x = \{1,4,6,9\}\). EI function and Revised EI with \(\gamma\)=2 are adopted as acquisition functions. As shown in Fig. 4, the EI function itself has a tendency to fall into the local optimum, and this shortcoming can be avoided by Revised EI.

Fig. 4
figure 4

contrastive test to explain the greediness of EI

Full size image
Fig. 5
figure 5

The PEI function of initial design

Full size image

To help understanding each item in equation (16), Fig. 5 displays the breakdown of PEI just after the initial design. \(E{I_p}(x)\) in equation (16) incorporates the prediction mean and the prediction uncertainty, while the proportion between exploitation and exploration is adjusted during the search process, this term is independent of the fidelity level, we can see that the left domain of the searching space is preferred. Here, the value of \({\alpha _1}(x,1)\) is based on the distribution difference of different fidelities, and it measures the credibility of expected improvement when a lower-fidelity evaluation is added. Here, \(\eta\) and \(\kappa\) in equation (21) are set as 0.5 and 1, respectively. As the random error and the constraint are not considered, \({\alpha _3}(x,l) \cdot {\alpha _4}(x,l) = 1\), based on the costs of evaluation, let \({\alpha _2}(1) = 4\) and \({\alpha _2}(2) = 1\). The PEI values of different fidelities are shown in Fig. 5.

Fig. 6
figure 6

The values of \({\alpha _1}(x,l)\) during the 9th–14th iteration

Full size image

Fig. 6 shows the value of \({\alpha _1}(x,1)\) from the 9th to the 14th iteration; according to the figure, the values are very small near the tested points, and after six iterations, the values in the whole design space of lower fidelity are too small to be selected as the next sample points, which is consistent with the expectation of Bayesian optimization that the sample points in the later stage of optimization are all in high fidelity.

4.2 Other numerical tests

In this subsection, a series of test functions from literature will be used to further investigate the properties of the proposed PEI method. Seven tests are conducted as listed in Table 1. The first five test functions are unconstrained, the sixth one is constrained, and the seventh one is a three-fidelity function (Xiao et al. 2002).

Table 1 Test functions
Full size table

4.2.1 Contrast of optimization result

In this subsection, we focus on the optimization results of the test functions. In all of the test, Latin hypercube is used to generate the initial design.

Specially, the search pattern of Case 4 is shown in Fig. 7, from which we can see after 1 time of high fidelity and 3 times of low-fidelity search, the peak where the optimal value located is successfully searched. Within that peak, after 5 times of high fidelity and 8 times of low-fidelity search, the iteration stops and the optima is searched.

Fig. 7
figure 7

The search process of Case 4

Full size image

Case 6 is a multi-fidelity optimization problem with unknown constraint. Fig. 8 displays the contour map of MFSM after optimization and the sample points. The points without labels are the initial design, including 9 high-fidelity points and 15 low-fidelity points. After 3 times of low-fidelity observations and 5 times of high-fidelity observations, the search stops and got optimal value as (0.75, 1.75) and optimum \({f_h}({x_{best}}) = 3.2344\). If there is no constraint, the best advantage should be (0.1, 0.1), so the constraint comes into play.

Fig. 8
figure 8

The search process of Case 6

Full size image

Case 7 is a three-fidelity optimal problem, where \(l_1\) represents first-low fidelity, \(l_2\) represents second-low fidelity, and h represents the high fidelity. We set \(C_m\)/\(C_{l_{2}}\)=2 and \(C_m\)/\(C_{l_{1}}\)=4. The initial design is \(x=\left\{ 0.1,0.3,0.4,0.5,0.6,0.7,0.8,1\right\}\) at first-low fidelity, \(x=\left\{ 0.2,0.4,0.6,0.8\right\}\) at second-low fidelity, and \(x=\left\{ 0.35,0.65\right\}\) at high fidelity. As shown in Fig. 10, it is obvious that the Co-kriging model is closer to the real function compared with that in Fig. 9 and the PEI method finds the optimal value -6.02 after 13 iterations.

Fig. 9
figure 9

Initial design of Case 7

Full size image
Fig. 10
figure 10

The search process of Case 7 by PEI method

Full size image

Table 2 shows the results of PEI and MFSKO for the former five test functions. From Table 2, we can see that PEI can jump out of the local optimum. When both methods search into the peak of the real optimum, the results of PEI are still closer to the real optima than the results of MFSKO. When the observations especially the high-fidelity observations are inadequate or the observations are worse space-filling, there is insufficient information to metamodel the real system, and the expected improvement deduced by the constructed MFSM is sometimes underestimated and hence causes premature stopping. Toward the introduction of \(\gamma\) and selecting a large value of it, the probability of exploration will increase, then PEI can jump out of local optimum and have the chance to get a better point.

Table 2 The optimization results of the former five test functions
Full size table

Besides, to verify the efficiency and accuracy of the algorithm, we use the same number of iterations as the stopping criterion. As shown in Table 3, PEI can find the optima more accurate. Even when the accuracy is the same, PEI saves the cost, such as Case 3 and Case 4, because the different choices of two algorithms for high or low fidelity lead to different cost. For example, in Case 3, the total number of searches for both algorithms is 24, but the high-fidelity number of PEI is 9, which is less than that of MFSKO.

Table 3 The optimization results and total cost of the former five test functions when the stop criterion is iteration number
Full size table

4.2.2 Contrast of test cost

In this part, the performances of PEI method and MFSKO method are compared when the cost ratio changes are compared. Fig. 12 shows the cost change process in the search process of former five test functions, where the abscissa is the cost currently spent, and the ordinate is the optimal value observed so far. By comparison, we found that both the search process of PEI method and MFSKO method will change when the cost ratio changes. And as the cost ratio increases from 4:1 to 20:1, the cost increase of each step of both methods becomes slower, that means more observations on low-fidelity systems are carried out. Fig. 11 also reflects the higher optimization accuracy of PEI method than MFSKO method. The reason for this is that the KL divergence is more significant than correlation in describing the relationship between high and low fidelity, which is not affected by the cost ratio.

Fig. 11
figure 11

Computational cost changes as iterations proceed of PEI and MFSKO

Full size image
Fig. 12
figure 12

the value of \({\alpha _1}(x,1)\) as k changes in Case 1

Full size image
Table 4 The total cost of the former five test functions
Full size table

Table 4 shows the total cost of the MFSKO and PEI as cost ratio changes and the details for high- and low-fidelity sample can refer to Table B1 in Appendix B. Due to the increase of exploratory nature, one may consider the total cost of PEI criterion may increase compared with the MFSKO method; however, from Table 4, we can see it is not always true, especially when the convergence accuracy is the same, the cost of PEI is smaller than that of MFSKO. We attribute this to the adjustment of proportional factor \(\gamma\) during the sampling process. In this paper, we adopted a simple adjustment method, and we believe that a better adaptive criterion of \(\gamma\) will lead to the improvement of PEI method to achieve high accuracy and considerable cost.

4.2.3 Discussion of \({\alpha _1}({\textbf{x}},1)\)

This section focuses on discussing the value of \({\alpha _1}({\textbf{x}},1)\) in multi-fidelity sequential criteria. We want to know as the difference between low fidelity and high fidelity increases, what will happen to the value of \({\alpha _1}({\textbf{x}},1)\). Here, we use Case 1 as test function and take the value of k as 1, 3, and 5, and the value curves of \({\alpha _1}({\textbf{x}},1)\) are shown in Fig. 12. According to Fig. 12, as the value of k increases, i.e., the difference between low fidelity and high fidelity increases, the general trend of the curve will not change, but the overall value will always be smaller, that means on the same condition, the probability of point from lower fidelity will be selected reduces. This is consistent with the intuition.

\({\alpha _1}({\textbf{x}},1)\) measures the credibility of fidelity level and KL divergence method is used in this paper. From Fig. 12 and Fig. 6, we can see that the value curve of \({\alpha _1}({\textbf{x}},1)\) is basically continuous and valued as 0 at the test points. \({\alpha _1}({\textbf{x}},1)\) measures the credibility of fidelity level. That is similar to using the correlation, but we think it is more explanatory as it is based on the distribution difference. Furthermore, the method is more flexible as we can change the value of \(\eta , \;\kappa\) together with the cost ratio to meet the preference of fidelity level. For instanse, the parameters are set as \(\eta = 2,\;\kappa = 0.5\) in case 2 and \(\eta = 2,\;\kappa = 1\) in case 3.

4.3 Application to air drag minimization of the NACA 0012 airfoil

Aerodynamic shape optimization design of airfoil is one of the key problems in aircraft design. With the development of CFD Technology and optimization algorithms, the optimization design of aerodynamic shape has made great progress. In particular, the high-efficiency computer has shortened the cost of optimization design. However, a high-accuracy simulation still takes a long time. So, two major problems in aerodynamic shape optimization design should be considered: on the one hand, how to design an optimization algorithm that can quickly and accurately find the global optimal solution; on the other hand, in many practical instances, the evaluation of a real system of interest is too expensive, and one may consider drawing data from surrogate experiment systems with lower cost. Here, we will apply the proposed PEI method to optimize the NACA0012 airfoil.

Fig. 13
figure 13

Computational grid of NACA0012 airfoil

Full size image

The airfoil profile needs to be parameterized before optimizing. An excellent method of parameterized characterization of airfoil is to use as few design variables as possible to represent the design space with given constraints, so as to effectively reduce the computational cost. At present, the commonly used methods for the parametric characterization of airfoil include linear function perturbation method, characteristic parameter description method, and Class-Shape Function Transformation (CST) method (Ivanov et al. 2017), which is adopted in this paper.

The mathematical expression of CST parameterization method of NACA0012 airfoil is

$$\begin{aligned} y = ({x^{0.5}} \times (1 - x)) \cdot S(x) + x \cdot {z_{te}} \end{aligned}$$
(27)

in which x represents the dimensionless coordinate value in the chord direction of the airfoil, y represents the dimensionless coordinate value in the thickness direction of the airfoil, \({z_{te}}\) is the half thickness of the trailing edge, and S(x) represents the shape function, which is usually expressed by the N-order Bernstein polynomial given by

$$\begin{aligned} S(x) = \sum \limits _{i = 0}^N {{A_i} \cdot {S_i}(x)} \end{aligned}$$
(28)

where \({S_i}(x) = C_N^i{x^i}{(1 - x)^{N - i}} = \frac{N}{{i!(N - i)!}}{x^i}{(1 - x)^{N - i}}\). For n-order Bernstein polynomials, the upper and lower surfaces of NACA0012 airfoil have a total of \(N+1\) design variables, which are \({A_0},{A_1}, \cdots ,{A_N}\). However, since the design variable positions on the upper and lower surfaces of the leading edge position are the same, there are \(2N+1\) design variables that need to be optimized. In this example, the Bernstein polynomial order N is selected as 5, so the airfoil optimization design problem involves 11 design variables. The three most important design variables were screened out through sensitivity analysis, and were denoted as \({a_1}\), \({a_2},\) and \({a_3}\). The other eight design variables were fixed to optimize the airfoil. The value ranges of the three design variables are \({a_1} \in [0.153849,0.188038]\), \({a_2} \in [0.139910,0.171001],\) and \({a_3} \in [0.143035,0.1748200]\).

Table 5 The result of the last 8 samples before iteration stop
Full size table

The work aims at minimizing the air drag of the NACA0012 airfoil at a free-stream Mach number \({M_\alpha } = 0.8\) and an angle of attack \(\alpha = {0^\circ }\), Reynolds number \({\textrm{Re}} = 6.5 \times {10^6}\). When the Mach number is 0.8, the compressibility effect of the gas makes strong positive shock waves form on the airfoil surface, and then shock resistance is generated. This drag can be significantly reduced by changing the geometry of the airfoil, so airfoil drag reduction design examples at transonic speeds are often used to verify the algorithm. In our work, CFD is employed for aerodynamic analysis and a C-type grid is generated to divide the computing domain as shown in Fig. 13. Two kinds of grids with different sparsity, respectively, are 321\(\times\)65 and 193\(\times\)33 which are used to simulate and obtain high- and low-fidelity data for the NACA0012 airfoil. And the simulation time of high fidelity and low fidelity is treated as the cost, which is nearly 4:1. The CFD simulation is built by us, for details refer to (Duan et al. 2012, 2019).

We obtain 25 low-fidelity and 9 high-fidelity initial samples by using the Latin hypercube design. Table 5 shows the last 9 samples before stopping, and the right column of the table gives the airfoil drag value. It can be seen that the proposed PEI method still has a tendency to search low fidelity first and then high fidelity even near the stopping point. The high-fidelity point searched in step 42 is taken as the optimization result.

Fig. 14
figure 14

Optimized front and rear airfoils

Full size image

A total of 31 high-fidelity and 45 low-fidelity experiments were performed in the whole calculation, including the initial design. However, a total of 36 high-fidelity and 50 low-fidelity experiments were conducted by the MFSKO method. At the same time, we also adopted the particle swarm optimization algorithm(PSO) to optimize the design. As an engineering example, the real optimal value is unknown in advance, so the PSO algorithm is employed to approximate the real optimal value. 30 particle points were selected on the real system, and after 38 iterations, the optimal value 2.444136E-03 was obtained. As shown in Table 6, PEI and MFSKO are also compared.

Table 6 Comparison of airfoil optimization results with different methods
Full size table

The airfoil curves after optimization by the three method are shown in Fig. 14, we can see that compared to the baseline airfoil, the thickness and curvature are both reduced, and the maximum thickness of the airfoil moves to the right, which can reduce the drag. In addition, Fig. 15 shows the static pressure contours of the baseline and optimized airfoil. The results show that the pressure recovery of the trailing edge of the airfoil is delayed, the pressure distribution becomes flat, and the shock wave intensity is weakened.

Fig. 15
figure 15

Static pressure contours of NACA0012 airfoil

Full size image

5 Summary and future work

In this paper, a Co-Kriging-based multi-fidelity sequential optimization method is proposed for expensive black-box problem, and the objective of the paper is to develop a more efficient sequential sampling strategy, named proportional expected improvement (PEI). The PEI criterion is an extension of EI criterion and used an integrated criterion to determine both location and fidelity level of the subsequent search.

In the integrated criterion, a proportional factor \(\gamma\) which is adaptively adjusted according to the sample density is added to adjust the tendency between exploration and exploitation during the search process. Meanwhile, Kullback–Leibler divergence is used to measure the credibility or information contribution of a point from system with different fidelities. The PEI method was then validated by application to seven analytical functions, and we found that the introduction of factor \(\gamma\) helps to improve the greedy nature of EI criterion and helps to search for the global optima. However, theoretical analysis shows that a large value of \(\gamma\) may lead to the increase of total cost and sample points may cluster. To solve this problem, we suggest adaptively adjusting \(\gamma\) by the sample density, and it will make a tradeoff between the accuracy of optimum and the numbers of iterations. The contrast test for five analytical functions also shows that adaptively adjusting the value of \(\gamma\) can achieve high accuracy and considerable cost. Besides, when the accuracy of two methods is the same, PEI can save the total cost, which means that PEI is a more efficient method.

Moreover, a Kullback–Leibler divergence-based item is used to measure the credibility of point from different fidelities, and it decides the fidelity level of the next observation along with the cost item. The effectiveness and advantage of the proposed method were compared with MFSKO method by seven analytical functions, and also demonstrated for aerodynamic shape optimization of NACA0012 airfoil.

The research in this paper is based on the existing Co-Kriging method, and the currently widely used multi-fidelity surrogate model is mostly based on autoregressive architecture. This kind of treatment is relatively easy to handle, but if the autoregression hypothesis does not meet the actual situation, it will result in incorrect results. As the surrogate model may be more important to the optimization results than the sequential criterion, thus how to describe the fidelity difference and the consequently modeling problem is a creative potential. In this paper, Case 7 is an three-fidelity optimal problem, and the computational cost of building a Co-Kriging model increases as the sample size increases. So, the more advanced metamodel is worth studying. In the PEI sequential criterion proposed in this paper, an adaptive proportional factor is introduced to improve greedy and to achieve better optimization effect, which is also applicable to single-fidelity case, but how to adjust the proportional factor adaptively to achieve high accuracy and considerable cost remains to be further studied. And we will also focus on applying the PEI method to higher dimensional optimization, it will be challenging as the dimension is larger than 50. On the other hand, through in this paper, we can handle some kind of unknown constraints, it is still an essential direction.