1 Introduction

1.1 Background

The efficient global optimization method (EGO) (Jones et al. 1998) based on kriging model and expected improvement (EI) has received much attention and gained a great success in engineering design optimizations (Forrester et al. 2008; Liu et al. 2017; Queipo et al. 2005; Wang and Shan 2007), where high-fidelity (hi-fi) and expensive numerical simulations are often employed. It generally includes the following steps. First, a limited number of sample points in the design space are chosen by the method of design of experiments (DoE) (Giunta et al. 2003) and an expensive numerical analysis, such as computational fluid dynamics (CFD) or computational solid dynamics (CSD), is executed to get the functional responses; then an initial kriging model is built based on the sampled data. Second, new sample point(s) is selected by maximizing the expected improvement (EI) function calculated through the predicted functional values of the cheap-to-evaluate kriging model and its mean-squared error (MSE). Third, the newly selected sample point(s) is evaluated by the expensive numerical analysis and the functional response(s) is augmented to the sampled data. Fourth, the kriging model is rebuilt and this adaptive sampling process is repeated until the resulting sample-point sequence converges to the global optimum. The EGO method soon got popularity in engineering design after its birth, for it enables the searching of global optimum with much less number of expensive function evaluations than the methods such as genetic algorithm (GA) (Holland 1975) and particle swarm optimization algorithm (PSO) (Kennedy and Eberhart 1995).

The advent of the EGO method greatly inspired the research and development of a type of optimization method called surrogate-based optimization (SBO) (Forrester and Keane 2009; Han and Zhang 2012; Koziel et al. 2013). The SBO method can be viewed as a generalized EGO method, by using different types of surrogate models and infill-sampling criteria (ISC) (Forrester and Keane 2009; Jones 2001; Liu et al. 2012), without being limited to kriging and EI only. Despite the success of SBO, it is still suffering from the “curse of dimensionality” (Koch et al. 1999; Shan and Wang 2010). To tackle this problem, many researchers have devoted themselves to developing more accurate surrogate models, towards more efficient global optimization. Two kinds of methods are concerned. One is gradient-enhanced surrogate model (Han et al. 2017) with the cheap gradients computed by adjoint method, and the other is variable-fidelity model (VFM) (Park et al. 2017) using auxiliary low-fidelity (low-fi), cheaper function to assist the prediction of hi-fi, expensive function. This article is mainly concerned with the VFM method, and the use of cheap gradients to enhance the prediction is beyond the scope of this article.

Generally, the VFM methods can be classified into three categories. The first type is the correction-based method that corrects the low-fi model using a bridge function (or scaling function) to approximate the hi-fi function (Alexandrov et al. 1998, 2001). The correction can be multiplicative (Haftka 1991; Chang et al. 1993), additive (Choi et al. 2004, 2009), or hybrid (Gano et al. 2005; Han et al. 2013). The second type is the space mapping (Bakr et al. 2001; Leifsson et al. 2016). The design space of the low-fi function is distorted to cause its optimal point to match that of the hi-fi function (Robinson et al. 2008; Viana et al. 2014). The third type is variable-fidelity kriging such as cokriging (Kennedy and O’Hagan 2000; Han et al. 2012; Forrester et al. 2007) and HK (Han and Görtz 2012). The cokriging was originally proposed in geostatistics community (Journel and Huijbregts 1978) and then extended to deterministic computer experiments by Kennedy and O’Hagan (2000). Cokriging introduces the assistance of cheap low-fi function by constructing the cross covariance between the low- and hi-fi functions. The newly developed HK model (Han and Görtz 2012) directly takes the kriging of the cheap low-fi function as the model trend of the kriging for the expensive hi-fi function, and the difficulty associated with constructing the cross covariance as that in cokriging is avoided. The HK model turns out to be as simple and robust as the correction-based method and as accurate as cokriging method. Moreover, it provides a more reasonable mean-squared error (MSE) estimation than any of the existing kriging and cokriging methods. Recently, the HK model received much attention in engineering design such as uncertainty analysis in CFD (Palar and Shimoyama 2017), multi-objective optimization (Ha et al. 2014), aerodynamic shape optimization (Zhang et al. 2015), and structural optimization (Courrier et al. 2016).

With the development of VFM, there is a trend that the VFO has become more and more attractive for engineering design problems where numerical simulations of varying fidelity are available. The literatures in the research area, published since 2000, are summarized in Table 1, in chronological order. We found that most of the literatures are dealing with low-dimensional optimization problems (< 10 dimensions) and most of the ISC methods used are essentially for local optimization. To enable global optimization, EI or a combination of MSP (minimizing surrogate prediction) and MSE have been used. When the EI method proposed by Jones et al. (1998) for single-fidelity optimization is directly applied to a variable-fidelity kriging model such as HK or cokriging model, only hi-fi samples can be chosen to update the variable-fidelity surrogate model. To improve the optimization efficiency, there is a strong need for adaptively selecting the samples of both low fidelity and high fidelity. However, currently, the theory and method of infilling low-fi samples for the improvement of hi-fi function of interest are still a blank area.

Table 1 Summary of literatures about variable-fidelity surrogate-based optimization
Full size table

1.2 Objectives

This article is inspired by the motivation of developing an adaptive method that can select the new samples of both low fidelity and high fidelity to update the variable-fidelity surrogate model towards the global optimum of hi-fi function. The objectives of developing such a method are as follows:

  1. 1)

    The first objective is to solve the problem associated with how to adaptively infill both low-fi and hi-fi samples. A variable-fidelity surrogate model is generally built through a number of observed low-fi samples and a few observed hi-fi samples (Han and Görtz 2012). After the initial variable-fidelity surrogate model is built, it can be improved not only by adding a hi-fi sample but also by adding a low-fi sample. But the question is how to select the new sample points? One way, the traditional way, is to use a fixed number of low-fi samples during the design, while hi-fi samples are repetitively added based on the ISC. It is, of course, not the most efficient way, since it is always questionable that how many low-fi samples would be sufficient. The other way, and a potentially better way, is that both low-fi and hi-fi samples are adaptively added. This motivates us to develop a theory and method that the infilling of low-fi and hi-fi samples are both towards the improvement of hi-fi function.

  2. 2)

    The second objective is to develop a more efficient global optimization method based on numerical simulations of varying fidelity. Literature survey shows that most of the VFO methods reported by current literatures are essentially for local optimization. The reason is that it is not economic or possible to build a sufficiently accurate global surrogate model for a multi-dimensional optimization problem. Therefore, there is a strong need to extend the standard EI method, proposed by Jones et al. (1998), to a VFO. The only method that serves this target is the augmented EI method proposed by D Huang and T T Allen et al. (2006) and the improved version in 2014 (Reisenthel and Allen 2014). However, the performance of augmented EI method is dependent on the empirical setting of free parameters. This motivates us to develop a variable-fidelity EI method which is free of empirical parameters and mathematically more general.

2 Variable-fidelity optimization based on hierarchical kriging and standard EI

The aim of this study is to solve the following constrained optimization problem based on a hi-fi expensive numerical analysis with assistance of a low-fi but cheaper numerical analysis

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Min}}.\kern0.75em y\left(\mathbf{x}\right)\\ {}\mathrm{w}.\mathrm{r}.\mathrm{t}.\kern0.5em {\mathbf{x}}_{l\mathrm{ow}}\le \mathbf{x}\le {\mathbf{x}}_{up}\\ {}s.t.\kern1.25em {g}_i\left(\mathbf{x}\right)\le 0,\kern1.25em i=1,\cdots, {N}_C\\ {}\mathrm{w}\mathrm{ith}\ \mathrm{assistance}\ \mathrm{of}\kern0.5em {y}_{\mathrm{lf}}\left(\mathbf{x}\right)\ \mathrm{and}\ {g}_{\mathrm{lf},i}\left(\mathbf{x}\right),\end{array}} $$
(1)

where y(x) and gi(x) denote the objective and constraint functions, respectively, which are evaluated by expensive, hi-fi numerical analyses; ylf(x) and glf, i(x) are the low-fi objective and constraint functions, respectively, which are evaluated by cheap numerical analyses; NC is the number of constraint functions; xup and xlow are the upper and lower bounds of the design variables x, respectively. Note that here we are mainly concerned with the single-objective optimization, and the extension to multi-objective optimization is beyond the scope of this article.

2.1 Variable-fidelity optimization framework

The optimization is solved based on HK surrogate models (Han and Görtz 2012) for the objective and constraint functions, which are built through a few expensive hi-fi samples and many cheap low-fi samples. The HK models are repetitively updated by the adaptive addition of expensive hi-fi sample points suggested by maximizing the EI function (Jones et al. 1998), until the optimum is reached. The framework of this HK-based optimization is shown in Fig. 1. The basic steps are as follows:

  1. a.

    Two sets of sample points are generated by using a DoE method and they are evaluated by the low- and hi-fi numerical analyses, respectively.

  2. b.

    Based on the low-fi sample data, a kriging model is built. Then taking it as the model trend, a HK surrogate model is built through the hi-fi samples. The HK model(s) for constraint function(s) is built in a similar manner.

  3. c.

    New sample point(s) is selected by maximizing the constrained EI (CEI) function through a combination of GA, Hooke and Jeeves, and BFGS optimization methods, and then evaluated by the expensive, hi-fi numerical analysis. When BFGS method is used, the gradients of EI function are computed by a central difference based on the HK prediction. Please note that only hi-fi sample points are chosen, and the number of low-fi samples is fixed.

  4. d.

    The newly selected sample point and its functional responses are augmented to the sampled dataset, and then the HK surrogate models are rebuilt.

  5. e.

    The steps b–d are repeated until the termination condition is satisfied.

Fig. 1
figure 1

Flowchart of VFO based on hierarchical kriging model and the standard EI method

Full size image

2.2 Design of experiments

Before constructing the HK model, DoE method is used to generate initial low- and hi-fi sample points. Different from other VFM methods, such as cokriging model, the hi-fi sampling sites do not need to be a subset of the low-fi sampling sites, which enables us to use DoE method for each fidelity level separately. In this article, the Latin hypercube sampling (LHS) (Giunta et al. 2003) method is adopted.

2.3 Surrogate modeling via hierarchical kriging

Kriging is a statistical interpolation method suggested by Krige (1951) and mathematically formulated by Matheron (1963). Kriging gained popularity in design and analysis of deterministic computer experiments after the milestone research work of Sacks et al. (1989). The HK model, proposed by Han and Görtz (2012), is an extension of the Sacks' kriging model to one that approximates the expensive hi-fi function with assistance of a cheap low-fi function. The details about the formulation of HK can be found in Appendix A.1.

2.4 Infill-sampling criterion of EI method

After constructing the initial HK model, it can be improved by adding new sample points using the EI method, proposed by Jones et al. (1998). EI is defined as the mathematical expectation of improvement with respect to the best solution observed so far. Through maximizing the EI function, the next update point can be identified. The details about the formulation of EI method can be found in Appendix A.2.

2.5 Termination conditions

Several termination criteria can be used in the HK-based optimization, such as the criteria defined based on the distance between samples and difference of their objective responses, the allowable minimum value of CEImax, the thresholds about accuracy of surrogate models, and the affordable maximum number of expensive function evaluations.

3 Proposed method

3.1 Formulation of variable-fidelity EI

This article formulates a VF-EI function, which is an extension of the standard EI to consider not only the model uncertainty due to lack of a hi-fi sample but also the model uncertainty due to lack of a low-fi sample. When HK model (Han and Görtz 2012) is used, the uncertainty due to lack of a low-fi sample can be analytically derived, which might be difficult or even not possible for other kinds of models such as cokriging. This uncertainty is used to define the EI of hi-fi function due to lack of a low-fi sample. Combining this EI with the standard EI, the VF-EI is formulated as not only a function of the design variables x (or spatial location) but also the function of fidelity level denoted by l.

Recall that for a HK model (see Appendix A.1 for detailed formulation), the random process of hi-fi function is assumed as

$$ Y\left(\mathbf{x}\right)={\beta}_0{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)+Z\left(\mathbf{x}\right). $$
(2)

where β0 is a scaling factor representing how the low-fi kriging \( {\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right) \) matches the hi-fi function. Based on the assumption, the resulting HK predictor and its MSE is

$$ {\displaystyle \begin{array}{l}\widehat{y}\left(\mathbf{x}\right)=\underset{\mathrm{trend}\ \mathrm{term}}{\underbrace{\beta_0{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)}}+\underset{\mathrm{correction}\ \mathrm{term}}{\underbrace{{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{\hbox{-} 1}\left({\mathbf{y}}_{\mathrm{S}}\hbox{-} {\beta}_0\mathbf{F}\right)}}\\ {}\mathrm{MSE}\left\{\widehat{y}\left(\mathbf{x}\right)\right\}={s}^2\left(\mathbf{x}\right)={\sigma}^2\left\{1.0-{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{r}+{\left[{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{F}-{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right)\right]}^2/{\left({\mathbf{F}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}\right\},\end{array}} $$
(3)

where

$$ \mathbf{F}={\left[{\widehat{y}}_{\mathrm{lf}}\left({\mathbf{x}}^{(1)}\right),\cdots, {\widehat{y}}_{\mathrm{lf}}\left({\mathbf{x}}^{(n)}\right)\right]}^{\mathrm{T}}\in {\Re}^n. $$
(4)

The key issue of VF-EI is how to define the EI of hi-fi function associated with adding a low-fi sample point. As \( {\beta}_0{\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right) \) is its model trend, the uncertainty of the HK prediction associated with lack of a low-fi sample at x is found to be \( {\beta}_0^2{s}_{\mathrm{lf}}^2\left(\mathbf{x}\right) \). Note that the uncertainties in F are neglected and \( {s}_{\mathrm{lf}}^2\left(\mathbf{x}\right) \) is the uncertainty of the low-fi kriging model \( {\widehat{y}}_{\mathrm{lf}}\left(\mathbf{x}\right) \). Then, we extend the model uncertainty of a HK model to s2(x, l), which is a function of both the spatial location x and fidelity level l

$$ \kern0.1em {s}^2\left(\mathbf{x},l\right)=\left\{\begin{array}{cc}{\beta}_0^2{s}_{\mathrm{lf}}^2\left(\mathbf{x}\right)& l=1\ \mathrm{for}\ \mathrm{low}\hbox{-} \mathrm{fi}\ \mathrm{level}\\ {}{s}^2\left(\mathbf{x}\right)& l=2\ \mathrm{for}\ \mathrm{hi}\hbox{-} \mathrm{fi}\ \mathrm{level}\kern0.7em \end{array}\right., $$
(5)

where s2(x) is the uncertainty of the HK model. We can assume that the prediction of the HK model for the objective function at any untried site x obeys the normal distribution

$$ \widehat{Y}\left(\mathbf{x},l\right)\sim N\left[\widehat{y}\left(\mathbf{x}\right),{s}^2\Big(\mathbf{x},l\Big)\right],\kern1.5em l=1,2, $$
(6)

whose mean is the prediction of the HK model \( \widehat{y}\left(\mathbf{x}\right) \).

With the assumption above, we redefine the statistical improvement w.r.t. the best-observed hi-fi objective function ymin so far as:

$$ {I}_{\mathrm{vf}}\left(\mathbf{x},l\right)=\max \left({y}_{\mathrm{min}}-\widehat{Y}\left(\mathbf{x},l\right),0\right), $$
(7)

which is also a function of both the spatial location x and fidelity level l. Then the VF-EI can be derived in a similar manner as the standard EI by Jones et al. (1998) does:

$$ {EI}_{\mathrm{vf}}\left(\mathbf{x},l\right)\kern0.4em =\left\{\begin{array}{cc}\left({y}_{\mathrm{min}}-\widehat{y}\left(\mathbf{x}\right)\right)\Phi \left(\frac{y_{\mathrm{min}}-\widehat{y}\left(\mathbf{x}\right)}{s\left(\mathbf{x},l\right)}\right)+s\left(\mathbf{x},l\right)\phi \left(\frac{y_{\mathrm{min}}-\widehat{y}\left(\mathbf{x}\right)}{s\left(\mathbf{x},l\right)}\right),& if\kern0.8000001em s\left(\mathbf{x},l\right)>0\\ {}0,& if\kern0.8000001em s\left(\mathbf{x},l\right)=0\end{array}\right.. $$
(8)

It is worth to note that the VF-EI only relates to the improvement of the hi-fi function. The VF-EI for the hi-fi level, EIvf(x, l = 2) indicates the expected improvement of the hi-fi function if a hi-fi sample point is added, which is similar to the standard EI method. But the VF-EI for the low-fi level, EIvf(x, l = 1), is the expected improvement of the hi-fi function when a low-fi sample is added. Please note that here we are not concerned with the expected improvement of low-fi function predicted by a low-fi kriging model. Rather, the infillings of both low-fi and hi-fi samples are hi-fi-optimum oriented, which is a unique property of the proposed method.

For a unconstrained optimization, the new sample point x and its fidelity level l can be determined by solving the following sub-optimization problem

$$ \mathbf{x},l=\underset{{\mathbf{x}}_{low}\le \mathbf{x}\le {\mathbf{x}}_{up},l=1,2}{\arg \max }{EI}_{\mathrm{vf}}\left(\mathbf{x},l\right). $$
(9)

If the new sample is found to be a low-fi one (l = 1), which means that adding a low-fi sample will improve the hi-fi objective function most, it will be evaluated by the cheaper analysis. Otherwise, the new sample will be evaluated by the expensive analysis (l = 2).

During the design, we found that the VF-EI will automatically tend to add more low-fi samples, which is a preferred feature for the consideration of improving the overall optimization efficiency. And the addition of low- and hi-fi samples will be in an alternative manner, along with the change of predicted correlation between low- and hi-fi functions and the ratio of two kinds of uncertainties mentioned above, \( {s}_{\mathrm{lf}}^2/{s}^2 \). For a HK model (see eq. (3)), supposing that the low-fi function can correctly capture the trend of the hi-fi function, the uncertainty of HK model, due to lack of a hi-fi sample (correction term in HK), will be generally much smaller than that due to lack of a low-fi sample (trend term in HK). As a result, maximizing the VF-EI will automatically lead to the more addition of low-fi samples. On the contrary, if the low-fi function correlates poorly with the hi-fi function, the β0 will be very small (close to zero), and maximizing the VF-EI will tend to add hi-fi samples since adding a low-fi sample has a little contribution to the improvement of the hi-fi function. On the other hand, the addition of low- or hi-fi samples is also controlled by the ratio of uncertainties \( {s}_{\mathrm{lf}}^2/{s}^2 \). Besides the process variance, \( {s}_{\mathrm{lf}}^2/{s}^2 \) is related to the distance to the observed sample. At a point where the low-fi function is undersampled, the VF-EI may tend to add low-fi samples, simply because the process variance of the hi-fi HK model will be much smaller than that of the low-fi kriging. And at a point where low-fi function is densely sampled, the VF-EI may switch to add hi-fi samples.

3.2 Constraint handling

For a constrained optimization, the HK model for the constraint function, \( \widehat{g}\left(\mathbf{x}\right) \), is also built, and we also assume the prediction of the HK model for the constraint function at any site is a normal distribution

$$ G\left(\mathbf{x},l\right)\sim N\left[\widehat{\mathrm{g}}\left(\mathbf{x}\right),{s}_g^2\Big(\mathbf{x},l\Big)\right],\kern0.6em l=1,2, $$
(10)

where \( {s}_{\mathrm{g}}^2\left(\mathbf{x},1\right) \) and \( {s}_g^2\left(\mathbf{x},2\right) \)are the uncertainties of constraint function due to lack of low- and hi-fi samples, respectively. Therefore, the probability of satisfying the constraint is

$$ P\left[G\left(\mathbf{x},l\right)\le 0\right]=\Phi \left(\frac{-\widehat{g}\left(\mathbf{x}\right)}{s_{\mathrm{g}}\left(\mathbf{x},l\right)}\right). $$
(11)

Eventually, the constrained VF-EI can be expressed as

$$ {CEI}_{\mathrm{vf}}\left(\mathbf{x},l\right)={EI}_{\mathrm{vf}}\left(\mathbf{x},l\right)\cdot P\left[G\left(\mathbf{x},l\right)\le 0\right]. $$
(12)

For an optimization problem with multiple constraints, the corresponding constrained VF-EI is

$$ {CEI}_{\mathrm{vf}}\left(\mathbf{x},l\right)={EI}_{\mathrm{vf}}\left(\mathbf{x},l\right)\cdot {\prod}_{i=1}^{N_{\mathrm{C}}}P\left[{G}_i\left(\mathbf{x},l\right)\le 0\right], $$
(13)

where NC is the number of constraints. It can be seen that in the above equation, the constrained VF-EI is a function of both the design variable x and the fidelity level l.

Through maximizing the constrained VF-EI, the spatial location of new sample point x and fidelity level of next numerical evaluation l can be determined by

$$ \mathbf{x},l=\underset{{\mathbf{x}}_{low}\le \mathbf{x}\le {\mathbf{x}}_{up},l=1,2}{\arg \max }{CEI}_{\mathrm{vf}}\left(\mathbf{x},l\right). $$
(14)

3.3 Discussion about the difference with augmented EI

By literature survey, we found that there is a similar but different method called augmented EI, which is proposed by Huang et al. (2006) and formulated based on cokriging model (Kennedy and O’Hagan 2000). The formulation of augmented EI is

$$ {EI}_{\mathrm{aug}}\left(\mathbf{x},l\right)\kern0.4em = EI\left(\mathbf{x}\right)\cdot {\alpha}_1\cdot {\alpha}_2,\kern0.35em l=1,2, $$
(15)

where

$$ {\alpha}_1=\mathrm{corr}\left[{\widehat{y}}_l\left(\mathbf{x}\right),{\widehat{y}}_2\left(\mathbf{x}\right)\right],{\alpha}_2={t}_2/{t}_l, $$
(16)

where α1 is a cross-correlation coefficient between the low- and hi-fi models and α2 is the cost ratio between a single hi-fi numerical simulation and a single low-fi numerical simulation. As the cross-correlation coefficient \( \mathrm{corr}\left[{\widehat{y}}_l\left(\mathbf{x}\right),{\widehat{y}}_2\left(\mathbf{x}\right)\right] \) could be not easy to calculate for other kinds of surrogate models, an alternative formulation is given in (Reisenthel and Allen 2014)

$$ \mathrm{corr}\left[{\widehat{y}}_l\left(\mathbf{x}\right),{\widehat{y}}_2\left(\mathbf{x}\right)\right]={s}_l\left(\mathbf{x}\right)/\left(\left|{\widehat{y}}_2\left(\mathbf{x}\right)-{\widehat{y}}_l\left(\mathbf{x}\right)\right|+{s}_2\left(\mathbf{x}\right)\right). $$
(17)

Although the motivations and ideas are similar, the VF-EI method proposed in this article is different from the augmented EI method. The main difference is that the VF-EI is derived analytically, but the augmented EI is somehow heuristic and empirical. As a result, VF-EI is free of empirical parameters and the addition of low- and hi-fi samples is fully adaptive. In contrast, the performance of the augmented EI is dependent on the proper use of low-fi function and empirical setting of α1 and α2. From this point of view, we could infer that the VF-EI can be potentially better than or at least as good as the augmented EI. In fact, this hypothesis is confirmed by the analytical function test cases and engineering design problems provided in Sections 4 and 5.

3.4 Implementation of proposed VF-EI

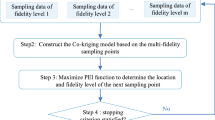
In this article, all the optimization test cases are performed based on an in-house optimization code called “SurroOpt” (Han 2016a, b). It is a surrogate-based generic optimization code that can be used to efficiently solve arbitrary single and multi-objective (Pareto front), unconstrained, and constrained optimization problems. The proposed VF-EI method and augmented EI were implemented in “SurroOpt.” Algorithm 1 is given as an implementation of the VFO and the corresponding framework is sketched in Fig. 2. The difference with the conventional optimization framework based on the standard EI method (see Fig. 1) is that both low-fi and hi-fi samples are added to update the HK model towards the global optimum of the hi-fi function,Algorithm 1: Procedure of VF-EI based optimization

0:

procedure

1:

set initial low- and hi-fi sample points, J = 0

2:

evaluate the samples by low-fi and hi-fi analyses, respectively

3:

while J < Jmax

4:

construct the low-fi kriging model \( {\widehat{\mathbf{y}}}_{\mathrm{lf}} \)

5:

construct the HK model \( {\widehat{\mathbf{y}}}_{\mathrm{hf}} \)

6:

find \( \kern0.1em {\mathbf{x}}_{\mathrm{lf}}^{\ast }=\arg \max {CEI}_{\mathrm{vf}}\left(\mathbf{x},l=1\right) \)

7:

find \( \kern0.1em {\mathbf{x}}_{\mathrm{hf}}^{\ast }=\arg \max {CEI}_{\mathrm{vf}}\left(\mathbf{x},l=2\right) \)

8:

if \( {EI}_{\mathrm{vf}}\left({\mathbf{x}}_{\mathrm{lf}}^{\ast },1\right)>{EI}_{\mathrm{vf}}\left({\mathbf{x}}_{\mathrm{hf}}^{\ast },2\right)\kern0.5em \) then:

\( {\mathbf{x}}_{\mathrm{new}}={\mathbf{x}}_{\mathrm{lf}}^{\ast },l=1 \)

9:

else \( {\mathbf{x}}_{\mathrm{new}}={\mathbf{x}}_{\mathrm{hf}}^{\ast },l=2 \)

endif

10:

if (l = 1) then

evaluate xnew using low-fi analysis, go to 4

11:

else

evaluate xnew using hi-fi analysis, J=J+1, go to 5

endif

12:

end while

13:

end procedure

Fig. 2
figure 2

Flowchart of VFO based on hierarchical kriging and the proposed VF-EI method

Full size image

4 Test cases of analytical functions

4.1 An illustrative example

In this sub section, a one-dimensional test function (Forrester et al. 2007) is used to verify the correctness of the proposed VF-EI method. The mathematical model is

$$ {\displaystyle \begin{array}{l}\min \kern1.5em y={\left(6x-2\right)}^2\sin \left(12x-4\right)\kern0.6em \\ {}\kern2.899999em {y}_{\mathrm{lf}}=0.5y+10\left(x-0.5\right)-5.\\ {}w.r.t.\kern1.1em x\in \left[0,1\right]\end{array}} $$
(18)

Please note that the theoretical optimal solution is at x∗ = 0.75725 with optimal functional value of f(x∗) =  − 6.020740.

The refining process of the HK model by using the proposed VF-EI is sketched in Table 2 and Fig 3. First, the initial HK model is built with six low-fi and three hi-fi sample points (Slf = {0.0,  0.1402,  0.3742,  0.4180,  0.7469,  0.9777}, S = {0.2223,  0.6128,  0.9877}), shown in Fig. 3a. Figure 3 (a, left) shows the low-fi kriging and HK models compared with the true functions. Although the low-fi kriging is not accurate enough, the trend is correctly mapped to three hi-fi samples. Figure 3 (a, right) is the distribution of the VF-EI function through the whole design space. It can be seen that the maximum of EI(x, 1) in the low-fi level is much higher than the maximum of EI(x, 2)in the hi-fi level, which implies that for the 1st update cycle, we should add a low-fi sample at location of x = 0.6423. Second, the low-fi kriging and HK models are rebuilt with the initial samples and the newly added low-fi sample (pink cross symbol), as shown in Fig. 3 (b, left). The low-fi kriging model is getting more accurate and the resulting HK model features the similar trend with the true hi-fi function. As the maximum of EI(x, 2) in hi-fi level is larger, shown in Fig. 3 (b, right), a hi-fi sample point at x = 0.7305 is added at the 2nd cycle. Then, the HK model is updated and becomes more accurate than the previous cycle. However, the exact optimal location is still not precisely reached, as shown in Fig. 3c. Then, two low-fi sample points are added into the sample dataset at the 3rd and 4th cycles and the low-fi kriging and HK models are both getting more and more accurate near the optimum, as shown Fig. 3d, e. Finally, a hi-fi sample point is added at a site that is very closing to the optimal location and the updating process terminates, see in Fig. 3f. The refining process of the HK model by using the augmented EI is sketched in Fig. 4. Here, we assume that the cost ratio t2/tl is 4. We find that only hi-fi samples are added during the optimization iterations. This is because the low- and hi-functions have a big difference in functional value, which results in a small value of correlation coefficient α1, consequently, and only hi-fi samples points are added during the entire design (see Table 3).

Fig. 3
figure 3figure 3

Refinement process of VFO of a 1-d analytical function based on HK surrogate model and the proposed VF-EI method (fidelity level of added samples: low-hi-low-low-hi)

Full size image
Fig. 4
figure 4

Refinement process of VFO of a 1-d analytical function based on HK surrogate model and the augmented EI method (fidelity level of added samples: hi-hi-hi)

Full size image
Table 2 Refinement process of the VF-EI based optimization of the 1-d illustrative test case
Full size table
Table 3 Refinement process of the augmented EI based optimization of the 1-d illustrative test case
Full size table

In this test case, only 5 hi-fi samples, including 3 initial samples, are used for VF-EI method to successfully find the global optimum (see Table 2), with assistance of 9 low-fi samples, which in turn verifies the correctness and effectiveness of the proposed VF-EI method. It is shown that the VF-EI method can adaptively determine both the location and fidelity level of a new design point, and the addition of both low- and hi-fi samples are in an alternative manner and hi-fi optimum oriented. During the updating process, the low-fi sample points are firstly used to depict the trend of the hi-fi function near the optimal solution; and then the hi-fi sample points are added to correct the absolute value until the hi-fi global optimum is reached.

4.2 Other test functions

To demonstrate the VF-EI method and make a reasonable comparison with the augmented EI method, six analytic functions with the number of dimensions in the range from 1 to 5 are tested. Among them, the test functions 5 and 6 are from the literature (Huang et al. 2006), in which the augmented EI was proposed. The expressions of adopted functions are shown in Table 4, and the definitions of analytical test cases are shown in Table 5.

Table 4 Test functions
Full size table
Table 5 Definition of variable-fidelity test cases
Full size table

The test cases include the following: (1) case 1–3, all of the hi-fi functions are the 1-d function from (Forrester et al. 2007) with different low-fi functions. For Forrester 1a, the low-fi function has a different optimal location with the hi-fi function; the Forrester 1b has the same trend but large difference in functional response with the hi-fi function; the Forrester 1c has a totally opposite trend with the hi-fi function; (2) case 4 is a 2-d function test case from Ref (Gano et al. 2005), where the low-fi function is obtained by adding linear and nonlinear noise factors to the hi-fi function. The low-fi function has similar trend and close optimal location with the hi-fi function; (3) case 5 is a 3-d “Hartman 3” function and the low-fi function is defined as adding systematic errors “MA 3” multiplied by 7.6 to the hi-fi functions. As a large deviation is introduced in the low-fi function, there is a big difference in functional responses between low- and hi-fi functions; (4) case 6 is a 5-d “Ackley 5” function, and the low-fi function is defined as adding systematic errors “MA 5” multiplied by 0.74 to the hi-fi function, which can retain the main trend of the hi-fi function. The 1-d and 2-d function cases, which can be visualized, are shown in Fig. 5.

Fig. 5
figure 5

Sketch of the low- and hi-fi functions for case 1 to 4 (left: case 1–3; right: case 4)

Full size image

In all of the three test cases, the initial numbers of low- and hi-fi sample points are 3 and 6 times of the number of dimensions and chosen by LHS respectively. The optimization using standard EI, augmented EI, and VF-EI are all repeated 10 times to consider the influence of the randomness due to initial sampling and the sub-optimization algorithms (when GA is used). The average test results are shown in Table 6.

Table 6 Comparison of VFOs with the standard EI, augmented EI, and the proposed VF-EI for analytical test cases
Full size table

From the test results, we can observe that, first, the global optima are successfully found in all of the cases, which validate the applicability of HK model-based optimization. Second, it is shown that the VF-EI can improve the optimization efficiency in all of the cases, in terms of the number of hi-fi sample points, compared with that using the standard single-fidelity EI method. Although the low-fi function has a poor correlation with hi-fi function (case 3), the performance of VF-EI is at least as good as the standard EI method. Third, as for the augmented EI, it only performs well in case 4, in which the low-fi function has similar trend and close optimal location with that of the hi-fi function. In case 6, it does improve the optimization efficiency but not as good as our VF-EI method. However, it does not work well in other analytical function cases and even worse than the standard EI in case 5. Please note that the similar result of case 5 was presented in the literature (Huang et al. 2006). We observed that unsatisfactory performance of the augmented EI method is due to the big difference in functional responses or optimal locations between low- and hi-fi functions.

In conclusion, the proposed VF-EI method can adaptively infill the low- and hi-fi sample points in an alternative manner, and is proved to be effective in all of the presented optimization cases. In contrast, the performance of the augmented EI method is problem dependent.

5 Application to engineering design problems

5.1 Drag minimization of RAE2822 airfoil in transonic viscous flow

5.1.1 Problem statement

The VF-EI method is applied to a benchmark problem of airfoil design, defined by the AIAA aerodynamic design optimization discussion group (ADODG) (Zhang et al. 2016), which is the drag minimization of a RAE 2822 airfoil, subject to area, and pitching moment constraints, at a freestream Mach number of 0.734, lift coefficient of 0.824, and Reynolds number of 6.5 × 106. It can be written as a standard nonlinear programming problem

$$ {\displaystyle \begin{array}{l}\min \kern0.6em {C}_d\\ {}s.t.\kern1.1em {C}_l=0.824\\ {}\kern2.1em {C}_m\ge -0.092,\\ {}\kern2.1em Area\ge {Area}_0\end{array}} $$
(19)

where Cl, Cd, and Cm is the lift, drag, and pitching moment coefficient respectively and Area is the airfoil cross-sectional area normalized by the chord length.

For convenience, in our study, the problem is reformulated as following:

$$ {\displaystyle \begin{array}{l}\min \kern0.6em {C}_d\\ {}s.t.\kern1.1em {C}_l\ge 0.824\\ {}\kern2.1em {C}_m\ge -0.092,\\ {}\kern2.1em Area\ge {Area}_0\end{array}} $$
(20)

where the angle of attack α is fixed at 2.8795 degree, at which the Cl of baseline RAE 2822 is 0.824. Please note that in the following text, the drag coefficient will be given in terms of drag count (cts) with 1 cts = 1 × 10−4.

5.1.2 Determination of low- and hi-fi CFD models

The high- and low-fi analysis models are defined as CFD simulations solving the same governing flow equations (Reynolds-averaged Naiver-Stokes equations) with different convergence criteria and computational meshes of varying resolutions. The flow solver used in this paper is an in-house solver called “PMNS2D” (Han et al. 2007; Xie et al. 2008). According to the grid study shown in Fig. 6, we choose the grid with 73,728 cells as the hi-fi model, and the grid with 18,432 cells as the low-fi model (see in Fig. 7). The low-fi CFD simulation terminates after 200 iterations and the hi-fi CFD simulate stops until the density residual has dropped 5.5 orders in magnitude, as shown in Fig. 8. As a result, the computational cost ratio of a hi-fi simulation to a low-fi simulation is approximately 100, which means that the cost of 100 low-fi CFD simulations is identical to that of a single hi-fi CFD simulation.

Fig. 6
figure 6

Determination of low- and hi-fi CFD models by grid convergence study for baseline RAE2822 airfoil (Ma = 0.734, α = 2.8795°, Re  = 6.5 × 106)

Full size image
Fig. 7
figure 7

Sketch of C type grids for low-fi (left) and hi-fi (right) CFD computations for baseline RAE2822 case

Full size image
Fig. 8
figure 8

Convergence histories of low-fi (left) and hi-fi (right) simulations for the baseline RAE2822 airfoil (Ma = 0.734, α = 2.8795°, Re  = 6.5 × 106)

Full size image

5.1.3 Results

The airfoil is parameterized by class-shape transformation (CST) method (Kulfan 2008), and 18 design variables are utilized to describe the airfoil. After parameterizing the baseline RAE2822 airfoil, the design space is obtained by expanding the initial parameters by 1.5 times and narrowing it by half.

Here, we compare VF-EI, augmented EI, and standard EI-based VFO with the single-fidelity optimization. 5 hi-fi and 100 low-fi samples are selected by DoE to construct the initial HK model. To increase the confidence of the statistical analysis, the optimization based on each method is repeated 10 times. Figure 9 shows the comparison of the shapes and pressure coefficient distributions of baseline and optimal airfoils. As one can see that the location of maximal thickness is moved backward, compared with the baseline RAE2822 airfoil, and the leading edge radius is reduced. Consequently, the shock intensity is decreased sharply.

Fig. 9
figure 9

Comparison of baseline RAE 2822 and optimal airfoils (upper: pressure coefficient distributions; lower: airfoil shapes, Ma = 0.734, α = 2.8795°, Re  = 6.5 × 106)

Full size image

Figure 10 shows the averaged convergence histories of the objective function. The vertical bars represent the standard deviation of the objective function caused by repeating the optimizations. Please note that the convergence history is plotted in a manner that shows the variation of the best hi-fi objective function observed so far versus the number of hi-fi functional evaluations only. It is obvious that both the VFOs with the proposed VF-EI, augmented EI, and the standard EI perform much better than the single-fidelity optimization, and both the VF-EI and augmented EI are dramatically more efficient than the standard EI. For using the VF-EI, although more low-fi samples are used, the total computational cost is reduced dramatically, since a low-fi CFD is much cheaper than a hi-fi CFD. Table 7 shows the comparison of optimization results using four different methods. It can be seen that the VF-EI-based method offers the best design on average and smallest standard deviation. Table 8 is for the comparison of optimization efficiency of using four different methods. We can see that when 25 hi-fi sample points are used for the VFO with the standard EI method, the drag is reduced by 36.03%. In contrast, only 13 hi-fi samples (including 5 initial hi-fi samples) are needed to achieve the same level of drag reduction when the VF-EI method is used, which means that the VF-EI is almost twice faster than the standard EI method.

Fig. 10
figure 10

Comparison of convergence histories of VFOs using proposed VF-EI, augmented EI, and the standard EI with the single-fidelity optimization based on kriging and EI (RAE2822 airfoil test case)

Full size image
Table 7 Comparison of optimization results using different methods (RAE2822 airfoil test case)
Full size table
Table 8 Comparison of optimization efficiency of using different methods for same level of drag reduction (RAE2822 airfoil test case)
Full size table

5.2 Drag minimization of ONERA M6 wing in transonic inviscid flow

5.2.1 Problem statement

This case is the drag minimization of a ONERA M6 wing at a freestream condition of Ma = 0.8395, α = 3.06°, subject to four constraints on the maximum thickness-to-chord ratio and one constraints on the lift coefficient. The wing is parameterized by four control sections with the planar shape being fixed (see Fig. 11). Each of the control section is parameterized by five-order CST method, resulting in 12 variables for each section and 48 design variables in total. It can be written as a standard nonlinear programming problem:

$$ {\displaystyle \begin{array}{l}\min \kern0.6em {C}_D\\ {}s.t.\kern0.8em 1\Big)\kern0.3em {C}_L\ge {C}_{L,0}\\ {}\kern2em 2\left)\kern0.4em {t}_1\ge {t}_{1,0}\kern0.5em 3\right)\kern0.4em {t}_2\ge {t}_{2,0}\\ {}\kern2em 4\left)\kern0.4em {t}_3\ge {t}_{3,0}\kern0.5em 5\right)\kern0.4em {t}_4\ge {t}_{4,0}\end{array}}, $$
(21)

where t denotes the maximum thickness-to-chord ratio of the control sections, and its subscript is the index of the control sections.

Fig. 11
figure 11

Parameterization of ONERA M6 wing using 4 control sections with the 48 design variables in total

Full size image

5.2.2 Determination of low- and hi-fi CFD models

The flow analyses are performed with the in-house code called PMNS3D. It solves the Euler equations to simulate the inviscid flow around the wing. With the structured grids of C-H topology generated by our in-house code, the low- and hi-fi CFD models are also defined in a similar way with the previous cases. According to the grid study shown in Fig. 12, we choose the grid with the distribution of 168 (chord-wise direction) × 36 (normal direction) × 44 (span direction) as the low-fi CFD, and the grid with the distribution of 312 (chord-wise direction) × 72 (normal direction) × 72 (span direction) as the hi-fi CFD (see in Fig. 13). The low-fi CFD simulation terminates after 20 iterations and the hi-fi CFD simulate stops until the density residual has dropped 5.2 orders in magnitude, as shown in Fig. 14. For this wing case, the computational cost ratio of hi-fi CFD to low-fi CFD is approximately 10.

Fig. 12
figure 12

Determination of low- and hi-fi CFD models by grid convergence study for baseline M6 wing (Ma = 0.8395, α = 3.06°)

Full size image
Fig. 13
figure 13

Sketch of C type grids for low-fi (left) and hi-fi (right) CFD computations for baseline M6 wing case

Full size image
Fig. 14
figure 14

Convergence histories of low-fi (left) and hi-fi (right) simulations for baseline M6 wing (Ma = 0.8395, α = 3.06°)

Full size image

5.2.3 Results

The design space is obtained by expanding the CST parameters of control sections of M6 wing by 1.25 times and narrowing it by a quarter. And 24 hi-fi and 300 low-fi samples are selected by DoE to construct the initial HK model. Here, only VFO based on HK model, using VF-EI, augmented EI, and standard EI are conducted, as it is difficult for single-fidelity method to optimize the wing with 48 design variables. The optimizations are also repeated for 10 times in this case. Table 9 compares the aerodynamic performance and thickness of the control sections between the baseline and optimized wings. The drag coefficient is reduced by 29.69 cts with all of the constraints are satisfied. Figure 15 shows the comparison of pressure contour of baseline and optimized wings. The result is further checked by comparison of the pressure distributions and shape at four span-wise sections of the wing. As we can see that, the shock is weakened for the optimal shape at all of the sections.

Table 9 The optimization results for ONREA M6 wing test case (Ma = 0.8395, α = 3.06°)
Full size table
Fig. 15
figure 15

Comparison of baseline ONREA M6 and the optimal wings (Ma = 0.8395, α = 3.06°)

Full size image

The averaged convergence histories with standard deviation of using different optimization strategies are sketched in Fig. 16. One can see that the optimization efficiency can be improved by using the proposed VF-EI method. Table 10 is for the comparison of the optimization results using three different methods. Again, it is shown that the VF-EI-based method offers the best design on average. Table 11 is for the comparison of optimization efficiency of using three different methods for the same level of drag reduction. We can see that the VF-EI method also performs the best. When 17 hi-fi sample points are added (41 in total) for the VFO with the VF-EI method, the drag is reduced by 19.65%. As for the augmented EI and standard EI method, to achieve the same level of drag reduction, 30 and 43 hi-fi sample points are need to be added. And the augmented EI method does improve the optimization efficiency, but not as good as our VF-EI method.

Fig. 16
figure 16

Comparison of convergence histories of VFOs using proposed VF-EI, augmented EI, and the standard EI based on HK (ONREA M6 wing test case)

Full size image
Table 10 Comparison of optimization results using different methods (ONREA M6 wing test case)
Full size table
Table 11 Comparison of optimization efficiency of using different methods for same level of drag reduction (ONREA M6 wing test case)
Full size table

6 Summary and future works

In this article, a variable-fidelity expected improvement (VF-EI) method was proposed for efficient global optimization of expensive-to-evaluate function with assistance of cheaper-to-evaluate function, based on a variable-fidelity model called hierarchical kriging (HK). The VF-EI method, as an extension of standard EI method, can select the new samples of both low fidelity and high fidelity to update the VFM towards the global optimum of the hi-fi function, and the infillings of both low-fi and hi-fi samples are hi-fi-optimum oriented.

By redefining the uncertainty of the HK model, the VF-EI was analytically derived. The VF-EI refers to the expected improvement of the hi-fi function by infilling either a low-fi or a hi-fi sample point at any untried x in the design space. The uncertainty and expected improvement of the hi-fi function due to lack of a low-fi sample was analytically derived, and then the resulting VF-EI function is formulated as a function of both the design variables x and the fidelity level l. By maximizing the VF-EI, the new sample point and its fidelity level can be determined. The VF-EI method was further extended to handle nonlinear constraints, by evaluating the probability of satisfying the constraints using the model uncertainty associated with lack of a low-fi sample as well.

Theoretical analysis shows that, when VF-EI is used, typically the addition of low- and hi-fi samples will be in an alternative way, which is controlled by the ratio of the two kinds of uncertainties, where are due to lack of low- and hi-fi samples, respectively. Besides, the VF-EI will tend to add more low-fi samples than hi-fi samples, if the low- and hi-fi functions are highly correlated. When compared to an existing method called augmented EI, we found that the main difference is that the VF-EI is analytically derived and free of empirical parameters, but the performance of the augmented EI is dependent on the proper setting of two empirical parameters.

The VF-EI method was then verified and validated by optimization of six analytical functions, and demonstrated for aerodynamic shape optimizations of the benchmark RAE 2822 airfoil in transonic viscous flow and a 48-dimensional ONREA M6 wing in transonic inviscid flow. It was shown that the proposed VF-EI method can adaptively infill the low-fi and hi-fi samples in an alternative manner, and is proved to be effective in all of the presented optimization cases. In contrast, the performance of augmented EI method is problem dependent.

Our future work will focus on applying the VF-EI method to higher dimensional optimization, in order to examine its performance for complex engineering design problems. This is still challenging for surrogate-based optimization method, especially when the number of dimension is larger than 100. We believe that extending the two-level VFMs to multi-fidelity models and developing dedicated ISC can be a remedy to tackle this problem. On the other hand, the use of cheap gradients obtained by adjoint method or automatic differentiation will be another promising way to ameliorate the “curse of dimensionality.”