Surface effects on vibration analysis of elastically restrained piezoelectric nanobeams subjected to magneto-thermo-electrical field embedded in elastic medium

Abstract

In the present study, a generalized nonlocal beam theory is utilized to study the magneto–thermo–mechanical vibration characteristic of piezoelectric nanobeam by considering surface effects rested in elastic medium for various elastic boundary conditions. The nonlocal elasticity of Eringen as well as surface effects, including surface elasticity, surface stress and surface density are implemented to inject size-dependent effects into equations. Using the Hamilton’s principle and Euler–Bernoulli beam theory, the governing differential equations and associated boundary conditions will be obtained. The differential transformation method (DTM) is used to discretize resultant motion equations and related boundary conditions accordingly. The natural frequencies are obtained for the various elastic boundary conditions in detail to show the significance of nonlocal parameter, external voltage, temperature change, surface effects, elastic medium, magnetic field and length of nanobeam. Moreover, it should be noted that by changing the spring stiffness at each end, the conventional boundary conditions will be obtained which are validated by well-known literature.

1 Introduction

In recent years, the tendency in studying the mechanical behavior of nanostructures has been grown. Among all nanostructures, the piezoelectric, for their unique mechanical properties, proved to be capable of designing the nano-electro-mechanical systems (NEMSs). It is apparent that these nanomaterials can be applicable for building blocks for nanodevices integrating mechanical and electrical functionality at nanoscale size [1]. So, according to their wide range of application such as nano-sensors, actuators, generators, transistors, and diodes, investigating the vibrational behavior of piezoelectric nanomaterials is significant [2].

It is known that the classical continuum mechanics cannot predict the size effects. Therefore, to inject the size-dependent response of nanostructures, several non-classical higher-order continuum theories have been employed, such as nonlocal elasticity theory [3], stress theory [4], strain gradient theory [5], surface elasticity [6], and micropolar theory [7]. Among all these theories, the nonlocal elasticity theory of Eringen [3] can be employed in a wide range of applications in the analysis of nanostructures. Due to simplicity and high computational efficiency of nonlocal elasticity theory, rapid extensions of this theory in various mechanical analysis for different nanostructures can be observed as [8–10].

One of the main size-dependent factors of nanostructures is surface effects, which are happening for increasing the surface-to-volume ratio in nanoscale. Due to high surface-to-volume ratio, the surface effects as well as the small scale effect become substantial, which leads to exceptional mechanical characteristics at the nanoscale. Therefore, as the surface layers energy is negligible compared with the bulk energy of material at the macroscale, the classical continuum mechanics is not applicable to predict the surface energy effect. Gurtin and Murdoch [11, 12], based on the continuum mechanics, developed a theoretical framework to take the surface energy effects into account. According to this theory, the surface layer is considered as an elastic two-dimensional membrane with zero thickness adhered to the underlying bulk material without slipping. It is also considered that the surface layers have distinct properties than the bulk of material which is characterized using the Lame constants of surface followed by surface residual stress. Many efforts have been done to investigate the surface effects [13–18] and nonlocal effects [19–27] on the mechanical properties of nanobeam separately, and simultaneously [2, 28–36].

Also, remarkable attention has been paid to investigate the mechanical characteristic of piezoelectric nanostructures in high-temperature conditions. So, the influence of temperature changing in the mechanical analysis is studied extensively. As for instance, Ebrahimi et al. [37] investigated the vibration characteristic of smart piezoelectrically actuated nanobeams in the magneto-electrical field and thermal environment. Further, Ke et al. [38] implemented the nonlocal elasticity theory into the thermo-electric-mechanical vibration analysis of piezoelectric nanobeam. Furthermore, Mohammadimehr et al. [39] studied the vibration and buckling analysis of triple-walled ZnO piezoelectric nanobeam based on the Timoshenko beam theory resting on Pasternak foundation under magneto-electro-thermo-mechanical loadings. In the work done by Marzbanrad et al. [40], the vibration behavior of size-dependent piezoelectric nanobeam resting on elastic under axial preload was studied by considering surface and thermal effects. Moreover, Ansari et al. [41] implemented the analytical solution to predict the postbuckling characteristics of FGM nanobeams subjected to thermal environment and surface stress effect.

It should be noted that all the mentioned works presented the numerical results for various mechanical properties of nanostructures for conventional boundary conditions (BCs) including Simply–Simply (S–S), Clamped–Clamped (C–C), Clamped–Simply (C–S) and Clamped–Free (C–F). In continuous systems, the type of BCs from their direct effect on vibration response of structures is so important. Mostly, in real systems, one of the mentioned BCs which has the nearest manner are chosen and assumed to satisfy the conditions exactly [42, 43]. Moreover, the rotational and transitional springs will substitute at the ends to introduce small deflections and moments. Further, Wattanasakulpong et al. [44] studied the linear and nonlinear vibration behavior of nanobeams which are elastically end-restrained. The numerical results are presented for Elastic–Elastic (E–E) and Simply–Elastic (S–E) boundary conditions. Besides, Zarepour et al. [45] investigated the electro-thermo-mechanical nonlinear characteristic of nanobeams resting on Winkler–Pasternak elastic medium for E–E and S–S BCs.

The present paper makes the first attempt to investigate the magneto-thermo-electric-mechanical vibration of piezoelectric nanobeam with elastic boundary condition by considering surface and nonlocal elasticity effects. Based on the Eringen’s nonlocal constitutive relations and using Gurtin–Murdoch theory to incorporate the surface effects, equilibrium equations of piezoelectric nanobeam subjected in magnet and thermal field is achieved. The differential transformation method (DTM) with an iterative algorithm on the basis of Taylor series expansion is utilized to solve resultant motion equations for various BCs. The natural frequencies for various elastic boundary conditions are obtained, while, by choosing right values for spring stiffness at each end of nanobeam, the corresponding natural frequencies for classical BCs will be achieved. To validate the accuracy of motion equations and numerical results, the resultant natural frequencies are compared with well-known literature which are in excellent agreement. The results are obtained for various spring stiffness constants, voltage values of piezoelectric field, temperature changing, magnetic field effect, nonlocal parameter, elastic foundation including Pasternak and Winkler foundations and nanobeam length for various elastic boundary conditions. It is shown that making changes to spring stiffness value and surface effect of piezoelectric nanobeam are two main approaches to achieve desired natural frequencies.

2 Formulation and theories

2.1 Eringen’s nonlocal elasticity theory

Among various types of nonlocal elasticity theory, Eringen’s theory proved to be capable and easy to use. The essence of nonlocal elasticity is that the stress field at a reference point x in an elastic medium does not only depend on the strain at that point, but also on the strains at all other points in the bulk of material [3].

This theory is based on the atomic theory of lattice dynamics and also the experimental observations of atomic and molecular scales which come from the observations on phonon dispersion. In this theory, the internal size as a material parameter is used to incorporate the scale effects into the equations [46]. The most general form of nonlocal elasticity relations will be indicated as an integral over the whole body of material, but by neglecting the body forces, the basic equations for stress tensor and electric displacement will be obtained as [47]:

$${{\sigma }_{ij}}-{{\mu }^{2}}{{\nabla }^{2}}{{\sigma }_{ij}}={{C}_{ijkl}}{{\varepsilon }_{kl}}-{{e}_{kij}}{{E}_{k}}-{{\lambda }_{ij}}\Delta T\ ,$$

(1)

$${{D}_{i}}-{{\mu }^{2}}{{\nabla }^{2}}{{D}_{i}}={{e}_{ikl}}{{\varepsilon }_{kl}}+{{\varepsilon }_{ik}}{{E}_{k}}+{{p}_{i}}\Delta T\ ,$$

(2)

where ${{\nabla }^{2}}$ is the Laplace operator, ${{\sigma }_{ij}},\ {{D}_{i}}$ denote the component of the stress, electric field; ${{\varepsilon }_{kl}},\ {{C}_{ijkl}},\ {{e}_{_{ikl}}},\ {{\lambda }_{ij}}$ are the strain, elastic constant, piezoelectric constants and thermal module. $\Delta T$ and ${{p}_{i}}$ are the temperature changes and piezoelectric constants; and also, $\mu ={{({{e}_{0}}a)}^{2}}$ represent the nonlocal parameter; moreover, ${{e}_{0}}a$ denotes the scale length coefficient revealing the size effect in obtaining the response of nanostructures.

2.2 Surface effects

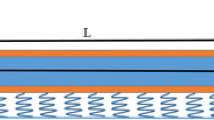
For the fact that the inter-atomic distance plays an important role in elastic constant of crystals, the bound contraction in the surface layers has a dominant influence than that in the bulk. To increase the surface-to-bulk ratio in nanoscale, the surface effects will become more significant and cannot be neglected. As this ratio increases, the surface effects role in response of nanobeam become more dominant. Accordingly, the energy which is produced by the atoms located in surface layers affects the mechanical properties of nanostructures which have been studied extensively by researchers. Gurtin et al. [11] proposed a continuum model which considered the surface layers as a zero-thickness film which subjected on the material body. In other words, the body and surface layers in the nanobeam are assumed such as a composite beam which is composed of a solid core with the bulk modulus and the surface shell with surface modulus as depicted in Fig. 1. The surface layer is assumed to be a two-dimensional thin film which attached perfectly to the bulk. Besides, the surface layers and the bulk material considered to be bonded, accordingly, the displacement field is continuous for both parts across the interface. It should be noted that this assumption is only for the modeling purpose which means that these layers do not actually exist; for this reason, the type of surface is not defined. For isotropic surfaces, the local stresses and electric displacement will be defined for piezoelectric nanobeam based on Gurtin model as [29]:

Fig. 1

Schematic of the nanobeam with elastic boundary conditions with length L, width b and height h

$$\tau _{\alpha \beta }^{sl}=\tau _{\alpha \beta }^{0}+C_{\alpha \beta \gamma \delta }^{s}{{\varepsilon }_{\gamma \delta }}-e_{\alpha \beta k}^{s}{{E}_{k}}\ ,$$

(3)

$$D_{i}^{\text{sl}}=D_{i}^{0}+e_{\alpha \beta i}^{s}{{\varepsilon }_{\alpha \beta }}+k_{ij}^{s}{{E}_{j}}\ ,$$

(4)

where $C_{\alpha \beta \gamma \delta }^{s}$, ${{\varepsilon }_{\gamma \delta }}$,$e_{\alpha \beta k}^{s}$ and $k_{ij}^{s}$ express the surface elastic, surface strains, surface piezoelectric and surface dielectric constants, respectively. $\tau _{\alpha \beta }^{sl}$, $\tau _{\alpha \beta }^{0}$ denote the nonlocal stress tensor and residual surface stress tensor, respectively.

By considering the same material properties for both top and bottom layers, the constitutive stress–strain relations for surface layers will be obtained as:

$${{\tau }_{xx}}={{\tau }_{0}}+{{E}^{s}}{{u}_{x,x~}},~~~~{{E}^{s}}=2{{\mu }_{0}}+{{\lambda }_{0}},~\ {{\tau }_{nx}}={{\tau }_{0}}{{u}_{n,x}}\ ,$$

(5)

while $\mathop{\sigma }_{zz}$ is often neglected in classical beam theories, which is assumed to satisfy the equilibrium equations by its linear relation with the beam thickness:

$${{\sigma }_{\mathbf{zz}}}=\frac{2z\nu }{h}({{\tau }_{o}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-{{\rho }_{o}}\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}})$$

(6)

2.3 Problem formulation

The vibration analysis of piezoelectric nanobeam embedded in elastic medium using the nonlocal and surface effects under the magnet and thermal environment with various elastic boundary conditions will be presented. The piezoelectric nanobeam with length L ($0\le x\le L$), thickness h ($-h/2\le z\le h/2$), and width b ($-{}^{b}\!\!\diagup\!\!{}_{2}\;\le y\le {}^{b}\!\!\diagup\!\!{}_{2}\;$) subjected to an applied voltage $\phi (x,\ z)$ and uniform temperature change $\Delta T$ is depicted in Fig. 1. The Euler–Bernoulli beam theory is utilized to obtain the motion equations. Following the Euler–Bernoulli beam theory (EBT), the displacement field for nanobeam at any arbitrary point is [48]:

$${{u}_{1}}=u\left( x,\,t \right)-z\frac{\partial w\left( x,t \right)}{\partial x},\ \ {{u}_{2}}=0,\ \ {{u}_{3}}=w(x,\,t)\ ,$$

(7)

where $u\left( x,\ t \right)$ and $w(x,\ t)$ denote the axial and transverse components of displacement, respectively.

The only nonzero strain component which can be defined based on EBT is:

$${{\varepsilon }_{xx}}=\frac{\partial u}{\partial x}-z\frac{{{\partial }^{2}}w}{{{\partial }^{2}}x}$$

(8)

And also, the electric displacement field for piezoelectric nanobeam can be expressed as [14]:

$$\begin{array}{*{20}l} {E_{x} = - \frac{{\partial \phi }}{{\partial x}};\;E_{z} = - \frac{{\partial \phi }}{{\partial z}},} \hfill \\ {D_{x} = \lambda _{{11}} E_{x} ;\;D_{z} = e_{{31}} \varepsilon _{x} + \lambda _{{33}} E_{z} ,} \hfill \\ {\frac{{\partial D_{x} }}{{\partial x}} + \frac{{\partial D_{z} }}{{\partial z}} = 0} \hfill \\ \end{array}$$

(9)

where ${{\lambda }_{11}}$ and ${{\lambda }_{33}}$ are the dielectric constants, while ${{D}_{x}}$and ${{D}_{z}}$express the electric displacements.

For the fact that ${{\lambda }_{11}}$and ${{\lambda }_{33}}$ are in the same order, ${{E}_{x}}<<{{E}_{z}}$ should be considered, ${{D}_{x}}$ in compare with ${{D}_{z}}$ should be ignored. The electrical BCs will be assumed as $\phi (x,\,\ -h/2)=0,\,\,\,\,\,\phi (x,\,\ h/2)=2V$combining with Eqs. (8) and (9), the electrical potential can be obtained as:

$$\phi (x,\,z)=-\frac{{{e}_{31}}}{{{\lambda }_{33}}}\left( \frac{{{z}^{2}}-{{h}^{2}}}{2} \right)\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\left( 1+\frac{z}{h} \right)V$$

(10)

Furthermore, the equivalent piezoelectric load can be expressed as follows:

$${{P}_{\text{electric}}}(x,t)=b\int\limits_{-h}^{h}{\sigma _{x}^{*}\,dz}=2\,V\,b\,{{e}_{31}}$$

(11)

Accordingly, using Hamilton’s principle, the governing motion equations and relative BCs will be obtained as [48]:

$$\int_{0}^{t}{\delta (U-T+{{W}_{\text{ext}}})\,dt=0}\ ,$$

(12)

where U, T and ${{W}_{\text{ext}}}$ are the strain energy, kinetic energy and the work done by external forces, respectively. The first variation of strain energy for piezoelectric nanobeams is:

$$\delta U = \int\limits_{0}^{L} {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\begin{array}{*{20}l} {} \hfill & {\sigma _{{xx}} \delta \varepsilon _{{xx}} + \sigma _{{xz}} \delta \gamma _{{xz}} - D_{x} \delta E_{x} - D_{z} \delta E_{z} + K_{{{\text{TL}}}} {\mkern 1mu} w(0,{\mkern 1mu} t){\mkern 1mu} \delta {\mkern 1mu} w(0,{\mkern 1mu} t)} \hfill \\ {} \hfill & { + {\mkern 1mu} K_{{{\text{RL}}}} \frac{{\partial w(0,t)}}{{\partial x}}{\mkern 1mu} \delta (\frac{{\partial w(0,t)}}{{\partial x}}) + K_{{{\text{TR}}}} {\mkern 1mu} w(L,{\mkern 1mu} t){\mkern 1mu} \delta {\mkern 1mu} w(L,{\mkern 1mu} t)} \hfill \\ {} \hfill & { + {\mkern 1mu} K_{{{\text{RR}}}} \frac{{\partial w(L,{\mkern 1mu} t)}}{{\partial x}}\delta (\frac{{\partial w(L,{\mkern 1mu} t)}}{{\partial x}})} \hfill \\ \end{array} } \right)dz{\mkern 1mu} dx} \;,}$$

(13)

where ${{K}_{\text{RL}}}$, ${{K}_{\text{TL}}}$,${{K}_{\text{RR}}}$and ${{K}_{\text{TR}}}$ express the corresponding rotational and translational spring constants at the left and right ends, respectively. Using Eq. (8) and Eq. (13) gives:

$$\delta U = \int\limits_{0}^{l} {\int_{{ - h/2}}^{{h/2}} {\left[ {\begin{array}{*{20}l} {N\delta u - M\delta \left( {\frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right) + D_{x} \delta \left( {\frac{{\partial \phi }}{{\partial x}}} \right) + D_{z} \delta \left( {\frac{{\partial \phi }}{{\partial z}}} \right)} \hfill \\ { + K_{{{\text{TL}}}} {\mkern 1mu} w(0,{\mkern 1mu} t){\mkern 1mu} \delta {\mkern 1mu} w(0,t) + K_{{{\text{RL}}}} \frac{{\partial w(0,t)}}{{\partial x}}{\mkern 1mu} \delta (\frac{{\partial w(0,t)}}{{\partial x}})} \hfill \\ { + K_{{{\text{TR}}}} {\mkern 1mu} w(L,{\mkern 1mu} t){\mkern 1mu} \delta {\mkern 1mu} w(L,t) + K_{{{\text{RR}}}} \frac{{\partial w(L,t)}}{{\partial x}}\delta (\frac{{\partial w(L,t)}}{{\partial x}})} \hfill \\ \end{array} } \right]dx} }$$

(14)

Accordingly, the axial force N and bending moment force M are defined as:

$$N=\int{{{\sigma }_{xx}}dz}\,,\ M=\int{\,{{\sigma }_{xx}}zdz}$$

(15)

After that, the kinetic energy will be determined as:

$$T=\frac{1}{2}\rho \,\iint{(\dot{u}_{1}^{2}+\dot{u}_{2}^{2}+\dot{u}_{3}^{2})\,}dA.dx=\frac{1}{2}\rho \int{\left( {{I}_{1}}{{\left( \frac{\partial u}{\partial t} \right)}^{2}}+{{I}_{2}}{{\left( \frac{{{\partial }^{2}}w}{\partial x\partial t} \right)}^{2}}+{{I}_{1}}{{\left( \frac{\partial w}{\partial t} \right)}^{2}} \right)}\,dx$$

(16)

Thus, the first variation of kinetic energy from Eq. (16) can be written as:

$$\delta T=-\int\limits_{0}^{l}{\left( {{I}_{1}}\left( \frac{{{\partial }^{2}}w}{\partial {{t}^{2}}} \right)\delta (w)-{{I}_{2}}\left( \frac{{{\partial }^{4}}w}{\partial {{x}^{2}}\partial {{t}^{2}}} \right)\delta (w)+{{I}_{1}}\left( \frac{{{\partial }^{2}}u}{\partial {{t}^{2}}} \right)\delta (u) \right)}dx$$

(17)

where:

$$I_{1} = \int_{-\frac{h}{2}}^{{\frac{h}{2}}} {\rho \,dz},\quad I_{2} = \int_{{- \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \,z^{2} \,dz}$$

(18)

The axial load which is obtained by the elastic medium based on the Winkler–Pasternak foundation is considered to be as:

$$f=-{{k}_{\text{w}}}w+{{k}_{\text{p}}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}$$

(19)

where k _w and k _p are the Winkler and Pasternak elastic medium constants.

The first variation of the work done by external forces will be determined by:

$$\delta {{W}_{\text{ext}}}=\int\limits_{0}^{t}{\left( f\delta (u)+q\delta (w) \right)}dt\ ,$$

(20a)

where q is defined as:

$$q=\left( H+{{N}_{T}}+{{P}_{\text{electric}}}+{{K}_{P}}+{{q}_{z}} \right)\left( \frac{{{\partial }^{2}}W}{\partial {{x}^{2}}} \right)-{{K}_{w}}\,W\ ,$$

(20b)

$${{N}_{T}}=-E{{\lambda }_{1}}\,A\,\Delta T$$

(21a)

$${{f}_{z}}=\eta \,H_{x}^{2}\left( \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}} \right)$$

(21b)

$${{q}_{z}}=\int_{A}{{{f}_{z}}\,dz}=\eta \,A\,H_{x}^{2}\left( \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}} \right)$$

(21c)

$$H=2b{{\tau }_{0}}$$

(21d)

Substituting Eqs. (14), (17) and (19) into Hamilton’s principle [Eq. (12)], the motion equations are obtained as:

$$\frac{\partial N}{\partial x}+f-{{I}_{1}}\left( \frac{{{\partial }^{2}}u}{\partial {{t}^{2}}} \right)=0$$

(22a)

$$\frac{{{\partial }^{2}}M}{\partial {{x}^{2}}}+q+{{I}_{2}}\left( \frac{{{\partial }^{4}}w}{\partial {{x}^{2}}\partial {{t}^{2}}} \right)-{{I}_{1}}\left( \frac{{{\partial }^{2}}w}{\partial {{t}^{2}}} \right)=0$$

(22b)

The bending moment and spring constants based on the obtained BCs from Hamilton’s principle will be described as:

$$-M-{{K}_{\text{RL}}}\frac{\partial w}{\partial x}=0,\quad \frac{\partial M}{\partial x}-{{K}_{\text{TL}}}\,w=0\,\text{at}\,x=0$$

(23a)

$$M-{{K}_{\text{RR}}}\frac{\partial w}{\partial x}=0,\quad -\frac{\partial M}{\partial x}-{{K}_{\text{TR}}}\,w=0\ \text{at}\ x=L$$

(23b)

The bending moment with considering surface and nonlocal effects for piezoelectric nanobeam will be obtained as:

$$M=\int{{{\sigma }_{xx}}zdA+\int{{{\tau }_{xx}}zdA-\int{{{e}_{31}}{{\phi }_{z}}zdA}}}$$

(24)

$$M=-{{(EI)}^{*}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\frac{2I\nu }{h}\left( {{\tau }_{0}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-{{\rho }_{0}}\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}} \right)+\frac{e_{31}^{2}}{{{\lambda }_{33}}}I\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}\ ,$$

(25)

where the effective bending stiffness of nanobeam will be determined as ${{\left( EI \right)}^{*}}=E\left( {\scriptstyle{}^{b{{h}^{3}}}\!\!\diagup\!\!{}_{12}\;} \right)+{{E}_{s}}\,({\scriptstyle{}^{{{h}^{3}}}\!\!\diagup\!\!{}_{6}\;}+{\scriptstyle{}^{b\,{{h}^{2}}}\!\!\diagup\!\!{}_{2}\;})$. The bending moment using the nonlocal elasticity will be obtained as:

$$M-\mu \frac{{{\partial }^{2}}M}{\partial {{x}^{2}}}=-{{(EI)}^{*}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\frac{2I\nu }{h}\left( {{\tau }_{0}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-{{\rho }_{0}}\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}} \right)+\frac{e_{31}^{2}}{{{\lambda }_{33}}}I\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}$$

(26)

$$M=\mu \left( -{{I}_{2}}\left( \frac{{{\partial }^{4}}w}{\partial {{x}^{2}}\partial {{t}^{2}}} \right)+{{I}_{1}}\left( \frac{{{\partial }^{2}}w}{\partial {{t}^{2}}} \right)-q \right)-{{(EI)}^{*}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}\ +\ \frac{2I\nu }{h}\left( {{\tau }_{0}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-{{\rho }_{0}}\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}} \right)+\frac{e_{31}^{2}}{{{\lambda }_{33}}}I\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}$$

(27)

Substituting Eqs. (27) into (22), the constitutive motion equation is as:

$$\begin{array}{*{20}l} {} \hfill & {\left( {1 - \mu \frac{{\partial ^{2} }}{{\partial x^{2} }}} \right)\left( { - I_{2} \left( {\frac{{\partial ^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right) + I_{1} \left( {\frac{{\partial ^{2} w}}{{\partial t^{2} }}} \right) - q_{w} } \right) - (EI)^{*} \frac{{\partial ^{4} w}}{{\partial x^{4} }} + \frac{{2I\nu }}{h}\left( {\tau _{0} \frac{{\partial ^{4} w}}{{\partial x^{4} }} - \rho _{0} \frac{{\partial ^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right)} \hfill \\ {} \hfill & { + \frac{{e_{{31}}^{2} }}{{\lambda _{{33}} }}I\frac{{\partial ^{4} w}}{{\partial x^{4} }} = 0} \hfill \\ \end{array}$$

(28)

For the free vibration response of piezoelectric nanobeam, a harmonic motion is assumed with the natural frequency of $\omega$ as:

$$w(x,\,t)=W(x){{e}^{i\omega t}}$$

(29)

Substituting Eqs. (29) into (28) resulted to:

$$\begin{array}{*{20}l} {} \hfill & {\left( {1 - \mu \frac{{\partial ^{2} }}{{\partial x^{2} }}} \right)\left( {\omega ^{2} I_{2} \left( {\frac{{\partial ^{2} W}}{{\partial x^{2} }}} \right) - \omega ^{2} I_{1} W(x) - q_{w} } \right) - (EI)^{*} \frac{{\partial ^{4} W}}{{\partial x^{4} }} + \frac{{2I\nu }}{h}\left( {\tau _{0} \frac{{\partial ^{4} W}}{{\partial x^{4} }} + \rho _{0} \omega ^{2} \frac{{\partial ^{4} W}}{{\partial x^{2} }}} \right)} \hfill \\ {} \hfill & { + \frac{{e_{{31}}^{2} }}{{\lambda _{{33}} }}I\frac{{\partial ^{4} W}}{{\partial x^{4} }} = 0} \hfill \\ \end{array}$$

(30)

2.4 Solution procedure

To derive an analytical solution for Eq. (30) due to the nature homogeneity is relatively difficult. In this condition, the DTM is utilized to translate the governing equations into ordinary equation. The manner of differential transform method is explained briefly in the following. In this method, differential transformation of k ^th derivative function y(x) and inverse of differential transformation of Y(k) are explained as [49]:

$$Y\left( k \right)=\text{ }\!\!~\!\!\text{ }\frac{1}{k!}{{\left[ \frac{{{\text{d}}^{k}}}{\text{d}{{x}^{k}}}y\left( x \right) \right]}_{x=0}}\ ,$$

(31a)

$$y\left( x \right)=\underset{k=0}{\overset{\infty }{\mathop \sum }}\,{{x}^{k}}Y(k)\ ,$$

(31b)

where y(x) is the original function and Y(k) is the transformed function. Equations (31) can be explored as:

$$y\left( x \right)=\text{ }\!\!~\!\!\text{ }\underset{k=0}{\overset{\infty }{\mathop \sum }}\,\frac{{{x}^{k}}}{k!}{{\left[ \frac{{{\text{d}}^{k}}}{\text{d}{{x}^{k}}}y\left( x \right) \right]}_{x=0}}$$

(32)

The theory of the differential transformation is derived from Taylor’s series expansion that can be deduced from Eq. (31a). The function y(x) in Eq. (31b) can be written in a finite form as:

$$y\left( x \right)=\underset{k=0}{\overset{N}{\mathop \sum }}\,{{x}^{k}}Y(k)$$

(33)

From the definitions of DTM in Equations (31), fundamental theorems of differential transforms method can be utilized that are listed in Table 1 and in Table 2 tabulated the differential transformation of boundary conditions. Applying the DTM into the equation of motion resulted as:

Table 1 Some basic theorems of DTM for equations of motion

Table 2 Transformed boundary conditions (BC) based on DTM

$$\begin{array}{*{20}l} {} \hfill & {\left( {\left( {EI} \right)^{*} + {\mkern 1mu} \frac{{2{\mkern 1mu} I_{3} {\mkern 1mu} \nu }}{h}\tau _{0} - \frac{{e_{{31}}^{2} }}{{\lambda _{{33}} }} - \mu ^{2} \left( {N_{T} + P_{{{\text{electric}}}} + H + K_{P} + q_{z} } \right)} \right)\frac{{\left( {k + 4} \right)!}}{{k!}}W[k + 4]{\mkern 1mu} } \hfill \\ {} \hfill & { + \left( {\frac{{2{\mkern 1mu} I_{3} {\mkern 1mu} \nu {\mkern 1mu} \rho _{0} {\mkern 1mu} \omega ^{2} }}{h} + \left( {N_{T} + P_{{{\text{electric}}}} + H + K_{P} + q_{z} } \right) + \mu ^{2} K_{w} - I_{1} {\mkern 1mu} \mu ^{2} {\mkern 1mu} \omega ^{2} } \right)\frac{{\left( {k + 2} \right)!}}{{k!}}W[k + 2]{\mkern 1mu} } \hfill \\ {} \hfill & { - \left( {K_{w} + I_{1} {\mkern 1mu} \omega ^{2} } \right)W[k]{\mkern 1mu} = 0} \hfill \\ \end{array}$$

(34)

By simplifying Eq. (34), the following relation will be obtained:

$$W{\mkern 1mu} [k + 4{\mkern 1mu} ] = \frac{{ - \left( {\frac{{2{\mkern 1mu} I_{3} {\mkern 1mu} \nu {\mkern 1mu} \rho _{0} {\mkern 1mu} \omega ^{2} }}{h} + \left( {N_{T} + P_{{{\text{electric}}}} + H + K_{P} + q_{z} } \right) + \mu ^{2} K_{w} - I_{1} {\mkern 1mu} \mu ^{2} {\mkern 1mu} \omega ^{2} } \right)\frac{{\left( {k + 2} \right)!}}{{k!}}W{\mkern 1mu} [k + 2{\mkern 1mu} ]{\mkern 1mu} + \left( {K_{w} + I_{1} {\mkern 1mu} \omega ^{2} } \right)W[k]{\mkern 1mu} }}{{\left( {\left( {EI} \right)^{*} + {\mkern 1mu} \frac{{2{\mkern 1mu} I_{3} {\mkern 1mu} \nu }}{h}\tau _{0} - \frac{{e_{{31}}^{2} }}{{\lambda _{{33}} }} - \mu ^{2} \left( {N_{T} + P_{{{\text{electric}}}} + H + K_{P} + q_{z} } \right)} \right)\frac{{\left( {k + 4} \right)!}}{{k!}}}}$$

(35)

Besides, applying the Table 2 relations to boundary conditions results:

Clamped–Elastic supported (C–E):

$$\begin{gathered} W\left[ 0 \right] = 0{\mkern 1mu} ,~\;W\left[ 1 \right] = 0,~\;W\left[ 2 \right] = C_{1} ,~\;W\left[ 3 \right] = C_{2} \hfill \\ \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;EI_{s} {\mkern 1mu} k(k - 1)\;W[k] - \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;K_{{{\text{RR}}}} k\;W[k] = 0 \hfill \\ \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;EI_{s} {\mkern 1mu} k(k - 1){\mkern 1mu} (k - 2)\;W[k]\; + \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;K_{{{\text{TR}}}} \;W[k] = 0 \hfill \\ \end{gathered}$$

(36a)

Simply–Elastic supported (S–E):

$$\begin{gathered} W\left[ 0 \right] = 0{\mkern 1mu} ,~\;W\left[ 2 \right] = C_{1} ,~\;W\left[ 1 \right] = 0,~\;W\left[ 3 \right] = C_{2} \hfill \\ \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;EI_{s} {\mkern 1mu} k(k - 1)\;W[k] - \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;K_{{{\text{RR}}}} k\;W[k] = 0 \hfill \\ \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;EI_{s} {\mkern 1mu} k(k - 1){\mkern 1mu} (k - 2)\;W[k] + \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;K_{{{\text{TR}}}} \;W[k] = 0 \hfill \\ \end{gathered}$$

(36b)

Elastic–Elastic supported (E–E):

$$\begin{array}{*{20}l} {} \hfill & {W\left[ 0 \right] = C_{1} {\mkern 1mu} ,~\;W\left[ 1 \right] = C_{2} {\mkern 1mu} ,~\;W\left[ 2 \right] = - \frac{{K_{{{\text{RL}}}} C_{2} }}{{2EI_{s} }},~\;W\left[ 3 \right] = \frac{{K_{{{\text{TL}}}} C_{1} }}{{6EI_{s} }}} \hfill \\ {} \hfill & {\mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;EI_{s} {\mkern 1mu} k(k - 1)\;W[k] - \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;K_{{{\text{RR}}}} k\;W[k] = 0} \hfill \\ {} \hfill & {\mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;EI_{s} {\mkern 1mu} k(k - 1){\mkern 1mu} (k - 2)\;W[k] + \mathop {\mathop \sum \limits^{\infty } }\limits_{{k = 0}} {\mkern 1mu} \;K_{{{\text{TR}}}} \;W[k] = 0} \hfill \\ \end{array}$$

(36c)

It should be noted that the transitional and rotational spring constants at each end of nanobeam will be expressed in the terms of moment of inertia and the Young’s modulus as:

$${{K}_{\text{TL}}}=\frac{{{\beta }_{\,\text{TL}}}{{E}_{c}}\,I}{{{L}^{3}}},\ \ {{K}_{\text{RL}}}=\frac{{{\beta }_{\,\text{RL}}}{{E}_{c}}\,I}{L},\ \,{{K}_{\text{TR}}}=\frac{{{\beta }_{\,\text{TR}}}\,{{E}_{c}}\,I}{{{L}^{3}}},\ \ {{K}_{\text{RR}}}=\frac{{{\beta }_{\,\text{RR}}}\,{{E}_{c}}I}{L}\ ,$$

(37)

where $\beta$ denotes the spring constant factor.

3 Numerical results and discussion

This section is dedicated to results obtained for analysis of megneto-thermo-mechanical vibration behavior of piezoelectric nanobeam incorporating nonlocal parameter, surface effect, elastic foundation for various elastic boundary conditions based on the Euler–Bernoulli beam theory. The material properties of nanobeam made of AL are given in Table 3.

Table 3 Al material properties

It should be noted that in the case in which the spring constants at each end in Elastic–Elastic boundary condition set to be a high value as ${{10}^{6}}$, the resultant natural frequencies correspond to the clamped boundary condition. Moreover, other conventional boundary conditions will be obtained for various values of spring constants, for instance, in Simply–Elastic (S–E) boundary condition by substituting ${{\beta }_{\text{RR}}}={{10}^{-6}},\ {{\beta }_{\text{TR}}}={{10}^{6}}$ is corresponding to S–S case and ${{\beta }_{\text{RR}}}={{\beta }_{\text{TR}}}={{10}^{6}}$ related to S-C case. And also for clamped–elastic (C–E) boundary condition, by substituting ${{\beta }_{\text{RR}}}={{\beta }_{\text{TR}}}={{10}^{-6}}$ is equivalent to C-F boundary condition and if by assuming ${{\beta }_{\text{RR}}}={{\beta }_{\text{TR}}}={{10}^{6}},$ the obtained boundary condition is C–C. To validate the accuracy of the numerical results, comparison between the present results and available results obtained by Reddy [48] for simply-supported boundary condition and Eltaher [50] for clamped–clamped, simply–clamped and clamped–free boundary condition are tabulated in Tables 4 and 5, respectively. As it is indicated from Tables 4 and 5, an excellent agreement is obtained for all classical boundary conditions. And also, for the fact that the experimental tests do not exist in detail for various conditions, in this study, the first dimensional frequency versus aspect ratio is also compared with the results which are obtained by molecular dynamic simulation respresented in Ansari and Sahmani [51] and showed to be in acceptable agreement which is depicted in Fig. 2.

Table 4 Comparison of the non-dimensional fundamental frequency for a nanobeam with various nonlocal parameters for simply-supported boundary condition (L = 10 nm, h/b = 2)

Table 5 Comparison of the non-dimensional fundamental frequency for a nanobeam with various nonlocal parameters for Clamped–Simply, Clamped–Clamped, Clamped–Free boundary condition (L = 10 nm, h/b = 2)

Fig. 2

The variation of the first frequency of classical beam versus aspect ratio in compare with the molecular dynamic results represented in Ref [51]

After that, the convergence study is performed to determine the minimum number of iterations required to obtain stable and accurate results for classical boundary condition as it is mentioned above in Table 6. As it can be observed for C–F boundary condition, the first three natural frequencies converge after 17th, 23rd and 35th iterations with four digit precisions, respectively. And also for S–S case, these natural frequencies converge after 17th, 27th^, and 35th iterations, while for C-S, they converge after 19th, 29th, and 37th iterations, and at last, for C–C boundary condition, the resultant natural frequencies converge after 23th, 33th, and 41st iterations. Therefore, the number of iterations is selected as k = 25 for the results reported here for first natural frequencies.

Table 6 Convergence study of nanobeam for the first three natural frequencies by considering surface effects ($L/h=10,\ L=20\ \text{nm},\ \ \mu =2\ \text{n}{{\text{m}}^{2}},h/b=2)$

First, natural frequencies of nanobeam are presented in Table 7 for various elastic boundary condition with different nonlocal parameter and spring constant factors. It can be found from the results that by incorporating the surface effects, the natural frequencies corresponding to all values of nonlocal parameters increase which indicates the fact that by considering the surface effects, the stiffness of nanobeam will be increased. Also, it is observed from Table 7 that for spring constant factor between 10⁻⁶ and 1, increasing nonlocal parameter causes an increase in natural frequencies for C–E and E–E boundary conditions. Also, for spring constant factor between 1 and 10⁶, the increase in nonlocal parameter tends to decrease the natural frequency in C–E and E–E boundary conditions and also for all values of spring stiffness in S-E boundary condition.

Table 7 Non-dimensional fundamental frequency corresponding to first mode obtained with various elastic boundary condition (L = 20 nm, L/h = 10, T = 20, V = 0.02)

Table 8 illustrates the effect of the natural frequencies for various elastic boundary conditions with different length and spring constant factors. As shown in Table 8, the surface effect is very sensitive to beam length and thickness. At the nanoscale, the fundamental frequency of the nanobeam by considering surface effect is approximately 3–4 orders higher than that of a classical beam including nonlocal parameters. At the microscale, the surface effect decreases and it is approximately 1.5–2 times greater than the classical. At a macroscale, surface effects are completely ignored and natural frequency of beam is similar to the classical beam.

Table 8 The natural frequency of nanobeam with various length and spring constant factor by considering surface effect ($L/h=10\text{,}\ \,b/h=2\text{,}\,\,\Delta T=20{}^\circ C,\ \ V=0.02,\ \ \mu =2\ \text{n}{{\text{m}}^{\text{2}}}$)

Table 9 implies the influences of elastic foundation including Winkler and Pasternak foundation on the natural frequencies. It can be readily observed that the value of the natural frequency has a direct relation with the stiffness of the elastic foundation. By increasing the value of Winkler–Pasternak foundation coefficients, the natural frequency increases which indicates the fact that by considering the elastic foundation, the stiffness of nanobeam will be increased, and hence, natural frequency will be grown.

Table 9 The natural frequency of nanobeam with various spring constant factor by considering surface effect and nonlocal effect for differenr values of elastic foundation ($L=20\,\ \text{nm},\ L/h=10\text{,}\,\ b/h=2\text{,}\,\,\Delta T=20\,{}^\circ \text{C},\ V=0.02,\ \mu =2\ \text{n}{{\text{m}}^{\text{2}}}$)

In Table 10, effects of temperature change on the natural frequency of nanobeam are tabulated. With the increase of temperature change, generally, the natural frequencies increase; the reason is that the increase in temperature change brings in more increase in the nanobeam stiffness and finally tends to grow in natural frequency. This behavior is right just for spring constant factor between 1 and 10⁶ and for S–E completely. For C–E and E–E boundary condition, the natural frequency decreases in the range of 10⁻⁶–1.

Table 10 The natural frequency of nanobeam by considering surface and nonlocal effects for various spring constant factor and temperature change ($L=20\text{ nm},\text{ }L/h=10,\text{ }h/b=0.2,\ \ V=0.2,\text{ }\mu =2\,\text{n}{{\text{m}}^{2}}$)

Table 11 presents the effect of the external voltage on the first natural frequency of nanobeam for various elastic boundary conditions. As it is observed, the positive voltage decreases the natural frequency and negative voltage increases the natural frequency generally. This is due to the fact that positive voltage weakens the nanobeam stiffness and negative voltage strengthens the nanobeam stiffness. But for C–E and E–E, this is opposite in the range of 10⁻⁶–1 that natural frequency increases.

Table 11 The natural frequency of nanobeam by considering surface and nonlocal effects for various spring constant factor and voltage external ($L=20\text{ nm},\text{ }L/h=10,\text{ }h/b=2,\ \mu =2\text{n}{{\text{m}}^{2}},\text{ }\Delta T={{20}^{\text{0}}}\text{C}$)

The effects of magnetic field on the natural frequency are examined in Table 12. It is found that natural frequency of nanobeam increases with increasing the value of magnetic potential. Obviously, the effect of external voltage is opposite to the magnetic potential. For this analysis, the behaviors of C–E and E–E boundary conditions are opposite to S–E within 10⁻⁶–1 that the natural frequency decreases.

Table 12 The natural frequency of nanobeam by considering surface and nonlocal effects for various spring constant factor and magnetic field $(L=20\,\text{nm},\ \text{L/h}\,\text{=}\,\text{10,}\,\ \text{b}\,\text{=}\,\text{0.5}\,\text{h,}\,\ \Delta T=0{}^\circ \text{C},\ \mu =2\,\text{n}{{\text{m}}^{2}})$

According to Tables 13, 14 and 15, the influences of each rotational and transitional spring constant factor change on the natural frequencies for C–E, S–E, and E–E boundary conditions are listed, respectively. As indicated from numerical results which are presented in detail, for a constant value of transitional spring, as the rotational spring increases, the natural frequencies increase. Moreover, for a constant value of transitional spring, with the increase in the value of rotational spring, the natural frequencies tend to increase.

Table 13 The natural frequency of nanobeam for C–E boundary condition ($L=20\text{ nm},\text{ }L/h=10,\text{ }h/b=2,\text{ }\mu \text{ }=2\text{n}{{\text{m}}^{2}},\text{ }\Delta T=20$)

Table 14 First natural frequency of nanobeam for S-E boundary condition ($L=20\text{ nm},\text{ }L/h=10,\text{ }h/b=2,\text{ }\mu \text{ }=2\,\text{n}{{\text{m}}^{2}},\text{ }\Delta T={{20}^{0}}\text{C}$)

Table 15 First natural frequency of P-FG nanobeam for E-E boundary condition ($L=20\text{ nm},\text{ }L/h=10,\text{ }h/b=2,\text{ }\mu \text{ }=2\,\text{n}{{\text{m}}^{2}},\text{ }\Delta T=20$)

The effects of external voltage and temperature change on the natural frequencies are investigated in Table 16. It can be seen that by increasing external voltage, for the spring stiffness within 10⁻⁶–1 in C–E and E–E, the natural frequencies increase and for S–E, natural frequency declines. Also, in the range of 1–10⁶, by growing external voltage, for all boundary condition, the natural frequency decreases. Also, by rising temperature change for C–E and E–E within 10⁻⁶–1, the natural frequency decreases, whereas for S–E, natural frequency rises. Also, in the range of 1–10⁶, growing temperature changes, natural frequency increases.

Table 16 The natural frequency of nanobeam with various spring constant factor by considering surface effect and nonlocal effect ($L=20\text{ nm},\text{ }L/h=10,\text{ }h/b=2,\text{ }\mu \text{ }=2\ \text{n}{{\text{m}}^{2}}$)

Depicted in Figs. 3, 4 and 5 are the variation of natural frequency for C–E, S–E, E–E boundary conditions by incorporating coupling of surface effect and nonlocal effect and just by considering nonlocal effect without surface effects, corresponding to various values of nonlocal parameters and spring constant factor. It can be observed that by considering the surface effect and by increasing the value of spring constant factor, natural frequency increases. It means that surface energy effects and spring constant factor play more important role than the nonlocal parameter.

Fig. 3

The variation of the first dimensionless frequency of nanobeam with spring constant factor for different nonlocal parameters for C–E boundary condition (L = 20 nm, L/h = 10, h/b = 2)

Fig. 4

The variation of the first dimensionless frequency of nanobeam with spring constant factor for different nonlocal parameters with considering surface effect for S–E boundary condition (L = 20 nm, L/h = 10, h/b = 2)

Fig. 5

The variation of the first dimensionless frequency of nanobeam with spring constant factor for different nonlocal parameters with considering surface effect for E–E boundary condition (L = 20 nm, L/h = 10, h/b = 2)

And also, the efficiency of piezoelectric material is described as follows:

$$\text{Efficiency}\ \text{of}\ \text{piezoelectric}\ \text{material}\ \text{=}\ \frac{\text{Natural}\,\,\text{frequency}\,\,\text{of}\,\text{piezoelectric}\,\,\text{nanobeam}}{\text{Natural}\,\text{frequency}\,\,\text{of}\,\,\text{nanobeam}}$$

The variation of efficiency of piezoelectric material versus voltage is depicted in Fig. 6 for various classical boundary conditions. As it can be observed, the negative voltage tends to increase the natural frequency of nanobeam, while the positive voltage decreases the value of natural frequencies. Also, for the C–F boundary condition, the voltage sign has inverse influence on the natural frequencies in comparison with other boundary conditions.

Fig. 6

Variation of efficiency of piezoelectric material versus voltage for various boundary conditions

4 Conclusion

In the present study, the magneto-thermo-mechanical vibration analysis of piezoelectric nanobeam rested in elastic medium is studied by considering surface and nonlocal effects for various elastic boundary conditions. To assume the elastic boundary condition, the rotational and transitional springs at each end are located which are used to introduce small deflections and moments. The main goal of the presented study is to investigate the influence of nonlocal parameter, piezoelectric voltage, temperature change, surface effects, elastic medium, magnetic field and length of nanobeam natural frequencies for different values of spring constants in elastic supports. As it is shown, the Hamilton’s principle is used to derive the motion equations based on the Euler–Bernoulli beam model. Then, DTM as an efficient and accurate numerical tool was implemented to solve vibration equations of piezoelectric nanobeam with elastic boundary condition. The convergence study and validation were also presented as well as the numerical results which clarified the influence of nonlocal parameter, piezoelectric voltage, temperature change, surface effects, elastic medium, magnetic field, length of nanobeam and spring constants on the first dimensionless natural frequency of piezoelectric nanobeam. Based on the presented numrecal results:

• 1. Increasing the spring constants leads to increase in the natural frequencies for all named boundary conditions.

• 2. For the variation of spring constant from ${{10}^{-6}}$ to 1 in C–E and E–E, the obtained result has the manner near the C–F boundary condition which shows different behavior in each case.

• 3. As the temperature change increases, the natural frequencies increase.

• 4. Increasing the voltage parameter from negative to positive amount tends to decrease the fundamental natural frequencies.

• 5. The natural frequencies decrease in the case that the nonlocal parameter increases.

• 6. As the length of nanobeam increases from the nanoscale to macroscale, the natural frequencies decrease and reach the classical value.

• 7. The surface effects tend to increase the natural frequencies which means the stiffness of nanobeam increases.