1 Introduction

With the advent of technology in the micro- and nanosizes, microbeams and nanobeams are often used in micro- and nanoelectromechanical systems (MEMS and NEMS) such as those employed in sensors, chemical sensing, signal filtering, actuators, fluid and mass transport. Moreover, beams are the core structures used widely in MEMS and NEMS and their properties are closely in correlation with their microstructures. Due to their micro- and nanosizes, the size effect is in consideration which is shown experimentally [1–4]. As a result, lacking a material length scale parameter, classical deformation theories cannot calculate the mechanical behavior of micro- and nanosystems. Therefore, in order to take into account the scale effects, size-dependent continuum theories have been developed by several researchers. For instance, couple stress theory [5–7], the nonlocal elasticity theory [8] and strain gradient theory [3] are proposed by diverse researches in the last several decades. Moreover, due to the severity of determining the material length scale parameters, Yang et al. [2] have proposed the modified couple stress theory which shows that the couple stress tensor is symmetric and the symmetric curvature tensor is in correlation with the strain energy of the system.

These features make the nonlocal elasticity theory and modified couple stress theory easier to use compared to the classical couple stress theory. Consequently, the research effort on mechanical behavior such as bending, buckling and vibration of micro- and nanosizes structures like microbeams, macroactuators, nanotubes and atomic force microscope are of great interests and have received a considerable attention. Asghari et al. [9]. presented a nonlinear size-dependent Timoshenko beam model based on the modified couple stress theory. They have investigated free vibration behavior of beam. Pirmohammadi et al. [10] have investigated active vibration suppression of a single-walled carbon nanotube under the action of a moving harmonic load using nonlocal elasticity theory. Bin et al. [11] have presented an analytical solution for the bending of a beam based on the couple stress elasto-plastic theory. Yin et al. [12] have analyzed the dynamic behavior of microscale plates based on the modified couple stress theory in which they have included material length scale parameter. Ke et al. [13] investigated dynamic stability of functionally graded microbeams based on the modified couple stress and Timoshenko beam theory. In this work, free vibration and buckling were also discussed. Akgöz et al. [14] employed this model to investigate vibration response of nonhomogeneous microbeams. Kim et al. [15] investigated the vibration, bending and buckling of microplates based on the modified couple stress theory. Simsek and Reddy [16] have employed this model to investigate the static bending and free vibration of functionally graded microbeams. Wang et al. [17] have studied the vibrations of three dimensional cylindrical microbeams by employing the modified couple stress theory. Ansari et al. [18] investigated the vibrational behavior of functionally graded microplates based on this theory. Kahrobaiyan et al. [19] have developed a new comprehensive Timoshenko beam element on the basis of the modified couple stress theory. Simsek [20] studied the free vibration analysis of microbeams based on the nonlinear elastic foundation using modified couple stress theory. Tang et al. [21] analyzed flexural vibrations of microbeams based on modified couple stress theory using a differential quadrature method to formulate the discrete forms of the governing equations. Al-Basyouni et al. [22] have studied bending and dynamic behavior of functionally graded beams. Ansari et al. [23] studied the vibration characteristic of a postbuckled microbeam based on the modified couple stress theory. Dai et al. [24] have developed a new nonlinear theoretical model for microbeams to explore the nonlinear dynamics based on the modified couple stress theory. Dehrouyeh-Semnani et al. [25] have investigated the dynamic characteristics of axially moving Timoshenko microbeams on the basis of this theory. He et al. [26] have proposed a new size-dependent model for functionally graded microplates by utilizing the modified couple stress theory and have analyzed bending, buckling and free vibration responses for simply supported microplates. Mohammdabadi et al. [27, 28] analyzed vibration and thermal effect on size-dependent buckling of composite laminated beams by using the modified couple stress, which is capable to capture the size effect by considering the material length scale parameters. Euler–Bernoulli, Timoshenko and Reddy beam models were investigated. Fakhrabadi et al. [29] presented the size-dependent mechanical behavior of the carbon nanotubes and nanoelectromechanical systems based on couple stress theory. Thai et al. [30] investigated static bending, buckling and free vibration behavior of size-dependent functionally graded sandwich microbeams based on the modified couple stress theory. Ghadiri et al. [31] have studied the vibration of rotating functionally graded Timoshenko microbeam based on this theory. And Kakhki et al. [32] have considered an analytical solution for thermoelastic damping in a microbeam based on the modified couple stress theory.

On the other hand, in various mechanical structures cracked problems are common. The presence of cracks in these structures has a significant impact on their health and safety [33, 34]. Henceforth, the detection of cracks is of great interests. Due to the fact that the presence of cracks alter the dynamic response of structures, the dynamical characteristics like vibration modes are used to detect the crack locations [35, 36]. So, in order to understand mechanical behaviors of cracked structures, there have been several theoretical investigations. Various analyses have been developed to study the natural frequencies and corresponding vibration modes. Hasheminejad et al. [37] have studied the flexural vibrations of cracked micro- and nanobeams in the presence of surface effects. Hosseini-Hashemi [38] have considered free transverse vibration of cracked nanobeams using Euler–Bernoulli and Timoshenko beam theories. Hsu et al. [39] have studied the longitudinal frequency of a cracked nanobeam. It is found that the frequency decreases with an increase of the crack parameter. Loya et al. [40] have considered a free transverse vibrations of cracked nanobeams using a nonlocal elasticity model. Roostai et al. [41] have studied the free vibration of nanobeams with multiple cracks. Torabi et al. [42] investigated an analytical method for free vibration analysis of Timoshenko beam theory, which is applied to cracked nanobeams on the basis of nonlocal elasticity model. Wang et al. [43] considered the free vibration and transverse shear deformation of a cracked nanobeam and Zhao et al. [44] have presented an explicit expression of the steady state responses of a cracked Euler–Bernoulli beam under a harmonic force.

This paper aims to investigate a transverse free vibration of a cracked microbeam based on the modified couple stress theory. The cracked beam will be divided into two segments connected by a rotational spring at the cracked position. Natural frequencies for a cracked micro- and nanobeam will be studied by applying boundary conditions, and numerical results are calculated for diverse crack positions, crack severities, material length scale parameter and various Poisson’s parameter.

2 The modified couple stress theory

Based on the modified couple stress theory introduced by [2] the strain energy density is a function of both strain tensor and curvature tensor. As a consequence, the strain energy of a deformed isotropic linear elastic body occupying a volume V is given as:

$$U = \frac{1}{2}\int\limits_{V}^{{}} {\left( {\sigma_{ij} \,\varepsilon_{ij} + m_{ij} \,\chi_{ij} } \right)\text{d}V,\quad i,\,j = 1,\,2,\,3}$$
(1)

where σ ij is the stress tensor, ɛ ij is the strain tensor, m ij are the components of the deviatoric part of the couple stress tensor and χ ij is the symmetric curvature tensor. The strain and the curvature tensors are expressed as:

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)$$
(2)
$$\chi_{ij} = \frac{1}{2}\left( {\theta_{i,j} + \theta_{j,i} } \right)$$
(3)

where u i are the components of the displacement vector and θ i are the components of the rotation vector which is defined as:

$$\theta_{i,j} = \frac{1}{2}e_{ijk} u_{k,j}$$
(4)

in which e ijk is the permutation symbol. Also, the constitutive relations can be expressed by:

$$\sigma_{ij} = \lambda \varepsilon_{kk} \delta_{ij} + 2\mu \varepsilon_{ij}$$
(5)
$$m_{ij} = 2\mu \ell^{2} \chi_{ij}$$
(6)

where δ ij is the Kronecker delta and 2ℓ 2  is defined as l 2, in which ℓ is the material length scale parameter which reflects the effect of the couple stress. Besides, λ and μ are Lame’s constants which is defined as:

$$\lambda = \frac{E\upsilon }{(1 + \upsilon )\,(1 - 2\upsilon )},\quad\mu = \frac{E}{2(1 + \upsilon )\,}$$
(7)

In the aforementioned equations, υ is the Poisson’s ratio and μ is the shear modulus.

3 Formulation of the problem

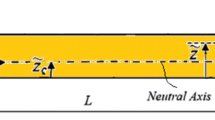
A microbeam has the length L, the width b and the height h which is depicted in Fig. 1. The microbeam has crack which is modeled with a longitude and a rotational spring at the crack position. The free transverse of the microbeam is in consideration. Hence, the governing equation will be calculated with the help of Hamilton’s principle.

Fig. 1
figure 1

Schematic of a cracked beam

Full size image

Based on Euler–Bernoulli beam theory, the displacement field at any point in the beam along its axis can be expressed as:

$$u_{x} (x,z,t) = - z\frac{{{\partial }w(x,t)}}{\partial x}$$
$$u_{y} (x,z,t) = 0$$
$$u_{z} (x,z,t) = w(x,t)$$
(8)

in which w is the transverse deflection of any point on the beam on the neutral axis and t expresses time. By the virtue of Eqs. (2) and (8), the only nonzero strain component can be obtained as:

$$\varepsilon_{xx} = - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}$$
(9)

What is more, with substitution of Eq. (8) into Eq. (4) the only nonzero component is obtained:

$$\theta_{y} = - \frac{\partial w(x,t)}{\partial x}$$
(10)

And substituting the above equation into Eq. (3), the curvature tensor components will be written as:

$$\chi_{xy} = - \frac{1}{2}\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}$$
$$\chi_{xx} = \chi_{yy} = \chi_{zz} = \chi_{xz} = \chi_{yz} = 0$$
(11)

Thereby, by utilizing Eqs. (1) to (11), the potential energy of the microbeam based on the modified couple stress theory can be expressed as:

$$U_{SE} = \frac{1}{2}\int\limits_{0}^{L} {\left( {\frac{E(1 - \upsilon )\,I}{(1 + \upsilon )\,(1 - 2\upsilon )} + \frac{1}{2}\mu Al^{2} } \right)\,\left( {\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right)^{2} \text{d}x}$$
(12)

On the other hand, the kinetic energy of the beam can be obtained as:

$$V = \frac{1}{2}\int\limits_{0}^{L} {\left[ {\rho A\,\left( {\frac{\partial w(x,t)}{\partial t}} \right)^{2} + \rho I\left( {\frac{{\partial^{2} w(x,t)}}{\partial x\partial t}} \right)^{2} } \right]} \;\text{d}x$$
(13)

where ρ is the density of the beam. Consequently, Lagrangian functional of the problem can be written as:

$$L = V - U_{SE}$$
(14)

So, the governing equation and the boundary conditions will be derived by Hamilton’s principle as:

$$\delta \int\limits_{0}^{t} {L\,\text{d}t} = 0$$
(15)

By calculating the first variation of the functional:

$$\int\limits_{0}^{t} {\int\limits_{0}^{L} {\left( {\rho A\,\frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t} + \rho I\frac{{\partial^{2} w}}{\partial x\partial t}\frac{{\partial^{2} \delta w}}{\partial x\partial t} - \left( {\frac{E(1 - \upsilon )\,I}{(1 + \upsilon )\,(1 - 2\upsilon )} + \frac{1}{2}\mu Al^{2} } \right)\,\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} \delta w}}{{{\partial }x^{2} }}} \right)\;{\text{d}}x\;{\text{d}}t = 0} }$$
(16)

Integrating the Eq. (16) by parts and considering the fundamental lemma of calculus of variations, coefficients of δw will be set to zero. Therefore,

$$\begin{aligned}& \left( {\frac{EI(1 - \upsilon )\,}{(1 + \upsilon )\,(1 - 2\upsilon )} + \frac{1}{2}\mu A\,l^{2} } \right)\frac{{\partial^{4} w(x,t)}}{{\partial x^{4} }} \\ & \quad + \rho A\,\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }} - \rho I\frac{{\partial^{4} w(x,t)}}{{\partial x^{2} \partial t^{2} }} = 0 \end{aligned}$$
(17)

It is worth mentioning that the classical governing equations of Euler–Bernoulli beam theory will be obtained as long as the material scale parameter l and the Poisson’s ratio are zero.

Also, the following boundary conditions of the beam at the edges (x = 0 and x = L) can be expressed as:

$$\begin{aligned} & {\text{Either}}\;\left( {\frac{EI(1 - \upsilon )\,}{(1 + \upsilon )\,(1 - 2\upsilon )} + \frac{1}{2}\mu A\,l^{2} } \right)\frac{{\partial^{3} w(x,t)}}{{\partial x^{3} }} \\ & \quad + \rho I\frac{{\partial^{3} w(x,t)}}{{\partial x\,\partial t^{2} }} = 0\quad {\text{Or}}\quad w = 0 \end{aligned}$$
$${\text{Either}}\;\left( {\frac{EI(1 - \upsilon )\,}{(1 + \upsilon )\,(1 - 2\upsilon )} + \frac{1}{2}\mu A\,l^{2} } \right)\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} = 0\quad {\text{Or}}\quad \frac{\partial w(x,t)}{\partial x} = 0$$
(18)

where EI and ρI are the flexural rigidity and the mass moment of inertia of the beam, respectively.

The steady state solution to Eq. (17) can be written in the form of w(x, t) = V(x)e iΩt. By inserting the expression V(x)e iΩt into Eq. (17), the time variable will be omitted and as a result it can be written as:

$$\begin{aligned} & \left( {\frac{EI(1 - \upsilon )\,}{(1 + \upsilon )\,(1 - 2\upsilon )} + \frac{1}{2}\mu A\,l^{2} } \right)V^{(4)} (x) + \rho I\varOmega^{2} V^{\prime\prime}(x) \\ & \quad - \rho A\varOmega^{2} V(x) = 0 \end{aligned}$$
(19)

where double prime symbol represents second derivative with respect to x and Ω represent second derivative with respect to x and frequency of vibrations, respectively. Considering the dimensionless variables and constants as:

$$\overline{V} = \frac{V}{L},\quad \xi = \frac{x}{L},\quad \lambda^{4} = \frac{{\rho AL^{4} \varOmega^{2} }}{E\,I}$$
(20)

and substituting Eq. (20) into (19) the transverse free vibration may be expressed as:

$$\bar{V}^{(4)} (\xi ) + m^{2} q^{4} \lambda^{4} V^{\prime\prime}(\xi ) - q^{4} \lambda^{4} V(\xi ) = 0$$
(21)

in which:

$$q^{4} = \frac{E\,I}{{\frac{EI(1 - \upsilon )\,}{(1 + \upsilon )\,(1 - 2\upsilon )} + \frac{1}{2}\mu A\,l^{2} }},\quad m^{2} = \frac{I}{{L^{2} A}},$$
(22)

It should be noted that A is the area of the cross section of the beam.

By solving the differential Eq. (21) and finding the roots for the related characteristic equation, the general solution is obtained as:

$$\begin{aligned} \bar{V}(\xi ) & = A_{1} \,\sinh (\beta_{r} \xi ) + A_{2} \,\cosh (\beta_{r} \xi ) \\ & \quad + A_{3} \,\sin (\beta_{i} \xi ) + A_{4} \,\cos (\beta_{i} \xi ) \end{aligned}$$
(23)

where β r and β i are:

$$\beta_{r} = q\lambda \left( {\frac{{\sqrt {m^{4} q^{4} \lambda^{4} + 4} - m^{2} q^{2} \lambda^{2} }}{2}} \right)^{1/2}$$
$$\beta_{i} = \,q\lambda \left( {\frac{{\sqrt {m^{4} q^{4} \lambda^{4} + 4} + m^{2} q^{2} \lambda^{2} }}{2}} \right)^{1/2}$$
(24)

4 Cracked beam model

The beam with an edge crack of length a located at a distance L C from the left end with the corresponding dimensionless variable b = L C/L is in consideration. In order to apply the effect of the crack which is shown in Fig. 1, the cracked beam has been considered to be divided into two sections connected by a rotational and a longitudinal elastic spring at the cracked position. The springs are introduced to consider the additional strain energy caused by the presence of the crack [40]. Therefore, the strain energy Ψ of the microbeam can be expressed as:

$$\varPsi = \frac{1}{2}\int\limits_{0}^{L} {\text{d}x} \int\limits_{A}^{{}} {\sigma_{xx} \left(\frac{\partial u}{\partial x} - y\frac{{\partial^{2} w}}{{\partial x^{2} }}\right)} \text{d}A +\Delta \varPsi_{c}$$
(25)

in which ΔΨ c is the additional strain energy caused by the crack. This equation can be stated in terms of the axial force and the bending moment as:

$$\varPsi = \frac{1}{2}\int\limits_{0}^{L} {\left( {N\frac{\partial u}{\partial x} + M\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \text{d}x +\Delta \varPsi_{c}$$
(26)

The increment due to the presence of an edge crack can be expressed as:

$$\Delta \varPsi_{c} = \frac{1}{2}k_{MM} M(L^{k} ,t)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}k_{NN} N(L^{k} ,t)\frac{\partial u}{\partial x} + \frac{1}{2}k_{MN} M(L^{k} ,t)\frac{\partial u}{\partial x} + \frac{1}{2}k_{NM} N(L^{k} ,t)\frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(27)

where k MM , k NN , k MN and k NM are the flexibility constants [40]. The last two terms are considered to take into account the coupled effects between axial force and bending moment. The increment of strain energy could be written as:

$$\Delta \varPsi_{c} = \frac{1}{2}M\Delta \theta + \frac{1}{2}N\Delta u$$
(28)

where Δθ is the angle rotated by the rotational spring and Δu the relative horizontal displacement at the edge crack section. Δθ and Δu may be stated as:

$$\Delta \theta = k_{MM} \frac{{\partial^{2} w}}{{\partial x^{2} }} + k_{MN} \frac{\partial u}{\partial x}$$
$$\Delta u = k_{NN} \frac{\partial u}{\partial x} + k_{NM} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(29)

In this investigation, the transverse free vibrations are studied; thereby, no longitudinal displacement is considered. Besides, the flexibility constants, k NN , k MN and k NM , are generally assumed to be small so that the only constant related to the bending moment, k MM , is considered. The slope increment Δθ in the cracked section is then expressed using dimensionless variables as:

$$\Delta \theta = \left. {\frac{{k_{MM} }}{L}\frac{{\partial^{2} \bar{W}}}{{\partial x^{2} }}\,} \right|_{{\xi = L^{c} }} = \left. {K\frac{{\partial^{2} \bar{W}}}{{\partial x^{2} }}\,} \right|_{{\xi = L^{c} }}$$
(30)

After defining how the crack beam is modeled, the analysis of free transverse vibration of the beam can be proceeded by applying the equation of motion in the vertical direction to each of the two segments:

$$\bar{V}^{(4)} (\xi ) + m^{2} q^{4} \lambda^{4} \bar{V}^{\prime\prime}(\xi ) - q^{4} \lambda^{4} \bar{V}(\xi ) = 0,\quad 0 \le \xi \le b$$
$$\bar{V}^{(4)} (\xi ) + m^{2} q^{4} \lambda^{4} \bar{V}^{\prime\prime}(\xi ) - q^{4} \lambda^{4} \bar{V}(\xi ) = 0,\quad b \le \xi \le 1$$
(31)

where λ 4 is the natural frequency parameter. The general solution for each segment can be stated as:

$$\begin{aligned} \bar{V}(\xi ) & = A_{1} \sinh (\beta_{r} \xi ) + A_{2} \cosh (\beta_{r} \xi ) \\ & \quad + A_{3} \sin (\beta_{i} \xi ) + A_{4} \cos (\beta_{i} \xi ),\quad 0 \le \xi \le b \end{aligned}$$
$$\begin{aligned} \bar{V}(\xi ) & = B_{1} \sinh (\beta_{r} \xi ) + B_{2} \cosh (\beta_{r} \xi ) \\ & \quad + B_{3} \sin (\beta_{i} \xi ) + B_{4} \cos (\beta_{i} \xi ),\quad b \le \xi \le 1 \end{aligned}$$
(32)

The above equations containing eight unknown constants that must be solved by applying the boundary conditions and the following expressed compatibility conditions at the cracked section:continuity of the vertical displacement,

$$\bar{V}_{2} (b) = V_{1} (b)$$
(33)

jump in bending slope,

$$\bar{V}_{2}^{\prime } \,(b) - \bar{V}_{1}^{\prime } \,(b) = K\bar{V}_{1}^{\prime \prime } \,\,(b)$$
(34)

continuity of the bending moment,

$$\bar{V}_{2}^{\prime \prime } (b) = \bar{V}_{1}^{\prime \prime } (b)$$
(35)

continuity of the shear force,

$$\bar{V}_{2}^{\prime \prime \prime } (b) = \bar{V}^{\prime\prime\prime}_{1} \,\,\,(b)$$
(36)

By applying the simply support boundary conditions and the aforementioned conditions into the Eq. (32), a linear system of equation is obtained. It is worth mentioning that this is a homogeneous system; thus, to avoid the trivial solution, it is necessary to impose nullity of the determinant of the coefficients’ matrix whose roots are the natural frequencies.

5 Results

The results presented in this section correspond to the natural frequencies of a microbeam based on the Euler–Bernoulli model and on the basis of the modified couple stress for different edge crack positions, several crack severities K, various Poisson’s ration and the material length scale parameter. Results have been compared with those of Loya et al. [40] which is presented in Tables 1 and 2. It is worth mentioning that these results are given by neglecting the rotational inertia, and setting material length scale parameter and Poisson’s ratio to zero.

Table 1 Comparison of the first four frequencies with crack positioned at ξ = 0.25
Full size table
Table 2 Comparison of the first four frequencies with crack positioned at ξ = 0.5
Full size table

In addition, in order to investigate the four natural frequencies, the width of the beam is assumed to be b = 10 h, and the length of the beam is chosen to be L = 100 h. Also, the dimensionless parameter η = h/l, the ratio of beam height to material length scale parameter, is introduced to study the effect of material length scale parameter, l, on the natural frequencies. The first four frequencies are calculated for various crack severities, Poisson’s ratio, different parameter η and crack positions which are given in Tables 3, 4, 5 and 6. It can be seen that the first four frequencies decrease gradually while crack severity increases. Furthermore, it is evident that the fourth natural frequency is constant for the considered microbeam for diverse Poisson’s ratio and various crack severities while it is at ξ = 0.25. In addition, it is found that the overall amount of frequencies is correlated positively with the increasing amount of Poisson’s ratio. What is more, the effect of dimensionless material scale length parameter η illustrates that the amount of natural frequencies plummets approximately 15 % by doubling η. Moreover, it is shown that the second and fourth frequencies are constants. This behavior is due to the fact that the second derivative of displacement is omitted at the crack section. Also, the overall amount of frequencies is slightly more for a crack positioned at quarter of the beam than the ones when the crack is at the middle of the beam.

Table 3 First four natural frequencies with a crack positioned at ξ = 0.25 and η = 1
Full size table
Table 4 First four natural frequencies with a crack positioned at ξ = 0.25 and η = 2
Full size table
Table 5 First four natural frequencies with a crack positioned at ξ = 0.50 and η = 1
Full size table
Table 6 First four natural frequencies with a crack positioned at ξ = 0.50 and η = 2
Full size table

Besides, the influence of Poisson’s ratio, dimensionless scale length parameter and crack position on the first natural frequency are investigated and shown in corresponding figures. According to the Figs. 2, 3, 4 and 5, natural frequency goes up steadily while Poisson’s ratio increases. Also, it is found that the natural frequency declines dramatically as long as crack severity parameter increases. Additionally, it can be seen that the natural frequency is almost twice as many when crack severity parameter quadruples. What is more, according to the figures presented, the natural frequency goes down considerably so long as the dimensionless material length scale parameter rises. Furthermore, Figs. 6, 7, 8 and 9 depict that crack severity and Poisson’s ratio correlate negatively and positively with the natural frequency, respectively. It is also crystal clear that the natural frequency drops approximately in half as crack severity quadruples. In addition, the overall natural frequency for a cracked positioned at 0.25 is far more than the ones when it is positioned at 0.5.

Fig. 2
figure 2

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.5 on natural frequency while η = 1

Full size image
Fig. 3
figure 3

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.5 on natural frequency while η = 2

Full size image
Fig. 4
figure 4

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.5 on natural frequency while η = 3

Full size image
Fig. 5
figure 5

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.5 on natural frequency while η = 3

Full size image
Fig. 6
figure 6

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.25 on natural frequency while η = 1

Full size image
Fig. 7
figure 7

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.25 on natural frequency while η = 2

Full size image
Fig. 8
figure 8

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.25 on natural frequency while η = 3

Full size image
Fig. 9
figure 9

Effect of Poisson’s ratio for diverse crack severity at ζ = 0.25 on natural frequency while η = 4

Full size image

Figure 10 illustrates the effect of crack position on natural frequency. Obviously, due to the symmetric boundary conditions applied to the microbeam, it was widely assumed that the natural frequency would vary symmetrically by changing the crack position from one edge of the beam to the opposite side. Besides, the minimum amount of natural frequency is shown to be where crack is positioned at the middle of the microbeam. Additionally, dimensionless material length scale parameter has almost no effect on natural frequencies for amounts more than 4.

Fig. 10
figure 10

Effect of crack position for diverse η on natural frequency with υ = 0.3 and K = 1.5

Full size image

Results, illustrated in Fig. 11, depict that the natural frequency for a microbeam with a crack positioned at ξ = 0, i.e., a microbeam with no crack, is the same for all crack severities. However, there is a striking difference when crack moves further through the length of the microbeam. It decreases considerably and hits its minimum amount at ξ = 0.5.

Fig. 11
figure 11

Effect of crack position for diverse K on natural frequency with υ = 0.3 and η = 1

Full size image

According to results shown in Fig. 12, Poisson’s ratio plays a significant role on the natural frequency as well as crack position. It is shown that for a microbeam with a Poisson’s ratio between 0.15 and 0.35, the natural frequencies almost remain the same. It, however, increases drastically so long as it is more than 0.35.

Fig. 12
figure 12

Effect of crack position for diverse υ on natural frequency with K = 1.5 and η = 1

Full size image

6 Conclusion

In this investigation, free transverse vibration of a cracked microbeam within the framework of Euler–Bernoulli beam theory on the basis of the modified couple stress theory is analyzed. Analytical solution and numerical results are presented. In this work, the impact of Poisson’s ratio, material scale length parameter, crack position and the crack severity on the natural frequencies were investigated. It has been found that the crack severity correlates negatively with natural frequencies. However, the fourth frequency for a crack at the quarter of the beam and the second and fourth frequencies for a crack at the middle of the crack remain constants, which is due to the symmetry of the beam and cancelation of the second derivative of the displacement. Crack severity plays a significant role on natural frequency. Also, natural frequency increases while Poisson’s ratio rises. The overall amounts of natural frequency decrease while crack moves toward the middle of the beam. Besides, the material scale length parameter as a considerable impact on natural frequency, which reduces the natural frequency when it rises.