1 Introduction

Nowadays nanotechnology is one of the most interesting technologies, which has greatly influenced many fields of science and industry such as human health science, aerospace industry, as well as civil and mechanical engineering [1]. There have been many efforts to enhance the physical, electrical and mechanical performance of nanodevices and nanostructures. In this regard, some kind of nanostructures like nanobeam, nanoplate and nanotube have been developed. Recently, these structural elements have been widely used in modern and innovative technologies like micro/nano electro mechanical systems (MEMS/NEMS). Designing and manufacturing such systems with high precision, is strongly affected by an accurate understanding of the mechanical behaviour of nanostructures, which play key role in the performance of these systems [2, 3]. Therefore, studies based on investigating the mechanical behaviour of nanostructures have been an area of active research.

Advanced nanocomposite materials have great application in nanotechnology due to their superior properties, however, nanocomposite materials inherently have distinct interface with sudden variation in material properties. This characteristic threatens the reliability of nanocomposite based instruments [4]. In order to solve this problem, there is an urgent need to employ materials with smooth variation in material properties to eliminate stress concentration at the constituent material interface [2, 5]. Functionally graded materials satisfy this requirement with continuous gradation of their compositions [5], thus with the growing amounts of nanostructures, FGMs are widely employed in MEMS and NEMS as AFMs, micro switches, microsensors and thin films [2, 5–9]. Veith et al. [10] investigated the transformation of core/shell aluminium/alumina nanoparticles into nanowires. Core/shell nanowires of Al/Al2O3 are obtained by decomposition of tert-butoxyalane on metal, silicon or glass substrates heated up to 650 °C without use of a noble metal seed. These biphasic nanowires are characterized by X-ray diffraction (XRD), scanning electron microscopy (SEM), scanning energy dispersive X-ray spectroscopy (EDX), transmission electron microscopy (TEM) and high-resolution TEM. They have uniform diameters of about 20–30 nm, are composed of an inner aluminium wire, wrapped up by aluminium oxide at a constant molar ratio, and have lengths of several micro-meters. With the quick growth of nanostructures, FGMs are extensively used in micro- and nano-structures such as thin films [11–14], micro-switches [15–17], micro piezoactuator [18], and micro/nano-electromechanical systems (MEMS and NEMS) [19–23]. Jia et al. [16] investigated the forced vibration of non-homogeneous FG micro-switches under combined electro-static, intermolecular forces and axial residual stress. In this study the effects of material composition, gap ratio, slenderness ratio, intermolecular force, axial residual stress on the pull-in instability were shown. In another study, they investigated the nonlinear pull-in characteristics of the microswitches made of either homogeneous material or non-homogeneous functionally graded material (FGM) with two material phases under the combined electrostatic and intermolecular Casimir force [15]. As it is challenging for a single layer to encounter all material and economical necessities pretended to an MEMS structural layer, Witvrouw and Mehta [24] recommended the use of a non-homogenous functionally graded material layer, to attain the favorite mechanical and electrical properties. Fine-tuning of the stress gradient was achieved by the use of a top stress compensation layer, whose optimum thickness was estimated from an assessment of the stress gradient shape through thickness. It should be noted that because of high sensitivity of micro and nanoelectromechanical systems (MEMS/NEMS) in response to external loading and stimulations, the accurate understanding of mechanical behavior of these systems is an important issue. In this regard, several investigations have been done to study the mechanical behavior of FG MEMS/NEMS [2, 6]. Eltaher et al. [25] through the investigation of static–buckling behavior of functionally graded nanobeams as a core structure of micro and nano electro mechanical systems, derived equilibrium equations by applying the principle of virtual displacement. Their study addressed the significant role of parameters such as material gradient index, boundary conditions and nonlocal effect on the static–buckling behavior of FG nanobeam. In another study, Eltaher et al. [26] by investigating the static and buckling behavior of nonlocal functionally graded Timoshenko nanobeam shown the importance of the material distribution profile effect on the buckling and bending behavior of nanobeams. Kiani et al. [4] investigated the effect of power-law parameter, small-scale parameter and length of the functionally graded nanobeam, on the frequencies and stability of the moving nanobeam. This study was done based on the mathematical model which have proposed for functionally graded nano beam moving with constant velocity. Nonlinear free vibration analysis of FG nanobeam based on nonlocal theory for two kind of boundary conditions, was studied by Nazemnezhad and Hosseini-Hashemi [27].

All of these studies and investigations have done to analyze behavior of nanostructures and they indicate that at the nanoscale, mechanical characteristic of the nanostructures behave in a different manner in comparison with macro scales. This behavior is due to inherent size effect. It is clear that, investigation of the mechanical behavior of nanostructures, extremely requires an efficient theory which could correctly predict the size dependent behavior of the nanostructures [27, 28]. This efficiency is obtained through considering the size effect in the theory. Classical continuum theories failed to analyze the mechanical behavior of the nanostructures, because they don’t consider the nanoscale effect [27, 28], however, classical continuum theories could be extended to be applicable for prediction of mechanical behavior of nanostructures through considering nanoscale effect [29–36]. Eringen’s nonlocal theory is an extended form of continuum theory which is largely used in nanostructures investigations [27]. Based on the assumption in nonlocal theory, stress at a reference point is a function of the strain at all neighbor points in the body [27]. The growing amount of studies, which have done based on nonlocal theory in recent years, have proved the applicability and functionality of this theory in nanostructures analysis [37–39]. Niknam and Aghdam [5] obtained a closed form solution for nonlinear vibration and buckling behavior of Euler–Bernoulli based FG nanobeam using nonlocal theory. Rahmani and Pedram [40] by using nonlocal beam theory, presented a closed-form solution for Timoshenko FG nanobeam to analyze the size effect on vibration behavior of the functionally graded nanobeam. Nonlocal beam theory could be used to analyze nanotube structures. Ebrahimi et al. [2] by using nonlocal theory, shown the applicability of differential transformation method to vibration analysis of functionally graded nanobeam.

Vibration, as an important mechanical behavior should be analyzed for structural elements to help designers to avoid resonance in engineering problems [41]. In the other hand, as the amount of functionally graded nano structures are growing, some studies have been done to investigate vibration behavior of functionally graded nano-structural elements. Eltaher et al. [42] investigated free vibration behavior of FG nanobeam on the basis of nonlocal elasticity theory. According to their results, dynamic characteristic and vibration behavior of the FG nanobeam is highly affected by material gradient index, nonlocal effect and boundary conditions.

Kiani [43] studied the dynamic response of a single-wall carbon nanotube (SWCNT) under a moving nano particle based on nonlocal theory. He also formulated the inertial effect of the moving nano scale particle and the friction, which exists between the nanoparticle surface and the inner surface of the SWCNT. Simsek [44] by investigating the forced vibration of a simply supported single-walled carbon nanotube (SWCNT) under a moving harmonic load, based on nonlocal Euler–Bernoulli beam theory, represented that dynamic deflection of the SWCNT is strongly affected by nonlocal parameter, and also its dynamic behavior is affected by other parameters like load velocity and the excitation frequency. In another study, Simsek [45] analytically studied the force vibration of an elastically connected double-carbon nanotube system (DCNTS) under a moving nanoparticle. The result of his study showed that dynamic response of the DCNTS is strongly affected by the nonlocal effect. He also addressed the important role of the velocity of the moving nanoparticle and the stiffness in the elastic layer on the dynamic response of DCNTS. Recently Pourseifi et al. [46], studied the vibration behavior of nanotubes particularly for designing a control system to suppress the vibration of nanotube in response to the action of a moving nanoparticle. In another study, Pirmohammadi et al. [47], used a linear classical optimal control to suppress the vibration of a single-walled carbon nanotube under action of a harmonic moving load.

Based on the above review, it is clearly observed that reports related to the investigation of FG nanobeam behavior in both transverse and axial mode in response to forced vibration due to moving load are limited. Due to this fact, this paper aimed to study the transverse and axial dynamic response of an FG nanobeam by using nonlocal and Euler–Bernoulli theories to derive governing equations and Laplace transform to solve the derived differential equations. It should be noted that an exact solution for both transverse and axial responses is obtained as a result of this effort. Through parametric study, valuable results have been concluded which are related to the effect of important parameters such as FG material distribution index, nonlocal parameters, aspect ratio and load velocity on the dynamic response of the FG nanobeam in axial and transverse modes. The presented results in this study are validated by obtaining good agreement which compares with available results in the literature.

2 Theory and formulation

2.1 Materials properties in functionally graded beam

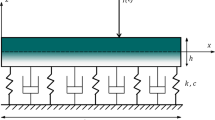
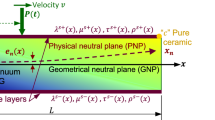
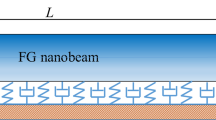
In this study, the FG beam, which is schematically shown in Fig. 1, consists of ceramic and metal. The FGM profile that is defined across the thickness direction of the beam is assumed to follow the power law form:

$$\begin{aligned} & f(z) = f_{m} + f_{cm\,} \left( {\frac{2z + h}{2h}} \right)^{p} \\& f(z) = f_{m} + f_{cm\,} \left( {\frac{2z + h}{2h}} \right)^{k} \\ & f_{cm} = f_{c} - f_{m} \\ \end{aligned}$$
(1)

f, f m , f c denotes the material properties of FGM, metal properties of FGM, ceramic properties of FGM, respectively and p and k are the power law index. The other material properties of FGM such as density and modulus of elasticity can be assumed to follow the power law.

Fig. 1
figure 1

Schematic of a simply supported FG nanobeam under a moving load

Full size image

The FG beam becomes a fully ceramic beam when p and k are set to be zero. Therefore from Eq. (1), the effective material properties of the FG nanobeam can be expressed as follows:

$$\begin{aligned} E(z) & = \left( {E_{c} - E_{m} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} + E_{m} \\ \rho (z) & = \left( {\rho_{c} - \rho_{m} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} + \rho_{m} \\ \end{aligned}$$
(2)

2.2 Kinematic relations based on Hamilton’s principle

The equations of motion is derived based on the Euler–Bernoulli beam theory according to which the displacement field at any point of the beam can be written as:

$$u_{x} \left( {x,z,t} \right) = u\left( {x,t} \right) - z\frac{\partial w(x,t)}{\partial x}$$
(3a)
$$u_{z} (x,z,t) = w(x,t)$$
(3b)

where t is time, u and w are displacement components of the mid-plane along x and z directions, respectively. Therefore, according to Euler–Bernoulli beam theory, every elements of strain tensor vanish except normal strain in the x-direction. Thus, the only nonzero strain is:

$$\varepsilon_{\text{xx}} = \varepsilon_{xx}^{0} - zk_{x}^{0} ,\quad \varepsilon_{xx}^{0} = \frac{\partial u(x,t)}{\partial x},\quad k^{0} = \frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}$$
(4)

where \(\varepsilon_{xx}^{0}\) and k 0 are the extensional strain and bending strain respectively. Based on the Hamilton’s principle, which states that, the motion of an elastic structure during the time interval t 1 < t < t 2 is such that the time integral of the total dynamics potential is extremum:

$$\int_{0}^{t} {\delta (U - T + V)dt = 0}$$
(5)

Here U is strain energy, T is kinetic energy and V is work done by external forces. The virtual strain energy can be calculated as:

$$\delta U = \int_{v} {\sigma_{ij} \delta \varepsilon_{ij} dV} = \int_{v} {\left( {\sigma_{xx} \delta \varepsilon_{xx} } \right)dV}$$
(6)

Substituting Eq. (4) into Eq. (6) yields:

$$\delta U = \int_{0}^{L} {\left( {N\left( {\delta \varepsilon_{xx}^{0} } \right) - M\left( {\delta k^{0} } \right)} \right)dx}$$
(7)

In which N, M are the axial force and bending moment respectively. These stress resultants used in Eq. (7) are defined as:

$$N = \int_{A} {\sigma_{xx} dA} ,\quad M = \int_{A} {\sigma_{xx} zdA}$$
(8)

The kinetic energy for Euler–Bernoulli beam can be written as:

$$T = \frac{1}{2}\int_{0}^{L} {\int_{A} {\rho (z)\left( {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right)dAdx} }$$
(9)

Also the virtual kinetic energy can be expressed as:

$$\delta T = \int_{0}^{L} {\left[ {I_{0} \left( {\frac{\partial u}{\partial t}\frac{\partial \delta u}{\partial t} + \frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}} \right) - I_{1} \left( {\frac{\partial u}{\partial t}\frac{{\partial^{2} \delta w}}{\partial t\partial x} + \frac{\partial \delta u}{\partial t}\frac{{\partial^{2} w}}{\partial t\partial x}} \right) + I_{2} \frac{{\partial^{2} w}}{\partial t\partial x}\frac{{\partial^{2} \delta w}}{\partial t\partial x}} \right]} dx$$
(10)

where (I 0, I 1, I 2) are the mass moment of inertias, defined as follows:

$$\left( {I_{0} ,I_{1} ,I_{2} } \right) = \int_{A} {\rho (z)\left( {1,z,z^{2} } \right)dA}$$
(11)

The first variation of external forces work of the beam can be written in the form:

$$\delta W_{ext} = \int_{0}^{L} {\left( {f(x)\delta u + q(x)\delta w} \right)dx}$$
(12)

where f(x) and q(x) are external axial and transverse loads distribution along length of beam, respectively.

By Substituting Eqs. (7), (10) and (12) into Eq. (5) and setting the coefficients of δu, δw and \(\frac{\delta \partial w}{\partial x}\) to zero, the following Euler–Lagrange equation can be obtained:

$$\frac{\partial N}{\partial x} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}$$
(13.a)
$$\frac{{\partial^{2} M}}{{\partial x^{2} }} = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}$$
(13.b)

Under the following boundary conditions:

$$N = 0\;\;{\text{or}}\;\;u = 0\quad {\text{at}}\;\;x = 0\;\;{\text{and}}\;\;x = L$$
(14.a)
$$\frac{\partial M}{\partial x} - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} = 0\;\;{\text{or}}\;\;w = 0\quad {\text{at}}\;\;x = 0\;\;{\text{and}}\;\;x = L$$
(14.b)
$$M = 0\;\;{\text{or}}\;\;\frac{\partial w}{\partial x} = 0\quad {\text{at}}\;\;x = 0\;\;{\text{and}}\;\;x = L$$
(14.c)

2.3 Nonlocal governing equations for FG nanobeam

Despite the elastic continuum theory that the stress field at point X depends only on the strain at the same point, based on Eringen nonlocal theory stress field at point X not only depends on strain at that point but also depends to all other points of the body. Thus the nonlocal stress tensor at point X can be obtained as follows:

$$\sigma^{nl} (X) = \int\limits_{V} {k\left( {\left| {X^{{\prime }} - X} \right|,\tau } \right)T\left( {X^{{\prime }} } \right)dV\left( {X^{{\prime }} } \right)}$$
(15.a)
$$T(X) = C(X):\varepsilon (X)$$
(15.b)

T(X) represents the classical macroscopic stress tensor at point X, the kernel function \(K\left| {\left( {X^{{\prime }} - X} \right),\tau } \right|\) denotes the nonlocal modulus, (X′ − X)indicates the distance and τ is the material constant which depends on type of material. The macroscopic stress tensor at a point X in a Hookean solid is represented by T and is depends to the strain at the same point which is based on the generalized Hook’s law. C is the fourth-order elasticity tensor which represents the double-dot product. A simplified equation of differential form is utilized due to the complicated solution of the integral constitutive equation, which is as follows:

$$L\sigma^{nl} (X) = \left( {1 - \mu \nabla^{2} } \right)\sigma^{nl} = T,\quad \mu = \tau^{2} l^{2}$$
(16)

\(L = \left( {1 - \mu \nabla^{2} } \right)\) and ∇2 indicates nonlocal differential and the Laplacian operator, respectively. τ is determined by τ = e 0 α/l where e 0 is a constant which varies based on each material and α and l represents the internal and external characteristic length. The nonlocal parameter which is represented by μ varies in accordance with different materials.

For an elastic material in the one dimensional case, the nonlocal constitutive relations may be simplified as:

$$\sigma^{nl} (x) - (e_{0} a)^{2} \frac{{\partial^{2} \sigma^{nl} (x)}}{{\partial x^{2} }} = E\varepsilon (x)$$
(17)

where σ and ɛ are the nonlocal stress and strain, respectively and E is the Young’s modulus. For Euler–Bernoulli nonlocal FG beam, Eq. (17) can be rewritten as:

$$\sigma_{xx} - \mu^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E(z)\varepsilon_{xx}$$
(18)

where (μ = (e 0 a)). Integrating Eq. (18) over the beam’s cross-section area, the force–strain and the moment–strain relations for the nonlocal FG beam can be obtained as follows:

$$N - \mu^{2} \frac{{\partial^{2} N}}{{\partial x^{2} }} = A_{xx} \frac{\partial u}{\partial x} - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(19)
$$M - \mu^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} = B_{xx} \frac{\partial u}{\partial x} - C_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(20)

In which the cross-sectional rigidities are defined as follows:

$$\left( {A_{xx} ,B_{xx} ,C_{xx} } \right) = \int_{A} {E(z)\left( {1,z,z^{2} } \right)dA}$$
(21)

The explicit relation of the nonlocal normal force can be derived by substituting for the second derivative of N from Eq. (13.a) into Eq. (19) as follows:

$$N = A_{xx} \frac{\partial u}{\partial x} - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \mu^{2} \left( {I_{0} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{1} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right)$$
(22)

Also the explicit relation of the nonlocal bending moment can be derived by substituting for the second derivative of M from Eq. (13.b) into Eq. (20) as follows:

$$M = B_{xx} \frac{\partial u}{\partial x} - C_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \mu^{2} \left( {I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right)$$
(23)

The nonlocal governing equations of FG nanobeam in terms of the displacement can be derived by substituting for N and M from Eqs. (22) and (23), respectively, into Eq. (13) as follows:

$$A_{\text{xx}} \frac{{\partial^{2} u}}{{\partial x^{2} }} - B_{\text{xx}} \frac{{\partial^{3} w}}{{\partial x^{3} }} + \mu^{2} \left( {I_{0} \frac{{\partial^{4} u}}{{\partial t^{2} \partial x^{2} }} - I_{1} \frac{{\partial^{5} w}}{{\partial t^{2} \partial x^{3} }}} \right) - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}} = 0$$
(24)
$$\begin{aligned} B_{\text{xx}} \frac{{\partial^{3} u}}{{\partial x^{3} }} - C_{\text{xx}} \frac{{\partial^{4} w}}{{\partial x^{4} }} + \mu^{2} \left( {I_{0} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + I_{1} \frac{{\partial^{5} u}}{{\partial t^{2} \partial x^{3} }} - I_{2} \frac{{\partial^{6} w}}{{\partial t^{2} \partial x^{4} }} - \frac{{\partial^{2} q}}{{\partial x^{2} }}} \right) - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} u}}{{\partial t^{2} \partial x}} + I_{2} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + q = 0 \end{aligned}$$
(25)

Transverse force for a nanobeam, under constant moving load can be defined as follow:

$$q = P\delta \left( {x - v_{0} t} \right)$$
(26)

where P is concentrated moving load, and δ(·) is Dirac delta function.

3 Analytical solution

The assumed mode method is utilized for discretization of the unknown fields of the problem in the spatial domain; therefore \(u\left( {x,t} \right) = \sum\nolimits_{n = 1}^{\infty } {U_{n} (t)\varphi_{n}^{u} (x)}\) and \(w\left( {x,t} \right) = \sum\nolimits_{n = 1}^{\infty } {W_{n} (t)\varphi_{n}^{w} (x)}\) in which the parameters \(\varphi_{n}^{u} (x)\) and \(\varphi_{n}^{w} (x)\) denote in turn the appropriate n th mode shapes associated with the axial and transverse deflection fields of the FG beam. Moreover \(\varphi_{n}^{u} (x) = \cos \left( {{\raise0.7ex\hbox{${n\pi x}$} \!\mathord{\left/ {\vphantom {{n\pi x} L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)\) and \(\varphi_{n}^{w} (x) = \sin \left( {{\raise0.7ex\hbox{${n\pi x}$} \!\mathord{\left/ {\vphantom {{n\pi x} L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)\) are derived as the mode shapes of the simply supported of the FG nanobeam. By using the general property of Dirac-Delta function, \(\delta \left( {x - v_{0} t} \right) = 2\sum\limits_{n = 1}^{\infty } {\sin \left( {{\raise0.7ex\hbox{${n\pi x}$} \!\mathord{\left/ {\vphantom {{n\pi x} L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)\sin \left( {{\raise0.7ex\hbox{${n\pi v_{0} t}$} \!\mathord{\left/ {\vphantom {{n\pi v_{0} t} L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)}\), the following set of ODEs is obtained:

$$\begin{aligned} - A_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{2} U_{n} (t) + B_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{3} W_{n} (t) - \mu^{2} I_{0} {\ddot{U}}_{n} (t)\left( {\frac{n\pi }{L}} \right)^{2} + \mu^{2} I_{1} {\ddot{W}}_{n} (t)\left( {\frac{n\pi }{L}} \right)^{3} - I_{0} {\ddot{U}}_{n} (t) + I_{1} {\ddot{W}}_{n} (t)\left( {\frac{n\pi }{L}} \right) = 0 \end{aligned}$$
(27)
$$\begin{aligned} B_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{3} U_{n} (t) - C_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{4} W_{n} (t) - \mu^{2} I_{0} \left( {\frac{n\pi }{L}} \right)^{2} {\ddot{W}}_{n} (t) + \mu^{2} I_{1} \left( {\frac{n\pi }{L}} \right)^{3} {\ddot{U}}_{n} (t) - \mu^{2} I_{2} \left( {\frac{n\pi }{L}} \right)^{4} {\ddot{W}}_{n} (t) - I_{0} {\ddot{W}}_{n} (t) + I_{1} \left( {\frac{n\pi }{L}} \right){\ddot{U}}_{n} (t) - I_{2} \left( {\frac{n\pi }{L}} \right)^{2} {\ddot{W}}_{n} (t) = - 2P\left( {1 + \mu^{2} \left( {\frac{n\pi }{L}} \right)^{2} } \right)\sin \left( {\frac{{n\pi v_{0} }}{L}t} \right) \end{aligned}$$
(28)

With the initial condition:

$$W_{n} (0) = U_{n} (0) = \dot{W}_{n} (0) = \dot{U}_{n} (0) = 0$$
(29)

The unknown parameters \(W_{n} (t)\) and \(U_{n} (t)\) of the Eqs. (27) and (28) should be determined by a suitable method. To solve the system of the differential Eqs. (27) and (28) in time domain, Laplace transform is utilized. By recalling of this transform, \(L\left[ {{\ddot{W}}_{n} (t)} \right] = s^{2} \varpi (s) - sW(0) - \dot{W}(0)\) where \(\varpi (s) = L\left[ {W(t)} \right]\) and \(L\left[ {{\ddot{U}}_{n} (t)} \right] = s^{2} \vartheta (s) - sU(0) - \dot{U}(0)\) where \(\vartheta (s) = L\left[ {U(t)} \right]\) and then by using Eq. (29) and applying Laplace Transform in Eqs. (27) and (28), the system of equation is obtained as follow:

$$\begin{aligned} & \left( { - A_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{2} - \mu^{2} I_{0} \left( {\frac{n\pi }{L}} \right)^{2} s^{2} - I_{0} s^{2} } \right)\vartheta (s) \\ & \quad + \left( {B_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{3} + \mu^{2} I_{1} \left( {\frac{n\pi }{L}} \right)^{3} s^{2} + I_{1} \left( {\frac{n\pi }{L}} \right)s^{2} } \right)\varpi (s) = 0 \\ \end{aligned}$$
(30)
$$\begin{aligned} \left( {B_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{3} + \mu^{2} I_{1} \left( {\frac{n\pi }{L}} \right)^{3} s^{2} + I_{1} \left( {\frac{n\pi }{L}} \right)s^{2} } \right)\vartheta (s) + \left( { - C_{\text{xx}} \left( {\frac{n\pi }{L}} \right)^{4} - \mu^{2} I_{0} \left( {\frac{n\pi }{L}} \right)^{2} s^{2} - \mu^{2} I_{2} \left( {\frac{n\pi }{L}} \right)^{4} s^{2} - I_{0} s^{2} - I_{2} \left( {\frac{n\pi }{L}} \right)^{2} s^{2} } \right)\varpi (s) = \frac{{ - 2P\left( {1 + \mu^{2} \left( {\frac{n\pi }{L}} \right)^{2} } \right)\left( {\frac{{n\pi v_{0} }}{L}} \right)}}{{s^{2} + \left( {\frac{{n\pi v_{0} }}{L}} \right)^{2} }} \end{aligned}$$
(31)

By solving the Eqs. (30) and (31), W n (s) and U n (s) are obtained as:

$$W_{n} (s) = - \frac{{2v_{0} \alpha \varepsilon P}}{{\left( {s^{2} + v_{0}^{2} \alpha^{2} } \right)\left( { - C_{xx} \alpha^{4} - \varepsilon \left( {I_{0} + I_{2} \alpha^{2} } \right)s^{2} + \frac{{\left( {B_{xx} \alpha^{3} + I_{1} \alpha \varepsilon s^{2} } \right)^{2} }}{{A_{xx} \alpha^{2} + I_{0} \varepsilon s^{2} }}} \right)}}$$
(32)

and

$$U_{n} (s) = \frac{{B_{xx} \alpha^{3} + I_{1} \alpha \varepsilon s^{2} }}{{A_{xx} \alpha^{2} + I_{0} \varepsilon s^{2} }}W_{n} (s)$$
(33)

where

$$\alpha = \left( {\frac{n\pi }{L}} \right),\quad \varepsilon = \left( {1 + \mu^{2} \left( {\frac{n\pi }{L}} \right)^{2} } \right)$$
(34)

By applying in inverse Laplace transform to Eq. (32) and then Eq. (33) the transverse and axial dynamic response of FG nanobeam are obtained:

$$w\left( {x,t} \right) = \sum\limits_{n = 1}^{\infty } {\frac{1}{{d_{2} }}\left\{ {\begin{array}{*{20}l} {\frac{{d_{1} \sin \left( {\sqrt {a_{2} } t} \right)}}{{\sqrt {a_{2} } }} - \frac{\sqrt 2 }{{4d_{5} \varphi }}} \hfill \\ { \times \left( \begin{aligned} \sqrt {\frac{{ - d_{6} - \varphi }}{{d_{7} }}} \left( {2d_{4} d_{5} + d_{3} \left( { - d_{6} + \varphi } \right)} \right)\sinh \left( {\sqrt {\frac{{ - d_{6} + \varphi }}{{2d_{7} }}} t} \right) \hfill \\ + \sqrt {\frac{{ - d_{6} + \varphi }}{{d_{7} }}} \left( { - 2d_{4} d_{5} + d_{3} \left( { - d_{6} + \varphi } \right)} \right)\sinh \left( {\sqrt {\frac{{ - d_{6} - \varphi }}{{2d_{7} }}} t} \right) \hfill \\ \end{aligned} \right)} \hfill \\ \end{array} } \right\}\sin \left( {\frac{n\pi x}{L}} \right)}$$
(35)

and

$$u\left( {x,t} \right) = \sum\limits_{n = 1}^{\infty } {\frac{1}{{d_{2} }}\left\{ {\begin{array}{*{20}l} {\frac{{d_{8} \sin \left( {\sqrt {a_{2} } t} \right)}}{{\sqrt {a_{2} } }} - \frac{\sqrt 2 }{{4d_{5} \varphi }}} \hfill \\ { \times \left( \begin{aligned} \sqrt {\frac{{ - d_{6} - \varphi }}{{d_{7} }}} \left( {2d_{10} d_{5} + d_{9} \left( { - d_{6} + \varphi } \right)} \right)\sinh \left( {\sqrt {\frac{{ - d_{6} + \varphi }}{{2d_{7} }}} t} \right) \hfill \\ + \sqrt {\frac{{ - d_{6} + \varphi }}{{d_{7} }}} \left( { - 2d_{10} d_{5} + d_{9} \left( {d_{6} + \varphi } \right)} \right)\sinh \left( {\sqrt {\frac{{ - d_{6} - \varphi }}{{2d_{7} }}} t} \right) \hfill \\ \end{aligned} \right)} \hfill \\ \end{array} } \right\}} \cos \left( {\frac{n\pi x}{L}} \right)$$
(36)

where

$$\varphi = \sqrt {d_{6}^{2} - 4d_{5} d_{7} }$$
(37)

For k = 1, 2, …, 10, dk are obtained as follow:

$$\begin{aligned} d_{1} & = a_{1} a_{8} - a_{1} a_{2} a_{9} \\ d_{2} & = a_{5} + a_{2}^{2} a_{6} - a_{2} a_{7} + a_{3} a_{8} - a_{2} a_{4} a_{8} - a_{2} a_{3} a_{9} + a_{2}^{2} a_{4} a_{9} \\ d_{3} & = a_{1} a_{2} a_{6} a_{8} - a_{1} a_{7} a_{8} - a_{1} a_{4} a_{8}^{2} + a_{1} a_{5} a_{9} + a_{1} a_{2} a_{4} a_{8} a_{9} \\ d_{4} & = - a_{1} a_{6} a_{8} + a_{1} a_{2} a_{6} a_{9} - a_{1} a_{4} a_{8} a_{9} + a_{1} a_{2} a_{4} a_{9}^{2} \\ d_{5} & = a_{5} + a_{3} a_{8} \\ d_{6} & = a_{7} + a_{4} a_{8} + a_{3} a_{9} \\ d_{7} & = a_{6} + a_{4} a_{9} \\ d_{8} & = a_{1} \sqrt {a_{5} } - a_{1} a_{2} \sqrt {a_{6} } \\ d_{9} & = a_{1} a_{5} \sqrt {a_{6} } + a_{1} a_{2} \sqrt {a_{5} } a_{6} - a_{1} \sqrt {a_{5} } a_{7} - a_{1} a_{4} \sqrt {a_{5} } a_{8} \\ & \quad + a_{1} a_{3} \sqrt {a_{6} } a_{8} - a_{1} a_{3} \sqrt {a_{5} } a_{9} + a_{1} a_{2} a_{4} \sqrt {a_{5} } a_{9} \\ d_{10} & = - a_{1} \sqrt {a_{5} } a_{6} + a_{1} a_{2} a_{6}^{{\frac{3}{2}}} - a_{1} a_{4} \sqrt {a_{5} } a_{9} + a_{1} a_{2} a_{4} \sqrt {a_{5} } a_{9} \\ \end{aligned}$$
(38)

where

$$\begin{aligned} & a_{1} = - 2v_{0} \alpha \varepsilon P,\quad a_{2} = v_{0}^{2} \alpha^{2} ,\quad a_{3} = - C_{xx} \alpha^{4} ,\quad a_{4} = - \varepsilon \left( {I_{0} + I_{2} \alpha^{2} } \right), \\ & a_{5} = \left( {B_{xx} \alpha^{3} } \right)^{2} ,\quad a_{6} = \left( {I_{1} \alpha \varepsilon } \right)^{2} ,\quad a_{7} = 2B_{xx} \alpha^{3} I_{1} \alpha \varepsilon ,\quad a_{8} = A_{xx} \alpha^{2} \quad {\text{and}}\quad a_{9} = I_{0} \varepsilon \\ \end{aligned}$$
(39)

4 Numerical results and discussions

In this section, a numerical testing of the procedure as well as parametric studies were performed in order to establish the validity and usefulness of the analytical approach. The effect of FG distribution, non-locality effect and thickness ratios on the natural frequencies of the FG nanobeam were investigated. The functionally graded nanobeam is composed of aluminium and alumina and its properties are shown in Table 1. The bottom surface of the beam consists of pure aluminium (Al), whereas the top surface of the beam is pure alumina (Al2O3). The relations described in Eq. (40) are performed in order to calculate non-dimensional natural frequencies.

$$\bar{\omega }_{1} = \omega_{1} L^{2} \sqrt {\uprho_{{{\text{Al}}_{2} {\text{O}}_{3} }} {\text{A/E}}_{{{\text{Al}}_{2} {\text{O}}_{3} }} {\text{I}}}$$
(40)

where \({\text{I}} = {\text{bh}}^{3} /12\) is the moment of inertia of the cross section of the beam.

Table 1 Material properties of FGM
Full size table

To evaluate the accuracy of the natural frequencies predicted by the present method, natural frequencies of simply supported FG nanobeam with various volume fraction index and L/h ratios previously analyzed by finite element method were re-examined. Tables 2 and 3 compares the results of the present study and the results presented by Eltaher et al. [42] were obtained by finite element method for FG nanobeam with different FG distribution indexes, length-to-thickness ratios and non-local parameters. The non-dimensional fundamental frequencies of simply-supported FG nanobeam are presented in Tables 2 and 3 and determines the effect of nonlocal parameter (varying from 0 to 5), material distribution index (varying from 0 to 10) and length-to-thickness ratios (varying from 20 to 100) on the natural frequency characteristics of FG nanobeam.

Table 2 Comparison of non-dimensional fundamental natural frequencies (\(\bar{\omega }_{1} = \omega_{1} L^{2} \sqrt {\uprho_{{{\text{Al}}_{2} {\text{O}}_{3} }} {\text{A/E}}_{{{\text{Al}}_{2} {\text{O}}_{3} }} {\text{I}}}\)) of simply supported FG nanobeams (b = 1000 nm, L = 10,000 nm, h = 100 nm, p = 0, 0.1, 0.2, 0.5 [42])
Full size table
Table 3 Comparison of non-dimensional fundamental natural frequencies (\(\bar{\omega }_{1} = \omega_{1} L^{2} \sqrt {\uprho_{{{\text{Al}}_{2} {\text{O}}_{3} }} {\text{A/E}}_{{{\text{Al}}_{2} {\text{O}}_{3} }} {\text{I}}}\)) of simply supported FG nanobeams (b = 1000 nm, L = 10,000 nm, h = 100 nm, p = 1, 2, 5, 10 [42])
Full size table

One may clearly notice here that the non-dimensional fundamental frequency parameters obtained in the present investigation are in excellent agreement with the results presented by analytical solution and finite element method for all cases used for comparison and validates the proposed method of solution. First of all, when the two parameters vanish (μ × 10−12 = 0 and p = 0) the classical isotropic beam theory is rendered. Furthermore, the effects of slenderness ratios on the dimensionless frequency are presented in Tables 2 and 3. From the results, it can be observed that, when the slenderness ratio of the FG nanobeam decreased (thickness reduces), the frequencies increased. As seen in Tables 2 and 3, by fixing the nonlocal parameter and varying the material distribution parameter results in decreasing fundamental frequencies due to increasing ceramics phase constituent and hence, stiffness of the beam. However, increasing nonlocal parameter causes a decrease in fundamental frequency at a constant material graduation index.

In this section the axial and transverse dynamic response of FG nanobeam under a moving constant load is analyzed. The dimensionless axial and transverse dynamic deflection are defined as the ratio of u and w with h; thickness of nanobeam are shown as \((\bar{u},\bar{w}) = (u,w)/h\). The transverse moving constant load is v 0 = 5, 10, 15, 20 nm/ns and also the width of the curve is 10 nm.

The variation of transverse dynamic deflection versus time for v 0 = 5, 10, 15, 20 nm/ns velocity of moving constant load and at different power law index of FG material as p = 0, 0.2, 1, 5 is illustrated in Fig. 2. In this figure the length of the nanobeam is equal to 100 nm and the non-local parameter is constant and equal to 1. It should be said that the deflection shown in Fig. 2 is the deflection at midspan (x = L/2). It can be seen that by passing time, the value of \(\bar{w}\) decreases or increases. Before the 3 ns, the values of \(\bar{w}\) that have higher velocities are higher than those of lower velocities which changes with passing time. By increasing the power law index of FG material, dynamic deflection increases. For instance, the amount of mentioned increase in Fig. 2c is twice that in Fig. 2d and this shows the importance of FG materials.

Fig. 2
figure 2

Variation of non-dimensional transverse dynamic deflection versus time for four different velocity of moving load and also for different power law index of FG material as a p = 0, b p = 0.2, c p = 1, d p = 5 (µ = 1 nm, h = L/100, k = p)

Full size image

In continuance, it can be understood that by increasing p, maximum dynamic deflection in transverse direction increases approximately in an exponential manner. Furthermore, an increase in velocity of each moving load parameter affects this procedure by a particular rate. In addition, by increasing time and power-law exponent, the dependency of dimensionless dynamic deflection on the velocity of moving load variations is insignificant.

Figure 3 illustrates the axial dynamic deflection \(\bar{u}\), versus time for the mentioned parameters in Fig. 2.

Fig. 3
figure 3

Variation of non-dimensional axial dynamic deflection versus time for four different velocity of moving load and also for different power law index of FG material as a p = 0, b p = 0.2, c p = 1, d p = 5 (µ = 1 nm, h = L/100, k = p)

Full size image

Except case (a), the amounts of (\(\bar{u}\)) increase or decrease at various times. Before 2.5 ns, the values of \(\bar{u}\) that have higher velocities are higher than those of lower velocities. In comparing Figs. 2b and 3b, it is distinctly clear that the amounts of \(\bar{w}\) are almost 1000 times as high as those of \(\bar{u}\). This is obvious as the FG nanobeam is under the transverse loading and consequently, the axial dynamic deflection should be negligible. It can be seen from Fig. 3 that when the power law index of FG is equal to zero, the amount of axial dynamic deflection for all of the loading velocities is also equal to zero. This is because of the fact that when p = 0, the nanobeam has homogenous properties. This behaviour seems predictable considering that as p increases, the FG nanobeam tends to a purely aluminum one, and that the Young’s modulus of aluminum is smaller than alumina. In this condition the amounts of I 1 and B are equal to zero and therefore, the differential equations of (24) and (25) become decoupled and the transverse dynamic deflection has no effect on axial dynamic deflection or vice versa.

The variation of maximum dynamic deflection versus the velocity of moving load for different non-local parameters and different aspect ratios is shown in Fig. 4. As shown, maximum dynamic deflection due to increasing velocity of the moving load initially decreases, then increases and finally decreases again. By increasing the nonlocal parameter in a constant aspect ratio (length to thickness), the amount of maximum deflection increases. Maximum difference occurred where nonlocal parameters are equal to 2 and 3.

Fig. 4
figure 4

Variation of the maximum non-dimensional dynamic deflection of the FG nano beam with respect to the moving load velocity, for different values of nonlocal parameters and also for various aspect ratios. a L/h = 50, b L/h = 70, c L/h = 80, d L/h = 100 (p = 1, k = p)

Full size image

By increasing the aspect ratio, the maximum dynamic deflection transfers to the lower velocities from the higher ones. For an instance the maximum dimensionless dynamic deflection in Fig. 4a occurred at a velocity of 70 nm/ns while for Fig. 4d, it occurs at 35 nm/ns.

The maximum transverse and axial dynamic deflection versus the velocity and for different power laws index of FG material are shown in Fig. 5a, b, respectively.

Fig. 5
figure 5

a Variation of maximum non dimensional transverse dynamic deflection versus moving load velocity and for different values of power law index, b variation of maximum non dimensional axial dynamic deflection versus moving load velocity and for different values of power law index (L/h = 100, µ = 1 nm, k = p)

Full size image

It is distinctly clear that increasing the velocity firstly, results in increasing the maximum dynamic deflection and secondly, results in its decrease. In Fig. 5a, by increasing the power index law of FG material, the maximum dynamic deflection increases and then decreases which is not the same in Fig. 5b. In Fig. 5b as the power law index increases (by up to 5), the maximum dynamic deflection approaches its highest value but as the power law index increases from 5 to 10, it decreases. Finally, as the power law index increases again (p > 10), the maximum dynamic deflection decreases. By more careful observation, it is seen from Fig. 5b that the two diagrams are coincident and their maximum dynamic deflection is equal to zero. This is due to the fact that when the power law index of FG material extends to infinity, the material becomes homogenous and shows the ceramic or metal material, respectively. In this condition there is no axial dynamic deflection in transverse loading.

The variation of maximum transverse and axial deflection versus nonlocal parameter for different power law index of FG material is shown in Fig. 6. In order to have more general results, the power law index p is not same for the elastic modulus and the density is presented (Fig. 7). Figure 7 shows the variation maximum non-dimensional transverse as well as axial dynamic deflection versus non-local parameter and for different values of density power law index. As shown, the amount of maximum transverse dynamic deflection variation is higher than those of axial dynamic deflection. According to Figs. 6a and 7a, as the nonlocal parameter increases the variation of maximum transverse dynamic deflection increases and in addition, the slope increases with increasing non-local parameter and the power law index of FG material. Figures 6b and 7b shows that increasing the non-local parameter tends to increase the maximum transverse dynamic deflection but when p = 0, the value of maximum dynamic deflection is equal to zero and increasing the non-local effect does not have any effect on it. By increasing the non-local parameter, strength and stability of the nanobeam reduces; therefore, the amount of deflection increases. Generally, Figs. 6 and 7 show the importance of the non-local parameter and the theory used in this study.

Fig. 6
figure 6

a Variation of maximum non dimensional transverse dynamic deflection versus nonlocal parameter and for different values of power law index, b variation of maximum non dimensional axial dynamic deflection versus nonlocal parameter and for different values of power law index (L/h = 100, v = 100 m/s, k = p)

Full size image
Fig. 7
figure 7

a Variation of maximum non dimensional transverse dynamic deflection versus nonlocal parameter and for different values of power law index, b variation of maximum non dimensional axial dynamic deflection versus nonlocal parameter and for different values of power law index (L/h = 100, v = 100 m/s, p = 1)

Full size image

5 Conclusion

An exact solution for the transverse and axial dynamic response of a FG nanobeam which is under moving constant load was analyzed in this study. Using the Hamilton principle, the differential equation and boundary condition is obtained and then based on the non-local Euler–Bernoulli theory the governing equations are derived. Considering the simply supported boundary condition and the Laplace transform, an exact analytical solution for the transverse and axial response of FG nanobeam was found. The results showed that increasing the power law index of FGM tends to increase the transverse dynamic deflection. Also, when the power index law is equal to zero or infinity, the amount of axial dynamic deflection is equal to zero which is due to the fact that in this condition, the material is homogenous and the transverse loading does not have any effect on the transverse dynamic deflection. Also, the effect of nonlocal parameter was analysed and the importance of using the non-local parameter in nanoscale was clarified.