1 Introduction

Since carbon nanotubes (CNTs) have possessed excellent mechanical and physical properties, they have vast prospective application as structural elements in nanoscale devices, such as nanobiological devices and nanoelectromechanical systems (NEMS) [1, 2]. Currently, CNT beams are being used as nanoscale materials and play important roles in designing sensor structures and improving the function of sensors in the nanoscale devices. Some researchers have explored the potential of using CNT-based resonators as nanomass detection sensor [3–6]. The principle of mass detection using CNT-based resonators is based on the fact that the resonant frequency of CNTs is sensitive to the changes in the nanomass attached to the CNTs, which causes the frequency shifts of CNT resonators. The idea of using individual CNTs as high-sensitivity mass sensor was first proposed by Poncharal et al. [4]. Since controlled experiments at nanoscale are difficult, computer simulation can be used to predict the frequency changes and to design reasonable structures of CNT-based resonators. The molecular dynamics simulation is very time-consuming and remains formidable for large-scale systems; therefore, the continuum mechanics or the molecular mechanics methods have been widely used to study the computation of large systems. [7–11]. Patel and Joshi [12, 13] reported the dynamic analysis of double-walled carbon nanotubes (DWCNTs) using atomistic finite element method (FEM). They suggested that defective DWCNTs could further be explored for mass sensing. Based on FEM analysis and continuum mechanics, Govind and Bansal investigated the potentials of cantilevered single-walled boron nitride nanotubes (SWBNNTs) and H model beam of SWBNNTs as nanomechanical resonators [14]. Li et al. [15] studied the free vibration and mass detection capability of CNT-based sensors using the molecular mechanics approach. The obtained results indicated that the nonlocal effect decreased the resonance frequency except for the fundamental frequency of nanocantilever sensor.

The more theoretical approaches of analyzing CNT-based resonators have been based on the Euler–Bernoulli beam model. In our previous work [16], the resonant frequencies and frequency shifts of the CNTs with attached mass were investigated by the Euler–Bernoulli beam theory. The local elastic theory does not consider about the long-range forces between atoms. However, the theory of nonlocal continuum mechanics considers that the stress field at a given reference point is a function of the strain distribution over a certain representative volume of the material centered at that point. In this way, the internal length scale enters into the constitutive equations simply as a material parameter. The nonlocal elasticity theory could potentially play a useful role in analysis related to nanoscale materials. Considering the small length scale effect of nanostructures, in the present study, we will analyze the resonant frequency of CNTs with clamped boundary condition under axial tensile loads using the nonlocal Euler–Bernoulli beam model.

2 Theoretical approaches

2.1 Nonlocal elasticity theory

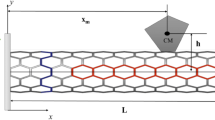
We considered a CNT clamped at both ends and subjected to an axial tensile load. The schematic diagram of the clamped CNT beam carrying an attached concentrated mass m c along its length position x = a is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of clamped CNT beam model with attached mass under tensile load

Full size image

In the study, the nonlocal Euler–Bernoulli beam model is applied to investigate a free vibration of CNT. The governing equation of motion for a beam subjected to an axial tensile load N is given by

$$EI\frac{{\partial^{4} w^{*} \left( {x,t} \right)}}{{\partial x^{4} }} - N\frac{{\partial^{2} w^{*} \left( {x,t} \right)}}{{\partial x^{2} }} + \rho A\frac{{\partial^{2} w^{*} \left( {x,t} \right)}}{{\partial t^{2} }} + \left( {ea} \right)^{2} \left[ {N\frac{{\partial^{4} w^{*} \left( {x,t} \right)}}{{\partial x^{4} }} - \rho A\frac{{\partial^{4} w^{*} \left( {x,t} \right)}}{{\partial x^{2} \partial t^{2} }}} \right] = 0$$
(1)

where x and t are the axial coordinate and time, respectively. w *(x, t) is the flexural deflection, e 0 a is the nonlocal parameter relative to carbon material, and a is the internal characteristic length of the C–C bond which was found to be 0.142 nm. E is the elastic modulus, I is the moment of inertia of the cross-sectional area A, and ρ is the mass density of the CNT.

As shown in Fig. 1, when a concentrated mass is attached to an arbitrary position (x = a) of nanotube length, the CNT beam can be considered as two parts which are 0 ≤ x ≤ a and a ≤ x ≤ L. That is, the CNT is treated as two separate beams connected to each other through the attached mass. According to Eq. (1), the governing differential equations for each beam are given by

$$EI\frac{{\partial^{4} w_{1} \left( {x,t} \right)}}{{\partial x^{4} }} - N\frac{{\partial^{2} w_{1} \left( {x,t} \right)}}{{\partial x^{2} }} + \rho A\frac{{\partial^{2} w_{1} \left( {x,t} \right)}}{{\partial t^{2} }} + \left( {e_{0} a} \right)^{2} \left[ {N\frac{{\partial^{4} w_{1} \left( {x,t} \right)}}{{\partial x^{4} }} - \rho A\frac{{\partial^{4} w_{1} \left( {x,t} \right)}}{{\partial x^{2} \partial t^{2} }}} \right] = 0,\quad 0 \le x \le a$$
(2)
$$EI\frac{{\partial^{4} w_{2} \left( {x,t} \right)}}{{\partial x^{4} }} - N\frac{{\partial^{2} w_{2} \left( {x,t} \right)}}{{\partial x^{2} }} + \rho A\frac{{\partial^{2} w_{2} \left( {x,t} \right)}}{{\partial t^{2} }} + \left( {e_{0} a} \right)^{2} \left[ {N\frac{{\partial^{4} w_{2} \left( {x,t} \right)}}{{\partial x^{4} }} - \rho A\frac{{\partial^{4} w_{2} \left( {x,t} \right)}}{{\partial x^{2} \partial t^{2} }}} \right] = 0,\quad a \le x \le L$$
(3)

where w j , j = 1, 2, are the flexural deflections of the left and the right with respect to the location of the concentrated mass.

We assume that the harmonic vibration of CNT resonator has the circular frequency of ω, and the vibration amplitudes of Y j , j = 1, 2. Thus, the solutions of the flexural deflection may be expressed as

$$w_{j} \left( {x,t} \right) = Y_{j} \left( x \right)\,e^{i\omega t} ,\quad j = 1,\;2$$
(4)

Substituting Eq. (4) into the differential Eqs. (2) and (3), we have

$$\left[ {1 + \left( {e_{0} a} \right)^{2} \frac{N}{EI}} \right]Y_{j}^{\left( 4 \right)} - \left[ {\frac{N}{EI} + \left( {e_{0} a} \right)^{2} \frac{{\rho A\omega^{2} }}{EI}} \right]Y^{\prime\prime}_{j} - \frac{{\rho A\omega^{2} }}{EI}Y_{j} = 0,\quad j = 1,\;2$$
(5)

Moreover, we can obtain the general solutions of Eq. (5) given by

$$Y_{j} \left( x \right) = C_{j1} \cosh \eta x + C_{j2} \sinh \eta x + C_{j3} \cos \xi x + C_{j4} \sin \xi x,\quad j = 1,\;2$$
(6)

where

$$\eta = \left( {\phi_{1} + \sqrt {\phi_{1}^{2} + \phi_{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\quad \xi = \left( {\sqrt {\phi_{1}^{2} + \phi_{2} } - \phi_{1} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$
(7)

and

$$\phi_{1} = \frac{N}{2EI} \cdot \frac{{1 + \left( {e_{0} a} \right)^{2} \frac{{\rho A\omega^{2} }}{N}}}{{\,1 + \left( {e_{0} a} \right)^{2} \frac{N}{EI}}},\quad \phi_{2} = \frac{{\rho A\omega^{2} }}{EI}$$
(8)

In Eq. (6), the constants C jk , j = 1, 2, k = 1 − 4, can be obtained from the corresponding boundary conditions given by

$$w_{1} \left( {0,t} \right) = \left. {\frac{{\partial w_{1} \left( {x,t} \right)}}{\partial x}} \right|_{x = 0} = w_{2} \left( {L,t} \right) = \left. {\frac{{\partial w_{2} \left( {x,t} \right)}}{\partial x}} \right|_{x = L} = 0$$
(9)
$$\left. {w_{1} \left( {a,t} \right) = w_{2} \left( {a,t} \right),\;\frac{{\partial w_{1} \left( {x,t} \right)}}{\partial x}} \right|_{x = a} = \left. {\frac{{\partial w_{2} \left( {x,t} \right)}}{\partial x}} \right|_{x = a} ,\;\left. {\frac{{\partial^{2} w_{1} \left( {x,t} \right)}}{{\partial x^{2} }}} \right|_{x = a} = \left. {\frac{{\partial^{2} w_{2} \left( {x,t} \right)}}{{\partial x^{2} }}} \right|_{x = a}$$
(10)
$$\left. {EI\frac{{\partial^{3} w_{1} \left( {x,t} \right)}}{{\partial x^{3} }}} \right|_{x = a} - EI\left. {\frac{{\partial^{3} w_{2} \left( {x,t} \right)}}{{\partial x^{3} }}} \right|_{x = a} = m_{c} \frac{{\partial^{2} w_{1} \left( {a,t} \right)}}{{\partial t^{2} }}$$
(11)

where m c is the attached mass to be detected.

Substituting Eq. (6) into the boundary conditions of Eqs. (9–11), the resonant frequencies of the CNT resonators with an attached concentrated mass can be determined by considering the nontrivial solutions.

2.2 Rayleigh’s energy method

In this analysis, we used a method of energy principle to investigate the vibration frequencies of CNTs used as nanoresonators. Considering the effect of nonlocal parameter on the vibrational behavior of CNT, the kinetic energy of the CNT carrying a concentrated mass can be expressed as

$$T = \frac{{\rho A\omega^{2} }}{2}\int {Y^{2} \left( x \right){\text{d}}x} + \frac{{m_{c} }}{2}Y^{2} \left( {\frac{L}{2}} \right) + \left( {e_{0} a} \right)^{2} \frac{{\rho A\omega^{2} }}{2}\int {\left( {\frac{{{\text{d}}Y\left( x \right)}}{{{\text{d}}x}}} \right)^{2} {\text{d}}x}$$
(12)

where ω is the circular frequency of vibration. Y(x) is the deflection shape of CNT with the first mode of vibration.According to our previous study [16], the deflection shape in Eq. (12) yielded

$$Y\left( x \right) = \frac{y}{{y_{\hbox{max} } }} = \beta \left( {1 - \cosh \alpha x} \right) + \gamma \left( {\sinh \alpha x - \alpha x} \right),\quad 0 \le x \le \frac{L}{2}$$
(13)

and

$$\alpha^{2} = \frac{N}{EI},\;\beta = \frac{{\tanh \frac{\alpha l}{4}}}{{2\tanh \frac{\alpha L}{4}\sinh^{2} \frac{\alpha L}{4} + \left( {\frac{\alpha L}{2} - \sinh \frac{\alpha L}{2}} \right)}},\;\beta = \frac{{\tanh \frac{\alpha l}{4}}}{{2\tanh \frac{\alpha L}{4}\sinh^{2} \frac{\alpha L}{4} + \left( {\frac{\alpha L}{2} - \sinh \frac{\alpha L}{2}} \right)}},\;\gamma = \frac{1}{{2\tanh \frac{\alpha L}{4}\sinh^{2} \frac{\alpha L}{4} + \left( {\frac{\alpha L}{2} - \sinh \frac{\alpha L}{2}} \right)}}$$
(14)

Substituting the deflection function in Eq. (13) into Eq. (12), we can obtain the equivalent mass of the combined system given as

$$m_{eq} = \left( {\phi + \mu } \right)\rho AL + m_{c}$$
(15)

and

$$\phi = \frac{{3\beta^{2} }}{2} - \frac{\alpha \beta \gamma L}{2} + \frac{{\alpha^{2} \gamma^{2} L^{2} }}{12} + \left( {2\beta \gamma + \frac{{4\gamma^{2} - 4\beta^{2} }}{\alpha L}} \right)\sinh \frac{\alpha L}{2} - 2\gamma^{2} \cosh \frac{\alpha L}{2} + \frac{{\beta^{2} + \gamma^{2} }}{2\alpha L}\sinh \alpha l - \frac{2\beta \gamma }{\alpha L}\sinh^{2} \frac{\alpha L}{2} - \frac{{\gamma^{2} }}{2}$$
(16)
$$\mu = \left( {\frac{{\alpha \left( {\beta^{2} + \gamma^{2} } \right)L}}{2}\sinh \alpha L - \cosh \alpha L + 4\alpha \beta \gamma L\cosh \frac{\alpha L}{2} - 4\alpha \gamma^{2} L\sinh \frac{\alpha L}{2} + \frac{{3\alpha^{2} L^{2} \left( {\gamma^{2} - \beta^{2} } \right)}}{2} - 3\alpha \beta \gamma L} \right)\left( {\frac{{e_{0} a}}{L}} \right)^{2}$$
(17)

where μ is the effect coefficient on the nonlocal parameter. Thus, the resonant frequency expression of the CNTs carrying concentrated mass yields

$$f = \frac{1}{2\pi }\sqrt {\frac{{k_{eq} }}{{\phi \rho AL + m_{c} }}}$$
(18)

where

$$k_{eq} = \frac{P}{{y_{\hbox{max} } }} = \frac{2N\alpha }{{2\tanh \frac{\alpha L}{4}\sinh^{2} \frac{\alpha L}{4} + \left( {\frac{\alpha L}{2} - \sinh \frac{\alpha L}{2}} \right)}}$$
(19)

3 Analytical results and discussion

In this simulation, the influences of the nonlocal parameter, the aspect ratio and the axial force on the resonant frequency of the CNT beam attached with nanomass are investigated in detail. We considered the CNT to be a diameter of 1.0 nm, and carrying concentrated mass on its center. The effective thickness of the CNTs was taken to be 0.34 nm. The elastic modulus and the density of the CNTs are 1.0 TPa and 2.3 g/cm3, respectively [17]. In the previous study, the result shows that the resonant frequencies of CNTs are affected by its vibration mode. The variations of vibration frequency in CNT resonator with the attached mass are little sensitive to the attached mass for the vibration modes larger than 1. In this paper, we focus on the investigation of the resonant frequency of CNT with attached nanomass for the first mode of vibration.

Figure 2 shows the effect of the nonlocal coefficient on the resonant frequency of the CNTs with the aspect ratio of 20 under attached different nanomasses. The axial tensile load applied to the CNTs is 20 nN, corresponding to the tensile stress of about 19 GPa. Because CNTs have the tensile strength up to 63 GP [18], the axial force over 20 nN can be also loaded to the CNT. For the choice of the nonlocal parameter e 0 a used in this simulation, we take that e 0 a/L is 0.2 [19, 20]. It is found that the effect of the nonlocal coefficient on the resonant frequency is significant to the attached mass <10−2 zg. The reason that the small nanomass makes the CNTs more flexible as the nonlocal model can be viewed as atoms linked by elastic springs [21]. Figure 3 shows the variation of the resonant frequency of the clamped CNT with the attached mass. Here, the frequency variation is defined as the difference between the frequency of the CNTs with and without attached mass, that is Δω = Δ(ω) − Δ(ω + m c ). The result shows that frequency shift of CNTs increases and tends to a plateau value with increasing attached mass. The influence of the nonlocal parameter on the frequency shift is larger in the attached mass larger than 1.0 zg. The mass sensitivity of CNT resonator usually depends on the variation of the frequency or the frequency shift with attached mass. It is seen from Figs. 2 and 3 that the nanomass in the order of 0.001–1.0 zg has higher sensitivity to the CNT resonator since the frequency or the frequency shift has large changes with the attached nanomass. The vibration characteristics of CNTs are affected by the mass attached to the CNTs. For very small mass, the variation of the frequency is insignificant because the vibration response depends mainly on the natural frequency of CNTs. On the other hand, the response of vibration frequency would hardly depend on the vibration characteristics of CNT beam because the larger mass is attached to the CNTs.

Fig. 2
figure 2

Effect of the nonlocal coefficient on the resonant frequency of the CNTs under attached different nanomasses (L/D = 20, N = 20 nN)

Full size image
Fig. 3
figure 3

Resonant frequency shifts of CNT beam under different concentrated masses (L/D = 20, N = 20 nN)

Full size image

The relationship between the resonant frequency of CNTs and the aspect ratio is shown in Fig. 4. The effects of the nonlocal coefficient on the resonant frequency of CNTs are small for different CNT lengths. Figure 5 shows the effect of the axial force on the resonant frequency of CNT with attached concentrated mass. This result suggests that higher mass sensitivity can be obtained by increasing tensile force acting on CNTs. For example, the vibration frequency of CNT resonator will increase up to 52 % for the attached mass larger than 0.1 zg and the axial force of 20 nN. This can be explained that the natural frequency of CNTs increases when the CNT beam is subjected to a tensile axial force, resulting in higher mass sensitivity.

Fig. 4
figure 4

Effect of the nonlocal coefficient on the resonant frequency of the CNTs under different aspect ratios (m c  = 0.1 zg, N = 20 nN)

Full size image
Fig. 5
figure 5

Effect of the axial force on the resonant frequency of CNT with attached concentrated mass (L/D = 20, e 0 a = 0)

Full size image

Moreover, we adopt another theoretical approach that is Raleigh’s energy method to confirm the feasibility of the proposed continuum beam model. Figure 6 shows the comparison of the resonant frequency between the nonlocal Euler–Bernoulli beam model and the Raleigh’s energy method as a function of the attached mass for different aspect ratios. It can be seen that the two results are very consistent with each other in increasing attached mass. The maximum error between the two simulation methods exists small mass of nanoparticles, which is <2.5 %.

Fig. 6
figure 6

Comparison of the resonant frequency between the Euler–Bernoulli beam model and the Raleigh’s energy method (L/D = 20, mc = 0.1 zg)

Full size image

4 Conclusion

We explored the potential of CNTs as a nanomechanical mass sensor when an axial tensile load is applied on the CNTs. Based on the nonlocal Euler–Bernoulli beam model, the influences of the nonlocal parameter, the aspect ratio and the axial force on the resonant frequencies and frequency shifts are investigated in detail. The effect of the nonlocal coefficient on the resonant frequency is significant to the attached mass <10−2 zg. The results indicate that the nanomass in the order of 0.001–1.0 zg has higher sensitivity to the CNT resonator. The nanomechanical mass sensor is expected to have higher sensitivity when an axial tensile load is applied on the CNTs.