1 Introduction

Reliability-based design optimization (RBDO) aims to obtain optimal design results under the satisfaction of reliability requirement while minimizing the lifecycle cost of products. During the operational stage, time-variant properties of working conditions, strength degradation and motion will greatly affect product reliability under uncertainties, and therefore time-variant reliability-based design optimization (t-RBDO) methods should be developed to obtain high confidence in design results. Compared with the time-invariant RBDO, more computational expenses are needed since stochastic processes and their correlations should be considered in the t-RBDO (Suksuwan and Spence 2018). Efficient time-variant reliability analysis methods can increase the computational efficiency and several kinds of corresponding methods have been developed, e.g., out-crossing-based methods (Jiang et al. 2017a), extreme value-based methods (Hu and Du 2013), stochastic process decomposition methods (Yu et al. 2018), and surrogate model-based methods (Tayyab et al. 2020).

Furthermore, time-variant reliability analysis and design optimization are nested in the typical t-RBDO, which will decrease computational efficiency. To address this issue, many studies have been conducted. A time-invariant equivalent method is proposed to solve t-RBDO problems as a sequence of time-invariant reliability analysis and RBDO (Jiang et al. 2017b). A two-step decoupling model is constructed to handle the t-RBDO, where a transformed time-invariant RBDO is performed in the first step while time-invariant reliability analysis and deterministic optimization are alternately conducted in the second step (Shi et al. 2020a). For a complicated case of systems with multiple temporal and spatial parameters, a general decoupling method by establishing a mapping between design variables and time-invariant system reliability is presented, which can be employed to conduct t-RBDO of systems under time-varying working conditions (Yu and Wang 2019). A nested extreme response surface method where the surrogate model is constructed between input variables and extreme time response of the performance function is proposed (Wang and Wang 2012). A sequential Kriging modeling approach is provided, where the surrogate model of the performance function of probabilistic constraints is built by a design-driven adaptive sampling scheme by decomposing stochastic process into random variables (Li and Chen 2019). A t-RBDO method is provided by using a simultaneously refined Kriging model, which employs a global Kriging surrogate model built in an artificially augmented reliability space to approximate the performance function of a probabilistic constraint (Hawchar et al. 2018). A single-loop surrogate method is presented, where only those sample points having large contribution to the time-variant limit state surface are selected to enhance the surrogate model, and hence the computational efficiency is very high (Hu and Mahadevan 2016). For more t-RBDO methods, please refer to Jiang et al. (2017b), Shi et al. (2020b), and Wang et al. (2019).

In engineering practices, it is usually difficult to build probabilistic models since there are not enough built-in sensors or sampling time to collect sufficient data. Therefore, some non-probabilistic models, e.g., evidence theory (Zhang et al. 2018), possibility theory (Mourelatos and Zhou 2005), fuzzy set (Wang et al. 2012), and interval variable (Zhao et al. 2021) can be implemented. A sequential single-loop procedure is established when probability and interval variables are involved in the time-variant hybrid reliability-based design optimization (t-HRBDO) (Wang et al. 2016). While parameters of probability function are interval, the incremental shifting vector technique is used to transform the nested optimization into equivalent deterministic optimization and hybrid reliability analysis to increase the computational efficiency (Huang et al. 2017). An efficient method integrating the hybrid perturbation random moment and hybrid perturbation inverse mapping is proposed for the t-HRBDO problem under probabilistic and interval variables (Xia et al. 2015). The enhanced chaos control technique is employed for the non-probabilistic RBDO based on a convex model, which can check and re-update the control factor during the optimization process (Hao et al. 2017a). The adaptive-loop approach is an improved method of the enhanced chaos control technique for the t-HRBDO (Hao et al. 2017b). For a thermal structure under random, interval, and fuzzy uncertainties, a non-probabilistic RBDO model is established based on an interval ranking strategy, and furthermore the subinterval vertex method is provided to improve the computational efficiency (Wang et al. 2017).

For a t-HRBDO problem, only the worst-case scenario is considered during the design stage in most of the studies to ensure higher safety, which will lead to the increase of resources and also the decrease of dynamic performance. However, reliability is an interval restricted by the lower and upper bound of reliability due to the existence of hybrid uncertainties. In order to balance the reliability and resources effectively within the reliability bounds during the design stage, a novel flexible-constrained t-HRBDO framework and corresponding algorithms are proposed in this paper. The contributions of the paper can be summarized as (1) a novel flexible-constrained t-HRBDO framework is presented by accounting for the balance of reliability and resources during the design stage, (2) an infeasible region pruning-based Kriging surrogate model is built for hard constraints under uncertainty to improve the computational efficiency, (3) a determination method for the design preference parameter is provided to quantitatively build the relationship between reliability and resources, and (4) a new metaheuristic algorithm is presented to effectively conduct the flexible-constrained t-HRBDO.

The organization of the paper is as follows. The framework of the flexible-constrained t-HRBDO model is proposed in Sect. 2. Algorithms to solve the flexible-constrained t-HRBDO problem are elaborated in detail in Sect. 3. Two examples are provided in Sect. 4 to testify and validate the proposed methods. Conclusions are drawn in Sect. 5.

2 The framework of the flexible-constrained t-HRBDO model

In this Section, random variables are employed to describe the aleatory uncertainty and interval variables to describe the epistemic uncertainty during the construction of the flexible-constrained t-HRBDO model, since interval variables need less data only the upper and lower bounds of variables and other non-probabilistic variables can be transformed to interval variables easily.

2.1 The t-HRBDO model under probabilistic and interval uncertainties

The time-variant reliability under the mixture of random and interval variables can be expressed by

$$R(t_{\text{s}} ,t_{\text{e}} ) = \Pr \left\{ {g({\mathbf{d}},{\mathbf{X}}^{{\varvec{R}}} ,{\mathbf{X}}^{{\varvec{I}}} ,{\mathbf{Y}}(t),t) > 0,\forall t \in (t_{\text{s}} ,t_{\text{e}} )} \right\},$$
(1)

where \(g({\mathbf{d}},{\mathbf{X}}^{{\varvec{R}}} ,{\mathbf{X}}^{{\varvec{I}}} ,{\mathbf{Y}}(t),t)\) is the time-variant limit state function, \({\mathbf{d}}\) is the vector of deterministic variables,\({\mathbf{X}}^{{\varvec{R}}} = \left[ {X_{1}^{R} ,X_{2}^{R} ,...,X_{nx}^{R} } \right]\) is the vector of random variables, \({\mathbf{Y}}(t) = \left[ {Y_{1} \left( t \right),Y_{2} \left( t \right),...,Y_{ny} \left( t \right)} \right]\) is the vector of stochastic processes, \({\mathbf{X}}^{{\varvec{I}}} = \left[ {X_{1}^{I} ,X_{2}^{I} ,...X_{nI}^{I} } \right] \in \left[ {{\mathbf{\underline {X} }}^{{\varvec{I}}} ,{\overline{\mathbf{X}}}^{{\varvec{I}}} } \right]\) is the vector of interval variables with the lower bound \(\varvec{\underline {X} }^{{\varvec{I}}}\) and upper bound \(\overline{\varvec{X}}^{{\varvec{I}}}\), \(t \in (t_{\text{s}} ,t_{\text{e}} )\) denotes the time. \(g({\mathbf{d}},{\mathbf{X}}^{{\varvec{R}}} ,{\mathbf{X}}^{{\varvec{I}}} ,{\mathbf{Y}}(t),t) > 0\) denotes that the system operates safely while \(g({\mathbf{d}},{\mathbf{X}}^{{\varvec{R}}} ,{\mathbf{X}}^{{\varvec{I}}} ,{\mathbf{Y}}(t),t) \le 0\) means failure during the time interval \(t \in (t_{\text{s}} ,t_{\text{e}} )\).

Since \({\mathbf{X}}^{{\varvec{I}}}\) is a vector of interval variables, the time-variant reliability \(R(t_{\text{s}} ,t_{\text{e}} )\) is also interval restricted by the lower and upper bounds. In engineering applications, the lower bound \(R^{L} (t_{\text{s}} ,t_{\text{e}} )\) and upper bound \(R^{U} (t_{\text{s}} ,t_{\text{e}} )\) of \(R(t_{\text{s}} ,t_{\text{e}} )\) can be calculated based on optimization. Basically, \(R^{L} (t_{\text{s}} ,t_{\text{e}} )\) reflects the worst-case scenario of a system while \(R^{U} (t_{\text{s}} ,t_{\text{e}} )\) reflects the best-case scenario of a system and they can be estimated by

$$\left\{ \begin{gathered} R^{L} (t_{\text{s}} ,t_{\text{e}} ) = \Pr \left\{ {\mathop {\min }\limits_{{{\varvec{X}}^{{\varvec{I}}} \in \left[ {{\varvec{X}}^{{\varvec{I(L)}}} ,{\varvec{X}}^{{\varvec{I(U)}}} } \right]}} \left[ {\mathop {\min }\limits_{{t \in (t_{\text{s}} ,t_{\text{e}} )}} g({\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} \varvec{,Y}(t),t) > 0} \right]} \right\} \hfill \\ R^{U} (t_{\text{s}} ,t_{\text{e}} ) = \Pr \left\{ {\mathop {\max }\limits_{{{\varvec{X}}^{{\varvec{I}}} \in \left[ {{\varvec{X}}^{{\varvec{I(L)}}} ,{\varvec{X}}^{{\varvec{I(U)}}} } \right]}} \left[ {\mathop {\min }\limits_{{t \in (t_{\text{s}} ,t_{\text{e}} )}} g({\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} \varvec{,Y}(t),t) > 0} \right]} \right\} \hfill \\ \end{gathered} \right.$$
(2)

Please refer to Ref. (Zhao et al. 2021) for the estimation method of \(R^{L} (t_{\text{s}} ,t_{\text{e}} )\) and \(R^{U} (t_{\text{s}} ,t_{\text{e}} )\). With the estimated lower bound \(R^{L} (t_{\text{s}} ,t_{\text{e}} )\) and upper bound \(R^{U} (t_{\text{s}} ,t_{\text{e}} )\), the conservative and radical t-HRBDO models are receptively provided by

$$\begin{gathered} {\text{find }}{\mathbf{d}},{{\mathbf{u}}}_{{{\varvec{X}}^{{\varvec{R}}} }} \hfill \\ \min \, C({\mathbf{d}},{{\mathbf{u}}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) \hfill \\ s.t. \, R_{j}^{L} \ge R_{j}^{tar} , \, j = 1,2,...,nc \hfill \\ \mathbf{ d}^{\mathbf{L}} \le {\mathbf{d}} \le {\mathbf{d}}^{\mathbf{U}} ,{{\mathbf{u}}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{L}} \le {{\mathbf{u}}}_{{{\varvec{X}}^{{\varvec{R}}} }} \le {{\mathbf{u}}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{U}} \mathbf{,} \hfill \\ \mathbf{ d} \in \Omega^{nd} ,{{\mathbf{u}}}_{{{\varvec{X}}^{{\varvec{R}}} }} \in \Omega^{nx} \hfill \\ \end{gathered}$$
(3)
$$\begin{gathered} {\text{find }}{\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \hfill \\ \min \, C({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) \hfill \\ s.t. \, R_{j}^{U} \ge R_{j}^{tar} , \, j = 1,2,...,nc \hfill \\ \mathbf{ d}^{\mathbf{L}} \le {\mathbf{d}} \le {\mathbf{d}}^{\mathbf{U}} ,{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{L}} \le {\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \le {\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{U}} \mathbf{,} \hfill \\ \mathbf{ d} \in \Omega^{nd} ,{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \in \Omega^{nx} \hfill \\ \end{gathered},$$
(4)

where \({\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}\) is the vector of mean values of random variables, \(R_{j}^{tar}\) is the target reliability, \(C( \cdot )\) denotes the cost function, and \(\Omega^{nd}\) and \(\Omega^{nx}\) are the design domains of \({\mathbf{d}}\) and \({\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}\).

For the conservative t-HRBDO in Eq. (3), the higher reliability is ensured with the higher resources while the radical t-HRBDO in Eq. (4), the resources will be the least but the reliability can not be ensured. Therefore it is necessary to balance the reliability and cost for a reasonable optimal results.

2.2 The flexible-constrained t-HRBDO model

For a system, the lower bound \(R^{L} (t_{\text{s}} ,t_{\text{e}} )\) and upper bound \(R^{U} (t_{\text{s}} ,t_{\text{e}} )\) depend on the hybrid uncertainties. However, cost paid for the same amount of reliability increase may be greatly discriminating for different engineering problems. It will be not reasonable to conduct conservative t-HRBDO when huge cost is needed for a small increment of initial reliability and to conduct the radical t-HRBDO when the higher reliability should be ensured. Therefore it is required to combine the lower bound \(R^{L} (t_{\text{s}} ,t_{\text{e}} )\) and upper bound \(R^{U} (t_{\text{s}} ,t_{\text{e}} )\) and furthermore the relationship between the reliability and cost should be quantified during the design procedure. Different from the traditional weight-sum method by combining the lower bound \(R^{L} (t_{\text{s}} ,t_{\text{e}} )\) and upper bound \(R^{U} (t_{\text{s}} ,t_{\text{e}} )\) directly, here we propose a flexible-constrained t-HRBDO model by introducing the relationship between the reliability and cost. The flexible-constrained t-HRBDO model can be provided typically by

$$\begin{gathered} {\text{find }}{\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \hfill \\ \min \, \frac{{C({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) - C_{0} }}{{C_{tar} - C_{0} }} + \gamma \max \left\{ {\frac{{R_{j}^{tar} - R_{j}^{L} }}{{R_{j}^{tar} - R_{0} }}} \right\} \hfill \\ s.t. \, R_{j}^{U} \ge R_{j}^{tar} {,}\; \, j = 1,2,...,nc \hfill \\ \, \gamma \ge 0 \hfill \\ \mathbf{ d}^{\mathbf{L}} \le {\mathbf{d}} \le {\mathbf{d}}^{\mathbf{U}} ,{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{L}} \le {\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \le {\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{U}} \hfill \\ \mathbf{ d} \in \Omega^{nd} ,{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \in \Omega^{nx} \hfill \\ \end{gathered},$$
(5)

where \(C_{0}\) is the cost under the radical design while \(C_{tar}\) is the cost under the conservative design, \(R_{0}\) is the lower bound of reliability under the radical design, \(\gamma\) is the design preference parameter. In this model, \(R_{j}^{U} \ge R_{j}^{tar} { ( }j = 1,2,...,nc.)\) is called hard constraints under uncertainty, which should be satisfied during the optimization process while \(\max \left\{ {\frac{{R_{j}^{tar} - R_{j}^{L} }}{{R_{j}^{tar} - R_{0} }}} \right\}\) is designed in the objective as the flexible constraint. The introduction of the flexible constraint into the objective function can not only build the relationship between cost and reliability by considering the conservative and radical t-HRBDOs but also improve the efficiency of the t-HRBDO than being as constraints under uncertainties.

3 Algorithms of the flexible-constrained t-HRBDO

Reliability analysis will be conducted for uncertain constraints in the typical t-HRBDO model while reliability analysis will be performed in both uncertain constraints and the objective function in the flexible-constrained t-HRBDO model. The classification-based surrogate will be built for the hard uncertain constraints and the global approximation-based surrogate for the flexible uncertain constraints to improve computational efficiency. The determination of the design preference parameter will be then made by considering the relationship between cost and reliability within the bounds of the time-variant reliability, which will help designers to make a more reasonable decision to balance the required reliability and cost for different engineering problems. In order to effectively solve the flexible-constrained t-HRBDO model, a metaheuristic algorithm is finally provided.

3.1 Improved infeasible region pruning technology for surrogate models of hard uncertain constraints

During the procedure of the RBDO, the current design point will be judged whether it is feasible or not and then substantial reliability analysis evaluations are needed. If the relationship between design points and reliability can be constructed, the feasibility of the current design point will be directly judged to decrease the number of reliability analysis evaluations.

For constrained optimization problems, the task is to find optimal solutions in the feasible domain. Design points in the infeasible domain are usually not to be concerned. In order to effectively divide the design domain into feasible domain and infeasible domain, the relationship between uncertain constraint and design points should be established. Here we define \(HC_{{R_{j} }} ({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) = R_{j} - R^{tar}\), then the uncertain constraint can be expressed by

$$HC_{{R_{j} }} ({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) \ge 0.$$
(6)

This can be considered as a classification problem. If a classification surrogate model is built with less computational expense, the computational efficiency of reliability analysis will be improved greatly. Therefore we propose a novel infeasible region pruning technology by changing the strategy of selecting new samples.

3.1.1 Initial surrogate modeling

The sample space of the constrained surrogate model under uncertainty is first determined. Samples will be drawn from the domain formed by the lower and upper limits of \(S_{candi} = \{ {\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \}\) uniformly. After generating candidate samples, \(N_{\text{ini}}\) samples are randomly selected as the set of training samples \(S_{\text{train}}\), and the remaining \(N_{\text{test}} = N_{candi} - N_{\text{ini}}\) samples will be used as the set of testing samples \(S_{\text{test}}\). The initial surrogate model of the j-th constraint is established by \([S_{{train(m)}}^{j} ,HC_{R} (S_{{train(m)}}^{j} )],\;m = 1,2,...,N_{{ini}}\) with the Kriging method.

For uncertain variables \({\varvec{U}}\), the expression of the Kriging model can be provided by

$$g({\varvec{U}}) = f({\varvec{U}}){\varvec{\beta}} + z({\varvec{U}}),$$
(7)

where \(f({\varvec{U}})\) is the polynomial of \({\varvec{U}}\), \(\beta\) is the regression coefficient, \(z({\varvec{U}})\) represents the stochastic error at \({\varvec{U}}\), \(f({\varvec{U}}){\varvec{\beta}}\) is known as the trend of prediction, \(z({\varvec{U}})\) can be fully expressed by a correlation function \(R(U_{i} ,U_{j} ,\theta )\) with \(\theta\) being the vector of unknown parameters. The vector \(\theta\) can be determined by the optimization

$$\theta * = \arg \mathop {\min }\limits_{\theta } (\left\| {{\varvec{R}}(\theta )} \right\|)\sigma,$$
(8)

where \(\sigma\) is the standard deviation.

3.1.2 Infeasible domain pruning

Due to the lack of sufficient data, the prediction accuracy of the initial surrogate model may be very poor, which will lead to a great error while judging whether the unknown design point is feasible or not. Therefore more samples are needed to improve the prediction accuracy of the surrogate model. Generally, some samples with effective information are selected to add into the training set to improve the model accuracy. Added samples will be determined based on acquisition functions, which usually cover statistical features of the current surrogate model, e.g., predictive mean and predictive variance.

In the most of current surrogate methods, the acquisition function should be evaluated for all testing samples before each updating of the set of testing samples and one or more testing samples are selected as added samples according to a certain rule. However, for a surrogate model with classification as the goal, one issue may be caused that the newly added samples could not provide relevant information on the classification boundary, since those samples for updating are selected from all testing samples. Meanwhile, the other issue is that the computational expense is usually very higher when the prediction is repeatedly conducted for all testing samples. In order to address the abovementioned issues well, a pruning method for the infeasible region sample pool is proposed.

For the current set of testing samples, the minimum probability that the set is a feasible point from the surrogate model is provided by

$$U_{test(*)}^{j} = \mu (S_{test(*)}^{j} )/\delta (S_{test(*)}^{j} ),$$
(9)

where \(\mu (S_{test(*)}^{j} )\) and \(\delta (S_{test(*)}^{j} )\) denote the mean value and standard deviation of \(S_{test(*)}^{j},\) respectively.

Error may be produced during the prediction with the surrogate model, but the set of samples with very small values of \(U_{test(*)}^{j}\) are mostly infeasible, which can be further clarified that the samples with small probability in Eq. (9) are almost infeasible points. Therefore these sets will be directly dropped and acquisition function evaluations will be no more required, which will further improve the computational efficiency.

At the early stage of the construction of the surrogate model, evaluation error is usually very large. In order not to omit the potential added samples for a high accuracy and meanwhile improve the computational efficiency at the early stage, the pruning principle considering dynamic updating is proposed. For the surrogate model of the j-the constraint, the pruning principle of dynamic updating is provided by

$$\begin{gathered} Cut^{j} = \left\{ {Cut_{1}^{j} \cap Cut_{2}^{j} } \right\} \hfill \\ Cut_{1}^{j} = \left\{ {S_{\text{test}}^{j} \left| {U_{\text{test}}^{j} \le \alpha_{1} } \right.} \right\} \hfill \\ \alpha_{1} { = } - \frac{1}{2}\exp \left( { - \frac{{N_{\text{train}} - N_{\text{ini}} }}{nx}} \right) \hfill \\ Cut_{2}^{j} = \left\{ {S_{\text{test}}^{j} \left| {U_{\text{test}}^{j} \le \alpha_{2} } \right.} \right\} \hfill \\ \alpha_{2} = Q_{Cut1}^{j} \left[ {\left( {\Phi_{\text{Gaussian}} ( - \frac{1}{2}) - 1} \right)\exp \left( { - \frac{{N_{\text{train}} - N_{\text{ini}} }}{nx}} \right){ + }1} \right] \hfill \\ \end{gathered},$$
(10)

where \(Cut^{j}\) is the pruning set, \(Cut_{1}^{j}\) is the collection of testing samples with too small values of \(U_{\text{test}}^{j}\) while \(Cut_{2}^{j}\) is the set of samples ranked at the back in \(Cut_{1}^{j}\), \(\Phi_{\text{Gaussian}} ( \cdot )\) is the cumulative probability function of standard normal distribution, \(Q_{Cut1}^{j} ( \cdot )\) indicates the quantile of \(Cut_{1}^{j}\), \(\alpha_{1}\) and \(\alpha_{2}\) are dynamic pruning coefficients.

The pruning coefficients \(\alpha_{1}\) and \(\alpha_{2}\) can dynamically update with the augment of the training set of the surrogate model, as shown in Fig. 1. The prediction accuracy will be higher with the continual updating of the surrogate model. When the surrogate model becomes more accurate, \(\alpha_{1}\) and \(\alpha_{2}\) will gradually be greater to exclude infeasible samples. But \(\alpha_{1}\) remains below 0, which indicates the minimum probability of becoming a feasible sample in the remaining testing samples is still \(\Phi_{\text{Gaussian}} (0){ = 0}{\text{.5}}\) to reserve the better potential updating samples when the surrogate model is accurate enough. The set of feasible samples \(FR\) after pruning is

$$FR{ = }\mathop \cap \limits_{j = 1}^{nc} \left( {{\complement }_{{S_{\text{test}}^{j} }} Cut^{j} } \right),$$
(11)

where \({\complement }_{{S_{\text{test}}^{j} }}\) means the complementary set of \(S_{\text{test}}^{j}\).

Fig. 1
figure 1

Dynamic pruning coefficients

Full size image

3.1.3 Principles of surrogate model updating

With the reduced set of testing samples by the infeasible domain pruning method, the acquisition function is used to select new samples. Here the acquisition function is employed for the selection.

$$\begin{gathered} Af\left( {S_{test(*)}^{j} } \right) = U_{test(*)}^{j} \times \frac{{\max \left\{ D \right\} - \min \left\{ D \right\}}}{{dis\left( {S_{test(*)}^{j} } \right) - \min \left\{ D \right\} + eps}} \hfill \\ D = \left\{ {dis\left( {S_{test(1)}^{j} } \right),dis\left( {S_{test(2)}^{j} } \right),...,dis\left( {S_{{test(N_{\text{test}} )}}^{j} } \right)} \right\} \hfill \\ \end{gathered},$$
(12)

where \(dis\left( {S_{test(*)}^{j} } \right){ = }\mathop {\min }\limits_{{i = 1,2,...,N_{\text{train}} }} \left\| {S_{test(*)}^{j} - S_{train(i)}^{j} } \right\|\) refers to the shortest distance between the testing sample and all training samples, eps is a minimal positive number. The acquisition function can select samples with the largest prediction uncertainty and ensure the uniformity between training samples at the same time. The testing sample with the minimal acquisition function value will be selected as the newly added sample, which is put into the training set for updating of the surrogate model. The procedure is repeated until the termination criteria is satisfied

$$U^{*} \ge 2 and \frac{{N_{FR}^{iter} - N_{FR}^{iter - 1} }}{{N_{FR}^{iter - 1} }} < \psi,$$
(13)

where \(N_{FR}^{iter}\) denotes the number of feasible points in the iter-th iteration. \(U^{*} \ge 2\) is used to control the accuracy of the surrogate model while \(\frac{{N_{FR}^{iter} - N_{FR}^{iter - 1} }}{{N_{FR}^{iter - 1} }} < \psi\) is employed to ensure that the feasible region will not change dramatically and \(\psi\) is usually chosen as 0.005.

The proposed surrogate method can effectively construct the feasible boundary surrogate model for uncertain constraints by classification based on Kriging. For the RBDO problem, the computational efficiency will increase since \(HC_{{R_{j} }} ({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} )\) is directly used to judge whether the design point is feasible or not to decrease the number of reliability analysis evaluations.

3.1.4 Kriging-HDMR-based surrogate model for flexible uncertain constraints

In this paper, the flexible uncertain constraints are converted into the objective function as \(\max \left\{ {\frac{{R_{j}^{tar} - R_{j}^{L} }}{{R_{j}^{tar} - R_{0} }}} \right\}(j = 1,2,...nc.)\), and it is necessary to build the mapping between \(R_{j}^{L}\) and \({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}\) based on surrogate methods. For simplicity, \(({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} )\) is denoted as \({\varvec{U}}\) here. High-Dimensional Model Representation (HDMR) is used to globally approximate the flexible constraint in the objective function. HDMR can decouple the high-dimensional model into the combination of low-dimensional models (Cheng and Lu 2019). For a response of \(g({\varvec{U}})\) with the input vector \({\varvec{U}}{ = }[U_{1} ,U_{2} ,...,U_{n} ]\), the expansion of \(g({\varvec{U}})\) based on the HDMR can be expressed by

$$g({\varvec{U}}) = g_{0} + \sum\limits_{{1 \le i_{1} \le n}} {g_{{i_{1} }} (U_{{i_{1} }} )} + \sum\limits_{{1 \le i_{1} \le i_{2} \le n}} {g_{{i_{1} i_{2} }} (U_{{i_{1} }} ,U_{{i_{2} }} )} + \sum\limits_{{1 \le i_{1} \le i_{2} \le i_{3} \le n}} {g_{{i_{1} i_{2} i_{3} }} (U_{{i_{1} }} ,U_{{i_{2} }} ,U_{{i_{3} }} )} + \cdots + \sum\limits_{{1 \le i_{1} \le ... \le i_{m} \le n}} {g_{{i_{1} i_{2} ...i_{m} }} (U_{{i_{1} }} ,U_{{i_{2} }} ,...U_{{i_{m} }} )} + g_{12...n} (U_{1} ,U_{2} ,...U_{n} ),$$
(14)

where \(g_{0}\) denotes the constant term, \(g_{{i_{1} }} (U_{{i_{1} }} )\) is the first-order term, \(\sum\limits_{{1 \le i_{1} \le i_{2} \le n}} {g_{{i_{1} i_{2} }} (U_{{i_{1} }} ,U_{{i_{2} }} )}\) is the interaction term between \(U_{{i_{1} }}\) and \(U_{{i_{2} }}\), \(\sum\limits_{{1 \le i_{1} \le i_{2} \le i_{3} \le n}} {g_{{i_{1} i_{2} i_{3} }} (U_{{i_{1} }} ,U_{{i_{2} }} ,U_{{i_{3} }} )}\) is the interaction term among \(U_{{i_{1} }}\), \(U_{{i_{2} }}\) , and \(U_{{i_{3} }}\), and \(g_{12...n} (U_{1} ,U_{2} ,...U_{n} )\) is the residual term. Terms in Eq. (14) can be estimated by analysis of variance-HDMR (ANOVA-HDMR) method or Cut-HDMR method. Compared with ANOVA-HDMR, Cut-HDMR has higher accuracy (Huang et al. 2015) and the expressions of terms with the Cut-HDMR with the initial point \({\varvec{U}}^{{\varvec{0}}} { = }[U_{1}^{0} ,U_{2}^{0} ,...,U_{n}^{0} ]\) are

$$\begin{gathered} g_{0} =g(\varvec{U}^{\varvec{0}} ) \hfill \\ g_{{i_{1} }} (U_{{i_{1} }} ) = g(U_{1}^{0} ,U_{2}^{0} ,...,U_{{i_{1} - 1}}^{0} ,U_{{i_{1} }} ,U_{{i_{1} + 1}}^{0} ,...,U_{n}^{0} ) - g_{0} \hfill \\ g_{{i_{1} i_{2} }} (U_{{i_{1} }} ,U_{{i_{2} }} ) = g(U_{1}^{0} ,U_{2}^{0} ,...,U_{{i_{1} - 1}}^{0} ,U_{{i_{1} }} ,U_{{i_{1} + 1}}^{0} ,...,U_{{i_{2} - 1}}^{0} ,U_{{i_{2} }} ,U_{{i_{2} + 1}}^{0} ,...,U_{n}^{0} ) \hfill \\ - g_{{i_{1} }} (U_{{i_{1} }} ) - g_{{i_{2} }} (U_{{i_{2} }} ) - g_{0} \hfill \\ g_{{i_{1} i_{2} i_{3} }} \left( {U_{{i_{1} }} ,U_{{i_{2} }} ,U_{{i_{3} }} } \right) = g(U_{1}^{0} ,...,U_{{i_{1} }} ,U_{{i_{1} + 1}}^{0} ,...,U_{{i_{2} }} ,U_{{i_{2} + 1}}^{0} ,...,U_{{i_{3} }} ,U_{{i_{3} + 1}}^{0} ,...,U_{n}^{0} ) \hfill \\ - g_{{i_{1} i_{2} }} (U_{{i_{1} }} ,U_{{i_{2} }} ) - g_{{i_{1} i_{3} }} (U_{{i_{1} }} ,U_{{i_{3} }} ) - g_{{i_{2} i_{3} }} (U_{{i_{2} }} ,U_{{i_{3} }} ) - g_{{i_{1} }} (U_{{i_{1} }} ) - g_{{i_{2} }} (U_{{i_{2} }} ) - g_{{i_{3} }} (U_{{i_{3} }} ) - g_{0} \hfill \\ \end{gathered}.$$
(15)

For most engineering problems, the accuracy will be high enough when \(g({\varvec{U}})\) is approximated by the first three terms (Rabitz and Aliş 1999). The combination of Kriging and HDMR is here presented to build the surrogate model of flexible constraint and the procedure is summarized as follows:

Step 1 the center point of the design space is selected as the cut point \({\varvec{U}}_{0}\), and then the lower bound of reliability \(R^{L}_{0} = R^{L} ({\varvec{U}}_{0} )\) is evaluated;

Step 2 two sample points \({\varvec{U}}_{i}^{upper}\) and \({\varvec{U}}_{i}^{lower}\) along \({\varvec{U}}_{i}^{{}}\) axis at the upper and lower limits of \({\varvec{U}}_{i}^{{}}\) are chosen, and corresponding lower and upper bounds of reliability \(R^{L}_{i} ({\varvec{U}}_{i}^{upper} ) = R^{L}_{i} ({\varvec{U}}_{i}^{upper} ,{\varvec{U}}_{0}^{i} ) - R^{L}_{0}\) and \(R^{L}_{i} ({\varvec{U}}_{i}^{lower} ) = R^{L}_{i} ({\varvec{U}}_{i}^{lower} ,{\varvec{U}}_{0}^{i} ) - R^{L}_{0}\) are evaluated, and then 1-Dimension Kriging model \(\hat{R}^{L}_{i} ({\varvec{U}}_{i}^{{}} )\) can be constructed;

Step 3 a new point \(({\varvec{U}}_{i} ,{\varvec{U}}_{j} ,{\varvec{U}}_{0}^{ij} )\) is randomly and jointly drawn similarly in Step 2, and its lower bound of reliability \(R^{L} ({\varvec{U}}_{i} ,{\varvec{U}}_{j} ,{\varvec{U}}_{0}^{ij} )\) is evaluated;

Step 4 if \(\left\| {\frac{{R^{L} ({\varvec{U}}_{i} ,{\varvec{U}}_{j} ,{\varvec{U}}_{0}^{ij} ) - \hat{R}^{L}_{i} ({\varvec{U}}_{i}^{{}} ) - \hat{R}^{L}_{j} ({\varvec{U}}_{j}^{{}} ) - R^{L} ({\varvec{U}}_{0} )}}{{R^{L} ({\varvec{U}}_{i} ,{\varvec{U}}_{j} ,{\varvec{U}}_{0}^{ij} )}}} \right\| \le \varepsilon_{1}\), then 1-Dimension Kriging model \(\hat{R}^{L}_{i} ({\varvec{U}}_{i}^{{}} )\) is satisfied and stops; otherwise go to the next step, \(\varepsilon_{1}\) is usually chosen as 0.001;

Step 5 four samples at the lower and upper limits of variables \({\varvec{U}}_{i}\) and \({\varvec{U}}_{j}\) are chosen, their lower bounds of reliability are evaluated and then 2-Dimension Kriging model \(\hat{R}^{L}_{i} ({\varvec{U}}_{i} ,{\varvec{U}}_{j} )\) is built;

Step 6 a new point \(({\varvec{U}}_{i}^{new} ,{\varvec{U}}_{j}^{new} ,{\varvec{U}}_{0}^{ij} )\) is generated similarly as that in Step 3, and check \(\left\| {\frac{{\hat{R}^{L}_{ij} ({\varvec{U}}_{i}^{new} ,{\varvec{U}}_{j}^{new} ) - R^{L}_{ij} ({\varvec{U}}_{i}^{new} ,{\varvec{U}}_{j}^{new} )}}{{R^{L}_{ij} ({\varvec{U}}_{i}^{new} ,{\varvec{U}}_{j}^{new} )}}} \right\| \le \varepsilon_{1}\); if the convergence criterion is satisfied and stops; otherwise go to the next step;

Step 7 \(({\varvec{U}}_{i}^{new} ,{\varvec{U}}_{j}^{new} ,{\varvec{U}}_{0}^{ij} )\) is added to the current set of samples, Step 5 and Step 6 are repeated until the convergence criterion is satisfied, the complete Kriging-HDMR model of the flexible constraint \(SC_{{R_{j} }} ({\varvec{U}})\) is finally obtained.

3.2 Determination of the design preference parameter

With the constructed surrogate model of hard and flexible uncertain constraints, Eq. (5) can be reformulated as

$$\begin{gathered} {\text{find }}{\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \hfill \\ \min \, \frac{{C({\mathbf{d}},{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) - C_{0} }}{{C_{tar} - C_{0} }}{ + }\gamma \max SC_{{R_{j} }} \hfill \\ s.t. \, \hfill \\ HC_{{R_{j} }} \ge 0, \, j = 1,2,...,nc \hfill \\ \gamma \ge 0 \hfill \\ {\mathbf{d}}^{\mathbf{L}} \le {\mathbf{d}} \le {\mathbf{d}}^{\mathbf{U}} ,{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{L}} \le {\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \le {\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }}^{\mathbf{U}} \hfill \\ {\mathbf{d}} \in \Omega^{nd} ,{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \in \Omega^{nx} \hfill \\ \end{gathered},$$
(16)

where \(\gamma\) denotes the design preference parameter to make a trade-off between reliability and other objective performance (e.g., mass, cost, et. al). The higher \(\gamma\) is, the reliability should be paid more attention as a prior objective. Specially, when \(\gamma \to 0\), the problem degenerates into a radical t-HRBDO model; while \(\gamma \to + \infty\), the problem will degenerate into a conservative t-HRBDO model. Therefore, the flexible-constrained t-HRBDO model is a general t-HRBDO model. Actually, a mapping function between the cost and reliability exists in the flexible-constrained t-HRBDO. A determination procedure of \(\gamma\) is proposed by considering lower and upper bounds of reliability under hybrid uncertainties to help designers to make a reasonable decision.

Step 1 the conservative t-HRBDO in Eq. (3) is conducted and the best objective function value is obtained as \(C(R^{tar} )\);

Step 2 the radical t-HRBDO in Eq. (4) is conducted and the best objective function value is obtained as \(C(R_{0} )\);

Step 3 the conservative t-HRBDO where \(R_{j}^{L} - \left( {R_{0} + R^{tar} } \right)/2 \ge 0\) is considered as a hard constraint is handled and the best objective function value is obtained as \(C\left( {\left( {R_{0} + R^{tar} } \right)/2} \right)\);

Step 4 Eq. (17) is solved for \(\gamma *\), which is defined as the breakpoint of \(\gamma\)

$$\frac{{C\left( {\left( {R_{0} + R^{tar} } \right)/2} \right) - C\left( {R_{0} } \right)}}{{C\left( {R^{tar} } \right) - C\left( {R_{0} } \right)}}\gamma * = \frac{a}{b},$$
(17)

where \(a\) and \(b\) , respectively, denote the importance of reliability and cost, which can be determined according to engineering practices. \(\gamma *\) can give designers a quantitatively narrowed bound to determine the value of \(\gamma\) further considering the importance of reliability and cost.

3.3 A metaheuristic framework of the flexible-constrained t-HRBDO

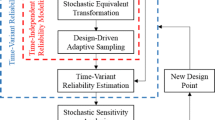
With the determined design preference parameter, the objective function of the flexible-constrained t-HRBDO can be obtained. However the objective function is implicit since the expression of the flexible constraint in the objective function is implicit. Because additional uncertain constraint evaluations are not needed in the procedure of the flexible-constrained t-HRBDO where surrogate models are built for uncertain constraints, a population metaheuristic algorithm will be implemented for this flexible-constrained t-HRBDO. The flowchart of the proposed framework for the flexible-constrained t-HRBDO is given in Fig. 2.

Fig. 2
figure 2

The proposed framework for flexible-constrained t-HRBDO

Full size image

The metaheuristic algorithm procedure to solve the proposed flexible-constrained t-HRBDO is described as follows:

  1. (1)

    \(N_{pop} = 50 \times (nd + nx)\) individuals are generated randomly as the feasible initial population, and the corresponding fitness values are evaluated based on the objective function;

  2. (2)

    according to the exploration and exploitation rules of the algorithm, the initial population is operated to generate the research direction and offspring population;

  3. (3)

    in the progeny population, the offspring are classified into feasible set and infeasible set according to their feasibility; for both the sets, offspring are sorted according to their fitness values respectively; the required number of offspring are chosen under the regulation of the feasible sample first, but for the infeasible set the better fitness first;

  4. (4)

    according to the requirements of different algorithms, certain operations are implemented on the offspring individuals and the corresponding fitness values are calculated;

  5. (5)

    if the termination condition satisfies and stops; otherwise go to step (2) and repeat the procedure until the optimal solution is obtained.

4 Examples

Two examples including one numerical example and one engineering case are employed to elaborate and testify the effectiveness of the proposed method. Since the flexible-constrained t-HRBDO is a newly proposed framework, currently no suitable methods but the general nested double loop method (GNDLM) can be taken as the reference for the accuracy comparison. The relative error of the proposed method and the GNDLM is defined as

$$err = \frac{{C_{P} - C_{G} }}{{C_{G} }} \times 100\%,$$
(18)

where \(C_{P}\) and \(C_{G}\) are the objective function value from the proposed method and GNDLM, respectively.

4.1 Numerical example

For this example, two random variables \(X_{1}^{R}\), \(X_{2}^{R}\), whose mean values are to be determined during the flexible-constrained t-HRBDO, and one interval variable \(X_{1}^{I}\) are included. The expression of the flexible-constrained t-HRBDO is provided by

$$\begin{gathered} {\text{find }}{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \hfill \\ \min \, C({\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ){ = }\left( {u_{{X_{1}^{R} }} - 3.7} \right)^{2} + \left( {u_{{X_{2}^{R} }} - 4.2} \right)^{2} \hfill \\ s.t. \, \hfill \\ P\left\{ {\mathop {\min }\limits_{{{\varvec{X}}^{{\varvec{I}}} }} g_{i} ({\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} ,t) > 0,\forall t \in (0,1)} \right\} \ge R_{j}^{tar} , \, j = 1,2 \hfill \\ g_{1} ({\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} ,t) = - X_{1}^{R} \sin (4X_{1}^{R} ) - 1.1X_{2}^{R} \sin (2X_{2}^{R} )X_{1}^{I} - 1.2t \hfill \\ g_{2} ({\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} ,t) = X_{1}^{R} + X_{2}^{R} - 3tX_{1}^{I} \hfill \\ 0 \le u_{{X_{1}^{R} }} \le 3.7,0 \le u_{{X_{2}^{R} }} \le 4.2 \hfill \\ X_{1}^{I} \in [1,1.4],X_{1}^{R} \sim N(u_{{X_{1}^{R} }} ,0.1^{2} ),X_{2}^{R} \sim N(u_{{X_{2}^{R} }} ,0.1^{2} ) \hfill \\ R_{j}^{tar} = \Phi (2) \approx 0.9772 \hfill \\ \end{gathered}.$$
(19)

The bounds of the limit state function at different values of interval variable are shown in Fig. 3. Meanwhile, the bounds of extreme response of the limit state function \(g_{i}^{L} = 0\) and \(g_{i}^{U} = 0\) are respectively shown in Fig. 4. From Figs. 3 and 4, we can see that the first limit state function is highly non-linear while the second is linear.

Fig. 3
figure 3

Safety boundaries of limit state function at different interval variables

Full size image
Fig. 4
figure 4

Boundaries of extreme response of the limit state function

Full size image

The surrogate model constructed by the improved infeasible region pruning technology based on Kriging for the hard constraint is provided in Fig. 5, while the surrogate model for the flexible constraint constructed by the Kriging-HDMR method is provided in Fig. 6.

Fig. 5
figure 5

Surrogate model for the hard constrain

Full size image
Fig. 6
figure 6

Surrogate models for flexible constraints

Full size image

When \(a/b = 1\) is assumed in this example, the breakpoint of the design preference parameter is obtained by \(\gamma {* = 1}.1864\). The optimal design results including design variables, objective function, function calls for uncertain constraints evaluation, and upper/lower bounds of reliability for the flexible-constrained t-HRBDO by the proposed method and the GNDLM method are given in Table 1.

Table 1 Optimal design results by the proposed method and the GNDLM method
Full size table

From Table 1, we can know that the calculated relative error is 3.8% of the objective function. For design variables and upper/lower bounds of reliability, they are very close and therefore the accuracy of the proposed method is very high. From the aspect of the computational efficiency, totally 58 + 91 = 149 function calls are required in the proposed method while 654 function calls are needed in the GNDLM method. The computational efficiency has improved by over 77.2%.

Conservative and radical flexible-constrained t-HRBDO models are respectively performed in this example. Optimal design results from the conservative, radical, and proposed flexible-constrained t-HRBDO strategies are provided in Table 2. From Table 2, we can see that design variables, objective function values, and upper/lower bounds of reliability from the proposed flexible-constrained method lie in the range bounded by the conservative and radical t-HRBDO. The reason is that the proposed method has made a balance between reliability and cost, which can suit for different engineering problems.

Table 2 Comparison between different t-HRBDO strategies
Full size table

The iteration history of the optimization procedure with case a/b = 1 is provided in Fig. 7. For this numerical example, only 20 iterations are needed to converge to the globally optimal design results.

Fig. 7
figure 7

Iteration history of optimization with case a/b = 1 for the numerical example

Full size image

4.2 The lower extremity exoskeleton

The lower extremity exoskeleton (LEEX) as a complicated engineering case is employed to elaborate and testify the proposed method. LEEX is a typical electromechanical system, which can be used to assist the disabled to move normally. The simplified model of the LEEX is given in Fig. 8. For the LEEX, the operational reliability when wearing and energy consumption should be considered at the early design stage. For the LEEX, each joint is similar and therefore the unilateral motion of the knee joint in the sagittal plane is employed for the flexible-constrained t-HRBDO. The structural diagram of the knee joint is shown in Fig. 9.

Fig. 8
figure 8

Simplified model of LEEX

Full size image
Fig. 9
figure 9

Diagram of the knee joint

Full size image

The knee joint is consisted of four links and a hydraulic cylinder. The lengths are defined as \({\varvec{k}} = \left[ {k_{1} ,k_{2} ,k_{3} ,k_{4} } \right]\). When manufacturing error \(\varvec{\Delta E} = \left[ {\Delta E_{1} ,\Delta E_{2} ,\Delta E_{3} ,\Delta E_{4} } \right]\) is considered, the lengths of links will be randomly distributed and represented by \({\mathbf{k}} = \left[ {k_{1} + \Delta E_{1} ,k_{2} + \Delta E_{2} ,k_{3} + \Delta E_{3} ,k_{4} + \Delta E_{4} } \right]\), which usually follow normal distribution. For the hydraulic rod, the manufacturing error \(\Delta L_{knee}\) and the wear \(wt\) for \(t\) gait cycles will be considered during its motion. The expression of the actual joint angle \(\alpha_{knee}^{^{\prime}}\) is derived by

$$\begin{gathered} \alpha_{knee}^{^{\prime}} \left( {{\varvec{k}},\varvec{\Delta E},\Delta L_{knee} ,w,p,t} \right) = \pi - \tan^{ - 1} \left( {\frac{{k_{1} + \Delta E_{1} }}{{k_{2} + \Delta E_{2} }}} \right) - \tan^{ - 1} \left( {\frac{{k_{3} + \Delta E_{3} }}{{k_{4} + \Delta E_{4} }}} \right) \hfill \\ \, - cos^{ - 1} \left[ {\frac{{\sum\limits_{l = 1}^{4} {\left( {k_{l} + \Delta E_{l} } \right)^{2} } - \left( {L_{knee} \left( {{\varvec{k}},p,t} \right) - wt{ + }\Delta L_{knee} } \right)^{2} }}{{2\sqrt {\sum\limits_{l = 1}^{2} {\left( {k_{l} + \Delta E_{l} } \right)^{2} } \sum\limits_{l = 3}^{4} {\left( {k_{l} + \Delta E_{l} } \right)^{2} } } }}} \right] \hfill \\ \end{gathered}.$$
(20)

The desired length of the hydraulic rod \(L_{knee} \left( {{\varvec{k}},p,t} \right)\) is

$$L_{knee} \left( {{\varvec{k}},p,t} \right){ = }\sqrt {\sum\limits_{l = 1}^{4} {k_{l}^{2} } - 2\sqrt {\sum\limits_{l = 1}^{2} {k_{l}^{2} } \sum\limits_{l = 3}^{4} {k_{l}^{2} } } \cos \left( {\theta_{knee} ({\varvec{k}},p,t)} \right)}$$
(21)
$$\theta_{knee} ({\varvec{k}},p,t){ = }\pi - \alpha_{knee} (p,t) - tan^{ - 1} \frac{{k_{1} }}{{k_{2} }} - tan^{ - 1} \frac{{k_{3} }}{{k_{4} }},$$
(22)

where \(p\) is the percentage of the gait cycle.

The ideal angle \(\alpha_{knee} (p,t)\) is fitted from the Clinical Gain Analysis (CGA) data, which can be expressed by

$$\alpha_{knee} (p,t) = \frac{{\sum\nolimits_{l = 1}^{6} {a_{l} \sin (b_{l} p + c_{l} + 2\pi t)} }}{180}\pi + \beta,$$
(23)

where \(\beta\) is a parameter affected by epistemic uncertainty for different people, which is considered as an interval variable and \(\beta \in [ - 0.20,0.20]\) here; \(a_{l} ,b_{l}\) and \(c_{l}\) are coefficients, which are listed in Table 3.

Table 3 Coefficients for al, bl, cl
Full size table

If the difference between the actual joint angle \(\alpha_{knee}^{^{\prime}}\) and the ideal angle \(\alpha_{knee} (p,t)\) is less than \(\varepsilon_{knee} { = }6^\circ {{\sim }}8^\circ\), the joint is considered to be safe. Then the time-variant reliability can be expressed by

$$R = \Pr \left\{ {\varepsilon_{knee} - \left| {\alpha_{knee}^{^{\prime}} \left( {{\varvec{k}},\varvec{\Delta E},\Delta L_{knee} ,w,p,t} \right) - \alpha_{knee} (p,t)} \right| > 0,\forall p \in (0,100{\text{\% }})} \right\}.$$
(24)

Take \(k_{1} + \Delta E_{1} ,k_{2} + \Delta E_{2} ,k_{3} + \Delta E_{3} ,k_{4} + \Delta E_{4}\) as random design variables \(X_{1}^{R} \sim X_{4}^{R}\), \(\Delta L_{knee}\) as the random design parameter \(X_{5}^{R}\), and \(\beta\) and \(w\) as the interval variables \(X_{1}^{I}\) and \(X_{2}^{I}\), the time-variant reliability in Eq. (24) can be rewritten by

$$R = \Pr \left\{ {\varepsilon_{knee} - \left| {\alpha_{knee}^{^{\prime}} \left( {{\varvec{k}},{\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} ,p} \right) - \alpha_{knee} (p)} \right| > 0,\forall p \in (0,100{\text{\% }})} \right\}.$$
(25)

The lower bound and upper bound of the time-variant reliability can be expressed by

$$\left\{ \begin{gathered} R^{L} = \Pr \left\{ {\mathop {\min }\limits_{{{\varvec{X}}^{{\varvec{I}}} }} \mathop {\min }\limits_{{p \in (0,100{\text{\% }})}} g\left( {{\varvec{k}},{\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} ,p} \right) > 0} \right\} \hfill \\ R^{U} = \Pr \left\{ {\mathop {\max }\limits_{{{\varvec{X}}^{{\varvec{I}}} }} \mathop {\min }\limits_{{p \in (0,100{\text{\% }})}} g\left( {{\varvec{k}},{\varvec{X}}^{{\varvec{R}}} ,{\varvec{X}}^{{\varvec{I}}} ,p} \right) > 0} \right\} \hfill \\ \end{gathered} \right.$$
(26)

The torque required per unit weight \(T_{knee} (p,t)\) can be obtained from the CGA data and

$$T_{knee} (p,t){ = }\sum\limits_{m = 1}^{6} {a_{m} \sin (b_{m} p + c_{m} + 2\pi t)},$$
(27)

where \(a_{m} ,b_{m}\) and \(c_{m}\) are coefficients, which are provided in Table 4.

Table 4 Coefficients for am, bm, cm
Full size table

The force arm \(H_{knee} (k,{\mathbf{X}}^{R} ,p,t)\) can be further calculated by

$$H_{knee} ({\varvec{k}},{\mathbf{X}}^{R} ,p,t){ = }\frac{{\sqrt {\sum\nolimits_{j = 1}^{2} {\left( {X_{j}^{R} } \right)^{2} } \sum\nolimits_{j = 3}^{4} {\left( {X_{j}^{R} } \right)^{2} } } \sin \left( {\theta_{k} (p,t)} \right)}}{{L_{knee} ({\varvec{k}},p,t){ + }X_{5}^{R} }}.$$
(28)

Therefore, the force in a gait cycle is

$$F_{knee} ({\varvec{k}},{\mathbf{X}}^{R} ,p,t){ = }\frac{{T_{knee} (p,t)}}{{H_{knee} ({\varvec{k}},{\mathbf{X}}^{R} ,p,t)}}.$$
(29)

The average driving force in a single gait cycle is approximated to describe the energy consumption, and then the objective function can be further simplified as

$$C_{knee} = \int_{0}^{100\% } {F_{knee} ({\varvec{k}},{\mathbf{X}}^{R} ,p,10^{5} )dp}.$$
(30)

For this case, \(t = 10^{5}\) is used.

The flexible-constrained t-HRBDO for the knee joint is then written as

$$\begin{gathered} {\text{find }}{\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} \hfill \\ \min \, SE_{knee} ({\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ){ = }\frac{{C_{knee} ({\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) - C_{0} }}{{C^{tar} - C_{0} }} + \gamma \frac{{R^{tar} - R^{L} ({\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} )}}{{R^{tar} - R_{0} }} \hfill \\ s.t. \, \hfill \\ R^{U} ({\mathbf{u}}_{{{\varvec{X}}^{{\varvec{R}}} }} ) \ge R^{tar} \hfill \\ 35 \le u_{{X_{1}^{R} }} \le 55,340 \le u_{{X_{2}^{R} }} \le 380,40 \le u_{{X_{3}^{R} }} \le 60,55 \le u_{{X_{4}^{R} }} \le 75 \hfill \\ X_{i}^{R} {{\sim }}N\left( {u_{{X_{i}^{R} }} ,0.5^{2} } \right), \, i = 1,2,3,4 \hfill \\ X_{5}^{R} {{\sim }}N\left( {0,3^{2} } \right),X_{1}^{I} \in [ - 0.2,0.2],X_{2}^{I} \in [0.5 \times 10^{ - 5} ,1.5 \times 10^{ - 5} ] \hfill \\ R^{tar} = \Phi (2) \approx 0.9772 \hfill \\ \end{gathered}.$$
(31)

In order to illustrate the effect of \(\gamma\) on optimal design results, \(a/b = 0.5,1,5,10\) are set during the flexible-constrained t-HRBDO. The corresponding optimal design results from the proposed method and the GNDLM method are, respectively, provided in Tables 5, 6, 7, and 8.

Table 5 Optimal design results with case \(a/b{ = }0.5\)
Full size table
Table 6 Optimal design results with case \(a/b{ = }1\)
Full size table
Table 7 Optimal design results with case \(a/b{ = }5\)
Full size table
Table 8 Optimal design results with case \(a/b{ = }10\)
Full size table

In order to illustrate the accuracy and efficiency of the proposed method compared with the GNDLM method, the relative error, efficiency improvement, and \(\gamma *\) are provided in Table 9 for different values of \(a/b\).

Table 9 Comparison of accuracy and efficiency with different \(a/b\)
Full size table

From Tables 5, 6, 7, and 8, we can see that function calls for constraints evaluation are the same regardless of \(a/b\), the reason is that function calls used for surrogate models of flexible and hard constraints have been determined before the optimization. With the increase of \(a/b\), the value of objective function become greater, which indicates that the higher reliability requires higher resource expenses. It shows that the computational efficiency has a great improvement over 94% under the satisfaction of computational accuracy, where the maximum error is 0.34% in Table 9.

Conservative, radical, and flexible-constrained t-HRBDO are also conducted for this engineering case. The corresponding optimal design results from conservative, radical, and proposed flexible-constrained t-HRBDO with \(a/b{ = }1\) strategies are provided in Table 10. The same conclusion as in the numerical example can be reached that design variables, objective function values, and upper/lower bounds of reliability from the proposed flexible-constrained method lie in the interval bounded from the conservative and radical t-HRBDO. Therefore, the cost and reliability can be balanced even for the complicated engineering case.

Table 10 Comparison between different t-HRBDO strategies
Full size table

The iteration history of optimization procedure with case a/b = 1 is provided in Fig. 10. For this engineering case, nearly 140 iterations are needed to converge to the globally optimal results.

Fig. 10
figure 10

Iteration history of optimization with case a/b = 1 for the engineering case

Full size image

5 Conclusions

This paper proposed a novel framework of the t-HRBDO by introducing flexible constraints in the objective function, which is called flexible-constrained t-HRBDO. Infeasible region pruning technique is improved based on the classification model to build the surrogate model for hard uncertain constraints, while Kriging-HDMR method is presented to build the surrogate model for flexible uncertain constraints, which increase the computational efficiency greatly. A determination method of the design preference parameter is provided to quantitatively build the relationship between reliability and cost in the flexible-constrained t-HRBDO, which can help designers to reasonably balance reliability and cost to avoid waste of resources and also risk according to engineering requirements during design stage. A new metaheuristic framework is given to effectively conduct the flexible-constrained t-HRBDO with higher efficiency. The results from the two examples show that the proposed framework can effectively balance cost and reliability within the lower bound and upper bound of reliability under hybrid uncertainties, and the proposed algorithms have the great efficiency improvement, e.g., over 77% for the numerical example and over 94% for the engineering case under the accuracy guarantee.