1 Introduction

In recent decades, adaptive filtering algorithms have been widely examined. These algorithms automatically adjust the filter parameters according to the changes in signal characteristics to make the filtering process more accurate. In practice, conventional adaptive algorithms are often designed with linear systems. The most popular conventional adaptive algorithms are recursive least squares (RLS) and least-mean squares (LMS) algorithms; see, e.g., [8, 25, 30]. Nonlinear problems such as time series prediction, pattern classification, radial basis function (RBF) networks, and nonlinear regression [1, 17, 22, 25, 33] have not attracted much attention. Kernel adaptive filtering (KAF), which is regarded as a nonlinear adaptive algorithm, has been developed to address the above problems. Kernel adaptive filtering algorithms have been applied in machine learning and nonlinear signal processing, showing better results. KAF algorithms use Mercer kernels [28] to map the input space into high-dimensional reproducing kernel Hilbert spaces (RKHS) and then perform linear learning in the feature space [30, 31]. However, the KAF needs to assign a new kernel unit as a dictionary center for every input sample. In other words, the network size will linearly grow with each new sample, which creates a growing structure.

Previously, kernel expansions of kernel algorithms have been observed, therefore various methods have been proposed to manage the growing network size of KAF algorithms, which are called sparse KAF (SKAFs). For instance, a sparse robust adaptive filtering algorithm based on the q-Renyi kernel function was extended in [34]. [22] proposed nonlinear adaptive filtering with a kernel set-Membership approach. To date, the existing SKAFs heavily rely on the well-selected sparse criteria, which can measure the similarity between two inputs. Several sparse criteria are commonly used to control the dimension of the kernel dictionary (or model) structure. In [28], the prediction variance criterion (PVC) was used for sparse, which has a medium complexity about quadratic. Concretely, sparsification methods include the surprise criterion (SC) [29], the quantization vector (QV) [5] method and the coherence criterion (CC) [13]. The novelty criterion (NC) [26] is widely studied as one of the simplest criteria. To significantly suppress the input space, the key idea of the NC is to establish two thresholds to evaluate the network performance. Among the NC family, examples include novelty criterion kernel least mean square (KLMS-NC) [22], as well as their numerous variations [29]. In the case of maintaining high learning performance, the use of sparse constraints can generate a small network. However, the mean square error (MSE) is adopted as a cost function, which leads to lower robust performance. The MSE-based SKAF algorithms only capture the second-order statistics of the data, so its performance may be seriously degraded in some non-Gaussian cases [15]. Therefore, a well-selected cost function is a good choice for kernel adaptive filtering, which plays an important role in the overall design of KAFs to gain high performance.

Recently, some non-quadratic error criteria have gained significant attention. For example, Gao proposed a kernel least mean square p-power algorithm (KLMP) [14] based on the fractional low-order statistical error criterion. Additionally, the algorithms associated with the maximum correntropy criterion (MCC) (i.e., Quantized kernel maximum correntropy (QKMC), Maximum correntropy Kalman filter and so on) [6, 32, 33] have shown their robust power against non-Gaussian circumstances. However, the above SKAFs are usually sparse with conventional sparsification methods, and the tracking capability of those algorithms can be reduced. NC, as a typical sparsification method, is quite effective and heuristic in nature. Nevertheless, when the measured data contain various noise distributions or large outliers, the NC may not always bring the best performance.

Motivated by this situation, we present an exponential loss function [18] as the sparse evaluation and construct a new sparse frame. In this paper, the modified novelty criterion is incorporated into the kernel fraction lower power order statistics error criterion based on the Softplus function (SKFLP) [29] to construct the sparse SKFLP algorithm for curbing the growing RBF network, namely, the modified novelty criterion robust kernel adaptive filtering algorithm based on the Softplus function (SKFLP-MNC). Our work here focuses on employing the exponential loss function as a sparse criterion and conducts some changes of the original. Based on the new sparse method, the SKFLP-MNC algorithm only contains the important input samples and uses them to build compact networks, which is effective for practical problems. In the SKFLP-MNC algorithm, the gradient descent methods are used to adjust the current desired output coefficient when a new input is selected as a dictionary center. The main features of our proposed algorithms are validated by simulation results. The rest of this paper is organized as follows. In Sect. 2, we review the SKFLP adaptive algorithm and related works of NC and then present the derivation of the proposed SKFLP-MNC algorithm, which has an update check similar to all sparse algorithms. In our proposed algorithms, when the update check ensures the updating of filter parameters, a modified NC sparsification follows to control the kernel dimension. Section 3 provides convergence analysis for SKFLP with the modified sparse criterion, referring to the exponential loss function. This section shows that the algorithm is convergent. Simulation results are discussed and described in Sect. 4 to show the performance of our algorithm. The algorithm yields a low steady-state MSE and a smaller dictionary dimension. Conclusions are given in Sect. 5.

2 Gaussian Kernel Adaptive Algorithm Based on Softplus Function with Sparse Criterion

In general, a structure can influence the convergence rate and filtering performance of filters. A modified novelty criterion is introduced in SKFLP to produce the SKFLP-MNC algorithm. Let us now consider the nonlinear adaptive algorithms based on the Gaussian kernel. The kernel algorithms learn an arbitrary nonlinear mapping developed in a sequence of samples. We use the Gaussian kernel to define the type of nonlinearity. A sequence of training samples {u(1), d(1),...(u(n), d(n))} are used as the input–output pairs, where u(n) is the input data vector and d(n) is the desired output at discrete time n. The mapping function is commonly known as Mercer kernels [27, 35].

2.1 Similarity Measures in Kernel Space

To overcome the performance degradation drawbacks based on MSE under various outliers, including impulsive interferences. Here, we propose a robust cost framework. First, we define a softplus function [28] as:

$$ s_{i} = {\text{log}}_{e} (1 + e^{{ - \alpha \left| {J(w)} \right|}} ) $$
(1)

where \(J(w)\) is an error function and the parameter \(\alpha\) is a positive value that controls the steepness of the Softplus function curve. Inspired by the saturation property of the Softplus function, we introduce a new cost function framework based on the Softplus function as follows:

$$ \begin{aligned} J_{s} (i) & = \frac{1}{\alpha }s_{i} = \frac{1}{\alpha }{\text{log}}_{e} (1 + e^{{ - J_{\omega } (i)}} ) \\ & = \frac{1}{\alpha }{\text{log}}_{e} (1 + e^{{ - \alpha \left| {e(i)} \right|^{p} }} ) \\ \end{aligned} $$
(2)

where \(J(w)\) is the fractional low-order statistical error criterion, as follows:

$$ J({{\varvec{\upomega}}}) = \left| {d(n) - {{\varvec{\upomega}}}^{T} (n)u(n)} \right|^{p} ,0 < p < 1 $$
(3)

\(\varphi (n)\) is a nonlinear function induced by the Mercer kernel \(\kappa (u, \cdot )\)[30], we can.

extend linear models to nonlinear models with a nonlinear transformation \(\varphi (n)\)

Then, we can use different sparsity criteria to obtain corresponding kernel adaptive filters. We choose the Gaussian kernel [23] as the nonlinear transformation, it can be defined by \(\kappa (u,u^{^{\prime}} {) = exp( - h}\left\| {u - u^{^{\prime}} } \right\|^{2} )\), where \(h\) is the kernel bandwidth. \(w(n)\) is the weight vector at \(n\), and \(E\) denotes the expectation operator. (2) is represented as:

$$ J_{s} = \frac{1}{\alpha }\log (1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} ) $$
(4)

e(n) is the prediction error, the desired signal is d(n) and the actual output is y(n) = w(n)T ϕ(u(n)). According to (4), when there has impulse noise interference, the gradient of the cost function tends to 0, which effectively inhibits the weight updating process of the algorithm. Then update equations of the weight vectors can be easily derived from the following gradient descent rule:

$$ \begin{aligned} \nabla_{\omega } J_{s} (i) & = \frac{{\partial J_{s} (i)}}{\partial \omega } = \frac{1}{\alpha }\frac{{\partial s_{i} }}{\partial J(e(i))}\frac{\partial J(e(i))}{{\partial \omega }} \\ & = \frac{1}{\alpha }\frac{1}{{1 + e^{ - ( - J(e(i)))} }}\frac{\partial J(e(i))}{{\partial \omega }} \\ & = \frac{1}{{1 + e^{{ - \alpha \left| {e(i)} \right|^{p} }} }}\frac{1}{{\left| {e(i)} \right|^{1 - p} }}{\text{sgn}}(e(i))\varphi (i) \\ \end{aligned} $$
(5)
$$ \omega (i) = \omega (i - 1) + \mu \sum\limits_{j = 1}^{i} {\frac{1}{{1 + e^{{ - \alpha \left| {e(j)} \right|^{p} }} }}\frac{1}{{\left| {e(j)} \right|^{1 - p} }}} $$
(6)

where \({\text{sgn}}()\) represents the sign operator and \(\mu\) is the step size that satisfies \(0 < \mu < 2\). The SKFLP algorithm achieves a fast convergence rate at the instant and a low steady-state error at the steady state. Nevertheless, it also has the limitation of a linearly increasing network structure.

2.2 Novelty Criterion

As we see, adaptive data selection that retains important data and removes redundant data is a natural method to tackle the issue of linearly increasing network structure. There are mainly two existing criteria for online kernel learning, the novelty criterion and the approximate linear dependency (ALD) [11]. To perform sparsification, the NC is supposed in the present learning system as:

$$ f_{i} = \sum\limits_{j = 1}^{n} {a_{j} (n)\kappa (c_{j} , \cdot )} $$
(7)

with \(c_{j}\) as the jth dictionary center and \(a_{j} (n)\) as the jth expansion coefficient. The dictionary \(C(n) = \{ c_{j} \}_{j = 1}^{n}\) stores a new input data pattern. When a new sample \({\{ }u(n + 1),d(n + 1{)\} }\) is raised, the NC needs to decide whether to accept \(u(n + 1)\) as a new center.

To understand how the NC operates, we focus on the distance and prediction error-based criteria. It first calculates the distance between \(u(n + 1)\) and the present dictionary, which can be defined by \(Dis = \mathop {\min }\limits_{{c_{j} \in C(n)}} \left\| {u(n + 1) - c_{j} } \right\|\). || || represents the Euclidean norm, U is the input space. There are two preset thresholds δ1 and δ2, where δ1 is the tolerance for the closeness of the new data to the dictionary, and δ2 is the tolerance for the a priori error. The parameter value needs to be set in advance for comparison; if \(Dis \le \delta_{1}\), \(u(n + 1)\) will not be added into the present dictionary center. Otherwise, it will calculate the prediction error

$$ e(n + 1) = d(n + 1) - f_{i} (u(n - 1)) $$
(8)

When \(\left| {e(n + 1)} \right| \ge \delta_{2}\), the new input sample \(u(n + 1)\) will be accepted as a new center.

2.3 Proposed Sparse Gaussian Kernel Adaptive Algorithm

In this section, we derive the proposed SKFLP-MNC algorithm in detail, which is inspired by Platt’s adaptive sparse strategies. The novelty criterion is very useful in reducing the numerical complexity and dynamic range requirements of the kernel adaptive algorithms. To further improve the filtering accuracy of the algorithm, the following improvement measures are proposed. Motivated by the discussion of the AdaBoost algorithm, we propose a new adaptive sparsification method as follows, namely, modified NC (MNC). The Adaboost algorithm [24] is a classification ability boosting algorithm that can generate a high-precision classification model with multiple low-precision models, and the exponential loss function(exp-loss) is the core of the AdaBoost algorithm. We define the exp-loss distribution \(g_{q}\) as follows:

$$ g_{q} (x) = {\text{exp}}( - q(f(x))) $$
(9)

where \(q\) is a regulatory factor. In this work, we focus mainly on applying the loss to define the modified NC theorem.

$$ \mathop {{\text{min}}}\limits_{{c_{j} \in C(n)}} ({\text{exp}}(\left\| {{\mathbf{u}}(n + 1) - c_{j} } \right\|^{2} {))} $$
(10)

\(\left\| {} \right\|^{2}\) denotes the Euclidean norm of a vector square, which can improve the convergence rate of the algorithm.

Similar to the SKFLP algorithm, the derivation of the SKFLP-MNC algorithm corresponds to solving the following optimization problem:

$$ \mathop {\min }\limits_{\Omega } \sum\limits_{n}^{N} {{(}\left| {d(n) - \Omega (n)^{T} \varphi (n)} \right|^{p} {)},0 < p < 1} $$
(11)

where \(\Omega ( \cdot )\) are the weights in the feature space. Then, a sparse operator \(O[ \cdot ]\) in the feature vector used to build the constraint is given by (10). As mentioned in (6), given the SKFLP update equation, the update form of SKFLP-MNC can be obtained by performing the sparse operator in the feature vector \(\varphi (u(n))\), namely,

$$ \Omega (n) = \Omega (n - 1) + \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n{))}O{[}\varphi (n{)]} $$
(12)

Remark

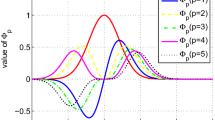
Gaussian kernel is used to algorithm, function κ(·, ·) used to calculate the inner product κ(·, ·) =  < ϕ(·)T, ϕ(·) > . Figure 1 shows the aforementioned Gaussian kernel with various values of the parameter h. We can see that the kernel width h affects the smoothness of the algorithm. To balance the data loss caused by the sparse discarding, we choose a smoothing Gaussian kernel width h = 0.2.

Fig. 1
figure 1

The element ϕ(× 0) = κ(·, × 0) of the feature space induced by the Gaussian kernel with h = 5, h = 3, h = 1, h = 0.2

Full size image

Let the form of input vector u(n) in the RKHS is ϕ(u(n)). Substituting (12) into (11) we arrive at:

$$ e(n) = d(n) - \Omega (n - 1)\varphi (n) - \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n{))}O{[}\varphi (n{)]}\varphi (n) $$
(13)

Using κ(·, ·) to evaluate the dot products, the previous equation turns into:

$$ e(n) = e(n - 1) - \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n{))}\kappa (O{[}\varphi (n{)]},\varphi (n{))} $$
(14)

Then, from Eq. (14), we can take into account that the update only occurs if the error is not very large and if the dictionary changed. We can then compute \(\Omega\) recursively as follows:

$$ \begin{aligned} \Omega (n) & = \Omega (n - 1) + \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n)){\rm O}[\varphi (n)] \\ & = [\Omega (n - 2) + \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n - 1)} \right|^{p} }} }}\frac{1}{{\left| {e(n - 1)} \right|^{1 - p} }}{\text{sgn}}(e(n - 1)){\rm O}[\varphi (n - 1)]] \\ & \; + \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n)){\rm O}[\varphi (n)] \\ & \ldots \\ \end{aligned} $$
(15)
$$ = \Omega (0) + \mu \sum\limits_{i = 1}^{n} {\frac{1}{{1 + e^{{ - \alpha \left| {e(i)} \right|^{p} }} }}\frac{1}{{\left| {e(i)} \right|^{1 - p} }}{\text{sgn}}(e(i)){\rm O}[\varphi (i)]} $$
(16)

Setting \(\Omega (0)\) to zero leads to:

$$ \Omega (n) = \mu \sum\limits_{i = 1}^{n} {\frac{1}{{1 + e^{{ - \alpha \left| {e(i)} \right|^{p} }} }}\frac{1}{{\left| {e(i)} \right|^{1 - p} }}{\text{sgn}}(e(i)){\rm O}[\varphi (i)]} $$
(17)

Based on this modified NC, we can decide whether the current data are available \(Dis_{1} > \delta_{1}\), \(\left| {e(n + 1)} \right| > \delta_{2}\) or redundant \(Dis_{1} < \delta_{1}\), and the thresholds \(\delta_{1}\) and \(\delta_{2}\) need to be set in advance and need to be greater than or equal to 0. \(C(n)\) note the dictionary at \(n\), and \(c_{j}\) are the elements of dictionary \(C(n)\). We initialize the dictionary \(C(1) = \{ u(1)\}\) and coefficient vector \(a(1) = \left[ {\mu \frac{1}{{1 + e^{{ - \alpha \left| {d(1)} \right|^{p} }} }}\frac{1}{{d(1)^{1 - p} }}{\text{sgn}}(d(1))} \right]\).

According to (10), calculate the distance between input \(u(n)\), which is the current input sample. Then, compare \(Dis_{1}\) with \(\delta_{1}\). If the distance Dis1 ≤ δ1, u(n + 1) will not be added into the present dictionary center, then we have C(n) = C(n − 1), and the dictionary remains unchanged. Otherwise, the prediction error is calculated by Eq. (8), if the prediction error |e(n + 1)|> δ2, we have C(n) = {C(n − 1), u(n)}.

Incorporate the MNC method into the SKFLP to generate the SKFLP-MNC algorithm. For the SKFLP-MNC, if Dis1 ≤ δ1 and |e(n + 1)|> δ2, we have:

$$ O{[}{\mathbf{u}}(n){]} = {\mathbf{u}}(n) $$
$$ C(n) = {\text{\{ }}C(n - 1),O{[}{\mathbf{u}}(n\user2{)]}{\text{\} }} $$
$$ {\mathbf{a}}(n) = \left[ {{\mathbf{a}}(n - 1),\mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n{))}} \right] $$
(18)

When a new training datum \(\{ u(n),d(n)\}\) is observed, the corresponding output of SKFLP-MNC can be calculated by:

$$ y(n) = f_{n - 1} (u(n)) = \sum\limits_{j = 1}^{n} {a_{j} (n - 1)\kappa (u(n),c_{j} )} $$
(19)

\(f_{n}\) is expressed as the estimate of the kernel mapping at iteration n. It can be seen from (10), the SKFLP-MNC only accepts the data that satisfy the modified NC criterion. A smaller framework is generated by discarding some input data. Equations (10), (11), (16), (18), and (19) summarize the proposed SKFLP-MNC algorithm.

3 Convergence Analysis for SKFLP-MNC

SKFLP-MNC algorithm is a novel kernel adaptive filter algorithm with sparsification. By examining the convergence properties of the SKFLP-MNC algorithm, the success of its learning mechanism is verified, which shows that the algorithm has inherent learning and prediction ability. We first derive the energy conservation relation of SKFLP-MNC and then present a sufficient condition for mean square convergence.

3.1 Energy Conservation Relation

First, a nonlinear mapping \(f^{*}\) is proposed to mark the estimated value of filtering. We know the universal approximation property [17]. We have an optimal weight vector \(\Omega^{*}\), which can be seen as \(f^{*} = \Omega^{*} \varphi ( \cdot )\). Specifically, the desired signal d(n) is expressed as:

$$ d(n) = f^{*} (u(n{))} + v(n) $$
(20)

Then, the output error of the algorithm can be expressed as

$$ e(n) = d(n) - \Omega (n - 1)^{{\text{T}}} \varphi (u(n{))} $$
(21)

Equation (20) is substituted into (21):

$$ \begin{aligned} e(n) & = \mathop \Omega \limits^{\sim} (n - 1)^{{\text{T}}} \varphi (u(n{))} + v(n) \\ & = e_{m} (n) + v(n) \\ \end{aligned} $$
(22)

where \(e_{m} (n) = \mathop \Omega \limits^{\sim} (n - 1)^{T} \varphi (u(n{))}\) is the priori error and \(\mathop \Omega \limits^{\sim} (n - 1) = \Omega^{*} - \Omega (n - 1)\) denotes the weight error vector in the RKHS. Subtracting \(\Omega^{*}\) from both sides of the Eq. (12) to obtain the iteration expression of deviation, we have

$$ \mathop \Omega \limits^{\sim} (n) = \mathop \Omega \limits^{\sim} (n - 1) - \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n{))}O{[}\varphi (u(n\user2{))]} $$
(23)

Define a posteriori error \(e_{p} (n) = \mathop \Omega \limits^{\sim} (n)^{T} \varphi (u(n{))}\), we have

$$ e_{p} (n) = e_{m} (n) + (\mathop \Omega \limits^{\sim} (n)^{T} - \mathop \Omega \limits^{\sim} (n - 1)^{T} )\varphi (u(n{))} $$
(24)

By incorporating (23), we obtain:

$$ \begin{aligned} e_{p} (n) & = e_{m} (n) - \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n{))}O{[}\varphi (u(n\user2{))]}^{{\text{T}}} \varphi (u(n{))} \\ & =e_{m} (n) - \mu \frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n{))}\kappa {(O[}\varphi (u(n{))],}\varphi (u(n{)))} \\ \end{aligned} $$
(25)

Combining (23) and (25) to eliminate the prediction error \(e(n)\) yields

$$ \mathop \Omega \limits^{\sim} (n) = \mathop \Omega \limits^{\sim} (n - 1) + \frac{{e_{p} (n) - e_{m} (n)}}{\kappa (O(\varphi (u(n))),\varphi (u(n)))}O[\varphi (u(n))] $$
(26)

The expected energy relationship is obtained by using the square of the norm of two sides in Eq. (26), and we have

$$ \left\| {\mathop \Omega \limits^{\sim} (n)} \right\|^{2} = \left\| {\mathop \Omega \limits^{\sim} (n - 1)} \right\|^{2} + \frac{{e_{p} (n)^{2} - e_{m} (n)}}{{\kappa (O(\varphi (u(n))),\varphi (u(n)))^{2} }} - \frac{{e_{m} (n)^{2} }}{{\kappa (O(\varphi (u(n))),\varphi (u(n)))^{2} }} + m_{l} $$
(27)

where \(m_{l}\) is expressed as:

$$ m_{l} = \frac{{2(e_{p} (n) - e_{m} (n))\{ \mathop \Omega \limits^{\sim} (n - 1)^{{\text{T}}} O[\varphi (u(n))]\kappa (O(\varphi (u(n))),\varphi (u(n)) - e_{m} (n)\} }}{{\kappa (O(\varphi (u(n))),\varphi (u(n)))^{2} }} $$
(28)

Equation (27) shows the energy conservation relation for SKFLP-MNC. When the sparsification size \(\delta_{1}\) and \(\delta_{2}\) approach zero, we have \(\kappa (O(\varphi (u(n{)))},\varphi (u(n{)))} \to 1\), and in this case, (27) reduces to the energy conservation relation for the SKFLP algorithm.

3.2 Mean Square Convergence Analysis

Substituting Eq. (25) into Eq. (27) yields the following expression:

$$ \begin{aligned} \left\| {\mathop \Omega \limits^{\sim} (n)} \right\|^{2} & = \left\| {\mathop \Omega \limits^{\sim} (n - 1)} \right\|^{2} + \mu^{2} \left( {\frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n))} \right)^{2} \\ & - 2\mu \mathop \Omega \limits^{\sim} (n - 1)O[\varphi (u(n))] \\ \end{aligned} $$
(29)

we take expectations of both sides of (29) to obtain the mean square behavior of the.

SKFLP-MNC and written as

$$ \begin{aligned} E\left[ {\left\| {\mathop \Omega \limits^{\sim} (n)} \right\|^{2} } \right] & = E\left[ {\left\| {\mathop \Omega \limits^{\sim} (n - 1)} \right\|^{2} } \right] + \mu^{2} E\left[ {\frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}} (e(n)))^{2} } \right] \\ & \quad- 2\mu E[\mathop \Omega \limits^{\sim} (n - 1)O[\varphi (u(n))]] \\ \end{aligned} $$
(30)

\(E{[}\left\| {\mathop \Omega \limits^{\sim} (n)} \right\|^{2} {]}\) represents the weight error power. Now, we use (30) to analyze the mean square convergence of the SKFLP-MNC. If the mean square converges, then \(E[\left\| {\mathop \Omega \limits^{\sim} (n)} \right\|^{2} ] \le E[\left\| {\mathop \Omega \limits^{\sim} (n - 1)} \right\|^{2} ]\). Thus,

$$ \mu^{2} E\left[ {\frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n)))^{2} } \right] - 2\mu E[\mathop \Omega \limits^{\sim} (n - 1)O[\varphi (u(n))]] \le 0 $$
(31)
$$ \mu \le \frac{{2E[\mathop \Omega \limits^{\sim} (n - 1)O[\varphi (u(n))]]}}{{E\left[ {\frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n)))^{2} } \right]}} $$
(32)

Hence, to guarantee that the SKFLP-MNC algorithm monotonically decreases, we obtain that the step size \(\mu\) at every iteration should satisfy

$$ 0 < \mu \le \frac{{2E[\mathop \Omega \limits^{\sim} (n - 1)O[\varphi (u(n))]]}}{{E\left[ {\frac{1}{{1 + e^{{ - \alpha \left| {e(n)} \right|^{p} }} }}\frac{1}{{\left| {e(n)} \right|^{1 - p} }}{\text{sgn}}(e(n)))^{2} } \right]}} $$
(33)

The existence of such a step size requires \(\forall_{n} E[\mathop \Omega \limits^{\sim} (n - 1)O[\varphi (u(n))]] > 0\).

4 Simulation Results

In this section, we present two simulation examples to demonstrate the benefits of the proposed SKFLP-MNC algorithm, and to compare its performance with that of the NLMS [3] algorithm, that of the KLMS-SC algorithm, that of the KLMS-NC algorithm and the RAN algorithm. The first example is the Mackey–Glass time series prediction, which shows that our proposed SKFLP-MNC algorithm compares successfully to the NLMS algorithm, KLMS-SC algorithm, KLMS-NC algorithm, and RAN algorithm in terms of computational costs while achieving comparable steady-state prediction error. It also shows that our proposed algorithms offer a flexible trade-off between steady-state error and convergence speed. The second example shows the advantage in terms of adaptive noise cancellation compared to the KLMS-SC algorithm and the NLMS algorithm. The performance of the adaptive solution was estimated by the testing MSE metric.

4.1 Short Term Mackey–Glass Time Series Prediction

The first example is the short term Mackey–Glass sequence prediction, which is used to create a chaotic sequence. We take the previous points u(n) = [x(n − 7), x(n − 6),· · ·, x(n − 1)]T to predict the current one point x(n). We take advantage of the following time-delay ordinary differential equation to generate the time series:

$$ \frac{{{\text{d}}x(n)}}{{{\text{d}}n}} = - bx(t) + \frac{cx(n - \tau )}{{1 + x(n - \tau )^{10} }} $$
(34)

where b = 0.1, c = 0.2, τ = 25. When using time series, it is usually best to select the last part of the series for validation, especially when using the data for prediction. First, three representative sparsity criteria are selected to obtain the corresponding kernel adaptive filtering algorithms to verify the effectiveness of SKFLP-MNC algorithm. A Gaussian kernel with kernel parameter h = 0.2 is chosen. Two hundred Monte Carlo [19] simulations were performed, each with 500 iterations to compute the learning curve with different realizations of noise. The noise used here includes the zero-mean Gaussian noise with variance 0.009 and the uniform noise distributed over [− 0.3, 0.3] and [− 1, 1]. The step size for NLMS is 0.1. For RAN, the step size is 0.05, and the tolerance for prediction error is 0.05. The step size is 0.5 for KLMS-NC, δ1 and δ2 are used in this paper to be the same as those in NC. KLMS-SC uses a step size of 0.5, T2 =  − 1, and λ = 0.01. The distance resolution parameters are [0.05, 0.5].

The parameter setting of Ran is shown in [19]. SKFLP-MNC algorithm uses δ1 = 0.15, δ2 = 0.01, p = 0.9, and α = 1. The parameters are set by cross validation. Figure 2 shows the learning curves of the KLMS-NC, KLMS-SC, RAN, NLMS and SKFLP-MNC under zero-mean Gaussian noise with variance 0.009 noise environments in short term Mackey–Glass time series prediction.

Fig. 2
figure 2

Learning curves of the KLMS-NC, KLMS-SC, RAN, NLMS, and SKFLP-MNC under Gaussian noise environments in Mackey–Glass time series prediction

Full size image

It is seen from Fig. 2 that the performances of RAN, KLMS-NC, KLMS-SC, NLMS, and SKFLP-MNC are comparable, and SKFLP-MNC significantly outperforms conventional algorithms in the steady state. The network sizes are listed in Table 1. It can be seen that SKFLP-MNC has a much smaller network size than other methods, which shows the modified criterion over the heuristic NC. In addition, the MNC is better than the NC in the sense that it makes use of the exponential loss function to generate a high-precision classification model.

Table 1 Network sizes of RAN, KLMS-NC, KLMS-SC, and SKFLP-MNC
Full size table

Then, we focus on the filtering performance of the SKFLP-MNC algorithm with different noise. The proposed SKFLP-MNC algorithm with no fixed budget is tested in the uniform noise distributed over [− 0.3, 0.3] and [− 1, 1]. Figures 3 and 4 show the results of this experiment, one can observe that:

Fig. 3
figure 3

Learning curves of different algorithms under the uniformly distributed [− 0.3, 0.3] noise environment in Mackey–Glass time series prediction

Full size image
Fig. 4
figure 4

Learning curves of different algorithms under the uniformly distributed [− 1, 1] noise environment in Mackey–Glass time series prediction

Full size image

The SKFLP-MNC algorithm has fast convergence speed, and its steady-state error performance is the strongest under the same convergence speed. In other words, the proposed algorithm can achieve high filtering accuracy, respectively. We increase the distribution range of the uniform noise process from 0.3 to 1(− 1 to − 0.3), which will increase the size of outliers. Therefore, we can find that the proposed algorithm has strong robustness and low computational complexity to reach a steady-state error.

4.2 Adaptive Noise Cancellation

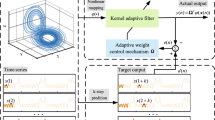
In the second trial, we compare the performance of the SKFLP-MNC with the KLMS-NC and the NLMS algorithms. The proposed algorithm is employed to the signal noise cancellation. A total of 200 simulations were averaged, each with 1000 iterations to compute the learning curve. Supposing the original input signal is s(n), and random noise v(n), the input signal of filter u(n) is obtained through the nonlinear distortion function. The filter system structure of this adaptive noise cancellation is shown in Fig. 5. The distortion function of the noise source is a nonlinear function. As a deterministic model, it is assumed that the relationship between v(n) and u(n) is

$$ u(n) = v(n) - 0.3u(n - 1) - u(n - 1)v(n - 1) + 0.5v(n - 1) + 0.2u(n - 2) $$
(35)
Fig. 5
figure 5

System structure of adaptive noise cancellation

Full size image

For our proposed SKFLP-MNC algorithm, the noise source used here includes the zero-mean Gaussian noise with variance 0.1 and the uniform noise distributed over [− 0.5, 0.5], where the waveform of the noise source is shown in Figs. 6 and 7. Hypothesis the original input s(n) = 0. Based on the simulation results above, the parameters are similar to experiment one, which are experimentally selected to achieve their optimal performance.

Fig. 6
figure 6

Uniform distributed noise over [− 0.5, 0.5]

Full size image
Fig. 7
figure 7

The zero-mean Gaussian noise

Full size image

In the stationary environment, Fig. 8 shows the learning curves of different algorithms in the same noise environment. It is seen from Fig. 8 that the steady state MSE of the SKFLP-MNC is smaller than that of the others algorithms in uniform noise environments. Interestingly, we observe the SKFLP-MNC algorithm has the fastest convergence rate. The averaged evolution curves for different adaptive algorithm are plotted in Fig. 9. The results indicate that our method produce a strong stability, which explains why its filtering behavior is outstanding to complex noise environment, although the rate of convergence is slower than that of KLMS-NC algorithm.

Fig. 8
figure 8

Learning curves of the NLMS, KLMS-NC, and SKFLP-MNC under uniform noise source environments in noise cancellation

Full size image
Fig. 9
figure 9

Learning curves of the NLMS, KLMS-NC, and SKFLP-MNC under Gaussian noise source environments in noise cancellation

Full size image

5 Conclusion

In this paper, we introduce a novel robust kernel adaptive filtering algorithm based on the Softplus function with sparsification in both Gaussian and non-Gaussian noise environments, which well solves the growth network size in kernel filtering. A novel NC structure with the exponential loss function is incorporated into SKFLP to curb the filtering network size. The proposed SKFLP-MNC algorithm’s characteristics, such as convergence speed, stability, and network size are presented for discussion. Meanwhile, to obtain a sufficient condition for mean-square convergence, the mean-square convergence analysis of the SKFLP-MNC algorithm is indirectly derived. Benefiting from this analysis, the SKFLP-MNC algorithm to reach filtering accuracy is better than the other adaptive algorithms under different noise levels. Simulation results on the MG timer series predictions and noise cancellation demonstrate the usefulness and effectiveness of our proposed method.