1 Introduction

The time series is regarded as a collection of data arranged in chronological order, and it is ubiquitous in nature, industrial production, financial technology, and other fields [11, 16, 17]. Generally, the time series extracted from the practical system has chaotic characteristics, which plays an important role in exploring the evolution rules of the system. However, the real-time property of streaming data and the complexity of the environment bring challenges for the accurate learning of chaotic dynamical systems [25]. Therefore, while mining the hidden information of time series, online prediction models also require to show strong performance for nonlinear, nonstationary, and non-Gaussian aspects of time series. In recent years, kernel adaptive filter (KAF) [21, 26] with universal approximation ability and excellent online learning ability has shown great vitality in various applications, such as time series prediction, channel equalization, nonlinear acoustic echo cancellation, etc. [1, 28, 33].

In the research of KAF, choosing a flexible and robust criterion [13, 14, 29] is crucial. Most classic KAF algorithms including kernel least mean square (KLMS) [20] and kernel recursive least squares (KRLS) [10] are presented under mean square error (MSE) which excel in terms of smoothness, convexity, and computational complexity. However, since MSE contains only second-order statistics and relies on Gaussian noise assumptions, it is difficult to handle the sharp spike and tail heaviness of signal noise in the environment, especially non-Gaussian noise. In order to improve the reliability and robustness of KAF in non-Gaussian environments, the maximum correntropy criterion (MCC) [15, 19, 34] based on information theoretic learning has received extensive attention. Replacing MSE in KRLS with MCC, kernel recursive maximum correntropy (KRMC) [35] is developed to enhance robustness to non-Gaussian noise. To further suppress the interference of nonzero mean noise, KRMC with variable center (KRMC-VC) [22] is proposed. Moreover, as a family criterion of correntropy, the generalized correntropy criterion (GCC) [6, 18] with more nonquadratic loss features is studied, and kernel recursive generalized maximum correntropy (KRGMC) [39] under GCC is developed to improve the flexibility and accuracy of correntropy. However, since GCC is not a strictly convex function [6], the existence of an optimal solution may not be guaranteed. Fortunately, the half-quadratic (HQ) [12, 36] theory can successfully convert a nonconvex problem into a global convex optimization problem, which ensures the best parameter estimates.

In addition, the optimization strategy [8, 9, 27] for obtaining optimal parameter estimates of criteria is also particularly attractive. Stochastic gradient descent (SGD) [23] is the most frequently adapted convex optimization method. However, it is difficult to guarantee both convergence speed and steady-state performance through SGD optimization. Afterward, optimization strategies based on recursive calculation or second-order optimization [7, 39] are proposed. Although they provide a more accurate solution, they take up excessive calculation and storage space. For the flaws mentioned above, the conjugate gradient (CG) [5] method comes up with a better solution. The nonlinear acoustic echo algorithm [3] achieves a good trade-off between complexity and performance by using the CG method. Kernel conjugate gradient (KCG) [37] algorithm not only solves the problem of slow convergence but also successfully avoids huge computing resources. Last but not least, suitable sparsification methods [2, 31], such as approximate linear dependency (ALD) [10, 26], coherence criterion (CC) [4, 38], and vector projection (VP) [40], are applied in KAF to deal with the high computational cost caused by the rapid growth of the kernel matrix, thereby improving the convergence speed. KCG-AC [37] directly controls data size growth through angle criteria (AC). Quantized KRGMC (QKRGMC) [30] is proposed to quantify the size of the kernel network in the input space by vector quantization.

Based on the above discussion, the main contributions are as follows:

  1. (1)

    The generalized HQ correntropy (GHC) criterion is proposed by combining HQ and GCC for the first time. It converts the maximum GCC into a global convex optimization problem via HQ, which makes the parameter estimation more accurate and further enhances the robustness with respect to non-Gaussian noise or outliers.

  2. (2)

    Furthermore, the KGHCG algorithm is proposed, which uses the CG method to solve the above GHC criterion of kernel space. The proposed algorithm can provide excellent convergence performance and high filtering accuracy. In addition, the VP method further constrains the infinite expansion mode of the kernel matrix in KGHCG, which greatly reduces the computational complexity, and we finally develop the KGHCG-VP algorithm.

  3. (3)

    Finally, we analyze the convergence performance, computational complexity and memory usage of the proposed method. Meanwhile, the efficiency of the proposed algorithms is verified by the Mackey–Glass (MG) dataset as well as real-world datasets including ENSO and Beijing air quality time series. Theoretical analysis and experimental results demonstrate that KGHCG and KGHCG-VP have better prediction ability and practicability for online tasks.

The rest of this article is structured as follows. In Sect. 2, related work is described briefly, including online kernel learning, GCC function, and its nonconvexity. In Sect. 3, we derive the proposed GHC criterion and KGHCG algorithm in detail, and the theoretical analysis of the proposed method is also investigated. In Sect. 4, simulation experiments are given. Finally, we summarize the conclusion in Sect. 5.

2 Related Works

2.1 Online Kernel Learning

Due to the complexity and dynamic nature of sequential arrival data flow, an online prediction model must demonstrate significant learning capacity for nonlinear and nonstationary. In recent years, KAF has become an efficient nonlinear modeling tool because of its excellent approximation ability and online learning ability. Its core concept is to exploit the online kernel learning framework, and the working principle of KAF is shown in Fig. 1.

Fig. 1
figure 1

Kernel adaptive filter for online multi-step prediction

Full size image

For online learning of chaotic time series \(\left\{ {\varvec{x}(n),d(n)} \right\} \), the classical KLMS [20] algorithm transforms the input of the original space \({{\mathcal {X}}}\) into a suitable high-dimensional feature space \({{\mathcal {F}}}\) through a nonlinear mapping \(\varphi (\cdot ) \) induced by kernel evaluation. Afterward, a suitable linear method is applied to the transformed sample and the expected output at each iteration n is estimated as

$$\begin{aligned} y(n) = {\varvec{\Omega }^T} \varphi (\varvec{x}(n)) \end{aligned}$$
(1)

where \(\varvec{\Omega }\) is the weight of the filter. According to the adaptive mechanism of KLMS, the learning rule for the weight is

$$\begin{aligned} {\varvec{\Omega }} (n) = {\varvec{\Omega }} (n - 1) + \eta e(n)\varphi (\varvec{x}(n)) \end{aligned}$$
(2)

where \(e(n)=d(n)-y(n)\) denotes the prediction error. \(\eta \) denotes the step parameter.

2.2 Generalized Correntropy Criterion

GCC [6] as the measure of the generalized similarity between two random variables A and B, is described by

$$\begin{aligned} L(A,B) = E\left[ {\kappa (A,B)} \right] = \iint {\kappa (A,B){f_{A,B}}(a,b){\textrm{d}}a{\textrm{d}}b} \end{aligned}$$
(3)

where \(\kappa ( \cdot , \cdot )\) denotes the Mercer kernel, \(E(\cdot )\) denotes the mathematical expectation, and \({f_{A,B}}(a,b)\) denotes the joint density function of A and B. Nevertheless, since \({f_{A,B}}(a,b)\) denotes an unknown function in practical applications, the mathematical expectation of the above formula can be approximated empirically through observed samples, which is

$$\begin{aligned} {\hat{L}}(A,B) = \frac{1}{N}\sum \limits _{n = 1}^N {\kappa (a(n),b(n))} \end{aligned}$$
(4)

where \(\kappa ( \cdot , \cdot )\) adopts the generalized Gaussian density function, and it is defined as:

$$\begin{aligned} \kappa (a,b) = \frac{\alpha }{{2\beta \Gamma ({1 / \alpha })}}\exp ( - {\beta ^{ - \alpha }}{\vert {a - b} \vert ^\alpha })= {\gamma _{\alpha ,\beta }}\exp ( - \lambda {\vert {a - b} \vert ^\alpha }) \end{aligned}$$
(5)

where \({\gamma _{\alpha ,\beta }} = \frac{\alpha }{{2\beta \Gamma ({1 / \alpha })}}\), \(\lambda = {\beta ^{ - \alpha }}\), \(\alpha > 0\) denotes the shape factor, \(\beta > 0\) denotes the scale factor, \(\Gamma (\cdot )\) denotes the gamma function, and \({\gamma _{\alpha ,\beta }}\) denotes the normalization constant.

Similar to MCC applied to KAF, the optimal weight vector of the filter can usually be solved by minimizing the generalized correntropy loss (GCL) function [30], and it is

$$\begin{aligned} \begin{aligned} {\ell _{\textrm{GCL}}}&= {\kappa _{\alpha ,\beta }}(0) - E\left[ {{\kappa _{\alpha ,\beta }}(e)} \right] = {\gamma _{\alpha ,\beta }} - \frac{1}{N}\sum \limits _{n = 1}^N {{\kappa _{\alpha ,\beta }}(e(n))} \\&= {\gamma _{\alpha ,\beta }}\left[ {1 - \frac{1}{N}\sum \limits _{n = 1}^N {\exp ( - \lambda {{\vert {e(n)} \vert }^\alpha })} } \right] \end{aligned} \end{aligned}$$
(6)

where \(e(n) = a(n) - b(n)\). Next, the Hessian matrix with respect to the error e of \(\ell _{\textrm{GCL}}\) is calculated to investigate the properties of the GCL function, which is

$$\begin{aligned} {{\textbf {H}}_{\textrm{GCL}}}(e)= & {} - \frac{{\alpha \lambda {\gamma _{\alpha ,\beta }}}}{N}diag({\Delta _1}(\alpha \lambda {\vert {e(1)} \vert ^\alpha } - (\alpha - 1)), \ldots ,\nonumber \\{} & {} {\Delta _N}(\alpha \lambda {\vert {e(N)} \vert ^\alpha } - (\alpha - 1))) \end{aligned}$$
(7)

where \({\Delta _n} = {\vert {e(n)} \vert ^{\alpha - 2}}\exp ( - \lambda {\vert {e(n)} \vert ^\alpha })\). From obtained Hessian matrix (7), we can obtain two properties as follows:

  1. (1)

    if \(0 < \alpha \le 1\), \({{\textbf {H}}_{\textrm{GCL}}}(e) \le 0\) for any e with \({e(n)} \ne 0(n = 1, \ldots ,N)\);

  2. (2)

    if \(\alpha > 1\), \({{\textbf {H}}_{\textrm{GCL}}}(e) \ge 0\) for any e with \(\vert {e(n)} \vert \le {\left[ {{{(\alpha - 1)}/{\alpha \lambda }}} \right] ^{{1/\alpha }}}(n = 1, \ldots ,N)\).

From the above properties we can get that if and only if \(\alpha > 1\) and \(\vert {e(n)} \vert \le {\left[ {{{(\alpha - 1)}/{\alpha \lambda }}} \right] ^{{1/\alpha }}}(n = 1, \ldots ,N)\), \({{\textbf {H}}_{\textrm{GCL}}}(e) \ge 0\). That is, the GCL is convex. When these conditions are not satisfied, GCL as the cost function is not strictly globally convex. As a result, the optimal value cannot be found when solving the cost function.

3 Proposed Algorithm

In this section, we derive the KGHCG algorithm in detail. Firstly, we create a GHC function based on GCC function and HQ modeling. Then, the parameters are optimally solved by the CG method for the GHC function of the kernel space. In addition, an online VP approach is adopted to propose KGHCG-VP to reduce the computational complexity. Finally, convergence properties and complexity of proposed method are investigated.

3.1 Generalized Half-Quadratic Correntropy

As mentioned in Sect. 2.2, the Hessian matrix of the GCL function is positive-definite if and only if certain conditions are met. In other words, the global convexity of GCL is difficult to guarantee since its Hessian matrix is not strictly positive definite, and thus GCL cannot directly handle convex optimization tasks. Luckily, the HQ framework ensures that the objective function is strictly convex. Specifically, a GHC criterion is proposed by introducing the intermediate variable \(\textbf{V}\) to transform nonconvex issues into fully convex issues.

The GCC criteria contain an exponential function as \(f(x) = \exp ( - x)\), and its conjugate function is \({\tilde{f}}(v) = v- v\ln ( - v) \) with \(v < 0\). For the convex function of the GCC criteria, the following proposition is made.

Proposition 1

The exponential function of GCC is conjugate functions of the convex functions \({\tilde{f}}(v) = - v\ln ( - v) +v \) with \(v < 0\). That is

$$\begin{aligned} \exp ( - \lambda {\vert {e(n)} \vert ^\alpha }) = {\sup _{v < 0}}\left\{ {v\lambda {{\vert {e(n)} \vert }^\alpha } - {\tilde{f}}(v)} \right\} \end{aligned}$$
(8)

where the upper bound value is obtained at \(v = - \exp ( - \lambda {\vert {e(n)} \vert ^\alpha })\).

Proof

By the conjugate function theory, we have the conjugate function of \({\tilde{f}}(v)\), which is

$$\begin{aligned} {{\tilde{f}}^*}(u) = {\sup _{v< 0}}\left\{ {uv - {\tilde{f}}(v)} \right\} = {\sup _{v < 0}}\left\{ {uv - v+ v\ln ( - v) } \right\} \end{aligned}$$
(9)

Then, we set \(h(v) = uv - v+ v\ln ( - v)\). h(v) reaches its maximum value when \(v = - \exp ( - u)\), expressed as \(h{}_{\max }(v) = \exp ( - u)\). Therefore, rewritten formula (9) is given by

$$\begin{aligned} {{\tilde{f}}^*}(u) = {\sup _{v < 0}}\left\{ {uv - v+ v\ln ( - v) } \right\} = \exp ( - u) \end{aligned}$$
(10)

where \(v = - \exp ( - u)\). In addition, we make \(u = \lambda {\vert {e(n)} \vert ^\alpha }\) and obtain

$$\begin{aligned} {{\tilde{f}}^*}(\lambda {\vert {e(n)} \vert ^\alpha }) = \mathop {\sup }\limits _{v < 0} \left\{ {v\lambda {{\vert e(n) \vert }^\alpha } - v+ v\ln ( - v) } \right\} = \exp ( - \lambda {\vert {e(n)} \vert ^\alpha }) \end{aligned}$$
(11)

where the upper bound value is obtained when \(v = - \exp ( - u)\), the maximum value is \(\exp ( - \lambda {\vert {e(n)} \vert ^\alpha })\), and the proposition is proved. \(\square \)

Based on the above discussion, the solution of GCL objective function (6) can be equivalent to solving the following optimization function; we have

$$\begin{aligned} \begin{aligned} \mathop {\max }\limits _{v < 0} \sum \limits _{n = 1}^N { \left\{ {v(n)\lambda {{\vert {e(n)} \vert }^\alpha } - {\tilde{f}}(v(n))} \right\} } \end{aligned} \end{aligned}$$
(12)

For a given v(n), optimization objective (12) is equivalent to minimizing the weighted least squares problem by GHC objective function, which is

$$\begin{aligned} \mathop {\min }\limits _{v < 0} \sum \limits _{n = 1}^N {\left( { - v(n)\lambda {{\vert {e(n)} \vert }^{\alpha - 2}}e{{(n)}^2}} \right) } \end{aligned}$$
(13)

where \(v(n) = - \exp ( - \lambda {\vert {e(n)} \vert ^\alpha })\).

Next, the Hessian matrix of GHC function (13) is calculated, and we get

$$\begin{aligned} {\textbf{H}_{\textrm{GHC}}}(e) = diag\left( { - 2\lambda v(1){{\vert {e(1)} \vert }^{\alpha - 2}}, - 2\lambda v(2){{\vert {e(2)} \vert }^{\alpha - 2}}, \ldots , - 2\lambda v(N){{\vert {e(N)} \vert }^{\alpha - 2}}} \right) \nonumber \\ \end{aligned}$$
(14)

Since \(v(n) < 0\), we can obtain Hessian matrix (14) of the GHC loss function strictly positive definite, ensuring that GHC is a strictly convex function. Compared to GCC, objective function (13) solves nonconvex to global convex optimization. Then, we utilize the conjugate gradient method to calculate.

First, we define minimizing GHC function (13) as a quadratic function optimization objective, which is given by

$$\begin{aligned} \min \frac{1}{2}{\left\| {\sqrt{\textbf{V}} \left( {{\varvec{d}^T} - {{\textbf{U}}^T}\varvec{w}} \right) } \right\| ^2} \Rightarrow \min \limits _{\varvec{w} } \frac{1}{2}{\varvec{w}^T}{\textbf{UV}}{{\textbf{U}}^{{T}}}\varvec{w} - \varvec{d}{\textbf{V}}{{\textbf{U}}^{{T}}}\varvec{w} \end{aligned}$$
(15)

where \(\varvec{d} = [d(1),d(2), \ldots ,d(N)]\), \({\textbf{U}} = [\varvec{u}(1),\varvec{u}(2), \ldots ,\varvec{u}(N)]\), \(\varvec{w}\) is the weight vector, and \(\textbf{V}\) is the intermediate variable, which is denoted as

$$\begin{aligned} \textbf{V}= diag( - 2v(1)\lambda {\vert {e(1)} \vert ^{\alpha - 2}}, \ldots , - 2v(N)\lambda {\vert {e(N)} \vert ^{\alpha - 2}}) \end{aligned}$$
(16)

Then, we utilize the CG approach to minimize the GHC objective function to propose the GHC-CG algorithm, which is similar to CGLS [24]. For a given data stream \(\left\{ {\varvec{u}(n),d(n)} \right\} \), initializations are set to \(\varvec{w}(0) = 0\), \(\varvec{r}(0) = {\textbf{V}}({\varvec{d}^T} - {{\textbf{U}}^T}\varvec{w}(0))\), \(\varvec{s}(0) = {\textbf{U}}\varvec{r}(0)\) and \(\varvec{p}(1) = \varvec{s}(0)\), and the optimization mechanisms are described as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} { \varvec{v}(n) = {\textbf{V}}{{\textbf{U}}^T}\varvec{p}(n)}\\ {{\varsigma _1}(n) = {{\left\langle {\varvec{s}(n - 1),\varvec{s}(n - 1)} \right\rangle }/{\left\langle {{{\textbf{U}}^T}\varvec{p}(n),\varvec{v}(n)} \right\rangle }}}\\ {\varvec{w}(n) = \varvec{w}(n - 1) + {\varsigma _1}(n)\varvec{p}(n)}\\ {\varvec{r}(n) = \varvec{r}(n - 1) - {\varsigma _1}(n)\varvec{v}(n)}\\ {\varvec{s}(n) = {\textbf{U}}\varvec{r}(n)}\\ {{\varsigma _2}(n+1) = {{\left\langle {\varvec{s}(n),\varvec{s}(n)} \right\rangle }/{\left\langle {\varvec{s}(n - 1),\varvec{s}(n - 1)} \right\rangle }}}\\ {\varvec{p}(n + 1) = \varvec{s}(n) + {\varsigma _2}(n+1)\varvec{p}(n)} \end{array}} \right. \end{aligned}$$
(17)

where \(\varvec{v} \) denotes the intermediate vector, \( \varsigma _1\) and \(\varsigma _2\) denote learning parameters, \( \varvec{r} \) is the residual vector, \(\varvec{s}\) denotes the residual vector of normal equations, and \(\varvec{p}\) denotes the search direction.

3.2 Kernel Generalized Half-Quadratic Correntropy Conjugate Gradient Algorithm

According to the GHC objective function, the weighted least squares problem is applied to the kernel space, which is

$$\begin{aligned} \mathop {\min }\limits _{v < 0} \sum \limits _{n = 1}^N {\left( { - v(n)\lambda {{\vert {e(n)} \vert }^{\alpha - 2}}e{{(n)}^2}} \right) = } \min \limits _{\varvec{\theta }} \frac{1}{2}{\left\| {\sqrt{\textbf{V}} \left( {{\varvec{d}^T} - \textbf{K}\varvec{\theta }} \right) } \right\| ^2} \end{aligned}$$
(18)

where \(\varvec{\theta }\) is the expansion coefficient, which needs to be estimated. \(\textbf{K}\) is the kernel matrix, which is expressed as

$$\begin{aligned} \textbf{K}= {\left[ {\begin{array}{*{20}{l}} {\kappa ({\varvec{u}(1)},{\varvec{u}(1)})}&{} \quad {\kappa ({\varvec{u}(1)},{\varvec{u}(2)})}&{} \quad \cdots &{}\quad {\kappa ({\varvec{u}(1)},{\varvec{u}(N)})}\\ {\kappa ({\varvec{u}(2)},{\varvec{u}(1)})}&{}\quad {\kappa ({\varvec{u}(2)},{\varvec{u}(2)})}&{} \quad \cdots &{}\quad {\kappa ({\varvec{u}(2)},{\varvec{u}(N)})}\\ \vdots &{} \quad \vdots &{} \quad \ddots &{} \quad \vdots \\ {\kappa ({\varvec{u}(N)},{\varvec{u}(1)})}&{}\quad {\kappa ({\varvec{u}(N)},{\varvec{u}(2)})}&{}\quad \cdots &{}\quad {\kappa ({\varvec{u}(N)},{\varvec{u}(N)})} \end{array}} \right] _{N \times N}} \end{aligned}$$
(19)

Then, we minimize the GHC function using the CG method. For the KGHCG algorithm, the expansion coefficient \(\varvec{\theta }\) and kernel matrix \(\textbf{K}\) update mechanism are very important. We define the kernel matrix \(\textbf{K}\) as

$$\begin{aligned} {\textbf{K}(N)} = {\left[ {\begin{array}{*{20}{c}} {{\textbf{K}(N-1)}}&{}\quad {\varvec{g}(N)^T}\\ {{\varvec{{\bar{g}}}(N)}}&{}\quad {{q(N)}} \end{array}} \right] _{N \times N}} \end{aligned}$$
(20)

where \({\varvec{g}(N)} = \left[ {\kappa ({\varvec{u}(1)},{\varvec{u}(1)}), \ldots ,\kappa ({\varvec{u}(N-1)},{\varvec{u}(N)})} \right] \) and \({q(N)} = \kappa ({\varvec{u}(N)},{\varvec{u}(N)})\).

The weight vector \(\varvec{w}(N)\) is obtained by kernel trick and mathematical induction.

$$\begin{aligned} \begin{aligned} \varvec{w}(N)&= \varvec{w}(0) + \sum \nolimits _{n = 1}^N {\varsigma _1}(n) \varvec{p}(n)\\&= \sum \nolimits _{n = 1}^N {\varsigma _1}(n) \sum \nolimits _{i = 1}^N {\pi _{i + 1}^i\varvec{s}(i - 1)} \\&= \sum \nolimits _{n = 1}^N {\left( {\sum \nolimits _{i = n}^N {{\varsigma _1}(i)\pi _{n + 1}^i} } \right) } \varvec{s}(n - 1)\\ {}&= {\textbf{U}}\left[ {\sum \nolimits _{n = 1}^N {\left( {\sum \nolimits _{i = n}^N {{\varsigma _1}(i)\pi _{n + 1}^i} } \right) }\varvec{r}(n - 1)} \right] \\&= {\textbf{U}}\left( {{\textbf{E}}(N)\varvec{\xi }(N)} \right) = {\textbf{U}}\varvec{\theta }(N) \end{aligned} \end{aligned}$$
(21)

where \(\pi _{n+1}^i = {{\varsigma }_{2n+1}}{{\varsigma _{2n+2}}} \cdots {{\varsigma _2}_i}\) with \(\pi _{n + 1}^{n} = 1\). \({\textbf{E}}(N) = \left[ {\varvec{r}(0),\varvec{r}(1), \ldots ,\varvec{r}(N - 1)} \right] \), \(\varvec{\theta }(N) = {\textbf{E}}(N)\varvec{\xi }(N)\), where the nth element of \(\varvec{\xi }(N)\) is defined by

$$\begin{aligned} {\xi _n}(N) = \sum \nolimits _{i = n}^N {{\varsigma _1}(i)\pi _{n + 1}^i} = {\xi _n}(N - 1) + {\varsigma _1}(N)\pi _{n + 1}^N \end{aligned}$$
(22)

Since \([\varvec{\theta }(N-1);0]\) is a good approximation of \({\varvec{\theta }(N)}\), it does not need to iterate over the number of data streams, and only needs one or two iterations to obtain superior parameter performance. Hence, \([\varvec{\theta }(N-1);0]\) is used as the initial value to replace \({\varvec{\theta }(N)}\). And the update of \(\varvec{\theta }(N)\) about the KGHCG algorithm with two iterations is expressed as

$$\begin{aligned} \varvec{\theta }(N) = \left[ {\varvec{\theta }(N - 1);0} \right] + ({\varsigma _1}(1) + {\varsigma _2}(2){\varsigma _1}(2))\varvec{r}(0) + {\varsigma _1}(2)\varvec{r}(1) \end{aligned}$$
(23)

At this point, the initial residual calculation formula is given by

$$\begin{aligned} \begin{aligned} \varvec{r}(0)&= \textbf{V}(N)({\varvec{d}^T} - {\textbf{K}(N)}[\varvec{\theta }(N - 1);0])\\&= \textbf{V}(N)\left( {\left[ {\begin{array}{*{20}{c}} {\varvec{d}{{(N - 1)}^T}}\\ {d(N)} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {\textbf{K}(N - 1)}&{}{\varvec{g}{{(N)}^T}}\\ {\varvec{{\bar{g}}}(N)}&{}{q(N)} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {\varvec{\theta }(N - 1)}\\ 0 \end{array}} \right] } \right) \\&= \left[ {\begin{array}{*{20}{c}} \textbf{I}&{}\textbf{0}\\ {{\textbf{0}^T}}&{}{v(N)} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{\left( {\varvec{ d}(N - 1) - \varvec{\theta }{{(N - 1)}^T}\textbf{K}(N - 1)} \right) }^T}}\\ {d(N) - \varvec{{\bar{g}}}(N)\varvec{\theta }(N - 1)} \end{array}} \right] \\&= {\left[ {\varvec{e}(N - 1),v(N)\left( {d(N) - \varvec{{\bar{g}}}(N)\varvec{\theta }(N - 1)} \right) } \right] ^T} \end{aligned} \end{aligned}$$
(24)

where \({v(N)} = 2\lambda {\vert {{e(N)}} \vert ^{\alpha - 2}}\exp ( - \lambda {\vert {{e(N)}} \vert ^\alpha })\), \(\varvec{e}(N) = {(\varvec{r}(1) - {\varsigma _1}(2)\varvec{v}(2))^T}\) and \(e(N)=\left( {d(N) - \varvec{\bar{g}}(N)\varvec{\theta }(N - 1)} \right) \).

In addition, since the size of the kernel matrix is determined by data scale, more and more computing resources need to be undertaken with the passage of time. To deal with the drawback of infinite expansion of the kernel matrix, the VP method [41] as the sparsification strategy is used. This criterion generates a more compact network by selecting samples with valid information, which further reduces the computational complexity. And it is defined as

$$\begin{aligned} \cos (\varvec{u},\varvec{u}') = \frac{{{{\left\langle {\varphi (\varvec{u}),\varphi (\varvec{u}')} \right\rangle }_{{\mathcal {F}}}}}}{{{{\left\| {\varphi (\varvec{u})} \right\| }_{{\mathcal {F}}}}{{\left\| {\varphi (\varvec{u}')} \right\| }_\mathcal{F}}}} \end{aligned}$$
(25)

Then we compare the distance \(\cos (\varvec{u},\varvec{u}') \) with the predefined threshold \(\tau \) that determines the level of sample sparseness. If \(\cos (\varvec{u},\varvec{u}') > \tau \), \(\left( {\varphi (\varvec{u}),d(n)} \right) \) will be discarded. Otherwise, \(\left( {\varphi (\varvec{u}),d(n)} \right) \) will be added to the existing dictionary \({{\mathcal {D}}}\), and the expansion coefficient and residual will be updated in real time according to the adaptive mechanism, achieving a good compromise between prediction accuracy and computational efficiency.

The procedure of the KGHCG-VP algorithm is detailed in Algorithm 1.

figure a

3.3 Convergence Analysis of KGHCG

For the proposed KGHCG algorithm, the update rules of weight and direction vectors of (17) are as follows

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {\varvec{w}(n + 1) = \varvec{w}(n) + {\varsigma _1}(n)\varvec{p}(n)}\\ {\varvec{p}(n + 1) = \varvec{s}(n) + {\varsigma _2}(n)\varvec{p}(n)} \end{array}} \right. \end{aligned}$$
(26)

where \(\varvec{s}(n)\) is the residual vector of normal equations (negative gradient vector), and the core concept of the direction vector is to search for the minimum value of the loss function, where \(\mathop {\lim }\limits _{n \rightarrow \infty } \inf \left\| {\varvec{s}(n)} \right\| = 0\).

In [42], descent conditions \(\varvec{s}(n)\varvec{p}(n + 1) < 0\) [37] of conjugate gradient and (26) together constitute the Zoutendijk criteria, which are defined as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {\varvec{w}(n + 1) = \varvec{w}(n) + {\varsigma _1}(n)\varvec{p}(n)}\\ {\varvec{s}(n)\varvec{p}(n + 1) < 0} \end{array}} \right. \end{aligned}$$
(27)

where direction vector \(\varvec{p}(n)\) and negative gradient vector \(\varvec{s}(n)\) satisfy the following inequality

$$\begin{aligned} \sum \limits _{n = 1}^\infty {\frac{{{{\left( {\varvec{s}(n - 1)\varvec{p}(n)} \right) }^2}}}{{{{\left\| {\varvec{p}(n)} \right\| }^2}}}} < + \infty \end{aligned}$$
(28)

Then, we prove convergence by contradiction.

Proposition 2

Based on (26), the proposed algorithm converges to the minimum value of the loss function, where

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } \inf \left\| {s(n)} \right\| = 0 \end{aligned}$$
(29)

Proof

First, we assume that the above Proposition 2 is false, i.e., \(\mathop {\lim }\limits _{n \rightarrow \infty } \inf \left\| {\varvec{s}(n)} \right\| \ge \delta \), where \(\delta \) is an arbitrarily small constant. Multiplying both sides of the negative direction vector \(\varvec{s}(n)\) in (26), we have

$$\begin{aligned} \begin{array}{l} \varvec{s}{(n - 1)^T}\varvec{p}(n + 1) = \varvec{s}{(n - 1)^T}\varvec{s}(n) + \varvec{s}{(n - 1)^T}{\varsigma _2}(n + 1)\varvec{p}(n)\\ \Rightarrow {\varsigma _2}(n + 1) = \frac{{\varvec{s}{{(n - 1)}^T}\varvec{p}(n + 1)}}{{\varvec{s}{{(n - 1)}^T}\varvec{p}(n)}} \approx \frac{{\varvec{s}{{(n)}^T}\varvec{p}(n + 1)}}{{\varvec{s}{{(n - 1)}^T}\varvec{p}(n)}} \end{array} \end{aligned}$$
(30)

\(\square \)

Then, calculating the 2-norm on both sides of the direction vector \(\varvec{p}(n+1)\) of (26) at the same time, and it is

$$\begin{aligned} \begin{aligned} {\left\| {\varvec{p}(n + 1)} \right\| ^2}&= {\left\| {\varvec{s}(n) + {\varsigma _2}(n + 1)\varvec{p}(n)} \right\| ^2}\\&= {\left\| {\varvec{s}(n)} \right\| ^2} + 2\varvec{s}{(n)^T}{\varsigma _2}(n + 1)\varvec{p}(n) + {\varsigma _2}{(n + 1)^2}{\left\| {\varvec{p}(n)} \right\| ^2}\\&= {\left\| {\varvec{s}(n)} \right\| ^2} + 2\varvec{s}{(n)^T}\left[ {\varvec{p}(n + 1) - \varvec{s}(n)} \right] + {\varsigma _2}{(n + 1)^2}{\left\| {\varvec{p}(n)} \right\| ^2}\\&= {\varsigma _2}{(n + 1)^2}{\left\| {\varvec{p}(n)} \right\| ^2} + 2\varvec{s}{(n)^T}\varvec{p}(n + 1) - {\left\| {\varvec{s}(n)} \right\| ^2} \end{aligned}\nonumber \\ \end{aligned}$$
(31)

Substituting the learning factor into formula (31), we obtain

$$\begin{aligned} {\left\| {\varvec{p}(n + 1)} \right\| ^2} = {\left( {\frac{{\varvec{s}{{(n)}^T}\varvec{p}(n + 1)}}{{\varvec{s}{{(n - 1)}^T}\varvec{p}(n)}}} \right) ^2}{\left\| {\varvec{p}(n)} \right\| ^2} + 2\varvec{s}{(n)^T}\varvec{p}(n + 1) - {\left\| {\varvec{s}(n)} \right\| ^2}\nonumber \\ \end{aligned}$$
(32)

Next, dividing both sides of Eq. (32) by \({\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) ^2}\), we have

$$\begin{aligned} \frac{{{{\left\| {\varvec{p}(n + 1)} \right\| }^2}}}{{{{\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) }^2}}}= & {} \frac{{{{\left\| {\varvec{p}(n)} \right\| }^2}}}{{{{\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) }^2}}} + \frac{2}{{\varvec{s}{{(n)}^T}\varvec{p}(n + 1)}} - \frac{{{{\left\| {\varvec{s}(n)} \right\| }^2}}}{{{{\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) }^2}}} \nonumber \\= & {} \frac{{{{\left\| {\varvec{p}(n)} \right\| }^2}}}{{{{\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) }^2}}} - \left( {\frac{{\left\| {\varvec{s}(n)} \right\| }}{{\varvec{s}{{(n)}^T}\varvec{p}(n + 1)}} - \frac{1}{{\left\| {\varvec{s}(n)} \right\| }}} \right) + \frac{1}{{{{\left\| {\varvec{s}(n)} \right\| }^2}}}\nonumber \\\le & {} \frac{{{{\left\| {\varvec{p}(n)} \right\| }^2}}}{{{{\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) }^2}}} + \frac{1}{{{{\left\| {\varvec{s}(n)} \right\| }^2}}} \end{aligned}$$
(33)

Further, we can obtain the scaling inequality by

$$\begin{aligned} \begin{aligned} \frac{{{{\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) }^2}}}{{{{\left\| {\varvec{p}(n)} \right\| }^2}}}&\ge {\left[ {\frac{1}{{{{\left\| {\varvec{s}(0)} \right\| }^2}}} + \frac{1}{{{{\left\| {\varvec{s}(1)} \right\| }^2}}} + \cdots + \frac{1}{{{{\left\| {\varvec{s}(n - 1)} \right\| }^2}}}} \right] ^{ - 1}} \\&= {\left( {\sum \limits _{i = 0}^{n - 1} {\frac{1}{{{{\left\| {\varvec{s}(i)} \right\| }^2}}}} } \right) ^{ - 1}} \ge \frac{{{\delta ^2}}}{n} \end{aligned} \end{aligned}$$
(34)

As \(\sum \nolimits _{n = 1}^\infty {{{{\delta ^2}}/n}} = + \infty \), we get the inequality of direction vector \(\varvec{p}(n)\) and negative gradient vector \(\varvec{s}(n)\)

$$\begin{aligned} \sum \nolimits _{n = 1}^\infty {\frac{{{{\left( {\varvec{s}{{(n)}^T}\varvec{p}(n + 1)} \right) }^2}}}{{{{\left\| {\varvec{p}(n)} \right\| }^2}}}} \ge + \infty \end{aligned}$$
(35)

which is different from (28) in the Zoutendijk criteria. So the assumption \(\mathop {\lim }\limits _{n \rightarrow \infty } \inf \left\| {\varvec{s}(n)} \right\| \ge \delta \) is wrong.

Since \(\mathop {\lim }\limits _{n \rightarrow \infty } \inf \left\| {\varvec{s}(n)} \right\| = 0\) is guaranteed, the convergence of the proposed algorithm can be obtained, and its convergence is further verified by simulation experiments.

3.4 Computational Complexity and Memory Usage of KGHCG

According to the complete idea of the proposed algorithm KGHCG, Table 1 shows its computational complexity comparison with KLMS [20], KRMC [35], KRMC-VC [22], and KRGMC [39] at the Nth iteration. Due to its simple structure, although KLMS [20] has the smallest computational complexity, the prediction accuracy and convergence speed are the worst. Because of the introduction of variable centers c, the number of additions, multiplications, and divisions of KRMC-VC [22] is \(L+2\) (L is the number of sliding data), L, and 1 more than that of KRMC [35], respectively. Although the division operation increases at each iteration compared with KRMC [35] and KRMC-VC [22], the coefficient of \(O(N^2)\) of KGHCG is smaller, and computational complexity of KGHCG is still lower than their cost. In comparison with KRGMC [39] and KGHCG based on GCC and its variation GHC, the recursive calculation of the former consumes the largest computational burden, and the latter KGHCG based on the CG method has excellent performance at a low computational burden. It has \(2{N^2} + 8N\) additions, \(2{N^2} + 10N +2\) multiplications, and 3 divisions.

Overall, the computational complexity of the proposed KGHCG is in the middle of other algorithms, and its convergence speed and prediction capability are comparable to those of algorithms based on recursive calculation. When all algorithms are sparse, their computational complexity uses the number of dictionaries D instead of N, with no extra cost for additions, multiplications, and divisions.

Table 1 Computational complexity of different models
Full size table

Furthermore, memory usage depends on the size of the kernel matrix of the online algorithms. Specifically, KLMS [20] requires O(N) memory. The order of memory required for KRMC [35], KRMC-VC [22], and KRGMC [39], and KGHCG is \(O(N^2)\). When the dictionary size \(D<<N\), KGHCG-VP and other sparse algorithms need less memory budget, and their order is \(O(D^2)\).

4 Experimental Results

In this section, the robustness of KGHCG algorithm and its sparse version KGHCG-VP will be verified in three time series. One of them is the benchmark MG chaotic time series with alpha-stable, and the others are real-world datasets with ENSO time series and Beijing air quality time series. In addition, a variety of online algorithms, including KLMS [20], KRMC [35], KRGMC [39], KRMC-VC [22], KRMC-ALD, KCG-AC [37], and QKRGMC [30], are used to compare with proposed online algorithms to evaluate the superior performance.

For the online prediction algorithm, its goal is to effectively improve the convergence speed while ensuring the accuracy of time series prediction. As a result, the complexity of the algorithm is characterized by dictionary size, training, and testing time. MSE, root MSE (RMSE), symmetric mean absolute percentage error (SMAPE), and \(R^2\) are used to describe the prediction accuracy, which are given by

$$\begin{aligned} \begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {\mathrm{{MSE}} = \frac{1}{N}\sum \limits _{n = 1}^N {{{(y(n) - d(n))}^2}} }\\ {\mathrm{{RMSE}} = \sqrt{\frac{1}{N}\sum \limits _{n = 1}^N {{{(y(n) - d(n))}^2}} } }\\ {\mathrm{{SMAPE}} = \frac{{100\% }}{N}\sum \limits _{n = 1}^N {\frac{{2\vert {{y(n)} - {d(n)}} \vert }}{{\vert {{y(n)}} \vert + \vert {{d(n)}} \vert }}} }\\ {R^{2} = 1 - \frac{{\sum \limits _{n = 1}^N {{{\left( {y(n) - d(n)} \right) }^2}} }}{{\sum \limits _{n = 1}^N {{{\left( {d(n) - \bar{d}} \right) }^2}} }}} \end{array}} \right. \end{array} \end{aligned}$$
(36)

where d(n) and y(n) stand for the actual value and the estimated value, \({\bar{d}}\) stands for the average of the actual value, and N stands for the size of the samples.

4.1 Mackey–Glass Time Series

In this part, the benchmark MG chaotic time series is considered to investigate the influence of non-Gaussian noise for the proposed methods, and it is calculated by the nonlinear differential equation:

$$\begin{aligned} \frac{{{\textrm{d}}x(t)}}{{{\textrm{d}}t}} = 0.9x(t) + \frac{{0.2x(t - \zeta )}}{{1 + x{{(t - \zeta )}^{10}}}} \end{aligned}$$
(37)

where \(\zeta = 17\) and the initial value is 0.5. The anti-noise ability of KGHCG algorithm is demonstrated by adding alpha-stable noise (the characteristic exponent is 1.8, the skewness is 0.5, the scale and location are 0.0001 and 0.2). In the online task, we make the past 10 steps \(x(k),x(k -1),\ldots ,x(k -9)\) to predict the next 5 step \(x(k+5)\). And the shapes of training samples and clean testing samples are 1500*10 and 500*1, respectively.

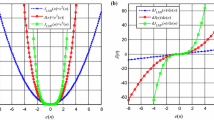
In the first trial, we explore the influence of the shape parameter \(\alpha \) on GCC and the proposed GHC criteria with non-Gaussian noise, and we set both the Gaussian kernel width \(\sigma \) and the scale parameter \(\beta \) to 1. Then, we plot the variation of the steady-state MSE with \(\alpha \in [1,3]\). As shown in Fig. 2, the filtering accuracy of the proposed GHC-based KGHCG algorithm dramatically outperforms the competitor in most conditions of \(\alpha \). In particular, the steady-state MSE of the proposed KGHCG is the smallest at \(\alpha = 2.25\).

Fig. 2
figure 2

The influence of the shape parameter \(\alpha \) under GCC and proposed GHC for MG chaotic time series with alpha-stable noise

Full size image

Furthermore, we explore the effects of the shape parameter \(\alpha \) and the scale parameter \(\beta \) of KGHCG. Considering \(\alpha ,\beta \in \left[ {1,4} \right] \), the grid search method is utilized to find the optimal parameter combination. We take the last 300 sets of data from the training set as the validation set and visualize the RMSE index to evaluate the prediction results of KGHCG in Fig. 3. It clearly shows that there is a positive correlation between parameter \(\beta \) and the RMSE index, and the value of RMSE increases after slightly decreases for parameter \(\alpha \) alone. Finally, when the optimal \(\alpha \) and \(\beta \) values are 2.25 and 1, the RMSE value of KGHCG reaches a minimum of 0.0439.

Fig. 3
figure 3

Error situations under different \(\alpha \) and \(\beta \) by KGHCG for MG chaotic time series with alpha-stable noise

Full size image
Table 2 Parameters setting of different methods for MG chaotic time series (\(\eta \) is the step parameter. \(\gamma \) is the regularization factor. \(\sigma '\) is the bandwidth of the correntropy. \(\alpha \) is the shape factor. \(\beta \) is the scale factor. c is the center location of the kernel. L is the number of sliding data. \(\nu \), \(\xi \) and \(\tau \) are the predefined threshold. \(\varepsilon \) is the quantization size)
Full size table

In the second trial, the robustness of KGHCG and KGHCG-VP is investigated by comparing the two groups, namely basic algorithms and sparse algorithms. Table 2 provides parameters setting of all online algorithms. As shown in Fig. 4, the convergence performance of different algorithms is visualized, and simulation results of different methods are obtained in Table 3. Based on the above experimental results, one can get the following conclusions:

  1. (1)

    Due to the poor adaptability of MSE to alpha-stable noise, KLMS [20] has the weakest convergence performance. In addition, compared with KRMC [35], KRGMC [39], and KRMC-VC [22], the proposed KGHCG, which combines GHC criterion and CG method, has the strongest adaptability to non-Gaussian noise in Fig. 4a.

  2. (2)

    Combining Fig. 4b and Table 3, KGHCG-VP, which introduced the sparse technique VP, can stably converge to the minimum value compared with the other three sparse algorithms under the condition that the dictionary is approximately the same. RMSE, SMAPE, and \(R^2\) of KGHCG-VP are 0.0502, 0.0427, and 0.9507, respectively, following KGHCG and still superior to KLMS [20], KRMC [35], KRGMC [39], and KRMC-VC [22]. Although the accuracy of KGHCG-VP is slightly lower than that of the original KGHCG, computation time is significantly shortened and the predicting speed is accelerated.

  3. (3)

    By observing prediction curves and error distributions for the MG chaotic time series in Fig. 5, KGHCG-VP can effectively track the change of the MG chaotic time series with excellent fitting results, and its final error distributions present the characteristics of a normal distribution. From the perspective of sparsity, KGHCG-VP can generate a compact dictionary structure and still maintain good prediction performance.

Fig. 4
figure 4

a Average learning curves of basic algorithms. b Average learning curves of sparse algorithms for MG chaotic time series with alpha-stable noise

Full size image
Table 3 Simulation results of different methods for MG chaotic time series
Full size table
Fig. 5
figure 5

Prediction curves and error distributions of KGHCG-VP for MG chaotic time series with alpha-stable noise

Full size image

4.2 El Nino-Southern Oscillation Time Series

The ENSO dataset is one of the most significant and widely influential chronological climate signals in the Earth’s system and has been proven to contain potentially chaotic properties [32]. Therefore, the accurate study of it not only contributes to the early warning of meteorological disasters, but also provides important assistance for the prediction of future climate trends. Hence, climate and sea surface temperature indicators are utilized to make a five-step prediction of the Nino 3.4 indicator. According to the phase space reconstruction theory (PSRT), we use the C-C method to reconstruct 1452 groups of ENSO datasets including monthly Pacific Decadal Oscillation and Southern Oscillation Index, Nino 1.2, Nino 3, Nino 3.4, and Nino 4 from January 1900 to December 2020 from the National Oceanic and Atmospheric Administration (http://www.psl.noaa.gov/gcos_wgsp/Timeseries/), and calculate that the embedding dimension and the delay time are [2, 2, 2, 2, 3, 3] and [4, 4, 3, 3, 4, 3], respectively. After that, we split the reconstructed data into training samples and testing samples with a ratio of 4:1.

Table 4 Parameters setting of different methods for ENSO time series ( \(\eta \) is the step parameter. \(\gamma \) is the regularization factor. \(\sigma '\) is the bandwidth of the correntropy. \(\alpha \) is the shape factor. \(\beta \) is the scale factor. c is the center location of the kernel. L is the number of sliding data. \(\nu \), \(\xi \) and \(\tau \) are the predefined threshold. \(\varepsilon \) is the quantization size)
Full size table
Fig. 6
figure 6

a Average learning curves of basic algorithms. b Average learning curves of sparse algorithms for ENSO time series

Full size image

For ENSO time series prediction, the parameters setting of different methods is shown in Table 4. Real-world datasets are often polluted by various adverse factors, which can degrade the performance of prediction models. Therefore, we demonstrate the adaptability and scalability of the proposed algorithms in natural environments by visualizing the testing MSE of different online algorithms for the prediction of Nino 3.4.

  1. (1)

    As shown in Fig. 6, whether the online algorithms are sparse or not, the testing MSE of KGHCG has the best convergence performance, followed by KGHCG-VP, and its stability gradually shows over time.

  2. (2)

    Table 5 summarizes the simulation results by different algorithms for the ENSO time series. Compared with the KGHCG algorithm, the testing time of KGHCG-VP significantly slumped by 66.3\(\%\). Although the prediction accuracy is slightly decreased, it is worth sacrificing tiny precision for a significant speedup in online tasks. In other words, KGHCG-VP has both low computational cost and high prediction accuracy. The prediction curves in Fig. 7 further confirm the high adaptability of the proposed algorithms on the ENSO dataset.

  3. (3)

    Error boxplots and scatter plots are drawn after each iteration, respectively, and the prediction accuracy is visually judged from Figs. 8 and 9. What is clearly presented in Fig. 8 is that the error range and the normal distribution curve of the proposed KGHCG and KGHCG-VP are small and concentrated. In addition, although the regression lines and baselines of KRGMC [39], KGHCG, KCG-AC [37], and KGHCG-VP have a small gap, KGHCG has the highest prediction accuracy, followed by KGHCG-VP when the \(R^2\) index and scatter distribution are considered at the same time.

Fig. 7
figure 7

Prediction curves and error distribution by KGHCG-VP for ENSO time series

Full size image
Fig. 8
figure 8

Boxplots and distributions of prediction errors by different methods for ENSO time series. The left side is the error boxplot, and the right side is the normal curve of error distributions. The black rectangle represents the median error. The shorter the height of the boxplot on the left, the closer the median is to zero, the smaller the vertical range of the error distribution curve on the right, and the fatter the horizontal range near the zero value, indicating the higher the prediction accuracy of the model

Full size image
Fig. 9
figure 9

Scatter plots of predicted and observed Nino3.4 by different methods for ENSO time series. The solid blue line is the regression line, and the dashed black line is the 1:1 baseline. The smaller the angle between the regression line and the baseline, the higher the prediction accuracy of the model

Full size image
Table 5 Simulation results by different methods for ENSO time series
Full size table

4.3 Beijing Air Quality Time Series

To further validate the efficacy of the proposed KGHCG-VP algorithm on large samples, we design multi-step prediction experiments using different sparse algorithms. In practical meteorology, the changes of atmospheric pollution concentrations are highly nonlinear and chaotic, and accurate prediction of them has an important effect on the improvement of human health and environmental quality. Therefore, we use the Beijing air quality time series to forecast PM2.5 concentration. Among them, the input variables are hourly PM2.5, PM10, SO2, NO2, O3, and CO in 2021. The output target is PM2.5 index and the horizons are one-step, five-step, and ten-step prediction. Through PSRT, the embedded dimension and delay time are calculated as [3,3,3,3,4,4] and [10,10,10,10,8,10], respectively. After that, we select 80\(\%\) of the reconstructed 8000 datasets as the training set and the rest as the testing set.

Table 6 Parameters setting of different methods for Beijing air quality time series ( \(\eta \) is the step parameter. \(\gamma \) is the regularization factor. \(\sigma '\) is the bandwidth of the correntropy. \(\alpha \) is the shape factor. \(\beta \) is the scale factor. c is the center location of the kernel. L is the number of sliding data. \(\nu \), \(\xi \) and \(\tau \) are the predefined threshold. \(\varepsilon \) is the quantization size)
Full size table

For the Beijing air quality time series, the parameters setting of different sparse algorithms is shown in Table 6. Table 7 summarizes simulation results for multi-step-ahead PM2.5 prediction. Obviously, compared with the KGHCG algorithm that loads complete dictionaries into the model, KGHCG-VP effectively filters the input data according to the sparsification strategy. Finally, a compact dictionary of size 250 is generated, which greatly improves computational efficiency and facilitates fast real-time prediction. For comparison of prediction precision, RMSE and \(R^2\) of KGHCG-VP are consistently excellent. On the contrary, the SMAPE indicator performs poorly. Therefore, we further calculate the change rate between different horizons of SMAPE and obtain the conclusion that the change rate of KGHCG-VP from five step to ten step is the smallest (12.17\(\%\)). Combining the testing time, RMSE, and \(R^2\), KGHCG-VP can still maintain high prediction accuracy while shortening the operation time.

In addition, we plot the variation trend of \(R^2\) under different steps in Fig. 10. It is intuitively observed that KGHCG-VP has the highest prediction accuracy for one-step prediction, and the change between different steps is the smallest. By calculating the change rates of \(R^2\) regarding all sparse algorithms, the change rates of KGHCG-VP are the smallest, which are 23.84\(\%\) and 55.82\(\%\), respectively. The numerical results are consistent with the observed results, which proves the superiority of the proposed algorithm.

Finally, we also visualize the learning curves of different sparse algorithms for multi-step prediction of the PM2.5 indicator in Beijing, and we conclude from Fig. 11 that the prediction accuracy gradually decreases as the prediction range increases, but the fitted curve of KGHCG-VP is still superior to the competitors. Especially in the prediction of ten-step, KGHCG can effectively track the changes of time series, which further demonstrates the efficiency of the algorithm.

Table 7 Simulation results of different sparsity methods for Beijing air quality time series
Full size table
Fig. 10
figure 10

The \(R^2\) index of different sparse methods for multi-step prediction of PM2.5 concentration in Beijing

Full size image
Fig. 11
figure 11

Prediction curves of different sparsity methods for multi-step prediction of PM2.5 concentration in Beijing

Full size image

5 Conclusion

This paper proposes a robust KGHCG algorithm. To be specific, our work is the first to develop a GHC criterion applied to KAF, which utilizes HQ optimization to cope with the nonconvex property of the GCC function. After that, the usage of the CG method has a positive effect on the convergence performance and prediction accuracy of KGHCG. In addition, the KGHCG-VP algorithm using the sparse strategy can resist the non-Gaussian noise while reducing the computational burden significantly. Experimental results show that KGHCG and its sparse variants have superior performance for online prediction tasks.

In our future work, we will consider the combination of KAF and evolving fuzzy systems to design an approach with strong structural adaptation and excellent adaptability in non-Gaussian noise environments. In addition, proper sparsification methods will also enhance the online prediction performance of the model, which is worthy of further study.