Adaptive Sparse Quantization Kernel Least Mean Square Algorithm for Online Prediction of Chaotic Time Series

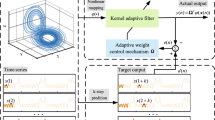
Abstract

Kernel least mean square (KLMS) algorithm is a popular method for time series online prediction. It has the advantages of good robustness, low computational complexity, model simplicity and online learning ability. Unfortunately, as input data grows, the dictionary size increases and the computational complexity raises significantly. In addition, how to improve the adaptability in time-varying environments with noise is also one of the main challenges. Therefore, we propose an improved KLMS algorithm from sparse perspective in response to the above problems, called adaptive sparse quantization kernel least mean square (ASQ-KLMS) algorithm. In the new model, sequential outlier criterion for sparsification and weights adaptive adjustment are combined with coherence criterion and quantization to form ASQ-KLMS algorithm. Firstly, it makes full use of effective information and ignores the interference of abnormal information to obtain a more accurate and compact dictionary. Then, a good balance between algorithm efficiency and accuracy can be achieved by controlling the choice of parameters. In addition, it can adaptively adjust weights in time-varying environment. At last, the Lorenz chaotic time series, the ENSO chaotic time series and the Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series are used to prove the reliability of the ASQ-KLMS algorithm.

1 Introduction

Online prediction of chaotic time series has been widely applied to various fields, including medicine systems, biomedicine, environment, engineering [4, 11, 13, 26, 32], etc. In practical prediction applications, most time series are nonlinear and require online processing, such as stock trend forecasting, real-time traffic flow prediction, and real-time monitoring of air quality. This real data generally contains noise. Therefore, it is highly desirable to have an anti-noise online prediction algorithm that has fast and accurate computing ability.

In the time series online prediction field, some methods based on nonlinear models, for example, dynamic neural networks [29, 39], online support vector regression (Online SVR) [14] and kernel adaptive filter (KAF) algorithms [2, 18, 34] have been proposed. Among these methods, dynamic neural network can improve the offline model network structure, and achieve dynamic update, but it is computationally intensive and easy to fall into local optimum. Online SVR and KAF algorithms are the classical kernel methods, which has the advantages of the kernel method and can handle time series prediction problems with nonlinear characteristics. The kernel method is an effective method to solve the nonlinear time series prediction problem. The Mercer core in reproducing kernel Hilbert space (RKHS) [1] is continuous, positive definite and reproducible which are desirable properties. Based on these properties, we cannot update the weight vector (it is also uncalculated in high-dimensional space), and use the Mercer kernel to expand the kernel function mapped to the high-dimensional space into the form of eigenvalues and eigenvectors. The output after mapping to the RKHS space is obtained, thereby realizing the combination of the kernel method and the SVR or the adaptive filter. However, it is necessary to continuously add new samples and update the model in online prediction of chaotic time series. The ever-increasing sample size and the amount of computation required for model updates pose significant challenges to the computational efficiency of online kernel methods.

As we know, Liu et al. [18] make a comprehensive introduction to the KAF algorithms. The KAF algorithms use a linear adaptive filtering algorithm in RKHS to implement nonlinear signal processing [12]. The KAF algorithms can adaptively update the model and are applied to many areas [40]. When new samples are acquired, it can be updated in recursive increments for online prediction. In addition, it solves nonlinear problems by using kernel mapping [6], which reduces computational complexity and can effectively solve time series online prediction problem with nonlinear characteristics. The KAF algorithms generally include KLMS [16] algorithm, kernel affine projection algorithm (KAPA) [17], kernel recursive least squares (KRLS) [5], and so on. The KAF algorithms are suitable for small samples, nonlinear modeling, and online recursive updating. However, it is necessary to continuously add new samples and update the model in online prediction of chaotic time series. The amount of calculation raises significantly when the sample size and the nuclear matrix dimension increase.

Among them, the KLMS algorithm is a typical kernel adaptive filter algorithm that Liu et al. proposed [16]. The KLMS algorithm has the advantages of good computational robustness and model simplicity. It has a good application prospect for online prediction of chaotic time series. But one of its main challenges is that the size of dictionary and the computational complexity increases dramatically with input data increasing [10]. If the real data contains outliers as training data, this will greatly reduce the accuracy of the prediction [21, 23]. Therefore, the ability to track the time-varying characteristics of the time series and the anti-noise ability in the dynamic environment needs to be improved.

Based on the above discussions, we improve the KLMS algorithm from the sparse perspective. In this paper, first, the outlier is eliminated using sequential outlier criterion to prevent it from being accepted as a new center, and then, the coherence criterion is added to the quantized kernel least mean square (QKLMS) [3] algorithm. The quantization method establishes a standard that distinguishes whether the data is informative or redundant. Redundant data is quantified to its nearest center. It can be said that we have fully explored the informative nature of the data. It also reduces the size of the dictionary, which decreases the complexities of computation. Moreover, a good trade-off between algorithm efficiency and accuracy is achieved by controlling the choice of parameters. In addition, we consider adding weight adaptive adjustment to the algorithm to improve the noise immunity of KLMS in the time-varying environment. In this process, the weight coefficients is adaptively adjusted, which obviously improves the dynamic tracking ability. Finally, the validity of the algorithm is verified in the Lorenz, ENSO and Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series for online prediction.

The remainder of this paper is structured as follows. Section 2 presents the relevant research progress of KLMS and sparse methods, and points out the current problems. Section 3 briefly introduces the KLMS algorithm and quantization method. Section 4 gives the detailed introduction and explanation of the relevant parts of the algorithm and the ASQ-KLMS algorithm. Section 5 presents the simulation results for online prediction of chaotic time series to demonstrate the effectiveness of ASQ-KLMS algorithm. Section 6 provides a conclusion and points out the prospects for further research.

2 Background and Related Works

2.1 Chaotic Time Series and Applications

Chaos refers to the uncertain signal generated in the deterministic system, which is similar to the random signal to a certain extent. Chaos is not simply disorder, but has no obvious periodicity and symmetry, but it is an ordered structure with rich internal levels, and is a new form of existence in nonlinear systems. The discrete situation of chaos is often expressed as chaotic time series. In chaotic time series modeling research, phase space reconstruction is a key step in system modeling [9]. According to the Takens embedding theorem [22], the chaotic dynamic system can be reconstructed from the time series and reproduce the evolution information of the chaotic system, providing strong support for accurate prediction.

Modeling and forecasting chaotic time series with multiple variables, noise and non-stationary is a current research hotspot. For chaotic time series containing multivariate, Zhang et al. [35] used principal component analysis (PCA) to perform dimensionality reduction and feature extraction on 13 local physical factors, and used the reduced fusion features as the input of a multi-layer perceptron to achieve a wide range of short-term rainfall predictions. For noisy chaotic time series, Lu et al. [20] constructed a new robust loss function by considering the mean and variance of the sample, which increases the noise immunity of the model to a certain extent. For non-stationary signals, Sharma et al. [27] proposed a Hank matrix-based eigenvalue decomposition, which can decompose the positive and negative frequency components of complex signals separately, and its performance is better than the comparison method.

2.2 Online Sparse Methods

In the past ten years, many scholars have proposed several improved KLMS algorithms and applied them to the field of time series online prediction. In 2008, C. Richard et al. [25] first added the normalization criterion into the KLMS algorithm, effectively reducing the size of the learning dictionary. And since then, Chen et al. [3] used the quantization method to reduce the input space dimension, and proposed the QKLMS algorithm in 2012. In the same year, M. Yukawa et al. [34] studied the multi-core algorithm and added a weighted norm penalty to the original. A sparse multi-nuclear normalized least mean square algorithm based on coherent criteria was proposed. Chen et al. [37] proposed the QKLMS algorithm based on fixed memory budget (FB-QKLMS) in 2013. It adds a rejection mechanism that limits the size of the dictionary and enables tracking time-varying features. In 2014, Gao et al. [8] proposed a kernel least mean square algorithm with the norm regularization FOBOS-KLMS algorithm. Then, Van Vaerenbergh et al. [7] proposed the probability least mean square (ProbLMS), which adds Bayesian machine learning to adaptive filtering. Zhao et al. [38] simplified the normalized variable step size and proposed a decorrelated kernel least mean square (DKLMS) algorithm in 2017. Zhang et al. [36] proposed a sequential outlier criterion to limit the interference of outliers in 2018. This method gives two conditions for judging whether the information is an abnormal value, and improves the anti-noise ability of the system. In 2018, Liu et al. [19] proposed the reduced Gaussian kernel least mean square (RGKLMS) algorithm, which avoids the continuous growth of weighted networks in non-stationary environments through implicit feature maps. In 2019, the kernel least mean square based on the Nystrom method (NysKLMS) proposed by Wang et al. [33] can significantly reduce the computational complexity.

In addition, some online sparse methods have been proposed to suppress the dictionary growth in the learning process, for example, an algorithm with a fixed dictionary size is studied in [28, 30]. The novelty criterion (NC) proposed in [24] proposes two constraints to suppress the growth of the dictionary. An approximate linear dependency (ALD) is proposed in [5] to verify the linear dependency between the new data and the elements in the dictionary, and if the approximation is irrelevant, the input is added to the dictionary. The coherence criterion (CC), which limits the size of the dictionary based on the similarity of the input, has been described in [25]. In the online sparse method based on the surprising standard (SC) [15] of Gaussian process, the information content of samples is quantified as a surprise, which can prevent outliers from being used as new centers, thereby a more reliable network will be obtained. Chen et al. [3] used quantization conditions to determine and quantify redundant data for network coefficient updates, thus taking advantage of more efficient information. Sequential outlier criterion (SOC) established the measurement of sample information based on the historical data sequence information, and then, the learning system processes the information measurement samples according to the sample information, redundancy or exception.

However, the form of the above sparse methods is very simple, only one aspect is considered, and the characteristics of the nonlinear system cannot be described comprehensively. Therefore, there is still room for improvement in these algorithms. In addition, KLMS and the extended algorithm based on sparse method are very sensitive to time-varying environments with noise, so it needs to improve the anti-noise ability of the model.

In the above-mentioned sparse methods, we find that the SOC criterion showed good ability to exclude outliers. KLMS-CC [25] and QKLMS show excellent predictive power, efficiency and nonlinear fitting ability. Combining the advantages of the above sparse methods, the ASQ-KLMS algorithm is proposed for online prediction of chaotic time series.

Table 1 shows an explanation of the parameters used in the ASQ-KLMS algorithm.

Table 1 The explanation of the parameters

3 Preliminary

3.1 Kernel Least Mean Square

The KLMS algorithm is suitable for online learning. It is a generalized and evolved form of the traditional least-mean-square (LMS) method in kernel space. The KLMS algorithm maps the input into a high-dimensional feature space by introducing a kernel function based on this linear method, retains the nonlinear characteristics of the data, and then uses a simple linear LMS method for online prediction in the kernel space.

$\mathbf{{X}}$ is the input data, then there is a nonlinear mapping $\Omega :\mathbf{{X}} \rightarrow \mathbf{{F}}$, the original data is mapped to the feature space and then the LMS algorithm linearly filters the converted data $\Omega \left( \mathbf{{x}} \right)$, $\mathbf{{x}} \in \mathbf{{X}}$. When the time step is n, the system output is expressed as

$$\begin{aligned} \mathbf{{y}}\left( n \right) = {{\varvec{\alpha }}_{n - 1}}^T\Omega \left( {\mathbf{{x}}\left( n \right) } \right) \end{aligned}$$

(1)

where $\mathbf{{x}}(n) \in \mathbf{R}^{M}$ is the input vector, $\mathbf{{y}}(n) \in \mathbf{R}$ is the output of the system, ${{{\varvec{\alpha }}}_n}$ is the weight vector.

In the LMS method, the update of the weight vector can be calculated by

$$\begin{aligned} {{{\varvec{\alpha }}}_n} = {{{\varvec{\alpha }}}_{n - 1}} + \eta \cdot \mathbf{{e}}\left( n \right) \Omega \left( {\mathbf{{x}}\left( n \right) } \right) \end{aligned}$$

(2)

where $\mathbf{{e}}$ means the prediction error at the n-th iteration, $\eta$ represents the step size, and $\Omega (\mathbf{{x}}(n))$ represents the conversion of the input $\mathbf{{X}}$ to the feature space $\mathbf{{F}}$. The weight vector ${{{\varvec{\alpha }}}_n}$ can be represented by the following equation:

$$\begin{aligned} {{{\varvec{\alpha }}}_n} = \eta \sum \limits _{i = 1}^n {\mathbf{{e}}\left( i \right) } \Omega \left( {\mathbf{{x}}\left( i \right) } \right) \end{aligned}$$

(3)

Nonlinear mapping can be implemented by means of kernel functions.

$$\begin{aligned} {{\varvec{\kappa }}}\left( {\mathbf{{x}}\left( i \right) ,\mathbf{{x}}\left( j \right) } \right) = \Omega {\left( {\mathbf{{x}}\left( i \right) } \right) ^T}\Omega \left( {\mathbf{{x}}\left( j \right) } \right) \end{aligned}$$

(4)

Therefore, the filter output of KLMS is given by

$$\begin{aligned} \mathbf{{y}}\left( n \right) = \eta \sum \limits _{i = 1}^{n - 1} {\mathbf{{e}}\left( i \right) {{\varvec{\kappa }}}\left( {\mathbf{{x}}\left( i \right) ,\mathbf{{x}}\left( n \right) } \right) } \end{aligned}$$

(5)

Kernel functions [31] provide a convenient way to solve complex nonlinear regression problems. We choose the Gaussian kernel as the kernel function to complete the output calculation. It is expressed as

$$\begin{aligned} {{\varvec{\kappa }}}\left( {\mathbf{{x}}\left( i \right) ,\mathbf{{x}}\left( j \right) } \right) = exp\left( { - \frac{{{{\left\| {\mathbf{{x}}\left( i \right) - \mathbf{{x}}\left( j \right) } \right\| }^2}}}{{2{\sigma ^2}}}} \right) \end{aligned}$$

(6)

where $\sigma$ denotes the kernel width.

3.2 Quantization

The quantization method represents the original input data using a smaller body. It does not directly discard the judged redundant input by the sparse correlation condition, but uses the quantization condition to judge, and quantizes the redundant variable for the network coefficient update, thereby utilizing more valid information. The objective function of QKLMS is defined as

$$\begin{aligned} \min \sum \limits _{i = 1}^n {\left| {\mathbf{{y}}\left( i \right) - {{{\varvec{\kappa }}}^T}\left( {{{\varvec{\mathrm{B}}}}\left( {i - 1} \right) ,\mathbf{{x}}\left( i \right) } \right) \cdot {{{\varvec{\alpha }}}_i}} \right| } \end{aligned}$$

(7)

where ${{\varvec{B}}}\left( \cdot \right)$ is the model dictionary. At the n-th iteration,${{\varvec{B}}}\left( n \right) = \mathrm{{O}}\left[ {\mathbf{{x}}\left( n \right) } \right]$,$O\left[ \cdot \right]$ is a quantization operator.

Chen et al. [3] proposed a simple online vector quantization method that satisfies the requirements of online prediction. They calculate the distance between $\mathbf{{x}}\left( n \right)$ and the dictionary $\mathbf{{B}}\left( {n - 1} \right)$:$dis\left( {\mathbf{{x}}\left( n \right) ,\mathbf{{B}}\left( {n - 1} \right) } \right) = \mathop {\min }\limits _{1 \le j \le size\left( {\mathbf{{B}}\left( {n - 1} \right) } \right) } \left\| {\mathbf{{x}}\left( n \right) - {\mathbf{{B}}_j}\left( {n - 1} \right) } \right\|$, where j means the j-th member of the dictionary $\mathbf{{B}}\left( {n - 1} \right)$, $\Vert \cdot \Vert$ denotes the Euclidean norm. If the calculated Euclidean distance is less than the set quantization parameter, the dictionary is not updated, $\mathbf{{B}}\left( n \right) = \mathbf{{B}}\left( {n - 1} \right)$, and the input data will be quantized to the ${\mathbf{{B}}_j}\left( {n - 1} \right)$. Otherwise, we will update the dictionary: $\mathbf{{B}}\left( n \right) = \mathbf{{B}}\left( {n - 1} \right) \cup \mathbf{{x}}\left( n \right)$, and it will become a new center in the existing dictionary.

Finally, the operation process of the QKLMS algorithm is described in detail in Algorithm 1.

4 Adaptive Sparse Quantization Kernel Least Mean Square Algorithm

In this section, we will introduce the reserve knowledge about our improved algorithm, and the ASQ-KLMS algorithm from the sparse perspective will be described in detail at the end.

4.1 Sequential Outlier Criterion for Sparsification

Generally, there are often some outliers in the actual data. When these outliers are used to update the network coefficients, the prediction accuracy will be seriously affected.

Therefore, Zhang et al. [36] proposed an online sparsification approach with sequential outlier criterion. Its major contribution is to propose conditions for checking whether new arriving data is an outlier. Based on historical data, there will be a range of expectations for new arriving datum. If this range is exceeded, we think the data is outlier.

The expected neighbor distance (END) and the expected neighbor direction vector (ENDV) are measures, which are used for determining whether data is an outlier or not. Given the information of all existing data, the END infers the reasonable distance of the neighbor data, and the ENDV infers the possible direction of the oriented data.

In the course of sequential learning, the END infers the expected distance from adjacent data. When an outlier occurs, the distance between the outlier and the previous data must be very large. Therefore, we use the END as one of the criteria to judge whether the data is an outlier or not. It is defined as

$$\begin{aligned} N D_{e}(n)=\sum _{i=1}^{n-2} \frac{2 i}{(n-2)(n-1)} \cdot d\langle {\mathbf {x}}(i+1), {\mathbf {x}}(i)\rangle \end{aligned}$$

(8)

where $d\langle {\mathbf{{x}}\left( {i + 1} \right) ,\mathbf{{x}}\left( i \right) } \rangle = \left\| {\mathbf{{x}}\left( {i + 1} \right) - {\mathbf {x}}\left( i \right) } \right\|$, and the main function of the coefficient $2i/(n-2)(n-1)$ is to give greater discourse power to the distance closer to the new data. The upper and lower bounds of the END for the n-th iteration are represented as

$$\begin{aligned} \left\{ \begin{array}{l}{B_{-} D_{\text {upper}}(n)=N D_{e}(n)+\lambda _{d} \sigma _{d}(n)} \\ {B_{-} D_{\text{ lower }}(n)=N D_{e}(n)-\lambda _{d} \sigma _{d}(n)}\end{array}\right. \end{aligned}$$

(9)

where $\lambda _d$ has different sizes according to different data sets. Its size determines the severity of the outlier determination conditions. $\sigma _{d}(n)$ is the standard deviation of $\{ d\langle {\varvec{x}}( {i + 1} ),{\varvec{x}}(i) \rangle ,i = 1,2,...,i - 2 \}$.

The ENDV establishes a historical vector trend based on the already existing data. When an outlier occurs, the difference between adjacent data vectors must be large. It is another criteria for judging whether the data is an outlier or not. The ENDV is described as

$$\begin{aligned} {\mathbf {N}} {\mathbf {V}}_{e}(n)=\sum _{i=1}^{n-2} \frac{2 i}{(n-2)(n-1)} \cdot \frac{[{\mathbf {x}}(i+1)-{\mathbf {x}}(i)]}{d\langle {\mathbf {x}}(i+1), {\mathbf {x}}(i)\rangle } \end{aligned}$$

(10)

where the coefficient $2i/(n-2)(n-1)$ is to give greater discourse power to the vector closer to the new data. The upper and lower bounds of the ENDV for the n-th iteration are represented as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{\mathbf {B\_}}{{\mathbf {V}}_{\text {upper}}} = {\mathbf {N}}{{\mathbf {V}}_e}\left( n \right) + {\lambda _v}{{{\varvec{\sigma }}}_v}\left( n \right) }\\ {{\mathbf {B\_}}{{\mathbf {V}}_{\text {lower}}} = {\mathbf {N}}{{\mathbf {V}}_e}\left( n \right) - {\lambda _v}{{{\varvec{\sigma }}}_v}\left( n \right) } \end{array}} \right. \end{aligned}$$

(11)

where $\lambda _v$ has different sizes according to different data sets. Its size determines the severity of the outlier determination conditions. $\varvec{\sigma }_{v}(n)$ is the standard deviation of $\left\{ {{{\left[ {{\mathbf {x}}\left( {i + 1} \right) - {\mathbf {x}}\left( i \right) } \right] } \big / {d\left\langle {{\mathbf {x}}\left( {i + 1} \right) ,{\mathbf {x}}\left( i \right) } \right\rangle ,i = 1,2,...,n - 2}}} \right\}$.

If the n-th data exceeds the specified range of END and ENDV, it will be considered as an outlier.

4.2 Coherence-sparsification Criterion

Correlation is a fundamental and effective indicator for detecting linear sparse approximations. In the past research, the dimensionality reduction of the kernel matrix by ALD conditions will be misjudged due to the inappropriate selection of thresholds, thus affecting the prediction effect. After that, the coherence coefficient was proposed as a standard by Richard et al. [25] in 2008. The coherence coefficient is written as

$$\begin{aligned} \mu \mathrm{{ = }}\mathop {\max }\limits _{i = 1,2,...,n} \left| {{{\varvec{\kappa }}}\left( {{\mathbf {x}}\left( n \right) ,{\mathbf {x}}\left( i \right) } \right) } \right| \le {\mu _0}\ \end{aligned}$$

(12)

where $\mu _{0}$ determines the size and sparseness of the sample dictionary, ${\mu _0} \in \left[ {0,1} \right]$. The calculation cost of the coherent criterion is not affected by the sample data, only depends on the size of the final dictionary. The calculation cost is small, and it can better measure the relationship between the input sample and the original sample dictionary; thus, the judgment of the input sample is more accurate.

4.3 Weight Adaptive Adjustment

If the input contains noise or sudden changes, or other factors that cause $\kappa _{n-1}$ to be very small, after updating $\alpha _{n}$, the effect will be amplified, even catastrophic. Therefore, we use the normalization strategy of Euclidean norm to improve the system adaptive ability. The weight can be updated:

$$\begin{aligned} {{\varvec{\alpha }}_n} = {{\varvec{\alpha }}_{n - 1}} + \frac{{\eta \cdot \left( {{\mathbf {y}}\left( n \right) - {\varvec{\kappa }}_{n - 1}^T{{\varvec{\alpha }}_{n - 1}}} \right) \cdot {{\varvec{\kappa }}_{n - 1}}}}{{\zeta + {{\left\| {{\varvec{\kappa }}_{n - 1}^T} \right\| }^2}}} \end{aligned}$$

(13)

where ${{\varvec{\kappa }}}_{n - 1} = {\varvec{\kappa }}\left( {{\mathbf {B}}\left( {n - 1} \right) ,{\mathbf {x}}\left( n \right) } \right)$ and $\zeta$ is a user-defined parameter whose purpose is to avoid the denominator being zero. This approach can significantly improve the ability of sequential learning systems to adapt to different data sets, especially those that contain noise and mutations.

4.4 ASQ-KLMS Algorithm

In order to achieve good performance, we combine the sequential outlier criterion, coherence-sparsification criterion and dynamic adjustment of weights with the quantization to form the ASQ-KLMS algorithm.

First, we use the sequential outlier criterion to determine whether the input is an outlier or not. If the current input data does not meet our given expected range, it will be discarded. Next, we combine quantization method with coherence criterion to determine whether input data is cached or not. The input data is cached when the current correlation coefficient does not exceed the threshold and the quantization condition is met. This greatly reduces the size of the dictionary, which helps to reduce the amount of calculations and speed up the calculation.

As we know, redundant data is fully utilized with quantization method, so that it still participates in the update of the weight coefficient. In addition, weight adaptive adjustment can improve the ability of KLMS to track time-varying features. This method can adaptively adjust coefficients according to input data, and improve the prediction accuracy in chaotic time online prediction.

The ASQ-KLMS algorithm is obtained from the sparse perspective, which can reduce computational complexity by limiting matrix dimensions and make full use of redundant information, so it can improve the calculation efficiency and prediction accuracy.

The specific steps of the ASQ-KLMS algorithm are described as follows:

First, calculate Eqs. (9) and (11). Then, we will make the following judgment.

• Case 1: If the neighbor distance and direction vector are outside the corresponding range, we will assume that the data is an outlier, then it will be discarded and we will continue to detect the next data.

• Case 2: If $dis\left( {{\mathbf {x}}\left( n \right) ,{\mathbf {B}}} \right) > \varepsilon$ and the coherence coefficient is less than threshold $\mu _{0}$, then it will become a member of the dictionary and become a new center. And update weight coefficient ${{\varvec{\alpha }}_n}$ using Eq. (14).

• Case 3: If $dis\left( {{\mathbf {x}}\left( n \right) ,{\mathbf {B}}} \right)$ is no more than $\varepsilon$, we suppose that this data is redundant, then the dictionary will not change: ${\mathbf {B}}\left( n \right) = {\mathbf {B}}\left( {n - 1} \right)$. And ${\mathbf {x}}\left( n \right)$ will be quantized to the j-th center: ${{\mathbf {B}}_j}\left( n \right) = \mathrm{{O}}\left[ {{\mathbf {x}}\left( n \right) } \right]$. And ${{{\varvec{\alpha }}}_n}$ is updated as (15).

• Case 4: If none of the above three conditions are met, it means that the input data is linearly related to the data in the current dictionary. So, it is considered as redundant data and discarded, and keep the existing dictionary unchanged. In this case, the weight coefficient will be dynamically adjusted and it will be calculated as shown in (16).

Finally, the output is calculated using Eq. (17).

In summary, the operation process of the ASQ-KLMS algorithm is described in detail in Algorithm 2.

4.5 Computational Complexity

Table 2 Comparing the computational complexity of each iteration

Table 2 summarizes the computational complexity analysis of KLMS, QKLMS, KLMS-CSL1, KLMS-SOC and ASQ-KLMS algorithms, including the time complexity of updating ${{{\varvec{\alpha }}}_n}$ during training and computing $\mathbf{{e}}\left( n \right)$ during testing. For KLMS, QKLMS and KLMS-CSL1, the time complexity of updating ${{{\varvec{\alpha }}}_n}$ during training data is $O\left( n \right)$ , and the time complexity of calculating $\mathbf{{e}}\left( n \right)$ during testing is $O\left( n \right)$, $O\left( m \right)$, $O\left( l \right)$, respectively, where n is the size of the dictionary when the model is not sparsified. m and l are close, but both are smaller than n. For KLMS-SOC and ASQ-KLMS, the time complexity of updating ${{{\varvec{\alpha }}}_n}$ during training data is $O\left( {{n^2}} \right)$, and the time complexity of calculating B during testing is $O\left( k \right)$ and $O\left( k \right)$, respectively, where k is close to m and l, but k is much smaller than n.

5 Experimental Results

In this section, experiments will be used to illustrate the good performance of our proposed algorithm regarding chaotic time series prediction. Three time series will be used for the simulation experiment. The first group is the Lorenz time series, which is a set of benchmark data. The second group and the third group are actual time series, which are the ENSO chaotic time series and the Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series, respectively. At the same time, our proposed algorithm is compared with KLMS, QKLMS, KLMS-CSL1, KLMS-SOC algorithms. In order to prevent accidental situations, we performed ten simulation experiments on the three sets of data, and calculated the average value as the final result.

We will use the root mean square error (RMSE) and ${R^2}$ as the prediction accuracy evaluation indicators. The RMSE can be defined as

$$\begin{aligned} \mathrm{{RMSE}} = \sqrt{\frac{{\sum \limits _{n = 1}^N {{{\left( {\mathop \mathbf{{y}}\limits ^ \wedge \left( n \right) - \mathbf{{y}}\left( n \right) } \right) }^2}} }}{N}} \end{aligned}$$

(18)

where n means the time step, and N is the number of samples calculated. If a method performs time series prediction, the smaller the RMSE of the calculated result, the higher the prediction accuracy of the method in time series prediction.

The ${R^2}$ can be calculated as

$$\begin{aligned} {R^2} = 1 - \frac{{\sum \limits _{n = 1}^N {{{\left( {\mathop \mathbf{{y}}\limits ^ \wedge \left( n \right) - \mathbf{{y}}\left( n \right) } \right) }^2}} }}{{\sum \limits _{n = 1}^N {{{\left( {\mathbf{{y}}\left( n \right) - \mathop \mathbf{{y}}\limits ^ - } \right) }^2}} }} \end{aligned}$$

(19)

where $\mathop {\mathbf {{y}}}\limits ^ -$ denotes average number of predicted targets, and N is the number of samples calculated. The larger the ${R^2}$ of the calculated result, the higher the prediction accuracy of the method in time series prediction.

In order to better describe the prediction results, training time and testing time are used as indicators for calculating time.

Parameter optimization methods mainly include cross-validation and grid search methods. The algorithm parameter tuning in this paper uses grid search method. The main idea is to use the current parameters that have the greatest impact on the model until the optimization; tune the parameters, and so on, until all the parameters are adjusted. The steps of our proposed algorithm tuning are to first adjust the step size $\eta$ and kernel bandwidth$\sigma$ ; then adjust the parameters ${\lambda _d}$ and${\lambda _v}$ of the SOC method, discarding about 1$\%$-5$\%$ outliers; finally adjust the $\mu _{0}$ ,$\varepsilon$ and $\zeta$ .

5.1 Lorenz Chaotic Time Series

The Lorenz data set is a set of classical time series with chaotic characteristics. In this part, the validity of the proposed algorithm is verified. The simulation results of 2501 Lorenz three-dimensional data are used:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\frac{{dx}}{{dt}} = e(-x +y )}\\ {\frac{{dy}}{{dt}} = fx - y - xz}\\ {\frac{{dz}}{{dt}} = xy - gz} \end{array}} \right. \end{aligned}$$

(20)

where e = 10, f = 28, g = 8/3, and this time series is deteriorated by adding white Gaussian noise.

In the experiment, we use the C-C method to calculate and select the appropriate phase space reconstruction parameters. The delay time of the three-dimensional variables x, y, and z is selected as 8, 7, 8, and the embedding dimension is 6, 6, 6. After that, the first 80% of the samples are used for training, and the last 20% are used for testing. Table 3 shows the parameter settings for the 5-step prediction of the Lorenz-x time series.

Table 3 Parameters setting of 5-step prediction of Lorenz-x chaotic time series

Fig. 1

The training MSE of ASQ-KLMS algorithm in Lorenz-x chaotic time series

Fig. 2

Lorenz-x chaotic time series 5-step prediction curve and error curve using ASQ-KLMS algorithm

Figure 1 shows the training MSE of ASQ-KLMS algorithm in Lorenz-x chaotic time series. Figure 2 shows the 5-step prediction curve of Lorenz-x chaotic time series using ASQ-KLMS algorithm, and Table 4 shows 5-step prediction results of Lorenz-x time series by KLMS, QKLMS, KLMS-CSL1, KLMS-SOC and ASQ-KLMS algorithm.

The RMSE and ${R^2}$ are important evaluation indicators, and the training time and testing time are efficiency assessment indicators. From Fig. 1, we can see that the model is well trained and has good convergence. From Table 4, we can see that the ASQ-KLMS algorithm simulation results are satisfactory on these four indicators. The shortest testing time means that the algorithm constitutes the most accurate and compact dictionary, which greatly reduces the computational complexity. Therefore, ASQ-KLMS algorithm has high efficiency online prediction capability. Because the SOC criterion is adopted, the training time is sacrificed, but the model has good anti-noise ability. From prediction accuracy, the ASQ-KLMS algorithm performs better than the KLMS-SOC algorithm, which means that the ASQ-KLMS algorithm improves the KLMS-SOC algorithm. At the same time, in Fig. 2, the blue line represents the original data curve and the orange line represents the predicted value curve from the upper subgraph, and the prediction curve can follow the original curve well. In the next subgraph, we can see that the error curve has less fluctuation. Therefore, the ASQ-KLMS algorithm is considered to have good performance for online prediction.

5.2 ENSO Chaotic Time Series

The ENSO is the abbreviation of El Nino-Southern Oscillation. ENSO is a climatic phenomenon that exists in the equatorial sea. Among them, the Southern Oscillation refers to the reversed-pressure vibration occurring between the Southeast Pacific and the Indian Ocean and Indonesia. It is one of the most prominent and important phenomena in the interannual variation of the tropical circulation. El Nino is an abnormal phenomenon in which the sea surface temperature in the equatorial Pacific Ocean in the Middle East continues to rise abnormally. The Southern Oscillation and El Nino are interrelated. When the El Nino phenomenon occurs, the sea surface temperature rises, the Pacific water temperature rises, and the global atmospheric circulation changes, while the Southern Oscillation is the most direct change. The ENSO occurs approximately every two to seven years and lasts for several months. It is one of the main culprits for natural weather disasters such as floods. The catastrophic climate problems such as the Yangtze River floods and the southern blizzards that have occurred in China are inextricably linked to ENSO. Therefore, timely and accurate prediction of ENSO related index has important significance and practical application value. The Pacific Decadal Oscillation (PDO) phenomenon occurs every 10 years. Many scholars believe that PDO and ENSO have strong correlations. Therefore, this paper combines the PDO and ENSO indices into a set of time series prediction data for simulation experiments.

By above knowable, we use the National Oceanic and Atmospheric Administration (NOAA) website (http://www.psl.noaa.gov/gcos_wgsp/Timeseries/) to obtain the monthly Nino 1.2, Nino 3, Nino 4, Nino3.4, SOI index and PDO index from 1949 to June 2018, including 834 samples. The acquired data is in standard PSL format. The Lyapunov exponent indicates that the ENSO time series is chaotic. At the same time, we use the C-C method to calculate and select the appropriate phase space reconstruction parameters. The embedding dimension is selected as 3, 3, 4, 3, 4, and 4. The delay time of the six-dimensional variables is selected as 2, 2, 3, 3, 2, and 2.

Table 5 shows parameter setting of five-step prediction for NINO 3.4 index. After that, the first 80% of the samples are used for training and the last 20% are used for testing.

Table 4 Five-step online prediction test results of Lorenz-x chaotic time series

Table 5 Parameter setting of five-step prediction for NINO 3.4 index

Fig. 3

The training MSE of ASQ-KLMS algorithm in Nino 3.4 chaotic time series

Fig. 4

Nino 3.4 chaotic time series 5-step prediction curve using KLMS, QKLMS, KLMS-CSL1, KLMS-SOC algorithm

Fig. 5

Nino 3.4 chaotic time series 5-step prediction curve and error curve using ASQ-KLMS algorithm

Figure 3 shows the training MSE of ASQ-KLMS algorithm in Nino 3.4 chaotic time series. Figure 5 shows Nino 3.4 chaotic time series 5-step prediction curve using ASQ-KLMS algorithm. Table 6 shows 5-step prediction results of Nino 3.4 chaotic time series by KLMS, QKLMS, KLMS-CSL1, KLMS-SOC and ASQ-KLMS algorithm.

Table 6 Five-step online prediction test results of NINO 3.4 chaotic time series

From Fig. 3, we can see that the model is well trained and has good convergence. It can be seen from the simulation results in Table 6 that the ASQ-KLMS algorithm shows excellent performance. ENSO is the actual data that contains noise, so there will be outliers in the sequence. The ASQ-KLMS algorithm has SOC criterion and weight adaptive adjustment, so it has good anti-noise ability, and the simulation results also illustrate this point. Specifically, we can see that the ASQ-KLMS algorithm has the shortest test time, which means that it constitutes the most accurate and compact dictionary, which greatly reduces the test time and has higher prediction efficiency. In addition, the accuracy index predicted by the ASQ-KLMS algorithm is also superior to other algorithms in Fig. 4. Therefore, the ASQ-KLMS algorithm has been proven to have a good predictive effect on the ENSO chaotic time series. Simultaneously, the blue line represents the original data curve, and the orange line represents the predicted value curve from the upper subgraph in Fig. 5, the prediction curve can follow the original curve well. In the next subgraph, error curve fluctuations are small. So we can get a conclusion that the ASQ-KLMS algorithm has excellent effectiveness for online prediction of ENSO chaotic time series.

Table 7 Parameters setting of five-step prediction of Beijing $\hbox {PM}_{2.5}$ chaotic time series

Fig. 6

The training MSE of ASQ-KLMS algorithm in Beijing PM$_{2.5}$ chaotic time series

Table 8 Five-step online prediction test results of Beijing $\hbox {PM}_{2.5}$ chaotic time series

Fig. 7

Beijing PM$_{2.5}$ chaotic time series 5-step prediction curve using KLMS, QKLMS, KLMS-CSL1, KLMS-SOC algorithm

Fig. 8

Beijing PM$_{2.5}$ chaotic time series five-step prediction curve and error curve using ASQ-KLMS algorithm

5.3 Beijing $\text {P}{{\text {M}}_{2.5}}$ Chaotic Time Series

As we all know, continuous smog weather has occurred in many places, seriously affecting the health of residents. Therefore, it is urgent to increase air quality research, especially to monitor and predict air pollution. $\text {P}{{\text {M}}_{2.5}}$ is one of the important indicators used to measure air quality. Therefore, predicting the value of $\text {P}{{\text {M}}_{2.5}}$ has important practical significance. The Lyapunov exponent indicates that the Beijing $\text {P}{{\text {M}}_{2.5}}$ time series data is chaotic.

In this section, we conduct simulations on Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series which consists of hourly $\text {P}{{\text {M}}_{2.5}}$, $\text {P}{{\text {M}}_{\text {10}}}$, $\text {C}\text {O}$, $\text {N}{{\text {O}}_{\text {2}}}$, ${{\text {O}}_{\text {3}}}$, $\text {S}{{\text {O}}_{\text {2}}}$ in Beijing in 2019. The original data set is confirmed by the test station. This data set comes from the website of Beijing Environmental Protection Inspection Center (http://www.bjmemc.com.cn/). After preprocessing the data, a total of 8300 samples will be used for simulation experiments, the first 90% will be used to train the model, and the remaining 10% will be used for testing. The C-C method is used to calculate and select the appropriate phase space reconstruction parameters. And the embedding dimensions are 3, 3, 4, 3, 4, and 3, and the delay times are 10, 10, 10, 10, 8, and 10. Table 7 shows the parameters setting of five-step prediction of Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series.

Figure 6 shows the training MSE of ASQ-KLMS algorithm in Lorenz-x chaotic time series. Figure 8 shows Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series five-step prediction curve using ASQ-KLMS algorithm. Table 8 shows five-step prediction results of Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series by KLMS, QKLMS, KLMS-CSL1, KLMS-SOC and ASQ-KLMS algorithm.

From Fig. 6, we can see that the model is well trained and has good convergence. The simulation results in Table 8 show that the ASQ-KLMS algorithm performs well in both prediction accuracy and efficiency. The Beijing $\hbox {PM}_{2.5}$ chaotic time series is the actual data containing noise, so there will be abnormal values in the sequence. The ASQ-KLMS algorithm has SOC criterion and weight adaptive adjustment, so it has good anti-noise ability, and the simulation results also illustrate this point. Although we added a SOC criterion, we sacrificed a little training time. Fortunately, we have formed an accurate and compact dictionary, which greatly reduces the test time and has higher prediction efficiency. Therefore, the ASQ-KLMS algorithm has been proven to have a good predictive effect on the Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series in Fig. 7. In Fig. 8, the blue line represents the original data curve and the orange line represents the predicted value curve; the prediction curve can follow the original curve well. In the next subgraph, the prediction error curve has a small fluctuation range. Therefore, the ASQ-KLMS algorithm is proved to be effective in completing the online prediction of Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series.

6 Conclusion

In this paper, the coherence criterion and the weight adaptive adjustment integrated with the quantization method form our proposed ASQ-KLMS algorithm. Compared with the other four algorithms, the ASQ-KLMS algorithm forms a more accurate and compact dictionary, and the prediction efficiency and prediction accuracy are very good. In addition, it also has good tracking time-varying characteristics and has certain adaptive ability to noise. The experiments of the Lorenz, the ENSO and the Beijing $\text {P}{{\text {M}}_{2.5}}$ chaotic time series prove the effectiveness of the ASQ-KLMS algorithm.

In order to improve the ability to track time-varying characteristics, we consider combining KAF and recurrent neural networks, drawing on the advantages of each other, and adding appropriate sparse methods to improve prediction accuracy in the future.