A Reduced Gaussian Kernel Least-Mean-Square Algorithm for Nonlinear Adaptive Signal Processing

Abstract

The purpose of kernel adaptive filtering (KAF) is to map input samples into reproducing kernel Hilbert spaces and use the stochastic gradient approximation to address learning problems. However, the growth of the weighted networks for KAF based on existing kernel functions leads to high computational complexity. This paper introduces a reduced Gaussian kernel that is a finite-order Taylor expansion of a decomposed Gaussian kernel. The corresponding reduced Gaussian kernel least-mean-square (RGKLMS) algorithm is derived. The proposed algorithm avoids the sustained growth of the weighted network in a nonstationary environment via an implicit feature map. To verify the performance of the proposed algorithm, extensive simulations are conducted based on scenarios involving time-series prediction and nonlinear channel equalization, thereby proving that the RGKLMS algorithm is a universal approximator under suitable conditions. The simulation results also demonstrate that the RGKLMS algorithm can exhibit a comparable steady-state mean-square-error performance with a much lower computational complexity compared with other algorithms.

1 Introduction

Currently, kernel-based learning algorithms demonstrate excellent performance in solving nonlinear problems. Successful kernel-based learning methods include support vector machines (SVMs), kernel Fisher discriminant analysis (KFDA), and kernel principal component analysis (KPCA) [20]. In the past few years, the kernel learning mechanism has been introduced into the field of adaptive filtering, leading to the emergence of kernel adaptive filtering (KAF) theory, which has attracted considerable attention [18]. KAF refers to a class of powerful nonlinear adaptive filters developed in reproducing kernel Hilbert spaces (RKHSs). In the framework of KAF, representative algorithms include the kernel least-mean-square (KLMS) algorithm [16], the kernel affine projection algorithm (KAPA) [17], the kernel recursive least-squares (KRLS) algorithm [5], and the extended KRLS algorithm [15]. The KLMS algorithm has been widely studied due to its simplicity and robustness. To benefit applications such as robotics and image recognition, the quaternion KLMS algorithm was proposed for quaternion-valued inputs [22]. In addition, the performance of KAF has been studied in other applications, such as time-series prediction [32] and system identification [7].

The main challenge of realizing KAF in online applications is the growth of the weighted network structure, which imposes a great computational burden. To decrease the computational complexity of KAF, several online sparsification criteria have been proposed to restrict the network growth, such as the approximate linear dependency (ALD) criterion [5], the novelty criterion (NC) [10], the surprise criterion (SC) [14], the coherence criterion (CC) [25], the quantization criterion [1], and sparsity-promoting regularization [2, 8]. Although these methods are quite effective in restricting network growth, the scale of the sample set will still continue to grow without a strategy for pruning redundant centers in the nonstationary scenario. The fixed-budget model [31] has the ability to prune redundant samples and limit the size of the network subject to an upper bound. However, the fixed network size needs to be preselected, and an excessively small preselected network size will cause the accuracy to suffer dramatically. The most recent state-of-the-art algorithm is the nearest-instance-centroid-estimation quantized kernel least-mean-square (NICEQKLMS) algorithm, which combines the vector quantization technique with the nearest-instance-centroid-estimation method to provide an appropriate time/space trade-off with good online performance [12]. Although sparsification criteria can be used to restrict the network growth by evaluating the contribution of each dictionary sample, the execution of the sparsification criteria itself requires a tremendous number of operations during the learning process.

Explicit kernel mapping has been widely verified to effectively accelerate the training of kernel machines. Williams and Seeger [29] showed that the feature maps of arbitrary kernels can be approximated using the Nystrom method. The technique of using factorization to approximate a given kernel matrix with a low-rank positive semidefinite matrix, which results in a lower computational cost, was introduced in [6]. Rahimi and Recht [24] proposed the random feature mapping method, which can be used to approximate a shift-invariant kernel. In addition, they introduced a concept for speeding up kernel-based training by mapping input data to a randomized low-dimensional feature space and applying linear optimization to search for the optimal solution. To take advantage of the temporal and spatial scalability of linear models, a series of kernel factorization algorithms has been proposed. The intent of the kernel factorization trick is to approximate the kernel mapping relationship via an explicit feature mapping function. Maji and Berg introduced an explicit feature map that can be used to approximate an intersection kernel [19]. In addition, to address the training problem under the non-i.i.d. (independently and identically distributed) assumption, a random Fourier features-based online kernel learning algorithm has been investigated [9]. Ring and Eskofier [26] proposed an efficient SVM benefiting from an approximative feature map, which can speed up training while maintaining nearly the same classification accuracy.

This paper examines an approximate mapping function for the Gaussian kernel by constructing an explicit-feature-mapped KAF algorithm. This can be carried out because for all KAF algorithms, kernel functions play a crucial role in performance, with the Gaussian kernel being the most common and most comprehensive kernel function used in KAF. In this paper, inspired by [23, 26], we introduce a reduced Gaussian kernel function and propose the corresponding reduced Gaussian kernel least-mean-square (RGKLMS) algorithm. To obtain an explicitly mapped kernel function, the Gaussian kernel is decomposed into two components, one of which is expanded to polynomial form via Taylor expansion. The approximate Gaussian kernel function is obtained by intercepting the finite-order terms of the Taylor expansion series and multiplying them by another factor. In this paper, the approximate Gaussian kernel function is called the reduced Gaussian kernel; the proof that the reduced Gaussian function is itself a kernel is given in Appendix. Each term of the polynomial of the reduced Gaussian kernel has an explicit feature mapping function, enabling the execution of corresponding iterative weight operations. Compared with calculating the kernel matrix and updating the dictionary based on sparsification criteria, the proposed combined reduced Gaussian kernel and iterative linear weight operations can significantly reduce the computational complexity.

The proposed RGKLMS algorithm for use in explicit feature mapping to approximate the Gaussian kernel has the following characteristics: 1) Because of the explicit mapping approach, the samples do not need to be stored. The iterative weight process also replaces the expansion of the weighted network structure, resulting in a considerable reduction in storage costs and enabling the development of fast recursive algorithms for computing. 2) Although the RGKLMS algorithm suffers from a slight loss in precision because low orders of the reduced Gaussian kernel are used, the computational complexity is dramatically decreased compared with that of the QKLMS algorithm and the QKLMS-FB algorithm. 3) Good tracking performance can be achieved without increasing the computational complexity in a nonstationary environment because the complexity of the proposed method depends mainly on the order of the reduced Gaussian kernel.

The remainder of this paper is organized as follows: Sect. 2 presents the general formulation of the reduced Gaussian kernel and exploits the methodology to develop an explicit-mapping-based RGKLMS algorithm. Section 3 demonstrates the computational complexity of the RGKLMS algorithm. Results for scenarios involving time-series prediction and nonlinear channel equalization are presented in Sect. 4. Finally, Sect. 5 presents our conclusions and a discussion.

2 Reduced Gaussian Kernel Least-Mean-Square Algorithm

Given a sequence of input–output pairs $\{\varvec{x}(n),d(n); n=1,2,\ldots ,m\}$, where $\varvec{x}(n)$ is the N-dimensional input vector, the objective is to learn a continuous nonlinear input–output mapping

$$\begin{aligned} \begin{aligned} d=f(\varvec{x}),\quad \varvec{x} \in X \subseteq R^N, \quad d \in R. \end{aligned} \end{aligned}$$

(1)

The task of a kernel adaptive filter is to find an approximation of the mapping $f(\cdot )$ based on the given data. Before we introduce the reduced Gaussian kernel least-mean-square algorithm, the QKLMS algorithm is described in detail.

2.1 Quantized Kernel Least-Mean-Square Algorithm

To the best of our knowledge, the QKLMS algorithm is the most representative KLMS algorithm with quantization criteria. The KLMS algorithm is a combination of the kernel method and the traditional least-mean-square algorithm [16]. The kernel method ensure the existence of a representation $\varPhi :X\rightarrow H$ that maps the elements of the space X to the elements of the high-dimensional feature space H. Afterward, the least-mean-square algorithm performs linear filtering of the transformed data $\varPhi (\varvec{x}),\varvec{x}\in X$. Given a sequence of samples $\{\varPhi (\varvec{x}_n),d(n)\}$, the original KLMS algorithm can be expressed as

$$\begin{aligned} \left\{ \begin{array}{lr} \varOmega (0)=0 &{} \\ e(n)=d(n)-\varOmega (n-1)^T\varPhi (\varvec{x}_n)\\ \varOmega (n)=\varOmega (n-1)+\mu e(n)\varPhi (\varvec{x}_n), &{} \end{array} \right. \end{aligned}$$

(2)

where $\varOmega (n)$ denotes an estimate of the weight vector in the mapped space, e(n) is the prediction error in iteration n, and $\mu$ is the step size. The QKLMS algorithm introduces the quantization techniques to select centers and utilizes “redundant” samples to update the coefficient of the closest center [1], thereby achieving the best performance compared with the other existing sparsification KLMS algorithms. The main procedures of the QKLMS algorithm are as follows. The filter output is computed as

$$\begin{aligned} \begin{aligned} y(n)&=\varOmega (n-1)^T\varPhi (\varvec{x}_n)=\sum _{i=1}^{\mathrm{size}(\varvec{C}(n-1))} \eta _i(n-1) K(\varvec{C}_i(n-1),\varvec{x}_n), \end{aligned} \end{aligned}$$

(3)

where K(, ) denotes the kernel operation. The predicted error is $e(n)=d(n)-y(n)$. Before the centers and coefficients are updated, the distance between $\varvec{x}_n$ and $\varvec{C}(n-1)$ is computed as follows: $\hbox {dis}(\varvec{C}(n-1),\varvec{x}_n)= \min (||(\varvec{C}_i(n-1)-\varvec{x}_n)||)_{i=1}^{\mathrm{size}(\varvec{C}(n-1))}$. Then, the magnitude of $\hbox {dis}(\varvec{C}(n-1),\varvec{x}_n)$ is compared against the preselected quantization size $\varepsilon$. If $\hbox {dis}(\varvec{C}(n-1),\varvec{x}_n) \le \varepsilon$, then the centers remain unchanged such that $\varvec{C}(n)=\varvec{C}(n-1)$, and the coefficient of the closest center is updated as follows: $\eta _i(n)=\eta _i(n-1)+\mu e(n)$. If $\hbox {dis}(\varvec{C}(n-1),\varvec{x}_n) > \varepsilon$, then a new center is added ($\varvec{C}(n)={\varvec{C}(n-1),\varvec{x}_n}$), with the coefficient $\eta (n)=[\eta (n-1),\mu e(n)]$. Let the quantization factor be $\gamma = \varepsilon /\sigma$. For the case of $\gamma =0$, the QKLMS algorithm reduces to the KLMS algorithm without the use of any sparsification strategy. Although the quantization technique can effectively reduce the sizes of the centers and the computational complexity of the kernel matrix [1], because the characteristics of the input sequence change in nonstationary situations, computing the growing kernel matrix (composed of centers) is a time-consuming task. To avoid the need to store a large number of samples and compute the kernel matrix, the weights can be computed iteratively by finding a suitable explicit kernel function.

2.2 Reduced Gaussian Kernel Function

Explicitly mapping the data can be a challenging task, as finding the actual mapping function of a kernel can be far from trivial. Thus, methods for approximating kernel functions have been widely studied. Inspired by [26], we introduce an approximate Gaussian kernel. Consider a finite input space X, and suppose that $K(\varvec{x},\varvec{x}')$ is a symmetric function on X. Let $F ={\phi (\varvec{x}): |\varvec{x} \in X}$ be the feature space under the feature mapping $\varvec{x}=(x_1, \ldots ,x_N)\mapsto \varPhi (\varvec{x})=(\varPhi _1(x), \ldots ,\varPhi _i(x), \ldots )$. Mercer’s theorem gives the necessary and sufficient conditions for a continuous symmetric function $K(\varvec{x},\varvec{x}')$ to be expressed as $K(\varvec{x},\varvec{x}')=\sum _{k=1}^{\infty }\lambda _k\varPhi _k(\varvec{x})^T\varPhi _k(\varvec{x}')=<\varPhi (\varvec{x}),\varPhi (\varvec{x}')>$ with nonnegative $\lambda _i$ [20]. First, the explicit mapping kernel must satisfy the following formulation:

$$\begin{aligned} K(\varvec{x}, \varvec{x}')=\varPhi (\varvec{x})^T\varPhi (\varvec{x}'), \end{aligned}$$

(4)

where $\varPhi (\cdot )$ denotes the feature mapping function from the original space to the high-dimensional feature space. To construct an approximate Gaussian kernel for which an explicit feature mapping function exists, we decompose the Gaussian function as follows:

$$\begin{aligned} \begin{aligned}&\hbox {exp}\left( -\frac{||\varvec{x}-\varvec{x}'||^2}{2\sigma ^2}\right) =\hbox {exp}(-a||\varvec{x}||^2)\hbox {exp}(-a||\varvec{x}'||^2) \hbox {exp}(2a\varvec{x}^T\varvec{x}'), \end{aligned} \end{aligned}$$

(5)

where $a=\frac{1}{2\sigma ^2}$. The first two factors have the form of Eq. (4), whereas the third factor does not. Therefore, via Taylor expansion, the third factor is rewritten as

$$\begin{aligned} \begin{aligned} \hbox {exp}(2a\varvec{x}^T\varvec{x}')&=1+2a\varvec{x}^T\varvec{x}'+\frac{(2a\varvec{x}^T\varvec{x}')^2}{2}+\cdots \\&=\sum _{p=0}^n \frac{(2a \varvec{x}^T\varvec{x}')^p}{p!}+R_n(2a\varvec{x}^T\varvec{x}'), \end{aligned} \end{aligned}$$

(6)

where $R_n(2a\varvec{x}^T\varvec{x}')$ is the Lagrange remainder of the Taylor expansion [26]. Substituting Eq. (6) into (5), we obtain the approximate Gaussian kernel function:

$$\begin{aligned} \begin{aligned} \hbox {exp}\left( -\frac{||\varvec{x}-\varvec{x}'||^2}{2\sigma ^2}\right)&=\hbox {exp}(-a||\varvec{x}||^2)\hbox {exp}(-a||\varvec{x}'||^2) \\&\qquad \left( \sum _{p=0}^n \frac{(2a \varvec{x}^T\varvec{x}')^p}{p!}+R_n(2a\varvec{x}^T\varvec{x}')\right) \\&=\sum _{p=0}^n \frac{(2a \varvec{x}^T\varvec{x}')^p}{p!}\hbox {exp}(-a(||\varvec{x}||^2+||\varvec{x}'||^2)\\&\quad +R_n(2a\varvec{x}^T\varvec{x}')\hbox {exp}(-a(||\varvec{x}||^2+||\varvec{x}'||^2)\\&=\sum _{p=0}^n \varPhi _p(\varvec{x})\varPhi _p(\varvec{x}')+ o(n), \end{aligned} \end{aligned}$$

(7)

where p is the order of the approximate Gaussian function, o(n) denotes the remainder $R_n\left( 2a\varvec{x}^T\varvec{x}')\hbox {exp}(-a(||\varvec{x}||^2+||\varvec{x}'||^2\right)$, and the feature mapping function of order p can be expressed as

$$\begin{aligned} \begin{aligned} \varPhi _p(\varvec{x})=\sqrt{\frac{(2a)^p}{p!}}\varvec{x}^p \hbox {exp}(-a||\varvec{x}||^2) \end{aligned} \end{aligned}$$

(8)

such that the form of Eq. (4) is satisfied. Here, we define this approximate Gaussian function of finite order as the reduced Gaussian kernel $K_\mathrm{RG}(,)$, which can be expressed as

$$\begin{aligned} \begin{aligned} K_\mathrm{RG}(\varvec{x},\varvec{x}')&= \sum _{p=0}^P \varPhi _p(\varvec{x})\varPhi _p(\varvec{x}')\\&=\sum _{p=0}^P \frac{(2a \varvec{x}^T\varvec{x}')^p}{p!}\hbox {exp}(-a(||\varvec{x}||^2+||\varvec{x}'||^2), \end{aligned} \end{aligned}$$

(9)

where P is the order parameter of the reduced Gaussian kernel. The kernel function satisfies Mercer’s theorem, and the reduced Gaussian function is proven (in “Appendix”) to be a kernel for finite P ($P\in N$).

The greatest concern regarding the reduced Gaussian kernel is the approximate error. As demonstrated via a study of the approximate error in [26], the relative approximate error $\frac{K_\mathrm{G}(,)-K_\mathrm{RG}(,)}{K_\mathrm{G}(,)}$ can be used to evaluate the difference between the Gaussian kernel and the reduced Gaussian kernel, where $K_\mathrm{G}(,)$ denotes the Gaussian kernel and $K_\mathrm{RG}(,)$ denotes the reduced Gaussian kernel. The relative approximate error decreases factorially as the order of the reduced Gaussian kernel linearly increases. The error also decreases as the kernel parameter $\sigma$ decreases.

To demonstrate the characteristics of the feature mapping function $\varPhi _p$ (8), in this paper, the feature mapping functions of orders 0–5 are shown in Fig. 1. In each case, the kernel parameter $\sigma$ is set to the same value of 0.707. For an input range of $[-\,4,6]$, each of the feature mapping functions of different orders exhibits characteristics similar to those of the well-known one-dimensional Gaussian function.

Fig. 1

Comparison of different-order terms of the mapping function in Eq. (14) when the filtering region is between 0 and 4 and $\sigma$ is 0.707

The curve for $\varPhi _p(p=0)$, as shown in Fig. 1, is equivalent to the Gaussian curve for $N(0,\sigma ^2)$. Compared with $\varPhi _p(p=0)$, the feature mapping curves of higher orders are similar to amplitude-modulated and mean-shifted Gaussian curves. As the order p increases, the maximum amplitude of $\varPhi _p$ becomes smaller. Meanwhile, for the inputs $x\le (0,1]$, the values of higher-order $\varPhi _p$ are smaller, indicating that the lower-order feature vectors make greater contributions.

To illustrate the characteristics of reduced Gaussian kernel functions of different orders, qualitative visualizations of the reduced Gaussian kernel functions and the Gaussian kernel with two-dimensional input are shown in Fig. 2. The x- and y-axes correspond to the value of the two-dimensional input, while the z-axis indicates the value of the kernel function. For the Gaussian kernel shown in Fig. 2a, the output is higher for inputs close to the center. For the reduced Gaussian kernels with P=2 and 3 shown in Fig. 2b, c, the output is higher for inputs that satisfy $|x|\rightarrow 0$ and $|y|\rightarrow 0$. For the higher-order reduced Gaussian kernels shown in Fig. 2d–f, the zones with notable output values gradually shift to the region of $|x|=|y|=C$, where C is a constant. Meanwhile, the maximal amplitudes of the reduced kernels gradually increase with increasing order.

Fig. 2

Qualitative visualizations of the Gaussian kernel and the reduced Gaussian kernels of orders $P =$ 2, 3, 6, 7, 10 under a one-dimensional input. a Gaussian kernel. b Reduced Gaussian kernel ($P =$ 2). c Reduced Gaussian kernel ($P =$ 3). d Reduced Gaussian kernel ($P =$ 6). e Reduced Gaussian kernel ($P =$ 7). f Reduced Gaussian kernel ($P =$ 10)

2.3 Reduced Gaussian Kernel LMS Algorithm

For the reduced Gaussian kernel, the corresponding RGKLMS algorithm is derived as follows. The output of the kernel adaptive filter can be represented as

$$\begin{aligned} \begin{aligned} y(n)=\varvec{\omega }(n-1)^T\varPhi (\varvec{x}_n). \end{aligned} \end{aligned}$$

(10)

Under the assumption that $a>0$, the explicitly mapped feature vector $\varPhi (\varvec{x}_n)$8 can be expressed as $\varPhi (\varvec{x}_n)=[\varPhi _p(\varvec{x}_n)]_{p=0}^P$, where P is the order of the reduced Gaussian kernel and the pth-order feature vector is

$$\begin{aligned} \begin{aligned} \varPhi _p(\varvec{x}_n)= \sqrt{\frac{(2a)^p}{p!}}\varvec{x}_n^p \hbox {exp}(-a\varvec{x}_n^2). \end{aligned} \end{aligned}$$

(11)

For $p=\{0,1,\ldots ,P\}$, we define

$$\begin{aligned} C_p=\sqrt{\frac{(2a)^p}{p!}} \end{aligned}$$

(12)

and adopt the notation $E(\varvec{x}_n)=\hbox {exp}(-\,a\varvec{x}_n^2)$. Then, the input vector in the feature space H can be represented as

$$\begin{aligned} \begin{aligned} \varPhi (\varvec{x}_n)&=[ C_0 E(\varvec{x}_n),C_1 \varvec{x}_n E(\varvec{x}_n),\ldots ,C_P \varvec{x}_n^P E(\varvec{x}_n)], \end{aligned} \end{aligned}$$

(13)

where $C_p \varvec{x}_n^p E(\varvec{x}_n)$ denotes the pth-order feature vector. According to the weight updating equation given in [16] (see equation (10) of that paper), the weight vector can be expressed as

$$\begin{aligned} \varvec{\omega }(n)=\mu e(n)\varPhi (\varvec{x}_n). \end{aligned}$$

(14)

We express the weight in vector form as

$$\begin{aligned} \varvec{\omega }(n-1)=[\varvec{\omega }_0(n-1),\varvec{\omega }_1(n-1),\ldots ,\varvec{\omega }_P(n-1)], \end{aligned}$$

(15)

where $\varvec{\omega }_p(n-1), p=0,1,\ldots ,P$, is the pth-order weight vector.

Based on Eqs. (13) and (15), the output of the reduced Gaussian kernel adaptive filter is

$$\begin{aligned} \begin{aligned} y(n)&=\varvec{\omega }(n-1)^T\varPhi (\varvec{x}_n)=\sum _{p=0}^P \varvec{\omega }_p^T(n-1) \varPhi _p(\varvec{x}_n). \end{aligned} \end{aligned}$$

(16)

The pth-order weight vector can be updated as follows:

$$\begin{aligned} \begin{aligned} \varvec{\omega }_p(n)=\varvec{\omega }_p(n-1)+\mu e_{n}C_p\varvec{x}_{n}^p E(\varvec{x}_n). \end{aligned} \end{aligned}$$

(17)

Remark 1

As seen from Eqs. (16) and (17), the explicit feature mapping allows the weight update to be performed as a linear adaptive filtering process. Because of the feature vector obtained by computing the explicit mapping function 8, the historical feature information can be stored in the weight information during the iterative process. Thus, a dictionary of samples is no longer necessary, and the expanding weighted network is replaced with a finite-dimensional nonlinear mapping network. Therefore, a sparsification method is no longer needed to limit the network size, and thus, the corresponding computational complexity (which is usually high) is avoided.

The RGKLMS algorithm is summarized in detail below. As shown in Algorithm 1, once the Gaussian kernel is substituted with the approximate explicit kernel, the kernel matrix computation is changed to a summation of products of finite-order feature vectors. Unlike in the case of the Gaussian kernel, these feature vectors can be directly obtained via the explicit feature mapping function. Working with the feature vectors allows the continued growth of the weighted network to be avoided via the recursive computing of the weight vectors, which can greatly reduce the required storage space and calculation cost.

3 Computational Complexity Analysis

To further reduce the computational complexity, the calculation process of the RGKLMS algorithm is optimized. When $p=0$, for the calculation of $\varPhi _0(\varvec{x})$, the number of multiplications is 3N and the number of $\hbox {exp}(\cdot )$ operations is N. The mapped vector is recursively computed using

$$\begin{aligned} \begin{aligned} \varPhi _{p+1}(x_i)= C_{p+1}^{'} \varvec{x} \varPhi _{p}(x_i), \end{aligned} \end{aligned}$$

(18)

where $C_{p+1}^{'}$ is precalculated as $C_{P+1}/C_{P}$. Therefore, for $i={1,2,\ldots ,P}$, the number of multiplications for the calculation of $\varPhi _p(\varvec{x})$ is 2N. For the calculation of $\{\varPhi _p(\varvec{x})\}_{p=0}^P$, the total number of multiplications is $(3P+3)N$ and the number of $\hbox {exp}(\cdot )$ operations is N. The computations carried out to calculate the filter output and update the weight vectors are the same.

For an input vector with a dimensionality of N and a Pth-order reduced Gaussian kernel, the computational complexity of the RGKLMS algorithm in each iteration is calculated as follows.

The complexity of the RGKLMS algorithm
i. To calculate the mapping vectors $\{\varPhi _p(x(n))\}_{p=0}^P$:
Number of multiplications $= (3P+3)N$;
Number of additions $= 0$;
Number of $\hbox {exp}(\cdot )$$= N$;
ii. To calculate the output of the filter:
Number of multiplications $= (P+1)N$;
Number of additions $= PN$;
iii. To update the weights:
Number of multiplications $= (N+1)(P+1)$;
Number of additions $= (P+1)N$;
All Operations:
Number of multiplications $= (5P+5)N+P+1$;
Number of additions $= (2P+1)N$;
Number of $\hbox {exp}(\cdot )= N$;

To show how the computational complexity of the RGKLMS algorithm increases with the order P, the dimensionality N of the input is taken to be 5. The resulting computational complexity curves are presented in Fig. 3.

Fig. 3

Computational complexity of the RGKLMS algorithm

Figure 3 shows that the numbers of multiplications and additions increase linearly with the order P. The number of $\hbox {exp}(\cdot )$ operations is equal to a constant value of N due to the recursive computation of the feature vector $\varPhi _p(\varvec{x})$ according to Eq. (18), which greatly reduces the computational cost of the RGKLMS algorithm, especially for high-order P.

Remark 2

The computational complexity of the explicit-mapping-based RGKLMS algorithm is markedly reduced by the recursive computation of the weight vectors. Compared with the complexity of an implicit-mapping-based kernel algorithm, the explicit mapping method has three advantages: 1) The required sample storage space is considerably reduced. 2) Calculating the mapped feature and weight vectors to obtain the filter output requires much less computational complexity than computing the kernel matrix with a large number of samples. 3) The implicit mapping method requires sparsification criteria and a dictionary updating strategy, thereby incurring a cost of O(D) for computation and storage, where D is the number of centers in the dictionary.

4 Simulation Results

To demonstrate the performance of the RGKLMS algorithm, two simulation experiments were conducted, one focusing on time-series prediction and one focusing on nonlinear channel equalization. The QKLMS and QKLMS-FB algorithms were chosen for comparison. The Gaussian kernel was adopted as the chosen kernel. The kernel parameter $\sigma$ and the step size $\mu$ were set to the same values for all compared algorithms. To clarify the principle applied for parameter setting, the characteristic parameters of all compared algorithms are introduced. The kernel parameter exerts a great influence on the computational complexity of the QKLMS and QKLMS-FB algorithms. A small kernel parameter value will result in a dramatic increase in the network size for the QKLMS and QKLMS-FB algorithms. Meanwhile, the performance will improve as the number of centers increases. The quantization factor $\gamma$ of the QKLMS and QKLMS-FB algorithms can be set to achieve a balance between complexity and accuracy. Increasing the value of $\gamma$ will reduce the complexity and affect the steady-state error. The forgetting factor $\beta$ of the QKLMS-FB algorithm helps the system to track statistical changes in the input data. A smaller value of $\beta$ can decrease the influence of historical data and restrict the growth of the network. Based on the complexity analysis presented in Sect. 3, the complexity of the RGKLMS algorithm depends on the order of the reduced Gaussian kernel. Therefore, the RGKLMS algorithm was simulated for multiple orders. The influence of the kernel parameter on the performance of the RGKLMS algorithm will be demonstrated via the following simulations. For visual clarity, the MSEs were computed in a running window of 50 samples. The computer used for the simulations had 4-Core i5-5200U processors and a 64-bit Windows operating system. Unless otherwise noted, the run-time mentioned in the following simulations is the time required for each iteration.

4.1 Time-Series Prediction

A benchmark problem of nonstationary data prediction is considered. The highly nonlinear system [25, 28] is described by the following difference equation:

$$\begin{aligned} \begin{aligned} d(n)&=(0.8-0.5\hbox {exp}(-d^2(n-1)))d(n-1)\\&\quad -(0.3+0.9\hbox {exp}(-d^2(n-1)))d(n-2)\\&\quad +0.1sin(d(n-1)\pi ), \end{aligned} \end{aligned}$$

(19)

where the initial state of the system is $d(-\,1)=d(-\,2)=0.1$.

4.1.1 Stationary Time-Series Prediction

To investigate the influence of the kernel parameter on the performance of the RGKLMS algorithm, simulations were conducted to compare the RGKLMS results obtained at orders of $P =$ 1, 2, 3. A set of 4000 generated samples was used as the training data. Zero-mean white Gaussian noise with a variance of 0.01 was added to the data set. The five most recent samples $\{d(n-1),d(n-2),d(n-3),d(n-4),d(n-5)\}$ were used to predict the current value d(n).

Simulations were performed using the RGKLMS algorithm at orders $P =$ 1, 2, 3. The step size was 0.1. The value of the kernel parameter $\sigma$ was varied from 0.2 to 1.6 to thoroughly demonstrate the performance of the RGKLMS algorithm at different orders. The final MSE curves, which were obtained after performing over 100 Monte Carlo simulations, are shown in Fig. 4. The final MSE of the RGKLMS algorithm with P=3 is better than those for $P =$ 1 and 2 under the same kernel parameter and step size setting. As the value of the kernel parameter increases from 0.6 to 3, the final MSEs of RGKLMS ($P =$ 1, 2, 3) first decrease and then gradually increase. The advantage of the RGKLMS algorithm with $P =$ 3 in terms of the steady-state MSE relative to the RGKLMS algorithm with $P =$ 2 and that with $P =$1 gradually diminishes as the kernel parameter increases to 3. When the kernel parameter is smaller than 0.8, the performances of the RGKLMS algorithm with $P =$ 1 and that with $P =$ 2 decline dramatically as the kernel parameter further decreases. Moreover, the performance is not notably improved when the order of the reduced Gaussian kernel is greater than 3.

Fig. 4

Final MSE curves for the RGKLMS algorithm ($P =$ 1, 2, 3) for different values of the kernel parameter $\sigma$ in time-series prediction

Fig. 5

Final MSE curves for the QKLMS, QKLMS-FB, and RGKLMS ($P =$ 1, 2, 3) algorithms for time-series prediction, obtained by averaging over 100 simulations

For the performance comparison between the QKLMS, QKLMS-FB, RGKLMS ($P =$ 1), RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms, the parameters of the compared algorithms were set as follows to carry out predictions on the same data set. The kernel parameter was set to 1.3. The step size $\mu$ was 0.1. The parameter $\gamma$ of the QKLMS-FB and QKLMS algorithms was set to 0.5. The parameter $\beta$ of the QKLMS-FB algorithm was set to 0.96, and the fixed budget was set to 12.

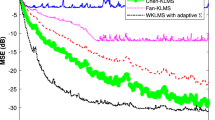
The simulation results are shown in Fig. 5. The final MSEs of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 1), RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms are − 17.93, − 17.67, − 17.43, − 17.43, and − 17.64 dB, respectively. The run-times of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 1), RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms for the last iteration are 0.0240, 0.0961, 0.0052, 0.0059, and 0.0062 ms, respectively. Although the coverage speed of the RGKLMS ($P =$ 3) algorithm is only slightly slower than that of the QKLMS-FB algorithm, the QKLMS-FB algorithm requires more than 15 times the training time of the RGKLMS ($P =$ 3) algorithm to achieve almost the same final MSE. The accumulative run-time curves, which demonstrate the clear advantage of the RGKLMS algorithm in terms of the computational complexity, are shown in Fig. 6.

Fig. 6

Run-time curves for the QKLMS, QKLMS-FB, and RGKLMS ($P =$ 1, 2, 3) algorithms for time-series prediction, obtained by averaging over 100 simulations

4.1.2 Nonstationary Time-Series Prediction

To evaluate the tracking ability of the proposed algorithm, an initial set of 6000 data points was generated using Eq. 20. Then, for $n>6000$, the system model was changed to

$$\begin{aligned} \begin{aligned} d(n)&=(0.2-0.7 \hbox {exp}(-d^2(n-1)))d(n-1)\\&\quad -(0.8+0.8 \hbox {exp}(-d^2(n-1)d(n-2))\\&\quad +0.2sin(d(n-1)\pi ), \end{aligned} \end{aligned}$$

(20)

which was investigated in [27]. For all compared algorithms, the kernel parameter was set to 1.3. The step size was chosen to be 0.1. The parameter $\gamma$ of the QKLMS-FB and QKLMS algorithms was set to 0.5. The parameter $\beta$ of the QKLMS-FB algorithm was set to 0.96. The fixed budget of the QKLMS-FB algorithm was set to 14. The RGKLMS algorithm was simulated at orders of $P =$ 1, 2, 3 to thoroughly demonstrate the performance of the proposed method. The MSE was averaged over 100 Monte Carlo simulations.

The MSE learning curves are shown in Fig. 7. The final MSE was calculated by averaging the last 200 samples. The training data for $n\le 6000$ are called segment I (Seg I), and the training data for $n>6000$ are called segment II (Seg II). The final MSEs of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 1), RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms are listed in Table 1. The final MSEs of the RGKLMS ($P =$ 3), QKLMS, and QKLMS-FB algorithms are almost the same for segment I. However, for segment II, the final MSEs of all versions of the RGKLMS algorithm ($P =$ 1, 2, 3) are much better than those of the QKLMS and QKLMS-FB algorithms. The QKLMS and QKLMS-FB algorithms each have the same final network size of 14 for time-series prediction, determined over 100 independent runs. As shown in Fig. 8, the network size is increased when the time series is changed. For a fair comparison of complexity, the run-times of all algorithms are compared, as shown in Fig. 9. The run-times of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 1), RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms for the last iteration are 0.0223, 0.0873, 0.0052, 0.0055, and 0.0063 ms, respectively. The run-times of the QKLMS and QKLMS-FB algorithms during the steady state are more than 3 times and 13 times that of the RGKLMS ($P =$ 3) algorithm. The complexity of the RGKLMS algorithm is much lower than that of the other compared algorithms. The coverage speeds of all versions of the RGKLMS algorithm ($P =$ 1, 2, 3) are lower than those of the QKLMS and QKLMS-FB algorithms in Seg I. However, in Seg II, the RGKLMS algorithm can much more rapidly track the change in the input. Therefore, the RGKLMS algorithm has better overall tracking performance compared to the QKLMS and QKLMS-FB algorithms.

Fig. 7

Final MSE curves for the QKLMS, QKLMS-FB, and RGKLMS ($P =$ 1, 2, 3) algorithms for nonstationary time-series prediction, obtained by averaging over 100 simulations

Table 1 Final MSEs when adapting to an abrupt change in channel conditions

Fig. 8

Network size curves for the QKLMS and QKLMS-FB algorithms for nonstationary time-series prediction, obtained by averaging over 100 simulations

Fig. 9

Run-time curves for the QKLMS, QKLMS-FB, and RGKLMS ($P =$ 1, 2, 3) algorithms for nonstationary time-series prediction, obtained by averaging over 100 simulations

4.2 Nonlinear Channel Equalization

Consider a nonlinear channel consisting of a linear filter and a memoryless nonlinearity, as shown in Fig. 10. The kernel adaptive filter is used in this paper as an adaptive equalizer to reverse the distortion of the signal transmitted through this nonlinear channel by updating the equalizer parameters (another name for the filter coefficients).

Fig. 10

Nonlinear channel model for equalization

4.2.1 Stationary Channel Equalization

In several practical nonlinear channel models, the channel impulse response of the linear part is described as follows:

$$\begin{aligned} h(i)=\frac{1}{2}\left[ 1+\cos \left( \frac{2*pi}{\varLambda }\right) (i-2)\right] \hbox {for}\quad ~ i=1,2,3, \end{aligned}$$

(21)

where the parameter $\varLambda$ determines the eigenvalue ratio (EVR) of the channel, which represents the difficulty in equalizing the channel [21, 30]. Here, $\varLambda$ is chosen to be 2.9. The corresponding normalized channel impulse response in the z-transform domain is given by

$$\begin{aligned} \begin{aligned} \hbox {Channel} (\varLambda =2.9)\hbox {:}\, H(z)=0.209+0.995z^{-1}+0.209z^{-2}.\\ \end{aligned} \end{aligned}$$

(22)

The output of the nonlinear channel is defined as $r(i)=x(i)+0.2x^2(i)-0.1x^3(i)+n(i)$, where n(i) is a 20 dB SNR white Gaussian noise component. A series of binary signals $s_i\in \{+\,1, -\,1\}$ is used as the channel input.

To demonstrate the influence of the kernel parameter on the steady-state error performance, the RGKLMS algorithm with $P =$ 1, 2, 3 is used, with a step size setting of 0.1. The final MSE curves are shown in Fig. 11. The RGKLMS ($P =$ 3) algorithm has better steady-state MSE performance than the other RGKLMS ($P =$ 1, 2) algorithms.

As the value of the kernel parameter varies from 0.2 to 1.5, the final MSEs of the RGKLMS ($P =$ 1, 2, 3) algorithms first decrease and then increase. The final MSE of the RGKLMS ($P =$ 3) algorithm reaches its minimum of − 21.842 dB when the value of the kernel parameter is 0.8.

Fig. 11

Final MSE curves of the RGKLMS ($P =$ 1, 2, 3) algorithms under kernel parameter values from 0.2 to 1.5 for stationary channel equalization

In the simulations of stationary channel equalization, the kernel size was set to $\sigma =0.8$ and the step size was set to $\mu =0.1$. The parameter $\gamma$ was set to the same value of 0.5 for both the QKLMS and QKLMS-FB algorithms. The parameter $\beta$ and the fixed budget of the QKLMS-FB algorithm were chosen to be 0.96 and 60, respectively.

Fig. 12

Learning curves of the QKLMS, QKLMS-FB, and RGKLMS ($P =$ 2, 3) algorithms for stationary channel equalization

Fig. 13

Network size curves for the QKLMS and QKLMS-FB algorithms for channel equalization, obtained by averaging over 100 simulations

Fig. 14

Run-time curves for the QKLMS, QKLMS-FB, and RGKLMS ($P =$ 2, 3) algorithms for channel equalization, obtained by averaging over 100 simulations

The final MSEs of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms shown in Fig. 12 are − 22.34, − 21.76, − 20.90, and − 21.84 dB, respectively. The final MSE of the RGKLMS ($P =$ 3) algorithm is better than that of the QKLMS-FB algorithm, which is also a fixed-budget online algorithm. The final network sizes of the QKLMS and QKLMS-FB algorithms for channel equalization are 76 and 60, respectively. The growth curves of the network size are shown in Fig. 13. The coverage speed of the RGKLMS algorithm is faster than those of the QKLMS and QKLMS-FB algorithms. Figure 14 demonstrates that the consumed run-time of the RGKLMS algorithm during the iteration is much lower than that of the QKLMS and QKLMS-FB algorithms. The run-times of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms for the last iteration are 0.0330, 0.1154, 0.0055, and 0.0063 ms, respectively.

4.2.2 Time-Varying Channel Equalization

The time-varying nonlinear channel model used in these simulations is often encountered in satellite communication links, as mentioned in [3, 11]. The linear channel impulse response is $h=[h_0, h_1, h_2]^\mathrm{T}$. Here, the channel parameter set $h=[0.3482, 0.8704, 0.3482]$, which is typical of the parameters commonly encountered in real communication systems, is used. For the time-varying channel model, the transfer function is defined as

$$\begin{aligned} H(z)=(h_0+h_0(i))+(h_1+h_1(i))z^{-1}+(h_2+h_2(i))z^{-2}, \end{aligned}$$

(23)

where $h_0(i)$, $h_1(i)$, and $h_2(i)$ are the time-varying coefficients and are generated by using a second-order Markov model, in which a white Gaussian noise source drives a second-order Butterworth low-pass filter. The simulation code used to generate the time-varying coefficients can be found in [13]. The output of the nonlinear channel is described by

$$\begin{aligned} r(i)=x(i)+0.2x^2(i)+n(i), \end{aligned}$$

(24)

where n(i) is a 20 dB white Gaussian noise component.

To investigate the effect of the kernel parameter on the performance of the RGKLMS algorithm for time-varying channel equalization, the RGKLMS algorithm with $P =$ 1, 2, 3 was simulated. The step size was set to 0.1. The final MSE curves are shown in Fig. 15. As the value of the kernel parameter increases, the time-varying channel equalization performance initially improves and then gradually degrades. The performance of the RGKLMS ($P =$ 3) algorithm is better than that of the RGKLMS ($P =$ 2) algorithm, which has a similar final MSE to that of the RGKLMS ($P =$ 1) algorithm. When the value of the kernel parameter is less than 0.3, as it decreases, the performance of the RGKLMS ($P =$ 1, 2, 3) algorithms becomes significantly worse. The RGKLMS ($P =$ 3) algorithm reaches its lowest final MSE of − 15.44 dB when the value of the kernel parameter is 0.4.

Fig. 15

Final MSE curves of the RGKLMS ($P =$ 1, 2, 3) algorithms for time-varying channel equalization

Now, we compare the performance of the RGKLMS algorithm for time-varying channel equalization with that of the QKLMS and QKLMS-FB algorithms. Their kernel parameters were chosen to be 0.4. All step sizes were set to 0.1. The parameter $\gamma$ was set to 0.5 for both the QKLMS and QKLMS-FB algorithms. The parameter $\beta$ and the budget D of the QKLMS-FB algorithm were set to 0.96 and 25, respectively. The MSE curves after 100 independent runs are shown in Fig. 16.

Fig. 16

Learning curves of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms for time-varying channel equalization

Fig. 17

Network size curves for the QKLMS and QKLMS-FB algorithms for time-varying channel equalization, obtained by averaging over 100 simulations

Fig. 18

Run-time curves for the QKLMS, QKLMS-FB, and RGKLMS ($P =$ 2, 3) algorithms for time-varying channel equalization, obtained by averaging over 100 simulations

As shown in Fig. 16, the final MSEs of the QKLMS-FB and QKLMS algorithms are − 10.76 and − 10.27 dB, respectively. In the initial stage, the learning curves remain consistent, but after 3000 iterations, the performance of the QKLMS-FB algorithm becomes worse. The final network sizes of the QKLMS and QKLMS-FB algorithms are 128 and 60, respectively. Although the QKLMS-FB algorithm achieves a much smaller network size than does the QKLMS algorithm, the steady-state MSE may degrade because the preselected budget is smaller than the required value. The final MSEs of the RGKLMS ($P =$ 2) and RGKLMS ($P =$ 3) algorithms are − 15.00 and − 15.32 dB, respectively. The network size growth curves of the QKLMS and QKLMS-FB algorithms are shown in Fig. 17. The run-times of the QKLMS, QKLMS-FB, RGKLMS ($P =$ 2), and RGKLMS ($P =$ 3) algorithms for the last iteration are 0.0331, 0.1004, 0.0054, and 0.0059 ms, respectively. The accumulative run-times of the compared algorithms are demonstrated in Fig. 18, which also shows the advantage of the RGKLMS algorithm in terms of the computational complexity. The simulation results clearly indicate that the RGKLMS algorithm with $P =$ 2 and 3 not only exhibits much better performance in terms of the steady-state error than the QKLMS and QKLMS-FB algorithms under the same kernel parameter and step size, but also achieves a faster training speed. In the time-varying channel simulations, the RGKLMS algorithm showed a dominant advantage over the online sparsification-criteria-based QKLMS and QKLMS-FB algorithms.

5 Conclusions and Discussion

In contrast to the existing methods for solving the problem posed by network growth in KAF with sparsification criteria, an approximate Gaussian kernel (called the reduced Gaussian kernel) is introduced in this paper, and the corresponding RGKLMS algorithm is proposed. The explicit feature mapping function of the reduced Gaussian kernel enables recursive updating of the weight vectors. A computational complexity analysis shows that the numbers of multiplications and additions increase linearly with the order of the RGKLMS algorithm. The number of $\hbox {exp}(\cdot )$ operations is fixed and depends on the dimensionality of the input vector. From simulation-based run-time comparisons, it can be concluded that compared with the kernel trick, the RGKLMS algorithm offers greatly reduced complexity and storage space requirements for the reasons discussed in Remark I. Extensive simulations also show that the RGKLMS algorithm performs better than the QKLMS and QKLMS-FB algorithms in terms of the steady-state error in a nonstationary environment. The reduced-Gaussian-kernel-based RGKLMS algorithm exhibits universal approximation capabilities in scenarios involving time-series prediction and nonlinear channel equalization. The proposed RGKLMS algorithm is an excellent choice for pursuing an effective online KAF algorithm, especially for applications with computational complexity and storage space constraints in a nonstationary environment.

The kernel parameter of the RGKLMS algorithm is discussed based on the analysis and the simulation results presented above. First, the effect of the kernel parameter on the performance of the RGKLMS algorithm is an important issue. As the simulation results show, for both time-series prediction and channel equalization, the kernel parameter has a significant effect on the steady-state error performance. Since the kernel parameter will not influence the complexity, according to the complexity analysis presented in Sect. 3, it is better to determine the optimal setting for the kernel parameter $\sigma$ prior to the application of the algorithm. Second, the order of the RGKLMS algorithm is also a crucial factor. Although the corresponding simulation results are not reported in this paper, we have found that the performance does not significantly improve when the order P is larger than 3. As shown in Fig. 1, in the input range of (0,1], the value of $\varPhi _p(\cdot )$ decreases as the order p increases, indicating that the effects of higher-order feature vectors are smaller than those of lower-order feature vectors. Therefore, as the order increases, the steady-state performance will not notably improve. Finally, the influence of the step size on the performance of the RGKLMS algorithm was not studied in this paper. A variable step strategy can also be used to improve the convergence speed based on the theoretical upper bound on the step size for dynamic convergence.

Appendix

To prove that the reduced Gaussian kernel function expressed in Eq. (7) is a kernel, the characteristics of kernels are used. The following proposition is given [4]. Let $K_1$ and $K_2$ be kernels over $X\times X$, where $X\subseteq R$; let $\alpha \in R^{+}$; let $f(\cdot )$ be a real-valued function on the space X; and let $\varPhi X \rightarrow R^m$. Then, the following propositions can be established:

Proposition 1

$K=K_1+K_2$ is a kernel if $K_1$ and $K_2$ are kernels.

Proposition 2

Due to the characteristics of kernels, $K=\alpha K_1 (k>0)$ is a kernel.

Proposition 3

$K=f(x_i)f(x_j)$.

Hypothesis I Each order term of Eq. (7) is a kernel. Based on Proposition 1, Eq. (7) is a kernel if Hypothesis I is satisfied. This is equivalent to saying that for any $p=\{1,2,\ldots ,P\}$, the function $\sum _{p=1}^{P}\frac{(2a)^p}{p!}x_i^p x_j^p \hbox {exp}(-a(x_i^2+x_j^2))$ is a kernel. Therefore, we need to identify only the pth-order term as a kernel, where $p=\{1,2,\ldots ,P\}$, because a sum of kernels is itself a kernel.

Hypothesis II The kernel parameter a is assumed to be larger than 0.

If Hypothesis I is satisfied, then the coefficients $\frac{(2a)^2}{p!}$ of each order are larger than 0. Based on Proposition 2, Hypothesis II can be said to be satisfied if the function $x_i^p x_j^p \hbox {exp}(-a(x_i^2+x_j^2))$ is a kernel for any $p=\{1,2,\ldots ,P\}$. Clearly, based on Proposition 3, $x_i^p x_j^p \hbox {exp}(-a(x_i^2+x_j^2))=x_i^p x_j^p \hbox {exp}(-ax_i^2) \hbox {exp}(-ax_j^2)=f(x_i)f(x_j)$ holds. Therefore, the reduced Gaussian kernel function given in Eq. (7) is a kernel.