Abstract
This paper aims to provide the complete analysis on the threshold dynamics of an age-space structured malaria epidemic model. We formulate the model in a spatially bounded domain by assuming that: (i) the density of susceptible humans at space x stabilizes at H(x); (ii) the force of infection between human population and mosquitoes is given by the mass action incidence. By appealing to the theory of fixed point problem and Picard sequences and iteration, the well-posedness of the model is shown by verifying that the solution exists globally and the model admits a global attractor. In the spatially homogeneous case, we establish the explicit formula for the basic reproduction number, which governs the malaria extinction and persistence. The local and global stability of equilibria is achieved by studying the distribution of characteristic roots of characteristic equation and constructing the suitable Lyapunov functions, respectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well known that malaria is a parasitic infections in humans, caused by the genus Plasmodium. In general, humans acquire malaria through effective biting by several species of infectious female anopheles mosquitoes [23, 25]. Susceptible mosquitoes acquire malaria through effective bites of infectious human host. It has been reported in [15] that about more than one hundred countries are under prevalence of malaria. Every year, two billion people are at risk affected by Plasmodium falciparum.
Reaction–diffusion model frameworks have been proved to be a powerful tool to generalize the classical Ross–Macdonald malaria models [4, 6, 11, 20,21,22, 32, 34]. For a spatial transmission dynamics of malaria, it is usually assumed that human and mosquitoes are confined in a bounded domain \(\Omega \). Laplacian operator \(\partial /\partial x^2\), \(x\in \Omega \subset {\mathbb {R}}^n (n\ge 1)\) are introduced to reflect the spatial random movement of humans and mosquitoes. Recent publications [13, 14, 21] demonstrated that the spatial heterogeneity is a more meaningful and important factor in disease transmission. In reality, as environmental conditions vary spatially, for example, temperature and humidity, etc., it comes natural to demonstrate spatial heterogeneity for disease transmission parameters. It is also argued in [26] that “the non-random distribution of humans and mosquitoes across the landscape can generate spatially heterogeneous biting patterns”.
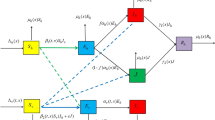
In typical and pioneering work of malaria transmission model [1, 18,19,20, 23, 25], humans are categorized into susceptible and infected class. The adult female mosquitoes (termed as vector) are categorized into susceptible and infected mosquito classes. The mosquitoes have to breed in water, and the adult female mosquitoes emerge from aquatic mosquitoes. The adult female mosquitoes transmit malaria to human hosts. The infected mosquitoes may spend a incubation period of 10 to 14 days (termed as extrinsic incubation period (EIP)) to survive (during which the infected mosquitoes cannot transmit malaria to human hosts) and transmit malaria to human hosts [18]. Taking EIP and mobility of human and mosquitoes in a spatial domain into account, Lou and Zhao [21] generalized the model in [25] and proposed a nonlocal and time-delayed diffusive malaria model, for \(x\in \Omega ,\ t>0\),
with
Here, \(S_m(t,x)\), \(I_m(t,x)\) and \(I_h(t,x)\) denote the density of susceptible, infected adult female mosquitoes and infected humans at space x and time t, respectively, which are equipped with diffusion rates \(D_m\), \(D_m\) and \(D_h\), respectively. The total population stabilizes at H(x). \(\beta (x)\) and \(\mu (x)\) stand for the space-dependent biting rate and recruitment rate of adult female mosquitoes, respectively. \(d_m\) represents the natural death rate of mosquitoes. b and c stand for the transmission probabilities per bite from \(I_h\) to \(S_m\) and from \(I_m\) to \(H(x)-I_h\), respectively. \(d_h\) and \(\rho \) represent the death rate and recovery rate of humans. \(\Gamma \) is the Green function corresponding to the operator \(D_m\Delta \) subject to the Neumann boundary condition. \(\tau \) represents the fixed incubation period constant.
Since the latent mosquitoes in one location can fly around during EIP, and arrive at any location in the domain when they can transmit malaria to human hosts, the spatial movement of mosquitoes in EIP will result in non-local infection [3, 13, 14]. In model (1.1), the nonlocal time delay term is obtained by introducing an infection age variable a. At time t and space x, denote by \(i_m(t,a,x)\) the density of the mosquitoes with infection age a. Suppose that \(\tau \) is a fixed latent period. It then follows that \(E_m(t,x)=\int \limits _0^{\tau }i_m(t,a,x)\mathrm{d}a\) and \(I_m(t,x)=\int \limits _{\tau }^{\infty }i_m(t,a,x)\mathrm{d}a\) are the density of latent and infected mosquitoes, respectively. Then, the evolution of \(i_m(t,a,x)\) satisfies
where \(i_m(t,0,x)\) is the newly infected mosquitoes. The nonlocal time delay term in (1.1) comes from the key point that \(i_m(t,\tau ,x)\) can be determined by the integration along characteristics line \(t-a=const.\),
where \(i_{m0}\) is initial condition, and \(\Pi (a)=e^{-d_ma}\). Hence,
From the standpoint of mathematical analysis, the authors in [21] confirmed that the threshold dynamics of (1.1) is governed by the sign of the principle eigenvalue of the associated linear and nonlocal eigenvalue problem. Subsequently, a typical feature of malaria termed as vector-bias, was introduced to describe the difference between the probability (denote by p and l) of a mosquito picking the human when he/she is infected and susceptible (see, e.g., [8, 29, 33, 34]). To explore the seasonal patterns of malaria epidemics (may be caused by annual temperature and rainfall variation (see, e.g., [12])), Bai et al. [4] further extended the models in [21, 33] by incorporating the seasonality, vector-bias, EIP and the spatial heterogeneity, and formulated a time-delayed periodic reaction-diffusion model. Their results suggest that the sharp threshold results can be achieved by defining the basic reproduction number. They also confirmed the existence of a periodic solution for the proposed models, which built an interesting biological implication: Seasonal patterns of malaria epidemics will occur. It is important to mention that recent studies on diffusive Zika epidemic models (see, e.g., [11, 22, 32]) can also be regarded as a generalization of the classical model in [25]. Like other vector-borne disease models, Zika epidemic models share the same cross-infection mechanism between humans and mosquitoes.
Our goal of this paper is to perform an original analysis of (1.1). A more complete understanding of (1.1) can help to get better understanding of the malaria transmission in regions. As in studies of Zika outbreak in Rio De Janerio, Bastos et al. [28] argued that compared to the total population, infected human density takes a fairly small number [28]. Subsequently, Fitzgibbon et al. [11], Magal et al. [22] and Wang and Chen [32] proposed the diffusive vector-borne disease model by assuming the density of susceptible humans to be H(x), which depends only on space x, and will not be altered within a short time. On the other hand, in (1.1), the force of infection for humans and mosquitoes is described by adopting standard infection mechanism, \(\frac{b\beta (x)}{H(x)}S_mI_h\) and \(\frac{c\beta (x)}{H(x)}(H(x)-I_h)I_m\), respectively, where \(H(x)-I_h\) represents the density of susceptible humans. It comes naturally to wonder what happens if standard incidence is replaced by the mass action. In this work, we continue to borrow the idea in [11, 22, 32] that the density of susceptible humans is H(x) and adopt the mass action incidence, which result in the force of infection for humans and mosquitoes at space x and time t given by \(b\beta (x)S_mI_h\) and \(c\beta (x)H(x)I_m\), respectively.
This work is also inspired by some recent works on diffusive disease models with age structure (see, for example, [5, 9, 10, 35, 36], aiming to understand the effects of the spatial heterogeneity and infection age on disease transmission. For the standard age-space structured susceptible–infective–recovered (SIR) model, Chekroun and Kuniya [5] reformulated the model by a hybrid system of one diffusive equation and one Volterra integral equation, and studied the threshold dynamics for the disease extinction and persistence in one-dimensional domain. Further, the global stability problem of a constant equilibrium was achieved by constructing Lyapunov function. In another works, the existence of travelling wave solutions of age-space structured SIR model with or without birth and death processes was established in a spatially unbounded domain [9, 10]. For a age-space structured SIR model with seasonality, Zhang and Wang [36] established the threshold dynamics that basic reproduction number more than one or less than one determines whether or not disease extinction. Yang et al. [35] made an attempt to extend the methods and ideas in [5] to propose a model for the spatial spreading of brucellosis in a continuous bounded domain. Some basic mathematical arguments, including the existence and uniqueness of the solution and threshold dynamics, were successfully addressed.
Unlike in [13, 21] where disease transmission is modeled with a fixed incubation period in a spatial bounded domain, here we intend to incorporate an infection age to be a continuous variable and the fixed incubation period is ignored. This work can be considered as a continuation of the work [21]. For convenience, we shall adopt some notations used in [21], as proceeded below. With these considerations, we propose the following age-space-structured malaria model:
with the following initial condition
and boundary condition
Here, \(\beta (x)\) and \(\beta _1(a)\in L_+^\infty ({\mathbb {R}}_+)\) are the age-dependent disease transmission rate. All the location-dependent parameters are continuous, strictly positive and uniformly bounded functions on \({\overline{\Omega }}\).
We point here that the main difficulty lies in that (1.4) is formulated in a non-uniform Banach space. The existence and positivity of the solution should be carefully verified, to which adopt the methods used in [5, 35]. Comparing to [5, 35], we need to turn the existence of global nonnegative classical solution into a fixed point problem by inserting the first and third equation to the second equation due to the cross-infection mechanism. On the other hand, the cross-infection mechanism brings us difficulties in obtaining the explicit formula for the basic reproduction number through defining the next generation operator. Finally, in a homogeneous case, the local stability of equilibria achieved by studying the distribution of characteristic roots of characteristic equation, the strong persistence result and the global stability of equilibria achieved by Lyapunov functions in different cases are indeed not trivial, as proceed below.
We proceed the paper as follows: In section 2, we present the preliminary results on (1.4) with (1.5) and (1.6), and the well-posedness of the model is shown by verifying that the solution exists globally and the model admits a global attractor. Section 3 is spent on giving the basic reproduction number for (1.4) by appealing to the theories of the next generation operator and renewal equations. In section 4, the local and global stability problem for space-independent equilibria of (1.4) is studied in a homogeneous case. A brief conclusion section ends the paper.
2 Preliminaries
Denote by \({\mathbb {X}} = C({\overline{\Omega }},{\mathbb {R}})\) the Banach space endowed with the norm \(\Vert \phi \Vert _{\mathbb {X}} = \sup \limits _{x\in {\overline{\Omega }}}\{|\phi (x)|\}\), and let \({\mathbb {X}}_+\) be its positive cone. Denote by \({\mathbb {Y}} = L_1({\mathbb {R}}_+, {\mathbb {X}})\) the space of Lebesgue integrable functions endowed with the norm \(\Vert \varphi \Vert _{{\mathbb {Y}}} = \int \limits _0^\infty |\varphi (a)|_{{\mathbb {X}}}\mathrm{d}a\). The positive cone of \({\mathbb {Y}}\) is \({\mathbb {Y}}_+\).
Suppose that \(T_1(t), T_2(t): {\mathbb {X}}\rightarrow {\mathbb {X}},\ t\ge 0\) are the strongly continuous semigroups corresponding to the operators, \(D_m \Delta \) and \(D_h\Delta \), subject to (1.6), respectively. Clearly,
where \(\Gamma _i(t, x, y), i=1,2\) is the Green function associated with \(D_m \triangle \) and \(D_h\triangle \) subject to (1.6). It then follows from [27, Corollary 7.2.3] (see also in [24, Theorem 1.5]) that \(T_i(t) : {\mathbb {X}}\rightarrow {\mathbb {X}},\ t\ge 0\), \(i = 1, 2\), is strongly positive and compact. Further, \(T(t) = (T_1(t), T_1(t), T_2(t)): {\mathbb {X}}^3\rightarrow {\mathbb {X}}^3,\ t\ge 0\) forms a strongly continuous semigroup.
We place our problem on the state space \({\mathbb {X}}\times {\mathbb {Y}}\times {\mathbb {X}}\). For convenience, in what follows, we denote
where \(\chi =\mu , \beta , H\), respectively.
We next aim to prove that the solution of (1.4) exists globally and (1.4) admits a global attractor. For simplicity, we denote by \(\mathbb {{\tilde{X}}}={\mathbb {X}}\times {\mathbb {Y}}\times {\mathbb {X}}\) and \(\mathbb {{\tilde{X}}}_+={\mathbb {X}}_+\times {\mathbb {Y}}_+\times {\mathbb {X}}_+\). We first present the main result.
Theorem 2.1
For any \(\phi =(\phi _1, \phi _2, \phi _3)\in \mathbb {{\tilde{X}}}\), (1.4) admits a unique global nonnegative classical solution. Further, the solution semiflow, i.e.,
possesses a global attractor in \(\mathbb {{\tilde{X}}}_+\).
We shall first introduce the following lemmas and then combine with them to prove Theorem 2.1. For convenience, we always denote
For positive T, we define the space
Lemma 2.2
For any \(\phi \in \mathbb {{\tilde{X}}}_+\), (1.4) admits a unique nonnegative solution defined on \([0,T]\times {\overline{\Omega }}\) with \(T>0\).
Proof
In view of the \(S_m\) equation of (1.4), direct calculation yields
where \({\mathbb {F}}_1(t,x) = e^{-d_m t}\int \limits _\Omega \Gamma _1(t,x,y)\phi _1(y)\mathrm{d}y\). Similarly, in view of the \(I_h\) equation of (1.4), we get
where \({\mathbb {F}}_2(t,x) = e^{-(d_h+\rho )t}\int \limits _\Omega \Gamma _2(t,x,y)\phi _3(y)\mathrm{d}y\). It follows from (1.3) that
where \({\mathbb {F}}_3(t,x) = \int \limits _0^\infty \beta _1(a+t)\frac{\Pi (a+t)}{\Pi (a)}\int \limits _\Omega \Gamma _1(t,x,y)\phi _2(a,y)\mathrm{d}y\mathrm{d}a\).
Plugging (2.5) into (2.4) and then substituting (2.3) and (2.4) in (2.2) yield
where \({\mathbb {F}}_4(t,x)=\int \limits _0^t e^{-(d_h+\rho ) (t-s)}\int \limits _\Omega \Gamma _2(t-s,x,y)H(y)\int \limits _0^\infty \beta _1(a+s)\frac{\Pi (a+s)}{\Pi (a)}\int \limits _\Omega \Gamma _1(s,y,z)\phi _2(a,z)\mathrm{d}z\mathrm{d}a\mathrm{d}y\mathrm{d}s\).
Next, we claim that the nonlinear operator \({\mathbb {F}}\) has a fixed point, which in turn ensures that (1.4) admits a unique solution on [0, T]. For ease of notations, we denote
It then follows that the nonlinear operator \({\mathbb {F}}\) can be rewritten as:
By appealing the Banach–Picard fixed point theorem, we only need to verify that the nonlinear operator \({\mathbb {F}}\) is a strict contraction in \({\mathbb {Y}}_T\). To this end, we choose any \({\mathcal {B}}_1, {\mathcal {B}}_2\in {\mathbb {Y}}_T\) and let \(\widetilde{{\mathcal {B}}} = {\mathcal {B}}_1 - {\mathcal {B}}_2\) such that
where
and
Putting
which leads to
Choosing sufficiently small \(T >0\) such that \({\tilde{h}}(T)<1\). We arrive at the conclusion that \({\mathbb {F}}\) is a strict contraction in \({\mathbb {Y}}_T\), that is, the nonlinear operator \({\mathbb {F}}\) has a unique fixed point. This proves Lemma 2.2.
\(\square \)
We next to prove that the local solution of (1.4) remains positive for any \(\phi \in \mathbb {{\tilde{X}}}_+\).
Lemma 2.3
For any \(\phi \in \mathbb {{\tilde{X}}}_+\), we have that \(\forall t\in [0,T]\) and \(x\in \Omega \),
Proof
It is easily seen that due to the positivity of \(\mu (x)\) and \(\phi _1\),
where \(\widehat{{\mathbb {F}}}_1 = e^{-\int \limits _{s-t}^s\left( d_m + \frac{{\mathcal {B}}(\tau ,y)}{S_m(\tau ,y)}\right) d\tau } \int \limits _\Omega \Gamma _1(t,x,y)\phi _1(y)\mathrm{d}y\).
We next to prove the positivity of \({\mathcal {B}}(t,x)\) by the method of Picard sequences. We first set
where \(\overline{{\mathbb {F}}}_2(t,x)\) is defined in (2.7). Assume that \({\mathcal {B}}_n(t, x)>0\ (n\in {\mathbb {N}})\). We then directly get
It remains to show that the sequence \(\{{\mathcal {B}}_n(t,x)\}_{0}^{\infty }\) converges to \({\mathcal {B}}(t,x)\) in the sense that \(\lim \limits _{n\rightarrow \infty }{\mathcal {B}}_n(t,x)={\mathcal {B}}(t,x)\). To achieve this, we introduce
Hence,
Note that both sides of above equality always hold. It allows us to choose \({\tilde{x}}\in {\overline{\Omega }}\) such that \({\mathcal {B}}^*(t,{\widetilde{x}}) = \max \limits _{t\in [0,T], x\in {\overline{\Omega }}}{\widehat{{\mathcal {B}}}(t,x)}\). Hence, for any \(n\in {\mathbb {N}}\),
where \(H^*=\max \limits _{x\in \Omega }\{H(x)\}\) and \(S^*_m = \max \limits _{t\in [0,T]}\left\| S_m(t,\cdot )\right\| _{\mathbb {X}}\). By repeating the iteration, it is easily seen that
where \(L_\lambda = \frac{\beta ^*S^*_m{\overline{\beta }}_1H^*}{\lambda ^2}\). Hence, for any \(m, n\in {\mathbb {N}}\),
Choose \(\lambda \) large enough that \(L_\lambda < 1\). Consequently, as \(n\rightarrow \infty \), \(\left\| {\mathcal {B}}^*_{m}-{\mathcal {B}}^*_{n}\right\| _\infty \rightarrow 0\), implying that \(\lim \limits _{n\rightarrow \infty }{\mathcal {B}}_n(t,x)={\mathcal {B}}(t,x)\), \(\forall t\in [0,T]\) and \(x\in \Omega \). The positivity of \({\mathcal {B}}_n(t,x)\) directly implies that \({\mathcal {B}}(t,x)\) is positive.
We next to show that \(I_h(t,x)>0\) by contradiction. Assume to the contrary that there exist \(x_*\in \Omega \) and \(t_1\in (0, T)\) such that
By (2.4), together with the positivity of \({\mathcal {B}}(t,x)\), we can easily obtain
which results in a contradiction with \(I_h(t_1+\epsilon , x_*)< 0\). Hence, \(I_h(t,x)>0\) directly follows. This completes the proof. \(\square \)
Next, we confirm that the solution of (1.4) exists globally by extending solution existence interval from \([0, T]\times {\overline{\Omega }}\) to \([0,+\infty )\times {\overline{\Omega }}\).
Lemma 2.4
For any \(\phi \in \tilde{{\mathbb {X}}}_+\), (1.4) admits a unique nonnegative solution defined on \([0,\infty )\times {\overline{\Omega }}\).
Proof
In view of \(S_m\) equation of system (1.4), we know that \(S_m\) is governed by
According to [21, Lemma 1] and comparison principle, \(S_m\) is bounded above by the upper solution \(\frac{\mu ^*}{d_m}\), i.e., \(S_m \le \frac{\mu ^*}{d_m}=M_S\) for all \(t>0\) and \(x\in {\overline{\Omega }}\).
We now claim that for all \(t>0\) and \(x\in \Omega \), \({\mathcal {B}}(t,x)<\infty \) by contradiction. Assume to the contrary that there exist \(t^*>0\) and \(x^*\in \Omega \) such that \(\lim _{t\rightarrow t^*}{\mathcal {B}}(t,x^*) = +\infty \). In view of \(S_m\) equation of system (1.4), we get \(\lim _{t\rightarrow t^*}\partial _{t}S_m(t,x^*) = -\infty \), i.e., \(S_m(t,x^*)<0\) in near of \(t^*\). This leads to a contradiction to the positivity of \(S_m\) (see Lemma 2.3). Hence, \({\mathcal {B}}(t,x)<\infty \). Based on this fact, we assume that there exists \(M_B>0\) such that \({\mathcal {B}}(t,x)<M_B\).
Finally, we determine the boundedness of \(I_h(t,x)\). Let \({\widetilde{I}}= \int \limits _0^\infty i_m(t,a,x)\mathrm{d}a\), then it satisfies
It then follows that
Therefore, the solution of (1.4) exists globally. This proves Lemma 2.4. \(\square \)
By utilizing the previous lemmas, we shall give the proof of Theorem 2.1.
Proof of Theorem 2.1
By the assertions in Lemmas 2.2, 2.3 and 2.4, we know that the solution of (1.4) with initial condition \(\phi =(\phi _1, \phi _2, \phi _3)\in \mathbb {{\tilde{X}}}_+\) exists globally. Let \(\Phi (t) : \mathbb {{\tilde{X}}}_+\rightarrow \mathbb {{\tilde{X}}}_+, t \ge 0\), be the semiflow generated by the solution of (1.4), i.e.,
From Lemma 2.4, solution semiflow \(\Phi (t)\) is ultimately bounded. Hence, we can apply [16, Theorem 2.4.6] to confirm that (1.4) possesses a global attractor. This proves Theorem 2.1.
Throughout of the paper, we define the following positively invariant set, at which the dynamics of (1.4) are confined.
Letting \({\mathcal {M}}(t):=\int \limits _\Omega S_m \mathrm{d}x+\int \limits _\Omega {\widetilde{I}}\mathrm{d}x\). Integrate the \(i_m\) equation from 0 to \(\infty \), and integrating the \(S_m\) and \(i_m\) equation of system (1.4) over \(\Omega \) and then adding them up, yield
Hence, we obtain the a priori estimate
This implies
Hence, there exists \(t_0>0\) such that for any \(t > t_0\), \({\mathcal {M}}(t) \le \frac{\mu ^*|\Omega |}{d_m}\).
Denote by \({\widehat{I}}_h(t) = \int \limits _\Omega I_h(t,x)\mathrm{d}x\). We directly have
We integrate this differential inequality to obtain that for \(t_1 > t_0\),
Consequently, we can define the following positively invariant set
\(\square \)
3 The basic reproduction number
Obviously, (1.4) has a disease-free steady state \(E_0 = (\frac{\mu (x)}{d_m},0,0)\). Assuming that both humans and mosquitos are near \(E_0\). Following the standard procedures as those in [30] and [7], this section is spent on defining basic reproduction number of model (1.4).
Linearizing system (1.4) at \(E_0\) for infectious components yields
We integrate the \(i_m\) equation of (3.1) along the characteristic line \(t-a=const.\)
We substitute (3.2) in \(I_h\) (defined in (2.4)) resulting in
where \({\mathbb {F}}_2\) and \({\mathbb {F}}_4\) are defined in (2.4) and (2.6), respectively. Since (3.3) is a renewal equation, we can make Laplace transformation to (3.3)
Interchanging the order of integration (t and s) and letting \(t-s={\tilde{t}}\) (for simplicity, still denote \({\tilde{t}}\) by t) yield
Interchanging the order of integration (t and a) and letting \(t-a={\bar{t}}\) (for simplicity, still denote \({\bar{t}}\) by t) yield
Consequently, interchanging the order of integration (t and z) yields
Setting \(\lambda =0\) leads to
Hence, the following operator \({\mathcal {L}}\) is termed as the next generation operator
The following result indicates that \({\mathcal {L}}\) defined in (3.6) is strictly positive and compact.
Lemma 3.1
Let \({\mathcal {L}}\) be defined in (3.6). Then, \({\mathcal {L}}\) is strictly positive and compact.
Proof
It is easily seen that the operator \({\mathcal {L}}\) is positive. Due to the properties of \(\Gamma _1\) and \(\Gamma _2\), we can select a bounded sequence \(\{\phi _n\}_{n\in {\mathbb {N}}}\) in \({\mathbb {X}}\) such that for \({\mathbb {M}} > 0\) and \(\forall x\in \Omega \),
Hence,
that is, \({\mathcal {L}}\) is uniformly bounded. According to the Arzelà–Ascoli theorem, it remains to confirm that \({\mathcal {L}}\) is equicontinuous. In fact, for any \(x,{\bar{x}}\in \Omega \) with \(|x-{\bar{x}}|<\delta \) and \(y\in {\overline{\Omega }}\),
Due to the compactness of the operator \(\Delta \) and the uniform continuity of \(\Gamma _2(s,x,y)\), finding \(\varepsilon _0>0\) ensures
where \({\mathcal {M}}=|\Omega |\int \limits _0^{\infty }e^{-(d_h+\rho )s}ds\int \limits _0^\infty \beta _1(a)\Pi (a)\mathrm{d}a \) and \(|\Omega |\) is the volume of \(\Omega \). Using this \(\delta \) and \(\epsilon _0\), we know that \(|{\mathcal {L}}[\phi ](x)-{\mathcal {L}}[\phi ]({\bar{x}})|<\epsilon _0\), for all \(|x-{\bar{x}}|<\delta \). Consequently, the compactness of \({\mathcal {L}}\) directly follows (as \({\mathcal {L}}\) is uniformly bounded and equicontinuous). This proves Lemma 3.1. \(\square \)
According to the general results as those in [30] and [7], we define the basic reproduction number as:
where \(r(\cdot )\) is the spectral radius of the operator \({\mathcal {L}}\). As usual, it is difficult to obtain spectral radius of the next-generation operator \({\mathcal {L}}\), if not impossible, so that we cannot get further information on dynamical properties of (1.4). To proceed further, we will consider the homogeneous case that
4 Global stability problem of space-independent steady states
This section is spent on exploring the global stability problem of the space-independent equilibria of the following system:
Note that the assertions of model (1.4) in previous sections, including the existence and uniqueness of the solution, existence of global attractor, and definition of the basic reproduction number, still hold for (4.1). Obviously, (4.1) has a space-independent disease-free equilibrium \({\tilde{E}}_0 = (S_m^0,0,0)\), where \(S_m^0=\frac{\mu }{d_m}\). Similar to (1.3) and (3.2), \(i_m(t,a,x)\) takes the following form:
with \({\mathcal {B}}(t-a,y):=i_m(t-a,0,y)=\beta S_m(t-a,y)I_h(t-a,y)\).
Lemma 3.1, together with Krein–Rutman theorem (see, e.g., [2, Theorem 3.2]), implies that the basic reproduction number is the only positive eigenvalue of \({\mathcal {L}}\), with a positive eigenvector. Substituting \(\phi (x)\equiv \mathbf{1 } > 0\) in (3.6) and using \(\int \limits _{\Omega }\Gamma _i(\cdot ,x,y)\mathrm{d}y=1 (i=1,2)\), one gets
In this setting, the basic reproduction number of (4.1), \([\mathfrak {R}_0]\), is
Denote by \(E^* = (S_m^*, i_m^*(\cdot ), I_h^*)\) the space-independent endemic equilibrium of (4.1), if it exists. Then, it satisfies
Direct calculation gives
where \(K=\int \limits _0^\infty \beta _1(a)\Pi (a)\mathrm{d}a\) and \(i_m^*(0)=\frac{d_m (d_h+\rho )([\mathfrak {R}_0]-1)}{HK\beta }\).
Obviously, we have the following assertion.
Lemma 4.1
If \([\mathfrak {R}_0] > 1\), (4.1) has a space-independent endemic equilibrium \(E^*=(S^*_m, i^*_m(0)\Pi (a), I_h^*)\), which is unique and defined by (4.5).
4.1 Local dynamics
This subsection is spent on the local stability problem of \({\tilde{E}}_0\) and \(E^*\). To this end, letting \(E=({\bar{S}}_m, {\bar{i}}_m(\cdot ), {\bar{I}}_h)\) be any equilibrium of (4.1). We linearize (4.1) around E
We proceed to determine the characteristic equation of E. Since the linear system contains Laplacian term, we introduce the related theory from [6]. Denote by \(\lambda _j (j= 1,2,\ldots )\) the eigenvalues of operator \(-\Delta \) on a bounded set \(\Omega \) with boundary condition (1.6), that is, \(\Delta \nu (x)= -\zeta _i \nu (x)\). Hence,
corresponding to which there is the space of eigenfunctions in \(C^1(\Omega )\), denoted by \(E(\lambda _i)\).
Denote by \(\{\phi _{ij}|\ j =1,2,\ldots ,\dim E(\lambda _i)\}\) the orthogonal basis of \(E(\lambda _i)\). Further, let \({\mathbb {X}}_{ij} =\{c\phi _{ij}|\ c\in {\mathbb {R}}^3\}\) such that
It is well known that the parabolic problem \(\frac{\partial u(t,x)}{\partial t}=\Delta u(t,x)\) with \(\frac{\partial u(t,x)}{\partial n} = 0\), admits the exponential solution \(u(t,x)= e^{\eta t}\nu (x)\), where \(\nu (x)\in {\mathbb {X}}_i\). Substituting \((S_m, i_m(t,a,x), I_h)=e^{\eta t}(\psi (x), \xi (a,x), \phi (x))\) in (4.6) gets
Combined with the second and third equation of (4.7), we get that
We prove the following claim.
Claim
\(\eta \ne -(D_m\lambda _i+d_m)\) and \(\eta \ne -(D_h\lambda _i+d_h+\rho )\).
In fact, if \(\eta =-(D_m\lambda _i+d_m)\), together with the first equation of (4.7), implies that \( \xi (0,x)=0\). Hence, from the fourth equation of (4.7), we directly have \(\eta =-(D_h\lambda _i+d_h+\rho )\), which results in a contradiction. \(\eta \ne -(D_h\lambda _i+d_h+\rho )<0\) can be proved in a similar way.
This claim together with the first and fourth equation of (4.7) implies that
where \(f(\eta )=H\int \limits _0^\infty \beta _1(a)e^{-\eta a}{\tilde{\Pi }}(a)da\). Plugging (4.8) into the third equation of (4.7) and canceling \(\xi (0,x)\), we get
Hence, (4.9) indeed admits a principal eigenvalue \(\eta ^*\) (see, for example, [17, Lemma 2.2]).
The following result indicates that both \({\tilde{E}}_0\) and \(E^*\) are locally asymptotically stable (LAS) under threshold conditions, which is achieved by studying the distribution of characteristic roots of (4.9).
Theorem 4.2
Let \([\mathfrak {R}_0]\) be defined by (4.3).
-
(i)
If \([\mathfrak {R}_0]<1\), then \({\tilde{E}}_0\) is LAS;
-
(ii)
If \([\mathfrak {R}_0]>1\), then \(E^*\) is LAS.
Proof
Let us first prove (i). For \({\tilde{E}}_0\), that is, \({\bar{S}}_m=\frac{\mu }{d_m}\) and \({\bar{I}}_h=0\), (4.9) can be reduced to
Suppose, by contradiction, (4.10) admits a real root \(\eta >0\). We estimate (4.10)
which leads to a contradiction with \([\mathfrak {R}_0]<1\). Hence, all the real roots of (4.10) are negative. On the other hand, if (4.10) admits a pair of complex roots, denote by \(\eta =c\pm di\) with \(c\ge 0\) and \(d>0\), we then have
again a contradiction with \([\mathfrak {R}_0]<1\). This proves (i).
We next prove (ii). For \(E^*\), that is, \({\bar{S}}_m=S_m^*\) and \({\bar{I}}_h=I_h^*\), (4.9) can be reduced to
With \(\eta =c+di\) with \(c\ge 0\), we estimate the left-hand side (4.12),
The right-hand side (4.12) can be estimated as
which is a contradiction. Consequently, if \([\mathfrak {R}_0]>1\), all roots of (4.12) have negative real parts. This proves (ii). \(\square \)
4.2 Global dynamics
This subsection is spent on the global stability problem of \({\tilde{E}}_0\) and \(E^*\). Combined with local asymptotic stability (in subsection (4.1)) and global attractivity of equilibria, we shall confirm that both \({\tilde{E}}_0\) and \(E^*\) are globally asymptotically stable (GAS).
Theorem 4.3
If \([\mathfrak {R}_0]<1\) and \(\phi =(\phi _1, \phi _2,\phi _3)\in {\mathcal {D}}\), then \({\tilde{E}}_0\) is GAS.
Proof
It is well known that function
and \(G(u,u)=0\). By using this function, we define
where \({\mathbb {L}}_{S_m}=G(S_m(t,x), S_m^0)\), \({\mathbb {L}}_{i_m}=\int \limits _0^\infty \Theta _1(a)i_m(t,a,x)\mathrm{d}a\), \({\mathbb {L}}_{I_h}=\frac{S_m^0\beta }{d_h+\rho }I_h(t,x)\) and \(\Theta _1(a)\in L_1(\infty )\) will be determined later.
We take the derivative of \({\mathbb {L}}_{S_m}\),
With the help of (4.2), we rewrite \({\mathbb {L}}_{i_m}\)
We take the derivative of \({\mathbb {L}}_{i_m}\)
Collecting the terms with the form of (4.17), together with the fact that \(\frac{\partial \Gamma _1(t,x,y)}{\partial t}=D_m\Delta \Gamma _1(t,x,y)\) a.e. for \(x\in \Omega \), we get
We take the derivative of \({\mathbb {L}}_{I_h}(t,x)\)
With the help of (4.16), (4.18) and (4.20), we get the derivation of \({\mathbb {L}}(t)\)
Setting
Then, it satisfies
Hence, (4.21) becomes
Hence, the global attractiveness of \({\tilde{E}}_0\) holds in \({\mathcal {D}}\) when \([\mathfrak {R}_0] < 1\) (see, e.g., [31, Theorem 4.2 ]). This together with Theorem 4.2 indicates that the \({\tilde{E}}_0\) is GAS. This proves Theorem 4.3. \(\square \)
Define
In the following, we pay attention to the persistence problem of system (4.1) when \([\mathfrak {R}_0] > 1\). We first give the following lemma.
Lemma 4.4
Let \({\mathcal {D}}_0\) be defined by (4.22). If \([\mathfrak {R}_0] > 1\), then there exists \(\epsilon _1>0\) such that
Proof
Due to \([\mathfrak {R}_0] > 1\), we can select \(\epsilon _1 > 0\) such that
We will prove the assertion by contradiction. Assume, by contradiction, that there exists \(T_1>0\) such that for all \(t\ge T_1\) and \(x\in \Omega \), we have \({\mathcal {B}}(t,x)\le \epsilon _1\). By the inequality in (4.23), choosing \(T_2>T_1\) (denote by \(h=T_2-T_1\)) and \(\lambda >0\) small enough that
Note that \(S_m\) satisfies
Hence, direct integrating (4.25) yields
Further from (2.4),
Combined with the above two inequalities, we have
Note that \(\int \limits _0^\infty e^{-\lambda t}{\mathcal {B}}(t,x)\mathrm{d}t < \infty \) for all \(x\in \Omega \). Choose \({\widetilde{x}}\in \Omega \) that \({\mathcal {B}}(t,{\widetilde{x}}) = \min _{x\in \Omega }{\mathcal {B}}(t,x)\). By (4.26), we have
Interchanging the order of integration (t and s) and letting \(t-s={\bar{t}}\) (for simplicity, still denote \({\bar{t}}\) by t) yield
Interchanging the order of integration (t and a) and letting \(t-a={\bar{t}}\) (for simplicity, still denote \({\bar{t}}\) by t) yield
Consequently, we have
which results in a contradiction with (4.24). This proves Lemma 4.4. \(\square \)
Lemma 4.5
If \([\mathfrak {R}_0] > 1\), then \(\liminf _{t\rightarrow \infty }|{\mathcal {B}}(t,\cdot )|_{\mathbb {X}} > \epsilon _1\), \(\forall \phi \in {\mathcal {D}}_0\).
Proof
Suppose, by contradiction, that \(\lim \inf _{t\rightarrow \infty }|{\mathcal {B}}(t,\cdot )|_{\mathbb {X}} < \epsilon _1\). This together with Lemma 4.4 allows us to choose increasing sequences \(\{t_{1j}\}_{j=1}^\infty \), \(\{t_{2j}\}_{j=1}^\infty \), \(\{t_{3j}\}_{j=1}^\infty \) and a decreasing sequence \(\{t_{4j}\}_{j=1}^\infty \) such that \(t_{1j}>t_{2j}>t_{3j}\), \(\lim \limits _{j\rightarrow +\infty }t_{4j}=0\) that
It is easy to see that \(|{\mathcal {B}}(t,\cdot )|_{\mathbb {X}}<\epsilon _1\), for all \(t\in (t_{2j},t_{1j})\). When \(t=t_{2j}\), we denote by \(\{{S_m}_j\}_{j=1}^\infty \), \(\{{\mathcal {B}}_j\}_{j=1}^\infty \) and \(\{{I_h}_j\}_{j=1}^\infty \) be functional sequences in \({\mathbb {X}}\), which satisfies \(S_{mj}=S_m(t_{2j},\cdot )\in {\mathbb {X}}\), \({\mathcal {B}}_j= {\mathcal {B}}(t_{2j},\cdot )\in {\mathbb {X}}\) and \(I_{hj}=I_h(t_{2j},\cdot )\in {\mathbb {X}}\), respectively. From the expressions in (2.2)-(2.4), we can conclude that there exist \((\breve{S}_m, \breve{{\mathcal {B}}}, \breve{I}_h)\in {\mathbb {X}}^+\times {\mathbb {Y}}^+\times {\mathbb {X}}^+\) such that
In this setting, for all \(a\ge 0\) and \(x\in \Omega \), denote by \((S_m^\diamond ,i_m^\diamond (t,a, x),I_h^\diamond )\) the solution of (4.1) with
Here, the choice of \(\phi _2\) is based on (1.3). According to Lemma 4.4, there exists \(\tau ^*>0\) and \(\ell >0\) such that
Denote by \({\mathcal {B}}_j^\diamond (t,\cdot ) = {\mathcal {B}}(t+\theta _j,\cdot )\). The above inequalities imply that for sufficiently large j that
Corresponding to this, however, by letting \({\widetilde{t}}_j:=t_{1j}-t_{2j}\), (4.27) indicates that
For the cases where \(\tau ^*<{\widetilde{t}}_j\) and \(\tau ^*>{\widetilde{t}}_j\), it is easily seen that (4.28) and (4.29) contradict each other. This proves Lemma 4.5. \(\square \)
Combined with Lemmas 4.4 and 4.5, we directly have:
Theorem 4.6
If \([\mathfrak {R}_0] > 1\), system (4.1) is uniformly strongly persistent, that is, there exists \(\epsilon _0>0\) such that for \(x\in \Omega \) and \(a\ge 0\),
where \(U=S_m, i_m(t,a,x), I_h\), respectively.
Proof
For all \(a\ge 0, x\in \Omega \), Lemma 4.5 implies that there exist \(\epsilon _1>0\) and \(t_2>0\) such that \(i_m(t,a,x)>\epsilon _1 \Pi (a):=\epsilon _{i_m}\) for all \(t > t_2\). By using this estimate, the \(I_h\) equation of (4.1) satisfies
By a comparison principle, we have
where \(\frac{\epsilon _2HK}{d_h + \rho }\) is the unique positive steady state of the following system
In view of \(S_m\) equation of (4.1) and (2.9), there exists \(t_3>0\) such that
Again, from comparison principle, we have
Consequently, the theorem is proved by letting \(\epsilon _0=\min \{\epsilon _{S_m}, \epsilon _{i_m}, \epsilon _{I_h}\}\). \(\square \)
Theorem 4.7
If \([\mathfrak {R}_0] > 1\), then \(E^*\) is GAS for \(\phi \in {\mathcal {D}}_0\).
Proof
Let us define
where
and \(G(u,v) = u - v - v\ln \frac{u}{v},\ \text{ for }\ u,v>0\), and \(\Psi _1(a)\) will be determined later. We next wish to calculate the derivative of \(\overline{{\mathbb {L}}}_{S_m}\), \(\overline{{\mathbb {L}}}_{i_m}\), and \(\overline{{\mathbb {L}}}_{I_h}\), respectively.
We derivative \(\overline{{\mathbb {L}}}_{S_m}\) along the solution of (4.1)
Here, the equality, \(\mu = d_mS_m^*+i_m^*(0)\), is used. Using (4.2), rewriting \(\overline{{\mathbb {L}}}_{i_m}\) as
For convenience, let
and
It follows from the relations \(i^*(a) = i^*(0)e^{-d_ma}\) and \(\Pi (0)=1\) that
With the equality that \(u\frac{\partial }{\partial u}G[u, v] + v\frac{\partial }{\partial v}G[u, v] =G[u, v]\), we have
Note that \(\frac{\partial }{\partial t}\Gamma _1=D_m\Delta \Gamma _1\), \(\frac{\partial }{\partial u}G[u,v]=1-\frac{v}{u}\) and semigroup \((T(0)[\phi ])(x)=\int \limits _\Omega \Gamma _1(0,x,y)\phi (y)\mathrm{d}y\) is an unit semigroup. It follows that
Now we let
Then, it satisfies
Hence, (4.32) becomes
Taking derivative of \(\overline{{\mathbb {L}}}_{I_h}\) yields
For simplicity, we let
With the help of (4.31), (4.34) and (4.35), we then have
where
Collecting terms with \(i_m^*(0)\), \(i_m(t,0,x)\) and \(\frac{HS_m^*\beta }{d_h + \rho }\), respectively,
Here, we have used the fact that \(\left[ 1-\frac{I^*_h}{I_h}\right] S_m^*\beta I_h=i_m(t,0,x)\frac{S_m^*}{S_m}-i_m^*(0)\). Canceling the zero terms, together with \(i^*_m(0)=\frac{HS_m^*\beta }{d_h + \rho } \int \limits _0^\infty \beta _1(a)i^*_m(a)\mathrm{d}a\), yields
By a zero trick that \(1-\frac{S_mI_hi_m^*(0)}{S_m^*I^*_h i_m(t,0,x)}=0\), we have
where \(g(\alpha )=\alpha -1-\ln \alpha , \alpha \in {\mathbb {R}}_+\) possesses the properties that \(g(\alpha )\ge 0\) when \(\alpha \ge 1\) and \(g(1)=0\). Hence,
Hence, with the help of the property of g, \(\frac{\partial \overline{{\mathbb {L}}}(t,x)}{\partial t} = 0\) if and only if \(S_m = S_m^*\), \(i_m(t,a,x) = i_m^*(a)\) and \(I_h= I^*_h\). According to the invariance principle (see, e.g., [31, Theorem 4.2]), the global attractivity of \(E^*\) directly follows. This together with the local stability of \(E^*\), as stated in Theorem 4.2, implies that \(E^*\) is GAS for all \(a\ge 0, x\in \Omega \). This proves Theorem. \(\square \)
5 Conclusion and discussion
This paper provides the complete analysis on the threshold dynamics of an age-space structured malaria epidemic model. Unlike in [21] where the spatial movement of mosquitoes in EIP will result in non-local infection, here we intend to incorporate an infection age to be a continuous variable and the fixed incubation period is ignored. We conducted a complete analysis of model (1.4) by adopting the density of susceptible population to be H(x) and the mass action incidence, which can be regarded as a continuous work of [21]. In Lemma 2.2, we confirmed that (1.4) admits a unique local solution through investigating the fixed point problem, which is defined in (2.6). It is also proved that the local solution of (1.4) is positive for initial conditions (see Lemma 2.3). The positivity of \(i_m(t,a,x)\) is implied by the positivity of \({\mathcal {B}}(t,x)\), which is proved by the methods of Picard sequences and iteration. The proof of which is indeed not trivial, as \({\mathcal {B}}(t,x)\) involves the product of \(S_m\) and \(I_h\), as demonstrated in (2.6). In addition, we have extended the interval of existence of the local solution to \([0,+\infty )\). To achieve this, we verified that in a finite time interval, the solution does not blow up (see Lemma 2.4). Consequently, the solution semiflow generated by the solution of (1.4) possesses a global attractor in \(\mathbb {{\tilde{X}}}_+\).
By introducing the renewal equation and Laplace transformation, we identified that the next-generation operator \({\mathcal {L}}\) defined in (3.6) is strictly positive and compact (see Lemma 3.1), which allow us to define \(\mathfrak {R}_0\). It is important to mention that it is difficult to obtain spectral radius of \({\mathcal {L}}\), if not impossible, so that we cannot get further information on dynamical properties of (1.4). To proceed further, we considered the special case where parameters are all independent of x. In such a setting, the Krein–Rutman theorem ensures that \([\mathfrak {R}_0]\) can be explicitly obtained if the positive eigenvector (corresponding to \([\mathfrak {R}_0]\)) is a constant. It is also identified that if \([\mathfrak {R}_0]<1\), then space-independent disease-free equilibrium \({\tilde{E}}_0 = (S_m^0,0,0)\), where \(S_m^0=\frac{\mu }{d_m}\), is GAS (see Theorem 4.3); if \([\mathfrak {R}_0]>1\), then the model is uniformly persistent (see Theorem 4.6) and the space-independent endemic equilibrium \(E^*=(S^*_m, i^*_m(0)\Pi (a), I_h^*)\) is GAS (see Theorem 4.7). The local stability of \(E_0\) and \(E^*\) is achieved by studying the distribution of characteristic roots of characteristic equation (4.9) (see Theorem 4.2). The strong persistence result is implied by the weak persistence (see Lemmas 4.4 and 4.5), which is achieved by making the Laplace transformation and the way of contraction. Both \({\tilde{E}}_0\) and \(E^*\) are proved to be GAS by Lyapunov functions in different cases (see Theorem 4.3 and 4.7).
If the average incubation period is fixed as \(\tau \), and
as standard arguments in [13, 21], our model (1.4) can be reformulated into, for \(x\in \Omega ,\ t>0\),
with
where \(I_m = \int \limits _\tau ^\infty i_m(t,a,x)\mathrm{d}a\). As studied in [21, Section 4], with additional conditions, the global attractivity of endemic equilibrium in homogeneous case can be proved by using a fluctuation method.
If we further take seasonality into account, by using the standard arguments as those in [4, 36], our model (1.4) can be reformulated by following system, for \(x\in \Omega ,\ t>0\),
with
Here, \(\mu (t,x)\), \(\beta _2(t,x)\) and \(d_m(t,x)\) are the recruitment rate, biting rate and mortality rate involving the seasonality, respectively. The dynamics of (5.1) and (5.2) will be left for future investigation.
References
Aron, J.L., May, R.M.: The Population Dynamics of Malaria. In: Anderson, R.M. (ed.) The Population Dynamics of Infectious Diseases: Theory and Applications, pp. 139–179. Chapman and Hall, London (1982)
Amann, H.: Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rev. 18, 620–709 (1976)
Britton, N.F.: Spatial structures and periodic travelling waves in an integro-differential reaction-diffusion population model. SIAM J. Appl. Math. 50, 1663–1688 (1990)
Bai, Z., Peng, R., Zhao, X.-Q.: A reaction-diffusion malaria model with seasonality and incubation period. J. Math. Biol. 77, 201–228 (2018)
Chekroun, A., Kuniya, T.: An infection age-space structured SIR epidemic model with neumann boundary condition. Appl. Anal. 99(11), 1972–1985 (2020)
Cantrell, R.S., Cosner, C.: Spatial Ecology via Reaction-Diffusion Equations. Mathematical and Computational Biology, Wiley, West Sussex (2003)
Diekmann, O., Heesterbeek, J.A.P., Metz, J.A.J.: On the definition and the computation of the basic reproduction ratio \(R_0\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 (1990)
Chamchod, F., Britton, N.F.: Analysis of a vector-bias model on malaria transmission. Bull. Math. Biol. 73, 639–657 (2011)
Ducrot, A., Magal, P.: Travelling wave solutions for an infection-age structured model with diffusion. Proc. R. Soc. Edinb. 139, 459–482 (2009)
Ducrot, A., Magal, P.: Travelling wave solutions for an infection-age structured epidemic model with external supplies. Nonlinearity 24, 2891–2911 (2011)
Fitzgibbon, W.E., Morgan, J.J., Webb, G.: An outbreak vector-host epidemic model with spatial structure: the 2015–2016 Zika outbreak in Rio De Janeiro Theor. Biol. Med. Modell. 14, 7 (2017)
Grassly, N.C., Fraser, C.: Seasonal infectious disease epidemiology. Proc. R. Soc. B 273, 2541–2550 (2006)
Guo, Z., Wang, F.-B., Zou, X.: Threshold dynamics of an infective disease model with a fixed latent period and non-local infections. J. Math. Biol. 65, 1387–1410 (2012)
Gourley, S.A., Wu, J.: Delayed non-local diffusive systems in biological invasion and disease spread. In: Nonlinear Dynamics and Evolution Equations, AMS, Providence, RI (2006)
Gutierrez, J.B., Galinski, M.R., Cantrell, S., Voit, E.O.: From within host dynamics to the epidemiology of infectious disease scientific overview and challenges. Math. Biosci. 270, 143–155 (2015)
Hale, J.K.: Asymptotic Behavior of Dissipative Systems. Math. Survey Monogr, vol. 25. AMS, Providence (1988)
Hsu, S.B., Wang, F.-B., Zhao, X.-Q.: Dynamics of a periodically pulsed bio-reactor model with a hydraulic storage zone. J. Dynam. Differ. Equ. 23, 817–842 (2011)
Killeen, G.F., McKenzie, F.E., Foy, B.D., et al.: A simplified model for predicting malaria entomologic inoculation rates based on entomologic and parasitologic parameters relevant to control. Am. J. Trop. Med. Hyg. 62, 535–544 (2000)
Koella, J.C.: On the use of mathematical models of malaria transmission. Acta Trop. 49, 1–25 (1991)
Li, J., Zou, X.: Modeling spatial spread of infectious diseases with a fixed latent period in a spatially continuous domain. Bull. Math. Biol. 71, 2048–2079 (2009)
Lou, Y., Zhao, X.-Q.: A reaction-diffusion malaria model with incubation period in the vector population. J. Math. Biol. 62, 543–568 (2011)
Magal, P., Webb, G., Wu, Y.: On a vector-host epidemic model with spatial structure. Nonlinearity 31, 5589–5614 (2018)
Macdonald, G.: The Epidemiology and Control of Malaria. Oxford University Press, London (1957)
Pazy, A.: Semigroups of Linear Operators and Application to Partial Differential Equations. Springer, New York (1983)
Ross, R.: The Prevention of Malaria, 2nd edn. Murray, London (1911)
Smith, D.L., Dushoff, J., McKenzie, F.E.: The risk of a mosquito-borne infection in a heterogeneous environment. PLoS Biol. 2, 1957–1964 (2004)
Smith, H.L.: Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems. Math. Survey Monogr, vol. 41. AMS, Providence, RI (1988)
Villela, D.A.M., Bastos, L., Carvalho, L.M., et al.: Zika in Rio de Janeiro: assessment of basic reproduction number and comparison with dengue outbreaks. Epidemiol. Infect. 145, 1649–1657 (2016)
Vargas-De-León, C.: Global analysis of a delayed vector-bias model for malaria transmission with incubation period in mosquitoes. Math. Biosci. Eng. 9, 165–174 (2012)
Wang, W., Zhao, X.-Q.: Basic reproduction numbers for reaction-diffusion epidemic models. SIAM J. Appl. Dyn. Syst. 11, 1652–1673 (2012)
Walker, J.A.: Dynamical Systems and Evolution Equations: Theory and Applications. Plenum Press, New York (1980)
Wang, J., Chen, Y.: Threshold dynamics of a vector-borne disease model with spatial structure and vector-bias. Appl. Math. Lett. 100, 106052 (2020)
Wang, X., Zhao, X.-Q.: A periodic vector-bias malaria model with incubation period. SIAM J. Appl. Math. 77, 181–201 (2017)
Xu, Z., Zhao, X.-Q.: A vector-bias malaria model with incubation period and diffusion. Discrete Contin. Dyn. Syst. Ser. B 17, 2615–2634 (2012)
Yang, J., Xu, R., Li, J.: Threshold dynamics of an age-space structured brucellosis disease model with Neumann boundary condition. Nonlinear Anal. RWA. 50, 192–217 (2019)
Zhang, L., Wang, Z.: A time-periodic reaction-diffusion epidemic model with infection period. Z. Angew. Math. Phys. 67, 117 (2016)
Acknowledgements
The authors would like to thank the editor and the anonymous reviewers for his/her suggestions that have improved this paper.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and all of them read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
J. Wang was supported by National Natural Science Foundation of China (nos. 12071115, 11871179), Natural Science Foundation of Heilongjiang Province (nos. LC2018002, LH2019A021) and Heilongjiang Provincial Key Laboratory of the Theory and Computation of Complex Systems.
Rights and permissions
About this article
Cite this article
Wang, C., Wang, J. Analysis of a malaria epidemic model with age structure and spatial diffusion. Z. Angew. Math. Phys. 72, 74 (2021). https://doi.org/10.1007/s00033-021-01511-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-021-01511-z