A reaction–diffusion malaria model with seasonality and incubation period

Abstract

In this paper, we propose a time-periodic reaction–diffusion model which incorporates seasonality, spatial heterogeneity and the extrinsic incubation period (EIP) of the parasite. The basic reproduction number $\mathcal {R}_0$ is derived, and it is shown that the disease-free periodic solution is globally attractive if $\mathcal {R}_0<1$, while there is an endemic periodic solution and the disease is uniformly persistent if $\mathcal {R}_0>1$. Numerical simulations indicate that prolonging the EIP may be helpful in the disease control, while spatial heterogeneity of the disease transmission coefficient may increase the disease burden.

1 Introduction

Malaria is a mosquito-borne disease that is prevalent in about 100 countries in Africa, Southeast Asia, and the Americas (Gutierrez et al. 2015). The disease, caused by the protozoan plasmodium parasite, is spread in humans following an effective bite by an infected adult female Anopheles mosquito (after taking a blood meal from the human host) (Forouzannia and Gumel 2014). It directly threatens public health, and causes a large negative impact on local economies. The World Health Organization (WHO) estimates that approximately one million people die every year from malaria, with 85% of the mortality occurring in children under 5 years of age (Okuneye and Gumel 2017).

Mathematical models can help understand infectious disease dynamics, and thereby provide guides and suggestions for the control of the disease (Xiao and Zou 2014). The first model for malaria transmission was introduced by Ross (1911) and further extended by Macdonald (1957). Subsequent contributions have been made to the generalization of the Ross-Macdonald malaria models to consider various aspects related to epidemiological features of malaria, such as repeated age-structure (Forouzannia and Gumel 2014), effect of climate change (Lou and Zhao 2010) and exposure (Niger and Gumel 2008) etc. A typical feature is the “vector-bias”, which describes the difference between the probabilities of a mosquito picking humans.

A vector-bias model of malaria transmission was first proposed by Kingsolver in Kingsolver (1987). It investigated the greater attractiveness of infectious humans to mosquitoes. Empirical evidence shows that mosquitoes prefer to bite humans infected with malaria (Lacroix et al. 2005). Following Kingsolver’s work, Hosack et al. (2008) incorporated an extrinsic incubation time in mosquitoes into a vector-bias model to study the dynamics of the disease in term of a threshold index. Chamchod and Britton (2011) extended the vector-bias model from previous authors by defining the attractiveness in a different way. Buonomo and Vargas-De-León (2013) further provided a complete global analysis of the original vector-bias model in Chamchod and Britton (2011) and extended the model to incorporate both immigration and disease-induced death of humans. For other works on vector-bias model, we refer to Abboubakar et al. (2016), Buonomo and Vargas-De-León (2013), Vargas-De-León (2012), Xu and Zhao (2012) and references therein. However, the following two important biological factors related to malaria transmission seem to have received little attention among these studies:

• (i) the seasonality for vector-borne infections. It is widely accepted that climate change affects the distribution and seasonal dynamics of mosquito populations, with substantial implications for disease seasonality and persistence (Ewing et al. 2016). For example, seasonal variation in mosquito abundance due to annual variation in temperature and rainfall can lead to seasonal patterns of malaria epidemics in the Kenyan highlands (Grassly and Fraser 2006; Hay et al. 2003). Therefore, it is important to consider the seasonal influence of vector populations in the study of vector-borne diseases.

• (ii) the spatial heterogeneity of the habitats of hosts and vectors. Spatial dispersal of human and vector populations has also contributed to the spread of vector-borne diseases (Cosner et al. 2009; Lou and Zhao 2011; Tatem et al. 2006). In addition, the non-random distribution of humans and mosquitoes across the landscape can generate spatially heterogeneous biting patterns (Smith et al. 2004). In recent years, researchers have started to explore the spatial transmission dynamics of malaria (see, e.g., Lou and Zhao 2011; Xu and Zhao 2012).

In this paper, motivated by the malaria transmission models in Chamchod and Britton (2011), Lou and Zhao (2011) and Wang and Zhao (2017), we formulate a time-delayed periodic reaction–diffusion model by taking into account the seasonality and the spatial heterogeneity. The model contains a time delay accounting for the extrinsic incubation period (EIP) of mosquitoes. The EIP has a significant impact on the disease dynamics. The longevity of a female adult mosquito ranges from 3 to 100 days and the EIP varies from 10 to 30 days (Wang and Zhao 2017). These infected mosquitoes that survive the EIP will remain infectious for the rest of their lives. Thus, the EIP directly influences the number of infectious mosquitoes.

The rest of the paper is organized as follows. In the next section, we derive the model rigorously, and study its well-posedness. In Sects. 3 and 4, we introduce the basic reproduction number $\mathcal {R}_0$ for the model via the next generation operators approach, and study the threshold dynamics in terms of $\mathcal {R}_0$. In Sect. 5, based on the computational method for $\mathcal {R}_0$ in Liang et al. (2017), we use numerical simulations to reveal the influences of heterogeneous infection, the EIP and vector-bias on malaria transmission. And the paper ends with a brief discussion.

2 The model

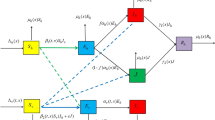
In order to take into account the mobility of individuals, seasonality effect and the EIP, we follow the ideas in Lou and Zhao (2011) and Wang and Zhao (2017) to develop a spatial model for malaria infection. The human population is divided into two epidemiological classes: susceptible $(S_h)$ and infectious $(I_h)$. Assume that the density of total human population, $N_h(t,x)=S_h(t,x)+ I_h(t,x)$, is described by the following reaction–diffusion equation

$$\begin{aligned} \frac{\partial N_h}{\partial t}=D_h \triangle N_h-d_h N_h+B(x,N_h)N_h,\,\,t>0, \,x\in \varOmega , \end{aligned}$$

(1)

where $\varOmega$ is the spatial habitat with smooth boundary $\partial \varOmega$, denoted by $\partial \varOmega$; $D_h>0$ is the diffusion coefficient; $d_h>0$ is the death rate of human; B, representing the birth rate of human, is a nonnegative function. Two prototypical birth rate functions in the biological literature are $B(x,u)=b_he^{-u/K(x)}$ and

$$\begin{aligned} \begin{array}{l} B(x,u)=\left\{ \begin{array}{l@{\quad }l} b_h\left[ 1-\frac{u}{K(x)}\right] , &{} 0\le u\le K(x), x\in \bar{\varOmega },\\ 0,&{} u>K(x), x\in \bar{\varOmega }, \end{array}\right. \end{array} \end{aligned}$$

where $b_h>0$ is the maximal individual birth rate of human, and K(x), standing for the local carrying capacity, is supposed to be a positive function of location x. Assume that no population flux crosses the boundary $\partial \varOmega$, and hence, we impose the Neumann boundary condition:

$$\begin{aligned} \frac{\partial N_h}{\partial \nu }=0,\,\,t>0, x\in \partial \varOmega , \end{aligned}$$

(2)

where $\nu$ is the outward unit normal vector on $\partial \varOmega$. Usually, system (1)–(2) admits a globally attractive positive steady state H(x) in $C(\bar{\varOmega }, {\mathbb {R}}_+){\setminus } \{0\}$ under appropriate assumptions [see, e.g., (Zhao 2017b, Theorems 3.1.5 and 3.1.6)]. For simplicity, we then assume that the total density of human at time t and location x stabilizes at H(x), that is, $N_h(t,x)\equiv H(x), \forall \,t\ge 0, x\in \varOmega .$

Let $S_m(t,x)$ and $I_m(t,x)$ be the spatial densities of susceptible and infectious female adult mosquitoes, respectively. Compared with the life span of a mosquito, the longevity of a human is quite long. The climate factor has little impact on human activities. Thus, we take all the parameters related to humans as constants. To incorporate a vector-bias term into the model, we introduce the parameters p and l to describe the probabilities with which a mosquito arrives at a human at random and picks the human if he is infectious and susceptible, respectively (Chamchod and Britton 2011; Wang and Zhao 2017). Since infectious humans are more attractive to mosquitoes, we assume that $p\ge l>0$. The biting rate $\beta (t,x)$ of mosquitoes is the number of bites per mosquito per unit time at time t and location x. Following the approach in Chamchod and Britton (2011) and Wang and Zhao (2017), the probabilities of a mosquito picking a susceptible human and an infectious human are

$$\begin{aligned} \frac{l[H(x)-I_h(t,x)]}{pI_h(t,x)+l[H(x)-I_h(t,x)]}\quad \text{ and }\quad \frac{pI_h(t,x)}{pI_h(t,x)+l[H(x)-I_h(t,x)]}, \end{aligned}$$

respectively. Then the number of newly infectious humans and newly infected mosquitoes per unit time at time t and location x is, respectively, given by

$$\begin{aligned} c\beta (t,x)\frac{l[H(x)-I_h(t,x)]}{pI_h(t,x)+l[H(x)-I_h(t,x)]} I_m(t,x), \end{aligned}$$

and

$$\begin{aligned} b\beta (t,x)\frac{pI_h(t,x)}{pI_h(t,x)+l[H(x)-I_h(t,x)]} S_m(t,x), \end{aligned}$$

where c(b) is the transmission probability per bite from infectious mosquitoes (humans) to susceptible humans (mosquitoes). We assume that $D_m$ is the diffusion coefficient for mosquitoes. Then the dynamics of infectious humans and susceptible adult mosquitoes can be described by

$$\begin{aligned} \begin{aligned} \frac{\partial I_h(t,x)}{\partial t}=D_h \triangle I_h(t,x)+\frac{c\beta (t,x)l[H(x)-I_h(t,x)]}{pI_h(t,x)+l[H(x)-I_h(t,x)]}I_m(t,x)-(d_h+\rho )I_h(t,x), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \frac{\partial S_m(t,x)}{\partial t}&=D_m \triangle S_m(t,x)+\mu (t,x)-d_m(t,x)S_m(t,x)\\&\quad -\frac{b\beta (t,x)p I_h(t,x)}{pI_h(t,x)+l[H(x)-I_h(t,x)]}S_m(t,x), \end{aligned} \end{aligned}$$

where $d_h$ is the natural death rate of humans, $\rho$ is the recovery rate of humans, $\mu (t,x)$ is the recruitment rate at which adult female mosquitoes emerge from larval at time t and location x, and $d_m(t,x)$ stands for the mortality rate for female adult mosquitoes. Here we assume that the recruitment rate of the mosquito population is independent of the actual density of adult mosquitoes. This is because only a fraction of a large reservoir of eggs and larvae matures to the adult stage, and the process does not depend directly on the size of the adult mosquito population (Esteva and Vargas 1998).

To incorporate the EIP into the model, the infected mosquito population is divided into two epidemiological categories: latent $(E_m)$ and infectious $(I_m)$. Since the latent mosquitoes can fly around during the incubation period, we introduce an infection age variable a. Let y(t, a, x) be the density of the mosquito population with infection age a at time t and location x. By a standard argument on structured population and spatial diffusion (see, e.g., Metz and Diekmann 1986), we get

$$\begin{aligned} \frac{\partial y(t,a,x)}{\partial t}+\frac{\partial y(t,a,x)}{\partial a}=D_m \triangle y(t,a,x)-d_m(t,x) y(t,a,x), \end{aligned}$$

(3)

where $d_m(t,x)$ is the mosquito death rate which is independent of the infection age. Suppose that $\tau$ is the average incubation period, we then have

$$\begin{aligned} E_m(t,x)=\int _0^\tau y(t,a,x)da,\,\,\,I_m(t,x)=\int _\tau ^{\infty } y(t,a,x)da. \end{aligned}$$

(4)

Differentiating (4) with respect to t and using (3), we obtain

$$\begin{aligned} \frac{\partial E_m(t,x)}{\partial t}=D_m\triangle E_m(t,x)-d_m(t,x)E_m(t,x)-y(t,\tau ,x)+y(t,0,x), \end{aligned}$$

(5)

and

$$\begin{aligned} \frac{\partial I_m(t,x)}{\partial t}=D_m\triangle I_m(t,x)-d_m(t,x)I_m(t,x)-y(t,\infty ,x)+y(t,\tau ,x), \end{aligned}$$

(6)

respectively. Biologically, we assume that $y(t,\infty , x) = 0$. Since the recruitment of newly infected mosquitoes y(t, 0, x) arise from the contact of susceptible mosquitoes and infectious humans, it follows that

$$\begin{aligned} y(t,0,x)=\frac{b\beta (t,x)p I_h(t,x)}{pI_h(t,x)+l[H(x)-I_h(t,x)]}S_m(t,x). \end{aligned}$$

Now we determine $y(t,\tau ,x)$ by the method of characteristics. For any $\xi \ge 0$, consider solutions of (3) along the characteristic line $t=a+\xi$ by letting $v(\xi ,a,x) =y(a+\xi ,a,x)$. Then for $a\in (0, \tau ]$, we have

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial v(\xi ,a,x)}{\partial a}&=\left[ \frac{\partial y(t,a,x)}{\partial t}+\frac{\partial y(t,a,x)}{\partial a}\right] _{t=a+\xi }\\&=D_m \triangle y(a+\xi ,a,x)-d_m(t,x) y(a+\xi ,a,x)\\&=D_m \triangle v(\xi ,a,x)-d_m(t,x) v(\xi ,a,x),\\ v(\xi ,0,x)&=y(\xi ,0,x)=\frac{b\beta (\xi ,x)p I_h(\xi ,x)}{pI_h(\xi ,x)+l[H(x)-I_h(\xi ,x)]}S_m(\xi ,x). \end{aligned} \right. \end{aligned}$$

Regarding $\xi$ as a parameter and solving the above equation, we obtain

$$\begin{aligned} v(\xi ,a,x)=\int _\varOmega \varGamma (\xi +a,\xi ,x,y)\frac{b\beta (\xi ,y)p I_h(\xi ,y)}{pI_h(\xi ,y)+l[H(y)-I_h(\xi ,y)]}S_m(\xi ,y)dy, \end{aligned}$$

(7)

where $\varGamma (t,s,x,y)$ is the fundamental solution of the operator $\partial _t-D_m\triangle +d_m(t,\cdot )$ associated with the Neumann boundary condition (see Friedman 1964, Chapter 1). Note that $\varGamma (t,s,x,y)=\varGamma (t+\omega ,s+\omega ,x,y)$ for all $t>s\ge 0$ and $x,y\in \varOmega$ due to $d_m(t,\cdot )=d_m(t+\omega ,\cdot )$. Since $y(t,a,x)=v(t-a,a,x), t\ge a$, it follows that

$$\begin{aligned} y(t,\tau ,x)=\int _\varOmega \varGamma (t,t-\tau , x,y)\frac{b\beta (t-\tau ,y)p I_h(t-\tau ,y)}{pI_h(t-\tau ,y)+l[H(y)-I_h(t-\tau ,y)]}S_m(t-\tau ,y)dy. \end{aligned}$$

(8)

Substituting (8) into (5) and (6) respectively, and dropping the $E_m(t,x)$ (since it is decoupled from the $I_h(t,x), S_m(t,x)$ and $I_m(t,x)$ equations), we obtain the following system

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial u_1(t,x)}{\partial t}&=D_h \triangle u_1(t,x)+\frac{c\beta (t,x)l[H(x)-u_1(t,x)]}{pu_1(t,x)+l[H(x)-u_1(t,x)]}u_3(t,x),\\&\quad -(d_h+\rho )u_1(t,x),\,\,t>0, x\in \varOmega ,\\ \frac{\partial u_2(t,x)}{\partial t}&=D_m \triangle u_2(t,x)+\mu (t,x)-d_m(t,x)u_2(t,x)\\&\quad -\frac{b\beta (t,x)p u_1(t,x)}{pu_1(t,x)+l[H(x)-u_1(t,x)]}u_2(t,x),\,\,t>0, x\in \varOmega ,\\ \frac{\partial u_3(t,x)}{\partial t}&=D_m\triangle u_3(t,x)-d_m(t,x)u_3(t,x)\\&\quad +\int _\varOmega \varGamma (t,t-\tau , x,y)\frac{b\beta (t-\tau ,y)p u_1(t-\tau ,y)}{pu_1(t-\tau ,y)+l[H(y)-u_1(t-\tau ,y)]}u_2(t-\tau ,y)dy,\\ t&>0, x\in \varOmega ,\\ \frac{\partial u_1(t,x)}{\partial \nu }&=\frac{\partial u_2(t,x)}{\partial \nu }=\frac{\partial u_3(t,x)}{\partial \nu }=0,\,\,\,t>0, x\in \partial \varOmega , \end{aligned} \right. \end{aligned}$$

(9)

where $(u_1(t,x),u_2(t,x),u_3(t,x))=(I_h(t,x),S_m(t,x), I_m(t,x))$. All constant parameters in model (9) are positive, and functions $\beta (t,x)$ and $\mu (t,x)$ are Hölder continuous and nonnegative nontrivial on ${\mathbb {R}}\times \bar{\varOmega }$, and $\omega$-periodic in t. The function $d_m(t,x)$ is Hölder continuous and positive on ${\mathbb {R}}\times \bar{\varOmega }$, and $\omega$-periodic in t.

Let $\mathbb {X}: = C(\bar{\varOmega }, {\mathbb {R}}^3)$ be the Banach space with the supremum norm $\Vert {\cdot }\Vert _{\mathbb {X}}$. For $\tau > 0$, define $C:=C([-\tau , 0],\mathbb {X})$ with the norm $\Vert \phi \Vert = \max _{\theta \in [-\tau ,0]}\Vert \phi (\theta )\Vert _\mathbb {X}, \forall \,\phi \in C$. Then C is a Banach space. Define $\mathbb {X}^+: =C(\bar{\varOmega }, {\mathbb {R}}_+^3)$ and $C^+: =C([-\tau ,0], \mathbb {X}^+)$, then both $(\mathbb {X},\mathbb {X}^+)$ and $(C, C^+)$ are strongly ordered spaces. Given a function $z: [-\tau ,\sigma )\rightarrow \mathbb {X}$ for $\sigma >0$, we define $z_t\in C$ by

$$\begin{aligned} z_t(\theta )=(z_1(t+\theta ), z_2(t+\theta ), z_3(t+\theta )),\,\,\forall \,\theta \in [-\tau ,0], \end{aligned}$$

for any $t\in [0,\sigma )$. Let $\mathbb {Y}:=C(\bar{\varOmega }, {\mathbb {R}})$ and $\mathbb {Y}^+:=C(\bar{\varOmega }, {\mathbb {R}}_+)$. Set

$$\begin{aligned}&\mathbb {Y}_H:=\{\varphi \in \mathbb {Y}^+: 0\le \varphi (x)\le H(x), \forall \,x\in \bar{\varOmega }\},\\&W_H: = C\left( [-\,\tau ,0], \mathbb {Y}_H \times \mathbb {Y}^+\times \mathbb {Y}^+\right) . \end{aligned}$$

Suppose that $T_1(t,s), T_2(t,s): \mathbb {Y}\rightarrow \mathbb {Y},$ are, respectively, the evolution operators associated with

$$\begin{aligned} \frac{\partial u_1(t,x)}{\partial t}=D_h \triangle u_1(t,x)-(d_h+\rho )u_1(t,x),\,\,t>0,x\in \varOmega , \end{aligned}$$

and

$$\begin{aligned} \frac{\partial u_2(t,x)}{\partial t}=D_m \triangle u_2(t,x)-d_m(t,x)u_2(t,x), \,\,t>0,x\in \varOmega , \end{aligned}$$

subject to the Neumann boundary condition. Noting that $T_1(t,s)=T_1(t-s)$, we have $T_1(t+\omega ,s+\omega )=T_1(t,s)$ for $(t,s)\in {\mathbb {R}}^2$ with $t\ge s$. Since $d_m(t,\cdot )$ is $\omega$-periodic in t, (Daners and Koch 1992, Lemma 6.1) implies that $T_2(t+\omega ,s+\omega )=T_2(t,s)$ for $(t,s)\in {\mathbb {R}}^2$ with $t\ge s$. Moreover, for $(t,s)\in {\mathbb {R}}^2$ with $t>s$, $T_1(t,s)$ and $T_2(t,s)$ are compact and strongly positive. Then $T(t,s)=\mathrm{diag}(T_1(t,s),T_2(t,s),T_2(t,s)): \mathbb {X}\rightarrow \mathbb {X}$ is an evolution operator for $(t,s)\in {\mathbb {R}}^2$ with $t\ge s$.

Define $F=(F_1,F_2,F_3): [0,+\,\infty )\times W_H\rightarrow \mathbb {X}$ by

$$\begin{aligned} F_1(t,\phi ):&=\frac{c\beta (t,\cdot )l[H(\cdot )-\phi _1(0,\cdot )]}{p\phi _1(0,\cdot )+l[H(\cdot )-\phi _1(0,\cdot )]}\phi _3(0,\cdot ),\\ F_2(t,\phi ):&=\mu (t,\cdot )-\frac{b\beta (t,\cdot )p \phi _1(0,\cdot )}{p\phi _1(0,\cdot )+l[H(\cdot )-\phi _1(0,\cdot )]}\phi _2(0,\cdot ),\\ F_3(t,\phi ):&=\int _\varOmega \varGamma (t,t-\tau , \cdot ,y)\frac{b\beta (t-\tau ,y)p \phi _1(-\tau ,y)}{p\phi _1(-\tau ,y)+l[H(y)-\phi _1(-\tau ,y)]}\phi _2(-\tau ,y)dy \end{aligned}$$

for $t\ge 0, x\in \bar{\varOmega }$ and $\phi =(\phi _1,\phi _2,\phi _3)\in W_H$. Then system (9) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \frac{\partial u(t,x)}{\partial t} =A(t)u(t,x)+F(t,u_t), &{}t>0,x\in \varOmega ,\\ u(\theta ,x)=\phi (\theta ,x), &{}\theta \in [-\tau ,0], x\in \varOmega , \end{array} \right. \end{aligned}$$

(10)

where $u(t,x):=(u_1(t,x),u_2(t,x),u_3(t,x))$, $A(t)=\mathrm{diag}(A_1, A_2(t), A_2(t))$, $A_1$ is defined by

$$\begin{aligned}&D(A_1)=\left\{ \varphi \in C^2(\bar{\varOmega })\,:\,\frac{\partial \varphi }{\partial \nu }=0\,\text{ on }\,\partial \varOmega \right\} ,\\&A_1\varphi =D_h \triangle \varphi -(d_h+\rho )\varphi , \,\,\,\forall \,\varphi \in D(A_1), \end{aligned}$$

and $A_2(t)$ is defined by

$$\begin{aligned}&D(A_2(t))=\left\{ \varphi \in C^2(\bar{\varOmega })\,:\,\frac{\partial \varphi }{\partial \nu }=0\,\text{ on }\,\partial \varOmega \right\} ,\\&A_2(t)\varphi =D_m \triangle \varphi -d_m(t,x)\varphi , \,\,\forall \,\varphi \in D(A_2(t)). \end{aligned}$$

Lemma 1

For any $\phi \in W_H$, system (9) has a unique solution, denoted by $z(t,\cdot ,\phi )$, on its maximal existence interval $[0,\bar{t}_\phi )$ with $z_0=\phi$, where $\bar{t}_\phi \le \infty$. Furthermore, $z(t,\cdot ,\phi )\in \mathbb {Y}_H\times \mathbb {Y}^+\times \mathbb {Y}^+, \forall \,t\in [0,\bar{t}_\phi )$ and $z(t,\cdot ,\phi )$ is a classical solution of (9) for all $t>\tau$.

Proof

According to the abstract setting of Martin and Smith (1990), one can see that a mild solution of (10) is a continuous solution to its associated integral equation

$$\begin{aligned} \left\{ \begin{aligned}&u(t,\phi )=T(t,0)\phi (0)+\int _0^t T(t,s)F(s,u_s)ds,\,\,\forall \,t>0,\\&u_0=\phi . \end{aligned} \right. \end{aligned}$$

Let $\bar{\beta }=\max _{t\in [0,\omega ],x\in \bar{\varOmega }}\beta (t,x)$ and $\tilde{H}=\min _{x\in \bar{\varOmega }} H(x)$. Clearly, F is locally Lipschitz continuous. For any $(t,\phi )\in [0,+\,\infty )\times W_H$ and $k> 0$, in view of $p\ge l>0$, we have

$$\begin{aligned}&\phi (0,x)+k F(t,\phi )(x)\\&\quad =\left( \begin{array}{c} \phi _1(0,x)+k \frac{c\beta (t,x)l[H(x)-\phi _1(0,x)]}{p\phi _1(0,x)+l[H(x)-\phi _1(0,x)]}\phi _3(0,x)\\ \phi _2(0,x)+k\left( \mu (t,x)-\frac{b\beta (t,x)p \phi _1(0,x)}{p\phi _1(0,x)+l[H(x)-\phi _1(0,x)]}\phi _2(0,x)\right) \\ \phi _3(0,x)+k\int _\varOmega \varGamma (t,t-\tau , \cdot ,y)\frac{b\beta (t-\tau ,y)p \phi _1(-\tau ,y)}{p\phi _1(-\tau ,y)+l[H(y)-\phi _1(-\tau ,y)]}\phi _2(-\tau ,y)dy \\ \end{array} \right) \\&\quad \ge \left( \begin{array}{c} \phi _1(0,x)+k \frac{c\beta (t,x)l}{pH(x)}[H(x)-\phi _1(0,x)]\phi _3(0,x)\\ \phi _2(0,x)+k \left( \mu (t,x)-\frac{b\beta (t,x)p }{l H(x)}\phi _1(0,x)\phi _2(0,x) \right) \\ \phi _3(0,x)+k\int _\varOmega \varGamma (t,t-\tau , \cdot ,y)\frac{b\beta (t-\tau ,y) }{H(y)}\phi _1(-\tau ,y)\phi _2(-\tau ,y)dy \\ \end{array} \right) \\&\quad \ge \left( \begin{array}{c} \phi _1(0,x)\left( 1-k\frac{c\bar{\beta }l}{p \tilde{H}}\phi _3(0,x)\right) \\ \phi _2(0,x)\left( 1-k\frac{b\bar{\beta }p}{l\tilde{H}}\phi _1(0,x) \right) \\ \phi _3(0,x) \\ \end{array} \right) , \end{aligned}$$

where the vector inequalities are understood componentwise, and

$$\begin{aligned}&H(x)-[\phi _1(0,x)+k F_1(t,\phi )(x)]\\&\quad =[H(x)-\phi _1(0,x)]\left[ 1-\frac{k c\beta (t,x)l}{p\phi _1(0,x)+l[H(x)-\phi _1(0,x)]}\phi _3(0,x)\right] \\&\quad \ge [H(x)-\phi _1(0,x)]\left[ 1-\frac{k c\beta (t,x)}{H(x)}\phi _3(0,x)\right] . \end{aligned}$$

This implies that

$$\begin{aligned} \lim _{k\rightarrow 0^+} \frac{1}{k}\mathrm{dist}\left( \phi (0,\cdot )+k F(t,\phi ), \mathbb {Y}_H\times \mathbb {Y}^+\times \mathbb {Y}^+\right) =0,\,\,\forall \,(t,\phi )\in {\mathbb {R}}_+\times W_H. \end{aligned}$$

Since H(x) is a steady state of system (1)–(2), it easily follows that $D_h \varDelta H(x)-d_hH(x)\le 0$, and hence

$$\begin{aligned} T(t,s): \mathbb {Y}_H\times \mathbb {Y}^+\times \mathbb {Y}^+\rightarrow \mathbb {Y}_H\times \mathbb {Y}^+\times \mathbb {Y}^+,\,\,\forall \,t\ge s\ge 0. \end{aligned}$$

Consequently, by Martin and Smith (1990, Corollary 4) with $K=\mathbb {Y}_H\times \mathbb {Y}^+\times \mathbb {Y}^+$ and $S(t,s) =T(t,s)$, system (9) has a unique non-continuable mild solution $z(t,\cdot ,\phi )$ with $z_0=\phi$ on its maximal existence interval $t\in [0, \bar{t}_{\phi })$, where $\bar{t}_{\phi }\le \infty$, and $z(t,\cdot , \phi )\in \mathbb {Y}_H\times \mathbb {Y}^+\times \mathbb {Y}^+$, $t\in [0,\bar{t}_{\phi })$. Moreover, by the analyticity of T(t, s) with respect to $(t,s)\in {\mathbb {R}}^2, t>s$, $z(t,\cdot ,\phi )$ is a classical solution when $t>\tau$. $\square$

To proceed further, we need some information on the following scalar periodic reaction–diffusion equation

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial w(t,x)}{\partial t}=D\triangle w(t,x)+g(t,x)-\mu (t,x)w(t,x),\,\,t>0,x\in \varOmega ,\\&\frac{\partial w}{\partial \nu }=0, \,\,t>0,x\in \partial \varOmega , \end{aligned} \right. \end{aligned}$$

(11)

where $D>0, g(t,x)\not \equiv 0$ is a Hölder continuous and nonnegative function for $t>0$ and $x\in \bar{\varOmega }$, $\mu (t, x)$ is Hölder continuous and positive for $t>0$ and $x\in \bar{\varOmega }$. Furthermore, $g(t,\cdot )$ and $\mu (t,\cdot )$ are $\omega$-periodic in t. Then we have the following observation.

Lemma 2

(Zhang et al. 2015, Lemma 2.1) System (11) admits a unique positive $\omega$-periodic solution $w^*(t,\cdot )$ which is globally attractive in $\mathbb {Y}^+$.

Let $C_H: = C([-\tau ,0], \mathbb {Y}_H)\times C([-\tau ,0],\mathbb {Y}^+)\times \mathbb {Y}^+$. For any given $\varphi \in C_H$, we define $\hat{\varphi }=(\varphi _1,\varphi _2,\hat{\varphi }_3)$, where $\hat{\varphi }_3(\theta ,\cdot )=\varphi _3(\cdot )\in \mathbb {Y}^+, \forall \,\theta \in [-\tau ,0]$. Clearly, $\hat{\varphi }\in W_H$. By the uniqueness of solutions, we have $u(t,\cdot ,\varphi )=z(t,\cdot ,\hat{\varphi }), \,\forall \,t\ge 0$. It then follows from Lemma 1 that system (9) has a unique solution $u(t,\cdot ,\varphi )$ with $u_0=\varphi$ on its maximal existence interval $[0,\bar{t}_{\varphi })$, where

$$\begin{aligned} u_t(\varphi )(\theta ,x)= & {} (u_1(t+\theta ,x, \varphi ),u_2(t+\theta ,x, \varphi ),u_3(t,x,\varphi )),\\&\forall \,t\ge 0, (\theta ,x)\in [-\,\tau ,0]\times \bar{\varOmega }. \end{aligned}$$

The following result shows that solutions of system (9) exist globally on $[0,\infty )$ and the Poincaré map associated with system (9) admits a global attractor in $C_H$.

Lemma 3

For any $\varphi \in C_H$, system (9) has a unique bounded solution $u(t,\cdot ,\varphi )$ on $[0,\infty )$ with $u_0=\varphi$. Moreover, system (9) generates an $\omega$-periodic semiflow $Q(t): =u_t(\cdot ): C_H\rightarrow C_H$, i.e., $Q(t)\varphi =u_t(\varphi ), \, \, \forall \,t\ge 0$, and $Q:=Q(\omega )$ has a global attractor in $C_H$.

Proof

Clearly, $0\le u_1(t,\cdot , \varphi )\le H(\cdot )$ for all $t\in [0,\bar{t}_{\varphi })$. Note that the second and third equation of (9) are dominated, respectively, by the following equation

$$\begin{aligned} \begin{aligned} \frac{\partial w_1(t,x)}{\partial t}&= D_m\triangle w_1(t,x)+\mu (t,x)-d_m(t,x)w_1(t,x),\,\,t>0, x\in \varOmega ,\\ \frac{\partial w_2(t,x)}{\partial t}&= D_m\triangle w_2(t,x)-d_m(t,x)w_2(t,x)\\&\quad +\frac{b\bar{\beta }p}{l}\int _\varOmega \varGamma (t,t-\tau , x,y)w_1(t-\tau ,y)dy,\,\,t>0, x\in \varOmega , \\ \frac{\partial w_1}{\partial \nu }&=\frac{\partial w_2}{\partial \nu }=0,\,\,t>0, x\in \partial {\varOmega }. \end{aligned} \end{aligned}$$

(12)

It is easy to see that there exists a positive vector $\varsigma =(\varsigma _1,\varsigma _2):=(\frac{\bar{\mu }}{\underline{d_m}}, \frac{b\bar{\beta }p\bar{\mu }}{l\underline{d_m^2}})$ such that

$$\begin{aligned} \mu (t,x)-d_m(t,x)\varsigma _1 \le 0,\,\,\frac{b\bar{\beta }p\bar{\mu }}{l\underline{d_m}}-d_m(t,x)\varsigma _2 \le 0, \end{aligned}$$

where $\bar{\mu }=\max _{t\in [0,\omega ],x\in \bar{\varOmega }}\mu (t,x)$ and $\underline{d_m}=\min _{t\in [0,\omega ],x\in \bar{\varOmega }} d_m(t,x)$. Then for any $q\ge 1$, $q\varsigma$ is an upper solution of (12). The comparison principle implies that solutions of system (9) are uniformly bounded, and hence, $\bar{t}_\varphi = +\,\infty$.

Define a semiflow $Q(t): C_H \rightarrow C_H$ of (9) by $Q(t)\varphi =u_t(\varphi ),\,\forall \,\varphi \in C_H$. By the proof of Zhang et al. (2015, Lemma 2.1), we can show that $\{Q(t)\}_{t \ge 0}$ is an $\omega$-periodic semiflow on $C_H$, and $Q^n=Q(n\omega ), \forall \,n\ge 0$. For any fixed $\varphi \in C_H$, there is a $t_1=t_1(\varphi )$ such that $u_2(t,\cdot ,\varphi ) \le 2\frac{\bar{\mu }}{\underline{d_m}}$ when $t>t_1$ and

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u_3(t,x)}{\partial t}\le D_m\triangle u_3(t,x)-\underline{d_m} u_3(t,x)+2b\bar{\beta }\frac{p\bar{\mu }}{l\underline{d_m}},\,\,t>t_1,x\in \varOmega ,\\&\frac{\partial u_3}{\partial \nu }=0, \,\,t>t_1,x\in \partial \varOmega , \end{aligned} \right. \end{aligned}$$

where $\bar{\mu }=\max _{t\in [0,\omega ],x\in \bar{\varOmega }}\mu (t,x)$ and $\underline{d_m}=\min _{t\in [0,\omega ],x\in \bar{\varOmega }} d_m(t,x)$. By Lemma 2, there is a $t_2(\varphi )>t_1$ such that $u_3(t,\cdot ,\varphi )\le 4\frac{b\bar{\beta }p\bar{\mu }}{l\underline{d_m^2}}, \forall \,t>t_2(\varphi )$. Therefore, the solution semiflow $Q(t): C_H\rightarrow C_H$ is point dissipative. Note that for each $t>\tau$, $Q(t): C_H\rightarrow C_H$ is compact (see Wu 1996, Theorem 2.1.8). It then follows from Magal and Zhao (2005, Theorem 2.9) that Q has a strong global attractor in $C_H$. $\square$

3 The basic reproduction number

Let $\mathbb {E}:= C(\bar{\varOmega },{\mathbb {R}}^2)$ and $\mathbb {E}^+:= C(\bar{\varOmega },{\mathbb {R}}_+^2)$, and $C_\omega ({\mathbb {R}}, \mathbb {E})$ be the Banach space consisting of all $\omega$-periodic and continuous functions from ${\mathbb {R}}$ to $\mathbb {E}$, where $\Vert \psi \Vert _{C_\omega ({\mathbb {R}},\mathbb {E})}:=\max _{\theta \in [0,\omega ]}\Vert \psi (\theta )\Vert _\mathbb {E}$ for any $\psi \in C_\omega ({\mathbb {R}},\mathbb {E})$. Below we use the method proposed in Zhao (2017a) to introduce the basic reproduction number for system (9). Setting $u_1=u_3=0$ in (9), we obtain the equation for the density of susceptible mosquitoes

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial u_2(t,x)}{\partial t}=D_m \triangle u_2(t,x)+\mu (t,x)-d_m(t,x)u_2(t,x),\,\,\,t>0,x\in \varOmega , \\&\frac{\partial u_2}{\partial \nu }=0, \,\,\,t>0,x\in \partial \varOmega . \end{aligned} \right. \end{aligned}$$

(13)

By Lemma 2, (13) admits a positive solution $m^*(t, \cdot )$, which is globally attractive in $\mathbb {Y}^+$ and $\omega$-periodic in $t\in \mathbb {R}$. Linearizing system (9) at $(0,m^*, 0)$ and then considering only the equations of infective compartments, we have

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial v_1}{\partial t}=D_h\triangle v_1(t,x)+c\beta (t,x)v_2(t,x)-(d_h+\rho )v_1(t,x),\,\,t> 0,x\in \varOmega ,\\&\frac{\partial v_2}{\partial t}=D_m\triangle v_2(t,x)-d_m(t,x)v_2(t,x)\\&\quad +\int _\varOmega \varGamma (t,t-\tau ,x,y)\frac{b\beta (t-\tau ,y)p}{lH(y)}m^*(t-\tau ,y)v_1(t-\tau ,y)dy,\\&\qquad t>0,x\in \varOmega ,\\&\frac{\partial v_1}{\partial \nu }=\frac{\partial v_2}{\partial \nu }=0, \,\,t>0, x\in \partial \varOmega , \end{aligned} \right. \end{aligned}$$

(14)

where $\varGamma$ is the same as in (7). Let

$$\begin{aligned} F(t)\left( \begin{array}{c} \phi _1 \\ \phi _2 \\ \end{array} \right) =\left( \begin{array}{cc} c\beta (t,\cdot )\phi _2(0,\cdot ) \\ \int _\varOmega \varGamma (t,t-\tau ,\cdot ,y)\frac{b\beta (t-\tau ,y)p}{lH(y)}m^*(t-\tau ,y)\phi _1(-\tau ,y)dy\\ \end{array} \right) \end{aligned}$$

for any $t\in {\mathbb {R}}, (\phi _1,\phi _2)\in C([-\,\tau ,0],\mathbb {E})$ and

$$\begin{aligned} -\,V(t) v=D\triangle v-W(t) v, \end{aligned}$$

where $D=\mathrm{diag}(D_h, D_m)$ and

$$\begin{aligned} -\,[W(t)](x)=\left( \begin{array}{c@{\quad }c} -\,(d_h+\rho ) &{} 0 \\ 0 &{} -\,d_m(t,x) \\ \end{array} \right) ,\,\,x\in \bar{\varOmega }. \end{aligned}$$

Let $\varPhi (t,s)=\mathrm{diag}(T_1(t,s), T_2(t,s)), t\ge s,$ be the evolution operators associated with the following system

$$\begin{aligned} \frac{dv}{dt}=-V(t)v \end{aligned}$$

subject to the Neumann boundary condition.

Recall that the exponential growth bound of $\varPhi (t,s)$ is defined as

$$\begin{aligned} \bar{\omega }(\varPhi )=\inf \{\tilde{\omega }: \exists M\ge 1\,\text{ such } \text{ that }\,\Vert \varPhi (t+s,s)\Vert \le Me^{\tilde{\omega }t},\,\,\forall \,s\in {\mathbb {R}}, t\ge 0\}. \end{aligned}$$

It is easy to see that

$$\begin{aligned} 0<r(\varPhi (\omega ,0))=\max \{r(T_1(\omega ,0)), r(T_2(\omega ,0))\}<1. \end{aligned}$$

By Thieme (2009, Proposition 5.6) with $s=0$, we obtain $\bar{\omega }(\varPhi )<0$. Therefore, F(t) and W(t) satisfy the following assumptions:

• (H1) Each F(t) maps $C([-\tau ,0],\mathbb {E}^+)$ into $\mathbb {E}^+$;

• (H2) Each matrix $-W(t)$ is cooperative, and $\bar{\omega }(\varPhi )<0$.

Following (Zhao 2017a, Section 2), we assume that $v\in C_\omega ({\mathbb {R}}, \mathbb {E})$ and $v(s,x)=v(s)(x)$ is the initial distribution of infectious humans and mosquitoes at time $s\in {\mathbb {R}}$ and the spatial location $x\in \bar{\varOmega }$. For any given $s\ge 0$, $F(t-s)v(t-s+\cdot ,x)$ represents the density distribution of newly infected humans and mosquitoes at time $t-s (s<t)$ and at location x which is produced by the infectious humans and mosquitoes who were introduced over the time interval $[t-s-\tau , t-s]$. Then $\varPhi (t,t-s)F(t-s)v(t-s+\cdot ,x)$ is the distribution at location x of those infected humans and mosquitoes who were newly infected at time $t-s$ and still survive in the environment at time t for $t \ge s$. Hence, the integral

$$\begin{aligned} \int _0^\infty \varPhi (t,t-s)F(t-s)v(t-s+\cdot ,x)ds \end{aligned}$$

is the distribution of accumulative infective humans and mosquitoes at time t and at location x produced by all those infectious humans and mosquitoes introduced at all previous times to t.

Define two linear operators on $C_\omega ({\mathbb {R}}, \mathbb {E})$ by

$$\begin{aligned}{}[Lv](t):= \int _0^\infty \varPhi (t,t-s)F(t-s)v(t-s+\cdot )ds, \,\,\forall \,t\in {\mathbb {R}}, v\in C_\omega ({\mathbb {R}},\mathbb {E}), \end{aligned}$$

and

$$\begin{aligned}{}[\hat{L}v](t):= F(t) \left( \int _0^\infty \varPhi (t+\cdot ,t-s+\cdot )v(t-s+\cdot )ds \right) , \,\,\,\forall \,t\in {\mathbb {R}}, v\in C_\omega ({\mathbb {R}},\mathbb {E}). \end{aligned}$$

Let A and B be two bounded linear operators on $C_\omega ({\mathbb {R}},\mathbb {E})$ defined by

$$\begin{aligned}{}[Av](t)=\int _0^\infty \varPhi (t,t-s)v(t-s)ds,\,\,[Bv](t)=F(t)v_t,\,\,\forall \,t\in {\mathbb {R}}, v\in C_\omega ({\mathbb {R}},\mathbb {E}). \end{aligned}$$

It then follows that $L=A\circ B$ and $\hat{L}=B\circ A$, and hence, L and $\hat{L}$ has the same spectral radius. Motivated by the concept of next generation operators in Bacaër and Guernaoui (2006), Thieme (2009) and Zhao (2017a), we define the spectral radius of L as the basic reproduction number for (9), namely,

$$\begin{aligned} \mathcal {R}_0:=r(L)=r(\hat{L}). \end{aligned}$$

For any given $t\ge 0$, let $\hat{P}(t)$ be the solution map of (14) on $C([-\tau ,0], \mathbb {E})$, that is $\hat{P}(t)\phi =v_t(\phi )$, where

$$\begin{aligned} v_t(\phi )(\theta ,x)= & {} v(t+\theta ,x,\phi )=(v_1(t+\theta ,x, \phi ),v_2(t+\theta ,x, \phi )),\\&\forall \,(\theta ,x)\in [-\tau ,0]\times \bar{\varOmega }, \end{aligned}$$

and $v(t,x,\phi )$ is the unique solution of (14) with $v(\theta ,x)=\phi (\theta ,x)$ for all $\theta \in [-\,\tau ,0], x\in \bar{\varOmega }$. Then $\hat{P}:=\hat{P}(\omega )$ is the Poincaré map associated with system (14). Let $r(\hat{P})$ be the spectral radius of $\hat{P}$. By the same arguments as in Zhao (2017a, Theorem 2.1), we have the following result.

Lemma 4

$\mathcal {R}_0-1$ has the same sign as $r(\hat{P})-1$.

Define $\mathcal {E}:=C([-\tau ,0],\mathbb {Y})\times \mathbb {Y}$ and $\mathcal {E}^+:=C([-\tau ,0],\mathbb {Y}^+)\times \mathbb {Y}^+$. For any $\varphi \in \mathcal {E}$, let $\bar{v}(t,x,\varphi )=(\bar{v}_1(t,x,\varphi ),\bar{v}_2(t,x,\varphi ))$ be the unique solution of (14) with $\bar{v}_0(\varphi )(\theta ,x)=\varphi (\theta ,x)$ for all $\theta \in [-\tau ,0], x\in \bar{\varOmega }$, where

$$\begin{aligned} \bar{v}_t(\varphi )(\theta ,x)= & {} \bar{v}(t+\theta ,x,\varphi )=(\bar{v}_1(t+\theta ,x, \varphi ),\bar{v}_2(t,x, \varphi )),\\&\forall \,t\ge 0, (\theta ,x)\in [-\tau ,0]\times \bar{\varOmega }. \end{aligned}$$

Let P be the Poincaré map of (14) on the space $\mathcal {E}$, that is, $P(\varphi )=\bar{v}_\omega (\varphi ), \,\forall \,\varphi \in \mathcal {E}$. Let r(P) be the spectral radius of P. Similar to the arguments in Lou and Zhao (2011, Section 3), we can show that $\bar{v}(t,x,\varphi )\gg 0$ for all $t> \tau , x\in \bar{\varOmega }, \varphi \in \mathcal {E}^+$ with $\varphi \not \equiv 0$. Moreover, Wu (1996, Theorem 2.1.8) implies that $\bar{v}_t$ is compact on $\mathcal {E}$ for all $t>\tau$. Thus, $P^{n}$ is compact and strongly positive whenever $nw>2\tau$. It then follows from Liang and Zhao (2007, Lemma 3.1) that r(P) is a simple eigenvalue of P having a strongly positive eigenvector $\bar{\varphi }\in \mathrm{int}{(\mathcal {E}^+)}$, and the modulus of any other eigenvalue is less than r(P).

Lemma 5

Let $\mu =\frac{\ln r(P)}{\omega }$. Then there exists a positive $\omega$-periodic function $v^*(t,x)$ such that $e^{\mu t}v^*(t,x)$ is a solution of (14).

Proof

Let $\bar{v}(t,x,\bar{\varphi })=(\bar{v}_1(t,x,\bar{\varphi }),\bar{v}_2(t,x,\bar{\varphi }))$ be the solution of (14) with $\bar{v}_0(\bar{\varphi })={\bar{\varphi }}$. Since $\bar{\varphi }\gg 0$, it is easy to see that $\bar{v}_t(\bar{\varphi })\gg 0$ for all $t\ge 0$. Denote

$$\begin{aligned} \begin{array}{l@{\quad }l} v_1^*(t,x)=e^{-\mu t}\bar{v}_1(t,x,\bar{\varphi }), &{}\,\,t\ge -\,\tau , x\in \bar{\varOmega },\\ v_2^*(t,x)=e^{-\mu t}\bar{v}_2(t,x,\bar{\varphi }), &{}\,\,t\ge 0, x\in \bar{\varOmega }. \end{array} \end{aligned}$$

Then $v^*(t,x)=(v_1^*(t,x),v_2^*(t,x)) \gg 0$ for all $t\ge 0, x\in \bar{\varOmega }$, and $v^*$ satisfies the following linear-periodic system with parameter $\mu$:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial v_1^*}{\partial t}&=D_h\triangle v_1^*(t,x)+c\beta (t,x)v_2^*(t,x)-(d_h+\rho +\mu )v_1^*(t,x),\\ \frac{\partial v_2^*}{\partial t}&=D_m\triangle v_2^*(t,x)-(d_m(t,x)+\mu )v_2^*(t,x)\\&\quad +\int _\varOmega \varGamma (t,t-\tau ,x,y)\frac{b\beta (t-\tau ,y)p}{lH(y)}m^*(t-\tau ,y)e^{-\mu \tau }v_1^*(t-\tau ,y)dy \end{aligned} \right. \end{aligned}$$

(15)

for all $(t, x)\in (0,\infty )\times \bar{\varOmega }$. Thus, $v^*(t,x)$ is a solution of the $\omega$-periodic system (15) with $\frac{\partial v^*_1}{\partial \nu }=\frac{\partial v^*_2}{\partial \nu }=0$ on $(0,\infty )\times \partial \varOmega$ and $v_0^*(\theta ,x)=(v_1^*(\theta ,x), v_2^*(0,x))=(e^{-\mu \theta }\bar{\varphi }_1(\theta ,x), \bar{\varphi }_2(x))$ for all $\theta \in [-\,\tau ,0], x\in \bar{\varOmega }$, where $v_t^*(\cdot ,\cdot )=(v_{1t}^*(\cdot ,\cdot ),v_2^*(t,\cdot ))$ for any $t\ge 0$ with

$$\begin{aligned} \begin{array}{l@{\quad }l} v_{1t}^*(\theta ,x)=v_1^*(t+\theta ,x)=e^{-\mu (t+\theta )}\bar{v}_1(t+\theta ,x,\bar{\varphi }),&{}\,\,\forall \,(\theta ,x)\in [-\tau ,0]\times \bar{\varOmega },\\ v_2^*(t,x)=e^{-\mu t} \bar{v}_2(t,x,\bar{\varphi }),&{}\,\,\forall \,x\in \bar{\varOmega }. \end{array} \end{aligned}$$

For any $\theta \in [-\,\tau ,0],x\in \bar{\varOmega },$ we have

$$\begin{aligned} v_1^*(\omega +\theta , x)&=e^{-\mu (\omega +\theta )}(P(\bar{\varphi }))_1(\theta ,x)=e^{-\mu (\omega +\theta )}r(P)\bar{\varphi }_1(\theta ,x)\\&=e^{-\mu \theta }\bar{\varphi }_1(\theta ,x)=v_1^*(\theta ,x),\\ v_2^*(\omega , x)&=e^{-\mu \omega }(P(\bar{\varphi }))_2(\theta ,x)=e^{-\mu \omega }r(P)\bar{\varphi }_2(x)=\bar{\varphi }_2(x)=v_2^*(0,x). \end{aligned}$$

Therefore, $v^*_0(\theta ,\cdot )=v^*_\omega (\theta ,\cdot )$ for all $\theta \in [-\tau , 0]$, and hence, the existence and uniqueness of solutions of (15) imply that

$$\begin{aligned} \begin{array}{l@{\quad }l} v_1^*(t,x)=v_1^*(t+\omega ,x),\,\,\,\forall \,t\ge -\tau , x\in \bar{\varOmega },\\ v_2^*(t,x)=v_2^*(t+\omega ,x),\,\,\,\forall \,t\ge 0, x\in \bar{\varOmega }. \end{array} \end{aligned}$$

Therefore, $v^*(t,x)$ is an $\omega$-periodic solution of (15) and $e^{\mu t}v^*(t,x)$ is a solution of (14). $\square$

By arguments similar to those in Wang and Zhao (2017, Lemma 8), we have the following observation.

Lemma 6

$r(\hat{P})=r(P)$.

As a consequence of Lemmas 4 and 6, we see that $\mathcal {R}_0-1$ has the same sign as $r(P)-1$.

4 Threshold dynamics

In this section, we establish a threshold-type result on the extinction and uniform persistence of the disease in terms of $\mathcal {R}_0$.

Let $\tau$ be a positive real number, X be a Banach space, and $\mathcal {C}:=C([-\tau ,0], X)$. For any $\phi \in \mathcal {C}$, define $\Vert \phi \Vert =\sup \nolimits _{-\tau \le \theta \le 0}\Vert \phi (\theta )\Vert _X$. Then $(\mathcal {C},\Vert {\cdot }\Vert )$ is a Banach space. Let $\mathcal {A}$ be the infinitesimal generator of a $C_0$-semigroup $\{\mathcal {T}(t)\}_{t\ge 0}$ on X. Assume that $\mathcal {T}(t)$ is compact for each $t>0$, and there exists $M>0$ such that $\Vert \mathcal {T}(t)\Vert \le M$ for all $t\ge 0$. We consider the abstract functional differential equation

$$\begin{aligned} \begin{array}{l@{\quad }l} \frac{du(t)}{dt}=\mathcal {A}u(t)+\mathcal {F}(t,u_t), &{} t>0,\\ u_0=\phi \in \mathcal {C}. \end{array} \end{aligned}$$

(16)

Here $\mathcal {F}: [0,\infty )\times \mathcal {C}\rightarrow X$ is continuous and maps bounded sets into bounded sets and $u_t\in \mathcal {C}$ is defined by $u_t(\theta )=u(t+\theta ), \forall \,\theta \in [-\,\tau ,0]$.

Lemma 7

(Zhao 2017b, Theorem 3.5.1) Assume that for each $\phi \in \mathcal {C}$, Eq. (16) has a unique solution $u(t,\phi )$ on $[0,\infty )$, and solutions of (16) are uniformly bounded in the sense that for any bounded subset $\mathcal {B}_0$ of $\mathcal {C}$, there exists a bounded subset $\mathcal {B}_1=\mathcal {B}_1(\mathcal {B}_0)$ of $\mathcal {C}$ such that $u_t(\phi )\in \mathcal {B}_1$ for all $\phi \in \mathcal {B}_0$ and $t\ge 0$. Then for any given $r>0$, there exists an equivalent norm $\Vert {\cdot }\Vert _r^*$ on $\mathcal {C}$ such that the solution maps $\mathcal {Q}(t):=u_t$ of Eq. (16) satisfy $\kappa (\mathcal {Q}(t)\mathcal {B})\le e^{-rt}\kappa (B)$ for any bounded subset $\mathcal {B}$ of $\mathcal {C}$ and $t\ge 0$, where $\kappa$ is the Kuratowski measure of noncompactness in $(\mathcal {C},\Vert {\cdot }\Vert _r^*)$.

Lemma 8

For each $r>0$, there exists an equivalent norm $\Vert {\cdot }\Vert _r^{*}$ on C such that for each $t>0$, the solution map $\hat{Q}(t):=z_t$ of system (9) satisfies $\kappa (\hat{Q}(t)B)\le e^{-rt}\kappa (B)$ for any bounded subset B of $W_H$.

Proof

Let $\hat{T}_1, \hat{T}_2: \mathbb {Y}\rightarrow \mathbb {Y}$ be the $C_0$ semigroups associated with $D_h\triangle -(d_h+\rho )$ and $D_m\triangle$ subject to the Neumann boundary condition, respectively. From Smith (1995, Section 7.1 and Corollary 7.2.3), it follows that $\hat{T}_i(t): \mathbb {Y}\rightarrow \mathbb {Y}, i=1,2$, is compact and strongly positive for each $t >0$. Furthermore, $\hat{T}(t): =\mathrm{diag} (\hat{T}_1(t), \hat{T}_2(t), \hat{T}_2(t)): \mathbb {X}\rightarrow \mathbb {X}$ is a $C_0$ semigroup for $t\ge 0$. Let $\hat{A}_i: D(\hat{A}_i)\rightarrow \mathbb {Y}$ be the generator of $\hat{T}_i, i=1,2$. Then $\hat{T}(t): \mathbb {X}\rightarrow \mathbb {X}$ is a semigroup generated by the operator $\hat{A}=\mathrm{diag}(\hat{A}_1, \hat{A}_2, \hat{A}_3)$ defined on $D(\hat{A})=D(\hat{A}_1)\times D(\hat{A}_2)\times D(\hat{A}_2)$.

Define $\hat{F}=(\hat{F}_1,\hat{F}_2,\hat{F}_3): [0,+\,\infty )\times C\rightarrow \mathbb {X}$ by

$$\begin{aligned} \hat{F}_1(t,\phi )&:=\frac{c\beta (t,\cdot )l[H(\cdot )-\phi _1(0,\cdot )]}{p\phi _1(0,\cdot )+l[H(\cdot )-\phi _1(0,\cdot )]}\phi _3(0,\cdot ),\\ \hat{F}_2(t,\phi )&:=\mu (t,\cdot )-\left[ d_m(t,\cdot )+\frac{b\beta (t,\cdot )p \phi _1(0,\cdot )}{p\phi _1(0,\cdot )+l[H(\cdot )-\phi _1(0,\cdot )]} \right] \phi _2(0,\cdot ),\\ \hat{F}_3(t,\phi )&:=-d_m(t,\cdot )\phi _3(0,\cdot )\\&\quad +\int _\varOmega \varGamma (t,t-\tau , \cdot ,y)\frac{b\beta (t-\tau ,y)p \phi _1(-\tau ,y)}{p\phi _1(-\tau ,y)+l[H(y)-\phi _1(-\tau ,y)]}\phi _2(-\tau ,y)dy \end{aligned}$$

for $t\ge 0, x\in \bar{\varOmega }$ and $\phi =(\phi _1,\phi _2,\phi _3)\in C$. Then system (9) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \frac{\partial u(t,x)}{\partial t} =\hat{A} u(t,x)+\hat{F}(t,u_t), &{}t>0,x\in \varOmega ,\\ u(\theta ,x)=\phi (\theta ,x), &{}\theta \in [-\tau ,0], x\in \varOmega , \end{array} \right. \end{aligned}$$

(17)

where $u(t,x):=(u_1(t,x),u_2(t,x),u_3(t,x))$.

Define $\hat{Q}(t)\varphi =z_t(\varphi ), \forall \varphi \in W_H$, where $z(t,\cdot ,\varphi )$ is the unique solution of (17) with $z_0=\varphi \in W_H$. Let $u(t,\cdot ,\phi )$ be the unique solution of (9) with $u_0=\phi \in C_H$. By the uniqueness of solutions, we have $u(t,\cdot ,\phi )=z(t,\cdot ,\varphi ),\,\forall \,t\ge 0$, provided that $\phi =(\phi _1,\phi _2,\phi _3)\in C_H$ and $\varphi =(\varphi _1,\varphi _2,\varphi _3)\in W_H$ satisfy $\phi _1\equiv \varphi _1, \phi _2\equiv \varphi _2$ and $\phi _3(\cdot )=\varphi _3(0,\cdot )$. It then follows from Lemma 3 and its proof that $\hat{Q}(t): W_H \rightarrow W_H,\, \forall t\ge 0$, and solutions of system (17) are uniformly bounded on $W_H$. By Lemma 7, there exists an equivalent norm $\Vert {\cdot }\Vert _r^{*}$ on C such that for each $t>0$, the map $\hat{Q}(t): W_H\rightarrow W_H$ is a $\kappa$-contraction with the contraction constant being $e^{-rt}$ for the Banach space $(C,\Vert {\cdot }\Vert _r^{*})$. $\square$

Lemma 9

Let $u(t,x, \phi )$ be the solution of system (9) with $u_0=\phi \in C_H$. If there exists some $t_0\ge 0$ such that $u_i(t_0,\cdot ,\phi )\not \equiv 0$, for some $i\in \{1,3\}$, then $u_i(t,x,\phi )>0, \forall \,t>t_0, x\in \bar{\varOmega }$. Moreover, for any $\phi \in C_H$, we have $u_2(t,x,\phi )>0, \forall \,t>0, x\in \bar{\varOmega }$ and $\liminf _{t\rightarrow \infty } u_2(t,x,\phi )\ge \gamma$ uniformly for $x\in \bar{\varOmega }$, where $\gamma$ is a $\phi$-independent positive constant.

Proof

Let $\bar{d_m}=\max _{t\in [0,\omega ],x\in \bar{\varOmega }}d_m(t,x)$. One easily sees that $u_1(t, x, \phi )$ and $u_3(t, x, \phi )$ satisfy

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \frac{\partial u_1}{\partial t}\ge D_h\triangle u_1(t,x)-(d_h+\rho )u_1(t,x), &{} t>0, x\in \varOmega ,\\ \frac{\partial u_3}{\partial t}\ge D_m\triangle u_2(t,x)-\bar{d_m}u_3(t,x), &{} t>0, x\in \varOmega ,\\ \frac{\partial u_1}{\partial \nu }=\frac{\partial u_3}{\partial \nu }=0, &{} t>0, x\in \partial \varOmega . \end{array} \right. \end{aligned}$$

If there exists $t_0\ge 0$ such that $u_i(t_0,\cdot ,\phi )\not \equiv 0$ for some $i=\{1,3\}$, it then follows from the parabolic maximum principle that $u_i(t,\cdot ,\phi )>0$ for all $t>t_0, x\in \bar{\varOmega }$.

Let $v(t,x,\phi _2)$ be the solution of

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial v(t,x)}{\partial t} = D_m \triangle v(t,x)+\mu (t,x)-\left( \frac{b\beta (t,x)p}{l} + d_m(t,x)\right) v(t,x),\,\,t> 0, x\in \varOmega ,\\&\frac{\partial v}{\partial \nu }=0,\,\,\,\,t>0, x\in \partial \varOmega ,\\&v(0,x)=\phi _2(0,x), \,\,\,\,x\in \varOmega . \end{aligned} \right. \end{aligned}$$

(18)

Note that $\mu (t,x)$ is Hölder continuous and nonnegative nontrivial on ${\mathbb {R}}\times \bar{\varOmega }$. An application of the comparison principle yields

$$\begin{aligned} u_2(t,x,\phi )\ge v(t,x,\phi _2)>0, \,\,\,\forall \,t>\omega , x\in \bar{\varOmega }. \end{aligned}$$

Furthermore, by Lemma 2, one finds that

$$\begin{aligned} \liminf _{t\rightarrow \infty } u_2(t,x,\phi )\ge \gamma :=\inf _{t\in [0,\omega ],x\in \bar{\varOmega }} v_*(t,x) \end{aligned}$$

uniformly for $x\in \bar{\varOmega }$, where $v_*(t,x)$ is the unique positive $\omega$-periodic solution of (18). $\square$

Theorem 1

Let $u(t,x, \phi )$ be the solution of (9) with $u_0 = \phi \in C_H$. Then the following two statements are valid:

• (i) If $\mathcal {R}_0 <1$, then the disease free $\omega$-periodic solution $(0,m^*(t,x),0)$ is globally attractive;

• (ii) If $\mathcal {R}_0 >1$, then system (9) admits at least one positive $\omega$-periodic solution $(u_1^*(t,x),u_2^*(t,x),u_3^*(t,x))$, and there exists $\eta >0$ such that for any $\phi \in C_H$ with $\phi _1(0,\cdot )\not \equiv 0$ and $\phi _3(\cdot )\not \equiv 0$, we have $\liminf _{t\rightarrow \infty } u_i(t,x,\phi )\ge \eta ,\,\, i=1,2,3$, uniformly for all $x\in \bar{\varOmega }$.

Proof

(i) In the case where $\mathcal {R}_0<1$, Lemmas 4 and 6 imply that $r(P)<1$, and hence $\mu =\frac{\ln r(P)}{\omega }<0$. Consider the following equation with parameter $\varepsilon >0$:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial v_1^{\varepsilon }}{\partial t}&=D_h\triangle v_1^{\varepsilon }(t,x)+c\beta (t,x)v_2^{\varepsilon }(t,x)-(d_h+\rho )v_1^{\varepsilon }(t,x), \,\,t>0,x\in \varOmega ,\\ \frac{\partial v_2^{\varepsilon }}{\partial t}&=D_m\triangle v_2^{\varepsilon }(t,x)-d_m(t,x)v_2^{\varepsilon }(t,x)\\&\quad +\int _\varOmega \varGamma (t,t-\tau ,x,y)\frac{b\beta (t-\tau ,y)p}{lH(y)}(m^*(t-\tau ,y)+\varepsilon )v_1^{\varepsilon }(t-\tau ,y)dy,\\ t&>0,x\in \varOmega ,\\ \frac{\partial v_1^{\varepsilon }}{\partial \nu }&=\frac{\partial v_2^{\varepsilon }}{\partial \nu }=0, \,\,t>0, x\in \partial \varOmega . \end{aligned} \right. \end{aligned}$$

(19)

For any $\psi \in \mathcal {E}$, let $v^{\varepsilon }(t,x,\psi )=(v_1^{\varepsilon }(t,x,\psi ),v_2^{\varepsilon }(t,x,\psi ))$ be the unique solution of (19) with $v_0^{\varepsilon }(\psi )(\theta ,x)=\psi (\theta ,x)$ for all $\theta \in [-\,\tau ,0], x\in \bar{\varOmega }$, where

$$\begin{aligned} v_t^{\varepsilon }(\psi )(\theta ,x)= & {} v^{\varepsilon }(t+\theta ,x,\psi )=(v_1^{\varepsilon }(t+\theta ,x, \psi ),v_2^{\varepsilon }(t,x, \psi )),\\&\forall \,t\ge 0, (\theta ,x)\in [-\,\tau ,0]\times \bar{\varOmega }. \end{aligned}$$

Let $P_{\varepsilon }: \mathcal {E} \rightarrow \mathcal {E}$ be the Poincaré map of (19), i.e., $P_{\varepsilon }(\psi )=v_{\omega }^{\varepsilon }(\psi ),\,\forall \,\psi \in \mathcal {E}$, and let $r(P_\varepsilon )$ be the spectral radius of $P_\varepsilon$. Since $\lim _{\varepsilon \rightarrow 0}r(P_\varepsilon )=r(P)<1$, we can fix a sufficiently small number $\varepsilon >0$ such that $r(P_\varepsilon )<1$. According to Lemma 5, there is a positive $\omega$-periodic function $v^*_\varepsilon (t, x)$ such that $v^\varepsilon (t, x) =e^{\mu _\varepsilon t}v_\varepsilon ^*(t, x)$ is a solution of (19), where $\mu _\varepsilon =\frac{\ln r(P_\varepsilon )}{\omega }<0$. For fixed $\varepsilon >0$, by Lemma 2 and the comparison principle, there exists a sufficiently large integer $n_1>0$ such that $n_1\omega \ge \tau$ and

$$\begin{aligned} u_2(t,x)\le m^*(t,x)+\varepsilon ,\,\forall \,t\ge n_1\omega -\tau , x\in \bar{\varOmega }. \end{aligned}$$

Then we have

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial u_1}{\partial t}&\le D_h\triangle u_1(t,x)+c\beta (t,x)u_3(t,x)-(d_h+\rho )u_1(t,x),\,\,\,t\ge n_1\omega , x\in \varOmega ,\\ \frac{\partial u_3}{\partial t}\le&D_m\triangle u_3(t,x)-d_m(t,x)u_3(t,x),\\&\quad +\int _\varOmega \varGamma (t,t-\tau ,x,y)\frac{b\beta (t-\tau ,y)p}{lH(y)}(m^*(t-\tau ,y)+\varepsilon )u_1(t-\tau ,y)dy,\\ t&\ge n_1\omega , x\in \varOmega ,\\ \frac{\partial u_1}{\partial \nu }&= \frac{\partial u_3}{\partial \nu }=0, \,\,t\ge n_1\omega , x\in \partial \varOmega . \end{aligned} \right. \end{aligned}$$

(20)

For any given $\phi \in C_H$, there exists some $\alpha _1 > 0$ such that

$$\begin{aligned} (u_1(t,x,\phi ),u_3(t,x,\phi ))\le \alpha _1 v^\varepsilon (t,x), \,\forall \,t\in [n_1\omega -\tau , n_1\omega ], x\in \bar{\varOmega }. \end{aligned}$$

Thus, using (19), (20) and the comparison theorem for abstract functional differential equation (Martin and Smith 1990, Proposition 1), we have

$$\begin{aligned} (u_1(t,\cdot ,\phi ),u_3(t,\cdot ,\phi ))\le \alpha _1 e^{\mu _{\varepsilon } t}v_\varepsilon ^*(t, \cdot ), \,\,\,\forall \,t\ge n_1\omega , \end{aligned}$$

and hence, $\lim _{t\rightarrow \infty } (u_1(t,x,\phi ),u_3(t,x,\phi ))=(0,0)$ uniformly for $x\in \bar{\varOmega }$. Then, the equation $u_2$ in (9) is asymptotic to

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial w(t,x)}{\partial t}=D_m\triangle w(t,x)+\mu (t,x)-d_m(t,x)w(t,x),\,\,t>0,x\in \varOmega ,\\&\frac{\partial w}{\partial \nu }=0, \,\,t>0,x\in \partial \varOmega . \end{aligned} \right. \end{aligned}$$

(21)

Next, we use the theory of internally chain transitive sets (see, e.g., Zhao 2017b) to prove that $\lim _{t\rightarrow \infty } (u_2(t,x,\phi )-m^*(t,x))=0$ uniformly for $x\in \bar{\varOmega }$, where $m^*(\cdot ,\cdot )$ is a global attractive solution of (21).

Let Q be defined as in Lemma 3, and $\mathcal {J}=\omega (\phi )$ be the omega limit set of $\phi =(\phi _1,\phi _2,\phi _3)\in C_H$ for Q. Since $\lim _{t\rightarrow \infty } u_i(t,x,\phi )=0, i=1,3$ uniformly for $x\in \bar{\varOmega }$, we have $\mathcal {J}=\{\hat{0}\}\times \bar{\mathcal {J}}\times \{0\}$. By Lemma 9, we know $\hat{0}\not \in \bar{\mathcal {J}}$, where $\hat{0}(\theta ,\cdot )=0, \theta \in [-\,\tau ,0]$.

For any $\varphi \in C([-\,\tau ,0],\mathbb {Y}^+)$, let $w(t,x,\varphi (0,\cdot ))$ be the solution of (21) with initial value $w(0,x)=\varphi (0,x)$. Define a solution semiflow of (21) on $C([-\,\tau ,0],\mathbb {Y}^+)$ by

$$\begin{aligned} w_t(\theta ,x,\varphi )=\left\{ \begin{array}{l@{\quad }l} w(t+\theta ,x,\varphi (0)), &{} \hbox {if}\,t+\theta>0, t>0,\theta \in [-\,\tau ,0], \\ \varphi (t+\theta ,x), &{}\hbox {if}\,t+\theta \le 0, t>0,\theta \in [-\,\tau ,0]. \end{array} \right. \end{aligned}$$

Let $\bar{P}(\varphi )=w_\omega (\varphi )$. It follows from (Zhao 2017b, Lemma 1.2.1) that $\mathcal {J}$ is an internally chain transitive set for Q, and hence $\bar{\mathcal {J}}$ is an internally chain transitive set for $\bar{P}$. Define $m_0^*\in C([-\,\tau ,0],\mathbb {Y}^+)$ by $m_0^*(\theta ,\cdot )=m^*(\theta ,\cdot )$ for $\theta \in [-\,\tau ,0]$. Since $\bar{\mathcal {J}}\ne \{\hat{0}\}$ and $m_0^*$ is globally attractive in $C([-\,\tau ,0],\mathbb {Y}^+){\setminus } \{\hat{0}\}$, we have $\bar{\mathcal {J}} \cap W^s(m_0^*)\ne \emptyset$, where $W^s(m_0^*)$ is the stable set of $m_0^*$. By Zhao (2017b, Theorem 1.2.1), we then get $\bar{\mathcal {J}}=\{m_0^*\}$. This proves $\mathcal {J}=\{(\hat{0},m_0^*,{0})\}$, and hence

$$\begin{aligned} \lim _{t\rightarrow \infty } \Vert (u_1(t,\cdot ,\phi ), u_2(t,\cdot ,\phi ),u_3(t,\cdot ,\phi ))-(0,m^*(t,\cdot ),0)\Vert _\mathbb {X}=0. \end{aligned}$$

(ii) In the case of $\mathcal {R}_0>1$, we have $r(P)>1$, and hence $\mu =\frac{\ln r(P)}{\omega }>0$. Let

$$\begin{aligned} \mathbb {C}_0=\{\phi \in C_H: \phi _1(0,\cdot )\not \equiv 0\,\text{ and }\,\phi _3(\cdot )\not \equiv 0\}, \end{aligned}$$

and

$$\begin{aligned} \partial \mathbb {C}_0:= C_H{\setminus } \mathbb {C}_0=\{\phi \in C_H: \phi _1(0,\cdot )\equiv 0\,\text{ or }\,\phi _3(\cdot )\equiv 0\}. \end{aligned}$$

Note that for any $\phi \in \mathbb {C}_0$, Lemma 9 implies $u_i(t,x,\phi )>0, i=1,3, \forall \,t>0, x\in \bar{\varOmega }$. It follows that $Q^n(\mathbb {C}_0)\subset \mathbb {C}_0, \forall \,n\in \mathbb {N}$. From Lemma 3, we know that $Q: C_H\rightarrow C_H$ has a strong global attractor in $C_H$.

Let

$$\begin{aligned} M_\partial :=\{\phi \in \partial \mathbb {C}_0: Q^n(\phi )\in \partial \mathbb {C}_0, \forall \,n\in \mathbb {N}\}, \end{aligned}$$

and $\omega (\phi )$ be the omega limit set of the orbit $\gamma ^+(\phi ):=\{Q^n(\phi ): \forall \,n\in \mathbb {N}\}$. Set $M=(\hat{0},m_0^*,{0})$. For any given $\psi \in M_\partial$, $Q^n(\psi )\in \partial \mathbb {C}_0, \forall \,n\in \mathbb {N}$. Thus, for each $n\in \mathbb {N}$, either $u_1(n\omega ,\cdot ,\psi ) \equiv 0$ or $u_3(n\omega ,\cdot ,\psi ) \equiv 0$. Moreover, by a contradiction argument with the help of Lemma 9, it is clear that for each $t\ge 0$, either $u_1(t,\cdot ,\psi )\equiv 0$ or $u_3(t,\cdot ,\psi )\equiv 0$. If $u_1(t,\cdot ,\psi ) \equiv 0$ for all $t\ge 0$, Lemma 2 ensures that $\lim _{t\rightarrow \infty } u_2(t,x,\psi )=m^*(t,x)$ uniformly for $x\in \bar{\varOmega }$. Note that the $u_3$ equation in (9) satisfies

$$\begin{aligned} \frac{\partial u_3(t,x,\psi )}{\partial t}\le D_m\triangle u_3(t,x,\psi )-\underline{d_m} u_3(t,x,\psi ). \end{aligned}$$

By the comparison principle, we have $\lim _{t\rightarrow \infty }u_3(t,x,\psi )=0$ uniformly for $x\in \bar{\varOmega }$. If $u_1(t_0,\cdot ,\psi ) \not \equiv 0$ for some $t_0\ge 0$, it follows from Lemma 9 that $u_1(t,\cdot ,\psi )>0, \forall \,t\ge t_0$. Thus, we have $u_3(t_0,\cdot ,\psi ) \equiv 0, \forall \,t\ge t_0$. From the $u_1$ equation in (9), we see that $\lim _{t\rightarrow \infty }u_1(t,x,\psi )=0$ uniformly for $x\in \bar{\varOmega }$. Thus, the $u_2$ equation in (9) is asymptotic to the following periodic equation

$$\begin{aligned} \frac{\partial u_2(t,x,\psi )}{\partial t}=D_m \triangle u_2(t,x,\psi )+\mu (t,x)-d_m(t,x)u_2(t,x,\psi ). \end{aligned}$$

(22)

By Lemma 2, (22) admits a unique positive $\omega$-periodic solution $m^*(t,\cdot )$, which is globally attractive in $\mathbb {Y}^+$. It then follows from the theory of asymptotically periodic system (see Zhao 2017b, Section 3.2) that $\lim _{t\rightarrow \infty }(u_2(t,x,\psi )-m^*(t,x))=0$ uniformly for $x\in \bar{\varOmega }$. As a result, $\omega (\psi )=M$ for any $\psi \in M_\partial$, and M cannot form a cycle for Q in $\partial \mathbb {C}_0$.

Consider the following time-periodic parabolic system with parameter $\delta >0$:

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial v_1^\delta }{\partial t}&=D_h\triangle v_1^\delta (t,x)+\frac{c\beta (t,x)l(H(x)-\delta )}{p\delta +l(H(x)-\delta )} v_2^\delta (t,x)-(d_h+\rho )v_1^\delta (t,x), t>0, x\in \varOmega ,\\ \frac{\partial v_2^\delta }{\partial t}&=D_m\triangle v_2^\delta (t,x)-d_m(t,x)v_2^\delta (t,x)\\&\quad +\int _\varOmega \varGamma (t,t-\tau ,x,y)\frac{b\beta (t-\tau ,y)p}{(p-l)\delta +lH(y)}(m^*(t-\tau ,y)-\delta )v_1^\delta (t-\tau ,y)dy,\\ t&>0, x\in \varOmega ,\\ \frac{\partial v_1^\delta }{\partial \nu }&=\frac{\partial v_2^\delta }{\partial \nu }=0, \,\,t>0, x\in \partial \varOmega . \end{aligned} \right. \end{aligned}$$

(23)

For any $\varphi \in \mathcal {E}$, let $v^{\delta }(t,x,\varphi )=(v_1^{\delta }(t,x,\varphi ),v_2^{\delta }(t,x,\varphi ))$ be the unique solution of (23) with $v_0^{\delta }(\varphi )(\theta ,x)=\varphi (\theta ,x)$ for all $\theta \in [-\,\tau ,0], x\in \bar{\varOmega }$, where

$$\begin{aligned} v_t^{\delta }(\varphi )(\theta ,x)= & {} v^{\delta }(t+\theta ,x,\varphi )=(v_1^{\delta }(t+\theta ,x, \varphi ),v_2^{\delta }(t,x, \varphi )),\\&\forall \,t\ge 0, (\theta ,x)\in [-\,\tau ,0]\times \bar{\varOmega }. \end{aligned}$$

Let $P_{\delta }: \mathcal {E} \rightarrow \mathcal {E}$ be the Poincaré map of (23), i.e., $P_{\delta }(\varphi )=v_{\omega }^{\delta }(\varphi ),\,\forall \,\varphi \in \mathcal {E}$. Let $r(P_\delta )$ be the spectral radius of $P_\delta$. Since $\lim _{\delta \rightarrow 0}r(P_\delta )=r(P)>1$, we can fix a small number $\delta >0$ such that

$$\begin{aligned} \delta <\min \left\{ \min _{t\in [0,\omega ], x\in \bar{\varOmega }} m^*(t,x),\min _{x\in \bar{\varOmega }} H(x)\right\} \,\,\,\text{ and }\,\,\, r(P_\delta )>1. \end{aligned}$$

For fixed $\delta >0$, by the continuous dependence of solutions on the initial value, there exists $\delta ^*>0$ such that for all $\phi$ with $||\phi -M||<\delta ^*$, we arrive at $\Vert Q(t)\phi -Q(t)M\Vert <\delta$ for all $t\in [0,\omega ]$. We now prove the following claim.

Claim. $\limsup _{n\rightarrow \infty } \Vert Q^n(\phi )-M\Vert \ge \delta ^*, \forall \,\phi \in \mathbb {C}_0.$

Suppose, by contradiction, that $\limsup _{n\rightarrow \infty } \Vert Q^n(\phi _0)-M\Vert <\delta ^*$ for some $\phi _0\in \mathbb {C}_0$. Then there exists $n_2\ge 1$ such that $\Vert Q^n(\phi _0)-M\Vert <\delta ^*$ for all $n\ge n_2$. For any $t\ge n_2\omega$, letting $t=n\omega +t'$ with $n=[t/\omega ]$ and $t'\in [0,\omega )$, we have

$$\begin{aligned} \Vert Q(t)\phi _0-Q(t)M\Vert =\Vert Q(t')(Q^n(\phi _0))-Q(t')M\Vert <\delta . \end{aligned}$$

(24)

It then follows from (24) and Lemma 9 that

$$\begin{aligned} u_2(t,x,\phi _0)>m^*(t,x)-\delta \,\,\text{ and }\,\, 0<u_i(t,x,\phi _0)<\delta ,\,\,i=1,3 \end{aligned}$$

for any $t\ge n_2\omega$ and $x\in \bar{\varOmega }$. Thus, $u_1(t,x,\phi _0)$ and $u_3(t,x,\phi _0)$ satisfy

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial u_1}{\partial t}\ge&D_h\triangle u_1(t,x)+\frac{c\beta (t,x)l[H(x)-\delta ]}{p\delta +l[H(x)-\delta ]} u_3(t,x)\\&-(d_h+\rho )u_1(t,x), \,\,\,\,\,t\ge n_2\omega +\tau , x\in \varOmega ,\\ \frac{\partial u_3}{\partial t}\ge&D_m\triangle u_3(t,x)-d_m(t,x)u_3(t,x)\\&+\int _\varOmega \varGamma (t,t-\tau ,x,y)\frac{b\beta (t-\tau ,y)p}{(p-l)\delta +lH(y)}(m^*(t-\tau ,y)-\delta )u_1(t-\tau ,y)dy,\\&t\ge n_2\omega +\tau , x\in \varOmega ,\\ \frac{\partial u_1}{\partial \nu }&=\frac{\partial u_3}{\partial \nu }=0,\,\,t\ge n_2\omega +\tau , x\in \partial {\varOmega }. \end{aligned} \right. \end{aligned}$$

(25)

Since $u(t,x,\phi _0)\gg 0$ for all $t> 0$ and $x\in \bar{\varOmega }$, there exists $\alpha _2>0$ such that

$$\begin{aligned} (u_1(t,x,\phi _0), u_3(t,x,\phi _0))\ge \alpha _2 e^{\mu _\delta t}v^*_\delta (t,x), \,\forall \,t\in [n_2\omega ,n_2\omega +\tau ],\, x\in \bar{\varOmega }, \end{aligned}$$

where $v^*_\delta (t,x)$ is a positive $\omega$-periodic function such that $e^{\mu _\delta t}v^*_\delta (t, x)$ is a solution of (23), where $\mu _\delta =\frac{\ln r(P_\delta )}{\omega }$. According to (25) and the comparison theorem, we have

$$\begin{aligned} (u_1(t,x,\phi _0),u_3(t,x,\phi _0))\ge \alpha _2 e^{\mu _{\delta } t}v^*_\delta (t,x), \,\,\,\,\,\forall \,t\ge n_2\omega +\tau ,\, x\in \bar{\varOmega }. \end{aligned}$$

Since $\mu _\delta >0$, it is easy to see that $u_i(t,\cdot ,\phi _0)\rightarrow +\,\infty , i=1,3$ as $t\rightarrow +\,\infty$. This leads to a contradiction.

The above claim implies that M is an isolated invariant set for Q in $C_H$, and $W^s(M)\cap \mathbb {C}_0=\emptyset$, where $W^s(M)$ is the stable set of M for Q. By the acyclicity theorem on uniform persistence for maps (see Zhao 2017b, Theorem 1.3.1 and Remark 1.3.1), $Q: C_H\rightarrow C_H$ is uniformly persistent with respect to $(\mathbb {C}_0,\partial \mathbb {C}_0)$ in the sense that there exists $\tilde{\eta }>0$ such that

$$\begin{aligned} \liminf _{n\rightarrow \infty } d(Q^n(\phi ), \partial \mathbb {C}_0)\ge \tilde{\eta },\,\,\forall \,\phi \in \mathbb {C}_0. \end{aligned}$$

(26)

Since for any integer n with $n\omega >\tau$, $Q^n=Q(n\omega )$ is compact, it follows that Q is asymptotically smooth on $C_H$. In addition, Lemma 3 implies that Q has a global attractor on $C_H$. By Magal and Zhao (2005, Theorem 3.7), Q admits a global attractor $A_0$ in $\mathbb {C}_0$.

Now we derive the desired practical persistence. Since $A_0=Q(A_0)=Q(\omega )(A_0)$, we have that $\phi _1(0,\cdot )>0$ and $\phi _3(\cdot )>0$ for all $\phi \in A_0$. Let $B_0: =\cup _{t\in [0,\omega ]} Q(t)A_0$. Then $B_0\subset \mathbb {C}_0$ and $\lim _{t\rightarrow \infty }d(Q(t)\phi ,B_0)=0, \forall \,\phi \in \mathbb {C}_0$. Define a continuous function $p: C_H\rightarrow {\mathbb {R}}_+$ by

$$\begin{aligned} p(\phi ):=\min \left\{ \min _{x\in \bar{\varOmega }}\phi _1(0,x), \min _{x\in \bar{\varOmega }}\phi _3(x) \right\} , \,\,\,\forall \,\phi =(\phi _1,\phi _2,\phi _3)\in C_H. \end{aligned}$$

Since $B_0$ is a compact subset of $\mathbb {C}_0$, it follows that $\inf _{\phi \in B_0} p(\phi )=\min _{\phi \in B_0} p(\phi )>0$. Consequently, there exists an $\eta ^*>0$ such that

$$\begin{aligned} \liminf _{t\rightarrow \infty } \min \left( u_1(t,\cdot ,\phi ), u_3(t,\cdot ,\phi ) \right) = \liminf _{t\rightarrow \infty } p(Q(t)\phi )\ge \eta ^*,\,\,\,\forall \,\phi \in \mathbb {C}_0. \end{aligned}$$

Furthermore, in view of Lemma 9, there exists an $\eta \in (0,\eta ^*)$ such that

$$\begin{aligned} \liminf _{t\rightarrow \infty } u_i(t,\cdot ,\phi )\ge \eta ,\,\,\,\forall \,\phi \in \mathbb {C}_0, i=1,2,3. \end{aligned}$$

It remains to prove the existence of a positive periodic solution. For a given real number $r>0$, we equip C with an equivalent norm $\Vert {\cdot }\Vert ^*_r$ as in Lemma 8. Define

$$\begin{aligned} \mathbb {W}_0=\{\phi \in W_H: \phi _1(0,\cdot )\not \equiv 0\,\text{ and }\,\phi _3(0,\cdot )\not \equiv 0\}, \end{aligned}$$

and

$$\begin{aligned} \partial \mathbb {W}_0:= W_H{\setminus } \mathbb {W}_0=\{\phi \in W_H: \phi _1(0,\cdot )\equiv 0\,\text{ or }\,\phi _3(0,\cdot )\equiv 0\}. \end{aligned}$$

Let $\hat{Q}=\hat{Q}(\omega )$, where $\hat{Q}(t)$ is defined as in Lemma 8. By the uniqueness of solutions, we see that $\hat{Q}$ is point dissipative, $\rho$-uniformly persistent with $\rho (\psi )=d(\psi ,\partial \mathbb {W}_0)$, and $\hat{Q}^n=\hat{Q}(n\omega )$ is compact for any integer n with $n\omega >\tau$. Moreover, Lemma 8 implies that $\hat{Q}$ is $\kappa$-condensing. Thus, it follows from (Magal and Zhao 2005, Theorem 4.5), as applied to $\hat{Q}$, that system (17) has an $\omega$-periodic solution $(z_1^*(t,\cdot ),z_2^*(t,\cdot ),z_3^*(t,\cdot ))$ with $(z_{1t}^*,z_{2t}^*,z_{3t}^*) \in \mathbb {W}_0$. Let $u_{10}^*=z_{10}^*, u_{20}^*=z_{20}^*, u_3^*(0,\cdot )=z_3^*(0,\cdot )$. Again by the uniqueness of solutions, we see that $(u_1^*(t,\cdot ), u_2^*(t,\cdot ), u_3^*(t,\cdot ))$ is a periodic solution of (9) and it is also strictly positive due to Lemma 9. $\square$

5 Numerical simulations

In this section, we carry out numerical simulations to reveal the influence of the EIP, the spatial heterogeneous infection and seasonality on the malaria transmission.

5.1 Numerical computation of $\mathcal {R}_0$

Let F(t) and V(t) be given as in Section 3. For any $\lambda \in (0,\infty )$, we consider the following linear and periodic system

$$\begin{aligned} \frac{\partial u}{\partial t} = \frac{1}{\lambda } F(t)u_t-V(t)u,\,\,t\ge 0, \end{aligned}$$

(27)

subjects to the Neumann boundary condition. Let $U(t, s, \lambda ) (t \ge s)$ be the evolution operators on $C([-\,\tau ,0],\mathbb {E})$ associated with system (27). By using arguments similar to those in Zhao (2017a, Theorem 2.2), we have the following result (see also Liang et al. 2017, Theorem 3.8).

Lemma 10

If $\mathcal {R}_0>0$, then $\lambda =\mathcal {R}_0$ is the unique solution of $r(U(\omega ,0,\lambda ))=1$.

In view of Lemma 10, we can use the standard bisection method to obtain the numerical solution $\lambda _0$ to $r(U(\omega , 0, \lambda )) = 1$, and hence, $\mathcal {R}_0 =\lambda _0$. Note that for each $\lambda \in (0,\infty )$, $r(U(\omega , 0, \lambda ))$ can be computed numerically via the following algorithm.

Lemma 11

(Liang et al. 2017, Lemma 2.5) Assume that $(E,E_+)$ is an ordered Banach space with $E_+$ being normal and $\mathrm{Int}(E_+)\ne \emptyset$, which is equipped with the norm $\Vert {\cdot }\Vert _E$. Let $\mathcal {L}$ be a positive bounded linear operator. Choose $v_0\in \mathrm{Int}(E_+)$ and define $a_n=\Vert \mathcal {L}v_{n-1}\Vert _E$, $v_n=\frac{\mathcal {L}v_{n-1}}{a_n}, \forall \,n\ge 1$. If $\lim \nolimits _{n\rightarrow \infty } a_n$ exists, then $r(\mathcal {L})=\lim \nolimits _{n\rightarrow \infty } a_n$.

5.2 Long term behavior

We concentrate on one dimensional domain $\varOmega =[0,\pi ]$ to simulate the long-time behavior of system (9). The time unit is taken as month. Baseline parameters are $d_h=\frac{1}{70 \times 12}\,\text{ month }^{-1}, \rho =0.0187\,\text{ month }^{-1}, d_m=3.2\,\text{ month }^{-1}, D_h=0.4\,\mathrm{km}^2\cdot \text{ month }^{-1}$ and $D_m=0.02\,\mathrm{km}^2\cdot \text{ month }^{-1}$, which are chosen or adapted from Lou and Zhao (2011) and Wang and Zhao (2017), $b=0.2, c=0.011, p=0.8, l=0.2,$ which are from Wang and Zhao (2017). Since the EIP takes from 10 to 30 days, we choose $\tau =0.5\,\text{ month }^{-1}$. For the sake of convenience, we assume that the density of total human population is $H(x)\equiv 110$, and $\beta (x)=4(1.1+\cos (2x))$, which describes the influences of spatially heterogeneous infection. Moreover, to reflect the seasonality, we suppose that the recruitment rate of mosquitoes from larvae is $\mu (t)=600(1+0.6\cos (\pi t/6 ))\,\text{ month }^{-1}$. It should be pointed out that these parameters are chosen for illustrative purpose only, and may not necessarily be realistic epidemiologically.

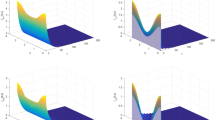
With this set of parameters, we have $\mathcal {R}_0=1.1339>1$, and the infection is persistent in human and mosquito populations (see Fig. 1). This is coincident with Theorem 1(ii). Note that we truncate time interval by [100, 200] so as to demonstrate the existence of positive periodic solution. If we take the same parameters as above except that $\mu (t)\equiv 600$, then $\mathcal {R}_0=1.1327$. This indicates that the time-averaged system may underestimate the disease risk.

Fig. 1

The evolution of $u_1$ and $u_3$, and x-intersections of numerical periodic solutions $u_1^*(t,x)$ and $u_3^*(t,x)$ at location $x=0.4054$. The initial data are chosen as $u_1(\theta ,x)= 3.3-\cos (2x), u_2(\theta ,x)=10-0.3\cos (2x)$ and $u_3(0,x)=2-0.2\cos (2x)$ for $\theta \in [-0.5,0], x\in [0,\pi ]$. a The evolution of $u_1$, b the evolution of $u_3$, c x-intersection of $u_1^*(t,x)$, d x-intersection of $u_3^*(t,x)$

5.3 Effects of parameters on $\mathcal {R}_0$

First, we examine the influences of the EIP and population diffusion. Let $\tau$ vary in [0.3, 1] and keep other parameters as above. Numerical computations demonstrate that $\mathcal {R}_0$ is a decreasing function (see Fig. 2a). This means that extending the incubation period with chemical measures may reduce the risk of disease transmission. For fixed $\tau =0.5$, we change $D_h$ from 0.04 to 0.2, but keep other parameters the same as those in Fig. 1. Although $\mathcal {R}_0$ decreases as $D_h$ increases, there is only a small change in the value of $\mathcal {R}_0$ (see Fig. 2b). This shows that increasing population mobility to control the disease is not a good strategy. Such observation is well understood biologically, since host-seeking by mosquitoes and blood-feeding are the key aspects for malaria transmission, and humans don’t find mosquitoes to be bitten.

Fig. 2

The effects of the EIP and population diffusion

Secondly, we explore the influence of spatially heterogeneous infection and the vector-bias level on malaria transmission. Take $\beta (x)=4(1.1+\delta \cos (2x)), 0\le \delta \le 1$. Numerical computations show that $\mathcal {R}_0$ is an increasing function of $\delta$ on [0, 1] (see Fig. 3a). Thus, more spatially heterogeneous infection can increase the basic reproduction number. To investigate the vector-bias effect, we use l / p to describe the relative attractivity of susceptible host versus infection one. Figure 3b shows that $\mathcal {R}_0$ decreases as l / p increases. Thus, the ignorance of the vector-bias effect will eventually underestimate the disease transmission risk. Below we prove the monotonicity of $\mathcal {R}_0$ with respect to $q:=l/p$.

Fig. 3

The effects of heterogeneous infection and vector-bias

Let A and B be defined as in Section 3. Motivated by the arguments in Liang et al. (2017, Section 4.2), we write

$$\begin{aligned} Av=(A_1v_1, A_2v_2)\,\,\text{ and }\,\,Bv=(B_1v_2, B_2v_1),\,\,\,\forall \,v=(v_1,v_2)\in C_\omega ({\mathbb {R}},\mathbb {E}), \end{aligned}$$

where

$$\begin{aligned}{}[A_1v_1](t)=\int _0^\infty T_1(t,t-s)v_1(t-s)ds,\,\, [A_2v_2](t)=\int _0^\infty T_2(t,t-s)v_2(t-s)ds, \end{aligned}$$

and

$$\begin{aligned}&[B_1v_2](t)= c\beta (t,\cdot )(v_2)_t(0,\cdot ),\\&[B_2v_1](t)=\frac{1}{q}\int _\varOmega \varGamma (t,t-\tau ,\cdot ,y)\frac{b\beta (t-\tau ,y)}{H(y)}m^*(t-\tau ,y)(v_1)_t(-\,\tau ,y)dy. \end{aligned}$$

Since $L(q)v=ABv=(A_1B_1v_2, A_2B_2v_1)$, it follows that

$$\begin{aligned} L^2(q)v =(A_1B_1A_2B_2v_1, A_2B_2A_1B_1v_2)=\frac{1}{q}L^2(1)v, \end{aligned}$$

and hence, $L^2(q)=\frac{1}{q}L^2(1)$. In view of $r^2(L(q))=r(L^2(q))$, we obtain

$$\begin{aligned} \mathcal {R}_0(q):=r(L(q))=\frac{1}{\sqrt{q}}r(L(1))=\frac{1}{\sqrt{q}}\mathcal {R}_0(1). \end{aligned}$$

(28)

Therefore, the simulation result in Fig. 3b is consistent with the analytical result.

6 Discussion

In this paper, taking into account the spatial heterogeneity, the EIP of the parasite in infected mosquitoes and the seasonality, we have proposed a vector-bias model for malaria transmission. Using the theory developed in Zhao (2017a), we have derived $\mathcal {R}_0$ for the model. It is shown that $\mathcal {R}_0$ serves as a threshold parameter for the persistence and extinction of the disease. In particular, we have proved that there is a positive $\omega$-periodic solution in the case where $\mathcal {R}_0>1$. This is a new finding for periodic and time-delayed reaction–diffusion models.

The mathematical difficulty in the establishment of positive $\omega$-periodic solution lies in the fact that we cannot directly verify the third condition in Magal and Zhao (2005, Theorem 4.5), namely, “either Q is $\kappa$-condensing or Q is convex $\kappa$-contracting $(0\le \kappa <1)$”. To overcome it, we used the idea in Zhao (2017b, Section 3.5) to construct an equivalent norm on C and prove that the solution maps of system (9) are $\kappa$-contractions on $W_H$. Accordingly, the existence of $\omega$-periodic solution follows from Magal and Zhao (2005, Theorem 4.5).

For periodic and time-delayed reaction diffusion models, the numerical approximation of the basic reproduction number $\mathcal {R}_0$ is difficult. In Section 5, we have numerically calculated $\mathcal {R}_0$ with the help of Lemmas 10 and 11, and explored the influences of some key parameters in (9) on the basic reproduction number $\mathcal {R}_0$. In the study of effect of heterogeneous infection, we have observed that the spatial heterogeneity of the disease transmission coefficient increases $\mathcal {R}_0$. This observation may provide some preventive strategies for the control of the malaria disease. Furthermore, it is found that $\mathcal {R}_0$ is a decreasing function of the EIP and the quotient l / p, which implies that the disease can be relieved by prolonging the length of the EIP, and that ignoring the impact of vector-bias will underestimate the infection risk of the disease.

Note that when $\frac{l}{p}\rightarrow 0$, the limit system corresponding to model (9) is of the form

$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial \hat{u}_1(t,x)}{\partial t}&=D_h \triangle \hat{u}_1(t,x)-(d_h+\rho )\hat{u}_1(t,x),\,\,t>0, x\in \varOmega ,\\ \frac{\partial \hat{u}_2(t,x)}{\partial t}&= D_m \triangle \hat{u}_2(t,x)+\mu (t,x)-(d_m(t,x)+b\beta (t,x))\hat{u}_2(t,x),\,\,t>0, x\in \varOmega ,\\ \frac{\partial \hat{u}_3(t,x)}{\partial t}&=D_m\triangle \hat{u}_3(t,x)-d_m(t,x)\hat{u}_3(t,x)\\&\quad +\int _\varOmega \varGamma (t,t-\tau , x,y)b\beta (t-\tau ,y)\hat{u}_2(t-\tau ,y)dy,\,\,\,t>0, x\in \varOmega ,\\ \frac{\partial \hat{u}_1(t,x)}{\partial \nu }&=\frac{\partial \hat{u}_2(t,x)}{\partial \nu }=\frac{\partial \hat{u}_3(t,x)}{\partial \nu }=0,\,\,\,\,t>0, x\in \partial \varOmega . \end{aligned} \right. \end{aligned}$$

(29)

Since model (29) is uncoupled, it follows from Lemma 2 that system (29) admits a unique $\omega$-periodic solution $(0,\hat{u}_2^*(t,\cdot ), \hat{u}_3^*(t,\cdot ))$, which is globally attractive in $C_H$. Clearly, $(0,\hat{u}_2^*(t,\cdot ),0)$ is not a solution of (29). Thus, we cannot define the basic reproduction number for the limiting system (29) in the same way as we did for the model system (9). In addition, we see from (28) that $\mathcal {R}_0\rightarrow \infty$ as $l/p\rightarrow 0$. One may conjecture that model (9) has a globally attractive and positive periodic solution when l / p is sufficiently small. We leave this interesting problem for future investigation.