Abstract
A significant proportion of malaria infections in humans exhibit no symptoms, but it is a reservoir for maintaining malaria transmission. A time periodic reaction-diffusion model for malaria spread is introduced in this paper, incorporating spatial heterogeneity, incubation periods, symptomatic and asymptomatic carriers. This paper introduces the concept of the basic reproduction number \(\mathcal {R}_{0}\), which is defined as the spectral radius of the next generation operator, and we present some preliminary results by elementary analysis. The threshold dynamic behavior analysis shows that when \(\mathcal {R}_{0}<1\), the disease is extinct, and when \(\mathcal {R}_{0}>1\), the disease is persistent. We investigate the case of constant system parameters, focusing on the global asymptotic stability of the disease-free steady state when \(\mathcal {R}_{0}=1\). In the numerical simulation section, we validate the theoretical results obtained, and then use elasticity analysis methods to explore the influence of parameters on the output solution. In addition, sensitivity analysis of the basic reproduction number under homogeneous conditions indicates direction of controlling malaria transmission. And several control measures are evaluated in the following steps.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Malaria is one of the most deadly and sophisticated parasitic diseases in underdeveloped countries, especially in Sub-Saharan Africa, causing high incidence rate and mortality, inducing a monstrous economic, social, and health burden [1], for which nearly half of the world population is at risk. There are currently approximately 219 million cases worldwide, with nearly 3.3 billion people exposed to contact the disease [2]. It stems from plasmodium parasite of protozoa spread in human after being effectively bitten by infected adult female Anopheles mosquitoes. P. vivax, P. falciparum, P. malariae, P. ovale and P. knowlesi are five types of malaria parasites that can infect humans.
The employment of mathematical models in the study of malaria transmission enables a deeper understanding of disease prevalence in communities and the exploration of how various factors, including migration, influence the evolution of the epidemic. Concerning this subject, researchers have developed rich mathematical models from the basic model of [3] and [4] to the spatiotemporal dynamic transmission of diseases. Epidemiologists widely use mathematical models as tools for predicting the prevalence of epidemics and infectious diseases, as well as guiding current study on malaria eradication [5]. Reaction-diffusion equations are usually used to comprehend the affect of the movement of humans and mosquitoes on diseases transmission taking into account the spatial structure [6, 7].
In recent years, malaria has become increasingly prominent due to the unexpected impact of climate change or global warming on the incidence rate of malaria. The rise and undulate of temperature can affect the vectors and life process of parasites. As is well known, mosquito reproduction is subjected to temperature - a temperature vary from 12 to \(31^\circ \)C decreases the number of days needed for reproduction from 65 to 7.3 days [8]. The spore formation of the parasites in mosquito is finished within 55 days at \(16^\circ \)C and reduced to 7 days at \(28^\circ \)C [9]. Climate change will shift from low latitude areas to areas where the population has not yet developed immunity to malaria, thereby affecting the epidemic patterns of the disease [10, 11]. The heightened interest in the relationship between global warming and malaria transmission has underscored the significance and relevance of modelling the impact of environmental factors on malaria spread. [11, 12]. Consequently, we need to consider these factor in the model.
The presence or absence of immunity constitutes a key determinant in the manifestation of clinical symptoms among malaria patients [13]. In high transmission regions of malaria, individuals maintain their susceptibility to malaria infection, potentially leading to the acquisition of immunity against the disease. The improvement of immunity reduces the parasite density of individuals and alleviates the severity of symptoms [14]. The clinical manifestations of malaria vary from severe and complex to mild and uncomplicated to asymptomatic [15]. According to reports, asymptomatic malaria infections have occurred in multiple high and medium transmission areas such as Kenya and Nigeria [16], which can be defined as individuals who have no recent history of symptoms and/or signs of malaria carrying parasites that can transmit the disease [17]. The number of asymptomatic carriers in a specific population within a specific time interval may affect the dynamics of disease transmission. Interestingly, simulation studies to date have shown that targeting asymptomatic infected individuals can reduce the spread of malaria [17, 18]. Therefore, it is believed that identifying and treating asymptomatic populations is an important path forward. By considering both symptomatic and asymptomatic cases of malaria, our aim is to gain insights into the influence of asymptomatic malaria individuals on the disease dynamics. A correct understanding of the impact of asymptomatic individuals on transmission dynamics will comprehensively describe the complex interplay between identified female Anopheles mosquitoes, intermediaries human, and pathogens (Plasmodium parasite). We hope that this qualitative analysis will fill the current gap in knowledge about asymptomatic malaria and help develop strategies that will further develop malaria control and eradication efforts. Understanding the contribution of asymptomatic carriers to the transmission of malaria among humans is crucial for the elimination of the disease.
The organizational structure of the remaining parts of this paper is as follows. A time-periodic reaction-diffusion model includes asymptomatic carriers, incubation periods and spatial heterogeneity is developed in Section 2. Section 3 brings some preliminary results. In Section 4, by applying to the theory of the next generation operator a threshold value, namely basic reproduction number \(\mathcal {R}_{0}\) is introduced. In Section 5, we analyze the threshold dynamic behavior: if \(\mathcal {R}_{0}<1\), then the disease becomes extinct, and if \(\mathcal {R}_{0}>1\), then the disease persists. Just as importantly, numerical simulations are conducted in the next section to explain the main theoretical results, sensitivity analysis, and evaluate control measures. Finally, a summary concludes the paper.
2 Model description
Due to the fact that malaria is transmitted among humans by mosquitos, two populations of mosquitoes and humans are considered here, and in a bounded domain \(\Omega \) which has smooth boundary \(\partial \Omega \). Describe \(N_{h}(t,x)\) and \(N_{v}(t,x)\) as the total population size of the humans and mosquitoes, respectively, at time t and location x. We further decompose the human population into susceptible, exposed, symptomatic, asymptomatic and recovered compartments, and are expressed by \(S_{h}\), \(E_{h}\), \(I_{h}\), J and R, respectively. Thus, \(N_{h}=S_{h}+E_{h}+I_{h}+J+R\). In addition, the recovered compartment dose not contain asymptomatic carriers and there is no associated transmission probability, as it does not cause mosquito infection. Although asymptomatic carriers may not develop clinical disease, their blood may still contain gametocytes with low levels wich could transmit the infection to mosquitoes [19]. The occurrence of asymptomatic infection is often due to the individual’s partial immunity to malaria caused by repeated exposures, so here we introduce a quantity c, \(0\le c\le 1\), which indicates a factor in reducing the infectivity of asymptomatic infections. It deems that the vector population consists only of female Anopheles mosquitoes, which are categorized into susceptible (\(S_{v}\)), exposed (\(E_{v}\)), and infectious compartments (\(I_{v}\)). The life span of mosquitoes is short, once they get infected they will not recover and can leave the infected class only through death. Accordingly, the total mosquito population is determined by \(N_{v}=S_{v}+E_{v}+I_{v}\). To address the impact of seasonal variation, we suppose that for some \(\omega >0\), the coefficients \(\Lambda _{v}(t,x)\), \(\mu _{v}(t,x)\), \(\alpha _{v}(t,x)\), \(\beta _{1}(t,x)\) and \(\beta _{2}(t,x)\) are all \(\omega \)-periodic with respect to t. As the human population is not significantly affected by seasonal temperature, the coefficients only related to mosquitoes are periodic. Furthermore, the dispersal pattern is an unbiased random walk, where a single walker randomly walks on a solid line with a fixed step [20]. Especially, according to [21], \(S_{h}\), \(E_{h}\), \(I_{h}\), J and \(R_{h}\) have the same coefficients represented by \(D_{h}>0\), while \(S_{v}\), \(E_{v}\) and \(I_{v}\) own the same coefficient denoted by \(D_{v}>0\).
Figure 1 is employed to elaborate on how humans and mosquitoes transition between various compartments. Therefore, for \(t>0\), our model subjects to the ensuing reaction-diffusion system,
where \(\frac{\partial }{\partial \nu }\) denotes the differentiation along the outward normal \(\nu \) to \(\partial \Omega \), \(\Delta \) is a Laplacian operator. The last equation of system (2.3) is boundary condition which means that the individuals do not move across the boundary \(\partial \Omega \). About initial data,
where \(A=S_{h}, E_{h}, I_{h}, J, R_{h}, S_{v}, E_{v}, I_{v}\). All position-dependent parameters are strictly positive, continuous and uniformly bounded functions on \(\Omega \).
The other equations in system (2.1) are not coupled with \(R_{h}\), then it is enough to explore the next system,
for \(t>0\). The biological significance of parameters is described in Table 1.
3 Preliminary results
Define \(\mathbb {X}:=C\left( \overline{\Omega }, \mathbb {R}^{7}\right) \) as the Banach space consisting of continuous functions mapping \(\overline{\Omega }\) to \(\mathbb {R}^{7}\). The space is equipped with the supremum norm, denoted by \(\Vert \cdot \Vert _{\mathbb {X}}\), and \(\mathbb {X}^{+}:=C\left( \overline{\Omega }, \mathbb {R}_{+}^{7}\right) \). Set \(\mathbb {Y}:=C\left( \overline{\Omega },\mathbb {R}\right) \) and \(\mathbb {Y}^{+}:=C\left( \overline{\Omega },\mathbb {R}_{+}\right) \). Suppose that \(T_{i}(t,s) (i=1,\ldots ,6):\mathbb {Y}\rightarrow \mathbb {Y}\), are evolution operators intimately related to
depending on the Neumann boundary condition, respectively. To clarify that \(T_{j}(t,s)=T_{j}(t-s)\), then \(T_{j}(t+\omega ,s+\omega )=T_{j}(t,s)\) (\(j=1,2,3,4\)) with \(t\ge s\) for \((t,s)\in (0,\infty )\times (0,\infty )\). Given that \(\mu _{v}(t,\cdot )\) and \(\alpha _{v}(t,\cdot )\) is \(\omega \)-periodic in t, Lemma 6.1 in [22] signifies that for \((t,s)\in \mathbb {R}^{2}\) with \(t\ge s\), \(T_{5}(t+\omega ,s+\omega )=T_{5}(t,s)\) and \(T_{6}(t+\omega ,s+\omega )=T_{6}(t,s)\). Additionally, based on [23, Corollary 7.2.3 ], \(T_{i}\) \((i=1,\ldots ,6)\) is compact and strongly positive. Then for \((t,s)\in \mathbb {R}^{2}\) with \(t\ge s\), \(T(t,s)=\text {diag}(T_{1}(t,s),T_{2}(t,s),T_{3}(t,s),T_{4}(t,s), T_{5}(t,s),T_{6}(t,s),T_{5}(t,s)):\mathbb {X}\rightarrow \mathbb {X}\) is an evolution operator.
For \(t>0\), \(x\in \overline{\Omega }\) and \(\phi \in \mathbb {X}^{+}\), denote a family operator \(\{\Phi (t)\}_{t>0}\) on \(\mathbb {X}^{+}\) by \(\Phi (t)(\phi )(x)=u(t,x;\phi )\). According to the proof of Lemma 2.1 in [24], it is straightforward to get that \(\{\Phi _{t}\}_{t\ge 0}\) is an \(\omega \)-periodic semiflow on \(\mathbb {X}^{+}\), which means that \(\Phi (t)\) is point dissipative. Furthermore, Theorem 2.1.8 in [25] reveals that \(\Phi (t)\) is compact.
Denote \(F=(F_{1},F_{2},F_{3},F_{4},F_{5},F_{6},F_{7}):[0,+\infty )\times \mathbb {X} \rightarrow \mathbb {X}\) by
for \(\phi =(\phi _{1},\cdots ,\phi _{7})\in \mathbb {X}^{+}\), \(t\ge 0\) and \(x\in \overline{\Omega }\). Let \(A(t)=\text {diag}(A_{1},A_{2},A_{3},A_{4},A_{5}(t),A_{6}(t),A_{5}(t))\), then T(t) is a simgroup generated by the operaator A defined on \(D(A)=(D(A_{1})\times D(A_{2})\times D(A_{3}) \times D(A_{4}) \times D(A_{5}) \times D(A_{6}(t)) \times D(A_{7}(t)))\). Then (2.3) can be rewritten as
where \(u=\left( S_{h},E_{h},I_{h},J, S_{v},E_{v},I_{v}\right) \). Here, \(A_{i} (i=1,\ldots ,4)\) is decided by
where \(m_{1}(x)=\mu _{h}(x)\), \(m_{2}(x)=\mu _{h}(x)+\alpha _{h}(x)\), \(m_{3}(x)=\mu _{h}(x)+\gamma _{1}(x)\) and \(m_{4}(x)=\mu _{h}(x)+\gamma _{2}(x)\). \(A_{j}(t) (j=5,6)\) is defined by
where \(p_{5}=\mu _{v}\), \(p_{6}=\mu _{v}+\alpha _{v}\).
Model (2.3) can be construed as
For each \(\phi \in \mathbb {X}^{+}\), according to [27, Theorem 1.1 and Remark 1.1], it can be inferred that (2.3) allows a single mild solution meeting \(u_{0}=\phi \) and \(u(t,\phi )\in \mathbb {X}^{+}\) for any t on its maximum existence interval \([0,\sigma _{\phi })\). According to the analytically of T(t, s), \(t>s\) and \((t,s)\in (0,\infty )\times (0,\infty )\), \(u(t,x,\phi )\) is a classical solution.
Theorem 3.1
For all \(\phi \in \mathbb {X}^{+}\), system (2.3) has a single solution \(u(t,;\phi )\in \mathbb {X}^{+}\) on \([0,\infty )\) with \(u_{0}=\phi \). Moreover, system (2.3) yields an \(\omega \)-periodic semiflow \(\Phi (t)=u(t,\cdot )\), that is, \(\Phi (t)(\phi )(x)=u(t,x;\phi )\), for \((t,x)\in (0,+\infty )\times \Omega \), additionally, \(\Phi :=\Phi (\omega )\) admits a global compact attractor in \(\mathbb {X}^{+}\).
Proof
According to the comparison principle, it is easy to know that on \([0,\sigma _{\phi })\), \(S_{h}(t,\cdot ;\phi )\) is bounded. There is some positive integer \(l_{1}=l_{1}(\phi )>0\) fulfilling \(S_{h}(t,x;\phi )\le M_{1}\), for \(t>l_{1}\omega \) and \(x\in \overline{\Omega }\). Let \((S_{h}(t,x),E_{h}(t,x),I_{h}(t,x),J(t,x),S_{v}(t,x), E_{v}(t,x),I_{v}(t,x)): =S_{h}(t,\phi )(x),E_{h}(t,\phi )(x),I_{h}(t,\phi )(x),J(t,\phi )(x), S_{v}(t,\phi )(x), E_{v}(t,\phi )(x),I_{v}(t,\phi )(x))\), \(t\ge 0\), \(x\in \Omega \) and
Denote \(\hat{f}=\max \limits _{t\in [0,\omega ],x\in \overline{\Omega }}f(t,x)\), \(\underline{f}=\min \limits _{t\in [0,\omega ],x\in \overline{\Omega }}f(t,x)\), \(\hat{g}=\max \limits _{x\in \overline{\Omega }}g(x)\), and \(\tilde{g}=\min \limits _{x\in \overline{\Omega }}g(x)\) where \(f=\Lambda _{v}(t,x), \mu _{v}(t,x),\alpha _{v}(t,x)\) and \(g=\Lambda _{h}(x), \mu _{h}(x), \alpha _{h}(x), \gamma _{1}(x), \gamma _{2}(x)\).
Integrating of the \(S_{h}\) equation of (2.3), gets
That is,
Application of the Green’s formula to the integrated form of the \(E_{h}\) equation in (2.3) yields
For \(t>l_{1}\omega \), we get
which gives rise to
where \(l_{2}>l_{1}\) is some integer. Thereupon,
Integrating the \(I_{h}\) and J equations in (2.3), respectively, and applying Green’s formula obtains
Thus,
where \(M_{2}=\hat{\alpha }_{h}\left[ \frac{\hat{\Lambda }_{h}|\Omega |+M_{1}|\Omega | (1+\tilde{\mu }_{h}+\tilde{\alpha }_{h})}{\tilde{\mu }_{h} +\tilde{\alpha }_{h}}+1\right] |\Omega |\) and \(m=\min \left\{ \tilde{\mu }_{h}+\tilde{\gamma }_{1}, \tilde{\mu }_{h}+\tilde{\gamma }_{2}\right\} \). Then \(\bar{I}_{h}(t)+\bar{J}(t)\le \frac{M_{2}}{m}\) for \(t\ge l_{3}\omega \) \((l_{3}\ge l_{2})\).
Based on comparison principle, on \([0,\sigma _{\phi })\), \(S_{v}(t,\cdot ;\phi )\) is bounded, then there is some positive integer \(l_{4}=l_{4}(\phi )\) meeting \(S_{v}(t,\cdot ;\phi )\le M_{3}\) for \(t\ge l_{4}\omega \) and \(x\in \overline{\Omega }\).
Integrate the \(S_{v}\) equation in system (2.3) produces
That is
Integrating of the sixth equation of model (2.3) and applying Green’s formula acquires
For \(t>l_{4}\omega \),
which leads to
where \(l_{5}>l_{4}\) is positive integer. Consequently,
Integrating the seventh equation of model (2.3)
Thus,
By Lemma 3.1 in [28], there exist constants \(K_{1}\) and \(K_{2}\) independent \(\phi \) satisfying
and
Therefore, \(S_{h}\), \(E_{h}\), \(I_{h}\), J, \(S_{v}\), \(E_{v}\) and \(I_{v}\) are uniformly bounded. Hence, \(\sigma _{\phi }=\infty \) for \(\phi \in \mathbb {X}^{+}\). \(\square \)
Describe a operator family \(\{\Phi (t)\}_{t>0}\) by \(\Phi (t)(\phi )(x)=u(t,x,\phi )\) for \(\phi \in \mathbb {X}^{+}\), and \((t,x)\in \mathbb {R}\times \overline{\Omega }\). Then \(\{\Phi _{t}\}_{t\ge 0}\) is an \(\omega \)-periodic semiflow according to the proof of Lemma 2.1 in [24]. In addition, \(\Phi (t)\) is point dissipative and Theorem 2.1.8 in [25] implies that \(\Phi (t)\) is compact. As a consequence, \(\Phi =\Phi (t)\) owns a global compact attractor [26, Theorem 2.9].
4 Basic reproduction number
The primary aim of this study is to explore the threshold dynamics of model (2.3). Basic reproduction number \(\mathcal {R}_{0}\) is among the most critical concepts in the study of infectious diseases, which will perform as the threshold for disease extinction and persistence. It is usually construed as the mean number of secondary infections that occur when a type of infected individual is introduced into a utterly susceptible population during the full infection period [29]. Here, according to the theory developed in [30, 32,33,34], the \(\mathcal {R}_{0}\) is introduced.
Set \(\mathbb {E}:=C\left( \overline{\Omega },\mathbb {R}^{5}\right) \), \(\mathbb {E}^{+}:=C\left( \overline{\Omega },\mathbb {R}^{5}_{+}\right) \) and \(C_{\omega }(\mathbb {R}, \mathbb {E})\) to be the Banach space consisting of wholly \(\omega \)-periodic and continuous functions from \(\mathbb {R}\) to \(\mathbb {E}\), and for \(\psi \in C_{\omega }(\mathbb {R}, \mathbb {E})\), \(\Vert \psi \Vert _{C_{\omega }(\mathbb {R}, \mathbb {E})}:=\max \limits _{\theta \in [0,\omega ]}\Vert \psi (\theta )\Vert _{\mathbb {E}}\). Then use [32] to acquire \(\mathcal {R}_{0}\) for model (2.3). Setting \(E_{h}=I_{h}=J=E_{v}=I_{v}=0\) in system (2.3), one gets
Lemma 2.1 in [24] suggests that model (4.1) has a positive globally attractive \(\omega \)-periodic solution \(\left( \tilde{S}_{h}(\cdot ), \tilde{S}_{v}(t,\cdot )\right) \) on \(C\left( \overline{\Omega }, \mathbb {R}^{2}_{+}\right) \). Linearizing model (2.3) at \(\left( \tilde{S}_{h}(\cdot ), 0,0,0, \tilde{S}_{v}(t,\cdot ),0,0\right) \) and regarding infection compartments, for \(t>0\), one obtains
Define \(\mathcal {F}(t):\mathbb {E}\rightarrow \mathbb {E}\) by
for \((\varphi _{1},\varphi _{2},\varphi _{3},\varphi _{4},\varphi _{5})\in \mathbb {E}\), \(t\in \mathbb {R}\), \(-V(t)v=\mathcal {D}\Delta v-W(t)v\), with \(\mathcal {D}=diag(D_{h},D_{h},D_{h},D_{v},D_{v})\) and
Allow \(\Psi (t,s)=\text {diag}(T_{2}(t,s),T_{3}(t,s),T_{4}(t,s),T_{6}(t,s),T_{5}(t,s))\), \(t\ge s\) to be the evolution operators intimately related to the subsequent mechanism
Then [35, Theorem 3.12] reveals that \(-V(t)\) is resolvent positive.
Recall that the exponential growth bound of \(\Psi (t,s)\) is defined by
Proposition A.2 in [35] shows that
According to [36, Lemma 14.2] and Krein-Rutman theorem, one has
and \(r(\Psi (\omega ,0))\) is the spectral radius of \(\Psi (\omega ,0)\). Let \(s=0\) in [35, Proposition 5.6], one brings \(\bar{\omega }(\Psi )<0\). Clarify that \(\Psi (t,s)\) is a positive operator, as meaning that for \(t\ge s\), \(\Psi (t,s)\mathbb {E}^{+}\subset \mathbb {E}^{+}\). Thus \(\mathcal {F}(t)\) and W(t) satisfying (i) for any \(t>0\), \(\mathcal {F}(t)\) maps \(\mathbb {E}^{+}\) into \(\mathbb {E}^{+}\); (ii) \(-W(t)\) is cooperative.
In order to introduce \(\mathcal {R}_{0}\) for system (2.3), keeping both human and mosquito populations are near the disease-free \(\omega \)-periodic solution \(\left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(t,x),0,0\right) \). Suppose that \(\bar{v}\in C(\mathbb {R},\mathbb {E})\) and \(\bar{v}(t,x)=\bar{v}(t)(x)\) is the initial distribution of infectious humans and mosquitoes introduced at \(t\in \mathbb {R}\), \(x\in \overline{\Omega }\). Note that for \(s\ge 0\), \(\mathcal {F}(t-s)\bar{v}(t-s,x)\) represents the density distribution of lately infected individuals at \(t-s\) \((s<t)\) and location x. Subsequently,
represents the distribution of cumulative infected individuals, which is created by whole infected individuals at prior to time t. Define
Subsequently \(\mathcal {L}\) is a continuous and positive operator, which maps the distribution of initial infection \(\bar{v}(t)\) to the whole infected distribution developed during among the infectious periodic. Encouraged by the doctrine of the next generation operators in [32, 35], \(\mathcal {R}_{0}\) for model (2.3) is described as the spectral radius of \(\mathcal {L}\),
For all \(\varphi \in \mathbb {E}\), P(t) is the solution map of (4.2) on \(\mathbb {E}\), namely, \(P(t)(\varphi )=v_{t}(\varphi )\), \(t\ge 0\), with \(v_{t}(\varphi )(x)=(v_{1}(t,x;\varphi ),v_{2}(t,x;\varphi ), v_{3}(t,x;\varphi ),v_{4}(t,x;\varphi ), v_{5}(t,x;\varphi ))\) and \(v(t,x;\varphi )\) is a single solution of (4.2) and \(v_{0}(x)=\varphi (x)\), for all \(x\in \overline{\Omega }\). Hence, \(P:=P(\omega )\) is the Poincaré map intimately related to (4.2). r(P) is set to be the spectral radius of P. Similar to [7, Section 3], one has \(v(t,x,\varphi )\gg 0\). According to [25, Theorem 2.1.8], for \(t>0\), \(v(t,x,\varphi )\) is compact on \(\mathbb {E}\). Thereby, \(P^{n}\) is compact and strongly positive. Based on [30, Lemma 3.1], r(P) is a simple eigenvalue of P which is intimately related to a positive eigenfunction \(\varphi \in Int(\mathbb {E}^{+})\).
In order to characterize \(\mathcal {R}_{0}\), we consider the following linear \(\omega \)-periodic equation
Based on [30, 31], we can obtain the following lemma.
Lemma 4.1
Problem (4.3) admits a unique principal eigenvalue \(\mu ^{*}>0\), associated with a strictly positive eigenvector \((\varphi _{1}^{*},\varphi _{2}^{*},\varphi _{3}^{*},\varphi _{4}^{*},\varphi _{5}^{*})\), then \(\mathcal {R}_{0}=\frac{1}{\mu ^{*}}\).
According to [32, Theorem 2.1], one gets the subsequent result.
Lemma 4.2
The sign of \(\mathcal {R}_{0}-1\) and \(r(P)-1\) are the same.
5 Threshold dynamics
Next analysis the strictly positive of the solution for system (2.3).
Lemma 5.1
Allow \(u(t,x,\phi )\) to be the solution of (2.3) with \(u_{0}=\phi \in \mathbb {X}^{+}\). In the event that there exists \(t_{0}\ge 0\) in such a way that \(E_{h}(t_{0},\cdot ;\phi )\not \equiv 0\) , \(I_{h}(t_{0},\cdot ;\phi )\not \equiv 0\), \(J(t_{0},\cdot ;\phi )\not \equiv 0\), \(E_{v}(t_{0},\cdot ;\phi )\not \equiv 0\) and \(I_{v}(t_{0},\cdot ;\phi )\not \equiv 0\), then the solution of (2.3) meets
Besides, for all initial data \(\phi \in \mathbb {X}^{+}\), \(\forall t\ge 0\), \(x\in \overline{\Omega }\), one has \(S_{h}>0\), \(S_{v}>0\), and
where \(\tilde{\varepsilon }>0\) is \(\phi \)-independent constant.
Proof
We know that for \(t>0\), \(E_{h}\), \(I_{h}\), J, \(E_{v}\) and \(I_{v}\) meet
Suppose there exists \(t_{0}\ge 0\), in such a way that \(E_{h}(t_{0},\cdot ;\phi )\not \equiv 0\), \(I_{h}(t_{0},\cdot ;\phi )\not \equiv 0\), \(J(t_{0},\cdot ;\phi )\not \equiv 0\), \(E_{v}(t_{0},\cdot ;\phi )\not \equiv 0\) and \(I_{v}(t_{0},\cdot ;\phi )\not \equiv 0\), then according to parabolic maximum principle, one has that \(E_{h}(t,\cdot ;\phi )>0\), \(I_{h}(t,\cdot ;\phi )>0\), \(J(t,\cdot ;\phi )>0\), \(E_{v}(t,\cdot ;\phi )>0\) and \(I_{v}(t,\cdot ;\phi )>0\), for \(t>t_{0}\). Set \(\hat{S}_{h}(t,\cdot ;\phi )\) to be the solution of
In virtue of the comparison principle, one concludes that \(S_{h}\ge \hat{S}_{h}\) for \(x\in \overline{\Omega }\). Additionally, system (5.1) has a single positive global attractive \(\omega \)-periodic solution \(\hat{S}^{*}_{h}(t,x)\) based on [24, Lemma 2.1]. Then
Denote \( \hat{S}_{v}\) to be the solution of
for \(t>0\), with \( \hat{S}_{v}(0,x)=\phi _{5}(x)\). Similarly, \(S_{v}\ge \hat{S}_{v}\) for \(x\in \overline{\Omega }\). Indisputably, system (5.2) has a single positive global attractive \(\omega \)-periodic solution \(\hat{S}^{*}_{v}(t,\cdot )\). Then
Choosing \(\tilde{\varepsilon }=\min \{\varepsilon _{1},\varepsilon _{2}\}\). The proof is complete. \(\square \)
Lemma 5.2
Define \(\mu =\frac{\ln r(P)}{\omega }\). There exists a \(\omega \)-periodic function \(v^{*}(t,x)\), which is positive, in such a way that \(e^{\mu t}v^{*}(t,x)\) is a solution of (4.2).
The proof of Lemma 5.2 is given in Appendix A.
Theorem 5.1
Denote \(u(t,x,\phi )\) to be the solution of (2.3) with \(u_{0}=\phi \in \mathbb {X}^{+}\). The following statements are true.
-
(i)
If \(\mathcal {R}_{0}<1\), then the disease-free \(\omega \)-periodic solution \(\left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(t,x),0,0\right) \) is globally attractive.
-
(ii)
If \(\mathcal {R}_{0}>1\), then model (2.3) admits no less than one positive \(\omega \)-periodic solution, and there exists an \(\eta >0\) such that for \(\phi \in \mathbb {X}^{+}\) with \(\phi _{2}(\cdot )\not \equiv 0\), \(\phi _{3}(\cdot )\not \equiv 0\), \(\phi _{4}(\cdot )\not \equiv 0\), \(\phi _{6}(\cdot )\not \equiv 0\) and \(\phi _{7}(\cdot )\not \equiv 0\), we have
$$\begin{aligned} \begin{aligned} \liminf \limits _{t\rightarrow \infty }S_{h}&\ge \eta , ~~ \liminf \limits _{t\rightarrow \infty }E_{h}\ge \eta , ~~\liminf \limits _{t\rightarrow \infty }I_{h}\ge \eta ,~~ \liminf \limits _{t\rightarrow \infty }J\ge \eta ,~~&\liminf \limits _{t\rightarrow \infty }S_{v}\ge \eta ,~~ \liminf \limits _{t\rightarrow \infty }E_{v}\ge \eta ,~~ \liminf \limits _{t\rightarrow \infty }I_{v}\ge \eta , \end{aligned} \end{aligned}$$uniformly for \(x\in \overline{\Omega }\).
Proof
-
(i)
If \(\mathcal {R}_{0}<1\), from Lemma 4.2, we know that \(r(P)<1\), and thereupon \(\mu =\frac{\ln r(P)}{\omega }<0\). For \(t>0\), view the following equations with \(\epsilon >0\),
$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial v^{\epsilon }_{1}}{\partial t}=D_{h}\Delta v^{\epsilon }_{1}+\beta _{1}(t,x)\left( \tilde{S}_{h}(x)+\epsilon \right) v^{\epsilon }_{5}-(\mu _{h}(x)+\alpha _{h}(x))v^{\epsilon }_{1},&x\in \Omega ,\\&\frac{\partial v^{\epsilon }_{2}}{\partial t}=D_{h}\Delta v^{\epsilon }_{2}+f\alpha _{h}(x)v^{\epsilon }_{1}-(\mu _{h}(x)+\gamma _{1}(x))v^{\epsilon }_{2},&x\in \Omega ,\\&\frac{\partial v^{\epsilon }_{3}}{\partial t}=D_{h}\Delta v^{\epsilon }_{3}+(1-f)\alpha _{h}(x)v^{\epsilon }_{1}-(\mu _{h}(x)+\gamma _{2}(x))v^{\epsilon }_{3},&x\in \Omega ,\\&\frac{\partial v^{\epsilon }_{4}}{\partial t}=D_{v}\Delta v^{\epsilon }_{4}+\beta _{2}(t,x)\left( \tilde{S}_{v}^{\epsilon }+\epsilon \right) v^{\epsilon }_{2} -(\mu _{v}(t,x)+\alpha _{v}(t,x))v^{\epsilon }_{4},&x\in \Omega ,\\&\frac{\partial v^{\epsilon }_{5}}{\partial t}=D_{v}\Delta v^{\epsilon }_{5}+\alpha _{v}(t,x)v^{\epsilon }_{4} -\mu _{v}(t,x)v^{\epsilon }_{5},&x\in \Omega ,\\&\frac{\partial v^{\epsilon }_{1}}{\partial \nu }= \frac{\partial v^{\epsilon }_{2}}{\partial \nu }= \frac{\partial v^{\epsilon }_{3}}{\partial \nu }= \frac{\partial v^{\epsilon }_{4}}{\partial \nu }= \frac{\partial v^{\epsilon }_{5}}{\partial \nu }=0,&x\in \partial \Omega . \end{aligned} \right. \end{aligned}$$(5.3)For \(\varphi \in \mathbb {E}\), we assume that \(v^{\epsilon }=(v^{\epsilon }_{1},v^{\epsilon }_{2}, v^{\epsilon }_{3},v^{\epsilon }_{4})\) is the unique solution of (5.3) with \(v_{0}^{\epsilon }(\varphi )(t,x)=v^{\epsilon }(t,x;\varphi )=(v^{\epsilon }_{1}(t,x;\varphi ), v^{\epsilon }_{2}(t,x;\varphi ),v^{\epsilon }_{3}(t,x;\varphi ),v^{\epsilon }_{4}(t,x;\varphi ))\), \(t\ge 0\), \(x\in \overline{\Omega }\). Let \(P_{\epsilon }:=\mathbb {E}\rightarrow \mathbb {E}\) be the Poincaré map of (5.3), i.e., \(P_{\epsilon }(\varphi )=v_{\omega }^{\epsilon }(\varphi )\), \(\varphi \in \mathbb {E}\). Allow \(r(P_{\epsilon })\) to represent the spectral radius of \(P_{\epsilon }\). Given that \(\lim \limits _{\epsilon \rightarrow 0}r(P_{\epsilon })=r(P)<1\), one can choose sufficiently small \(\epsilon >0\) in such a way that \(r(P_{\epsilon })<1\). On the basis of Lemma 5.2, there can be a positive \(\omega \)-periodic function \(v_{\epsilon }^{*}(t,x)\), then \(v^{\epsilon }=e^{\mu t} v_{\epsilon }^{*}\) is a solution of model (5.3), where \(\mu _{\epsilon }=\frac{\ln r(P_{\epsilon })}{\omega }<0\). For given \(\epsilon >0\), applying the comparison principle, there is some adequately large integer \(n_{1}>0\) in such manner as to
$$\begin{aligned} \begin{aligned} S_{h}\le \tilde{S}_{h}(x)+\epsilon , ~~ S_{v}\le \tilde{S}_{v}(t,x)+\epsilon ,~~t\ge n_{1}\omega ,~~x\in \overline{\Omega }. \end{aligned} \end{aligned}$$Then, for \(t\ge n_{1}\omega \),
$$\begin{aligned} \left\{ \begin{aligned} \frac{\partial E_{h}}{\partial t}&\le D_{h}\Delta E_{h}+\beta _{1}(t,x)\left( \tilde{S}_{h}(x)+\epsilon \right) I_{v}-(\mu _{h}(x)+\alpha _{h}(x))E_{h},&x\in \Omega ,\\ \frac{\partial I_{h}}{\partial t}&\le D_{h}\Delta I_{h}+f\alpha _{h}(x)E_{h}-(\mu _{h}(x)+\gamma _{1}(x))I_{h},&x\in \Omega ,\\ \frac{\partial J}{\partial t}&\le D_{h}\Delta J+(1-f)\alpha _{h}(x)E_{h}-(\mu _{h}(x)+\gamma _{2}(x))J,&x\in \Omega ,\\ \frac{\partial E_{v}}{\partial t}&\le D_{v}\Delta E_{v}+\beta _{2}(t,x)\left( \tilde{S}_{v}+\epsilon \right) I_{h}-(\mu _{v}(t,x)+\alpha _{v}(t,x))E_{v},&x\in \Omega ,\\ \frac{\partial I_{v}}{\partial t}&\le D_{v}\Delta I_{v}+\alpha _{v}(t,x)I_{v}-\mu _{v}(t,x)I_{v},&x\in \Omega ,\\ \frac{\partial E_{h}}{\partial \nu }&=\frac{\partial I_{h}}{\partial \nu } =\frac{\partial J}{\partial \nu } =\frac{\partial E_{v}}{\partial \nu } =\frac{\partial I_{v}}{\partial \nu }=0,&x\in \partial \Omega . \end{aligned} \right. \end{aligned}$$(5.4)Using (5.3), (5.4) and the comparison theorem, there is \(\alpha _{1}>0\) in such a manner that \((E_{h},I_{h}, J, E_{v},I_{v})\le \alpha _{1} e^{\mu _{\epsilon }t}v_{\epsilon }^{*}(t,\cdot )\), \(t\ge n_{1}\omega \), and
$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }(E_{h}, I_{h}, J, E_{v}, I_{v})=(0,0,0,0,0) ~\text {uniformly for}~x\in \overline{\Omega }. \end{aligned} \end{aligned}$$Then the equations of \(S_{h}\) and \(S_{v}\) are asymptomatic to (4.1). By the internally chain transitive sets [37, Section 2.1], we obtain that \(\lim \limits _{t\rightarrow \infty } \left[ \left( S_{h}(t,x),S_{v}(t,x)\right) -\left( \tilde{S}_{h}(x),\tilde{S}_{v}(t,x)\right) \right] =0\) uniformly for \(x\in \overline{\Omega }\), where \(\left( \tilde{S}(x),\tilde{S}_{v}(t,x)\right) \) is the globally attractive solution of (4.1).
-
(ii)
For \(\mathcal {R}_{0}>1\), one achieves \(r(P)>1\) and \(\mu =\frac{\ln r(P)}{\omega }>0\).
Denote
and
To highlight the fact that for \(\phi \in M_{0}\), \(t>0\), \(x\in \overline{\Omega }\), Lemma 5.1 reveals that
It follows that \(\Phi ^{n}(M_{0})\subset M_{0}\), \(n\in \mathbb {N}\). According to Theorem 3.1, \(\Phi \) allows a global attractor in \(\mathbb {X}^{+}\). Denote
meanwhile \(\omega (\phi )\) is the omega limit set of the orbit \(\gamma ^{+}(\phi )=\{\Phi ^{n}(\phi ):\forall n\in \mathbb {N}\}\). Set \(\mathcal {M}=\left\{ \left( \tilde{S}_{h}(\cdot ),0,0,0,\tilde{S}_{v}(t,\cdot ), 0,0\right) \right\} \). The fact that \(\mathcal {M}\) cannot develop a cycle for \(\Phi (\omega )\) in \(M_{0}\) is shown in the next claim. Claim 1 For any \(\tilde{\phi }\in M_{\partial }\), the omega limit set \(\omega (\tilde{\phi })=\mathcal {M}\). For \(\tilde{\phi }\in M_{\partial }\), \(\Phi ^{n}\left( \tilde{\phi }\right) \in \partial M_{0}\), \(n\in \mathbb {N}\). Hence, for each \(n\in \mathbb {N}\), either \(E_{h}\left( n\omega ,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(I_{h}\left( n\omega ,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(J\left( n\omega ,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(E_{v}\left( n\omega ,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(I_{v}\left( n\omega ,\cdot ;\tilde{\phi }\right) \equiv 0\). Accordingly, for each \(t\ge 0\), \(E_{h}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(I_{h}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(J\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(E_{v}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(I_{v}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\). Conversely, it contradicts with Lemma 5.1. If \(E_{h}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\), the third and forth equations in system (2.3) satisfy
By the comparison principle, one has \(\lim \limits _{t\rightarrow \infty }\left( I_{h}\left( t,x;\tilde{\phi }\right) ,J\left( t,x;\tilde{\phi }\right) \right) =(0,0)\) uniformly for \(x\in \overline{\Omega }\). From the \(E_{v}\) equation of model (2.3), it is easy to check that \(\lim \limits _{t\rightarrow \infty }E_{v}\left( t,x;\tilde{\phi }\right) =0\) uniformly for \(x\in \overline{\Omega }\), and then \(\lim \limits _{t\rightarrow \infty }I_{v}\left( t,x;\tilde{\phi }\right) =0\). Furthermore, \(S_{h}\) and \(S_{v}\) equations satisfy an nonautonomous system which is asymptomatic to the periodic system (4.1). Furthermore, it can be demonstrated through application of the internally chain transitive sets method, as presented in [37], that \(\lim \limits _{t\rightarrow \infty }\left( S_{h}\left( t,\cdot ;\tilde{\phi }\right) , S_{v}\left( t,\cdot ;\tilde{\phi }\right) \right) -\left( \tilde{S}_{h}(\cdot ), \tilde{S}_{v}(t,\cdot )\right) =0\). If \(E_{h}\left( t_{1},\cdot ;\tilde{\phi }\right) \not \equiv 0\), for some \(t_{1}\ge 0\). It follows from Lemma 5.1 that \(E_{h}\left( t_{1},\cdot ;\tilde{\phi }\right) >0\) for \(t\ge t_{1}\). Thus, \(I_{h}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(J\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(E_{v}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\) or \(I_{v}(t,\cdot ;\tilde{\phi })\equiv 0\), \(t\ge t_{1}\). For the case of \(I_{h}\left( t,\cdot ;\tilde{\phi }\right) \equiv 0\), \(t\ge t_{1}\), then \(\lim \limits _{t\rightarrow \infty }E_{h}\left( t,\cdot ;\tilde{\phi }\right) =0\). In this case, it is easy to get \(\lim \limits _{t\rightarrow \infty }J\left( t,\cdot ;\tilde{\phi }\right) =0\), \(\lim \limits _{t\rightarrow \infty }E_{v}\left( t,\cdot ;\tilde{\phi }\right) =0\) and then \(\lim \limits _{t\rightarrow \infty }I_{v}\left( t,\cdot ;\tilde{\phi }\right) =0\). Based on \(S_{h}\) and \(S_{v}\) equations, one obtains \(\lim \limits _{t\rightarrow +\infty }\Big (\left( S_{h}\left( t,\cdot ;\tilde{\phi }\right) , S_{v}\left( t,\cdot ;\tilde{\phi }\right) \right) -\left( \tilde{S}_{h}(\cdot ),\tilde{S}_{v}(t,\cdot )\right) \Big )=0\). The same way can also be used in other cases. Consequently, \(\omega (\tilde{\phi })=\mathcal {M}\) for any \(\tilde{\phi }\in M_{\partial }\).
Take into account the next equations with \(\delta >0\) and \(t>0\),
For \(\tilde{\psi }\in \mathbb {E}\) , denote \(v^{\delta } =\left( v^{\delta }_{1}, v^{\delta }_{2}, v^{\delta }_{3}, v^{\delta }_{4}\right) \) to be the solution of (5.5) with \(v^{\delta }_{0}\left( \tilde{\psi }\right) (t,x)=\tilde{\psi }(x)\). Let \(P_{\delta }:=P_{\delta }(\omega )\) is the Poincaré map of (5.5) in \(\mathbb {E}\), i.e., \(P_{\delta }\left( \tilde{\psi }\right) =v^{\delta }_{\omega }\left( \tilde{\psi }\right) \), \(\forall \tilde{\psi }\in \mathbb {E}\), and \(r(P_{\delta })\) be the spectral radius of \(P_{\delta }\). Due to \(\lim \limits _{\delta \rightarrow 0}r(P_{\delta })=r(P)>1\), select \(\delta >0\) to be sufficiently small, so that
For the above fixed \(\delta >0\), by the continuous dependence of solutions on initial value, there exists \(\bar{\delta }>0\) such that for all \(\tilde{\psi }\) with \(\left\| \tilde{\psi } -\mathcal {M}\right\| \le \bar{\delta }\), one has \(\Vert \Phi (t)\tilde{\psi }-\Phi (t)\mathcal {M}\Vert <\delta \) for \(t\in [0,\omega ]\). We now prove the following claim.
Claim 2 For every \(\phi \in M_{0}\), there holds \(\lim \limits _{n\rightarrow \infty }\Vert \Phi ^{n}\phi -\mathcal {M}\Vert \ge \bar{\delta }\).
Using contradictory proof, assume that for some \(\phi _{0}\in M_{0}\), there is \(\lim \limits _{n\rightarrow \infty }\Vert \Phi ^{n}\phi _{0}-\mathcal {M}\Vert < \bar{\delta }\). Given \(n_{2}\ge 1\), for \(n\ge n_{2}\), one has \(\Vert \Phi ^{n}(\phi _{0})-\mathcal {M}\Vert < \bar{\delta }\). For \(t\ge n_{2}\omega \), letting \(t=n\omega +t^{\prime }\) with \(n=[t / \omega ]\) and \(t^{\prime }\in [0,\omega )\), we obtain that
for \(t\ge n_{2}\omega \), \(x\in \overline{\Omega }\). As a consequence, when \(t\ge n_{2}\omega \), \(E_{h}\left( t,x;\phi _{0}\right) \), \(I_{h}\left( t,x; \phi _{0}\right) \), \(J\left( t,x; \phi _{0}\right) \), \(E_{v}\left( t,x;\phi _{0}\right) \) and \(I_{v}\left( t,x; \phi _{0}\right) \) meet
Given that \(u(t,x; \phi _{0})\gg 0\) for \((t,x)\in (0,+\infty )\times \overline{\Omega }\), there exists \(\alpha _{2}>0\) in such a way that
where \(v^{*}_{\delta }(t,x)\) is a positive \(\omega \)-periodic function in a manner that \(e^{\mu _{\delta }t}v^{*}_{\delta }(t,x)\) is a solution of system (5.5), and \(\mu _{\delta }=\frac{\ln r(P_{\delta })}{\omega }\). Since \(\mu _{\delta }>0\), it yields that \(E_{h}(t,\cdot ; \phi _{0})\rightarrow \infty \), \( I_{h}(t,\cdot ;\phi _{0})\rightarrow \infty \), \( J(t,\cdot ;\phi _{0})\rightarrow \infty \), \(E_{v}(t,\cdot ;\phi _{0})\rightarrow \infty \) and \(I_{v}(t,\cdot ;\phi _{0})\rightarrow \infty \) as \(t\rightarrow \infty \), which is a contradiction. Thence, \(\mathcal {M}\) is an isolated invariant set and \(W^{s}(\mathcal {M})\cap M_{0}= \emptyset \), \(W^{s}(\mathcal {M})\) is the stable set. Pursuant to [26, Theorem 3.7], \(\Phi \) allows a global attractor \(A_{0}\) in \(M_{0}\). Based on [37, Theorem 1.3.1 and Remark 1.3.1], one has that \(\Phi \) is uniformly persistent about \((M_{0}, \partial M_{0})\). That is to say, there exists \(\bar{\eta }>0\), in such a way that
Since \(A_{0}=\Phi A_{0}\), we find that \(\phi _{i}(\cdot )>0\), \(i=2,3,4,6,7\) for \(\phi \in A_{0}\). Denote \(B_{0}:=\bigcup \limits _{t\in [0,\omega ]}\Phi (t)A_{0}\). Subsequently, \(B_{0}\subset M_{0}\) and \(\lim \limits _{t\rightarrow \infty }\text {d}(\Phi (t),B_{0})=0\), \(\forall \phi \in M_{0}\). Define \(p:\mathbb {X}^{+}\rightarrow \mathbb {R}_{+}\) as a continuous function,
In view of \(B_{0}\) is compact subset of \(M_{0}\), it follows that \(\inf \limits _{\phi \in B_{0}}p(\phi )=\min \limits _{\phi \in B_{0}}p(\phi )>0\). Consequently, there is an \(\eta ^{*}>0\) that
Additionally, according to Theorem 5.1, there is a constant \(\hat{\eta }\in (0,\eta ^{*})\) such that
Based on [20, Theorem 4.6] and [26, Theorem 4.5], model (2.3) has at least one positive \(\omega \)-periodic solution. We complete the proof. \(\square \)
6 Global asymptotic stability analysis
We presume that \(\beta _{1}\), \(\beta _{2}\), \(\mu _{v}\) and \(\alpha _{v}\) are independent of time t. Following [38, 39], we cogitate the global asymptotic stability of the disease-free steady state in the critical case of \(\mathcal {R}_{0}=1\) for the next system at \(t>0\),
For simplicity, we still use the previous symbols.
Theorem 6.1
If \(\mathcal {R}_{0}=1\), then the disease-free steady state \(E^{0}=\left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \) of system (6.1) is globally asymptotical stable.
Proof
We first explore that \(\left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \) is locally asymptotically stable. Assume \(\delta _{1}>0\) and let \(u_{0}=\left( S_{h}^{0},E_{h}^{0},I_{h}^{0},J^{0}, S_{v}^{0},E_{h}^{0},I_{v}^{0}\right) \) with \(\left\| u_{0}-\left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \right\| \le \delta _{1}\). Denote
In view of
one has
Set \(\hat{T}_{1}(t)\) and \(\hat{T}_{2}(t)\) to be designated as the semigroups produced by the generator
and
subject to Nuemann boundary condition, respectively.
Choose \(\delta _{2}>0\) such that \(\Vert \hat{T}_{1}(t),\hat{T}_{2}(t)\Vert \le M_{5}e^{-\delta _{2}t}\) for some \(M_{5}>0\). Then
where \(r_{1}^{0}=\frac{S_{h}^{0}}{\tilde{S}_{h}(x)}-1\) and \(r_{2}^{0}=\frac{S_{v}^{0}}{\tilde{S}_{v}(x)}-1\).
Denote \(S=\min \left\{ \min \limits _{x\in \overline{\Omega }}\tilde{S}_{h}(x), \min \limits _{x\in \overline{\Omega }}\tilde{S}_{h}(x)\right\} \), then
Note that for \(t>0\), \((E_{h},I_{h},J,E_{v},I_{v})\) satisfies
Assuming \(\tilde{T}(t)=\left( \tilde{T}_{1}(t),\tilde{T}_{2}(t),\tilde{T}_{3}(t) ,\tilde{T}_{4}(t),\tilde{T}_{5}(t)\right) \) represents the semigroup of the system,
Then, one has
Since \(\mathcal {R}_{0}=1\), due to Proposition 4.15 in [40], there is \(M_{5}>0\), in such a way that \(\Vert \tilde{T}(t)\Vert \le M_{5}\) for \(t\ge 0\). Using \(z(s)\le \frac{\delta _{1}M_{5}e^{-\delta _{2}t}}{S}\), one deduces that
where \(M_{6}=\frac{M_{5}^{2}\Vert \beta _{1}\Vert ~\Vert \tilde{S}_{h}\Vert }{S}\) and \(M_{7}=\frac{M_{5}^{2}\Vert \beta _{2}\Vert ~\Vert \tilde{S}_{v}\Vert }{S}\). Applying Gronwall’s inequality yields
where \(M_{8}=\max \left\{ M_{5}\delta _{1}\frac{\delta _{1}M_{6}}{\delta _{2}}, 2M_{5}\delta _{1}\frac{\delta _{1}M_{7}}{\delta _{2}}\right\} \). Thus,
For \(t>0\), let \((\hat{v}_{1},\hat{v}_{2})\) be a solution of the system,
with \( \hat{v}_{1}(0,x)=S_{h}^{0},~~\hat{v}_{2}(0,x)=S_{v}^{0}\), for \(x\in \overline{\Omega }\). By the comparison principle, one has \((S_{h}(t,x), S_{v}(t,x))\ge (\hat{v}_{1}(t,x),\hat{v}_{2}(t,x))\), with \(t\ge 0\) and \(x\in \overline{\Omega }\). Let \(\left( S_{h}^{\delta _{1}}(x), S_{v}^{\delta _{1}}(x)\right) \) be the positive steady state of system (6.2) and \(w_{1}(t,x)=\hat{v}_{1}(t,x)-S_{h}^{\delta _{1}}(x)\), \(w_{2}(t,x)=\hat{v}_{2}(t,x)-S_{v}^{\delta _{1}}(x)\). Then for \(t>0\), \((w_{1}(t,x),w_{2}(t,x))\) satisfies
with \( w_{1}(0,x)=S_{h}^{0}-S_{h}^{\delta _{1}}(x),\) \(w_{2}(0,x)=S_{v}^{0} -S_{v}^{\delta _{1}}(x)\). Let \(P_{1}(t)\), \(P_{2}(t)\) be the semigroups generated by \(D_{h}\Delta -\mu _{h}(x)\) and \(D_{v}\Delta -\mu _{v}(x)\) with Neumann boundary condition, respectively. Set \(P(t)=(P_{1}(t), P_{2}(t))\). It is possible to select \(M_{5}\) in such a manner that \(\Vert P(t)\Vert \le M_{5}e^{\alpha _{3}t}\), provided that \(M_{5}\) is sufficiently large. By (6.3), we have
Hence,
Let \(K_{3}=M_{8}M_{5}\Vert \beta _{1}(\cdot )\Vert \) and \(K_{4}=M_{8}M_{5}\Vert \beta _{2}(\cdot )\Vert \). Then
Selecting \(\delta _{4}>0\) small enough to satisfy \(\max \{K_{3},K_{4}\}<-\frac{\alpha _{3}t}{2}\), one has
Now by (6.4), one has
Noticing that \(z(s)\le \frac{\delta _{1}M_{5}e^{-\delta _{2}t}}{S}\le \frac{\delta _{1}M_{5}}{S}\), we get that
and
In view of that \(\lim \limits _{\delta _{1}\rightarrow 0}\left( S_{h}^{\delta _{1}}(x),S_{v}^{\delta _{1}}(x)\right) =\left( \tilde{S}_{h}(x),\tilde{S}_{v}(x)\right) \), we can choose \(\delta _{1}\) sufficiently small, for \(t>0\), one derives that
proving the local stability of \(E_{0}=\left\{ \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right\} \).
Next, we prove the global attractivity of \(\left\{ \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right\} \). On view of Theorem 3.1, \(\Phi (t)\) has a global attractor \(\mathcal {A}\). Define
Claim 1. For \(u_{0}=(S_{h}^{0},E_{h}^{0},I_{h}^{0}, J^{0},S_{v}^{0},E_{v}^{0},I_{v}^{0})\in \mathcal {A}\), the omega limit set \(\omega (u_{0})\in \partial X_{1}\).
We know that \(S_{h}^{0}(\cdot )\le \tilde{S}_{h}(\cdot )\) and \(S_{v}^{0}(\cdot )\le \tilde{S}_{v}(\cdot )\). If \(E_{h}^{\varepsilon }=I_{h}^{\varepsilon }= J^{\varepsilon }= E_{v}^{\varepsilon }=I_{v}^{\varepsilon }=0\), the claim easily follows from the fact that \(\partial X_{1}\) is invariant for \(\Phi (t)\). Assuming that either \(E_{h}^{0}\ne 0\) or \(I_{h}^{0}\ne 0\) or \(J^{0}\ne 0\) or \(S_{v}^{0}\ne 0\) or \(E_{v}^{0}\ne 0\) or \(I_{v}^{0}\ne 0\), then one has \(E_{h}(t,x)>0\), \(I_{h}(t,x)>0\), \(E_{v}(t,x)>0\), \(I_{v}(t,x)>0\) and \(J(t,x)>0\) for \(t>0\) and \(x\in \overline{\Omega }\). Then for \(t>0\), \(S_{v}\) and \(S_{h}\) satisfy
with \(S_{h}(0,x)\le \tilde{S}_{h}(x)\), \(S_{v}(0,x)\le \tilde{S}_{v}(x)\) for \( x\in \overline{\Omega }\). Apply the comparison principle, \(S_{h}< \tilde{S}_{h}(x)\) and \(S_{v}< \tilde{S}_{v}(x)\) for \(t>0\) and \(x\in \overline{\Omega }\). According to [39], we introduce
Then for \(t>0\), \(c(t;u_{0})>0\). We conclude that \(c(t;u_{0})\) is strictly decreasing. Give \(t_{2}>0\) and set \(E_{h}^{\varepsilon }(t,\cdot )=c(t_{2};u_{0})\phi _{2}\), \(I_{h}^{\varepsilon }(t,\cdot )=c(t_{2};u_{0})\phi _{3}\), \(J^{\varepsilon }(t,\cdot )=c(t_{2};u_{0})\phi _{4}\), \(E_{v}^{\varepsilon }(t,\cdot )=c(t_{2};u_{0})\phi _{5}\), \(I_{v}^{\varepsilon }(t,\cdot )=c(t_{2};u_{0})\phi _{6}\) for \(t\ge t_{2}\). It follows from \(S_{h}<\tilde{S}_{h}(\cdot )\) and \(S_{v}<\tilde{S}_{v}(\cdot )\) that
Therefore, \(\left( E_{h}^{\varepsilon },I_{h}^{\varepsilon },J^{\varepsilon }, E_{v}^{\varepsilon },I_{v}^{\varepsilon }\right) \ge \left( E_{h},I_{h},J,E_{v},I_{v}\right) \) for \(t>t_{2}\) and \(x\in \overline{\Omega }\). For system (6.5), we see that \(c(t_{2};u_{0})\phi _{2}(x)=E_{h}^{\varepsilon }>E_{h}\) for \((t,x)\in (t_{2},+\infty )\times \overline{\Omega }\). Similarly, \(c(t_{2};u_{0})\phi _{3}(x)=I_{h}^{\varepsilon }>I_{h}\), \(c(t_{2};u_{0})\phi _{4}(x)=J^{\varepsilon }>J\), \(c(t_{2};u_{0})\phi _{6}(x)=E_{v}^{\varepsilon }>E_{v}\), \(c(t_{2};u_{0})\phi _{7}(x)=I_{v}^{\varepsilon }>I_{v}\), for \(t>t_{2}\) and \(x\in \overline{\Omega }\). Due to \(t_{2}\) is arbitrary, \(c(t;u_{0})\) is strictly decreasing. Let \(c_{*}=\lim \limits _{t\rightarrow \infty }c(t;u_{0})\). Then \(c_{*}=0\). Actually let \(Z=(Z_{1},Z_{2},Z_{3},Z_{4},Z_{5},Z_{6},Z_{7})\in \omega (u_{0})\). There is \(\{t_{n}\}\) with \(t_{n}\rightarrow +\infty \) as \(t\rightarrow +\infty \) such that \(\Phi (t_{n})u_{0}\rightarrow Z\). Then for \(t\ge 0\), one gets that \(c(t;Z)=c_{*}\) due to \(\lim \limits _{t\rightarrow +\infty }\Phi (t+t_{n})u_{0}=\Phi (t) \lim \limits _{t\rightarrow +\infty }\Phi (t_{n})u_{0}=\Phi (t)Z\). If \(Z_{2}\ne 0\), \(Z_{3}\ne 0\), \(Z_{4}\ne 0\), \(Z_{5}\ne 0\), \(Z_{6}\ne 0\) and \(Z_{7}\ne 0\), based on the above viewpoint, it can be concluded that c(t; Z) is strictly decreasing, which yields a contradiction to \(c(t;Z)=c_{*}\). Consequently, \(Z_{2}=Z_{3}=Z_{4}=Z_{6}=Z_{6}=0\).
Claim 2. \(\mathcal {A}=\left\{ \left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \right\} \).
Since \(\mathcal {A}\) is globally attractive in \(\partial X_{1}\), then \(\left\{ \left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \right\} \) is the only compact invariant subset of system (6.1). From the invariance of \(\omega (u_{0})\) and \(u_{0}\in \partial X_{1}\), one has \(\omega (u_{0})=\left\{ \left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \right\} \). Since the global attractor \(\mathcal {A}\) is compact invariant in \(\mathbb {X}^{+}\), \(\left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \) is stable, and by [38, Lemma 3.11], one has \(\mathcal {A}=\left\{ \left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \right\} \).
The globally asymptotical stability of \(\left( \tilde{S}_{h}(x),0,0,0,\tilde{S}_{v}(x),0,0\right) \) is immediately obtained based on the global attractivity and local stability. \(\square \)
7 Numerical simulation
This part uses numerical simulations to clarify the analytical results and to show how to gain some cognisance of epidemiology.
7.1 Long term behavior
The one-dimensional domain \((0,\pi )\) is generally employed to simulate the long-time dynamics as suggested by [6, 7, 21]. We refer to system (2.3) as a model for the spread of malaria in Maputo Province, Mozambique. Fix periodic \(\omega =12\) months. b means biting rate on humans, \(\frac{b}{N_{h}}\) is the per human biting rate. Denote \(\tilde{\beta }_{1}\) as the role of mosquito biting behavior in the probability of acquiring malaria from infectious humans, and \(\tilde{\beta }_{2}\) is expressed as the transmission probability of the infectivity of mosquito bites in transmitting malaria from human to mosquito. As a consequence, we can express \(\beta _{1}=\frac{b}{N_{h}}\tilde{\beta }_{1}\) and \(\beta _{2}=\frac{b}{N_{h}}\tilde{\beta }_{2}\), which represent the spread probability of the disease in mosquitoes and humans. [41] ascertained the interval of critical parameters about the temporal and spatial patterns of malaria. Since the climate in Maputo is conducive to the spread of malaria, [42] explored the seasonality impacts on the spread of malaria, containing seasonal forced biting rate b(t), mosquitoes mortality rate \(\mu _{v}(t)\) and recruitment rate \(\Lambda _{v}(t)\), where
and
The description of the parameters can be found in Table 2.
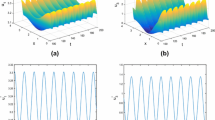
We choose \(\tilde{\beta }_{1}=0.17\), \(\tilde{\beta }_{2}=0.15\). Let \(\gamma _{1}=a_{1}\cdot (1.05-\cos (2x))~\text {Month}^{-1}\) and \(\gamma _{2}=a_{2}\cdot (1.05-\cos (2x))~\text {Month}^{-1}\), where \(a_{1}=0.055\), \(a_{2}=0.051\). It can be observed that individuals residing in urban areas, especially those nearer to the city center, have access to superior medical treatment due to a higher concentration of doctors, hospitals, and state-of-the-art medical equipment. Consequently, the recovery rate of patients is expected to be higher in urban areas compared to rural areas. The other parameters remain consistent with those in Table 2. For these given parameters, numerical calculations can yield \(\mathcal {R}_{0}=4.3652>1\), indicating that the disease is persistent. In this case, the long-term behavior of system (2.3) is illustrated in Figure 2, with initial data
This is consistent with the Theorem 5.1(ii).
By disinfection and sterilization mosquito breeding sites and take advantage of insecticide treated mosquito nets, the bite rate is reduced to 0.5b, and the death rate of mosquito is increased to \(1.5\mu _{v}\). People pay more attention to the spread of diseases and invest more and more medical resources. Therefore, it is assumed that the recovery rate of infected persons will increase to \(1.1\gamma _{1}\) and \(1.1\gamma _{2}\), then \(\mathcal {R}_{0}=0.5164<1\). Figure 3 describes that the infectious hosts and vectors go to 0, i.e., the disease will be eradicated.
7.2 Sensitivity analysis
Sensitivity analysis can be applied to quantify the impact of uncertainty on model input parameters and subsequently impact on model outputs [43, 44]. The purpose of sensitivity analysis is to quantify this relationship by using the ubiquitous derivative of the output as a function of the input and to accurately quantify the ratio of output perturbation relative to the input perturbation. This section analyzes the sensitivity of the output solution and the basic reproduction number.
7.2.1 Sensitivity analysis to output solutions
For our model, this involves under the \(13 \times 5\) sensitive coefficient matrix given by
for convenience, let
Since our model parameters are assessed in distinct units and of different orders of magnitude, which leads to a challenge to interpret the sensitivity results. First, we focus on elasticity analysis [45]. The field of elasticity analysis is concerned with studying the proportional response of a model’s output to proportional changes in its input parameters, as opposed to additive changes. The elasticity coefficient matrix is given by
Especially, elasticity is dimensionless due to it is proportional sensitivities and is scaled. Therefore, the elasticity between all model parameters can be directly compared.
In this study, we employ a basic finite differences approach to estimate the derivative and computationally solve the elasticity coefficient matrix. More precisely, we utilize the following formula to numerically calculate the elasticity coefficients
for \(i=1,2,3,4,5\) and \(j=1,\cdots ,13\) and \(\triangle \tilde{P}_{j}>0\). According to [46, 47], \(\frac{\partial \tilde{Q}_{i}(t,x;\tilde{P})}{\partial \tilde{P}_{j}} \frac{\tilde{P}_{j}}{\tilde{Q}_{i}(t,x;\tilde{P})}\) is called normalized sensitivity index. The aforementioned metric quantifies the ratio of the change in the output to a small proportionate variation in the input.
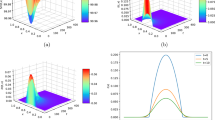
Figure 4 presents the full elasticity coefficient at the \(t=350\) and \(x=3\). The presented data illustrates in a lucid manner that collective equilibrium concentrations are primarily influenced by the parameter \(\mu _{v}\), while the parameter \(\Lambda _{v}\) exhibits a secondary level of sensitivity. And through observation, it finds that the influence of these parameters on the infected compartment is relatively large, while the impact on the susceptible compartment is almost negligible.
The following evaluates the effect of evolving model parameters over time on outbreak size, sensitivity analysis is performed by Latin Hypercube Sampling and partial rank correlation coefficient (PRCC) method [48]. To assess whether the significance of a parameter appears at a certain time interval during the progression of the model dynamics, PRCC indices are calculated at multiple time points and plotted against time. Figure 5 shows the significance of the effect of parameters on outputs \(E_{h}\), \(I_{h}\), J, \(E_{v}\) and \(I_{v}\). This figure shows the absolute value of the PRCC to make it easier to compare their relative magnitudes. Looking at Figure 5, the mathematical model is a dynamic system, PRCC can depend on time, and the relative importance of parameters can also be contingent on time. For \(E_{h}\), shown in Figure 5 (a), for example, for \(t_{1}\le t\le t_{2}\), the effect of parameters on the solution is \(\beta _{1}>N_{h}>\Lambda _{v}>f>\beta _{2}>\gamma _{1}>\gamma _{2}>\mu _{v}>\alpha _{h}\), while when \(t_{4}\le t\le t_{5}\), the order is \(\beta _{2}>\gamma _{1}>\mu _{v}>f>\Lambda _{v}>\beta _{1}>\Lambda _{h}>\alpha _{v}>\gamma _{2}>c>N_{h}>\alpha _{h}>\mu _{h}\). In addition, it is also found that in this time interval, when t is less than about 0.8, the influence of \(\beta _{1}\) might be the greatest on the solution, and when \(t>t_{3}\), \(\gamma \) is the greatest. For \(I_{h}\), shown in Figure 5 (b), when \(t_{1}<t< t_{2}\), the the effect of parameters on the solution is \(\gamma _{1}>f>\Lambda _{v}>N_{h}>\gamma _{2}>\mu _{h}>\Lambda _{h}>\beta _{1}>\alpha _{h}>c>\text {others}\), while when \(t_{4}<t< t_{5}\), the order is \(\alpha _{h}>\gamma _{2}(\gamma _{1})>\beta _{1}>f>\beta _{2}>\Lambda _{v}>\Lambda _{h}>\mu _{v}> c(\mu _{h})>N_{h}>\alpha _{v}\). Furthermore, during this time interval, if \(t<t_{3}\), the \(\gamma _{1}\) might have the greatest influence on \(I_{h}\). For J (see Figure (5) (c)), during \(t_{1}<t< t_{2}\), the influence of parameters on the output solution is in the order of \(\alpha _{h}>\gamma _{2}>\beta _{2}>\mu _{v}>\alpha _{v}>\gamma _{1}>f>c>\beta _{1}>N_{h}>\Lambda _{v}>\mu _{h}>\Lambda _{h}\), and when \(t_{3}<t< t_{4}\), the order is \(\mu _{v}>\alpha _{v}>f>\mu _{h}>\alpha _{h}>\gamma _{1}>N_{h}>\Lambda _{v}>\beta _{2}>\gamma _{2}>\beta _{1}>c>\Lambda _{h}\). For \(E_{v}\) (see Figure 5 (d)), when \(t_{1}<t< t_{2}\), the order of influence of parameters on output solution is \(\beta _{2}>c>N_{h}>\mu _{v}>f>\gamma _{1}>\alpha _{h}>\mu _{h}>\Lambda _{v}>\alpha _{v}>\beta _{1}>\gamma _{2}>\Lambda _{h}\), then it is \(\Lambda _{v}>\beta _{2}>\beta _{1}>c>\gamma _{1}>\alpha _{v}>f>\mu _{v}>\text {others} \) when \(t_{3}<t< t_{4}\). It is easy to see that when \(t<t_{3}\), \(\beta _{2}\) has the greatest impact on \(E_{v}\), while when \(t>t_{3}\), \(\Lambda _{v}\) has the greatest impact. Finally, for \(I_{v}\), when \(t_{1}<t< t_{2}\), the order of parameter influence is \(\beta _{2}>\alpha _{v}>\Lambda _{h}>\Lambda _{v}>\beta _{1}>c>f>\gamma _{2}>\mu _{v}>\alpha _{h}> \gamma _{1}>N_{h}>\mu _{h}\), while \(t_{3}<t< t_{4}\), the order is \(\beta _{2}>\beta _{1}(\Lambda _{v})>\alpha _{v}>\Lambda _{h}>f>\mu _{v}>c>\gamma _{2}>\alpha _{h}>\gamma _{1}> N_{h}>\mu _{h}\). During the entire time interval in Figure 5 (e), \(\beta _{2}\) is the parameter that has the greatest impact on the output solution \(I_{v}\).
7.2.2 Sensitivity analysis to basic reproduction number in a homogeneous case
When all coefficients are constants, we obtain a explicit formula of basic reproduction number, written by \(R_{0}\). It is easy to get
where \(R_{1}=\frac{f\alpha _{h}}{\mu _{h}+\alpha _{h}}\cdot \frac{\beta _{1}}{\mu _{h}+\gamma _{1}}\cdot \frac{\Lambda _{h}}{\mu _{h}}\), \(R_{2}=\frac{(1-f)\alpha _{h}}{\mu _{h}+\alpha _{h}}\cdot \frac{c\beta _{1}}{\mu _{h}+\gamma _{2}}\cdot \frac{\Lambda _{h}}{\mu _{h}}\) and \(R_{3}=\frac{\alpha _{v}}{\mu _{v}+\alpha _{v}}\cdot \frac{\beta _{2}}{\mu _{v}}\cdot \frac{\Lambda _{v}}{\mu _{v}}\). In addition, \(R_{1}\), \(R_{2}\) and \(R_{3}\) have their own biological meanings: \(R_{1}\) implies the impact of one symptomatic infected human on the susceptible mosquitoes, where \(\frac{f\alpha _{h}}{\mu _{h}+\alpha _{h}}\) is the proportion of exposed humans developing into symptomatic compartment, \(\frac{1}{\mu _{h}+\gamma _{1}}\) and \(\beta _{1}\) represent the period of infection and infection rate of symptomatic humans, respectively; \(R_{2}\) denotes the effect of one asymptomatic infected human on the susceptible mosquitoes, where \(\frac{(1-f)\alpha _{h}}{\mu _{h}+\alpha _{h}}\) is the proportion of exposed humans developing into asymptomatic compartment, \(\frac{1}{\mu _{h}+\gamma _{2}}\) and \(c\beta _{1}\) represent the period of infection and infection rate of asymptomatic humans, respectively; \(R_{3}\) denotes the effect of one infected mosquito on susceptible humans, where \(\frac{\alpha _{v}}{\mu _{v}+\alpha _{v}}\) is the proportion of exposed mosquitoes developing into infectious compartment, \(\frac{1}{\mu _{v}}\) and \(\beta _{2}\) represent the period of infection and infection rate of symptomatic humans, respectively.
As we all know, the basic reproduction number is one of the most important concepts in epidemiology. More meaningfully, it explains the threshold behavior of many infectious illness models. Therefore, it is necessary to analyze the affect of parameters on the basic reproduction number. Obviously, there are 14 parameters in system (2.3), however, it can be known from the expression of \(R_{0}\) that \(D_{v}\) and \(D_{h}\) have no influence on \(R_{0}\), so here we analyze the influence of the remaining eight parameters.
To analyze the effects of the parameter values on \(R_{0}\) by Latin Hypercube Sampling and PRCC method [48]. PRCC scatter plots in Figure 6 of parameters \(\Lambda _{h}\), f, c, \(\mu _{h}\), \(\gamma _{1}\), \(\gamma _{2}\), \(\alpha _{h}\), \(\alpha _{v}\), \(\beta _{1}\), \(\beta _{2}\), \(\mu _{v}\) and \(\Lambda _{v}\) (all eight parameters are changed concomitantly, sample size \(N = 8000\)). The abscissa stands for a uniform distribution of all input parameters with the minimum and maximum values. The ordinate denotes \(R_{0}\). From Figures 6 and 7, one can investigate the dependence of \(R_{0}\) on parameters to get more information. For instance, numeric plots indicate that \(R_{0}\) is monotonically decreasing with respect to \(\mu _{h}\), \(\mu _{v}\), \(\gamma _{1}\) and \(\gamma _{2}\), whereas \(R_{0}\) is a monotonically increasing function of \(\Lambda _{h}\), \(\Lambda _{v}\), f, c, \(\alpha _{h}\), \(\alpha _{v}\), \(\beta _{1}\) and \(\beta _{2}\), respectively. According to the biological significance of the parameters, the means of control like applying insecticide treated mosquito nets and spraying insecticides can reduce the bite rate of mosquitoes, increase death rate and then reduce \(R_{0}\). The reduction of bite rate can also decrease the recruitment rate of mosquitoes, thus reducing \(R_{0}\). Moreover, increasing medical resources can improve the recovery rate of host and then reduce the basic reproduction number. For parameters \(\mu _{h}\) and \(\Lambda _{h}\) related to host, increasing the death rate and reducing the recruitment rate can reduce the \(R_{0}\), but this is not desirable. Therefore, we ignored the related strategies when evaluating the control measures later. The result illustrated in Figure 7 suggests that, \(R_{0}\) is more sensitive to \(\mu _{h}\), followed by f, c and \(\beta _{1}\), which means that the presence of asymptomatic carriers cannot be ignored when exploring malaria transmission patterns and developing strategies to prevent and control malaria transmission.
Figure 8 provides more results on the analysis of basic reproduction number. The gray plane in this figure represents \(R_{0}=1\), which means that the values of the two parameters are combined below the gray plane, there will be \(R_{0}<1\) indicating that the disease is extinct, otherwise \(R_{0}>1\) meaning that the disease is persistent.
7.3 Effectiveness of preventive control measures
In view of the influence of the above parameters on the spread of disease, we propose the following measures to prevent and control the spread of disease, and analyze the effects of these measures. Let us consider seven cases of the intervening measures at vectors and hosts.
Baseline scenario (BS): The value of parameters in this case is consistent with that in Figure 2.
Strategy I: The contact of mosquitoes and humans can be reduced by using mosquito nets, mosquito repellent sprays, etc. Here has four steps:
Strategy I-I: Adjust \(\beta _{1}=0.65\times 0.17\).
Strategy I-II: Adjust \(\beta _{2}=0.65\times 0.44\).
Strategy I-III: Adjust \(\beta _{1}=0.65\times 0.17\) and \(\beta _{2}=0.65\times 0.44\).
The use of insecticides can increase mosquito mortality and improve the medical environment to increase the recovery rate of the host.
Strategy II-I: Adjust \(\gamma _{1}=1.3\times 0.04256~\text {Month}^{-1}\).
Strategy II-II: Adjust \(\gamma _{2}=1.3\times 0.045~\text {Month}^{-1}\).
Strategy II-III: Adjust \(\mu _{v}=1.3\times \mu _{v}(t)~\text {Month}^{-1}\).
Strategy II-IV: Adjust \(\gamma _{1}=1.3\times 0.04256~\text {Month}^{-1}\), \(\gamma _{2}=1.3\times 0.045~\text {Month}^{-1}\) and \(\mu _{v}=1.3\times \mu _{v}(t)~\text {Month}^{-1}\).
Strategy III: Adjust \(\beta _{1}=0.65\times 0.17\), \(\beta _{2}=0.65\times 0.44\), \(\gamma _{1}=1.3\times 0.04256~\text {Month}^{-1}\), \(\gamma _{2}=1.3\times 0.045~\text {Month}^{-1}\) and \(\mu _{v}=1.3\times \mu _{v}(t)~\text {Month}^{-1}\).
Figure 9 indicates that control measures can reduce the final size of infection mosquitoes and humans which helpful to lower the potential risk of the malaria transmission. Besides, we find that the use of both control measures delays the time to peak, which provides time for the department of disease control and prevention to take steps to control the disease when it emerges. However, the use of such control measures can also increase peaks, which in turn can lead to a shortage of medical resources such as hospital beds during peak disease. We point out that the comparison of strategies is not about which strategy is more effective (as they may be related to different costs), but more about which control measures can effectively control the spread of disease.
8 Discussion
This paper formulates a time periodic reaction-diffusion malaria model accounting for asymptomatic carriers. The genesis of this model is drawn from the following biological inquiries: (1) What is the impact of asymptomatic carriers on the transmission of malaria? (2) Are there regional variations in the role of mosquito and human propagation in the transmission of malaria? (3) What are the impacts of the seasonal changes in temperature on the malaria spread? For the model, our analyses include the stability of the infection-free \(\omega \)-periodic solution, the existence and uniform persistence of positive \(\omega \)-periodic solution. Assuming the parameter is not a time function, we can obtain the global asymptotic stability of the infection-free steady state in the critical case of \(\mathcal {R}_{0}=1\). Aguilar and Gutierrez [49] considered asymptomatic models, but did not take into account the impact of human and mosquito spread on malaria transmission.
The numerical simulation part first verify the theoretical results of long-term dynamic behavior. Second, we analyze the impact of parameters in model (2.3) on disease transmission, which is divided into two parts. The impact of parameters on the model state variables is analyzed using elasticity and PRCC indexes. When the mathematical model is a dynamic system, PRCC indexes depend on time, and the relative importance of parameters can also rely on time. In addition, this paper conducts sensitivity analysis on the basic reproduction number under special cases of spatial homogeneity. In this case, an explicit expression of the basic reproduction number can be obtained, elucidating the biological significance of each part, and it is found that \(R_{0}\) is more sensitive to \(\mu _{h}\), followed by f, c and \(\beta _{1}\), which means that the presence of asymptomatic carriers cannot be ignored when exploring malaria transmission patterns and developing strategies to prevent and control malaria transmission. The third part is the evaluation of control measures. It should be pointed out that the comparison of strategies is not about which strategies are more effective (as they may be related to different costs), but rather about which control measures can effectively control the spread of diseases. Based on the numerical results, it can be seen that, spraying insecticides, using mosquito nets and other means to disinfect vectors and reduce the contact between vector and host which can prevent or slow down the transmission of the malaria disease.
In our research, we’ve identified certain shortcomings that require improvement. In the course of theoretical analysis, the intricate nature of periodic has hindered a comprehensive discussion of all scenarios. Consequently, we have not yet addressed the global stability of the positive periodic solution in this model. In the realm of malaria transmission modeling, limited attention has been given to investigating the impact of infection age and spatial diffusion on disease transmission. In reality, the intensity of infectivity in malaria varies across different stages of infection. Referred to as the age of infection, this temporal factor significantly influences the number of secondary infections. Incorporating this crucial factor into the study of malaria transmission is essential. These issues hold significant importance in understanding the dynamics of malaria transmission and devising effective control measures. Therefore, in our future research, we aim to delve deeper into these aspects.
Data availibility
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
Gutierrez, J.B., Galinski, M.R., Cantrell, S., et al.: From within host dynamics to the epidemiology of infectious disease: scientific overview and challenges. Math. Biosci. 270, 143–155 (2015)
World Health Organization (2019), World Malaria Report, 2019
Ross, R.: The Prevention of Malaria. John Murray, London (1911)
Macdonald, G.: The analysis of infection rates in diseases in which super infection occurs. Trop. Dis. Bull. 47, 907–915 (1950)
Anderson, R.M., May, R.M.: Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, London (1991)
Bai, Z., Peng, R., Zhao, X.-Q.: A reaction-diffusion malaria model with seasonality and incubation period. J. Math. Biol. 77, 201–228 (2018)
Lou, Y., Zhao, X.-Q.: A reaction-diffusion malaria model with incubation period in the vector population. J. Math. Biol. 62, 542–568 (2011)
Li, J., Welch, R.M., Nair, U.S. et al.: Dynamic Malaria Models with Environmental Changes, Proceedings of the Thirty-Fourth Southeastern Symposium on System Theory Huntsville, AL, (2002) 396-400
Martens, W.J.M., Niessen, L., Rotmans, J., et al.: Climate change and vector-borne disease: a global modelling perspective. Global Environ. Change 5, 195–209 (1995)
Hay, S.I., Cox, J., Rogers, D.J., et al.: Climate change and the resurgence of malaria in East African highlands. Nature 415, 905–909 (2002)
Gething, P.W., Smith, D.L., Patil, A.P., et al.: Climate change and the global malaria recession. Nature 465, 342–346 (2010)
Jetten, T.H., Martens, W.J.M., Takken, W.: Model simulations to estimate malaria risk under climate change. J. Med. Entomol. 33, 361–371 (1996)
Lindblade, K.A., Steinhardt, L., Samuels, A., et al.: The silent threat: asymptomatic parasitemia and malaria transmission. Expert Rev. Anti-Infect. Ther. 11, 623–639 (2013)
Crompton, P.D., Moebius, J., Portugal, S., et al.: Malaria immunity in man and mosquito: insights into unsolved mysteries of a deadly infectious disease. Annu. Rev. Immunol. 32, 157–187 (2014)
Babikera, H.A., Gadalla, A.A., Ranford-Cartwright, L.C.: The role of asymptomatic P. falciparum parasitaemia in the evolution of antimalarial drug resistance in areas of seasonal transmission. Drug Resist. Updates 16, 1–9 (2013)
Eke, R.A., Chigbu, L.N., Nwachukwu, W.: High prevalence of asymptomatic Plasmodium infection in a suburb of Aba Town, Nigeria. Ann. Afr. Med. 5, 42–45 (2006)
Okell, L.C., Griffin, J.T., Kleinschmidt, I., et al.: The potential contribution of mass treatment to the control of Plasmodium falciparum malaria. PLoS One 6, e20179 (2011)
Griffin, J.T., Hollingsworth, T.D., Okell, L.C.: Reducing Plasmodium falciparum malaria transmission in Africa: a model-based evaluation of intervention strategies. PLoS Med. 7, e1000324 (2010)
Vinetz, J.M., Gilman, R.H.: Asymptomatic Plasmodium parasitemia and the ecology of malaria transmission. Am. J. Trop. Med. Hyg. 66, 639–640 (2002)
Cantrell, R.S., Cosner, C.: Spatial Ecology via Reaction-Diffusion Equations. In: Mathematical and Computational Biology. Wiley, West Sussex (2003)
Wu, R., Zhao, X.-Q.: A reaction-diffusion model of vector-borne disease with periodic delays. J. Nonlinear Sci. 29, 29–64 (2019)
Daners, D., Medina, P.K.: Abstract Evolution Equations, Periodic Problems and Applications, Pitman research notes in mathematics series, vol. 279. Longman, Harlow (1992)
Smith, H.L.: Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems. American Mathematical Society, Providence (1995)
Zhang, L., Wang, Z.-C., Zhao, X.-Q.: Threshold dynamics of a time periodic reaction-diffusion epidemic model with latent periodic. J. Differ. Equ. 258, 3011–3036 (2015)
Wu, J.: Theory and Applications of Partial Functional Differential Equations. Springer, New York (1996)
Magal, P., Zhao, X.-Q.: Global attractors and steady states for uniformly persistent dynamical systems. SIAM J. Math. Anal. 37, 251–275 (2005)
Martin, R.H., Smith, H.L.: Abstract functional differential equations and reaction-diffusion systems. Trans. Am. Math. Soc. 321, 1–44 (1990)
Peng, R., Zhao, X.-Q.: A reaction-diffusion SIS epidemic model in a time-periodic environment. Nonlinearity 25, 1451–1471 (2012)
Diekmann, O., Heesterbeek, J.A.P., Metz, J.A.J.: On the definition and the computation of the basic reproduction ratio \(R_{0}\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 (1990)
Liang, X., Zhang, L., Zhao, X.-Q.: Basic reproduction ratios for periodic abstract functional differential equations (with application to a spatial model for Lyme disease). J. Dyn. Diff. Equ. 31, 1247–1278 (2019)
Wang, J., Cui, R.: Analysis of a diffusive host-pathogen model with standard incidence and distinct dispersal rates. Adv. Nonlinear Anal. 10, 922–951 (2021)
Zhao, X.-Q.: Basic reproduction ratios for periodic compartmental models with time delay. J. Dyn. Differ. Equ. 29, 67–82 (2017)
Wang, B.-G., Xin, M.-Z., Huang, S., et al.: Basic reproduction ratios for almost periodic reaction-diffusion epidemic models. J. Differ. Equ. 352, 189–220 (2023)
Song, P., Lou, Y., Xiao, Y.: A spatial SEIRS reaction-diffusion model in heterogeneous environment. J. Differ. Equ. 267, 5084–5114 (2019)
Thieme, H.R.: Spectral bound and reproduction number for infinite-dimensional population structure and time heterogeneity. SIAM J. Appl. Math. 70, 188–211 (2009)
Hess, P.: Periodic-Parabolic Boundary Value Problem and Positivity, (Pitman reasearch notes in Mathematics vol 247) (Harlow: Longman Scientific and Technical), (1991)
Zhao, X.-Q.: Dynamical Systems in Population Biology, 2nd edn. Springer, New York (2017)
Wu, Y., Zou, X.: Dynamics and profiles of a diffusive host-pathogen system with distinct dispersal rates. J. Differ. Equ. 264, 4989–5024 (2018)
Cui, R., Lam, K.-Y., Lou, Y.: Dynamics and asymptotic profiles of steady states of an epidemic model in advective environments. J. Differ. Equ. 263, 2343–2373 (2017)
Webb, G.F.: Theory of Nonlinear Age-Dependent Population Dynamics. CRC Press (1985)
Chitnis, N., Hyman, J.M., Cushing, J.M.: Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 70, 1272–1296 (2008)
Wang, X., Zhao, X.-Q.: A malaria transmission model with temperature-dependent incubation period. Bull. Math. Biol. 79, 1155–1182 (2017)
Cacuci, D.G.: Sensitivity theory for nonlinear systems. I. Nonlinear functional analysis approach. J. Math. Phys. 22, 2794–2802 (1981)
Levy, A.B.: Solution sensitivity from general principles. SIAM J. Control Optim. 40, 1–38 (2001)
Caswell, H.: Matrix Population Models, vol. 1. Sinauer, Sunderland (2000)
Saltelli, A., Chan, K., Scott, E.: Sensitivity Analysis. Wiley Series in Probability and Statistics. Wiley, New York (2000)
Arriola, L., Hyman, J.M.: Sensitivity Analysis for Uncertainty Quantification in Mathematical Models. In: Chowell, G., Hyman, J.M., Bettencourt, L.M.A., Castillo-Chavez, C. (eds.) Mathematical and Statistical Estimation Approaches in Epidemiology. Springer, Dordrecht (2009)
Hoare, A., Regan, D.P., Wilson, D.G.: Sampling and sensitivity analyses tools (SaSAT) for computational modelling. Theor. Biol. Med. Model. 5, 4 (2008)
Aguilar, J.B., Gutierrez, J.B.: An epidemiological model of malaria accounting for asymptomatic carriers. Bull. Math. Biol. 82, 42 (2020)
Acknowledgements
The authors are grateful for the support and useful comments provided by Professor Xiaoqiang Zhao (Memorial University of Newfoundland).
Funding
The research is partially supported by the National Natural Science Foundation of China (12201007), Young Elite Scientists Sponsorship Program by BAST (No. BYESS2023036), Doctoral Research Initiation Fund (No. BS202328), The Shandong Provincial Natural Science Foundation (ZR2022MF278).
Author information
Authors and Affiliations
Contributions
YS is responsible for raising questions, modeling, and completing the entire manuscript for the manuscript. FC conducts a detailed examination and derivation of the theoretical analysis process. LW refines and modifies the language of the manuscript, as well as assists in theoretical analysis. XZ is responsible for numerical work and provides guidance on the results of numerical simulation and program development.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Consent for publication
All authors of this manuscript agree to publish in this journal.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
Proof of Lemma 5.2
Proof
Denote \(v=(v_{1},v_{2}, v_{3},v_{4},v_{5})\) to be the solution of (4.2) with \(v_{0}(\bar{\varphi })=\bar{\varphi }\). Let \(v_{1}^{*}=e^{-\mu t}v_{1}\), \(v_{2}^{*}=e^{-\mu t}v_{2}\), \(v_{3}^{*}=e^{-\mu t}v_{3}\), \(v_{4}^{*}=e^{-\mu t}v_{4}\), \(v_{5}^{*}=e^{-\mu t}v_{5}\). Since \(\bar{\varphi }\gg 0\), \(v(t,x;\bar{\varphi })\gg 0\) for \(t\ge 0\), then
and \(v^{*}\) meets the next system with \(\mu \),
Thence, \(v^{*}\) is a solution of (A.1) with \(\frac{\partial v^{*}_{1}}{\partial n}=\frac{\partial v^{*}_{2}}{\partial n}=\frac{\partial v^{*}_{3}}{\partial n}=\frac{\partial v^{*}_{4}}{\partial n} =\frac{\partial v^{*}_{5}}{\partial n}=0\) on \((0,+\infty )\times \partial \Omega \) and \(v^{*}(0,x) =(\bar{\varphi }_{1}(x),\bar{\varphi }_{2}(x), \bar{\varphi }_{3}(x), \bar{\varphi }_{4}(x),\bar{\varphi }_{5}(x))\) for \(x\in \overline{\Omega }\). Then \(v_{i}^{*}(\omega ,x)=e^{-\mu \omega }r(P)\bar{\varphi }_{i}(x)v_{i}^{*}(0,x)\), \((i=1,\ldots ,5)\). Thence
Thereby, \(e^{\mu t}v^{*}\) is a solution of (4.2). \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shi, Y., Chen, F., Wang, L. et al. Dynamics analysis of a reaction-diffusion malaria model accounting for asymptomatic carriers. Z. Angew. Math. Phys. 75, 43 (2024). https://doi.org/10.1007/s00033-023-02180-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-023-02180-w