1 Introduction

It is known that the Kadomtsev–Petviashvili-I (KPI) equation

$$\begin{aligned} (u_t+6uu_x+u_{xxx})_x+3\sigma ^2 u_{yy}=0, \, \sigma ^2=-1, \end{aligned}$$
(1.1)

is a (2+1)-dimensional extension of the integrable Korteweg-de Vries (KdV) equation [1]. The KdV and KP equations are two of the most significant mathematical models which possess abundant exact solutions in nonlinear science. The integrable positive KP hierarchy associated with the Lax operator of the KPI Eq. (1.1) is introduced in Ref [2, 3]. The first four forms can be expressed as follows:

$$\begin{aligned} u_{t_1}=u_x, \end{aligned}$$
(1.2a)
$$\begin{aligned} u_{t_2}=-2u_y, \end{aligned}$$
(1.2b)
$$\begin{aligned} u_{t_3}=-6uu_x-u_{xxx}+3\partial _{x}^{-1}u_{yy}, \end{aligned}$$
(1.2c)
$$\begin{aligned} u_{t_4}=12(2u_x\partial _{x}^{-1}u_{y}-\partial _{x}^{-2}u_{yyy}+u_{xxy}+4uu_{y}). \end{aligned}$$
(1.2d)

Note that third Eq. (1.2c) is just the KPI equation by setting \(t_3=t\), and fourth Eq. (1.2d) can be reduced to an equivalent expression of the normal KdV equation when \(y=x\). Besides, under the potential \(u=\phi _x\) and \(t_4=\frac{1}{24}t\), fourth Eq. (1.2d) is read as

$$\begin{aligned} \phi _{ xxxxy} + 4\phi _{xxy} \phi _ x + 2\phi _{ xxx} \phi _y + 6\phi _{xy} \phi _{xx}- \phi _ {yyy}-2\phi _{ xxt} = 0, \end{aligned}$$
(1.3)

which is named the (2+1)-dimensional Date–Jimbo–Kashiwara–Miwa (DJKM) equation [4, 5]. Because these two equations are the generalizations of the KdV equation in (2+1)-dimensions, a novel integrable KdV system

$$\begin{aligned} u_t=a(6uu_x+u_{xxx}-3w_y)+b(2wu_x-z_y+u_{xxy}+4uu_{y}), \, u_y=w_x,\,u_{yy}=z_{xx}, \end{aligned}$$
(1.4)

has been firstly constructed by Lou [6]. This equation is also called as the cKP3–4 equation, to reflect the combination of the third member and fourth member in the positive KP hierarchy. The Lax pair

$$\begin{aligned} \psi _y={\mathrm {i}}(\psi _{xx}+u\psi ), {\mathrm {i}}\equiv \sqrt{-1}, \end{aligned}$$
(1.5a)
$$\begin{aligned} \psi _t=2{\mathrm {i}}b\psi _{xxxx}+4a\psi _{xxx}+4{\mathrm {i}}bu\psi _{xx}+2(3au+2{\mathrm {i}}bu_{x}+bw)\psi _{x} \end{aligned}$$
$$\begin{aligned} -{\mathrm {i}}(3aw+bz-2bu^2+3a{\mathrm {i}}u_{x}-2bu_{xx}+{\mathrm {i}}bw_{x})\psi , \end{aligned}$$
(1.5b)

and the dual Lax pair

$$\begin{aligned} \psi _y=-{\mathrm {i}}(\psi _{xx}+u\psi ), {\mathrm {i}}\equiv \sqrt{-1},\end{aligned}$$
(1.6a)
$$\begin{aligned} \psi _t=-2{\mathrm {i}}b\psi _{xxxx}+4a\psi _{xxx}-4{\mathrm {i}}bu\psi _{xx}+2(3au-2{\mathrm {i}}bu_{x}+bw)\psi _{x} \end{aligned}$$
$$\begin{aligned} +{\mathrm {i}}(3aw+bz-2bu^2-3a{\mathrm {i}}u_{x}-2bu_{xx}-{\mathrm {i}}bw_{x})\psi , \end{aligned}$$
(1.6b)

have been proposed directly, which can indicate the integrability of the cKP3–4 Eq. (1.4). Furthermore, it has been found that the combined equation may possess soliton molecules and the missing D’Alembert-type solutions [6]. Some important properties such as the Painlevé property, Schwartz form and symmetry reductions for the cKP3–4 Eq. (1.4) have been discussed [7].

Motivated by these facts, we would like to investigate an extended form for the integrable cKP3–4 Eq. (1.4), written as

$$\begin{aligned} a(6\gamma u u_{x}+u_{xxx}+3\delta v_{xy})+b(u_{xxy}+2\gamma u_{x}v_{x}+4\gamma uu_{y}+\delta v_{yy})+cu_{t}=0,\quad v_{xx}=u_{y}, \end{aligned}$$
(1.7)

where \(a,b,c,\gamma\) and \(\delta\) are arbitrary real constants, which satisfy \(c\gamma (a^2+b^2)\ne 0\) to ensure the nonlinearity of the considered equation. By taking the choice

$$\begin{aligned} \gamma =1,\delta =c=-1, v_x=w, \end{aligned}$$
(1.8)

it is easy to see that the above form is just the cKP3–4 Eq. (1.4). For \(\delta \ne 0\), the considered model equation includes the KP equation and the (2+1)-dimensional DJKM equation as its special cases. For \(\delta = 0\), in the case

$$\begin{aligned} \delta =0, c=1,\gamma =\frac{e}{2b}, \end{aligned}$$
(1.9)

Equation (1.7) reduces to the (2+1)-dimensional generalized breaking soliton equation

$$\begin{aligned} u_t+au_{xxx}+bu_{xxy}+\frac{3ae}{b}uu_{x}+2euv_{x}+eu_{x}v=0, \,u_{y}=v_{x}, \end{aligned}$$
(1.10)

which was firstly proposed by Xu and can pass the Painlevé test [8]. In particular, using the potential \(u=\phi _x\) and setting \(a=0, b=1,e=-2\), Eq.  (1.10) transforms into the Bogoyavlenskii–Schiff (BS) equation, or named breaking soliton equation

$$\begin{aligned} \phi _{xt}+\phi _{xxxy}-2\phi _{xx}\phi _{y}-4\phi _{x}\phi _{xy}=0, \end{aligned}$$
(1.11)

which was introduced by Calogero and Degasperis [9]. This equation was also studies by Bogoyavlenskii and Schiff in different methods [10,11,12]. For all we know, the Painlevé property, integrability and various exact solutions of these two equations have been widely investigated [13,14,15,16,17,18,19]. For example, bilinear Bäcklund transformations, Lax pairs and infinitely many conservation laws have been constructed for the (2+1)-dimensional breaking soliton equation by using the binary Bell polynomial approach [20].

In various physical fields, the KP Eq. (1.1) is widely used to characterize the propagation of weakly dispersive and small amplitude waves in (2+1)-dimensions [1]. Besides, the breaking soliton Eq. (1.11) is a significant model to describe the (2+1)-dimensional interaction of a long wave propagating along the x-axis and a Riemann wave propagating along the y-axis [10, 11]. As an extended form of these two equations, we believe that the generalized Eq. (1.7) should have potential applications in many areas of nonlinear science. The extended form (1.7) can also be applied to physics as a way to model real (2+1)-dimensional shallow water waves due to the negative coefficients of two second-order linear dispersion terms.

As well-known, Hirota’s bilinear method is a pretty effective tool in the study of nonlinear integrable equations. Hirota bilinear forms play a crucial role in presenting exact solutions, particularly multi-soliton solutions. Most of nonlinear integrable equations can be written in bilinear forms. However, it was further found that some nonlinear evolution equations cannot be directly transformed into a bilinear form. For instance, the (2+1)-dimensional DJKM Eq. (1.3) does not possess a simple bilinear expression like the KdV equation in (1+1)-dimensions, and it has a trilinear form given by previous studies [4, 5, 21,22,23].

In this paper, we would like to study some integrable properties of the generalized Eq. (1.7) which can be given by a trilinear form instead of the bilinear form. The framework of this paper is as below. Firstly, a general multi-parameter bilinear Bäcklund transformation will be derived with the help of appropriate bilinear exchange formulas. The resulting bilinear Bäcklund transformation can be converted into the corresponding Lax pairs. Secondly, a generic class of lump solutions will be built from the existing nonlinear superposition formula when \(\delta <0\) to the extended nonlinear model Eq. (1.7). Our conclusions and remarks will be given in the last section.

2 Bilinear Bäcklund transformation and Lax pair

It is obvious that under the transformation

$$\begin{aligned} u=\frac{2}{\gamma }(\ln f)_{xx},\quad v=\frac{2}{\gamma }(\ln f)_{y}, \end{aligned}$$
(2.1)

the extended form (1.7) can be given by

$$\begin{aligned}&a(f^2f_{xxxxx}+2ff_{xx}f_{xxx}-5ff_{x}f_{xxxx}-6f_{xx}^2f_{x}+8f_{xxx}f_{x}^2+3\delta f^2f_{xyy}-3\delta ff_{x}f_{yy} \\ &\quad\quad -6\delta ff_{y}f_{xy}+6\delta f_{x}f_{y}^2)+b(f^2f_{xxxxy}-ff_{xxxx}f_{y}+2ff_{xx}f_{xxy}-4ff_{x}f_{xxxy}\\ &\quad\quad +4f_{x}f_{xxx}f_{y}-2f_{xx}^{2}f_{y}-4f_{xx}f_{x}f_{xy}+4f_{x}^{2}f_{xxy}+\delta f^2f_{yyy}+2\delta f_{y}^{3}-3\delta ff_{y}f_{yy})\\ &\quad\quad +c\,f^2f_{xxt}-c\,ff_{xx}f_{t}-2c\,ff_{x}f_{xt}+2c\,f_{x}^{2}f_{t}=0. \end{aligned}$$
(2.2)

The trilinear Eq. (2.2) does not exist a direct bilinear form, whereas can be written as

$$\begin{aligned} &\frac{3a}{2}D_x\left[\left(D_{x}^{4}+3 \delta D_{y}^2 \right)f\cdot f\right]\cdot f^2+D_x\left[\left(bD_{x}^{3}D_{y}+\frac{3}{2}cD_{x}D_{t}\right)f\cdot f\right]\cdot f^2\\ &\quad +\frac{b}{2}D_{y}\left[\left(D_{x}^{4}+3 \delta D_{y}^2 \right)f\cdot f\right]\cdot f^2=0,\end{aligned}$$
(2.3)

where the Hirota bilinear differential operators are defined by

$$\begin{aligned} D_{x{_1}}^{n_1}D_{x{_2}}^{n_2}f\cdot g=(\partial _{x{_1}}-\partial _{x{_{1}^{\prime}}})^{n_1}(\partial _{x{_2}}-\partial _{x{_{2}^{\prime}}})^{n_2}f(x_1,x_2)g(x_1^{\prime},x_2^{\prime})|_{{x_{1}^{\prime}}=x_1,{x_{2}^{\prime}}=x_2}, \end{aligned}$$

with \(n_1\) and \(n_2\) being arbitrary nonnegative integers [24].

In mathematical physics, bilinear Bäcklund transformations are significantly helpful to search for exact solutions to nonlinear equations, and they can connect with Lax pairs and construct the modified soliton equation [25,26,27,28,29,30,31]. In the following, let us present a bilinear Bäcklund transformation for the trilinear Eq. (2.3).

Theorem 2.1

Suppose that f and \(f'\) are two different solutions to the trilinear Eq. (2.3). Then, we have the following multi-parameter Bäcklund transformation to Eq. (2.3):

$$\begin{aligned} (\tilde{\delta } D_{y}+D_{x}^2+\mu D_{x}+\lambda )f \cdot f' = 0, \end{aligned}$$
(2.4a)
$$\begin{aligned} &\left[aD_{x}^{3}+bD_{x}^{2}D_{y}+(b\mu -3a\tilde{\delta }) D_{x}D_{y}-b\tilde{\delta }D_{y}^{2}-3a\lambda D_{x} \right. \\ &\left.\quad+(b\mu ^2-3b\lambda -3a\tilde{\delta }\mu )D_{y}+cD_t+\kappa (y,t)\right]f \cdot f' = 0,\end{aligned}$$
(2.4b)

where \(\tilde{\delta } =\pm \sqrt{\delta }\), \(\lambda ,\mu\) are two arbitrary constants and \(\kappa (y,t)\) is an arbitrary function.

Proof

Let us first introduce a key function

$$\begin{aligned} P_1=f^{'4}\Big\{\frac{3a}{2}D_x\big[(D_{x}^{4}+3 \delta D_{y}^2)f\cdot f\big]\cdot f^2\Big\}-f^{4}\Big\{\frac{3a}{2}D_x\big[(D_{x}^{4}+3 \delta D_{y}^2 )f'\cdot f'\big]\cdot f^{'2}\Big\}. \end{aligned}$$
(2.5)

By using the exchange identities (A.1)-(A.7) for Hirota’s bilinear operators in Appendix A in turn, \(P_1\) can be expressed as

$$\begin{aligned} P_1&=\frac{3a}{2}D_{x}\Big \{ f^{'2}(D_{x}^{4}+3\delta D_{y}^2)f\cdot f-f^2(D_{x}^{4}+3\delta D_{y}^2 )f'\cdot f'\Big \}\cdot f^2f^{'2} \\ &=\frac{3a}{2}D_{x}\Big \{6\delta D_{y}(D_{y}f\cdot f')\cdot ff'+2D_x(D_{x}^{3}f\cdot f')\cdot ff'-6D_{x}(D_{x}^{2}f\cdot f')\cdot ( D_{x} f\cdot f') \Big \}\cdot f^2f^{'2}\\ &=3aD_{x}\Big \{-3\tilde{\delta }D_{y}[(D_{x}^{2}+\mu D_x)f\cdot f']\cdot ff'+D_x(D_{x}^{3}f\cdot f')\\ &\quad\quad+3D_x[(\tilde{\delta }D_y+\lambda )f\cdot f']\cdot ( D_{x} f\cdot f') \Big \}\cdot f^2f^{'2}\\ &=3aD_{x}\Big \{-3\tilde{\delta }D_{x}[D_{x}D_{y}f\cdot f')\cdot ff'+(D_{y}f\cdot f')\cdot (D_{x}f\cdot f')]\\ &\quad\quad-3\tilde{\delta }\mu D_{y}(D_{x}f\cdot f')\cdot ff'+3\tilde{\delta }D_{x}(D_{y}f\cdot f')\cdot (D_{x}f\cdot f')\\ &\quad\quad+D_x(D_{x}^{3}f\cdot f')\cdot ff' -3 D_{x}(D_{x}f\cdot f')\cdot \lambda ff' \Big \}\cdot f^2f^{'2}\\ &=3D_x\Big \{D_x[(aD_{x}^{3}-3a\tilde{\delta }D_{x}D_{y} -3a\tilde{\delta }\mu D_{y} -3a\lambda D_{x})f\cdot f' ]\cdot ff'\Big \}\cdot f^2f^{'2}, \end{aligned}$$
(2.6)

\(\square\)

where we have applied (2.4a) in the above derivation. Let us second consider another key function

$$\begin{aligned} P_2&=f^{'4}\Big \{D_x\big [(bD_{x}^{3}D_{y}+\frac{3}{2}cD_{x}D_{t})f \cdot f\big ]\cdot f^2+\frac{b}{2}D_y\big [(D_{x}^{4}+3 \delta D_{y}^2 )f\cdot f\big ]\cdot f^2 \Big \}\\&\quad\quad-f^{4}\Big \{D_x\big [(bD_{x}^{3}D_{y}+\frac{3}{2}cD_{x}D_{t})f' \cdot f'\big ]\cdot f^{'2}+\frac{b}{2}D_y\big [(D_{x}^{4}+3 \delta D_{y}^2 )f'\cdot f'\big ]\cdot f^{'2} \Big \}. \end{aligned}$$
(2.7)

According to the bilinear Bäcklund transformation presented by Hu and Li [4, 5] for the (2+1)-dimensional DJKM Eq. (1.3) and using (2.42.4a), a similar direct computation leads to (see Appendix B for details)

$$\begin{aligned}P_2=3D_{x}\Big \{D_x\big [(bD_{x}^{2}D_{y}-3b\lambda D_y+c D_t-b \tilde{\delta }D_{y}^{2}+b\mu ^2D_y +b\mu D_{x}D_{y})f \cdot f'\big ]\cdot ff'\Big \}\cdot f^2f^{'2}. \end{aligned}$$
(2.8)

Moreover, we have

$$\begin{aligned} \\ P_1+P_2&=f^{'4}\Big \{\frac{3a}{2}D_x\big [(D_{x}^{4}+3 \delta D_{y}^2 )f\cdot f\big ]\cdot f^2+D_x\big [(bD_{x}^{3}D_{y}+\frac{3}{2}cD_{x}D_{t})f \cdot f\big ]\cdot f^2\\ &\quad\quad+\frac{b}{2}D_y\big [(D_{x}^{4}+3 \delta D_{y}^2 )f\cdot f\big ]\cdot f^{2} \Big \}-f^{4}\Big \{\frac{3a}{2}D_x\big [(D_{x}^{4}+3 \delta D_{y}^2 )f'\cdot f'\big ]\cdot f^{'2}\,\,\\&\quad\quad+D_x\big [(bD_{x}^{3}D_{y}+\frac{3}{2}cD_{x}D_{t})f' \cdot f'\big ]\cdot f^{'2}+\frac{b}{2}D_y\big [(D_{x}^{4}+3 \delta D_{y}^2 )f'\cdot f'\big ]\cdot f^{'2} \Big \} \\ &\quad\quad=3D_{x}\Big \{D_x\big [(aD_{x}^{3}-3a\tilde{\delta }D_{x}D_{y} -3a\tilde{\delta }\mu D_{y} -3a\lambda D_{x}+bD_{x}^{2}D_{y} -3b\lambda D_y\\ &\quad\quad+c D_t-b \tilde{\delta }D_{y}^{2}+b\mu ^2D_y +b\mu D_{x}D_{y})f\cdot f' ]\cdot ff'\Big \}\cdot f^2f^{'2}. \end{aligned}$$
(2.9)

Therefore, the system of bilinear equations (2.4) guarantees \(P_1+P_2=0.\) This shows that the system (2.4) presents a Bäcklund transformation for the trilinear Eq. (2.3).

We remark that if \(\tilde{\delta }=0\), the system (2.4) reduces to the Bäcklund transformations given in Refs. [8, 14] by choosing appropriate parameters. Next, we will derive a Lax pair for Eq.  (1.7), based on the above bilinear Bäcklund transformation. Taking

$$\begin{aligned} \psi =\frac{f}{f'},\, u=\frac{2}{\gamma }(\ln f')_{xx}, \end{aligned}$$
(2.10)

and applying the following identities:

$$\begin{aligned} \left\{ \begin{array}{lll} &{}(D_{x}f\cdot f')/f^{'2}&{}=\psi _{x},\\ &{} (D_{x}^{2}f\cdot f')/f^{'2}&{}=\psi _{xx}+\gamma u\psi , \\ &{} (D_{x}^{3}f\cdot f')/f^{'2}&{}=\psi _{xxx}+3\gamma u\psi _x, \\ &{}(D_{x}D_{y}f\cdot f')/f^{'2}&{}=\psi _{xy}+\gamma \partial _{x}^{-1}u_{y}\psi ,\\ &{}(D_{x}^{2}D_{y}f\cdot f')/f^{'2}&{}=\psi _{xxy}+2\gamma \partial _{x}^{-1}u_{y}\psi _{x}+\gamma u\psi _{y},\\ &{}\cdots \cdots \end{array}\right. \end{aligned}$$
(2.11)

the bilinear Bäcklund transformation (2.4) can be transformed into the following system:

$$\begin{aligned} \tilde{\delta }\psi _y+ \psi _{xx}+\mu \psi _{x}+(\lambda +\gamma u)\psi =0, \end{aligned}$$
(2.12a)
$$\begin{aligned} &c\psi _t+ a\psi _{xxx}+b\psi _{xxy}+(b\mu -3a\tilde{\delta })\psi _{xy}-b\tilde{\delta }\psi _{yy}+(3a\gamma u-3\lambda a \\ &\quad\,\, +2b\gamma \partial _{x}^{-1}u_{y})\psi _{x}+(b\gamma u-3a\tilde{\delta }\mu -3\lambda b+b\mu ^2)\psi _y+\big ( b \mu \gamma \partial _{x}^{-1}u_{y}\quad \\ &\quad\,\, -3a \tilde{\delta } \gamma \partial _{x}^{-1}u_{y}- b\tilde{\delta }\gamma \partial _{x}^{-2}u_{2y}+\kappa (y,t)\big )\psi =0.\qquad \qquad \qquad \qquad \quad \end{aligned}$$
(2.12b)

A direct computation shows that system (2.12) becomes

$$\begin{aligned} L_1\psi =\tilde{\delta }\psi _y+\psi _{xx}+\mu \psi _x+(\lambda +\gamma u)\psi =0,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$
(2.13a)
$$\begin{aligned} L_2\psi =c\psi _{t}+4a\psi _{xxx}-2b\tilde{\delta }\psi _{yy}+3a\mu \psi _{xx}+(6a\gamma u+2b\gamma \partial _{x}^{-1}u_{y})\psi _{x}+ (b\mu ^2-4\lambda b \qquad \quad \end{aligned}$$
$$\begin{aligned} \qquad \qquad \qquad -3a\tilde{\delta }\mu )\psi _{y}+\big (3a\gamma u_{x}-b\gamma u_{y}+\mu b\gamma \partial _{x}^{-1}u_{y}-3a\gamma \tilde{\delta }\partial _{x}^{-1}u_{y}-b\gamma \tilde{\delta }\partial _{x}^{-2}u_{2y}+\kappa (y,t)\big )\psi , \end{aligned}$$
(2.13b)

where

$$\begin{aligned} L_1=\tilde{\delta }\partial _y+\partial _{x}^{2}+\mu \partial _{x}+(\lambda +\gamma u),\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$
(2.14a)
$$\begin{aligned} L_2=c\partial _t+4a \partial _{x}^{3}-2b\tilde{\delta }\partial _{y}^{2}+3a\mu \partial _{x}^{2}+(6a\gamma u+2b\gamma \partial _{x}^{-1}u_{y})\partial _{x}+(b\mu ^2- 4\lambda b \qquad \qquad \qquad \end{aligned}$$
$$\begin{aligned} \qquad \qquad \quad -3a\tilde{\delta }\mu )\partial _{y}+\big (3a\gamma u_{x}-b\gamma u_{y}+\mu b\gamma \partial _{x}^{-1}u_{y}-3a\gamma \tilde{\delta }\partial _{x}^{-1}u_{y}-b\gamma \tilde{\delta }\partial _{x}^{-2}u_{2y}+\kappa (y,t)\big ). \end{aligned}$$
(2.14b)

We can check that the compatibility condition \([L_1,L_2]=0\) of the above system generates Eq.  (1.7), which means system (2.14) can be regarded as a Lax pair of Eq.  (1.7).

For simplicity, in the following discussion of this section, we adopt \(\lambda =\mu =\kappa (y,t)=0\) in the bilinear Bäcklund transformation (2.4). It is easily checked that system (2.13) becomes

$$\begin{aligned} \tilde{\delta }\psi _y+\psi _{xx}+\gamma u \psi =0, \,\tilde{\delta }=\pm \sqrt{\delta },\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$
(2.15a)
$$\begin{aligned} c\psi _t&-\frac{2b}{\tilde{\delta }}\psi _{xxxx}+4a\psi _{xxx}-\frac{4b\gamma }{\tilde{\delta }}u\psi _{xx}+2\Big (3a\gamma u-\frac{2b\gamma }{\tilde{\delta }}u_x+b\gamma \partial _{x}^{-1}u_y\Big )\psi _x \\ &-\Big (3a\gamma {\tilde{\delta }}\partial _{x}^{-1}u_y+b\gamma {\tilde{\delta }}\partial _{x}^{-2}u_{2y}+\frac{2b\gamma ^2}{{\tilde{\delta }}}u^2-3a\gamma u_x+\frac{2b\gamma }{{\tilde{\delta }}}u_{xx}-b\gamma u_y\Big )\psi =0, \end{aligned}$$
(2.15b)

which is equivalent to the Lax pair (1.5) or the dual Lax pair (1.6) to the cKP3–4 equation, under the choice (1.8). By the dependent variable transformation

$$\begin{aligned} \phi =\ln ({f}/{f'}),\, \rho =\ln (ff'), \end{aligned}$$
(2.16)

the bilinear Bäcklund transformation (2.4) can be transformed into the following coupled system:

$$\begin{aligned} \tilde{\delta }\phi _{y}+\rho _{xx}+\phi _{x}^2=0,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\, \end{aligned}$$
(2.17a)
$$\begin{aligned} a&(\phi _{xxx}+3\phi _{x}\rho _{xx}+\phi _{x}^3-3\tilde{\delta }\rho _{xy}-3\tilde{\delta }\phi _{x}\phi _{y})\\&+b(\phi _{xxy}+2\phi _{x}\rho _{xy}+\phi _{y}\rho _{xx}+\phi _{x}^2\phi _{y}-\tilde{\delta }\rho _{yy}-\tilde{\delta }\phi _{y}^2)+c\phi _t=0, \end{aligned}$$
(2.17b)

where \(\tilde{\delta }=\pm \sqrt{\delta }.\) By eliminating \(\rho\) and then taking the derivative with respect to x at both ends of the resulting equation, the coupled system (2.17) yields

$$\begin{aligned} a(\phi _{xxxx}-6\phi _{x}^2\phi _{xx}-6\tilde{\delta }\phi _{xx}\phi _{y}+3{\delta }\phi _{yy} )+b\big [\phi _{xxxy}-4\tilde{\delta }\phi _{xy}\phi _{y} \end{aligned}$$
$$\begin{aligned} -\big (2\phi _{x}+2\phi _{xx}\partial _{x}^{-1}-\tilde{\delta }\partial _{x}^{-1}\partial _{y}\big )\big ((\phi _{x}^{2})_y+\tilde{\delta }\phi _{yy}\big )\big ]+c\phi _{xt}=0, \end{aligned}$$
(2.18)

which can be regarded as a modified form of Eq.  (1.7). In particular, setting \(\delta =0\) and introducing the new dependent variable \(\varpi\) by \(\varpi =\phi _x\), the corresponding modified equation is

$$\begin{aligned} a(\varpi _{xxx}-6\varpi ^2\varpi _{x})+b[\varpi _{xxy}-4\varpi ^2\varpi _{y}-2\varpi _{x}\partial _{x}^{-1}(\varpi ^2)_{y}]+c\varpi _{t}=0, \end{aligned}$$
(2.19)

which is called as the (2+1)-dimensional modified KdV-CBS equation [32] and can be reduced to the modified KdV equation in the case of \(y=x\).

In addition, since the left-hand side of (2.4a) may be written as

$$\begin{aligned} (\tilde{\delta }D_{y}+D_{x}^{2})f\cdot f'/(ff')=\tilde{\delta }[\ln (f /f')]_{y}+[\ln (ff')]_{xx}+[\ln (f /f')]_{x}^{2}\qquad \qquad \qquad \qquad \end{aligned}$$
$$\begin{aligned} \qquad \qquad \qquad \qquad \qquad \qquad \qquad =\tilde{\delta }[\ln (f /f')]_{y}+2[\ln (f)]_{xx}-\big [\ln (f/f')\big ]_{xx}+[\ln (f /f')]_{x}^{2}, \end{aligned}$$
(2.20)

the bilinear equation \((\tilde{\delta }D_{y}+D_{x}^{2})f\cdot f'=0\) is equivalent to

$$\begin{aligned} \gamma u= \phi _{xx}-\phi _{x}^2-\tilde{\delta }\phi _{y}, \quad \tilde{\delta }=\pm \sqrt{\delta }, \end{aligned}$$
(2.21)

by using the following related variable transformation

$$\begin{aligned} u=\frac{2}{\gamma }[\ln (f)]_{xx},\, \phi =\ln (f/f'). \end{aligned}$$
(2.22)

This shows that formula (2.21) connects the solution u of the extended KdV Eq. (1.7) and the solution \(\phi\) of Eq.  (2.18).

3 Lump solutions with \(\delta \ne 0\)

Lump solutions are a kind of analytical rational solutions, which decay to zero in all directions in space. In particular, such solutions play a crucial role in revealing complex nonlinear phenomena in scientific fields such as nonlinear optics, ocean engineering, plasmas and fluid mechanics [33]. Hence, the study on the lump solution of nonlinear soliton equations can help us understand a variety of interesting phenomena and the related physical mechanisms in nature. It is reported that many kinds of methods can generate lump solutions, such as symbolic computations with Maple [21, 34,35,36,37], the long wave limit approach [22, 38, 39], the Hirota bilinear method and the use of nonlinear superposition formulae [25]. In this section, by using the nonlinear superposition formula associated with the bilinear Bäcklund transformation in Theorem 2.1, we would like to explore lump solutions for the extended KdV Eq. (1.7) with \(\delta \ne 0\). Now, let us set \(\lambda =0\) for convenience and rewrite (2.4) symbolically by \(f{\mathop {\rightarrow }\limits ^{\mu }}f'\). We have the following nonlinear superposition formula of Eq.  (2.3):

Theorem 3.1

[4, 5, 40] Let \(f_{0}\) be a nonzero solution of Eq.  (2.3) and assume that \(f_1\) and \(f_2\) are two nonzero solutions given by the bilinear Bäcklund transformation (2.4) such that \(f_{0}{\mathop {\rightarrow }\limits ^{\mu _{i}}}f_{i} (i=1,2)\). Then, \(f_{12}\) defined by

$$\begin{aligned} f_0 f_{12}=\hat{c}\big [D_{x}+\frac{1}{2}(\mu _2-\mu _1)\big ]f_1 f_2 \end{aligned}$$
(3.1)

is a new solution to Eq.  (2.3) which is interrelated to \(f_1\) and \(f_2\) under system (2.4) with parameters \(\mu _2\) and \(\mu _1\) , respectively. Here, \(\hat{c}\) is a nonzero real constant.

This theorem might be proved via a similar way to the one in the previous works [4, 5, 40]. Thus, we omit its proof in this paper.

In what follows, we take

$$\begin{aligned} f_0=1,\, f_{i}=\theta _i+\xi _i,\, \theta _i=k _i x+l_i y+m_i t+\zeta _i, \, i=1,2, \end{aligned}$$
(3.2)

where \(k _i, l_i, m_i, i=1, 2,\) are parameters to be determined, and \(\xi _i,\zeta _{i},i=1, 2,\) are arbitrary constants. By employing the bilinear Bäcklund transformation (2.4), we get

$$\begin{aligned} \mu _i=-\frac{l_i}{k_i}\tilde{\delta },\,m_i=-\frac{\delta }{c}\Big (\frac{3al_i^2}{k_i}+\frac{bl_i^3}{k_i^2}\Big ),\,i=1,2. \end{aligned}$$
(3.3)

Applying Theorem 3.1 and choosing \(\hat{c}=\frac{2}{\mu _2-\mu _1}\) in (3.1), a new solution of Eq.  (2.3) is presented as follows:

$$\begin{aligned} f_{12}&= \frac{2}{\mu _2-\mu _1}\left [f_{1x}f_2-f_{1}f_{2x}+\frac{1}{2}(\mu _2-\mu _1)f_1f_2\right] \\ & =\theta _1\theta _2+\left(\xi _1+\frac{2k _1}{\mu _2-\mu _1}\right)\theta _2+\left(\xi _2-\frac{2k _2}{\mu _2-\mu _1}\right)\theta _1 \\ &\quad+\xi _1\xi _2+\frac{2(k _1\xi _2-k _2\xi _1)}{\mu _2-\mu _1}. \end{aligned}$$
(3.4)

Upon selecting

$$\begin{aligned} \xi _1=\frac{2k_1}{\mu _1-\mu _2},\,\xi _2=\frac{2k_2}{\mu _2-\mu _1}\qquad \end{aligned}$$
(3.5)

and substituting (3.3) into (3.4), then \(f_{12}\) has the following form:

$$\begin{aligned} f_{12}=\theta _1\theta _2+B_{12}, \, B_{12}=\frac{4k_1^3k_2^3}{\delta (k_1l_2-k_2l_1)^2}.\qquad \end{aligned}$$
(3.6)

To establish lump solutions, we take

$$\begin{aligned} k_1=r_1+d_1\mathrm {i},\; l_1=r_2+d_2\mathrm {i},\; \zeta _1=r_4+d_4\mathrm {i},\;\mathrm {i}\equiv\sqrt{-1}, \end{aligned}$$
$$\begin{aligned} k_2=k_1^*,\; l_2=l_1^*, \;\zeta _2=\zeta _{1}^{*}, r_i, d_i\in \mathbb R, i=1,2,4,\qquad \quad \end{aligned}$$
(3.7)

where the asterisk denotes the complex conjugate. Substituting (3.2), (3.3) and (3.7) into (3.6) generates the following class of rational solutions:

$$\begin{aligned} f_{12}=(r_1 x+r_2y+r_3t+r_4)^2+(d_1x+d_2y+d_3t+d_4)^2+d, \end{aligned}$$
(3.8)

where \(r_3,d_3\) and d are given by

$$\begin{aligned} r_3=\frac{-3a\delta (r_1r_2^2-r_1d_2^2+2d_1d_2r_2)}{c(r_1^2+d_1^2)}-\frac{b\delta \big [(r_1^2-d_1^2)(r_2^3-3r_2d_2^2)-2r_1d_1(d_2^3-3r_2^2d_2)\big ]}{c(r_1^2+d_1^2)^2}, \end{aligned}$$
$$\begin{aligned} d_3=\frac{-3a\delta (d_1d_2^2-d_1r_2^2+2d_2r_1r_2)}{c(r_1^2+d_1^2)}-\frac{b\delta \big [(r_1^2-d_1^2)(3r_2^2d_2-d_2^3)-2r_1d_1(r_2^3-3r_2d_2^2)\big ]}{c(r_1^2+d_1^2)^2}, \end{aligned}$$
$$\begin{aligned} d=-\frac{(r_1^2+d_1^2)^3}{\delta (r_1d_2-r_2d_1)^2},\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$
(3.9)

where \(r_1d_2-r_2d_1\ne 0\) and the other parameters involved are arbitrary. Clearly, the conditions

$$\begin{aligned} r_1d_2-r_2d_1\ne 0 \,\, \mathrm {and}\,\, \delta <0, \end{aligned}$$
(3.10)

guarantee that the above class of function solutions is always positive. We remark that the class of function solutions reduces to the polynomial solutions of the extended bilinear second KP equation given by the long wave limit approach [22]. Under the constraint (3.10), the transformation (2.1) presents the following lump solutions to the extended form (1.7):

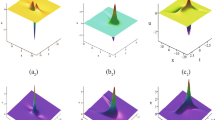
$$\begin{aligned} u=\frac{2}{\gamma }(\ln f_{12})_{xx}=\frac{2(f_{12,xx}f_{12}-f_{12,x}^2)}{\gamma f_{12}^2}, \quad v=\frac{2}{\gamma }(\ln f_{12})_{y}=\frac{2f_{12,y}}{\gamma f_{12}}, \end{aligned}$$
(3.11)

where \(f_{12}\) is defined by (3.8) and (3.9). Figures 1 and 2 exhibit three-dimensional plots and curves of the lump solutions (3.11) with choices of the involved parameters. We see that the lump solution u has a peak and two valleys, and decays algebraically in all directions in the (x, y)-plane.

Fig. 1
figure 1

Profile of u in the lump solution (3.11) with (3.8), (3.9) and parameters: \(r_1=\frac{1}{2},r_2=1, r_4= 3,d_1=2, d_2=-1, d_4=-2, a = -2, b = 1, c=-1, \gamma =1,\delta = -1, t=0\): (a) 3D plot, (b) contour plot and (c) x-curves

Full size image
Fig. 2
figure 2

Profile of v in the lump solution (3.11) with (3.8), (3.9) and same parameters as above: (a) 3D plot, (b) contour plot and (c) x-curves

Full size image

It is worth noting that extended Eq. (1.7) may possess abundant solution structures. We can also see if the analytic function \(f=f(x,y,t)\) in expression (2.2) satisfies

$$\begin{aligned} f_{y}=-\frac{a}{b}f_{x}, f_{t}=-\frac{2a^3\delta }{cb^2}f_{x},\qquad \qquad \end{aligned}$$
(3.12)

then the function f solves the trilinear Eq. (2.2). Thus, the trilinear Eq. (2.2) has the following solutions in the form

$$\begin{aligned} f=F(\eta ), \,\eta =kx-\frac{a}{b}ky-\frac{2a^3\delta }{cb^2}kt+h, \end{aligned}$$
(3.13)

where k is an arbitrary nonzero real constant, h is arbitrary and \(F(\eta )\) is an arbitrary function. As an example, let us consider a class of polynomial function solutions to the trilinear Eq. (2.2) in the form

$$\begin{aligned} f=\Big [k_1(x-\frac{a}{b}y-\frac{2a^3\delta }{cb^2}t)+h_1\Big ]^4+ \Big [k_2(x-\frac{a}{b}y-\frac{2a^3\delta }{cb^2}t)+h_2\Big ]^2+h_3, \end{aligned}$$
(3.14)

where the real constants \(k_1\) and \(k_2\) satisfy \(k_1^2+ k_2^2\ne 0\), but the constants \(h_i, 1\le i \le 3,\) are all arbitrary. It is easy to observe that the solutions in (3.14) are positive if the parameter \(h_3>0\) holds, and so the transformation in (2.1) with (3.13) present the nonsingular rational solutions u and v for the extended Eq. (1.7):

$$\begin{aligned} u&=\frac{2}{\gamma }\Big [\frac{12k_1^2(k_1\eta '+h_1)^2+2k_2^2}{(k_1\eta '+h_1)^4+(k_2\eta '+h_2)^2+h_3} -\frac{\big (4k_1 (k_1\eta '+h_1)^3+2k_2 (k_2\eta '+h_2)\big )^2 }{\big ((k_1\eta '+h_1)^4+(k_2\eta '+h_2)^2+h_3\big )^2 }\Big ],\\ v&=-\frac{2a}{\gamma b}\Big [\frac{4k_1(k_1\eta '+h_1)^3+2k_2(k_2\eta '+h_2)}{(k_1\eta '+h_1)^4+(k_2\eta '+h_2)^2+h_3}\Big ], \end{aligned}$$
(3.15)

where

$$\begin{aligned} \eta '=x-\frac{a}{b}y-\frac{2a^3\delta }{cb^2}t.\qquad \end{aligned}$$

Note that solution (3.15) is just a special case of the arbitrary travelling wave with

$$\begin{aligned} u=u_1(x-\frac{a}{b}y-\frac{2a^3\delta }{cb^2}t), \end{aligned}$$

which needs to satisfy \(ab\ne 0\). Besides, this solution does not tend to zero in the direction \(x-ay/b-2a^3\delta t/cb^2= \mathrm {constant}\), which yields the plane lump solution from [41]. The three-dimensional plots and curves generated by nonsingular rational solution (3.15) with the specific parameters are made by using Maple plot tools in Figs. 3 and 4.

Fig. 3
figure 3

Profile of u in the lump solution (3.15) with parameters: \(k_1 = 1, k_2 = 2, h_1=1,h_2=2, h_3=5, a = -2, b = 1,c = -1,\gamma =1,\delta =-1, t = 1\): (a) 3D plot, (b) contour plot and (c) y-curves

Full size image
Fig. 4
figure 4

Profile of v in the lump solution (3.15) with same parameters as Fig. 3: (a) 3D plot, (b) contour plot and (c) y-curves

Full size image

4 Concluding remarks

In summary, some meaningful integrable properties of the extended Eq. (1.7) have been explored, by means of a trilinear form. We first have computed a bilinear Bäcklund transformation to Eq.  (1.7), based on the exchange identities for Hirota’s bilinear operators and the existing research results. And then, associated with the obtained bilinear Bäcklund transformations, we have also derived a Lax pair and a modified equation to Eq.  (1.7) in detail. Lastly, two kinds of nonsingular rational solutions have been generated from the nonlinear superposition formula and arbitrary travelling wave solutions. The first class of rational solutions shows us that Eq.  (1.7) possesses a general class of lump solutions with \(\delta <0\), while the second class of nonsingular rational solutions is essentially travelling wave solutions due to special solution structures of Eq.  (1.7).

We point out that the generalized Eq. (1.7) includes many important nonlinear soliton equations as its special cases, such as the DJKM equation, the BS equation, the extended second KP equation and the generalized breaking soliton equation [4,5,6, 8, 14, 21, 22]. It is extremely important in soliton theory to search for nonlinear integrable systems and investigate their integrable characteristics. On the one hand, our work extends the above-mentioned equations to a new one which possesses many interesting integrable properties. The compatibility condition \([L_1,L_2] = 0\) of the general system (2.14) can generate the corresponding integrable equation with the selection of coefficients a, b, c and \(\delta\), which provides new (2+1)-dimensional nonlinear integrable equations to describe nonlinear phenomena in mathematical physics. On the other hand, the presented result enriches the existing theory on lumps to nonlinear soliton equations, adding new examples of employing trilinear forms to search for lump solutions.

As far as we know, there is still a lot of work to do with Eq.  (1.7), which is worth studying in depth. As Lou described in Ref. [6], some interesting exact solutions are also valid for the extended Eq. (1.7) with \(\delta \ne 0\), such as soliton molecule solutions and the D’Alembert-type solutions [6, 42,43,44,45]. Moreover, recent works exhibit that many (2+1)-dimensional nonlinear equations possess interaction solutions between lump or lump-type solutions and other kinds of exact solutions [36]. Therefore, it is meaningful for the extended Eq. (1.7) to look for interaction solutions including lump-kink interaction solutions and lump-soliton interaction solutions [46]. Another interesting work is to investigate Hirota N-soliton conditions [47,48,49] and linear superposition solutions [50] to the introduced Eq. (1.7), which will be carried out in our future research.