Integrability, lump solutions, breather solutions and hybrid solutions for the (2+1)-dimensional variable coefficient Korteweg-de Vries equation

Abstract

This paper focuses on the integrability and exact solutions of a (2+1)-dimensional variable coefficient Korteweg-de Vries equation. The bilinear form, Bäcklund transformations, and Lax pair of this equation are obtained using the Bell polynomial method. Soliton solutions, including lump solitons, breather solitons, and hybrid solutions, are constructed by assuming different auxiliary functions in the bilinear ansatz method. Additionally, the soliton solutions are presented as figures for different variable coefficient functions and undetermined items under appropriate parameter choices. The Bäcklund transformations also lead to Lax pair and the infinity conservation laws that ensure the integrability of the nonlinear system under study.

1 Introduction

Nonlinear partial differential equations (NLPDEs) play a key role in simulating various phenomena in mathematical theory, physical science and engineering technology [1]- [6]. Searching for the exact solutions of NLPDEs is crucial for deep understanding of these phenomena and developing new technologies, but it used to be difficult. Emergence of integrable system theory applicable to NLPDEs is a major breakthrough in this field. The developments of integrable systems theory with other mathematical tools make exact solutions of complex NLPDEs possible. Currently, further research on NLPDEs remains a vibrant field with many promising future opportunities.

In numerous NLPDEs, the Korteweg-de Vries (KdV) equation and its generalized equations have significance for their wide applications in engineering, plasma physics, water waves, hydrodynamics and quantum theory [7]–[11]. The classical KdV equation

$$\begin{aligned} u_t=u_{xxx}+6uu_x \end{aligned}$$

(1)

as first discovered in 1895 by Korteweg and de Vries while investigating the motion of long waves of small amplitude in shallow water [12]. On account of the importance and applicability of the KdV equations, the studies on them have spread and deepened more and more.

Boiti et al. [13] used the idea of the weak Lax pair to derive the (2+1)-dimensional KdV equation

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t+3(uv)_x+u_{xxx}=0,\\ u_x=v_y. \end{array}\right. } \end{aligned}$$

(2)

This equation falls under the category of NLPDEs and has garnered significant interest in studying the different forms of exact solutions. To achieve this, various distinguishing methods have been employed and contributed to finding the exact solutions of (2). For example, the Hirota bilinear method [14], the tanh-coth method, the cosh ansatz, the Exp-function method [15], the method combining positive quadratic function and hyperbolic function [16], and the extended homoclinic test technique [17].

The above research results are all based on the (2+1)-dimensional constant coefficient KdV equation. However, NLPDEs with variable coefficients are also a very important and constantly evolving research area that needs to be explored to gain a deeper understanding and clearer explanations of real physical phenomena. Compared with the constant coefficient KdV equations, the coefficients in the equations studied are the function(s) of the space variable or time variable. Currently, the main methods for finding the exact solutions of variable coefficient KdV equations include Bäcklund transformation [18, 19], Hirota’s direct method [20, 21], Darboux transformation [22, 23], Painlevé analysis [19, 24], nonlinear superposition principle [25] and auxiliary equation method [26, 27].

In this paper, we will aim at the (2+1)-dimensional variable coefficient KdV equation (vcKdV) from Eq. (2)

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho (t)u_t+3(uv)_x+u_{xxx}=0,\\ u_x=v_y, \end{array}\right. } \end{aligned}$$

(3)

where $u=u(x,y,t)$, $v=v(x,y,t)$, x and y are space variables, and t is time variable. And the coefficient function $\rho (t)$ is a function of time t. The bilinear ansatz method will be applied to construct the exact soliton solutions and hybrid solutions of the vcKdV equation (3) with different $\rho (t)$. The variable coefficient Equations more realistically model various situations, such as superconductors, plasmas, and optical-fiber communications, some of which have a distinct soliton character. We propose the idea of the ansatz method for solving constant coefficient equations, study the ansatz method for variable coefficient equations, and give the conditions on the parameters to get lump soliton, breather soliton, and hybrid solutions, which provide useful ideas for solving other equations with variable coefficients.

This paper is organized as follows. In Sect. 2.1, we first review the Bell polynomials and further derive the bilinear form, Bäcklund transformations, and Lax pair from the relationship between the Bell polynomial and the Hirota bilinear operator. In Sect. 3, soliton solutions including lump, breather, and line and hybrid solutions of the vcKdV Eq. (3) are constructed by ansatz method and their dynamics properties are illustrated by graphs. In Sect. 4, the infinite conservation laws are derived on the basis of Lax pair. In Sect. 5, certain conclusions end in full text.

2 Bilinear form and Lax integrability

In this section, Bell polynomials will be used to derive the bilinear form and Lax pair of the vcKdV equation (3). The exponential polynomial was first proposed by Bell in 1934 [28] and the generalized Bell polynomials have played an important role in studying various NLPDEs with constant or variable coefficients [29]–[36].

2.1 Bilinear from

The bilinear form of the vcKdV Eq. (3) will be obtained next on the basis of the connection between Bell polynomials, and the Hirota bilinear operator.

2.1.1 Bell polynomials

Firstly, we will briefly review the one-dimensional Bell polynomials, multi-dimensional Bell polynomials and the binary Bell polynomials.

The one-dimensional Bell polynomials [28] are defined as

$$\begin{aligned} Z_{mx}(g)=Z_m(g_x,\ldots ,g_{nx})=\exp (-g)\partial _x^m\exp (g),\nonumber \\ \end{aligned}$$

(4)

where $g_{ix}=\partial _x^ig$.

If $m_i$ ($i= 1,\;2, \ldots ,j$) are arbitrary nonnegative integers, $g=g(x_1,\ldots ,x_j)$ is a $C^\infty$ multi-variable function and $g_{s_1x_1,\ldots , s_jx_j}=\partial _{x_1}^{s_1}... \partial _{x_j}^{s_j}g \ \ (s_i=0,\ldots , m_i, i=1,\ldots , j)$, then the multi-dimensional Bell polynomials (Z-polynomials) [29]- [31] read

$$\begin{aligned} Z_{m_1x_1,\ldots ,m_jx_j}(g)=\exp (-g)\partial _{x_1}^{m_1}... \partial _{x_j}^{m_j}\exp (g). \end{aligned}$$

(5)

The binary Bell polynomials (${\mathscr {Z}}$-polynomials) have the following form

$$\begin{aligned} \begin{aligned}&{\mathscr {Z}}_{m_1x_1, \ldots , m_jx_j}(\iota ,\kappa )=Z_{m_1x_1, \ldots , m_jx_j}(g)|_{g_{s_1x_1,\ldots ,s_jx_j}}\\&\quad ={\left\{ \begin{array}{ll} \iota _{s_1x_1, \ldots , s_jx_j},&{}\text { if }\ s_1+ \ldots + s_j {\textrm{ is } \ \textrm{ odd }},\\ \kappa _{s_1x_1, \ldots , s_jx_j},&{}\text { if }\ s_1+ \ldots + s_j {\textrm{ is } \ \textrm{even }}. \end{array}\right. } \end{aligned} \end{aligned}$$

(6)

Here list several common terms of the binary Bell polynomials

$$\begin{aligned} \begin{aligned} {\mathscr {Z}}_x(\iota ,\kappa )&=\iota _x,\\ {\mathscr {Z}}_{2x}(\iota ,\kappa )&=\kappa _{2x}+\iota _x^2,\\ {\mathscr {Z}}_{xt}(\iota ,\kappa )&=\kappa _{xt}+\iota _x\iota _t,\\ {\mathscr {Z}}_{3x}(\iota ,\kappa )&=\iota _{3x}+3\iota _x\kappa _{2x}+\iota _x^3,\\ {\mathscr {Z}}_{2xt}(\iota ,\kappa )&=\iota _{2xt}+\kappa _{2x}\iota _t+2\kappa _{xt}\iota _x+\iota _x^2\iota _t,\\ {\mathscr {Z}}_{4x}(\iota ,\kappa )&=\iota _x^4+6\iota _x^2\kappa _{2x}+3\iota _{2x}^2+4\iota _x\iota _{3x}+\kappa _{4x}. \end{aligned} \end{aligned}$$

(7)

Define the Hirota bilinear operators $D_{x_i}^{m_i} \ \ (i=1,\ldots , j)$ as

$$\begin{aligned} \begin{aligned}&D_{x_1}^{m_1}\cdots D_{x_j}^{m_j}(F\cdot {G})=(\partial x_1-\partial x_{1'})^{m_1}\cdots \\&\quad (\partial x_j-\partial x_{j'})^{m_j}F(x_1,\ldots ,x_j)G(x_{1'},\ldots \\&\quad ,x_{j'})|_{x_1=x_{1'},\ldots ,x_j=x_{j'}},\\ \end{aligned} \end{aligned}$$

(8)

where $F=F(x_1,\ldots ,x_j)$, $G=G(x_{1'},\ldots ,x_{j'})$ and $m_i \ (i=1,\ldots , j)$ are nonnegative integers.

The binary Bell polynomials and the Hirota operator have the following relation

$$\begin{aligned}{} & {} {\mathscr {Z}}_{m_1x_1, \ldots , m_jx_j}(\iota =\ln {F/G},\kappa \nonumber \\{} & {} \quad =\ln {FG})=(FG)^{-1}D_{x_1}^{m_1}\cdots D_{x_j}^{m_j}F\cdot {G}, \end{aligned}$$

(9)

which can further be expressed by the Q-polynomials and the Z-polynomials

$$\begin{aligned} \begin{aligned}&(FG)^{-1}D_{x_1}^{m_1}\cdots D_{x_j}^{m_j}(F\cdot {G})\\&\quad ={\mathscr {Z}}_{m_1x_1, \ldots , m_jx_j}(\iota ,\kappa )\mid _{\iota =\ln {G/F},\kappa =\ln {FG}}\\&\quad ={\mathscr {Z}}_{m_1x_1, \ldots , m_jx_j}(\iota ,\iota +q)\mid _{\iota =\ln {F/G},q=2\ln {F}}\\&\quad {=}\sum _{m_1{+}\cdots m_j{=}even}\sum _{s_1=0}^{m_1}\cdots \sum _{s_j{=}0}^{m_j}\prod _{k{=}1}^j \left( {\begin{array}{c}m_k\\ s_k\end{array}}\right) Q_{s_1x_1,\ldots ,s_jx_j}(q)\\&\quad \times {\mathscr {Z}}_{(m_1-s_1)x_1,\ldots ,(m_j-s_j)x_j}(\iota ). \end{aligned} \end{aligned}$$

(10)

If $F=G$, then $\iota =\ln \frac{F}{G}=0$, $\kappa =\ln {F^2}=2\ln {F}$, and Eq. (10) turns into

$$\begin{aligned} \begin{aligned}&F^{-2}D_{x_1}^{m_1}\cdots D_{x_j}^{m_j}F^2={\mathscr {Z}}_{m_1x_1, \ldots , m_jx_j}(0,q=2\ln {F})\\&\quad ={\left\{ \begin{array}{ll} 0,&{}\text { if }\ m_1+\cdots +m_j {\textrm{ is }\ \textrm{ odd}},\\ Q_{m_1x_1, \ldots , m_jx_j}(q),&{}\text { if }\ m_1+\cdots +m_j {\textrm{ is }\ \textrm{ even }}, \end{array}\right. } \end{aligned}\nonumber \\ \end{aligned}$$

(11)

where $Q_{m_1x_1, \ldots , m_jx_j}(q)$ are Q-polynomials with even part partitional structure and a few terms to be used below are listed here

$$\begin{aligned} \begin{aligned}&Q_0=1,\\&Q_{2x}(q)=q_{2x},\\&Q_{x,y}(q)=q_{xy},\\&Q_{y,t}(q)=q_{yt},\\&Q_{3x,y}(q)=q_{3xy}+3q_{2x}q_{xy}.\\ \end{aligned} \end{aligned}$$

(12)

Under the Hopf-Cole transformations

$$\begin{aligned} \iota =\ln {\mathbb {W}}, \ \ {\mathbb {W}}=F/G, \end{aligned}$$

(13)

the multi-dimensional Bell polynomials have the following property

$$\begin{aligned} Z_{m_1x_1,\ldots ,m_jx_j}(\iota )\mid _{\iota =\ln {{\mathbb {W}}}}={\mathbb {W}}_{m_1x_1,\ldots ,m_jx_j}/{\mathbb {W}}, \end{aligned}$$

(14)

and the binary Bell polynomials can be linearized.

2.1.2 Bilinear form of the vcKdV equation

Based on the relation (11) between the binary Bell polynomials and the bilinear operator, we will derive the bilinear transformations that convert the nonlinear vcKdV Eq. (3) into its equivalent bilinear Eq. will be obtained. The relevant conclusions will be presented as the following theorem.

Theorem 1

The bilinear form of the vcKdV Eq. (3) is

$$\begin{aligned}{} & {} (\rho (t)D_yD_t+D_x^3D_y+3\gamma D_x^2+3\delta D_xD_y)f\cdot \nonumber \\{} & {} \quad f=0, \end{aligned}$$

(15)

and the equivalent bilinear equation is

$$\begin{aligned}{} & {} \rho (t)(f_{yt}f-f_tf_y)+f_{xxxy}f-f_{xxx}f_y-3f_{xxy}f_x\nonumber \\{} & {} \quad +3f_{xx}f_{xy}+3\gamma (f_{xx}f-f_x^2)+3\delta (f_{xy}f-f_xf_y)\nonumber \\{} & {} \quad =0. \end{aligned}$$

(16)

Proof

For the vcKdV Eq. (3), we consider the transformations

$$\begin{aligned} u=\gamma +m_y, \ \ v=\delta +m_x, \end{aligned}$$

(17)

where $\gamma$ and $\delta$ are real parameters, and $m=m(x,y,t)$ is a differentiable function of x, y and t. Substituting the transformations (17) into Eq. (3), we have

$$\begin{aligned} \rho (t)m_{yt}+3[(\gamma +m_y)(\delta +m_x)]_x+m_{xxxy}=0.\nonumber \\ \end{aligned}$$

(18)

Taking the further transformations

$$\begin{aligned} m=q_x,\ \ q=2\ln {f}, \end{aligned}$$

(19)

and substituting the transformations (19) into Eq. (18), we get

$$\begin{aligned} \rho (t)q_{xyt}+3[(\gamma +q_{xy})(\delta +q_{xx})]_x+q_{xxxxy}=0,\nonumber \\ \end{aligned}$$

(20)

where $q=q(x,y,t)$ and $f=f(x,y,t)$ are two differentiable functions of x, y and t.

Integrating Eq. (20) with respect to x, we have

$$\begin{aligned} \rho (t)q_{yt}+3(\gamma +q_{xy})(\delta +q_{xx})+q_{xxxy}=C. \end{aligned}$$

(21)

We assume the combinations of the integral constant C and the constant term $3\gamma \delta$ to be zero, and denote

$$\begin{aligned} E(q)=\rho (t)q_{yt}++q_{xxxy}+3\gamma q_{xx}+3\delta q_{xy}=0.\nonumber \\ \end{aligned}$$

(22)

From the Q-polynomials (12) of the binary Bell polynomials, Eq. (22) can be rewritten as

$$\begin{aligned} E(q)=\rho (t)Q_{yt}+Q_{3xy}+3\gamma Q_{2x}+3\delta Q_{xy}=0.\nonumber \\ \end{aligned}$$

(23)

According to the formula (11), we confirm that the bilinear representation of the vcKdV Eq. (3) is Eq. (15). By the bilinear operator (8), the bilinear form (15) will be converted into the corresponding bilinear Eq. (16). $\square$

In the process of proving the theorem above, we also obtained the bilinear transformation

$$\begin{aligned} u=\gamma +(2\ln {f})_{xy},\,\,v=\delta +(2\ln {f})_{xx} \end{aligned}$$

(24)

of the vcKdV Eq. (3) obviously.

2.2 Lax integrability

Based on the bilinear form (15) and the Hopf-Cole transformations (13), the Bäcklund transformations and the relative Lax pair will be derived, which ensure the Lax integrability of the vcKdV Eq. (3). Two related theorems will be given in this part.

Theorem 2

The Bäcklund transformations of the vcKdV Eq. (3) are

$$\begin{aligned} {\left\{ \begin{array}{ll} (D_xD_y+\lambda D_x){\tilde{F}}\cdot {{\tilde{G}}}=0,\\ (\rho (t)D_t+D_{3x}){\tilde{F}}\cdot {{\tilde{G}}}=0,\\ (3\gamma D_x+3\delta D_{y}){\tilde{F}}\cdot {{\tilde{G}}}=0, \end{array}\right. } \end{aligned}$$

(25)

where $\lambda$ is an arbitrary constant and ${\tilde{F}}={\tilde{F}}(x,y,t)$ and ${\tilde{G}}={\tilde{G}}(x,y,t)$.

Proof

Suppose that q(x, y, t) and ${\hat{q}}(x,y,t)$ are two different solutions of Eq. (22). The new transformations

$$\begin{aligned} \iota =\frac{{\hat{q}}-q}{2}=\ln {\frac{{\tilde{F}}}{{\tilde{G}}}}, \ \ \kappa =\frac{{\hat{q}}+q}{2}=\ln {{\tilde{F}}{\tilde{G}}} \end{aligned}$$

with Eq. (22) and the binary Bell polynomials (7) lead to

$$\begin{aligned} \begin{aligned} 0&=E({\hat{q}})-E(q))\\&=\rho (t)({\hat{q}}-q)_{yt}+({\hat{q}}-q)_{xxxy}\\&\quad +3({\hat{q}}_{xy}{\hat{q}}_{xx}-q_{xy}q_{xx})\\&\quad +3\gamma ({\hat{q}}-q)_{2x}+3\delta ({\hat{q}}-q)_{xy}\\&=2(\rho (t)\iota _{yt}+\iota _{3xy}+3(\kappa _{2x}\iota _{xy}\\&\quad +\kappa _{xy}\iota _{2x})+3\gamma \iota _{2x}+3\delta \iota _{xy})\\&=2(\partial _{y}(\rho (t){\mathscr {Z}}_t+{\mathscr {Z}}_{3x})+\partial _x(3\gamma {\mathscr {Z}}_x\\&\quad +3\delta {\mathscr {Z}}_{y})+R(\iota ,\kappa )),\\ \end{aligned} \end{aligned}$$

(26)

in which

$$\begin{aligned} R(\iota ,\kappa )=3(\kappa _{xy}\iota _{2x}-\iota _x\kappa _{2xy}-\iota _x^2\iota _{xy}). \end{aligned}$$

(27)

Eq. (26) can be rewritten as

$$\begin{aligned}&0=\frac{E({\hat{q}})-E(q)}{2}=\partial _{y}(\rho (t){\mathscr {Z}}_t+{\mathscr {Z}}_{3x})\nonumber \\&\quad +\partial _x(3\gamma {\mathscr {Z}}_x+3\delta {\mathscr {Z}}_{y}). \end{aligned}$$

(28)

Introducing another constrained condition ${\mathscr {Z}}_{xy}+\lambda {\mathscr {Z}}_{x}$$=0$ and combining it with Eq. (28), we obtain a set of equations

$$\begin{aligned} \left\{ \begin{array}{c} {\mathscr {Z}}_{xy}+\lambda {\mathscr {Z}}_{x}=0,\\ \rho (t){\mathscr {Z}}_t+{\mathscr {Z}}_{3x}=0,\\ 3\gamma {\mathscr {Z}}_x+3\delta {\mathscr {Z}}_{y}=0, \end{array} \right. \end{aligned}$$

(29)

which with Eq. (9) can deduce the Bäcklund transformations (25) for the vcKdV Eq. (3). $\square$

Theorem 3

When $3\gamma {\mathbb {W}}_x+3\delta {\mathbb {W}}_{y}=0$, the Lax pair of the vcKdV Eq. (3) is as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} L_1({\mathbb {W}})={\mathbb {W}}_{xy}+\lambda {\mathbb {W}}_x+u{\mathbb {W}}=0,\\ L_2({\mathbb {W}})=\rho (t){\mathbb {W}}_t+3v{\mathbb {W}}_x+{\mathbb {W}}_{3x}=0. \end{array}\right. } \end{aligned}$$

(30)

Proof

According to the Hopf-Cole transformations (13) and Eqs. (10) and (14), there hold

$$\begin{aligned}&{\mathscr {Z}}_x(\iota ,\kappa )=\frac{{\mathbb {W}}_x}{{\mathbb {W}}}, \ \ {\mathscr {Z}}_y(\iota ,\kappa )=\frac{{\mathbb {W}}_y}{{\mathbb {W}}}, \nonumber \\&\quad \ \ {\mathscr {Z}}_{2x}(\iota ,\kappa )=q_{2x}+\frac{{\mathbb {W}}_{2x}}{{\mathbb {W}}},\nonumber \\&\quad {\mathscr {Z}}_{xy}(\iota ,\kappa )=q_{xy}+\frac{{\mathbb {W}}_{xy}}{{\mathbb {W}}},\nonumber \\&\quad \ \ {\mathscr {Z}}_{3x}(\iota ,\kappa )=3q_{2x}\frac{{\mathbb {W}}_{x}}{{\mathbb {W}}}+\frac{{\mathbb {W}}_{3x}}{{\mathbb {W}}}. \end{aligned}$$

(31)

For $3\gamma {\mathbb {W}}_x+3\delta {\mathbb {W}}_{y}=0$, we substitute (31) into (29) and obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {W}}_{xy}+\lambda {\mathbb {W}}_x+m_y\psi =0,\\ \rho (t){\mathbb {W}}_t+3m_x{\mathbb {W}}_x+{\mathbb {W}}_{3x}=0. \end{array}\right. } \end{aligned}$$

(32)

Taking the transformations (17) into Eq. (32), we prove that the Lax pair (30) holds. The compatibility condition ${\mathbb {W}}_{xyt}={\mathbb {W}}_{txy}$ leads to

$$\begin{aligned} \rho (t)m_{yt}+3[(\gamma +m_y)(\delta +m_x)]_x+m_{yxxx}=0.\nonumber \\ \end{aligned}$$

(33)

All these prove that the vcKdV Eq. (3) is completely integrable. $\square$

3 The exact solutions of the vcKdV equation

In this section, we will use ansatz-methods [37]- [41] to construct the solutions of the bilinear Eq. (16) and further obtain the exact solutions of the vcKdV Eq. (3). For convenience, we take $\gamma =0$ and $\delta =0$. The different expressions of auxiliary functions f and different choices of the parameters will determine the types of solitons, such as lump solitons, breather solitons and line solitons.

3.1 Lump soliton solutions

Lump soliton solution is a special rational solution, which is local in all spatial directions. Many scholars have used the positive quadratic function in ansatz-methods to construct the lump soliton solutions of NLPDEs [37]- [39].

To find the lump soliton solutions to the vcKdV Eq. (3), we start with the following solution f of the bilinear Eq. (16)

$$\begin{aligned} f=\zeta _1^2+\zeta _2^2+\eta , \end{aligned}$$

(34)

with

$$\begin{aligned} \zeta _i=k_ix+b_iy+c_i(t)+d_i,(i=1, 2), \end{aligned}$$

(35)

where $k_i, b_i$ and $d_i$ are undetermined real parameters, and $c_i(t)$ are functions of t. After taking (34) into Eq. (16) to collect the coefficients of x and y, and setting these coefficients equal to 0, we can get the conditions that $c_i(t)$ $(i=1, 2)$ and $\eta$ satisfy the following equalities

$$\begin{aligned}{} & {} c_1(t)=-\int {\frac{3(b_1^2k_1+b_1k_1^2-b_1k_2^2+b_2^2k_1+2b_2k_1k_2)}{\rho (t)(b_1^2+b_2^2)}}dt,\nonumber \\{} & {} c_2(t)=-\int {\frac{3(b_1^2k_2-b_2k_1^2+b_2k_2^2+b_2^2k_2+2b_1k_1k_2)}{\rho (t)(b_1^2+b_2^2)}}dt,\nonumber \\{} & {} \eta =-\frac{k_1^3b_1^3+k_1^3b_1b_2^2+k_1^2b_1^2k_2b_2+k_1^2k_2b_2^3+k_1b_1^3k_2^2+k_1b_1k_2^2b_2^2+b_1^2k_2^3b_2+k_2^3b_2^3}{(b_1k_2-b_2k_1)^2}, \end{aligned}$$

(36)

where $k_i$ and $d_i$ ($i=1,2$) are arbitrary, but conditions that $\eta >0$, $b_1\ne 0$, $b_2\ne 0$ and $b_1k_2-b_2k_1\ne 0$ should be satisfied simultaneously to avoid the singularity of the lump soliton.

When we choose $\rho (t)=1$, $k_1=4, b_1=-3, d_1=2, k_2=\frac{3}{2}, b_2=1, d_2=2$, the bilinear Eq. (16) becomes a constant-coefficient case, and its solution is

$$\begin{aligned}{} & {} f=(4x-3y-\frac{129}{40}t+2)^2+(\frac{3}{2}x\nonumber \\{} & {} \quad +y+\frac{417}{40}t+2)^2+\frac{7665}{289}. \end{aligned}$$

(37)

It is easy to obtain the lump soliton solutions u and v of the vcKdV Eq. (3) from (37) and (24). The explicit expressions are omitted here and in the rest of this paper for the sake of brevity. The corresponding figures of u and v are presented in Fig. 1 ($a_1$) and ($a_2$).

Fig. 1

As $y=0$, lump soliton solutions of Eq. (3) for the different variable coefficient function: (a) $\rho (t)=1$; (b) $\rho (t)=\frac{1}{t}$; (c) $\rho (t)=\frac{1}{t^2}$

When we choose $\rho (t)=\frac{1}{t}$, $k_1=2, b_1=-3, d_1=1, k_2=\frac{3}{2}, b_2=5, d_2=5$, the solution of bilinear Eq. (16) is

$$\begin{aligned} f= & {} (2x-3y-\frac{1113}{272}t^2+1)^2+(\frac{3}{2}x\nonumber \\{} & {} \quad +5y+\frac{291}{272}t+5)^2+\frac{1275}{841}. \end{aligned}$$

(38)

It is easy to obtain the lump soliton solutions u and v of the vcKdV Eq. (3) from (38) and (24). The corresponding figures of u and v are presented in Fig. 1 ($b_1$) and ($b_2$).

When we choose $\rho (t)=\frac{1}{t^2}$, $k_1=1, b_1=2, d_1=5, k_2=2, b_2=-3, d_2=-2$, the solution of bilinear Eq. (16) is

$$\begin{aligned} f= & {} \left( x+2y+\frac{5}{13}t^3+5\right) ^2+\Big (2x-3y\nonumber \\{} & {} \quad -\frac{25}{13}t^3-2\Big )^2+\frac{260}{49}. \end{aligned}$$

(39)

The lump soliton solutions u and v of the vcKdV Eq. (3) are obtained from (39) and (24). The corresponding figures of u and v are presented in Fig. 1 ($c_1$) and ($c_2$).

In the above three cases, $\rho (t)$ is the inverse of a power function. The shape of lumps takes a parabolic shape and cubic parabolic shape, which was related to the variable coefficient $\rho (t)$.

Fig. 2

Contour and characteristic lines of one-lump soliton solutions of Eq. (3) for $\rho (t)=1$: (a) characteristic lines map and contour map of u and v as $t=0$; (b) contour plots of u and v at $t=-2$ and $t=2$; (c) characteristic plots of u and v as $t=-2$ and $t=2$

Next, we will analyze the movement of the lump soliton in detail by the method of characteristic lines. From the expressions of $\zeta _i$ in (35), letting $\zeta _1=0$ and $\zeta _2=0$, we get respectively the two characteristic lines $L_1$ and $L_2$ of f. Because $b_1k_2-b_2k_1\ne 0$, these two lines must intersect and their angle is $\theta$ as shown in Fig. 2 ($a_1$) and ($a_2$). Under the given parameters and at $t=0$, $L_1:4x-3y+2=0$ and $L_2: \frac{3}{2}x+y+2=0$, which both cross the center of the lump. As time goes from $t=-2$ to $t=2$, the two characteristic lines will move parallelly and their angle does not change ($\theta =\theta _1=\theta _2$) in Fig. 2a and c. The red line $L_3:4x-3y+\frac{169}{20}=0$ and the green line $L_5:4x-3y-\frac{89}{20}=0$ parallel with $L_1$. The red line $L_4:\frac{3}{2}x+y-\frac{377}{20}=0$ and the green line $L_6:\frac{3}{2}x+y+\frac{457}{20}=0$ parallel with $L_2$. The connecting line between the intersection of two red lines and the intersection of two green lines is the moving trajectory of the center of the lump, seen in Fig. 2 (b) and (c).

Fig. 3

As $y=0$, lump soliton solutions of Eq. (3) for the different $\rho (t)$: (a) $\rho (t)=\frac{1}{\sin {\frac{t}{2}}}$; (b) $\rho (t)=\frac{1}{\sin {t}}$; (c) $\rho (t)=\frac{1}{\sin {2t}}$

When we choose $\rho (t)=\frac{1}{\sin {\frac{t}{2}}}$, $k_1=1, b_1=2, d_1=5, k_2=2, b_2=-3, d_2=-2$, the solution of bilinear Eq. (16) is

$$\begin{aligned} f= & {} \left( x+2y-\frac{30\cos {\frac{t}{2}}}{13}+5\right) ^2+\left( 2x-3y\right. \nonumber \\{} & {} \quad \left. +\frac{150\cos {\frac{t}{2}}}{13}-2\right) ^2+\frac{260}{49}. \end{aligned}$$

(40)

It is easy to obtain the lump soliton solutions u and v of the vcKdV Eq. (3) from (40) and (24). The corresponding figures of u and v are presented in Fig. 3 ($a_1$) and ($a_2$). Because $\rho (t)$ is the inverse of a trigonometric function, which also appears in the expression of f, the lump soliton solution has corresponding periodicity whose period is controlled by $\rho (t)$.

When we choose $\rho (t)=\frac{1}{\sin {t}}$, $k_1=1, b_1=2, d_1=5, k_2=2, b_2=-3, d_2=-2$, the solution of bilinear Eq. (16) is

$$\begin{aligned} f= & {} \left( x+2y-\frac{15\cos {t}}{13}+5\right) ^2+\left( 2x\right. \nonumber \\{} & {} \quad \left. -3y+\frac{75\cos {t}}{13}-2\right) ^2+\frac{260}{49}. \end{aligned}$$

(41)

It is easy to obtain the lump soliton solutions u and v of the vcKdV Eq. (3) from (41) and (24). The corresponding figures of u and v are presented in Fig. 3 ($b_1$) and ($b_2$).

Fig. 4

Periodic lump soliton solutions of Eq. (3) for $\rho (t)=\frac{1}{\sin {\frac{t}{2}}}$ for different y values: (a) $y=-4$; (b) $y=0$; (c) $y=4$

When we choose $\rho (t)=\frac{1}{\sin {2t}}$, $k_1=1, b_1=2, d_1=5, k_2=2, b_2=-3, d_2=-2$, the solution of bilinear Eq. (16) is

$$\begin{aligned} f= & {} (x+2y-\frac{15\cos {2t}}{26}+5)^2+(2x-3y\nonumber \\{} & {} \quad +\frac{75\cos {2t}}{26}-2)^2+\frac{260}{49}. \end{aligned}$$

(42)

It is easy to obtain the lump soliton solutions u and v of the vcKdV Eq. (3) from (42) and (24). The corresponding figures of u and v are presented in Fig. 3 ($c_1$) and ($c_2$).

From Fig. 1 and Fig. 3, it is obvious that the lump solitons of v are all bright ($a_2$, $b_2$ and $c_2$) and the ones of u are all anti-bright ($a_1$, $b_1$ and $c_1$). As for the periodicity, it depends on the period of the auxiliary function f. From the expressions of f in Eqs. (40)-(42), the period of the first lump soliton is $4\pi$, the period of the second lump soliton is $2\pi$, and the period of the last lump soliton is $\pi$.

Fig. 5

Two-dimensional cross-section graph of a periodic lump soliton solution of Eq. (3) for $\rho (t)=\frac{1}{\sin {\frac{t}{2}}}$ as $y=0$, $y=4$ and $y=10$

Figures 4 (a), (b) and (c) are the three-dimensional graphs of the periodic lump soliton solutions u and v in Fig. 3 (a) at $y=-4$, $y=0$ and $y=4$ respectively. The sectional diagrams of the components u and v with different y values are shown in Fig. 5 (a) and (b) respectively. In Fig. 5, the green, blue and red curves correspond to $y=-4$, $y=0$ and $y=4$ respectively. What y values can influence is only the amplitude of the soliton. It can also be clearly seen that the amplitudes of u and v at $y=0$ are the largest.

3.2 Breather soliton solutions

To construct the breather soliton solutions of the vcKdV Eq. (3), we assume that the solution f of the bilinear Eq. (16) is a combination of hyperbolic and trigonometric functions as follows [42, 43]

$$\begin{aligned} f= & {} a_1\cosh \zeta _1+a_2\cos \zeta _2\nonumber \\{} & {} \quad +a_3\sinh \zeta _3+a_4\sin \zeta _4, \end{aligned}$$

(43)

with

$$\begin{aligned} \zeta _i=k_ix+b_iy+c_i(t)+d_i, (i=1, 2, 3, 4), \end{aligned}$$

(44)

where $k_i, b_i$ and $d_i$ are undetermined real parameters, and $c_i(t)$ are functions of t. From (43), it is not difficult to find that hyperbolic functions affect the locality of the breather solitons and trigonometric functions control the period. From this perspective, the breather solitons can be viewed as consisting of the solitary wave and the periodic wave. Substituting (43) into Eq. (16), collecting the coefficients of different functions and setting these coefficients equal to 0, we can determine specific parameters, which will lead to different breather soliton solutions.

(1) From those parameters, we select the following values: $a_1\ne 0$, $a_2\ne 0$, $a_3\ne 0$, $a_4=0$, and other undetermined items satisfy

$$\begin{aligned} \begin{aligned}&c_1(t)=-\int {\frac{k_3(k_3^2+3)}{\rho (t)}},\ \ \ c_2(t)=\int {\frac{k_2(k_2^2+3)}{\rho (t)}},\\&\quad c_3(t)=-\int {\frac{k_3(k_3^2+3)}{\rho (t)}},\\&\quad k_1=k_3,\ \ \ b_1=-\frac{1}{k_3},\\&\quad b_2=\frac{1}{k_2},\ \ \ b_3=-\frac{1}{k_3}, \end{aligned} \end{aligned}$$

(45)

where $k_2\ne 0$ and $k_3\ne 0$. When we take different $\rho (t)$ and appropriate $a_1$, $a_2$, $a_3$, $k_2$, $k_3$, $d_1$, $d_2$, $d_3$, we get several solutions.

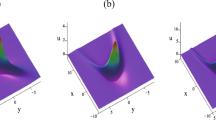
When taking $\rho (t)=1$, $a_1=3,\ a_2=-1,\ a_3=2,\ k_2=1,\ k_3=\frac{1}{2}$, $d_1=3$, $d_1=5$, $d_1=4$, this is a case of the constant coefficient KdV Eq. whose breather solitons will be the ordinary ones. The solution of the bilinear Eq. (16) is

$$\begin{aligned}{} & {} f=3\cosh \left( -\frac{1}{2}x+2y+\frac{13}{8}t-3\right) \nonumber \\{} & {} \quad -\cos (-x-y+2t-5)\nonumber \\{} & {} \quad -2\sinh \left( -\frac{1}{2}x+2y+\frac{13}{8}t-4\right) . \end{aligned}$$

(46)

From (46) and (24), we can obtain the expressions of the breather soliton solutions u and v whose figures are depicted in Fig. 6 ($a_1$) and ($a_2$). For $\rho (t)=1$, the vcKdV Eq. (3) is just constant-coefficient and the shape of the breather soliton depends only on the undermined function $\rho (t)$. From the expression of f, it can be inferred that the breather soliton is straight and the solitary wave propagates with a velocity of $\frac{13}{4}$ along the x-axis, while the periodic wave travels with a velocity of 2.

If the parameters are chosen as $\rho (t)=\frac{1}{t}$, $a_1=3,\ a_2=-1,\ a_3=2,\ k_2=1,\ k_3=\frac{1}{2}$, $d_1=3$, $d_1=5$, $d_1=4$, the solution of the bilinear Eq. (16) is

$$\begin{aligned}{} & {} f=3\cosh (-\frac{1}{2}x+2y+\frac{13}{16}t^2-3)-\cos (-x-y\nonumber \\{} & {} \quad +2t^2-5)-2\sinh (-\frac{1}{2}x+2y+\frac{13}{16}t^2-4).\nonumber \\ \end{aligned}$$

(47)

The breather soliton solutions were obtained from (47) and (24), whose figures are shown in Fig. 6 ($b_1$) and ($b_2$). From Eq. (47) and Fig. 6 ($b_1$) and ($b_2$), the shapes of the breather solitons are quadratic parabolic. The moving velocity of the solitary wave is $\frac{13}{8}$ along the direction of the x-axis, and the propagating velocity of the periodic wave is 2.

If the parameters are chosen as $\rho (t)=\frac{1}{t^2}$, $a_1=3,\ a_2=-1,\ a_3=2,\ k_2=1,\ k_3=\frac{1}{2}$, $d_1=2$, $d_1=3$, $d_1=4$. The solution to the bilinear Eq. (16) can be obtained as

$$\begin{aligned}{} & {} f=3\cosh \left( -\frac{1}{2}x+2y+\frac{13}{24}t^3-2\right) \nonumber \\{} & {} \quad -\cos \left( -x-y+\frac{2}{3}t^3-3\right) \nonumber \\{} & {} \quad -2\sinh \left( -\frac{1}{2}x+2y+\frac{13}{24}t^3-4\right) .\nonumber \\ \end{aligned}$$

(48)

The breather soliton solution obtained from (48) and (24), whose figures are presented in Fig. 6 ($c_1$) and ($c_2$) respectively. By going over Eq. (48) and Fig. 6 ($c_1$) and ($c_2$), we can determine that the shapes of the breather solitons are cubic parabolic, and the solitary wave moves in the direction of the x-axis with a velocity of $\frac{13}{12}$ and the periodic wave propagates with a velocity of $\frac{2}{3}$.

Fig. 6

As $y=0$, breather soliton solutions of Eq. (3) for different $\rho (t)$: (a) $\rho (t)=1$; (b) $\rho (t)=1/t$; (c) $\rho (t)=1/t^2$

2) If we select $a_1=a_1$, $a_2=a_2$, $a_3=a_3$, $a_4=a_4$,

$$\begin{aligned} \begin{aligned}&c_1(t)=-\int {\frac{k_3(k_3^2+3)}{\rho (t)}},\ \ \ c_2(t)=\int {\frac{k_2(k_2^2+3)}{\rho (t)}},\\&\quad c_3(t)=-\int {\frac{k_3(k_3^2+3)}{\rho (t)}},\ \ \ c_4(t)=\int {\frac{k_2(k_2^2+3)}{\rho (t)}},\\&\quad k_1=k_3,\ \ \ k_4=k_2,\ \ \ b_1=-\frac{1}{k_3},\ \ \\&\quad b_2=\frac{1}{k_2},\ \ \ b_3=-\frac{1}{k_3},\ \ \ b_4=\frac{1}{k_2}, \end{aligned}\nonumber \\ \end{aligned}$$

(49)

the resulting lump soliton solutions closely resemble those shown in Fig. 6. However, we will refrain from providing further elaboration on this topic.

3) If $a_2=0$ and $a_4=0$, the trigonometric functions disappear in the f expression (43). As a result, the breather soliton no longer exhibits any periodicity and instead degenerates into a solitary wave. Therefore, the parameters are chosen as follows

$$\begin{aligned}{} & {} c_1(t)=-\int {\frac{k_1(k_1^2+3)}{\rho (t)}},\ \ c_3(t)=-\int {\frac{k_3(k_3^2+3)}{\rho (t)}},\nonumber \\{} & {} \quad \ b_1=-\frac{1}{k_1},\ \ b_3=-\frac{1}{k_3}, \end{aligned}$$

(50)

where $k_1\ne 0$, $k_3\ne 0$, $a_1\ne 0$ and $a_3\ne 0$. When we take different $\rho (t)$ and appropriate $a_1$, $a_3$, $k_1$, $k_3$, $d_1$, $d_3$, we get different solutions.

Assuming $\rho (t)=1$, $a_1=3, a_3=1, k_1=1, k_3=1$, $d_1=-4$, $d_3=5$, we obtain the solution of the bilinear Eq. (16) is

$$\begin{aligned} f= & {} 3\cosh (-x+y+4t+4)\nonumber \\{} & {} \quad -\sinh (-x+y+4t-5). \end{aligned}$$

(51)

Fig. 7 ($a_1$) and ($a_2$) illustrate the line soliton solutions u and v, which are derived from Eq. (51) and Eq. (24). From Eq. (51), the velocity of the line soliton along the x-axis is 4.

Fig. 7

As $y=0$, line soliton solutions of Eq. (3) for different $\rho (t)$ and $\beta (t)$: (a) $\rho (t)=1$; (b) $\rho (t)=1/t$; (c) $\rho (t)=1/t^2$

Setting $\rho (t)=\frac{1}{t}$, $a_1=3, a_3=1, k_1=1, k_3=1$, $d_1=-4$, $d_3=5$, we get the solution to the bilinear Eq. (16) is

$$\begin{aligned} f= & {} 3\cosh (-x+y+2t^2+4)\nonumber \\{} & {} \quad -\sinh (-x+y+2t^2-5). \end{aligned}$$

(52)

Fig. 7 ($b_1$) and ($b_2$) exhibit the line soliton solutions u and v respectively, which are derived from Eqs. (52) and (24). Based on Eq. (52) and Fig. 7 ($b_1$) and ($b_2$), it can be concluded that the shapes of the line soliton are parabolic and the velocity of the line soliton along the x-axis is 2.

Taking $\rho (t)=\frac{1}{t^2}$, $a_1=3, a_3=1, k_1=1, k_3=1$, $d_1=-4$, $d_3=5$, the solution of the bilinear Eq. (16) is

$$\begin{aligned} f= & {} 3\cosh (-x+y+\frac{4}{3}t^3+4)\nonumber \\{} & {} \quad -\sinh (-x+y+\frac{4}{3}t^3-5). \end{aligned}$$

(53)

Fig. 7 ($c_1$) and ($c_2$) show the line soliton solutions u and v that can be obtained from Eqs. (53) and (24). By analyzing Eq. (53) and examining Fig. 7 ($c_1$) and ($c_2$), it can be concluded that the line solitons are cubic parabolic and the velocity of the line soliton along the x-axis is $\frac{4}{3}$.

When $a_4=0$ in Eq. (43), Fig. 6 presents the breather solitons of the vcKdV Eq. (3), where ($a_1$), ($b_1$) and ($c_1$) represent anti-bright solitons u, while ($a_2$), ($b_2$) and ($c_2$) represent bright solitons v. When $a_2=0$ and $a_4=0$ in Eq. (43), Fig. 7 depicts the line solitons of the vcKdV Eq. (3), which can be viewed as the degenerations of breather solitons. Similar to analysis in Fig. 6, ($a_1$), ($b_1$) and ($c_1$) in Fig. 7 represent the anti-bright solitons u, while ($a_2$), ($b_2$) and ($c_2$) in Fig. 7 correspond to the bright solitons v.

3.3 Hybrid solutions of lump and line solitons

To derive the hybrid solutions of lump soliton and line-soliton waves named lump-line soliton solutions for the vcKdV Eq. (3), we suppose that the solution f of the bilinear Eq. (16) is a combination of quadratic and exponential functions [37, 38, 40]

$$\begin{aligned} f=\zeta _1^2+\zeta _2^2+a\exp ({\zeta _3})+\eta , \end{aligned}$$

(54)

with

$$\begin{aligned} \zeta _i=k_ix+b_iy+c_i(t)+d_i, (i=1, 2, 3), \end{aligned}$$

(55)

where $k_i, b_i$ and $d_i$ are undetermined real parameters, and $c_i(t)$ are functions of t. By substituting (54) into Eq. (16) and setting the coefficients of x, y and $\exp {\zeta _3}$ to 0, we can obtain several sets of parameters. Among these sets, we will select one set of parameters

$$\begin{aligned} \begin{aligned}&c_1=\int {\frac{3(-b_3^2k_1k_3^2+b_1k_3^2-b_3^2k_1-2b_3k_1k_3)}{\rho (t)b_3^2}}dt,\\&c_2=\int {\frac{3(-b_3^2k_2k_3^2+b_2k_3^2-b_3^2k_2-2b_3k_2k_3)}{\rho (t)b_3^2}}dt,\\&c_3=-\int {\frac{k_3(b_3k_3^2+3b_3+3k_3)}{\rho (t)b_3}}dt, \end{aligned}\nonumber \\ \end{aligned}$$

(56)

where $k_i$, $d_i$ $(i=1, 2, 3)$, $b_1$, $b_2$, and $\eta$ are arbitrary, but $a\ne 0$, $b_3\ne 0$. It needs to be noted that if $a=0$, Eq. (54) will take the form of a lump soliton. To avoid this case, we set $a\ne 0$ here.

When we consider $\rho (t)=1$, $a=1$, $k_1=4$, $b_1=-3$, $d_1=2$, $k_2=2$, $b_2=5$, $d_2=2$, $k_3=-1$, $b_3=1$, $d_3=3$ and $\eta =2$, these parameters correspond to lump-line solitons for the constant coefficient vcKdV Eq. (3). The solution of the bilinear Eq. (16) can be expressed as

$$\begin{aligned}{} & {} f=(4x-3y+9t+2)^2+(2x+5y+15t+2)^2\nonumber \\{} & {} \quad +e^{-x+y+t+3}+2. \end{aligned}$$

(57)

The expressions of u and v can easily be obtained from Eqs. (57) and (24). Figures 8 ($a_1$) and ($a_2$) show the hybrid solutions of one lump and one line.

Fig. 8

As $y=0$, lump-line solutions of Eq. (3) for different $\rho (t)$: (a) $\rho (t)=1$; (b) $\rho (t)=1/t$; (c) $\rho (t)=1/t^2$

Assuming $\rho (t)=\frac{1}{t}$, $a=1$, $k_1=4$, $b_1=-3$, $d_1=-7$, $k_2=\frac{}{3}{2}$, $b_2=5$, $d_2=2$, $k_3=-1$, $b_3=2$, $d_3=3$, $\eta =2$, the solution to the bilinear Eq. (16) can be expressed as follows

$$\begin{aligned}{} & {} f=(4x-3y-\frac{57}{8}t^2-7)^2+(\frac{3}{2}x+5y\nonumber \\{} & {} \quad -\frac{3}{8}t^2+2)^2+e^{-x+2y+\frac{5}{4}t^2+3}+2. \end{aligned}$$

(58)

The hybrid solutions u and v obtained from (58) and (24) are shown graphically in Fig. 8 ($b_1$) and ($b_2$).

When we take $\rho (t)=\frac{1}{t^2}$, $a=1$, $k_1=4$, $b_1=-3$, $d_1=-1$, $k_2=-2$, $b_2=5$, $d_2=7$, $k_3=-1$, $b_3=1$, $d_3=3$, $\eta =2$, the solution of the bilinear Eq. (16) is

$$\begin{aligned}{} & {} f{=}(4x-3y-3t^3-1)^2{+}({-}2x{+}5y{+}5t^3+7)^2\nonumber \\{} & {} \quad +e^{-x+y+\frac{1}{3}t^3+3}+2. \end{aligned}$$

(59)

From (59) and (24), the expressions of the lump-line soliton solutions u and v of the vcKdV Eq. (3) can be obtained, whose graphs are depicted in Fig. 8 ($c_1$) and ($c_2$) respectively.

Figure 8 shows the lump-line solutions of the vcKdV Eq. (3), with the different time-dependent function $\rho (t)$. ($a_1$) and ($a_2$) show the lump-line solutions of constant coefficient equation. Similarly, the shapes of the lump-line solutions are determined by $\rho (t)$. In particular, ($b_1$) and ($b_2$) correspond to $\rho (t)=\frac{1}{t^2}$, resulting in parabolic shapes. On the other hand, ($c_1$) and ($c_2$) correspond to $\rho (t)=\frac{1}{t^3}$, resulting in cubic parabolic shapes.

4 Infinite conservation laws of the vcKdV equation

It is well known that the KdV Eq. (1) has infinite conservation laws. In this section, we will try to derive the infinite conservation laws of the vcKdV Eq. (3) starting with Lax pair which is a convenient and popular way.

Combining Eq. (29) with the binary Bell polynomials (7), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \kappa _{xy}+\iota _x\iota _y+\lambda {\iota _x}=0,\\ \rho (t)\iota _t+(\iota _{3x}+3\iota _x\kappa _{2x}+\iota _x^3)=0,\\ 3\gamma \iota _x+3\delta \iota _y=0. \end{array}\right. } \end{aligned}$$

(60)

Introducing a new variable $\varpi =\iota _x$, we have $\kappa _x=m+\iota _x$, which is substituted with the transformations (17) into Eq. (60), we have

$$\begin{aligned}{} & {} u-\gamma +\varpi _y+\varpi (\partial _x^{-1}\varpi _y)+\lambda {\varpi }=0, \end{aligned}$$

(61)

$$\begin{aligned}{} & {} \quad \rho (t)\partial _x^{-1}\varpi _t+[\varpi _{xx}+3\varpi (v-\delta +\varpi _x)+\varpi ^3]\nonumber \\{} & {} \quad =0, \end{aligned}$$

(62)

and

$$\begin{aligned} 3\gamma \varpi +3\delta \partial _x^{-1}\varpi _y=0. \end{aligned}$$

(63)

Differentiating Eqs. (62) and (63) with respect to x, we get

$$\begin{aligned} \rho (t)\varpi _t+\partial _x[\varpi _{xx}+3\varpi (v-\delta +\varpi _x)+\varpi ^3]=0,\nonumber \\ \end{aligned}$$

(64)

and

$$\begin{aligned} 3\gamma \varpi _x+3\delta \varpi _y=0, \end{aligned}$$

(65)

Substituting the series expansion

$$\begin{aligned} \varpi =\sum _{n=1}^\infty I_n(u,v,u_x,v_x,u_y,v_y,\ldots )\lambda ^{-n} \end{aligned}$$

(66)

into Eq. (61) leads to

$$\begin{aligned}{} & {} u-\gamma +\sum _{n=1}^\infty I_{n,y}\lambda ^{-n}+\left( \sum _{n=1}^\infty I_{n}\lambda ^{-n}\right) \nonumber \\{} & {} \quad \left( \partial _x^{-1}\sum _{n=1}^\infty I_{n,y}\lambda ^{-n}\right) +\lambda \sum _{n=1}^\infty I_n\lambda ^{-n}=0, \end{aligned}$$

(67)

in which the coefficients of $\lambda$ are collected as

$$\begin{aligned} \begin{aligned}&\lambda ^0 \ \ \ \ \,I_1=-(u-\gamma )=-m_y,\\&\quad \lambda ^{-1} \ \ \,I_2=-I_{1,y}=u_y=m_{yy},\\&\quad \lambda ^{-2} \ \ \,I_3=-I_{2,y}-I_1(\partial _x^{-1}I_{1,y})\\&\quad =-(u_{yy}+(u-\gamma )\partial _x^{-1}u_y)\\&\quad =-(m_{yyy}+m_y\partial _x^{-1}m_{yy}),\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\&\quad \lambda ^{-n+1}:I_n=-I_{n-1,y}\\&\quad -\sum _{i=1}^\infty I_{i}(\partial _x^{-1}I_{n-i,y}), \ \ (n=2, 3, 4, \ldots ). \end{aligned} \end{aligned}$$

(68)

Respective substitutions of the expansion (66) into Eqs. (64) and (65) make

$$\begin{aligned}{} & {} \rho (t)\sum _{n=1}^\infty I_{n,t}\lambda ^{-n}+\partial _x[\sum _{n=1}^\infty I_{n,xx}\lambda ^{-n}\nonumber \\{} & {} \quad +3(\sum _{n=1}^\infty I_n\lambda ^{-n})(v-\delta +\sum _{n=1}^\infty I_{n,x}\lambda ^{-n})\nonumber \\{} & {} \quad +(\sum _{n=1}^\infty I_n\lambda ^{-n})^3]=0, \end{aligned}$$

(69)

and

$$\begin{aligned} 3\gamma \sum _{n=1}^\infty I_{n,x}\lambda ^{-n}+3\delta \sum _{n=1}^\infty I_{n,y}\lambda ^{-n}=0. \end{aligned}$$

(70)

Collecting the coefficients of $\lambda$ in Eq. (69), we obtain the infinitely many conservation laws

$$\begin{aligned}{} & {} \rho (t)M_{n,t}+G_{n,x}+\rho (t)N_{n,y}=0, \ \ \nonumber \\{} & {} \quad (n=1, 2, 3, \ldots ), \end{aligned}$$

(71)

where $M_n$, $N_n$ and $G_n$ are shown as

$$\begin{aligned}{} & {} M_n=-\sum _{i=1}^\infty I_{i}(\partial _x^{-1}I_{n-i+1,y}),\ n=3, 4, 5, \ldots .\nonumber \\ \end{aligned}$$

(72)

$$\begin{aligned}{} & {} \quad N_n=-\partial _y^{-1}I_{n,t},\ n=1, 2, 3, \ldots . \end{aligned}$$

(73)

and

$$\begin{aligned} \begin{aligned} G_1&=(I_{1,xx}+3(v-\delta )I_1)=-(u_{xx}+3(v-\delta )(u-\gamma ))\\&=-(m_{xxy}+3m_xm_{y}),\\ G_2&=(I_{2,xx}+3(v-\delta )I_2+3I_1I_{1,x})\\&=u_{xxy}+3(u-\gamma )u_x+3(v-\delta )u_{y},\\&=m_{xxyy}+3m_ym_{xy}+3m_xm_{yy},\\ G_3&=(I_{3,xx}+3(I_1I_{2,x}+I_2I_{1,x}+(v-\delta )I_3)+I_1^3),\\&\ \ \ \ \ \ \vdots \\ G_n&=\left( I_{n,xx}+3\left( \sum _{i+j=n}I_iI_{j,x}+(v-\delta )I_n\right) \right. \\&\left. +\sum _{i+j+k=n}I_iI_jI_k\right) ,\ (n=1,2, 3, 4, \ldots ). \end{aligned} \end{aligned}$$

(74)

The first conservation law is

$$\begin{aligned} \rho (t)m_{yt}+m_{xxxy}+3m_xm_{xy}+3m_{xx}m_y=0, \end{aligned}$$

(75)

which is a distortion of the vcKdV Eq. (3). The second conservation law reads

$$\begin{aligned}{} & {} \rho (t)m_{yyt}+m_{xxxyy}+3m_{xy}m_{xy}\nonumber \\{} & {} \quad +3m_xm_{xyy}+3m_{xx}m_{yy}+3m_{y}m_{xxy}=0, \end{aligned}$$

(76)

which is just the derivative form of the first conservation law with respect to y. Similar operations will result in an infinite number of conservation laws which can correspond to different NLPDEs.

5 Conclusions

In this paper, we are concerned with the (2+1)-dimensional variable coefficient KdV Eq. (3). On one hand, the integrability of the vcKdV Eq. (3) is verified by Lax pair and infinite conservation laws that are derived from the Bell polynomials and Bäcklund transformations. On the other hand, based on the bilinear form and ansatz method, the soliton solutions and hybrid solutions of the the vcKdV Eq. (3) are constructed and are presented graphically. We also take into account the different coefficient functions and undetermined functions, and do some detailed analysis on the soliton solutions. What we have done and obtained here is conducive to further research on the NLPDEs with variable coefficients and may illustrate more phenomena in the fields of hydrodynamics, shallow water waves, plasma physics and quantum theory.