Keywords

1 Introduction

The theory of modern integrable systems originated from the work on the celebrated Korteweg-de Vries (KdV) equation. It is a prototype water wave model involving a broad variety of mathematical methods. This theory allows one to study a wide range of phenomena and problems arising from physics, biology, and pure and applied mathematics. The special significance of integrable systems is that they combine tractability with nonlinearity. Hence, these systems enable one to explore nonlinear phenomena while working with explicit solutions. One of the interesting explicit solutions in nonlinear dynamics is that of solitons. Kruskal and Zabusky first discovered solitons in the mid-1960s when they worked on the KdV equation. A soliton is essentially a localized object that may be found in diverse areas of physics, such as gravitation and field theory, plasma and solid state physics, and hydrodynamics. The importance of solitons stems from the exhibition of particle-type interactions and the characterization of the long time asymptotic behavior of the solution.

There are some other types of explicit solutions available in the literature. One of them is so-called rational solutions, which is important to be found for integrable equations. It provides us a criterion for integrability as the existence of an infinite sequence of rational solutions appears to be equivalent to the Painlevé property (Newell 1987), and the rational solutions are of, at least, potential value in physical applications. In this regard, of particularly interesting are an important class of what we called nonsingular rational solutions. To the best of our knowledge, the study of nonsingular rational solutions to integrable equations can be traced back to Ames (1967) where N.J. Zabusky found simplest nonsingular rational solution \(u=-\frac{4q}{1+4q^2x^2}\) to the Gardner equation

$$u_t+12quu_x+6u^2u_x+u_{xxx}=0.$$

In the literature, there are three types of nonsingular rational solutions: (1) Algebraic solitons; (2) Lump solutions; (3) Rogue wave solutions. There are some examples which exhibit nonsingular rational solutions. In the case of algebraic solitons, a typical example is the Benjamin-Ono (BO) equation

$$\begin{aligned} u_t+4uu_x+Hu_{xx}=0, \quad Hu(x,t)\equiv \frac{1}{\pi }\text {PV}\int ^{\infty }_{-\infty }\frac{u(y,t)}{y-x}dy. \end{aligned}$$
(1)

In Ono (1975), Ono obtained 1-soliton solution \(u=\frac{a}{a^2(x-at-x_0)^2+1}\). Some further results about the algebraic solitons of the BO equation could be found in Matsuno (1982a, (1982b), Case (1979). The second example of algebraic solitons is the mKdV equation \(v_t+6v^2v_x+v_{xxx}=0\), whose simplest algebraic solution was also given by Ono (1976) \( v=v_0-\frac{4v_0}{4v_0^2(x-6v_0^2t)^2+1}\). Furthermore, N-algebraic solitons were found in Ablowitz and Satsuma (1978). As for lump solutions, the result can be traced to Manakov et al. (1977) where Manakov et al. gave lump solutions to the KPI equation. In particular, in Ablowitz and Satsuma (1978); Satsuma and Ablowitz (1979), Ablowitz and Satsuma developed a new method to seek lump solutions to the KPI equation and DSI equation by taking the “long-wave” limit of the soliton solutions and there have been many results about this topic; please see Feng et al. (1999), Grammaticos et al. (2007), Ablowitz et al. (2000), Villarroel and Ablowitz (1999), Ma (2015), Villarroel and Ablowitz (1994), Gilson and Nimmo (1990), Hu and Willox (1996). The third line of research about nonsingular rational solutions is rogue wave solutions, which is of physical significance. As is known, the NLS equation \(iu_t+u_{xx}+2|u|^2u=0\) admits the following rogue wave solution \( u=\left( 1-\frac{4(1+4it)}{1+4x^2+16t^2}\right) e^{2it}. \) Obviously, by taking \(u\longrightarrow ue^{-2it}\), we may get a nonsingular rational solution of the equation

$$ iu_t+u_{xx}+2(|u|^2-1)u=0.$$

For more examples, please see, e.g., Kharif et al. (2009), Solli et al. (2007), Peregrine (1983), Dubard et al. (2010), Dubard and Matveev (2011), Gaillard (2011), Guo et al. (2012), Ohta and Yang (2012), Li et al. (2013), Ohta and Yang (2012, (2013) and references therein.

The purpose of this paper is to develop a new procedure to generate lump solutions to several integrable models. Different from those by Ablowitz and Satsuma by taking the “long-wave” limit of the soliton solutions obtained and those by Ablowitz and Villarroel based on inverse scattering transform, the technique we develop here is via Bäcklund transformations and nonlinear superposition formulae in Hirota’s bilinear formalism (Hirota and Satsuma 1978). We will apply our procedure to the some known examples such as KPI equation, two-dimensional Toda equation, BKP equation to show how it works and further to the DJKM equation, Novikov-Veselov equation and negative flow of BKP equation to show its effectiveness.

2 The Lump Solutions of KP Equation

The KP equation takes the form

$$\begin{aligned} (u_t+6uu_x+u_{xxx})_x+\alpha u_{yy}=0. \end{aligned}$$
(2)

Traditionally, the Eq. (2) with \(\alpha =-1\) is called KPI, and the one for \(\alpha =1\) is KPII. The KPI equation does not have stable soliton solutions but has localized solutions that decay algebraically as \(x^2+y^2\rightarrow \infty \) and are called lumps. The lump solutions of KPI have been first obtained by Manakov et al. (1977) and also by Ablowitz and Satsuma (1978). Subsequently, Ablowitz and Satsuma derived the determinant form of the N-lump solution for the KPI equation by taking limits of the corresponding soliton solutions in Satsuma and Ablowitz (1979). In the following, we will use the bilinear Bäcklund transformation and the nonlinear superposition formula to rederive the N-lump solutions of KPI equation.

Through the dependent variable transformation \(u=2(\ln f)_{xx}\), the Eq. (2) can be written in bilinear form

$$\begin{aligned} (D_xD_t+D^{4}_x+\alpha D^2_{y})f\cdot f=0, \end{aligned}$$
(3)

where the bilinear operator \(D^{m}_{x}D^{k}_{t}\) is defined by Hirota (2004)

$$\begin{aligned} D^{m}_{x}D^{k}_{t} a \cdot b\equiv \left. \left( {\partial \over \partial x}- {\partial \over \partial x'}\right) ^m\left( {\partial \over \partial t}-{\partial \over \partial t'}\right) ^k a(x,t)b(x',t')\right| _{x'=x,t'=t}.\nonumber \end{aligned}$$

A bilinear Bäcklund transformation for Eq. (3) is given by Nakamura (1981), Hu (1997)

$$\begin{aligned}&(aD_y+D^{2}_x+\lambda D_{x})f\cdot f'=0,\end{aligned}$$
(4)
$$\begin{aligned}&(D_t+D^{3}_x-3a\lambda D_{y}-3aD_xD_y)f\cdot f'=0, \end{aligned}$$
(5)

where \(a^2=\frac{1}{3}\alpha \) and \(\lambda \) is an arbitrary constant. We represent (4)–(5) symbolically by \(f\buildrel {\lambda }\over \longrightarrow f'\). The associated nonlinear superposition formula for the Eq. (3) is stated in the following proposition (Nakamura 1981; Hu 1997).

Proposition 1

Let \(f_0\) be a nonzero solution of (3) and suppose that \(f_1\) and \(f_2\) are solutions of (3) such that \(f_0 \buildrel {\lambda _i}\over \longrightarrow f_i \ (i=1,2)\). Then \(f_{12}\) defined by

$$\begin{aligned} f_0\,f_{12}=c[D_x+\frac{1}{2}(\lambda _2-\lambda _1)]f_1 \cdot f_2,\quad c\,\, \text {is a nonzero real constant} \end{aligned}$$
(6)

is a new solution to (3) which is related to \(f_1\) and \(f_2\) under bilinear BT (4)–(5) with parameters \(\lambda _2\) and \(\lambda _1\) respectively, i.e.

 

figure a

 

In Hu (1997), it has been shown if we choose \(\theta _i=x+p_iy-\alpha p_i^2t\), then the Bäcklund transformation tells us \(1 \buildrel {\lambda _i=-ap_i}\over \longrightarrow f_i=\theta _i+\beta _i\) (where \(\beta _i\) is a constant). By using proposition 1, we can obtain the following solution to the KP equation

$$\begin{aligned}&f_{12}=\frac{2}{a(p_1-p_2)}[f_{1x}f_2-f_1f_{2x}+\frac{1}{2}(\lambda _2-\lambda _1)f_1f_2]=\nonumber \\&\theta _1\theta _2+(\beta _1+\frac{2}{a(p_1-p_2)})\theta _2+(\beta _2-\frac{2}{a(p_1-p_2)})\theta _1+\beta _1\beta _2+\frac{2(\beta _2-\beta _1)}{a(p_1-p_2)},\nonumber \\ \end{aligned}$$
(7)

by taking \(c=\frac{2}{a(p_1-p_2)}\) in (6). If \(\alpha =-1, p_2=p_1^{*}, \beta _1=-\frac{2}{a(p_1-p_2)}, \beta _2=\frac{2}{a(p_1-p_2)}\) in (7), then we obtain the 1-lump solution

$$\begin{aligned} f_{12}=\theta _1\theta _1^{*}-\frac{12}{(p_1-p_1^{*})^2}>0.\nonumber \end{aligned}$$

Furthermore, we can obtain an N-lump solution of the KP equation by using the nonlinear superposition formula repeatedly. For this purpose, we have the following proposition.

Proposition 2

$$\begin{aligned} F_N=c_N\left| \begin{array}{cccc} f_1 &{} f_2 &{} \cdots &{} f_{N}\\ (-\partial _x+\frac{\lambda _1}{2})f_1 &{} (-\partial _x+\frac{\lambda _2}{2})f_2 &{} \cdots &{}(-\partial _x+\frac{\lambda _N}{2})f_{N}\\ \vdots &{} \vdots &{} &{} \vdots \\ (-\partial _x+\frac{\lambda _1}{2})^{N-1}f_1 &{} (-\partial _x+\frac{\lambda _2}{2})^{N-1}f_2 &{} \cdots &{}(-\partial _x+\frac{\lambda _N}{2})^{N-1}f_{N} \end{array}\right| \end{aligned}$$
(8)

is a determinant solution to the KP equation (3), where \(f_i (i=1,2,\ldots ,N)\) is obtained from the seed solution \(f_0\) by using Bäcklund transformation (4) and (5), i.e. \(f_0 \buildrel {\lambda _i}\over \longrightarrow f_i\).

In order to obtain the N-lump solution, we take \(f_i=\theta _i+\beta _i,\theta _i=x+p_iy-\alpha p_i^2t,\lambda _i=-ap_i,\) \(\beta _i=\sum \limits _{j\not =i}\frac{2}{\lambda _i-\lambda _j}\) for \(i=1,2,\ldots ,N\) and \(c_N=\prod \limits _{1\le i <j\le N}\frac{2}{\lambda _j-\lambda _i}\). In this case, from (8), we have

$$\begin{aligned} F_N=c_N\left| \begin{array}{ccc} \theta _1+\beta _1 &{} \cdots &{} \theta _N+\beta _N\\ -1+\frac{\lambda _1}{2}(\theta _1+\beta _1) &{} \cdots &{} -1+\frac{\lambda _N}{2}(\theta _N+\beta _N)\\ \vdots &{} &{} \vdots \\ (-N+1)(\frac{\lambda _1}{2})^{N-2}+(\frac{\lambda _1}{2})^{N-1}(\theta _1+\beta _1) &{} \cdots &{}(-N+1)(\frac{\lambda _N}{N})^{N-2}+(\frac{\lambda _N}{2})^{N-1}(\theta _N+\beta _N) \end{array}\right| . \end{aligned}$$

It can be verified that the above determinant can be written as the product of the determinants

$$\begin{aligned} \left| \begin{array}{cccc} 1 &{} \frac{\lambda _1}{2} &{} \cdots &{} (\frac{\lambda _1}{2})^{N-1}\\ 1 &{} \frac{\lambda _2}{2} &{} \cdots &{} (\frac{\lambda _2}{2})^{N-1}\\ \vdots &{} \vdots &{} &{} \vdots \\ 1 &{} \frac{\lambda _N}{2} &{} \cdots &{} (\frac{\lambda _N}{2})^{N-1} \end{array}\right| \times \left| \begin{array}{cccc} \theta _1 &{} \frac{2}{\lambda _1-\lambda _2} &{} \cdots &{} \frac{2}{\lambda _1-\lambda _N}\\ -\frac{2}{\lambda _1-\lambda _2} &{} \theta _2 &{} \cdots &{} \frac{2}{\lambda _2-\lambda _N}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ -\frac{2}{\lambda _1-\lambda _N}&{} -\frac{2}{\lambda _2-\lambda _N} &{} \cdots &{} \theta _N \end{array}\right| . \end{aligned}$$

By using the basic property of Vandermonde determinant, we know

$$\begin{aligned} F_N=\left| \begin{array}{cccc} \theta _1 &{} \frac{2}{\lambda _1-\lambda _2} &{} \cdots &{} \frac{2}{\lambda _1-\lambda _N}\\ -\frac{2}{\lambda _1-\lambda _2} &{} \theta _2 &{} \cdots &{} \frac{2}{\lambda _2-\lambda _N}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ -\frac{2}{\lambda _1-\lambda _N}&{} -\frac{2}{\lambda _2-\lambda _N} &{} \cdots &{} \theta _N \end{array}\right| . \end{aligned}$$
(9)

If we choose \(N=2M,\, p_{M+i}=(p_i)^{*} (i=1,2,\ldots ,M)\), then \(F_N\) gives the M-lump solutions of KPI equation which coincides with those obtained in Satsuma and Ablowitz (1979). The positivity of (9) could be found in Ohta and Yang (2013) for an affirmative answer.

3 The Lump Solutions of the DJKM Equation

The second equation of the KP hierarchy is the DJKM equation which is written as

$$\begin{aligned} w_{xxxxy}+2w_{xxx}w_y+4w_{xxy}w_x+6w_{xy}w_{xx}-w_{yyy}-2w_{xxt}=0. \end{aligned}$$
(10)

Through the dependent variable transformation \(w=2(\ln f)_{x}\), the Eq. (10) can be transformed into the multilinear form

$$\begin{aligned} D_x[(D^3_xD_y-D_xD_t)f\cdot f]\cdot f^2+\frac{1}{2}D_y[(D^4_x-3D^2_y)f\cdot f]\cdot f^2=0. \end{aligned}$$
(11)

A bilinear Bäcklund transformation for Eq. (11) is given by

$$\begin{aligned}&(D^2_x+iD_y+\lambda +\mu D_{x})f\cdot f'=0,\end{aligned}$$
(12a)
$$\begin{aligned}&(iD_t+\frac{3}{2}\lambda D_y-\frac{1}{2} D^2_{y}-\frac{i}{2}\mu ^2D_y-\frac{i}{2}\mu D_xD_y-\frac{i}{2} D^2_xD_y)f\cdot f'=0, \end{aligned}$$
(12b)

where \(\lambda ,\mu \) are arbitrary constants. If we take \(\lambda =0\) for simplicity, then Bäcklund transformation (12a) and (12b) can be symbolically written as \(f\buildrel {\mu }\over \longrightarrow f'\). The associated nonlinear superposition formula for the Eq. (11) is stated in the following proposition.

Proposition 3

Let \(f_0\) be a nonzero solution of (11) and suppose that \(f_1\) and \(f_2\) are solutions of (11) such that \(f_0 \buildrel {\mu _i}\over \longrightarrow f_i \ (i=1,2)\). Then \(f_{12}\) defined by

$$\begin{aligned} f_{0}\,f_{12}=c[D_x+\frac{1}{2}(\mu _2-\mu _1)]f_1 \cdot f_2, \end{aligned}$$
(13)

is a new solution to (11) which is related to \(f_1\) and \(f_2\) under bilinear BT with parameters \(\mu _2\) and \(\mu _1\) respectively. Here c is a nonzero real constant.

Similar with the KP case, we obtain the 1-lump solution to the DJKM equation by using the Bäcklund transformation and nonlinear superposition formula. By setting \(\theta _i=x+p_iy-\frac{1}{2}p_i^3t\), then from bilinear BT, one obtains \(1 \buildrel {\mu _i=-ip_i}\over \longrightarrow f_i=\theta _i+\beta _i\) (where \(\beta _i\) is a constant). Now from the nonlinear superposition formula (13), we obtain the following solution of the DJKM equation

$$\begin{aligned}&f_{12}=\frac{2}{\mu _2-\mu _1}[f_{1x}f_2-f_1f_{2x}+\frac{1}{2}(\mu _2-\mu _1)f_1f_2]=\nonumber \\&\theta _1\theta _2+(\beta _1+\frac{2}{\mu _2-\mu _1)})\theta _2+(\beta _2-\frac{2}{\mu _2-\mu _1})\theta _1+[\beta _1\beta _2+\frac{2(\beta _2-\beta _1)}{\mu _2-\mu _1}] \end{aligned}$$
(14)

by taking \(c=\frac{2}{\mu _2-\mu _1}\) in (13). If we choose \(p_2=p_1^{*},\,\beta _1=\frac{2}{\mu _1-\mu _2},\,\beta _2=\frac{2}{\mu _2-\mu _1}\) in (14), then we obtain \(\mu _2=-\mu _1^{*},\,\theta _2=\theta _1^{*}\) and the 1-lump solution

$$\begin{aligned} f_{12}=\theta _1\theta _1^{*}+\frac{4}{(\mu _1+\mu ^{*}_1)^2}=|\theta _1|^2+\frac{4}{(\mu _1+\mu ^{*}_1)^2}>0. \end{aligned}$$
(15)

The N-lump solution could be found by using the nonlinear superposition formula repeatedly.

Proposition 4

$$\begin{aligned} F_N=c_N\left| \begin{array}{cccc} f_1 &{} f_2 &{} \cdots &{} f_{N}\\ (-\partial _x+\frac{\mu _1}{2})f_1 &{} (-\partial _x+\frac{\mu _2}{2})f_2 &{} \cdots &{}(-\partial _x+\frac{\mu _N}{2})f_{N}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ (-\partial _x+\frac{\mu _1}{2})^{N-1}f_1 &{} (-\partial _x+\frac{\mu _2}{2})^{N-1}f_2 &{} \cdots &{}(-\partial _x+\frac{\mu _N}{2})^{N-1}f_{N} \end{array}\right| \end{aligned}$$

is a determinant solution to the DJKM equation (11), where \(f_i (i=1,2,\ldots ,N)\) are obtained from seed solution \(f_0\) by using BT (12a)–(12b) \(f_0 \buildrel {\mu _i}\over \longrightarrow f_i\).

In order to obtain the multi-lump solution, we take \(f_i=\theta _i+\beta _i,\,\theta _i=x+p_iy-\frac{1}{2} p_i^3t,\,\mu _i=-ip_i,\) \(\beta _i=\sum \limits _{j\not =i}\frac{2}{\mu _i-\mu _j}\) for \(i=1,2,\ldots ,N\). After the proper choices of parameters, the determinant \(F_N\) could be written as

$$\begin{aligned} F_N=c_N\left| \begin{array}{ccc} \theta _1+\beta _1 &{} \cdots &{} \theta _N+\beta _N\\ \vdots &{} &{} \vdots \\ (-N+1)(\frac{\mu _1}{2})^{N-2}+(\frac{\mu _1}{2})^{N-1}(\theta _1+\beta _1) &{} \cdots &{}(-N+1)(\frac{\mu _N}{N})^{N-2}+(\frac{\mu _N}{2})^{N-1}(\theta _N+\beta _N) \end{array}\right| . \end{aligned}$$

It can be verified that the above determinant is also a product of determinants

$$\begin{aligned} \left| \begin{array}{cccc} 1 &{} \frac{\mu _1}{2} &{} \cdots &{} (\frac{\mu _1}{2})^{N-1}\\ 1 &{} \frac{\mu _2}{2} &{} \cdots &{} (\frac{\mu _2}{2})^{N-1}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ 1 &{} \frac{\mu _N}{2} &{} \cdots &{} (\frac{\mu _N}{2})^{N-1} \end{array}\right| \times \left| \begin{array}{cccc} \theta _1 &{} \frac{2}{\mu _1-\mu _2} &{} \cdots &{} \frac{2}{\mu _1-\mu _N}\\ -\frac{2}{\mu _1-\mu _2} &{} \theta _2 &{} \cdots &{} \frac{2}{\mu _2-\mu _N}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ -\frac{2}{\mu _1-\mu _N}&{} -\frac{2}{\mu _2-\mu _N} &{} \cdots &{} \theta _N \end{array}\right| . \end{aligned}$$
(16)

The choice of \(c_N=\prod \limits _{1\le i <j\le N}\frac{2}{\mu _j-\mu _i}\) gives us

$$\begin{aligned} F_N=\left| \begin{array}{cccc} \theta _1 &{} \frac{2}{\mu _1-\mu _2} &{} \cdots &{} \frac{2}{\mu _1-\mu _N}\\ -\frac{2}{\mu _1-\mu _2} &{} \theta _2 &{} \cdots &{} \frac{2}{\mu _2-\mu _N}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ -\frac{2}{\mu _1-\mu _N}&{} -\frac{2}{\mu _2-\mu _N} &{} \cdots &{} \theta _N \end{array}\right| . \end{aligned}$$
(17)

For \(N=2M\) and \(p_{M+i}=(p_i)^{*}\,(i=1,2,\ldots ,M)\), we could find that \(\theta _{M+i}=(\theta _i)^{*},\,\mu _{M+i}=-(\mu _i)^{*}\) and the positivity of \(F_N\) is the same with KP case. Therefore, in this case, \(F_N\) is the M-lump solution of the DJKM equation.

4 The Lump Solutions of the Elliptic Toda Equation

We now consider the so-called elliptic Toda equation

$$\begin{aligned} (\frac{\partial ^2}{\partial {x^2}}+\frac{\partial ^2}{\partial {y^2}})(\log {u_n})=u_{n+1}-2u_n+u_{n-1}. \end{aligned}$$

This equation has been studied in Villarroel (1998); Villarroel and Ablowitz (1994), where the inverse scattering method was applied to obtain lump solutions. By the use of variable transformation \(u_n=\frac{f_{n+1}f_{n-1}}{f_n^2}\), we can obtain the following bilinear form

$$\begin{aligned} (D_x^2+D_y^2)f_n\cdot {f_n}=(2e^{D_n}-2)f_n\cdot {f_n} \end{aligned}$$
(18)

which admits a Bäcklund transformation as follows

$$\begin{aligned}&(D_x+iD_y+\lambda ^{-1}e^{-D_n}+\mu )f\cdot {g}=0, \end{aligned}$$
(19a)
$$\begin{aligned}&((D_x-iD_y)e^{-\frac{1}{2}D_n}-\lambda {e^{\frac{1}{2}D_n}}+\gamma {e^{-\frac{1}{2}D_n}})f\cdot {g}=0. \end{aligned}$$
(19b)

Furthermore, from the Bäcklund transformation, we may get the following superposition formula.

Proposition 5

Let \(f_0(n)\) be a nonzero solution of Eq. (18) and suppose that \(f_1(n)\) and \(f_2(n)\) are solutions of (18) such that \(f_0(n) \buildrel {\lambda _i}\over \longrightarrow f_i(n) \ (i=1,2)\), then there exists the following nonlinear superposition formula

$$\begin{aligned} e^{-\frac{1}{2}D_n}f_0\cdot {f_{12}}=c(\lambda _1e^{-\frac{1}{2}D_n}-\lambda _2e^{\frac{1}{2}D_n})f_1\cdot {f_2} \end{aligned}$$
(20)

where \(f_{12}\) is a new solution of (18) related to \(f_1\) and \(f_2\) with parameters \(\lambda _2\) and \(\lambda _1\) respectively. Here c is a nonzero constant.

In order to get the lump solution, we choose \(f_0=1\) and \(f_i (i=1,2)\) as linear functions with respect to x, y and n, i.e. \(1 \buildrel {\lambda _i}\over \longrightarrow f_i=\theta _i+\beta _i=n+p_ix+q_iy+\beta _i\). Then from the Bäcklund transformation (19a) and (19b), we may get \(\mu _i=-\lambda _i^{-1},\gamma _i=\lambda _i\), \(p_j=\frac{1}{2}(\lambda _j^{-1}+\lambda _j)\) and \(q_j=\frac{1}{2i}(\lambda _j^{-1}-\lambda _j)\). Therefore, we get the seed function of the lump solutions

$$\begin{aligned} \theta _j=n+\frac{1}{2}(\lambda _j^{-1}+\lambda _j)x+\frac{1}{2i}(\lambda _j^{-1}-\lambda _j)y,\quad j=1,2. \end{aligned}$$

Therefore the nonlinear superposition formula (20) becomes

$$\begin{aligned} f_{12}(n)=c(\lambda _1f_1(n-1)f_2(n)-\lambda _2f_1(n)f_2(n-1)). \end{aligned}$$
(21)

In this case, if we take \(c=\frac{1}{\lambda _1-\lambda _2}\) and \(f_i=\theta _i+\beta _i\), then (21) can be written as

$$\begin{aligned}&f_{12}(n)=\theta _1\theta _2+\frac{1}{\lambda _1-\lambda _2}(\lambda _1\beta _2-\lambda _2(\beta _2-1))\theta _1 \nonumber \\&\quad +\frac{1}{\lambda _1-\lambda _2}(\lambda _1(\beta _1-1)-\lambda _2\beta _1)\theta _2 +\beta _1\beta _2+\frac{1}{\lambda _1-\lambda _2}(\lambda _2\beta _1-\lambda _1\beta _2). \end{aligned}$$
(22)

Furthermore, if we take \(\beta _1=\frac{\lambda _1}{\lambda _1-\lambda _2},\beta _2=-\frac{\lambda _2}{\lambda _1-\lambda _2}\), then we have:

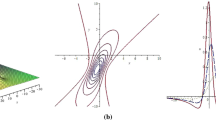
$$\begin{aligned} f_{12}(n)=\theta _1\theta _2+A, \end{aligned}$$
(23)

where \(A=\frac{\lambda _1\lambda _2}{(\lambda _1-\lambda _2)^2}\). Obviously, if we choose \(\lambda _1\not =\lambda _2\), then \(\theta _1=\theta _2^*\), \(A>0\), and therefore we get 1-lump solution of the elliptic Toda equation which is shown in Fig. 1.

Fig. 1
figure 1

1-lump solution of the elliptic Toda equation

Full size image

Proposition 6

The elliptic Toda equation admits the general nonlinear superposition formula

$$\begin{aligned} e^{-\frac{1}{2}D_n}F_{N-1}\cdot F_{N+1}=c(\lambda _Ne^{-\frac{1}{2}D_n}-\lambda _{N+1}e^{\frac{1}{2}D_n})F_N\cdot \hat{F}_N, \end{aligned}$$
(24)

where

$$\begin{aligned}&F_N(n)= \left| \begin{array}{ccc} f_1(n)&{}\cdots &{}f_N(n)\\ \vdots &{}&{}\vdots \\ (-\lambda _1)^{N-1}f_1(n-N+1)&{}\cdots &{}(-\lambda _N)^{N-1}f_N(n-N+1) \end{array} \right| \\&\qquad :=|1(n),\ldots ,N(n)|.\\&\hat{F}_N(n)=\left| 1(n),\ldots ,N-1(n), N+1(n) \right| . \end{aligned}$$

Here \(\{f_j(n,x,y),\, j=1,2,\ldots ,N+1\}\) are the seed functions \(f_j(n,x,y)=n+\frac{1}{2}(\lambda _j^{-1}+\lambda _j)x+\frac{1}{2i}(\lambda _j^{-1}-\lambda _j)y+\beta _j\).

Proof

It is noted that (24) can be alternatively written as:

$$\begin{aligned} F_{N-1}(n-1)F_{N+1}(n)=(\lambda _NF_N(n-1)\hat{F}_N(n)-\lambda _{N+1}F_N(n)\hat{F}_N(n-1)) \end{aligned}$$
(25)

and

$$\begin{aligned} F_{N-1}(n-1)=|1(n-1),\ldots ,N-1(n-1)|=\prod _{i=1}^{N-1}(-\lambda _i)D\left[ \begin{array}{c} 1\\ N \end{array} \right] \end{aligned}$$

where the determinant D means \(F_N(n)\) and \(D\left[ \begin{array}{c} j\\ k \end{array}\right] \) means the \((N-1)\)-th minor of D whose j-th row and k-th column are deleted. By taking the explicit forms of F and \(\hat{F}\) into the Eq. (25), we may see the nonlinear superposition formula is a Jacobi identity.

Inspired by the 1-lump solution, we now choose \(f_j(n)=\theta _j(n)+\beta _j=n+\frac{1}{2}(\lambda _j^{-1}+\lambda _j)x+\frac{1}{2i}(\lambda _j^{-1}-\lambda _j)y+\beta _j\), and therefore the solution \(F_N(n)\) can be written as

$$\begin{aligned} F_N(n)= \left| \begin{array}{ccc} \theta _1+\beta _1&{}\cdots &{}\theta _N+\beta _N\\ -\lambda _1(\theta _1+\beta _1-1)&{}\cdots &{}-\lambda _N(\theta _N+\beta _N-1)\\ \vdots &{}{}&{}\vdots \\ (-\lambda _1)^{N-1}(\theta _1+\beta _1-N+1)&{}\cdots &{}(-\lambda _N)^{N-1}(\theta _N+\beta _N-N+1) \end{array} \right| , \end{aligned}$$

from which we see that if and only if we take \(\beta _i=\lambda _i\sum \limits _{j\not =i}\frac{1}{\lambda _i-\lambda _j}\), we can get \(F_{2M}\) without the odd term. On the other hand, from the determinant identity, we may get

$$\begin{aligned} F_N(n)=\left| \begin{array}{cccc} 1&{}-\lambda _1&{}\cdots &{}(-\lambda _1)^{N-1}\\ 1&{}-\lambda _2&{}\cdots &{}(-\lambda _2)^{N-1}\\ \vdots &{}\vdots &{}{}&{}\vdots \\ 1&{}-\lambda _N&{}\cdots &{}(-\lambda _N)^{N-1} \end{array} \right| \times \left| \begin{array}{cccc} \theta _1&{}\frac{-\lambda _1}{\lambda _1-\lambda _2}&{}\cdots &{}\frac{-\lambda _1}{\lambda _1-\lambda _N}\\ \frac{-\lambda _2}{\lambda _2-\lambda _1}&{}\theta _2&{}\cdots &{}\frac{-\lambda _2}{\lambda _2-\lambda _N}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \frac{-\lambda _N}{\lambda _N-\lambda _1}&{}\frac{-\lambda _N}{\lambda _N-\lambda _2}&{}\cdots &{}\theta _N \end{array} \right| . \end{aligned}$$
(26)

In this case, we have the following determinant solution

$$\begin{aligned} F_N(n)=\left| \begin{array}{cccc} \theta _1&{}\frac{-\lambda _1}{\lambda _1-\lambda _2}&{}\cdots &{}\frac{-\lambda _1}{\lambda _1-\lambda _N}\\ \frac{-\lambda _2}{\lambda _2-\lambda _1}&{}\theta _2&{}\cdots &{}\frac{-\lambda _2}{\lambda _2-\lambda _N}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \frac{-\lambda _N}{\lambda _N-\lambda _1}&{}\frac{-\lambda _N}{\lambda _N-\lambda _2}&{}\cdots &{}\theta _N \end{array} \right| . \end{aligned}$$
(27)

In the following, we want to construct lump solutions from (27). Here we just consider the case of \(N=4\), and set the parameters as \(\lambda _3=\frac{1}{\lambda _1^*},\lambda _4=\frac{1}{\lambda _2^*}\). In this case, we have

$$\begin{aligned} F_4&=\theta _1\theta _1^*\theta _2\theta _2^*+\frac{\lambda _1\lambda _2}{(\lambda _1-\lambda _2)^2}\theta _1^*\theta _2^*+c.c +\frac{\lambda _1^*\lambda _2}{(\lambda _1^*\lambda _2-1)^2}\theta _1\theta _2^*+c.c\\ {}&+\frac{\lambda _1\lambda _1^*}{(\lambda _1\lambda _1^*-1)^2}\theta _2\theta _2^*+\frac{\lambda _2\lambda _2^*}{(\lambda _2\lambda _2^*-1)^2}\theta _1\theta _1^*+A, \end{aligned}$$

where c.c means the complex conjugate and A is greater than zero. It means \(F_4\) is 2-lump solution of the Toda equation and Fig. 2 shows 2-lump solution of the Toda equation.

Fig. 2
figure 2

The interaction of 2-lumps of the Toda equation

Full size image

In general, Villarroel has shown in Villarroel (1998) that the \(F_{2N}\) given by (27) is always greater than 0 if \(\lambda _{N+i}\lambda _i^*=1\) and \(\{\lambda _i,1\le i\le 2N\}\) are off the unit circle.

5 The Lump Solution of the BKP Equation

In Gilson and Nimmo (1990), the lump solution of the BKP equation has been considered by Claire Gilson and Jon Nimmo. In this part, we would like to show the Bäcklund transformation and nonlinear superposition formula can also provide us a Pfaffian form to the lump solution of BKP, which indicates this technique could also be used for the \(B_\infty \)-type equations and Pfaffian forms.

Consider the BKP equation

$$\begin{aligned} (u_t+15uu_{3x}+15u_x^3-15u_xu_y+u_{5x})_x+5u_{3x,y}-5u_{yy}=0. \end{aligned}$$

Through the bilinear transformation \(u=2(\log {f})_x\), we obtain the bilinear form for the BKP equation

$$\begin{aligned} (D_x^6-5D_x^3D_y-5D_y^2+9D_xD_t)f\cdot {f}=0, \end{aligned}$$
(28)

whose Bäcklund transformation is indicated as follows (Hirota 2004)

$$\begin{aligned}&(D_x^3-D_y-3kD_x^2+3k^2D_x)f\cdot {g}=0,\end{aligned}$$
(29a)
$$\begin{aligned}&(-D_x^5-5D_x^2D_y+5kD_x^4+5k^2D_x^3-10k^2D_y+10kD_xD_y+6D_t)f\cdot {g}=0. \end{aligned}$$
(29b)

Furthermore, we have the following nonlinear superposition formula.

Proposition 7

Let \(f_0\) be a nonzero solution of Eq. (28) and suppose that \(f_1\) and \(f_2\) are solutions such that \(f_0 \buildrel {\lambda _i}\over \longrightarrow f_i \ (i=1,2)\), then there exists the following nonlinear superposition formula

$$\begin{aligned}{}[D_x-(k_1+k_2)]f_0\cdot {f_{12}}=c[D_x+(k_1-k_2)]f_1\cdot {f_2} \end{aligned}$$
(30)

where \(f_{12}\) is a new solution related to \(f_1\) and \(f_2\) with parameters \(\lambda _2\) and \(\lambda _1\) respectively. Here c is a nonzero constant.

For the Bäcklund transformation (29a) and (29b), if we take \(f_0=1\) and \(f_i(i=1,2)\) as the linear functions, then \(f_i=\theta _i+\beta _i=x+3k_i^2y+5k_i^4t+\beta _i,\, i=1,2\). In this case, the nonlinear superposition formula becomes

$$\begin{aligned} -\frac{d}{dx}f_{12}-(k_1+k_2)f_{12}=f_2-f_1+(k_1-k_2)f_1\cdot {f_2}. \end{aligned}$$
(31)

By solving this ordinary differential equation, we may obtain the solution of the BKP equation

$$\begin{aligned}&f_{12}=\frac{k_2-k_1}{k_1+k_2}f_1f_2+\frac{2k_1}{(k_1+k_2)^2}f_1-\frac{2k_2}{(k_1+k_2)^2}f_2+2\frac{k_2-k_1}{(k_1+k_2)^3}\nonumber \\&\qquad =\frac{k_2-k_1}{k_1+k_2}\theta _1\theta _2+\frac{(k_2^2-k_1^2)\beta _2+2k_1}{(k_1+k_2)^2}\theta _1+\frac{(k_2^2-k_1^2)\beta _1-2k_2}{(k_1+k_2)^2}\theta _2+A, \end{aligned}$$

where \(A=\frac{k_2-k_1}{k_1+k_2}\beta _1\beta _2+\frac{\beta _1-\beta _2}{k_1+k_2}-\frac{k_2-k_1}{(k_1+k_2)^2}(\beta _1+\beta _2)+2\frac{k_2-k_1}{(k_1+k_2)^3}\). It can be verified that if we take \(\beta _1=\frac{-2k_2}{k_1^2-k_2^2},\beta _2=\frac{2k_1}{k_1^2-k_2^2}\), \(k_2=k_1^*\) and \(|Im k_1|>|Re k_1|\), then the 1-lump solution could be obtained.

Remark 1

Notice that the first order ordinary differential equation (31) may have a general solution, however, in the lump-solution case, we just consider the polynomial solution of f, hence this solution is unique in this sense.

In Fig. 3, the 1-lump solution of the BKP equation is drawn for a particular choice of the parameters.

Fig. 3
figure 3

The figure of 1-lump solution of the BKP equation

Full size image

Proposition 8

BKP equation has a general nonlinear superposition formula as follows

$$\begin{aligned}{}[D_x-(k_{2n+1}+k_{2n+2})]F_{2n}\cdot {F_{2n+2}}=[D_x+(k_{2n+1}-k_{2n+2})]\hat{F}_{2n+1}\cdot {{F}_{2n+1}}. \end{aligned}$$
(32)

In particular, the solution \(F_{2n}\), \(F_{2n+1}\) and \(\hat{F}_{2n+1}\) have the Pfaffian forms

$$\begin{aligned} F_{2n}=(1,\ldots ,2n),\,F_{2n+1}=(d_0,1,\ldots ,2n+1),\,\hat{F}_{2n+1}=(d_0,1,\ldots ,2n,2n+2), \end{aligned}$$
(33)

in which the Pfaff element satisfies the following relationship

$$\begin{aligned}&(d_0,i)=f_i=\theta _i+\beta _i=x+3k_i^2y+5k_i^4t+\beta _i,\nonumber \\&(d_1,i)=\frac{d}{dx}(d_0,i)+k_i(d_0,i)=1+k_if_i,\\&\frac{d}{dx}(i,j)+(k_i+k_j)(i,j)=(d_0,d_1,i,j),\,(d_0,d_1)=0.\nonumber \end{aligned}$$
(34)

In order to prove the proposition, we need following lemmas.

Lemma 1

Under the assumption of the Pfaff element (33), we have

$$\begin{aligned} \frac{d}{dx}(1,\ldots ,2n)+(\sum _{i=1}^{2n}k_i)(1,\ldots ,2n)=(d_0,d_1,1,\ldots ,2n). \end{aligned}$$
(35)

Proof

We will prove this conclusion by induction. For n=1, it is just the assumption we set in (33). By assumption, it is known that

$$\begin{aligned} \frac{d}{dx}(2,\ldots ,\hat{j},\ldots ,2n+2)+\sum _{i=2,i\not =j}^{2n+2}k_i(2,\ldots ,\hat{j},\ldots ,2n+2)=(d_0,d_1,2,\ldots ,\hat{j},\ldots ,2n+2) \end{aligned}$$

holds for Pfaffian of order n. Then for Pfaffian of order \(n+1\), we have

$$\begin{aligned}&(d_0,d_1,1,\ldots ,2n+2)\\&=\sum _{j=2}^{2n+2}(-1)^j[(d_0,d_1,1,j)(2,\ldots ,\hat{j},\ldots ,2n+2)+(1,j)(d_0,d_1,2,\ldots ,\hat{j},\ldots ,2n+2)]\\&=\sum _{j=2}^{2n+2}(-1)^j\{[\frac{d}{dx}(1,j)+(k_1+k_j)(1,j)](2,\ldots ,\hat{j},\ldots ,2n+2)\\&\qquad \quad +(1,j)[\frac{d}{dx}(2,\ldots ,\hat{j},\ldots ,2n+2)+\sum _{i\not =j}k_i(2,\ldots ,\hat{j},\ldots ,2n+2)]\}\\&=\frac{d}{dx}(1,\ldots ,2n+2)+\sum _{i=1}^{2n+2}k_i(1,\ldots ,2n+2), \end{aligned}$$

which completes the proof.

Lemma 2

Under the assumption of the Pfaffian element (33), we also have

 

$$\begin{aligned} (d_1,1,\ldots ,2n+1)&=\frac{d}{dx}(d_0,1,\ldots ,2n+1)+(\sum _{i=1}^{2n+1}k_i)(d_0,1,\ldots ,2n+1),\end{aligned}$$
(36a)
$$\begin{aligned} (d_1,1,\ldots ,2n,2n+2)&=\frac{d}{dx}(d_0,1,\ldots ,2n,2n+2)+(\sum _{i\not =2n+1}k_i)(d_0,1,\ldots ,2n,2n+2). \end{aligned}$$
(36b)

Proof

We just prove the first equation, and the second one can be verified in a similar way. By expansion of Pfaffian, one has

$$\begin{aligned}&(d_1,1,\ldots ,2n+1)\\&=\sum _{j=1}^{2n+1}(-1)^j(d_1,j)(1,\ldots ,\hat{j},2n+1)\nonumber \\&=\sum _{j=1}^{2n+1}(-1)^{j-1}[\frac{d}{dx}(d_0,j)+k_j(d_0,j)](1,\ldots ,\hat{j},\ldots ,2n+1)\nonumber \\&=\frac{d}{dx}(d_0,1,\ldots ,2n+1)+\sum _{j=1}^{2n+1}(-1)^{j-1}k_j(d_0,j)(1,\ldots ,\hat{j},\ldots ,2n+1)\\&-\sum _{j=1}^{2n+1}(-1)^{j-1}(d_0,j)[(d_0,d_1,1,\ldots ,\hat{j},\ldots ,2n+1)-(\sum _{i=1,i\not =j}^{2n+1}k_i)(1,\ldots ,\hat{j},\ldots ,2n+1)]\\&=\frac{d}{dx}(d_0,1,\ldots ,2n+1)+(\sum _{i=1}^{2n+1}k_i)(d_0,\ldots ,2n+1), \end{aligned}$$

and the equation is verified.

The Lemma 1 tells us the left side of the nonlinear superposition formula can be written as

$$\begin{aligned} (d_0,d_1,1,\ldots ,2n)(1,\ldots ,2n+2)-(1,\ldots ,2n)(d_0,d_1,1,\ldots ,2n+2), \end{aligned}$$
(37)

while the Lemma 2 shows the right side can be written as

$$\begin{aligned} -(d_1,1,\ldots ,2n+1)(d_0,1,\ldots ,2n,2n+2)+(d_0,1,\ldots ,2n+1)(d_1,1,\ldots ,2n,2n+2). \end{aligned}$$
(38)

Therefore, under these two lemmas, we find that the nonlinear superposition formula of BKP equation (30) can be written as

$$\begin{aligned}&(d_0,d_1,1,\ldots ,2n)(1,\ldots ,2n+2)-(1,\ldots ,2n)(d_0,d_1,1,\ldots ,2n+2)=\nonumber \\&\quad -(d_1,1,\ldots ,2n+1)(d_0,1,\ldots ,2n,2n+2)+(d_0,1,\ldots ,2n+1)(d_1,1,\ldots ,2n,2n+2),\nonumber \end{aligned}$$

which is the Pfaffian identity (Hirota 2004).

And then we would like to prove the \(F_{2n}\) given in (33) is always positive or always negative under some constrains. Following the method mentioned in Gilson and Nimmo (1990), we first consider the determinant of \(2n \times 2n\) skew-symmetric matrix \(A=(a_{i,j})_{1\le i,j \le 2n}\) which can be represented as the square of Pfaffian given in (33):

$$\begin{aligned} F^2_{2n}=(1,2,\ldots ,2n)^2=\det A. \end{aligned}$$
(39)

Applying Eqs. (33) and (39), we can derive:

$$\begin{aligned} a_{i,j}=\frac{k_i-k_j}{k_i+k_j}[(f_i+\frac{2k_j}{k_i^2-k_j^2})(f_j-\frac{2k_i}{k_i^2-k_j^2})+\frac{2(k_i^2+k_j^2)}{(k_i^2-k_j^2)^2}]. \end{aligned}$$
(40)

If we set \(k_i=k_{n+i}^*,\beta _i=\beta _{n+i}^*\) and \(|\mathrm {Im} k_i|>|\mathrm {Re} k_i|\), then the determinant of A can be written as the following form:

$$\begin{aligned} \det A=\det \left| \begin{array}{cc} \mathrm {C}&{}\mathrm {B}\\ \mathrm {-B^*}&{}\mathrm {C^*} \end{array} \right| , \end{aligned}$$
(41)

which is always positive. In Eq. (41), \( B=(b_{i,j})_{1\le i,j \le n}\), \( C=(c_{i,j})_{1\le i,j \le n}\) are two \(n\times n\) matrices, whose element \(b_{i,j}\), \(c_{i,j}\) are given by:

$$\begin{aligned}&b_{i,j}=\frac{k_i-k_j^\star }{k_i+k_j^\star }[(f_i+\frac{2k_j^\star }{k_i^2-k_j^{\star 2}})(f_j^\star -\frac{2k_i}{k_i^2-k_j^{\star 2}})+\frac{2(k_i^2+k_j^{\star 2})}{(k_i^2-k_j^{\star 2})^2}],\\&c_{i,j}=\frac{k_i-k_j}{k_i+k_j}[(f_i+\frac{2k_j}{k_i^2-k_j^2})(f_j-\frac{2k_i}{k_i^2-k_j^2})+\frac{2(k_i^2+k_j^2)}{(k_i^2-k_j^2)^2}]. \end{aligned}$$

Since \(F_{2n}^{2}>0\) by taking \(k_i=k_{n+i}^*,\beta _i=\beta _{n+i}^*\) and \(|\mathrm {Im} k_i|>|\mathrm {Re} k_i|\) in \(F_{2n}\) , and the lump solution is a continuous function, so the \(F_{2n}\) is always positive or always negative. Therefore, the solution \(F_{2n}\) with \(k_i=k_{n+i}^*,\beta _i=\beta _{n+i}^*\) and \(|\mathrm {Im} k_i|>|\mathrm {Re} k_i|\) is the nonsingular rational solution of the BKP equation.

6 The Lump Solutions of the Novikov-Veselov Equation

In this part, we want to discuss the lump solution of the Novikov-Veselov equation

$$\begin{aligned} 2u_t+u_{xxx}+u_{yyy}+3(u\partial _y^{-1}u_x)_x+3(u\partial _x^{-1}u_y)_y=0, \end{aligned}$$
(42)

which can be viewed as an extension the KdV equation in two spatial dimensions and one temporal dimension. Bäcklund Transformation and nonlinear superposition formula and 1,2-lump solutions have been studied in Hu and Willox (1996). Here we revisited some important facts.

Under the dependent variable transformation \( u=u_0+2(\log {f})_{xy} \) with \(u_0\) a constant, the Eq. (42) can be transformed into the multilinear form and enjoys the following Bäcklund transformation

$$\begin{aligned}&(D_xD_y-\mu {D_x}-\lambda {D_y}+\lambda \mu +u_0)f\cdot {f'}=0,\end{aligned}$$
(43a)
$$\begin{aligned}&(2D_t+D_x^3+D_y^3+3\lambda ^2D_x-3\lambda D_x^2+3\mu ^2D_y-3\mu D_y^2)f\cdot f'=0, \end{aligned}$$
(43b)

where \(\lambda \) and \(\mu \) are arbitrary constants. The nonlinear superposition formula can be stated as follows.

Proposition 9

Let \(f_0\) be a nonzero solution of (42) and suppose that \(f_1\) and \(f_2\) are solutions of (42) such that \(f_0 \buildrel {\mu _i}\over \longrightarrow f_i \ (i=1,2)\). Then \(f_{12}\) defined by

$$\begin{aligned}{}[D_x-(k_1+k_2)]f_0\cdot {f_{12}}=c[D_x+(k_1-k_2)]f_1\cdot {f_2}\quad \end{aligned}$$
(44)

is a new solution to (42) which is related to \(f_1\) and \(f_2\) under bilinear BT (43a) and (43b) with parameters \(k_2\) and \(k_1\) respectively. Here c is a nonzero real constant.

To obtain the lump solutions, we have to take \(f_0=1\) and \(f_i=\theta _i+\beta _i=k_i^2x+u_0y-\frac{3}{2(k_i^4+{u_0^3}/{k_i^2})}t+\beta _i\). For 1-lump solution, if we set \(k_2=k_1^*,\,\beta _1=\beta _2^*\) and \(\text {Im}{k_i}>\text {Re}{k_i},\,(i=1,2)\), then

$$\begin{aligned} f_{12}=(\theta _1+\frac{2k_1^2k_2}{k_1^2-k_2^2})\times c.c.+2\frac{k_1^2k_2^2(k_1^2+k_2^2)}{(k_1^2-k_2^2)^2}, \end{aligned}$$

where c.c. means the complex conjugate. Obviously, \(f_{12}\) is positive and it is a 1-lump solution. We depict the 1-lump solution of the Novikov-Veselov equation in Fig. 4.

Fig. 4
figure 4

1-lump solution of the Novikov-Veselov equation

Full size image

Noticing that the nonlinear superposition formula of the Novikov-Veselov equation (44) is the same as the BKP equation (30), the Novikov-Veselov equation (44) possesses the same structure of solution as the BKP equation except the seed function. Hence we have the following proposition.

Proposition 10

Novikov-Veselov equation owns a general nonlinear superposition formula

$$\begin{aligned}{}[D_x-(k_{2n+1}+k_{2n+2})]F_{2n}\cdot {F_{2n+2}}=[D_x+(k_{2n+1}-k_{2n+2})]\hat{F}_{2n+1}\cdot {{F}_{2n+1}}, \end{aligned}$$
(45)

where

$$\begin{aligned} F_{2n}=(1,\ldots ,2n),\,F_{2n+1}=(d_0,1,\ldots ,2n+1),\,\hat{F}_{2n+1}=(d_0,1,\ldots ,2n,2n+2), \end{aligned}$$
(46)

where the Pfaffian elements satisfy the following relationships

$$\begin{aligned}&(d_0,i)=f_i=\theta _i+\beta _i=k_i^2x+u_0y-\frac{3}{2(k_i^4+{u_0^3}/{k_i^2})}t+\beta _i,\nonumber \\&(d_1,i)=\frac{d}{dx}(d_0,i)+k_i(d_0,i),\nonumber \\&\frac{d}{dx}(i,j)+(k_i+k_j)(i,j)=(d_0,d_1,i,j),\,(d_0,d_1)=0. \end{aligned}$$
(47)

Since the proof of this proposition is similar to that of BKP equation, we omit it here. If we set \(k_i=k_{n+i}^*, \beta _i=\beta _{n+i}^*\) and \(|\mathrm {Im} k_i|>|\mathrm {Re} k_i|\), then we can show in a similar way in Sect. 5 that \(F_{2n}\) is always positive or always negative. Therefore, we get the N-lump solution of the Novikov-Veselov equation, which has the representation of (46) with \(k_i=k_{n+i}^*,\beta _i=\beta _{n+i}^*\) and \(|\mathrm {Im} k_i|>|\mathrm {Re} k_i|\).

7 The Lump Solutions for Negative Flow of BKP Equation

In Hirota (2004), Sect. 3.3, the author proposed another shallow wave equation, called the negative flow of BKP equation

$$\begin{aligned} u_{yt}-u_{xxxy}-3(u_xu_y)_x+3u_{xx}=0. \end{aligned}$$
(48)

By the dependent variable transformation \(u=2(\log {f})_x\), it can be transformed into a bilinear form

$$\begin{aligned}{}[(D_t-D_x^3)D_y+3D_x^2]f\cdot {f}=0, \end{aligned}$$

which possesses the following Bäcklund transformation

$$\begin{aligned}&(D_xD_y+\lambda ^{-1} D_x+\lambda D_y)f\cdot {f'}=0,\end{aligned}$$
(49a)
$$\begin{aligned}&(D_x^3+3\lambda D_x^2+3\lambda ^2D_x-D_t)f\cdot {f'}=0. \end{aligned}$$
(49b)

Furthermore, we have the following result.

Proposition 11

Let \(f_0\) be a nonzero solution of Eq. (48) and suppose that \(f_1\) and \(f_2\) are solutions of (48) such that \(f_0 \buildrel {\lambda _i}\over \longrightarrow f_i \ (i=1,2)\), then there exists a following nonlinear superposition formula

$$\begin{aligned} (D_x+(k_1-k_2))f_0\cdot {f_{12}}=c(D_x-(k_1-k_2))f_1\cdot {f_2}, \end{aligned}$$
(50)

where \(f_{12}\) is a new solution of (48) related to \(f_1\) and \(f_2\) under bilinear BT (49a) and (49b) with parameters \(k_2\) and \(k_1\) respectively. Here c is a nonzero constant.

A 1-lump solution of the negative flow for BKP equation is derived in the following. Starting with \(f_0=1,f_i=x-k_i^2y+3k_i^2t+\beta _i(i=1,2)\), we may obtain the following solution

$$\begin{aligned}&f_{12}=\frac{k_2-k_1}{k_1+k_2}f_1f_2+\frac{2k_1}{(k_1+k_2)^2}f_1-\frac{2k_2}{(k_1+k_2)^2}f_2+2\frac{k_2-k_1}{(k_1+k_2)^3}\nonumber \\&\qquad =\frac{k_2-k_1}{k_1+k_2}\theta _1\theta _2+\frac{(k_2^2-k_1^2)\beta _2+2k_1}{(k_1+k_2)^2}\theta _1+\frac{(k_2^2-k_1^2)\beta _1-2k_2}{(k_1+k_2)^2}\theta _2+A, \end{aligned}$$

where \(A=\frac{k_2-k_1}{k_1+k_2}\beta _1\beta _2+\frac{\beta _1-\beta _2}{k_1+k_2}-\frac{k_2-k_1}{(k_1+k_2)^2}(\beta _1+\beta _2)+2\frac{k_2-k_1}{(k_1+k_2)^3}\). If we take \(\beta _1=\frac{-2k_2}{k_1^2-k_2^2}, \,\beta _2=\frac{2k_1}{k_1^2-k_2^2}\), \(k_2=k_1^*\) and \(|\text {Im} k_1|>|\text {Re} k_1|\), we get the 1-lump solution.

In order to obtain N-lump solutions, we need to establish a general nonlinear superposition formula for the negative flow BKP equation.

Proposition 12

The negative flow BKP equation owns a general nonlinear superposition formula

$$\begin{aligned}{}[D_x-(k_{2n+1}+k_{2n+2})]F_{2n}\cdot {F_{2n+2}}=[D_x+(k_{2n+1}-k_{2n+2})]\hat{F}_{2n+1}\cdot {{F}_{2n+1}} \end{aligned}$$
(51)

and the solutions \(F_{2n}\), \(F_{2n+1}\) and \(\hat{F}_{2n+1}\) are expressed as Pfaffians

$$\begin{aligned} F_{2n}=(1,\ldots ,2n),\,F_{2n+1}=(d_0,1,\ldots ,2n+1),\,\hat{F}_{2n+1}=(d_0,1,\ldots ,2n,2n+2), \end{aligned}$$
(52)

where the Pfaff elements satisfy the following relations

$$\begin{aligned}&(d_0,i)=f_i=\theta _i+\beta _i=x-k_i^2y+3k_i^2t+\beta _i,\nonumber \\&(d_1,i)=\frac{d}{dx}(d_0,i)+k_i(d_0,i),\nonumber \\&\frac{d}{dx}(i,j)+(k_i+k_j)(i,j)=(d_0,d_1,i,j),\, (d_0,d_1)=0. \end{aligned}$$
(53)

The proof of Proposition 12 is similar to the case of BKP equation, so we omit it here. Furthermore, we can show in a similar way in Sect. 5 that \(F_{2n}\) in (52) with \(k_i=k_{n+i}^*, \beta _i=\beta _{n+i}^*\) and \(|\mathrm {Im} k_i|>|\mathrm {Re} k_i|\) gives the N-lump solution of the negative flow of BKP equation.

8 Conclusion

It is truly remarkable that the lump solutions of several integrable models could be obtained by Bäcklund transformations and nonlinear superposition formulae and the effectiveness presents itself in this paper. It is natural to expect that this technique can be applied to more equations in AKP and BKP type, also for CKP and DKP type equations. The lack of the bilinear Bäcklund transformation of CKP equation brings us essential difficulty to construct the nonlinear superposition formula, as well as the lump solution. In particular, we also expect to develop the similar technique to generate the lump solutions for the discrete integrable lattices.