1 INTRODUCTION

A plasma system containing more than one types of ions (both positive and negative) is known as multi-ion plasma [1]. The existence of multi-ion plasmas are found in abundance in space and astrophysical objects. Therefore, the study of linear and nonlinear propagation of ion-acoustic waves (IAWs) in multi-ion component plasmas is important for the understanding of space and laboratory plasma situations. Ionosphere and magnetosphere of Earth, solar wind, bow shock in front of the magnetopause boundary layers, heliosphere, Saturn’s magnetosphere, and cometary tails are subsumed of multi-ion plasmas [2–9]. As a result, the importance of multi-ion plasmas has been increased substantially and a large number of authors studied the evolution of solitons in plasma having both positive and negative ion species [10–15]. These investigations indicate that the collisionless multi-ion plasma can be a common medium for the nonlinear propagation of waves in space and laboratory plasma.

It is well known that the external magnetic field can modify the propagation properties of the electrostatic ion-acoustic solitary structures. The effect of an ambient external magnetic field on the electrostatic waves has been studied by a number of authors [16–19]. Yu et al. [16] extended the Sagdeev approach to study the IAWs in a magnetized plasma. Sultana et al. [20] studied obliquely propagating arbitrary amplitude ion-acoustic solitary waves (IASWs) in a magnetized electron–ion plasma with suprathermal electrons. Their results show how the external magnetic field affects the nature of the solitary wave profile. The combined effects of obliqueness and electron suprathermality have also been incorporated to analyze IAWs in a bi-ion magnetized plasma.

Due to the presence of accelerated particles or superthermal radiation fields [21], space plasma systems, as well as laboratory experiments [22], provide abundant evidence for the occurrence of nonthermal (non-Maxwellian) plasmas. Plasma distributions involving a population of superthermal particles characterizes a power-law behavior [21, 23], which is efficiently described by a kappa \((\kappa )\) parametric distribution function.

The isotropic three-dimensional (3D) kappa velocity distribution of particles of mass m has the form

$${{F}_{k}}(v) = \frac{{\Gamma ({{k}_{e}} + 1)}}{{{{{(\pi {{k}_{e}}\omega )}}^{{(3/2)}}}\Gamma ({{k}_{e}} - 1{\text{/}}2)}}\mathop {\left( {1 + \frac{{{{v}^{2}}}}{{{{k}_{e}}{{\omega }^{2}}}}} \right)}\nolimits^{ - ({{k}_{e}} + 1)} ,$$
((1))

where Γ is the gamma function; ω shows the most probable speed of the energetic particles, similar to thermal speed for Maxwellian distribution, given by \(\omega [{{(2k - 3{\text{/}}{{k}_{e}})}^{{1/2}}}{{({{k}_{B}}T{\text{/}}m)}^{{1/2}}}]\), with T being the characteristic kinetic temperature; and the parameter \({{k}_{e}}\) represents the spectral index of kappa (κ) distributed superthermal (hot) electrons [24], which defines the strength of the superthermality. The range of this parameter is \(3{\text{/}}2 < k < \infty \) [25]. In the limit \(k \to \infty \) [26–28], the kappa distribution function reduces to the well-known Maxwell–Boltzmann distribution.

Nowadays, several authors in their plasma models have considered the effects of finite ion temperature by assuming adiabatic ions and nonadiabatic electrons [29–35] following different types of distributions [36–40]. Mamun and Jahan [41] considered a dusty plasma system consisting of adiabatic inertial electrons and ions and negatively charged static dust and observed that the effects of adiabatic electrons and negatively charged static dust together significantly modify the basic properties of the Dust ion-acoustic Korteweg–de Vries (KdV) solitons. Choi et al. [42] considered a plasma system containing nonthermal electrons and heavy ions and obtained that the nonthermality of electrons determines the existence of the double layer solution. Mamun and Tasnim [43] considered a multi-ion plasma and studied the basic features of solitary and shock structures. Hossain et al. [40, 44, 45] considered a quantum multi-ion plasma and studied the striking features of solitary and double layer structures. Mamun et al. [46] considered a quantum multi-ion plasma and investigated the basic properties of arbitrary-amplitude solitary waves and double layers. Sayed et al. [47] also studied the basic features of solitary waves with small, but finite, amplitudes for a multi-ion plasma. Haider et al. [48, 49] considered arbitrarily charged heavy ions and, using the reductive perturbation technique, studied the obliquely propagating solitary structure in the presence of an external magnetic field. Hosen et al. [50, 51] considered a plasma system containing composed of nondegenerate inertial ions, degenerate electrons, and immobile positively charged heavy ions and studied the basic characteristics of IAWs in the presence of external magnetic field. Sultana et al. [19, 20] considered a magnetized plasma composed of kappa-distributed electrons and an inertial ion fluid and studied the properties of arbitrary-amplitude obliquely propagating IASWs via a mechanical motion analog. Sultana and Mamun et al. [52] also considered a multi-ion plasma with positrons and two-temperature superthermal kappa-distributed electrons and investigated nonlinear features of IAWs. Alam et al. [53] considered an unmagnetized dusty plasma system consisting of negatively charged immobile dust, inertial ions, and superthermal (kappa-distributed) electrons with two distinct temperatures and investigated it both numerically and analytically by deriving KdV, modified KdV (mKdV), and Gardner equations, along with its double layers (DLs) solutions by adopting the reductive perturbation technique. Recently, Uddin et al. [54] considered a plasma system containing immobile positive ions, mobile cold positrons, superthermal (kappa-distributed) hot positrons, and electrons and investigated the basic properties of the nonlinear propagation of the nonplanar (cylindrical and spherical) positron-acoustic shock waves in an unmagnetized electron−positron−ion plasma both analytically and numerically. They derived modified Burgers equation by using the reductive perturbation method.

Till now, there is not theoretical investigation in which multi-ion magnetized plasma system with superthermal (kappa-distributed) electrons has been considered. The superthermal electrons are modeled by a Lorentzian distribution function characterized by a spectral index κ. The thermal ions are assumed to obey Maxwellian distribution function. Therefore, in this work, our main intention is to study the basic features of IASWs by deriving the magnetized KdV and magnetized mKdV equations in a multi-ion magnetized plasma.

2 THEORETICAL MODEL AND BASIC EQUATIONS

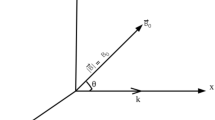
We consider a magnetized plasma system containing ions of both positive and negative charge and kappa-distributed electrons. Thus, at equilibrium condition, we have \({{n}_{{ + i0}}} = {{n}_{{ - i0}}} + {{n}_{{he0}}}\), where \({{n}_{{ + i0}}}\) and \({{n}_{{ - i0}}}\) are unperturbed positively and negatively charged ion number densities, respectively, and \({{n}_{{he0}}}\) is the number density of unperturbed hot electrons. In IAWs, the inertia comes from the ion which is 1836 times heavier than the electron. The ion will oscillate more slowly than electron in its equilibrium position. It is also notable that IAWs in a plasma system comprising N ion species has N modes [55, 56]. We have studied the slow wave mode, because our present plasma system contains inertial both positively and negatively charged ions and superthermal electrons where positively charged ions and negatively charged ions oscillate in antiphase with each other, but the electrons oscillate in an equal phase with ions. The nonlinear dynamics of the electrostatic waves propagating in such a magnetized plasma system is governed by the following (normalized) equations:

$$\frac{{\partial {{n}_{ + }}}}{{\partial t}} + \nabla \cdot ({{n}_{ + }}{{{\mathbf{u}}}_{ + }}) = 0,$$
((2))
$$\frac{{\partial {{n}_{ - }}}}{{\partial t}} + \nabla \cdot ({{n}_{ - }}{{{\mathbf{u}}}_{ - }}) = 0,$$
((3))
$$\frac{{\partial {{{\mathbf{u}}}_{ + }}}}{{\partial t}} + ({{{\mathbf{u}}}_{ + }} \cdot \nabla ){{u}_{ + }} = - \nabla \phi + {{\alpha }_{ + }}({{{\mathbf{u}}}_{ + }} \times \hat {z}),$$
((4))
$$\frac{{\partial {{{\mathbf{u}}}_{ - }}}}{{\partial t}} + ({{{\mathbf{u}}}_{ - }} \cdot \nabla ){{u}_{ - }} = \beta \nabla \phi + {{\alpha }_{ - }}({{{\mathbf{u}}}_{ - }} \times \hat {z}).$$
((5))

The system of equations is closed by Poisson’s equation

$${{\nabla }^{2}}\phi = \mu \mathop {\left( {1 - \frac{{\sigma \phi }}{{{{k}_{e}} - 3{\text{/}}2}}} \right)}\nolimits^{ - {{k}_{e}} + 1/2} - {{n}_{ + }} + \gamma {{n}_{ - }},$$
((6))

where \({{n}_{ + }}\) and \({{n}_{ - }}\) are the positive and negative ion particle number densities normalized by its equilibrium value \({{n}_{{ + i0}}}\) and \({{n}_{{ - i0}}}\); \({{{\mathbf{u}}}_{ + }}\) and \({{{\mathbf{u}}}_{ - }}\) are the positive and negative ion fluid speeds normalized by \({{C}_{ + }} = {{({{k}_{B}}{{T}_{e}}{\text{/}}{{m}_{ + }})}^{{1/2}}}\) and \({{C}_{ - }} = {{({{k}_{B}}{{T}_{e}}{\text{/}}{{m}_{ - }})}^{{1/2}}}\), respectively; ϕ is the electrostatic wave potential normalized by \({{k}_{B}}{{T}_{e}}{\text{/}}e\); \(\sigma = {{T}_{e}}{\text{/}}{{T}_{i}}\) is the hot electron to the positive ion temperature ratio; \(\beta = {{z}_{ - }}{{m}_{ + }}{\text{/}}{{z}_{ + }}{{m}_{ - }}\); \(\mu = {{n}_{{e0}}}{\text{/}}{{z}_{ + }}{{n}_{{ + i0}}}\) is the hot electron number density to the positive ion number density ratio; \(\gamma = {{z}_{ - }}{{n}_{{ - i0}}}{\text{/}}{{z}_{ + }}{{n}_{{ + i0}}}\) is the negative ion number density to positive ion number density ratio; \({{\alpha }_{ + }} = {{\omega }_{{ + c}}}{\text{/}}{{\omega }_{{pi}}}\) is the positive ion cyclotron frequency to the positive ion plasma frequency ratio; and \({{\alpha }_{ - }} = {{\omega }_{{ - c}}}{\text{/}}{{\omega }_{{pi}}}\)is the ratio the negative ion cyclotron frequency to the positive ion plasma frequency. It should be noted that \({{m}_{ + }}\) and \({{m}_{ - }}\) are the positive and negative ion mass, respectively; \({{n}_{{e0}}}\) is the total electron number density at equilibrium; \({{T}_{e}}\) is the hot electron temperature; \({{T}_{i}}\) is the positive ion temperature; \({{k}_{e}}\) is the spectral index; \({{\omega }_{{ + c}}}\) and \({{\omega }_{{ - c}}}\) are the positive and the negative ion cyclotron frequencies; \({{\omega }_{{pi}}}\) is the positive ion plasma frequency; \({{k}_{B}}\) is the Boltzmann constant, and e is the magnitude of the electron charge. The time variable t is normalized by \({{\omega }_{{pi}}} = {{(4\pi {{n}_{{ + i0}}}{{e}^{2}}{\text{/}}{{m}_{ + }})}^{{1/2}}}\), and the space variable \(x\) is normalized by \({{\lambda }_{D}} = {{({{m}_{e}}{{c}^{2}}{\text{/}}4\pi {{n}_{{ + i0}}}{{e}^{2}})}^{{1/2}}}\).

3 NONLINEAR EQUATIONS

3.1 Derivation of the Magnetized KdV Equation

At first we use reductive perturbation method to derive the well known KdV equation. We apply the reductive perturbation technique in which independent variables are stretched as

$$\xi = {{\epsilon }^{{1/2}}}({{L}_{x}}\hat {x} + {{L}_{y}}\hat {y} + {{L}_{z}}\hat {z} - {{V}_{p}}t),$$
((7))
$$\tau = {{\epsilon }^{{3/2}}}t,$$
((8))

where \({{V}_{p}}\) is the phase velocity of IASWs; \(\epsilon \) is a smallness parameter measuring the weakness of the dispersion \((0 < \epsilon < 1)\); and \({{L}_{x}}\), \({{L}_{y}}\), and \({{L}_{z}}\) are the directional cosines of the wave vector k along the x, y, and z axes, respectively, so that \(L_{x}^{2} + L_{y}^{2} + L_{z}^{2} = 1\). For a dynamical equation, we also expand the perturbed quantities \({{n}_{{( + , - )}}}\), \({{u}_{{( + , - )}}}\), and ϕ in power series of \(\epsilon \). We may expand \({{n}_{{( + , - )}}}\), \({{u}_{{( + , - )}}}\), and ϕ in power series of \(\epsilon \) as

$${{n}_{{( + , - )}}} = 1 + \epsilon n_{{( + , - )}}^{{(1)}} + {{\epsilon }^{2}}n_{{( + , - )}}^{{(2)}} + \cdot \cdot \cdot ,$$
((9))
$${{u}_{{( + , - )x,y}}} = 0 + {{\epsilon }^{{3/2}}}u_{{( + , - )x,y}}^{{(1)}} + {{\epsilon }^{2}}u_{{( + , - )x,y}}^{{(2)}} + \cdot \cdot \cdot ,$$
((10))
$${{u}_{{( + , - )z}}} = 0 + \epsilon u_{{( + , - )z}}^{{(1)}} + {{\epsilon }^{2}}u_{{( + , - )z}}^{{(2)}} + \cdot \cdot \cdot ,$$
((11))
$$\phi = 0 + \epsilon {{\phi }^{{(1)}}} + {{\epsilon }^{2}}{{\phi }^{{(2)}}} + \cdot \cdot \cdot .$$
((12))

Now, applying Eqs. (7)–(12) into Eqs. (2)–(6) and taking the lowest order coefficient of \(\epsilon \), we obtain \(u_{{ + x}}^{{(1)}} = - ({{L}_{y}}{\text{/}}{{\alpha }_{ + }})(\partial {{\phi }^{{(1)}}}{\text{/}}\partial \xi )\), \(u_{{ - x}}^{{(1)}} = (\beta {{L}_{y}}{\text{/}}{{\alpha }_{ - }})(\partial {{\phi }^{{(1)}}}{\text{/}}\partial \xi )\), \(u_{{ + y}}^{{(1)}} = ({{L}_{x}}{\text{/}}{{\alpha }_{ + }})(\partial {{\phi }^{{(1)}}}{\text{/}}\partial \xi )\), \(u_{{ - y}}^{{(1)}} = - (\beta {{L}_{x}}{\text{/}}{{\alpha }_{ - }})(\partial {{\phi }^{{(1)}}}{\text{/}}\partial \xi )\), \(u_{{ + z}}^{{(1)}} = {{L}_{z}}{{\phi }^{{(1)}}}{\text{/}}{{V}_{p}}\), \(u_{{ - z}}^{{(1)}} = - \beta {{L}_{z}}{{\phi }^{{(1)}}}{\text{/}}{{V}_{p}}\), \(n_{ + }^{{(1)}} = L_{z}^{2}{{\phi }^{{(1)}}}{\text{/}}V_{p}^{2}\), \(n_{ - }^{{(1)}} = - \beta L_{z}^{2}{{\phi }^{{(1)}}}{\text{/}}V_{p}^{2}\), \({{V}_{p}} = {{L}_{z}}\sqrt {(1 + \gamma \beta ){\text{/}}\mu {{c}_{1}}} \), and

$${{c}_{1}} = \frac{{(2{{k}_{e}} - 1)\sigma }}{{2{{k}_{e}} - 3}},$$

and find the dispersion relation for the IAWs that move along the propagation vector k. To the next higher order of \(\epsilon \), we obtain a set of equations after using the values of \(u_{{ + z}}^{{(1)}}\), \(u_{{ - z}}^{{(1)}}\), \(n_{{ + z}}^{{(1)}}\), \(n_{{ - z}}^{{(1)}}\), and \({{V}_{p}}\) and taking the z component of momentum equation as

$$\begin{gathered} \frac{{\partial n_{ + }^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial n_{ + }^{{(2)}}}}{{\partial \xi }} + {{L}_{x}}\frac{{\partial u_{{ + x}}^{{(2)}}}}{{\partial \xi }} \\ + \;{{L}_{y}}\frac{{\partial u_{{ + y}}^{{(2)}}}}{{\partial \xi }} + {{L}_{z}}\frac{{\partial u_{{ + z}}^{{(2)}}}}{{\partial \xi }} + {{L}_{z}}\frac{{\partial (n_{ + }^{{(1)}}u_{{ + z}}^{{(1)}})}}{{\partial \xi }} = 0, \\ \end{gathered} $$
((13))
$$\begin{gathered} \frac{{\partial n_{ - }^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial n_{ - }^{{(2)}}}}{{\partial \xi }} + {{L}_{x}}\frac{{\partial u_{{ - x}}^{{(2)}}}}{{\partial \xi }} \\ + \;{{L}_{y}}\frac{{\partial u_{{ - y}}^{{(2)}}}}{{\partial \xi }} + {{L}_{z}}\frac{{\partial u_{{ - z}}^{{(2)}}}}{{\partial \xi }} + {{L}_{z}}\frac{{\partial (n_{ - }^{{(1)}}u_{{ - z}}^{{(1)}})}}{{\partial \xi }} = 0, \\ \end{gathered} $$
((14))
$$\frac{{\partial u_{{ + z}}^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial u_{{ + z}}^{{(2)}}}}{{\partial \xi }} + {{L}_{z}}u_{{ + z}}^{{(1)}}\frac{{\partial u_{{ + z}}^{{(1)}}}}{{\partial \xi }} + {{L}_{z}}\frac{{\partial {{\phi }_{2}}}}{{\partial \xi }} = 0,$$
((15))
$$\frac{{\partial u_{{ - z}}^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial u_{{ - z}}^{{(2)}}}}{{\partial \xi }} + {{L}_{z}}u_{{ - z}}^{{(1)}}\frac{{\partial u_{{ - z}}^{{(1)}}}}{{\partial \xi }} - \beta {{L}_{z}}\frac{{\partial {{\phi }_{2}}}}{{\partial \xi }} = 0,$$
((16))
$$\begin{gathered} \frac{{{{\partial }^{2}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{2}}}} = \mu {{c}_{1}}{{\phi }_{2}} + \mu {{c}_{2}}\phi _{1}^{2} - n_{ + }^{{(2)}} + \gamma n_{ - }^{{(2)}}, \\ {{c}_{2}} = \frac{{(2{{k}_{e}} - 1)(2{{k}_{e}} + 1){{\sigma }^{2}}}}{{2{{{({{k}_{{he}}} - 3)}}^{2}}}}. \\ \end{gathered} $$
((17))

Again, taking the coefficient of \({{\epsilon }^{2}}\) for x and y components from the momentum equation, we get

$$u_{{ + y}}^{{(2)}} = \frac{{{{L}_{y}}{{V}_{p}}}}{{\alpha _{ + }^{2}}}\frac{{{{\partial }^{2}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{2}}}},$$
((18))
$$u_{{ - y}}^{{(2)}} = - \beta \frac{{{{L}_{y}}{{V}_{p}}}}{{\alpha _{ - }^{2}}}\frac{{{{\partial }^{2}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{2}}}},$$
((19))
$$u_{{ + x}}^{{(2)}} = \frac{{{{L}_{x}}{{V}_{p}}}}{{\alpha _{ + }^{2}}}\frac{{{{\partial }^{2}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{2}}}},$$
((20))
$$u_{{ - x}}^{{(2)}} = - \beta \frac{{{{L}_{x}}{{V}_{p}}}}{{\alpha _{ - }^{2}}}\frac{{{{\partial }^{2}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{2}}}}.$$
((21))

Now, combining Eqs. (13)–(21), we obtain an equation of the form

$$\frac{{\partial {{\phi }^{{(1)}}}}}{{\partial \tau }} + \lambda {{\phi }^{{(1)}}}\frac{{\partial {{\phi }^{{(1)}}}}}{{\partial \xi }} + \chi \frac{{{{\partial }^{3}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{3}}}} = 0.$$
((22))

This is the well-known KdV equation, which describes the obliquely propagating IAWs in a magnetized plasma, where

$$\lambda = \frac{1}{{1 + \beta \gamma }}\left[ {\frac{{3{{L}_{z}}(1 - {{\beta }^{2}}\gamma )}}{{2{{V}_{p}}}} - \frac{{\mu {{c}_{2}}V_{p}^{3}}}{{L_{z}^{2}}}} \right],$$
((23))
$$\chi = \frac{{V_{p}^{3}}}{{2L_{z}^{2}(1 + \beta \gamma )}}\left[ {1 + \frac{{(1 - L_{z}^{2})}}{{\alpha _{ + }^{2}}} + \frac{{\beta \gamma (1 - L_{z}^{2})}}{{\alpha _{ - }^{2}}}} \right].$$
((24))

The stationary localized solution of Eq. (22) is given by

$${{\phi }^{{(1)}}} = {{\phi }_{m}}\mathop {{\text{sech}}}\nolimits^2 \left( {\frac{\xi }{\Delta }} \right),$$
((25))

where \({{\phi }_{m}} = 3{{u}_{0}}{\text{/}}\lambda \) is the amplitude, with \({{u}_{0}}\) being the plasma species fluid speed, and \(\Delta = {{(4\chi {\text{/}}{{u}_{0}})}^{{1/2}}}\) is the width.

3.2 Derivation of the Magnetized mKdV Equation

The same stretched coordinates are applied to obtain the mKdV equation as we used in deriving KdV equation in Section 3.1 (i.e., Eqs. (7) and (8)) and also use the dependent variables, which are expanded as

$${{n}_{{( + , - )}}} = 1 + {{\epsilon }^{{1/2}}}n_{{( + , - )}}^{{(1)}} + \epsilon n_{{( + , - )}}^{{(2)}} + {{\epsilon }^{{3/2}}}n_{{( + , - )}}^{{(3)}} + \cdot \cdot \cdot ,$$
((26))
$$\begin{gathered} {{u}_{{( + , - )x,y}}} = 0 + \epsilon u_{{( + , - )x,y}}^{{(1)}} \\ + \;{{\epsilon }^{{3/2}}}u_{{( + , - )x,y}}^{{(2)}} + {{\epsilon }^{2}}u_{{( + , - )x,y}}^{{(3)}} + \cdot \cdot \cdot , \\ \end{gathered} $$
((27))
$${{u}_{{( + , - )z}}} = 0 + {{\epsilon }^{{1/2}}}u_{{( + , - )z}}^{{(1)}} + \epsilon u_{{( + , - )z}}^{{(2)}} + {{\epsilon }^{{3/2}}}u_{{( + , - )z}}^{{(3)}} + \cdot \cdot \cdot ,$$
((28))
$$\phi = 0 + {{\epsilon }^{{1/2}}}{{\phi }^{{(1)}}} + \epsilon {{\phi }^{{(2)}}} + {{\epsilon }^{{3/2}}}{{\phi }^{{(3)}}} {\cdot \cdot \cdot} .$$
((29))

We find the same expressions of \(n_{ + }^{{(1)}}\), \(n_{ - }^{{(1)}}\), \(u_{{ + z}}^{{(1)}}\), \(u_{{ - z}}^{{(1)}}\), \(u_{{( + )x,y}}^{{(1)}}\), \(u_{{( - )x,y}}^{{(2)}}\), and \({{V}_{p}}\) as like as that of KdV equation. To the next higher order of \(\epsilon \), by using the values of \(n_{ + }^{{(1)}}\), \(n_{ - }^{{(1)}}\), \(u_{{ + z}}^{{(1)}}\), \(u_{{ - z}}^{{(1)}}\), \(u_{{( + )x,y}}^{{(1)}}\), \(u_{{( - )x,y}}^{{(2)}}\), and \({{V}_{p}}\), we obtain a set of equations, which can be simplified as

$$u_{{ + z}}^{{(2)}} = \frac{{L_{z}^{3}{{\phi }^{{{{{(1)}}^{2}}}}}}}{{2\mathop {{{V}_{p}}}\nolimits^3 }} + \frac{{{{L}_{z}}{{\phi }^{{(2)}}}}}{{{{V}_{p}}}},$$
((30))
$$u_{{ - z}}^{{(2)}} = \frac{{{{\beta }^{2}}L_{z}^{3}{{\phi }^{{{{{(1)}}^{2}}}}}}}{{2\mathop {{{V}_{p}}}\nolimits^3 }} - \beta \frac{{{{L}_{z}}{{\phi }^{{(2)}}}}}{{{{V}_{p}}}},$$
((31))
$$n_{ + }^{{(2)}} = \frac{{3L_{z}^{4}{{\phi }^{{{{{(1)}}^{2}}}}}}}{{2V_{p}^{4}}} + \frac{{L_{z}^{2}{{\phi }^{{(2)}}}}}{{V_{p}^{2}}},$$
((32))
$$n_{ - }^{{(2)}} = \frac{{3{{\beta }^{2}}L_{z}^{4}{{\phi }^{{{{{(1)}}^{2}}}}}}}{{2V_{p}^{4}}} - \beta \frac{{L_{z}^{2}{{\phi }^{{(2)}}}}}{{V_{p}^{2}}},$$
((33))
$${{\rho }^{{(2)}}} = - \frac{1}{2}A{{\phi }^{{{{{(1)}}^{2}}}}} = 0,$$
((34))

where,

$$A = \left[ {\frac{{3L_{z}^{4}}}{{2V_{p}^{4}}} - \left( {\mu {{c}_{2}} + \frac{{3\gamma {{\beta }^{2}}L_{z}^{4}}}{{2V_{p}^{4}}}} \right)} \right].$$

To the next higher order of \(\epsilon \), we obtain a set of equations

$$\begin{gathered} \frac{{\partial n_{ + }^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial n_{ + }^{{(3)}}}}{{\partial \xi }} + {{L}_{x}}\frac{{\partial u_{{ + x}}^{{(2)}}}}{{\partial \xi }} + {{L}_{x}}\frac{\partial }{{\partial \xi }}(n_{ + }^{{(1)}}u_{{ + x}}^{{(1)}}) \\ + \;{{L}_{y}}\frac{{\partial u_{{ + y}}^{{(2)}}}}{{\partial \xi }} + {{L}_{y}}\frac{\partial }{{\partial \xi }}(n_{ + }^{{(1)}}u_{{ + y}}^{{(1)}}) + {{L}_{z}}\frac{{\partial u_{{ + z}}^{{(3)}}}}{{\partial \xi }} \\ + \;{{L}_{z}}\frac{\partial }{{\partial \xi }}(n_{ + }^{{(1)}}u_{{ + z}}^{{(2)}}) + {{L}_{z}}\frac{\partial }{{\partial \xi }}(n_{ + }^{{(2)}}u_{{ + z}}^{{(1)}}) = 0, \\ \end{gathered} $$
((35))
$$\begin{gathered} \frac{{\partial n_{ - }^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial n_{ - }^{{(3)}}}}{{\partial \xi }} + {{L}_{x}}\frac{{\partial u_{{ - x}}^{{(2)}}}}{{\partial \xi }} + {{L}_{x}}\frac{\partial }{{\partial \xi }}(n_{ - }^{{(1)}}u_{{ - x}}^{{(1)}}) \\ + \;{{L}_{y}}\frac{{\partial u_{{ - y}}^{{(2)}}}}{{\partial \xi }} + {{L}_{y}}\frac{\partial }{{\partial \xi }}(n_{ - }^{{(1)}}u_{{ - y}}^{{(1)}}) + {{L}_{z}}\frac{{\partial u_{{ - z}}^{{(3)}}}}{{\partial \xi }} \\ + \;{{L}_{z}}\frac{\partial }{{\partial \xi }}(n_{ - }^{{(1)}}u_{{ - z}}^{{(2)}}) + {{L}_{z}}\frac{\partial }{{\partial \xi }}(n_{ - }^{{(2)}}u_{{ - z}}^{{(1)}}) = 0, \\ \end{gathered} $$
((36))
$$\frac{{\partial u_{{ + z}}^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial u_{{ + z}}^{{(3)}}}}{{\partial \xi }} + {{L}_{z}}\frac{\partial }{{\partial \xi }}(u_{{ + z}}^{{(1)}}u_{{ + z}}^{{(2)}}) + {{L}_{z}}\frac{{\partial {{\phi }^{{(3)}}}}}{{\partial \xi }} = 0,$$
((37))
$$\frac{{\partial u_{{ - z}}^{{(1)}}}}{{\partial \tau }} - {{V}_{p}}\frac{{\partial u_{{ - z}}^{{(3)}}}}{{\partial \xi }} + {{L}_{z}}\frac{\partial }{{\partial \xi }}(u_{{ - z}}^{{(1)}}u_{{ - z}}^{{(2)}}) - \beta {{L}_{z}}\frac{{\partial {{\phi }^{{(3)}}}}}{{\partial \xi }} = 0,$$
((38))
$$\frac{{{{\partial }^{2}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{2}}}} = \mu {{c}_{1}}{{\phi }^{{(3)}}} + 2\mu {{c}_{2}}{{\phi }^{{(1)}}}{{\phi }^{{(2)}}} - n_{ + }^{{(3)}} + \gamma n_{ - }^{{(3)}}.$$
((39))

Now, combining Eqs. (35)–(39) we obtain an equation of the form

$$\frac{{\partial {{\phi }^{{(1)}}}}}{{\partial \tau }} + {{\alpha }_{1}}{{\alpha }_{3}}{{\phi }^{{(1)2}}}\frac{{\partial {{\phi }^{{(1)}}}}}{{\partial \xi }} + {{\alpha }_{2}}{{\alpha }_{3}}\frac{{{{\partial }^{3}}{{\phi }^{{(1)}}}}}{{\partial {{\xi }^{3}}}} = 0.$$
((40))

This is the well-known mKdV equation, which describes the obliquely propagating IAWs in a magnetized plasma. Here, \({{\alpha }_{1}}\), \({{\alpha }_{2}}\), and \({{\alpha }_{3}}\) are given by

$${{\alpha }_{1}} = \frac{{15L_{z}^{6}(1 + \gamma {{\beta }^{3}})}}{{2V_{p}^{6}}},$$
((41))
$${{\alpha }_{2}} = 1 + \frac{{(1 - L_{z}^{2})}}{{\alpha _{ + }^{2}}} + \frac{{\gamma \beta (1 - L_{z}^{2})}}{{\alpha _{ - }^{2}}},$$
((42))
$${{\alpha }_{3}} = {{L}_{z}}\sqrt {\frac{{1 + \gamma \beta }}{{\mu {{c}_{1}}}}} .$$
((43))

The stationary solitary wave solution of standard mKdV equation is obtained by considering a frame \(\xi = \eta - {{u}_{0}}T\) (moving with speed \({{u}_{0}}\)), and the solution is

$${{\phi }^{{(1)}}} = {{\phi }_{m}}{\text{sech}}\left( {\frac{\xi }{\varpi }} \right),$$
((44))

where the amplitude is \({{\phi }_{m}} = \sqrt {(6{{u}_{0}}{\text{/}}{{\alpha }_{1}}{{\alpha }_{3}})} \) and the width is \(\varpi = {{\phi }_{m}}\sqrt {({{\alpha }_{1}}{\text{/}}6)} \).

4 PARAMETRIC INVESTIGATION AND RESULTS

We are interested to numerically analyze the IAWs soliton structures of magnetized multi-ion plasma with kappa-distributed superthermal electrons by deriving KdV and mKdV equations, which are represented by Eqs. (22) and (40), respectively. At first, we focus on the stationary solitary wave solution of standard KdV equation (22) and the solution is

$${{\phi }^{{(1)}}} = {{\phi }_{m}}{\text{sec}}{{{\text{h}}}^{2}}\left( {\frac{\xi }{\Delta }} \right),$$
((45))

where the amplitude is \({{\phi }_{m}} = 3{{u}_{0}}{\text{/}}\lambda \) and the width is \(\Delta = {{(4\chi {\text{/}}{{u}_{0}})}^{{1/2}}}\).

The solitary waves are caused due to the balance between nonlinearity and dispersion. So, the nonlinear coefficient λ and dispersion coefficient χ play a crucial role to study the basic features of the solitary waves. The degree of nonlinearity is proportional to the potential of the plasma system, and a higher nonlinear medium causes higher electrostatic potential. From the above relation, it is obvious that the height of the amplitude of the solitary structures is directly proportional to the soliton speed moving with \({{u}_{0}}\) and inversely proportional to the nonlinear coefficient λ. Again, the width of these solitary structures is directly proportional to the dispersion constant χ and inversely proportional to the soliton speed \({{u}_{0}}\). It should be noted that KdV equation derived here is valid only for the limits \(\lambda = 0\), \(\lambda > 0\), and \(\lambda < 0\). The ranges of plasma parameters (\({{u}_{0}} = 0.01\)–1, \(\mu = 3.46\)–3.6, \(\sigma = \) 0.2–2.5, \(\gamma = 0.5\)–1.8, \(\beta = 0.15\)–0.37, \(\alpha = 0.2\)–0.6, \({{k}_{e}} = \) 5–40, and \(\delta = 10\)–70) used in this numerical analysis are very wide and correspond to space and laboratory plasma situations. In the framework of our plasma model, we have investigated how solitary waves and their basic features (amplitude, width) are modified by the relevant plasma parameters, such as μ, σ, γ, β, α, \({{k}_{e}}\), and δ.

We have found that, for \({{\mu }_{c}} = \mu = 3.49\), the amplitude of the IASWs breaks down due to the vanishing of the nonlinear coefficient λ for \({{u}_{0}} = 0.01\), \({{k}_{e}}\) = 20, \(\sigma = 2.5\), \(\delta = 30\), \(\gamma = 1.5\), and β = \(\alpha = 0.2\). So, in this investigation, it is observed that the magnetized KdV equation supports the space plasma system under consideration IASWs with the feature of hump (compressive, or positive) and dip (rarefactive, or negative) types, which depends on the critical value \({{\mu }_{c}}\). In Figs. 1 and 2, we have graphically presented the solitary profiles with positive to negative ion mass ratio β variation for both positive and negative potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\), respectively. From Figs. 1 and 2, we can say that, due to the maximum value of the positive to negative ion mass ratio, the nonlinearity becomes minimum. So, we obtained the maximum value of the potential.

Fig. 1.
figure 1

(Color online) Variation of the positive potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with β for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\sigma = 2.5\), \(\mu = 3.5\), \(\delta = 30\), \(\gamma = 1.5\), and \(\alpha = 0.2\).

Full size image
Fig. 2.
figure 2

(Color online) Variation of the negative potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with β for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\sigma = 2.5\), \(\mu = 3.49\), \(\delta = 30\), \(\gamma = 1.5\), and \(\alpha = 0.2\).

Full size image

The amplitude of the solitons determines its strength. Figures 3 and 4 proclaim the strength of the solitary profiles for the variation of hot electron number density to the positive ion number density ratio μ for both positive and negative potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\), respectively. For the maximum value of μ, the phase velocity \({{V}_{p}}\) becomes minimum, but the nonlinearity becomes maximum. Due to this maximum nonlinearity, the strength of the solitary profiles is minimum.

Fig. 3.
figure 3

(Color online) Variation of the positive potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with μ for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\sigma = 2.5\), \(\beta = 0.3\), \(\delta = 30\), \(\gamma = 1.5\), and \(\alpha = 0.2\).

Full size image
Fig. 4.
figure 4

(Color online) Variation of negative potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with μ for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\sigma = 2.5\), \(\beta = 0.3\), \(\delta = 30\), \(\gamma = 1.5\), and \(\alpha = 0.2\).

Full size image

Figures 5 and 6 are disclosed that the width and strength of the solitary profiles are very much dependent on the negative ion number density to positive ion number density ratio \(\gamma \) for both positive and negative potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\), respectively. With the increasing value of γ, the phase velocity \({{V}_{p}}\) and dispersion coefficient χ are increased. So, the width of the solitary profiles increases. When the width increases, the amplitude of the solitary profiles should be decreased and strength should become minimum. However, nonlinearity decreases with the increasing value of γ and, hence, strength increases. As a result of this investigation, it is observed that the width and strength of the solitary profiles are maximum, when the negative ion number density to positive ion number density ratio is maximum.

Fig. 5.
figure 5

(Color online) Variation of the positive potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with γ for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\sigma = 2.5\), \(\mu = 3.5\), \(\delta = 30\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image
Fig. 6.
figure 6

(Color online) Variation of the negative potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with γ for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\sigma = 2.5\), \(\mu = 3.49\), \(\delta = 30\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

In this investigation, we have executed excess hot electron to the positive ion temperature ratio σ causes more disturbance on the IAWs profile, as shown in Fig. 7. From this numerical analysis, it is clear that minimum width and amplitude occurred due to the maximum value of σ.

Fig. 7.
figure 7

(Color online) Variation of the amplitude of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with σ for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\gamma = 1.5\), \(\mu = 3.5\), \(\delta = 30\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

Effects of obliqueness δ on width and amplitude for positive potential magnetized KdV solitons \({{\phi }^{{(1)}}}\) is represented through the Fig. 8. From Fig. 8, it is obvious that amplitude falls and width reduces when δ rises.

Fig. 8.
figure 8

(Color online) Variation of positive potential KdV solitons \({{\phi }^{{(1)}}}\) with δ for \({{u}_{0}} = 0.01\), \({{k}_{e}} = 20\), \(\sigma = 2.5\), \(\mu = 3.5\), \(\gamma = 1.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

The strength of IASWs propagating in a magnetized plasma is very much sensitive to superthermal electrons. Hence, in this framework of our model, we have investigated the superthermality effect for a fixed soliton propagation speed within the accessible range. The effects of superthermality on obliquely propagating IAWs are depicted in Figs. 9 and 10 for both positive and negative potential of magnetized KdV solitons \({{\phi }^{{(1)}}}\). It is seen that the more strongly non-Maxwellian distributions (lower κ, i.e., increased excess superthermal particles) lead to both nonlinearity and change in phase velocity. It is found that the soliton amplitude increases with decreasing λ due to \({{k}_{e}}\) decreasing.

Fig. 9.
figure 9

(Color online) Variation of positive potential KdV solitons \({{\phi }^{{(1)}}}\) with \({{k}_{e}}\) for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\sigma = 2.5\), \(\mu = 3.5\), \(\gamma = 1.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image
Fig. 10.
figure 10

(Color online) Variation of negative potential KdV solitons \({{\phi }^{{(1)}}}\) with \({{k}_{e}}\) for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\sigma = 2.5\), \(\mu = 3.49\), \(\gamma = 1.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

The width Δ of magnetized KdV solitary waves very much depends on the values of hot electron number density to the positive ion number density ratio μ. A graphical view of width Δ vs. the positive or negative ion cyclotron frequency to the positive ion plasma frequency ratio α with the variation of μ is depicted in Fig. 11, where the mutation of the width is taken under consideration. It is found that the width of magnetized KdV SWs decreases with the increasing values of μ.

Fig. 11.
figure 11

(Color online) Variation of width Δ of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with μ for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\sigma = 2.5\), \({{k}_{e}} = 20\), \(\gamma = 1.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

It must be noticed from the Fig. 12 that the value of obliqueness δ and the amplitude of the solitary waves increase, while their width increases for the lower range of δ (from 0° to about 50°), and decrease for the higher range of δ (from 50° to about 90°). As \(\delta \to 90^\circ \), the width goes to zero, while the amplitude goes to infinity. It is likely that, for large angles, the assumption that the waves are electrostatic is no longer valid and we should look for fully electromagnetic structures. Our present investigation is only valid for small values of δ but invalid for arbitrary large value of δ. In case of larger values of δ, the wave amplitude becomes large enough to break the validity of the reductive perturbation method. We have observed from Fig. 12 that the amplitude and width of the solitary profile decreases with increasing values of the positive or negative ion cyclotron frequency to the positive ion plasma frequency ratio α.

Fig. 12.
figure 12

(Color online) Variation of the width of magnetized KdV solitons \({{\phi }^{{(1)}}}\) with α for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\sigma = 2.5\), \({{k}_{e}} = 20\), \(\gamma = 1.5\), \(\beta = 0.3\), and \(\mu = 3.5\).

Full size image

It is time to look at the stationary solitary wave solution of standard mKdV equation (40).

It is obvious from the above relation that the height of the amplitude of the solitary structures is directly proportional to the soliton speed \({{u}_{0}}\) and inversely proportional to the constants \({{\alpha }_{1}}\) and \({{\alpha }_{3}}\), while the width of these solitary structures is directly proportional to the constant \({{\alpha }_{1}}\) only. In this investigation, it is observed that the magnetized mKdV equation supports IASWs in the space plasma system under consideration with the feature of hump (compressive or positive) only. The compressive solitary waves are formed due to the magnetized mKdV equation, which does not depend on the critical value \({{\mu }_{c}}\).

We have numerically analyzed that, with the increasing of β, the phase speed increases, but \({{\alpha }_{1}}\) and \({{\alpha }_{3}}\) both decrease for magnetized mKdV solitons. Hence, strength of the solitary waves is maximum for maximum value of β depicted in Fig. 13.

Fig. 13.
figure 13

(Color online) Variation of the amplitude of magnetized mKdV solitons \({{\phi }^{{(1)}}}\) with β for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\sigma = 2.5\), \({{k}_{e}} = 20\), \(\gamma = 1.5\), \(\mu = 3.5\), and \(\alpha = 0.2\).

Full size image

However, Fig. 14 shows that the phase speed decreases and \({{\alpha }_{1}}\) increases with the increasing of μ. This implies that maximum amplitude for magnetized mKdV solitons \({{\phi }^{{(1)}}}\) is possible when μ is minimum.

Fig. 14.
figure 14

(Color online) Variation of the amplitude of magnetized mKdV solitons \({{\phi }^{{(1)}}}\) with μ for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\sigma = 2.5\), \({{k}_{e}} = 20\), \(\gamma = 1.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

Again, from Fig. 15, we observed that amplitude increases with increasing γ and, from Fig. 16, we found amplitude is reduced for increased value of σ. Confidently, it is clear that the magnetized mKdV solitons potential is maximum when γ is maximum, but σ is minimum.

Fig. 15.
figure 15

(Color online) Variation of the amplitude of magnetized mKdV solitons \({{\phi }^{{(1)}}}\) with γ for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\sigma = 2.5\), \({{k}_{e}} = 20\), \(\mu = 3.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image
Fig. 16.
figure 16

(Color online) Variation of the amplitude of magnetized mKdV solitons \({{\phi }^{{(1)}}}\) with σ for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\gamma = 1.5\), \({{k}_{e}} = 20\), \(\mu = 3.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

The amplitude of magnetized mKdV solitons \({{\phi }^{{(1)}}}\) also responses on superthermal parameter \({{k}_{e}}\) depicted in Fig. 17. We have investigated numerically that the multiplication of \({{\alpha }_{1}}\) and \({{\alpha }_{3}}\) decreases with increasing value of superthermal index \({{k}_{e}}\). The investigation shows that amplitude increment of the solitary profiles is possible when increment of the superthermality occurred.

Fig. 17.
figure 17

(Color online) Variation of the amplitude of magnetized mKdV solitons \({{\phi }^{{(1)}}}\) with \({{k}_{e}}\) for \({{u}_{0}} = 0.01\), \(\delta = 30\), \(\gamma = 1.5\), \(\sigma = 1.5\), \(\mu = 3.5\), \(\beta = 0.3\), and \(\alpha = 0.2\).

Full size image

5 DISCUSSION

We have studied the nonlinear propagation of IAWs in a magnetized collisionless multi-ion plasma containing both positive and negative ions and kappa-distributed superthermal hot electrons. In order to describe the dynamics of such solitary waves, we derived the magnetized KdV and mKdV equations by adopting reductive perturbation method. It is found that the soliton strength is maximum for the maximum value of the positive to negative ion mass ratio, for the maximum value of hot electron number density to the positive ion number density ratio, for the maximum negative ion number density to positive ion number density ratio, for the minimum value of hot electron to the positive ion temperature ratio, and for the minimum value of obliqueness, for lowest superthermality with the decreasing values of the positive or negative ion cyclotron frequency to the positive ion plasma frequency ratio. The width of the magnetized KdV solitons is also maximum for the maximum value of the positive to negative ion mass ratio, and the minimum values of hot electron number density to the positive ion number density ratio and superthermality, but the phase speed increases when the width decreases. The plasma system under consideration supports IASWs, whose basic properties are found to be significantly modified by the electron to ion temperature ratio, positive to negative ion mass ratio, positive and negative ion cyclotron frequency to the positive ion plasma f-requency ratio, and the plasma particle number densities.

It is noted here that we have studied the obliquely propagating IASWs and observed the amplitude variations for nonlinear compression (for KdV and mKdV solitons) and rarefaction (only for mKdV solitons) perturbations for small-amplitude limit. However, one can investigate IASWs in plasmas containing impurity ions or dust particles by showing the possible existence of large-amplitude nonlinear ion-acoustic wave structures [57–59], which is beyond the scope of our present work. We may conclude that the results of our present investigation should be useful for understanding the nonlinear features of localized electrostatic disturbances in some space and astrophysical plasma systems, particularly, the ionosphere and magnetosphere of the Earth, solar wind, bow shock in front of the magnetopause boundary layers, heliosphere, Saturn’s magnetosphere, and cometary tails, where the magnetized multi-ion and superthermal electrons are the dominant plasma species.