1 Introduction

Recently, there has been a great deal of interest in understanding linear and nonlinear features of multi-ion plasma system. A multi-ion plasma system is a system containing more than one types of ions. Plasmas with a significant amount of negative ions also called electro-negative plasmas (Hines et al. 1957; Buchsbaum 1957; Yakimenko 1957; Vender et al. 1995; Kimura et al. 1998; Mamun et al. 2009), have attracted a great deal of attention because of their potential applications in microelectronic and photo-electronic industries (Lieberman and Lichtenberg 2005). This type of plasmas have a great importance to various fields of plasmas science and technology. The presence of the negative ions in the Earth’s ionosphere (Massey 1976) and cometary comae (Chaizy et al. 2009) is well known. In different situations, (viz. plasma processing reactors (Gottscho and Gaebe 1986), neutral beam sources (Bacal and Hamilton 1986), low-temperature laboratory experiments (Jacquinot et al. 1977; Ichiki et al. 2002), etc.) the existence of positive-negative ion plasmas has also been found. The importance of negative ion plasmas to the field of plasma physics is growing because negative ions were found to outperform positive ions in plasma etching. It was conclusively showed by the Cassini spacecraft that the heavy negative ions are present in the upper region of Titan’s atmosphere (Coates et al. 2007). For even more complicated molecules these particles may act as organic building blocks. The population of second ion species of such space plasmas and many laboratory plasmas (Jacquinot et al. 1977; Watanabe et al. 2001; Weingarten et al. 2001) are noticeable (Mamun et al. 2004). Some new interesting features (Hines et al. 1957; Buchsbaum 1957; Yakimenko 1957) are introduced by this ion population and the existing electron-proton plasma waves are modified.

Recently some authors have included quantum diffraction of plasma particles in different plasma situations (Manfredi and Feix 1996; Chatterjee et al. 2009; Akbari-Moghanjoughi 2010). This type of plasma is known as quantum plasma. Quantum plasmas have attracted a great deal of attention because of their potential applications in dense plasma particularly in different astrophysical and cosmological systems (Opher et al. 2001; Jung 2001; Chabier et al. 1977), e.g. interstellar or molecular clouds, planetary rings, comets, the interior of Jupiter (Fortov 2009) and massive white dwarfs (Balberg and Shapiro 2000), magnetars (Lai 2001; Harding and Lai 2006), neutron stars (Chapman and Gericke 2011), etc. White dwarfs and neutron stars are the products of the final stages of stellar evolution. In such astrophysical compact objects, the density of charged particles is extremely high (about 1019–1026 cm−3). The properties of matter existing under such dense plasmas are different from the properties of classical plasmas. Quantum plasmas have extremely high plasma number densities and low temperatures. At extremely low temperatures, the thermal de Broglie wavelength becomes comparable to the interelectron distance and the electron temperature becomes comparable to the electron Fermi temperature (T Fe ) and the electrons follow Fermi Dirac distribution law. In this condition quantum mechanical effects are expected to play a significant role in the behavior of charged particles (Shukla and Ali 2005; Ali and Shukla 2006). As electrons are lighter than ions, the quantum behavior of electron is reached faster than ions. The electron gas in an ordinary metal is a good example where both plasma and quantum effects coexist do occur. At room temperature and standard metallic densities, quantum effects can not be ignored, so that the electron gas constitutes a true quantum plasma.

The dust particles are also quite common in various plasma systems. The presence of static charged dust in electron-ion plasmas leads to introduce a new mode. Shukla and Silin (1996) have first theoretically shown the existence of low-frequency dust ion-acoustic (DIA) waves in a dusty plasma, which was latter observed in laboratory experiments (Barkan et al. 1996; Merlino et al. 1998; Shukla and Mamun 2002). The nonlinear waves associated with the DIA and Quantum DIA (QDIA) waves particularly solitary waves (SWs) (Khan and Mushtaq 2007; Masood et al. 2007), shock waves (Masood et al. 2009), and double layers (Mamun and Shukla 2009), etc. have received a great deal of interest in understanding the basic properties of localized electrostatic perturbation in space (Goertz 1989; Mendis and Rosenberg 1994; Morfill and Ivlev 2009) and laboratory dusty plasmas (Merlino and Goree 1998). The formation of double layers (DLs) is possible in different dense plasma environments (Moslem et al. 2007; Khan et al. 2009; Misra and Samanta 2010) where the electron quantum statistical pressure and tunneling force associated with the Bohm potential play important roles in the propagation of quantum ion-acoustic waves (Khan et al. 2009), quantum dust-acoustic waves (Moslem et al. 2007), quantum electron-acoustic waves (Misra and Samanta 2008; Lee 2009), etc.

Very recently Hossain et al. (2011) have considered a plasma system composed of inertial ions, massless quantum electrons, and negatively charged immobile dust particles and have derived a higher order nonlinear equation, known as modified Gardner equation (MGE) (Hossain et al. 2011). They have studied the nonlinear features of the finite amplitude nonplanar QDIA SWs beyond the Korteweg-de Vries limit as well as DLs (Hossain and Mamun 2012). To the best of our knowledge, no attempt has been taken to study the DLs in multi-ion quantum plasma. Therefore, in this present paper, we attempt to study the basic features of cylindrical and spherical QDIA DLs by using more modern Gardner approach (Hossain et al. 2011).

The manuscript is organized as follows. The model equations and MGE are provided in Sect. 2. The analytical analysis of the MGE (for DLs) and a brief discussion are presented in Sect. 3.

2 Governing Equations and MGE

We consider the nonlinear propagation of an unmagnetized quantum plasma system composed of massless electrons, inertial positive as well as negative ions and negatively charged static dust. Thus at equilibrium overall charge neutrality condition implies

(1)

where Z p (Z n ) Z d0 are the charge states for positive ions (negative ions) dusts particles and n p0 (n n0) n e0 is the equilibrium positive ions (negative ions) electrons number density. The nonlinear dynamics of such QDIA waves in a nonplanar (cylindrical or spherical) geometry is governed by

(2)
(3)
(4)
(5)
(6)
(7)
(8)

where μ=n e0/Z n n n0, β=Z p n p0/Z n n n0 connected through the charge neutrality condition (see Eq. (1)), μ=β−1−δ with δ=Z d0 n d0/Z n n n0, m=Z p m n /Z n m p , ν=0 for 1D planar geometry, and ν=1(2) for cylindrical (spherical) geometry. We have considered the following set of equations for the normalizations: x=ω pp x/C s , t=ω pn x/C s , n α =n α /n α0, u α =u α /c s , ϕ=eϕ/K B T Fe with α=e for electrons, p for positive ions, n for negative ions, u α is the plasma fluid speed, ω pα =(n α0 e 2/ϵ 0 m α )1/2 is α-particle plasma frequency and C s =(k B T Fe /m n )1/2 is quantum ion-acoustic speed. In the above set of normalized equations, we introduce the non-dimensional quantum parameter H=ħω pe /k B T Fe . We have assumed that the ions are cold and the electrons obey the following pressure law

(9)

where V Fe =(2k B T Fe /m e )1/2 is the electron thermal Fermi speed at temperature T Fe and k B is the Boltzmann’s constant.

We first introduce the stretched coordinates to derive K-dV equation

(10)

where V p is the QDIA wave phase speed (ω/k) and ϵ is a smallness parameter measuring the weakness of the dispersion (0<ϵ<1). We then expand n α , u α , and ϕ in power series of ϵ

(11)
(12)
(13)
(14)

By developing equations in various powers of ϵ, we obtain in the lowest order of ϵ the dispersion law

(15)

By developing equations in various powers of ϵ and after some mathematical calculations and assuming ν=0, we obtain the well known K-dV equation of the form

(16)

where

(17)
(18)

This K-dV equation (16) is not valid for a parametric regime corresponding to A=0 or A∼0 (where A is the coefficient of the nonlinear term of the K-dV or Burger equation, and A∼0 means here that A is not equal 0, but A is around 0). This is because, the latter gives rise to infinitely large amplitude structures which break down the validity of the reductive perturbation method (Washimi and Taniuti 1966). This means that to study finite amplitude solitary waves or DLs beyond this K-dV/Burger limit, one must resort the other type of nonlinear dynamical equation which can be valid for A∼0. The technique of analyzing SWs and DLs, is Gardner approach, leads to a standard Gardner equation. To study QDIA DLs by analyzing the ingoing solutions of Eqs. (2)–(8), we now introduce the stretched coordinates (Hossain et al. 2011)

(19)

The nonlinear coefficient ‘A’ (16) vanishes at some critical value of β which can be found from the solution of A=0 as

(20)

For β around its critical value (β c ), i.e. for |β−β c |=ϵ corresponding to A=A 0, we can express A 0 as

(21)

where s=1 for β>β c and s=−1 for β<β c .

So, ρ (2) (found from the second order calculation of ϵ) can be expressed as

(22)

which, therefore, must be included in the third order Poisson’s equation.

We follow the assumptions and mathematical methods of Hossain et al. (2011) and obtain an equation of the form

(23)

where

(24)
(25)
(26)
(27)

Equation (23) is known as modified Gardner equation (MGE). The detailed calculations and assumptions can be seen in Hossain et al. (2011). The modification is due the extra term (viz. \(\frac{\nu}{2\tau}\psi\)), which arises due to the effects of the nonplanar geometry. It is important to note that if we neglect ψ 3 term, the MGE reduces to a modified K-dV equation. However, in this modified K-dV equation the nonlinear term vanishes at β=β c and is not valid near the critical value β=β c . But the MGE derived here is valid for β near its critical value. It should be noted here that Hossain et al. (2011) and Hossain and Mamun (2012) derived this MGE and discuss the possibility of the SWs (Hossain et al. 2011) and DLs (Hossain and Mamun 2012) solution beyond the K-dV limit in a DIA quantum plasma system.

3 Numerical analysis and discussion

We have already mentioned that ν=0 corresponds to a 1D planar geometry which reduces Eq. (23) to a standard Gardner equation (SGE). Our aim now is to numerically analyze MGE. However, for clear understanding, we first briefly discuss the stationary DLs solution of this SGE [i.e. Eq. (23) with ν=0]. The stationary DLs solution of this SGE is obtained by considering a moving frame (moving with speed U 0) ξ=ζ−U 0 τ, and imposing all appropriate boundary conditions for DLs solutions, including ψ (1)→0, dψ/dξ→0, d 2 ψ/dξ 2→0 at ζ→−∞. Thus, one can express the stationary DLs solution of this SGE as

(28)

where the amplitude (ψ m ) and the width (Δ) of the DLs are respectively

(29)

with γ=α 1/6α 2.

Equation (28) represents a DLs solution when α 1 and α 2 maintain the opposite sign, i.e., α 1/α 2<0 to make γ<0.

It may be noted here that if we would neglect the higher order nonlinear term [viz. the fourth term of (23) or the term containing ψ 3], but would keep the lower order nonlinear term [viz. the third term of (23) or the term containing ψ 2], we would obtain the solitary structures that are due to the balance between nonlinearity (associated with ψ 2 only) and dispersion. On the other hand, in our present work, we have kept both the terms containing ψ 2 and ψ 3, and have obtained the DLs structures which are formed due to the balance between the nonlinearity (associated with ψ 2 and ψ 3) and dispersion. It may be added here that the dissipation (which is usually responsible for the formation of the shock-like structures (Karpman 1975; Mamun and Shukla 2009)) is not essential for the formation of DLs structures (Bharuthram and Shukla 1992; Verheest and Pillay 2008). The stationary DLs solution of the SGE equation, and the conditions for the existence of DLs clearly imply that the DLs structures predicted in our present investigation is not due to the dissipation (which has been neglected in our present investigation), but is due to the balance between the harmonic nonlinearities and the dispersion caused by density correlation due to quantum fluctuation and charge separation effect.

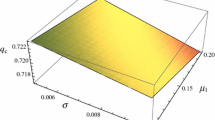
The results that we have found from the planar geometry are depicted in Figs. 2, 3, 4. Figure 1 shows the parametric regime of β c for different values of m and μ (obtained from the solutions of A=0). Figure 2 shows the profile of positive double layers in planer geometry for μ=0.6, U 0=0.1, m=0.5 and H=0.3. Figure 3 shows the profile of positive double layers in planer geometry for μ=0.6, U 0=0.1, m=0.5 and H=0.9. From Figs. 2 and 3, it is clear that the amplitude of positive DLs does not vary with the quantum diffraction parameter, but the width of the positive DLs decreases with the increase of it. We have found the same results for the negative double layers.

Fig. 1
figure 1

Showing the parametric regime of β c for different values of m and μ (obtained from the solutions of A=0) (Color figure online)

Full size image
Fig. 2
figure 2

Profile of positive double layers in planer geometry for μ=0.6, U 0=0.1, m=0.5 and H=0.3 (Color figure online)

Full size image
Fig. 3
figure 3

Profile of positive double layers in planer geometry for μ=0.6, U 0=0.1, m=0.5 and H=0.9

Full size image

It is also found that (from Fig. 4) magnitude of the amplitude of the DLs increases with the decrease of μ. The width of positive and negative DLs also increases with decrease of μ.

Fig. 4
figure 4

Profile of positive double layers in planer geometry for μ=0.2, U 0=0.1, m=0.5 and H=0.3 (Color figure online)

Full size image

We now turn to Eq. (23) with the term (ν/2τ)ψ, which is due to the effects of the nonplanar (cylindrical or spherical) geometry. An exact analytic solution of Eq. (23) is not possible. Therefore, we have numerically solved Eq. (23), and have studied the effects of cylindrical and spherical geometries on time-dependent QDIA DLs. The results are depicted in Figs. 5, 6, 7, 8. The initial condition, that we have used in our numerical analysis, is in the form of the stationary solution of Eq. (23) without the term (ν/2τ)ψ. Figure 5 (6) shows how the effects of a cylindrical geometry modify the QDIA positive (negative) DLs. On the other hand, Fig. 7 (8) shows how the effects of a spherical geometry modify the QDIA positive (negative) DLs.

Fig. 5
figure 5

Showing the effects of cylindrical geometry on QDIA positive DLs for μ=0.6, U 0=0.1, m=0.5 and H=0.3 (Color figure online)

Full size image
Fig. 6
figure 6

Showing the effects of cylindrical geometry on QDIA negative DLs for μ=0.6, U 0=0.1, m=0.5 and H=0.3 (Color figure online)

Full size image
Fig. 7
figure 7

Showing the effects of spherical geometry on QDIA positive DLs for μ=0.6, U 0=0.1, m=0.5 and H=0.3 (Color figure online)

Full size image
Fig. 8
figure 8

Showing the effects of spherical geometry on QDIA negative DLs for μ=0.6, U 0=0.1, m=0.5 and H=0.3 (Color figure online)

Full size image

The numerical solutions of Eq. (23) (displayed in Figs. 5, 6, 7, 8) reveal that for a large value of τ, the spherical and cylindrical DLs are similar to 1D structures. This is because for a large value of τ ( e.g. τ=−30) the term (ν/2τ)ψ, which is due to the effects of the cylindrical or spherical geometry, is no longer dominant. However, as the value of τ decreases, the term (ν/2τ)ψ becomes dominant, and both spherical and cylindrical DLs structures differ from 1D ones. It is found that as the value of τ decreases, the amplitude (the magnitude of the amplitude) of these localized pulses increases. It is also found that the amplitude of cylindrical QDIA DLs is larger than those of 1D ones, but smaller than that of the spherical ones.

To summarize, we have investigated cylindrical (ν=1) and spherical (ν=2) QDIA DLs in quantum multi ion dusty plasma by deriving MGE which is valid for β∼β c . It is found that the quantum dusty plasma system under consideration supports finite amplitude DLs, whose basic features (polarity, amplitude, width, etc.) depend on the ion and dust number densities as well as quantum diffraction (tunneling) parameter, H. It is also found that at β<β c , positive DLs exist, whereas at β>β c , negative DLs exist. We have used a wide range of the quantum dusty plasma parameters (viz. m=0.1–0.9, μ=0.1–0.6 and H=0.1–0.9) in our numerical analysis. Thus, the dust-plasma parameters are within the appropriate ranges for both space environments and laboratory devices.

It may be stressed here that the results of this investigation could be useful for understanding the nonlinear features of electrostatic disturbances in different astrophysical and cosmological systems (Opher et al. 2001; Jung 2001; Chabier et al. 1977), e.g. interstellar or molecular clouds, planetary rings, comets, the interior of Jupiter (Fortov 2009) and massive white dwarfs (Balberg and Shapiro 2000), magnetars (Lai 2001; Harding and Lai 2006), neutron stars (Chapman and Gericke 2011), etc. and also in the other plasma systems where the quantum effect of electron is important.