1 Introduction

Dusty plasmas have opened up a completely new and fascinating research area, because of their vital applications in understanding various collective processes in space environments (Shukla 2001; Mendis and Rosenberg 1994; Shukla and Mamun 2002) and laboratory devices (Barkan et al. 1995, 1996; Merlino et al. 1998; Homann et al. 1997). The presence of highly negatively charged and massive grains of dust particles in an electron ion plasma is responsible for the appearance of new types of waves, depending on whether the dust grains are considered to be static or mobile. One type of these waves is the dust-ion-acoustic (DIA) wave, which is the usual ion-acoustic wave modified by the presence of dust grains. In DIA waves, ion mass provides the inertia and restoring force comes from the thermal pressure of electrons. The phase speed of such DIA waves is much larger (smaller) than the ion (electron) thermal speed.

Shukla and Silin (1992) have first theoretically shown the existence of low frequency DIA waves in a dusty plasma system. Barkan et al. (1996) and Nakamura et al. (1999) have observed the DIA waves in laboratory experiments. Nowadays, the linear properties of the DIA waves in dusty plasmas are well understood from both theoretical and experimental points of view (Shukla and Mamun 2002; Barkan et al. 1996; Merlino et al. 1998; Shukla and Silin 1992; Shukla and Rosenberg 1999). Recently, the nonlinear waves particularly the DIA solitary waves (DIA SWs) have received an impressive interest in realizing the basic properties of localized electrostatic perturbations in space and laboratory dusty plasmas. The DIA SWs have been theoretically investigated by several authors (Popel et al. 2003; Mamun 2008; El-Labany et al. 2008; Mamun et al. 2009; Alinejad 2011; Hossain et al. 2011; Kundu et al. 2012). In those works (Popel et al. 2003; Mamun 2008; El-Labany et al. 2008; Mamun et al. 2009; Alinejad 2011; Hossain et al. 2011; Kundu et al. 2012), the interactions of multiple ions or electrons were not considered.

Yu and Luo (2008) provided an important note on multispecies model for identical particles. They proposed that unless the electrons are physically separated in the space/time domain of interest, it is fallacious to partition identical electrons into different species following different dynamics or kinetics. Thus, it is possible to partition identical electrons into different species following different dynamics or kinetics, when the electrons are physically separated in the space/time domain of interest.

During the last few decades, the DIA and IA waves in a two electron/ion components plasma in different plasma environments have been studied by several authors both theoretically (Alinejad 2011; Buti 1980; Moslem and El-Taibany 2005; Masood et al. 2009; Masud et al. 2012a, 2012b, 2013b; Masud and Mamun 2013) and experimentally (Nakamura and Sugai 1996). Most of the investigations have been focused on Maxwellian plasmas. However, a lot of theoretical observations of space plasmas (Vasyliunas 1968; Leubner 1982) are often characterized by a particle distribution function with high energy tail and they may deviate from the Maxwellian. Superthermal particles may arise due to the effect of external forces acting on the natural space environment plasmas or to wave particle interaction. Plasmas with an excess of superthermal non-Maxwellian electrons are generally characterized by a long tail in the high energy region. Such space plasmas can be modeled by generalized Lorentzian or kappa distribution (Vasyliunas 1968; Summers and Thorne 1991; Mace and Hellberg 1995; Baluku and Hellberg 2008; Hellberg et al. 2009) rather than the Maxwellian distribution.

A three dimensional generalized Lorentzian or kappa distribution function takes the form (Summers and Thorne 1991)

$$\begin{aligned} &F_\kappa(v)=\frac{\varGamma{(\kappa+1)}}{(\pi\kappa\theta ^2)^{3/2}\varGamma{(\kappa-1/2)}}\biggl(1+\frac{v^2}{\kappa\theta^2} \biggr)^{-(\kappa+1)}, \end{aligned}$$

where θ is the most probable speed (effective thermal speed), related to the usual thermal velocity V t =(K B T/m)1/2 by θ=[(2κ−3)/κ]V t , T being the characteristic kinetic temperature, i.e., the temperature of the equivalent Maxwellian with the same average kinetic energy (Hellberg et al. 2009), and K B is the Boltzmann constant. The most probable speed, and hence the κ distribution, is defined for κ>3/2. The parameter κ is the spectral index, which is a measure of the slope of the energy spectrum of the superthermal particles forming the tail of the velocity distribution function. Low values of κ represent a “hard” spectrum with a strong non-Maxwellian (power law-like) tail, an enhanced velocity distribution at low speeds, and a depressed distribution at intermediate speeds (Summers and Thorne 1991). In the limit κ→∞, the above kappa distribution function for electrons reduces to the well known Maxwell-Boltzmann distribution.

Recently, a numerous investigations have been made by many authors on DIA or IA SWs with single-temperature superthermal (kappa distributed) electrons (Baluku and Hellberg 2008; Baluku et al. 2010; Choi et al. 2011; Shah et al. 2011; Hussain 2012; Shahmansouri et al. 2013; Sultana and Kourakis 2011). In many non-equilibrium plasmas, electrons can often be grouped into two or more distinct components with different temperatures (Buti 1980; Moslem and El-Taibany 2005; Masood et al. 2009; Masud et al. 2012a, 2012b; Yu and Shukla 1988). This usually happen because certain electrons are preferentially heated by external sources (viz. waves and beams). Before reaching at the final equilibrium, there can exist a time scale in which the separation of the electrons into different temperature groups is possible. A plasma system containing two groups of electrons with different temperatures can excite/support the waves which are unique in the system. These two groups of electrons in such plasmas can be termed as two-temperature superthermal electrons, when both of the groups follow the kappa distributions with distinct temperatures.

Schippers et al. (2008) have combined a hot and a cold electron component, while both electrons are kappa distributed and found a best fit for the electron velocity distribution. Baluku et al. (2011) used this model as base of a kinetic theory study for electron-acoustic waves in Saturn’s magnetosphere and then they have studied IA solitons in a plasma with two-temperature kappa distributed electrons (Baluku and Hellberg 2012). Recently, Masud et al. (2013a) have studied the characteristic of DIA shock waves in an unmagnetized dusty plasma consisting of negatively charged static dust, inertial ions, positively charged positrons following Maxwellian distribution, and superthermal electrons with two distinct temperatures. Alam et al. (2013) have also analyzed the effects of DIA shock waves in an unmagnetized dusty plasma with two-temperature kappa distributed electrons. The plasmas composed of two-temperature superthermal (kappa-distributed) electrons (Shahmansouri et al. 2013; Schippers et al. 2008; Baluku et al. 2011; Baluku and Hellberg 2012; Masud et al. 2013a; Alam et al. 2013) are very relevant to the Saturnian magnetosphere (Baluku et al. 2011).

In the last few years, the formation of DIA GSs and DLs (Masud et al. 2012a; Deeba et al. 2012; Akhter et al. 2013a; Zobaer et al. 2013) has been a topic of great interest. Akhter et al. (2013b) investigated the DIA GSs and DLs in an unmagnetized dusty plasma system consisting of inertial positive and negative ions, negatively charged static dust, and single temperature kappa distributed electrons.

Recently, Saini and Kohli (2013) have studied the small amplitude dust-acoustic SWs and DLs. They have considered an unmagnetized four component dusty plasma system consisting of extremely massive, highly negatively charged inertial dust grains, inertialess nonextensively distributed electrons and two temperature ions (Masud and Mamun 2012, Tasnim et al. 2013a).

But up to now, there is no investigation has been made to study the DIA SWs and DLs with two temperature superthermal (kappa distributed) electrons in planar geometry. Therefore, in our present work, we consider a dusty plasma system containing inertial ions, negatively charged static dust, and superthermal electrons with two distinct temperatures. We analyze the basic features of DIA GSs and DLs, which exist beyond limits for the K-dV solitons. The manuscript is organized as follows: The governing equations are provided in Sect. 2. The K-dV, mK-dV, and standard Gardner (SG) equations are derived and numerically solved in Sects. 3, 4, and 5 respectively. The solitary wave solution of SG equation is given in Sect. 6, DL solution is discussed in Sect. 7, and a brief discussion is provided in Sect. 8.

2 Governing equations

We consider the nonlinear propagation of the DIA waves in an unmagnetized dusty plasma system containing inertial ions, negatively charged immobile dust, and kappa distributed electrons with two distinct temperatures. Hence, at equilibrium, n i0=n e10+n e20+Z d n d0, where n i0 is the unperturbed ion number density, n e10 (n e20) is the density of unperturbed lower (higher) temperature electron, n d0 is the unperturbed dust number density, and Z d is the number of electrons residing on the dust grain surface. The nonlinear dynamics of the DIA waves, whose phase speed is much smaller (larger) than the electron (ion) thermal speed in a planar geometry is governed by

$$\begin{aligned} &\frac{\partial n_i}{\partial t} + \frac{\partial}{\partial x} (n_iu_i) = 0, \end{aligned}$$
(1)
$$\begin{aligned} &\frac{\partial u_i}{\partial t} + u_i \frac{\partial u_i}{ \partial x} =-\frac{\partial\phi}{\partial x}, \end{aligned}$$
(2)
$$\begin{aligned} &\frac{\partial^{2}\phi}{\partial x^{2}} = \mu_{e1}\biggl(1-{\frac{\sigma_1\phi}{\kappa_{e1}-\frac{3}{2}} \biggr)^{-\kappa_{e1} +\frac{1}{2}}}-n_i+\mu \\ &\hphantom{\frac{\partial^{2}\phi}{\partial x^{2}} =}{}+\mu_{e2}\biggl(1-{\frac{\sigma_2\phi}{\kappa_{e2} -\frac{3}{2}} \biggr)^{-\kappa_{e2}+\frac{1}{2}}}=-\rho, \end{aligned}$$
(3)

where n i is the ion particle number density normalized by its equilibrium value n i0, u i is the ion fluid speed normalized by C i =(k B T ef /m i )1/2, ϕ is the electrostatic wave potential normalized by k B T ef /e, σ 1=T ef /T e1, σ 2=T ef /T e2, μ e1=n e10/n i0, μ e2=n e20/n i0, μ=Z d n d0/n i0=1−μ e1−μ e2 where T ef =n e0 T e1 T e2/(n e10 T e2+n e20 T e1). Here n e0 is the total electron number density at equilibrium. It should be noted that T e1 (T e2) is the lower (higher) electron temperature, T ef is the effective temperature of two electrons, T i is the ion temperature, k B is the Boltzmann constant, and e is the magnitude of the electron charge. The time variable t is normalized by \(\omega_{pi}^{-1}=(m_{i}/4\pi n_{i0}e^{2})^{1/2}\) and the space variable x is normalized by the effective electron Debye length λ Dm =(k B T ef /4πn i0 e 2)1/2.

3 Derivation of K-dV equation

We first derive the well known K-dV equation using the reductive perturbation method. The K-dV equation has been introduced by the stretched coordinates (Nahar et al. 2013):

$$\begin{aligned} &\zeta={\epsilon}^{\frac{1}{2}}(x - V_pt), \end{aligned}$$
(4)
$$\begin{aligned} &\tau={\epsilon}^{\frac{3}{2}}t, \end{aligned}$$
(5)

where V p is the phase speed of the DIA wave and ϵ is a smallness parameter measuring the weakness of the dispersion (0<ϵ<1). To obtain a dynamical equation, we also expand the perturbed quantities n i , u i , ϕ, and ρ in power series of ϵ. Let M be any of the system variables n i , u i , and ϕ, describing the system’s state at a given position and instant. We consider small deviations from the equilibrium state M (0)—which explicitly is \(n_{i}^{(0)}=1\), \(u_{i}^{(0)}=0\), and ϕ (0)=0 by taking

$$\begin{aligned} M= M^{(0)}+\sum\limits _{n=1}^\infty{ \epsilon^n M^{(n)}}. \end{aligned}$$
(6)

To the lowest order in ϵ, Eqs. (1)–(6) give

$$\begin{aligned} &u_i^{(1)}=\frac{1}{V_p}\psi,\qquad n_i^{(1)}= \frac{1}{V_p^2}\psi, \end{aligned}$$
(7)
$$\begin{aligned} &\frac{1}{V_p^2}=\frac{\mu_{e1}(\kappa_{e1}-\frac{1}{2})\sigma _1}{\kappa_{e1}-\frac{3}{2}}+\frac{\mu_{e2}(\kappa_{e2}-\frac {1}{2})\sigma_2}{\kappa_{e2}-\frac{3}{2}}, \end{aligned}$$
(8)

where ψ=ϕ (1). Equation (8) represents the linear dispersion relation for the DIA waves. To the next higher order of ϵ, we obtain a set of equations, which, after using Eqs. (7)–(8), can be simplified as

$$\begin{aligned} &\frac{\partial n_i^{(1)}}{\partial\tau} -V_p\frac{\partial n_i^{(2)}}{\partial\zeta} + \frac{\partial u_i^{(2)}}{\partial\zeta} +\frac{\partial}{\partial \zeta}\bigl[n_i^{(1)}u_i^{(1)} \bigr]=0, \end{aligned}$$
(9)
$$\begin{aligned} &\frac{\partial u_i^{(1)}}{\partial \tau}-V_p\frac{\partial u_i^{(2)}}{\partial \zeta}+u_i^{(1)} \frac{\partial u_i^{(1)}}{\partial \zeta}+\frac{\partial\phi^{(2)}}{\partial\zeta}=0, \end{aligned}$$
(10)
$$\begin{aligned} &\frac{\partial^2 \psi}{\partial \zeta^2}-\mu_{e1}{\frac{P_1 P_2\sigma_1^2 \psi^2 }{2 P_3^2}+ \mu_{e1}\frac{P_2 \sigma_1 \phi^{(2)} }{P_3}} \\ &\quad {}-\mu_{e2}{\frac{P_4 P_5\sigma_2^2 \psi^2 }{2 P_6^2}+\mu_{e2} \frac{P_5 \sigma_2 \phi^{(2)} }{P_6}}+n_i^{(2)}=0, \end{aligned}$$
(11)

where P 1=−1/2−κ e1, P 2=1/2−κ e1, P 3=−3/2+κ e1, P 4=−1/2−κ e2, P 5=1/2−κ e2, and P 6=−3/2+κ e2.

Now, combining Eqs. (9)–(11), we obtain a equation of the form:

$$ \frac{\partial\psi}{\partial\tau}+A\psi\frac{\partial \psi}{\partial\zeta} + \beta\frac{\partial^3 \psi}{\partial \zeta^3} = 0, $$
(12)

where

$$\begin{aligned} &A=\frac{V_p^3}{2} \biggl[\frac{3}{V_p^4}- \frac{\mu_{e1}P_1 P_2\sigma_{1}^2}{P_3^2} -\frac{\mu_{e2}P_4 P_5\sigma_{2}^2}{P_6^2} \biggr], \end{aligned}$$
(13)
$$\begin{aligned} &\beta=\frac{V_p^3}{2}. \end{aligned}$$
(14)

Equation (12) is known as K-dV (Korteweg-de Vries) equation. The stationary localized solution of Eq. (12) is given by

$$ \psi=\psi_m \mathrm{sech}^{2} \biggl(\frac{\zeta}{\delta_1}\biggr), $$
(15)

where the amplitude ψ m and the width δ 1 are given by ψ m =3U 0/A and \(\delta_{1}=\sqrt{4\beta/U_{0}}\), respectively. As U 0>0, Eq. (15) clearly indicates that (i) small amplitude SWs with ψ>0, i.e. hump shape (positive potential) solitons exist if μ e1>0.342, (ii) SWs with ψ<0, i.e. dip shape (negative potential) solitons exist if μ e1≤0.342. To have some numerical appreciations of our results, we have numerically analyzed the solitary height, the solitary width and solitary profile by using the general expressions for the coefficients A and β [i.e., by using Eqs. (13), (14), and (15)]. It is found that K-dV solitons associated with positive (negative) potential formed far above (below) the critical value (shown in Figs. 2 and 3). This is happened due to the fact that the amplitude of the K-dV solitons goes to the infinite value, which then breaks down the validity of the reductive perturbation method. Therefore, more higher order nonlinear equation should be taken into account to get the formation of solitons around critical value.

4 Derivation of mK-dV equation

A modified K-dV (mK-dV) equation (Tasnim et al. 2013b) is obtained by taking the next higher order calculation of ϵ. To analyze the nonlinear evolution near the critical parameter μ e1≃μ c , mK-dV equation is obtained from the third order calculation, which utilizes another set of stretched coordinates. The stretched co-ordinates for mK-dV equation (Nahar et al. 2013) is:

$$\begin{aligned} &\zeta={\epsilon}(x - V_pt), \end{aligned}$$
(16)
$$\begin{aligned} &\tau={\epsilon}^3t. \end{aligned}$$
(17)

By using Eqs. (16) and (17) in Eqs. (1)–(3) and (6), we have found the same values of \(n_{i}^{(1)}, u_{i}^{(1)}\), and V p as like as that of the K-dV equation. To the next higher order of ϵ, we obtain a set of equations, which, after using the values of \(n_{i}^{(1)}, u_{i}^{(1)}\), and V p can be simplified as

$$\begin{aligned} &u_i^{(2)}=\frac{1}{2V_p^3}\psi^2+ \frac{\phi ^{(2)}}{V_p},\qquad n_i^{(2)}=\frac{3}{2V_p^4} \psi^2+\frac{\phi^{(2)}}{V_p^2}, \end{aligned}$$
(18)
$$\begin{aligned} &\rho^{(2)}=-\frac{1}{2}A\psi^2 =0. \end{aligned}$$
(19)

To the next higher order of ϵ, we obtain a set of equations:

$$\begin{aligned} &\frac{\partial n_i^{(1)}}{\partial\tau} -V_p\frac{\partial n_i^{(3)}}{\partial\zeta} + \frac{\partial u_i^{(3)}}{\partial\zeta} +\frac{\partial}{\partial \zeta}\bigl(n_i^{(1)}u_i^{(2)} \bigr) \\ &\quad {} +\frac{\partial}{\partial \zeta}\bigl(n_i^{(2)}u_i^{(1)} \bigr)=0, \end{aligned}$$
(20)
$$\begin{aligned} &\frac{\partial u_i^{(1)}}{\partial \tau}-V_p\frac{\partial u_i^{(3)}}{\partial \zeta}+u_i^{(1)} \frac{\partial u_i^{(2)}}{\partial \zeta}+u_i^{(2)}\frac{\partial u_i^{(1)}}{\partial \zeta} \\ &\quad {}+\frac{\partial \phi^{(3)}}{\partial\zeta}=0, \end{aligned}$$
(21)
$$\begin{aligned} &\frac{\partial^2 \psi}{\partial \zeta^2}+\mu_{e1}\frac{P_1 P_2 P_3 \sigma_1^3 \psi^3 }{6P_3^3}- \mu_{e1}\frac{P_1 P_2\sigma_1^2 \psi\phi^{(2)} }{P_3^2} \\ &\quad {}+\mu_{e1}\frac{P_2\sigma_1 \phi^{(3)} }{P_3} +\mu_{e2} \frac{P_4 P_5 P_6\sigma_2^3 \psi^3 }{6 P_6 ^3} \\ &\quad {}-\mu_{e2}\frac{P_4 P_5 \sigma_2^2 \psi\phi^{(2)} }{P_6^2}+\mu_{e2}\frac{P_5\sigma_2 \phi^{(3)} }{P_6}+n_{i}^{(3)}=0. \end{aligned}$$
(22)

Now, combining Eqs. (20)–(22) we obtain a equation of the form:

$$\begin{aligned} \frac{\partial\psi}{\partial \tau}+\alpha_1\alpha_2\psi^2 \frac{\partial\psi}{\partial\zeta} + \alpha_2\frac{\partial^3 \psi}{\partial\zeta^3} = 0, \end{aligned}$$
(23)

where

$$\begin{aligned} &\alpha_1=\frac{15}{2V_p^6}+\mu_{e1} \frac{P_1 P_2 P_3\sigma_1^3}{2P_3^3}+\mu_{e2}\frac{P_4 P_5 P_6\sigma_2^3 }{2P_6^3}, \end{aligned}$$
(24)
$$\begin{aligned} &\alpha_2=\frac{V_p^3}{2}. \end{aligned}$$
(25)

Equation (23) is known as mK-dV equation. The stationary SW solution of Eq. (23) is, therefore, directly given by

$$ \psi=\psi_m \mathrm{sech} \biggl(\frac{\zeta}{\delta_2}\biggr), $$
(26)

where the amplitude ψ m and the width δ 2 are given by \(\psi_{m}=\sqrt{6U_{0}/\alpha_{1}\alpha_{2}}\) and \(\delta_{2}=\psi_{m} \sqrt{\gamma_{1}}\), γ 1=α 1/6. The amplitude and width variation of mK-dV solitons are nearly valid around critical value. The mK-dV equation has a solitary wave solution around μ e1=μ c , but not any DLs solution. Therefore, we proceed into next higher order equation known as standard-Gardner (sG) equation (higher order nonlinear equation), because the sG equation has both SWs and DLs.

5 Derivation of SG equation

To derive the DIA GSs we follow Eq. (19) by analyzing the ingoing solutions of Eqs. (1)–(3) which provides A=0 as ψ≠0. A feasible feature expressed from Eq. (15) is, for A>(<)0 the dusty plasma supports hump (dip) shape DIA SWs which are associated with a positive (negative) potential, and no SW can exist at A=0 and A∼0. It is to be noted that A is a function of μ e1, μ e2, κ e1, κ e2, σ 1, and σ 2. Hence, to find the parametric regimes corresponding to A=0, we have to express one (viz. μ e1) of these six parameters in terms of the other parameters (viz. μ e2, κ e1, κ e2, σ 1, and σ 2). Therefore, A(μ e1=μ c )=0, and the critical condition (μ c ) can be written as

$$\begin{aligned} \mu_{e1}=\mu_{c}&=\frac{1}{6 R_1 R_2 \sigma_{1}^2}\Bigl[Q_1 Q_2 \sigma_{1}^2-6 Q_3 Q_4 \mu_{e2}\sigma_{1}\sigma_{2} \\ &\quad {}+\sqrt{R_1 R_2 R_3 \sigma_{1}^2}\Bigr], \end{aligned}$$
(27)

where \(Q_{1}=-1+4\kappa_{e1}^{2}\), Q 2=(3−2κ e2)2, Q 3=3+4(−2+κ e1)κ e1, Q 4=3+4(−2+κ e2)κ e2, R 1=(1−2κ e1)2, R 2=(3−2κ e2)2, \(R_{3}=(1+2\kappa_{e1})^{2} R_{2} \sigma_{1}^{2}-12(-3+2\kappa_{e1})(1+2\kappa_{e1})Q_{4} \mu_{e2}\sigma_{1}\sigma_{2} +12(3-2\kappa_{e1})^{2} (-1+4\kappa_{e2}^{2})\mu_{e2}\sigma_{2}^{2}\).

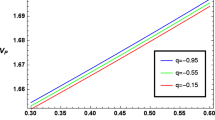
Equation (27) represents the critical value of μ e1 above (below) which the SWs with a positive (negative) potential exists, gives the value of μ c . We note that A=0 at its critical value μ e1=μ c ≃0.342 (which is a solution of A=0). One can find from Eq. (27) that μ c ≃0.342 for a set of dusty plasma parameters (Masud et al. 2013a) (viz. μ e2=0.04, σ 1=2.5, σ 2=0.1, κ e1=20, and κ e2=2). We note that μ c can vary with σ 1 and μ e2 (shown in Fig. 1), and one can take any other critical value within this range that supports the dusty plasma situation under consideration. Using this dusty plasma parameters (Masud et al. 2013a), σ 1=1.8−5, and μ e2=0.01−0.09, we have the existence of the small amplitude SWs with a positive potential for μ e1>μ c , and with a negative potential for μ e1<μ c . So, for μ e1 around its critical value (μ c ), A=A 0 can be expressed as

$$\begin{aligned} A_0\simeq s \biggl(\frac{\partial A}{\partial \mu_{e1}} \biggr)_{\mu_{e1}=\mu_{c}}| \mu_{e1}-\mu_{c}|=c_1s\epsilon, \end{aligned}$$
(28)

where |μ e1−μ c | is a small and dimensionless parameter, and can be taken as the expansion parameter ϵ, i.e. |μ e1−μ c |≃ϵ, and s=1 for μ e1>μ c and s=−1 for μ e1<μ c . c 1 is a constant depending on the dusty plasma parameters (κ e1, κ e2, σ 1, σ 2, μ e1, and μ e2) and is given by

$$\begin{aligned} c_1=\frac{6P_2^2\mu_{e1}\sigma_{1}^2}{P_3^2} +\frac{6P_2 P_5\mu_{e2}\sigma_{1}\sigma_{2}}{P_3P_6}-\frac{P_1P_2\sigma _{1}^2}{P_3^2}. \end{aligned}$$
(29)

The value of c 1 for a set of dusty plasma parameters (Masud et al. 2013a) (viz. μ e1=0.342, μ e2=0.04, σ 1=2.5, σ 2=0.1, κ e1=20, and κ e2=2) is 7.13865. Now, ρ (2) can be expressed as

$$\begin{aligned} \epsilon^2\rho^{(2)}\simeq-\epsilon^3 \frac{1}{2}c_1s\psi^2, \end{aligned}$$
(30)

which, therefore, must be included in the third order Poisson’s equation. To the next higher order in ϵ, we obtain the following equation

$$\begin{aligned} &\frac{\partial^2 \psi}{\partial \zeta^2}+\frac{1}{2}c_1s \psi^2+\mu_{e1}\frac{P_1 P_2 P_3 \sigma_1^3 \psi^3 }{6P_3^3}-\mu_{e1} \frac{P_1 P_2\sigma_1^2 \psi \phi^{(2)} }{P_3^2} \\ &\quad {}+\mu_{e1}\frac{P_2\sigma_1 \phi^{(3)} }{P_3} +\mu_{e2} \frac{P_4 P_5 P_6\sigma_2^3 \psi^3 }{6 P_6 ^3} \\ &\quad {}-\mu_{e2}\frac{P_4 P_5 \sigma_2^2 \psi\phi^{(2)} }{P_6^2}+\mu_{e2}\frac{P_5\sigma_2 \phi^{(3)}}{P_6}+n_{i}^{(3)}=0. \end{aligned}$$
(31)

After simplification, we can write from Eq. (31)

$$\begin{aligned} \frac{\partial\psi}{\partial\tau}+sc_1\alpha_2\psi\frac{\partial \psi}{\partial\xi} + \alpha_2\alpha_3\psi^2\frac{\partial \psi}{\partial\xi} + \alpha_2\frac{\partial^3 \psi}{\partial \xi^3}=0, \end{aligned}$$
(32)

where

$$ \alpha_3=\frac{15}{2V_p^6}+\mu_{e1} \frac{P_1 P_2 P_3\sigma_1^3}{2P_3^3}+\mu_{e2}\frac{P_4 P_5 P_6\sigma_2^3 }{2P_6^3}. $$
(33)

Equation (32) is known as SG equation. It is also called mixed mK-dV equation. It contains both ψ-term of K-dV and ψ 2-term of mK-dV equation. If we neglect ψ 2 term and put c 1 sα 2=A and α 2=β then the Gardner equation reduces to K-dV equation which is derived in Eq. (12). However, in this K-dV equation the nonlinear term vanishes at μ e1=μ c , and is not valid around μ e1=μ c , and μ e1≃μ c , which make soliton amplitude large enough to break down its validity. But the Gardner equation derived here is valid for μ e1∼μ c .

Fig. 1
figure 1

The A=0 graph which represents the variation of μ c with σ 1 and μ e2, where μ c is the critical value of μ e1 above (below) which compressive (rarefactive) DIA solitary structures are formed

Full size image

6 SW solution of SG equation

To analyze stationary GSs, we first introduce a transformation ζ=ξ−U 0 τ which allows us to write Eq. (32), under the steady state condition, as

$$ \frac{1}{2} \biggl(\frac{d\psi}{d\zeta} \biggr)^2+V(\psi)=0, $$
(34)

where the pseudo-potential V(ψ) is

$$\begin{aligned} V(\psi)=-\frac{U_0}{2\alpha_2}\psi^2+\frac{c_1s}{6} \psi^3+\frac{\alpha _3}{12}\psi^4. \end{aligned}$$
(35)

We note here that U 0 and α 2 are always positive. It is obvious from Eq. (35) that

$$\begin{aligned} &V(\psi)|_{\psi=0}=\frac{dV(\psi)}{d\psi}\bigg \vert _{\psi=0}=0, \end{aligned}$$
(36)
$$\begin{aligned} &\frac{d^2V(\psi)}{d\psi^2}\bigg \vert _{\psi=0}<0. \end{aligned}$$
(37)

The conditions Eqs. (36) and (37) imply that SW solutions of Eq. (34) exist if

$$\begin{aligned} V(\psi)|_{\psi=\psi_m}=0. \end{aligned}$$
(38)

The latter can be solved as

$$\begin{aligned} &U_{0}=\frac{c_1s\alpha_2}{3}\psi_{m1,2}+\frac{\alpha_2\alpha_3}{6}\psi _{m1,2}^2, \end{aligned}$$
(39)
$$\begin{aligned} &\psi_{m1,2}=\psi_m \biggl[1\mp\sqrt{1+\frac{U_0}{V_0}} \biggr], \end{aligned}$$
(40)

where ψ m =−c 1 s/α 3, and \(V_{0}=c_{1}^{2}s^{2}\alpha_{2}/6\alpha_{3}\). Now, using Eqs. (35) and (40) in Eq. (34) we have

$$\begin{aligned} \biggl(\frac{d\psi}{d\zeta} \biggr)^2+\gamma\psi^2(\psi- \psi_{m1}) (\psi -\psi_{m2})=0, \end{aligned}$$
(41)

where γ=α 3/6. The SW solution of Eq. (34) or Eq. (41) is, therefore, directly given by

$$\begin{aligned} \psi= \biggl[\frac{1}{\psi_{m2}}- \biggl(\frac{1}{\psi_{m2}} -\frac{1}{\psi_{m1}} \biggr)\cosh^2 \biggl(\frac{\xi}{\Delta} \biggr) \biggr]^{-1}, \end{aligned}$$
(42)

where ψ m1,2 are given in Eq. (40), and SWs width Δ is

$$\begin{aligned} \Delta=\frac{2}{\sqrt{-\gamma\psi_{m1}\psi_{m2}}}. \end{aligned}$$
(43)

Equation (42) represents the SW solution of SG equation (32).

7 DL solution

The DL solution of Eq. (32) is given by

$$\begin{aligned} \psi=\frac{\psi_m}{2} \biggl[1+\tanh \biggl(\frac{\zeta}{\Delta} \biggr) \biggr], \end{aligned}$$
(44)

with

$$\begin{aligned} &U_0=-\frac{s^2\alpha_2}{6\alpha_3}, \end{aligned}$$
(45)
$$\begin{aligned} &\psi_m=\frac{6U_0}{s\alpha_2}, \end{aligned}$$
(46)
$$\begin{aligned} &\Delta=\frac{2}{\psi_m\sqrt{-\gamma}}, \end{aligned}$$
(47)

where γ=α 3/6 and ψ m (Δ) is the DL height (thickness). This clearly indicates that Eq. (44) represents a DL solution if and only if γ<0, i.e., α 3<0. When α 2 α 3=0, then, in this case, we can find the value of the parameter μ e1 as the critical one (μ e1=μ d ≈0.271) for a set of dusty plasma parameters (viz. μ e2=0.04, σ 1=2.5, σ 2=0.1, κ e1=20, and κ e2=2) (Masud et al. 2013a). For μ d >0.271, α 3>0, DL does not form. Therefore, negative potential DLs exist for μ d <0.271 and s=−1 in our present considered plasma system.

8 Discussion

We have considered an unmagnetized dusty plasma system consisting of negatively charged immobile dust, inertial ions, and inertialess superthermal electrons with two distinct temperatures. We have investigated the basic features (amplitude, width, polarity etc.) of such a dusty plasma system by deriving the K-dV, mK-dV and SG equations using the reductive perturbation method. The DLs solution obtained from SG equation is also analyzed. The results that we have obtained from this investigation can be summarized as follows:

  1. 1.

    We have found that K-dV equation supports either compressive (positive) or rarefactive (negative) SWs, while depending on the critical value μ c , the co-existence of both compressive and rarefactive SWs are found in SG solitons. But only compressive structures are formed for mK-dV solitons and rarefactive structures are formed for DLs.

  2. 2.

    The basic features of hump and dip types DIA-GSs are identified, which are found to exist beyond the K-dV limit, i.e. for μ e1∼0.342. The DIA GSs are completely different from the K-dV solitons because μ e1=0.342 corresponds to the vanishing of the nonlinear coefficient of the K-dV equation, and μ e1∼0.342 corresponds to extremely large amplitude K-dV solitons for which the validity of the reductive perturbation method breaks down.

  3. 3.

    The critical value of μ e1 (μ c ) varies with relative electron number density μ e2 and relative temperature ratio σ 1 as displayed in Fig. 1. It is observed that the critical value μ c increases gradually with the increase of σ 1, but decreases abruptly with the increase of μ e2.

  4. 4.

    The K-dV solitons are found for both above or below the critical value (i.e., when μ e1>μ c or μ e1<μ c ).

  5. 5.

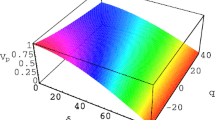
    It is observed that at μ e1>0.342, the positive potential K-dV solitons exist, whereas at μ e1<0.342, the negative potential K-dV solitons exist (shown in Figs. 2 and 3).

    Fig. 2
    figure 2

    Showing the variation of amplitude of the positive K-dV solitons with μ e2 for μ e1=0.45, σ 1=2.5, σ 2=0.1, κ e1=20, κ e2=2, and U 0=0.1. The upper (pink) curve is for μ e2=0.01, the middle (blue) one is for μ e2=0.05, and the lower (green) one is for μ e2=0.09

    Full size image
    Fig. 3
    figure 3

    Showing the variation of amplitude of the negative K-dV solitons with κ e2 for σ 1=2.5, σ 2=0.1, μ e1=0.25, μ e2=0.04, κ e1=20, and U 0=0.1. The upper (green) curve is for κ e2=2, the middle (blue) one is for κ e2=1.8, and the lower (pink) one is for κ e2=1.6

    Full size image
  6. 6.

    It is clear that the amplitude of the positive potential K-dV solitons decreases (increases) with the increase (decrease) of μ e2 (shown in Fig. 2). On the other hand, the amplitude of the negative potential K-dV solitons decreases (increases) with the increase (decrease) of spectral index parameter κ e2 (shown in Fig. 3).

  7. 7.

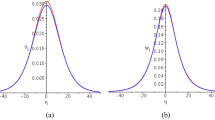
    Only positive potential (compressive) SWs are found for mK-dV solitons. It is observed that with the increase (decrease) of relative electron number density μ e1, the amplitude of the SWs decreases (increases) slightly as depicted in Fig. 4.

    Fig. 4
    figure 4

    Showing the variation of amplitude of the positive mK-dV solitons with μ e1 for μ e2=0.04, κ e1=20, κ e2=2, σ 1=2.5, σ 2=0.1, and U 0=0.1. The upper (green) curve is for μ e1=0.36, the middle (blue) one is for μ e1=0.38, and the lower (pink) one is for μ e1=0.4

    Full size image
  8. 8.

    We have found both compressive and rarefactive GSs co-exist in the system under consideration. It is to be noted that the amplitude of the positive potential GSs decreases (increases) abruptly with the increase (decrease) of relative temperature ratio σ 1 (displayed in Fig. 5) and the amplitude of the negative potential GSs increases (decreases) slightly with the increase (decrease) of relative temperature ratio σ 2 (depicted in Fig. 6).

    Fig. 5
    figure 5

    Showing the variation of amplitude of the positive GSs with σ 1 for μ e1=0.35, μ e2=0.04, κ e1=20, κ e2=2, σ 2=0.1, c 1=7.139, s=1, and U 0=0.1. The upper (green) curve is for σ 1=4.5, the middle (blue) one is for σ 1=3.5, and the lower (pink) one is for σ 1=2.5

    Full size image
    Fig. 6
    figure 6

    Showing the variation of amplitude of the negative GSs with σ 2 for μ e1=0.32, μ e2=0.04, κ e1=20, κ e2=2, σ 1=2.5, c 1=7.139, s=−1, and U 0=0.1. The upper (pink) curve is for σ 2=0.1, the middle (blue) one is for σ 2=0.3, and the lower (green) one is for σ 2=0.5

    Full size image
  9. 9.

    It is observed that negative potential (rarefactive) DLs exist around μ e1<μ d and s=−1. No DLs are found above the critical value (i.e. μ e1>μ d ). Furthermore, it is seen that for larger values of spectral index parameter κ e1, the amplitude of the negative potential DLs increases as displayed in Fig. 7.

    Fig. 7
    figure 7

    Formation of the negative potential DLs due to the variation of κ e1 for μ e1=0.18, μ e2=0.04, κ e2=2, σ 1=2.5, σ 2=0.1, and s=−1. The upper (pink) curve is for κ e1=20, the middle (blue) one is for κ e1=25, and the lower (green) one is for κ e1=30

    Full size image

The ranges of the dusty plasma parameters (Masud et al. 2013a) (viz. σ 1=1.8−5, σ 2=0.1−0.8, μ e1=0.1−0.9 and μ e2=0.01−0.09) used in this numerical analysis are very wide, and correspond to space and laboratory dusty plasma situations. It is observed that superthermality effects play an important role on the variation of amplitude of solitary structures as well as DLs. It may be stressed that the results of our current investigation should be useful in understanding the nonlinear features of electrostatic disturbances in space dusty plasmas, viz. Saturn’s magnetosphere (Baluku and Hellberg 2012), pulsar magnetosphere (Kundu et al. 2011), earth’s magnetospheric plasma sheet (Christon et al. 1988), solar wind (Pierrard and Lemaire 2013) etc., in which negatively charged dust fluid, ions, and electrons of two different temperatures (hot and cold) can be the major plasma species.