1 Introduction

Nowadays, waves in inhomogeneous dusty plasmas which occur in space (e.g., mesospheric noclitlucents clouds, in interstellar clouds, in ring systems of giant planets, in interplanetary space, in cometary tails as well as in laboratory discharges) have attracted a great deal of interest in understanding the electrostatic structures observed in different regions of space and laboratory devices discharges (Shukla and Mamun 2002; Mowafy et al. 2008; El-Wakil et al. 2006a; Asaduzzaman and Mamun 2012). Inhomogeneity may result from magnetic field gradients, temperature and density which appears significantly near the edges and the boundaries of the dusty plasma system. Samaryan et al. (2001) observed experimentally the dust density perturbation in a DC glow discharge in neon and showed that the phase velocity of the density changed along the plasma column. Mowafy et al. (2008) investigated the effect of positive and negative dust charge fluctuation on the amplitude and the width of the dust ion acoustic waves in a collisionless, unmagnetized inhomogeneous dusty plasma comprising cold positive ions, cold positive and negative stationary dust grains, as well as isothermal electrons. More specifically, Zhang and Xue (2005) investigated the properties of linear waves in inhomogeneous plasma with non-adiabatic dust charge fluctuation and nonthermal ions. However, the Maxwellian distribution function, which is in thermal equilibrium, is most frequently used in collisionless plasmas. Accordingly, various observations of fast ions and electrons in space environments indicated that these particles have velocity distributions that are not in thermal equilibrium. Accordingly, Cairns et al. (1995) studied the effect of electrons nonthermality for the observations made by the Freja satellite, while nonthermal ions have been observed in the Earth’s bow-shock (Asbridge et al. 1968). In the last few years, several other studies have been devoted for studying the non-thermal distribution of electrons and ions (Sahu and Roychoudhurya 2006; El-Shewy 2007; Singh and Lakhina 2004; El-Taibany and Sabry 2005; El-Shewy et al. 2008). Later, Asaduzzaman and Mamun (2012) investigated the effects of polarization force and non-Maxwellian nonthermal electrons on properties of DA waves in an inhomogeneous positively charged dusty plasma. Moreover, dusty plasma with dissipative properties supports the existence of shock waves instead of solitary waves. The dissipation in dusty plasma can be caused by Landau damping, dust fluid viscosity, dust-dust collision and dust charge fluctuation, which would modify the wave structures (Nakamura and Sarma 2001; Singh and Rao 1998a; Popel et al. 2000; Nakamura et al. 1999). Under some appropriate conditions, shock waves can be propagated in the system. Experimentally, the effects of dissipation caused by kinematic viscosity on the propagation of solitary wave structure are observed by Nakamura and Sarma (2001). However, the effects of trapped ion on nonlinear DA solitary and shock waves in a strongly coupled dusty plasma or in a magnetized dusty plasma were studied (Mamun 1998; Mamun et al. 2004; Anowar et al. 2009). More specifically, the behavior of the oscillatory shock waves caused by dust fluid viscosity in the dusty plasma has been investigated in two types dust fluid in unmagnetized, collisionless dusty plasma consisting of electrons, singly charged ions, hot and cold dust grains (El-Shewy et al. 2011a, 2011b). Recently, some papers have been devoted to study a theoretical models for the solitary existence in two types of dust fluids in a homogeneous/inhomogeneous plasmas, see for example (El-Wakil et al. 2006b; Mowafy et al. 2008; Mamun and Shukla 2002; Sayed and Mamun 2007; Mamun 2008). The effect of inhomogeneity on the dust fluid dissipation is one of the important problems in dust plasma. Xiao et al. (2006) studied the wave evolution in one-dimension inhomogeneous plasmas through the KdV-Burgers equation. Zhang and Xue (2008) studied the effects of the non-adiabatic dust charge fluctuation and the fast (nonthermal) ions on the instability linear DA waves in inhomogeneous dusty plasmas. They founded that, the presence of non-thermality of ions modifies the linear DA wave properties. Very recently, the bifurcation analysis of both magnetized and unmagnetized plasmas with q-nonextensive velocity distribution are studied via perturbation approaches (Saha and Chatterjee 2014a, 2014b). Therefore, we aim to study the effect of dust viscosity and electron-ion nonthermality fraction on the instability of DA waves in inhomogeneous dusty plasmas with non-adiabatic dust charge fluctuation. Moreover, the nonlinear investigation of the plasma system is carried out by studying the obtained KdV-Burgers equation. The organization of the paper is as follows: In Sect. 2, we present the basic equations. In Sect. 3, the linear dispersion relation has been derived. Section 4 is devoted to the nonlinear analysis of dusty dissipative plasma system via KdV-B equation. Section 5 is kept for conclusion.

2 Governing equations

We consider an inhomogeneous system of an unmagnetized dusty plasma. The system consists of extremely massive, micronsized, negatively charged dust fluid and nonthermal ions, electrons obeying a nonthermal distribution. The plasma is postulated to be inhomogeneous along the vertically oriented tube, chosen to be the x-axis. In case of the steady state, the charge neutrality becomes: n i0(x)=Z d0(x)n d0(x)+n e0(x), where n i0(x), n d0(x), n e0(x) and Z d0(x) refer to the unperturbed ion, dust, electron number densities and the unperturbed number of charges residing on the dust grain, respectively. The dynamics of the DA waves are governed by the basic set of equations

$$\begin{aligned} &\frac{\partial n_{d}}{\partial t}+\frac{\partial ( n_{d} \vartheta _{d} ) }{\partial x}=0, \end{aligned}$$
(1)
$$\begin{aligned} &\frac{\partial \vartheta _{d}}{\partial t}+\vartheta _{d}\frac{\partial \vartheta _{d}}{\partial x}=-q \frac{\partial \phi }{\partial x}+\eta \frac{\partial ^{2} \vartheta _{d}}{\partial x^{2}}, \end{aligned}$$
(2)
$$\begin{aligned} &\frac{\partial ^{2}\phi }{\partial x^{2}}=-qn_{d}+n_{e}-n_{_{i}}, \end{aligned}$$
(3)

where ϑ d refers to the dust fluid velocity normalized to the DA speed \(C_{d}=\sqrt{Z_{d0}(0)T_{i}/ m_{d}}\), with T i refers to the temperature of ions and m d refers to the mass of the negatively charged dust particles, n d refers to the dust grain number density normalized to n d0(0), ϕ refers to the electrostatic potential normalized to (T i /e) with e refers to the magnitude of the electron charge and η refers to the viscosity coefficient. The time and space variables are normalized by the dust plasma period \(\omega _{pd}^{-1}= \sqrt{m_{d}/ 4\pi n_{d0}(0)Z_{d0}^{2}(0)e^{2}}\) and the Debye length λ Dd =C d /ω pd , respectively.

The nonthermal distribution of the ions and the electrons is chosen to take the form

$$\begin{aligned} &n_{_{i}}=\frac{1}{1-\mu (0)} \bigl[ 1+\beta \bigl( \phi +\phi ^{2} \bigr) \bigr] \exp ( -\phi ), \end{aligned}$$
(4)
$$\begin{aligned} &n_{e}=\frac{\mu (x)}{1-\mu (0)} \bigl[ 1-\theta \sigma _{i}\phi + \theta (\sigma _{i}\phi )^{2} \bigr] \exp ( \sigma _{i}\phi ), \end{aligned}$$
(5)

where β=4α/(1+3α), α refers to a parameter determining the number of fast nonthermal ions, μ(x)=n e0(x)/n i0(0), θ=4Δ/(1+3Δ), Δ refers to a parameter determining the number of fast nonthermal electrons and σ i =T i /T e with T e refers to the temperature of electrons.

The charge q=Z d0 e which implies the charge’s sign is normalized by Z d0(0)e which refers to the dust charge at x=0. To determine q, we postulate the following orbital motion-limited (Allen 1992) charge current balance equation. In the normalized form, it will be in the form

$$ \frac{\tau _{ch}}{\tau _{d}} \biggl( \frac{\partial q}{\partial t}+\vartheta _{d} \frac{\partial q}{\partial x} \biggr) =\frac{\tau _{ch}}{Z_{d0}(0)e}(I_{e}+I_{i}), $$
(6)

where I e and I i refer to the electron and ion currents, respectively, and given as

$$\begin{aligned} &I_{e}=-\pi a^{2}e\sqrt{\frac{8T_{e}}{\pi m_{e}}}n_{e0}(x)e^{\sigma _{i}\phi}e^{zq}, \end{aligned}$$
(7)
$$\begin{aligned} &I_{i} =\pi a^{2}e\sqrt{\frac{8T_{i}}{\pi m_{i}}} \frac{n_{i0}(x)}{1+3\alpha } \biggl[ 1+\frac{24\alpha }{5}+\frac{16\alpha }{3}\phi +4\alpha \phi ^{2} \\ &\phantom{I_{i} =\,}- \frac{zq}{\sigma _{i}} \biggl( 1+\frac{8\alpha }{5}+ \frac{8\alpha }{3} \phi +4\alpha \phi ^{2} \biggr) \biggr] \exp ( -\phi ), \end{aligned}$$
(8)

where a refers to the dust grain’s radius and z=z d0(0)e 2/(4πε 0 aT e ), 4πε 0 a refers to the capacitance of the dust grain of radius a. And \(\tau _{d}\approx \omega _{pd}^{-1}\) refers to the dust hydrodynamical time scale and τ ch ≈(dq d /dt)−1 refers to the charging time scale given as

$$ \tau _{ch}= \biggl( \frac{a}{\sqrt{2\pi }}\frac{\omega _{pi}^{2}}{\vartheta _{thi}} \frac{5+8\alpha }{5+15\alpha } \biggl(1+z+\frac{5+24\alpha }{5+8\alpha }\sigma _{i} \biggr) \biggr) ^{-1}, $$
(9)

where ω pi and ϑ thi refer to the ion plasma frequency and the ion thermal velocity, respectively.

In case of the non-adiabatic charge variation, τ ch /τ d is small and finite, (Singh and Rao 1998b) we set

$$ \frac{\tau _{ch}}{\tau _{d}}=\lambda $$
(10)

3 Linear analysis

Firstly, one can study the dispersion properties of the linear waves, in which we express our dependent variables ϑ d , ϕ, q and n d according to the standard-normal mode analysis in terms of the equilibrium and perturbed parts, viz. \(\vartheta _{d}=0+\vartheta _{d}^{\prime }(x,t)\), ϕ=0+ϕ′(x,t), q=q 0(x)+q′(x,t), \(n_{d}=n_{d0}(x)+n_{d}^{\prime }(x,t)\) and substitute them into (1)–(8), we assume all perturbed quantities are proportional to exp[i(kx−ωt)], we get the following set of equations

$$\begin{aligned} &n_{d}^{\prime }(x,t)=\frac{1}{\omega } \biggl( kn_{d0}(x)-i \frac{dn_{d0}(x)}{dx} \biggr) \vartheta _{d}^{\prime }(x,t), \end{aligned}$$
(11)
$$\begin{aligned} &\vartheta _{d}^{^{\prime }}(x,t)=\frac{kq_{0}(x)}{\omega +i\eta k^{2}}\phi ^{^{\prime }}(x,t), \end{aligned}$$
(12)
$$\begin{aligned} &n_{d}^{^{\prime }}(x,t)=\frac{1}{\omega (\omega +i\eta k^{2})} \biggl[kq_{0}(x) \biggl( kn_{d0}(x) \\ &\phantom{n_{d}^{^{\prime }}(x,t)=\,}-i\frac{dn_{d0}(x)}{dx} \biggr) \biggr] \phi ^{^{\prime }}(x,t), \end{aligned}$$
(13)
$$\begin{aligned} &n_{_{i}}=\frac{1}{1-\mu (0)}(\beta -1)\phi ^{\prime }(x,t), \end{aligned}$$
(14)
$$\begin{aligned} &n_{e}=\frac{\mu (x)}{1-\mu (0)}\sigma _{i}(1-\theta )\phi ^{\prime }(x,t), \end{aligned}$$
(15)
$$\begin{aligned} &q^{\prime }(x,t)=\frac{1}{\beta _{1}-i\lambda \omega } \biggl( \beta _{2}- \frac{k\lambda q_{0}(x)}{\omega }\frac{dq_{0}(x)}{dx} \biggr) \phi ^{\prime }(x,t), \end{aligned}$$
(16)

where

$$\begin{aligned} &\beta _{1} =\frac{1+\delta \sigma _{i}}{(1+zq_{0}(x))(1+z+\delta \sigma _{i})},\qquad \delta = \frac{5+24\alpha }{5+8\alpha }, \\ &\beta _{2} =\frac{\sigma _{i}}{z(1+z+\delta \sigma _{i})} \biggl( \frac{zq_{0}(x)}{\sigma _{i}} \frac{15-16\alpha }{15+24\alpha } \\ &\phantom{\beta _{2} =\,}-\frac{\delta \sigma _{i}-zq_{0}(x)}{1+zq_{0}(x)}-\frac{15-8\alpha }{15+24\alpha } \biggr). \end{aligned}$$
(17)

According to this, we get the linear dispersion relation

$$\begin{aligned} &k^{2}-B-\frac{n_{d0}(x)}{\beta _{1}-i\lambda \omega } \biggl( \beta _{2}- \frac{k\lambda q_{0}(x)}{\omega }\frac{dq_{0}(x)}{dx} \biggr) \\ &\quad{}-\frac{kq_{0}^{2}(x)}{\omega ( \omega +i\eta k^{2} ) } \biggl( kn_{d0}(x)-i\frac{dn_{d0}(x)}{dx} \biggr) =0, \end{aligned}$$
(18)

where

$$ B=\frac{1}{1-\mu (0)} \bigl[ (\beta -1)-\mu (x)\sigma _{i}(1-\theta ) \bigr]. $$
(19)

If all the functions n d0(x), q 0(x) and μ(x) are characterized by the exponential forms as

$$\begin{aligned} \begin{aligned} &n_{d0}(x) =n_{d0}(0)\exp ( \alpha _{d}x), \\ &q_{0}(x) =q_{0}(0)\exp (\alpha _{q}x), \\ &\mu (x) =\mu (0)\exp (\alpha _{\mu }x), \end{aligned} \end{aligned}$$
(20)

we get a new dispersion relation in the form

$$\begin{aligned} &k^{2} ( \beta _{1}-i\lambda \omega ) \omega \bigl( \omega +i\eta k^{2} \bigr) -B ( \beta _{1}-i\lambda \omega ) \omega \bigl( \omega +i\eta k^{2} \bigr) \\ &\quad{}-\beta _{2}n_{d0}\omega \bigl( \omega +i\eta k^{2} \bigr) e^{\alpha _{d}x} \\ &\quad{}+k\lambda \alpha _{q}n_{d0}q_{0}^{2} \bigl( \omega +i\eta k^{2} \bigr) e^{2\alpha _{q}x}e^{\alpha _{d}x} \\ &\quad{}-k^{2} ( \beta _{1}-i\lambda \omega ) n_{d0}q_{0}^{2}e^{2\alpha _{q}x}e^{\alpha _{d}x} \\ &\quad{}+ik\alpha _{d}n_{d0}q_{0}^{2} ( \beta _{1}-i\lambda \omega ) e^{2\alpha _{q}x}e^{\alpha _{d}x}=0, \end{aligned}$$
(21)

which can be written in another form as

$$\begin{aligned} &i \bigl( B\lambda -k^{2}\lambda \bigr) \omega ^{3}+ \bigl( -k^{2}B\lambda \eta +k^{2}\lambda \eta -B\beta _{1}+k^{2}\beta _{1} \\ &\quad{}-n_{d0}\beta _{2}e^{\alpha _{d}x} \bigr) \omega ^{2} + \bigl( k^{2}i\lambda n_{d0}q_{0}^{2}e^{2\alpha _{q}x+\alpha _{d}x} \\ &\quad{}+k \lambda n_{d0}q_{0}^{2}\alpha _{d}e^{2\alpha _{q}x+\alpha _{d}x}+k \lambda n_{d0}q_{0}^{2} \alpha _{q}e^{2\alpha _{q}x+\alpha _{d}x} \\ &\quad{} -k^{2}iB\eta \beta _{1}+k^{4}i\eta \beta _{1}-k^{2}i\eta n_{d0}\beta _{2}e^{\alpha _{d}x} \bigr) \omega \\ &\quad{}+k^{3}i\lambda \eta n_{d0}q_{0}^{2} \alpha _{q}e^{2\alpha _{q}x+\alpha _{d}x} -k^{2}n_{d0}q_{0}^{2} \beta _{1}e^{2\alpha _{q}x+\alpha _{d}x} \\ &\quad{}+kin_{d0}q_{0}^{2} \alpha _{d} \beta _{1}e^{2\alpha _{q}x+\alpha _{d}x}=0, \end{aligned}$$
(22)

where \(i=\sqrt{-1}\). Let us consider

$$ \omega =\omega _{r}+i\omega _{i}, $$
(23)

where ω r and ω i refer to the real and imaginary parts.

Considering (22) in view of (23), we get

$$\begin{aligned} &-k^{2}B\lambda \eta \omega _{r}^{2}+k^{2} \lambda \eta \omega _{r}^{2}-k^{2}\lambda n_{d0}q_{0}^{2}\omega _{i}e^{2\alpha _{q}x+\alpha _{d}x} \\ &\quad{}-3B\lambda \omega _{r}^{2}\omega _{i} +3k^{2}\lambda \omega _{r}^{2}\omega _{i}+k^{2}B\lambda \eta \omega _{i}^{2}-k^{4} \lambda \eta \omega _{i}^{2} \\ &\quad{}+B\lambda \omega _{i}^{3}-k^{2}\lambda \omega _{i}^{3} +k\lambda n_{d0}q_{0}^{2} \alpha _{d} \omega _{r}e^{2\alpha _{q}x+\alpha _{d}x} \\ &\quad{}+k\lambda n_{d0}q_{0}^{2} \alpha _{q}\omega _{r}e^{2\alpha _{q}x+\alpha _{d}x} -k^{2}n_{d0}q_{0}^{2} \beta _{1}e^{2\alpha _{q}x+\alpha _{d}x} \\ &\quad{} -B\beta _{1}\omega _{r}^{2}+k^{2} \beta _{1}\omega _{r}^{2}+k^{2}B\eta \beta _{1}\omega _{i} -k^{4}\eta \beta _{1}\omega _{i} \\ &\quad{}+B\beta _{1}\omega _{i}^{2}-k^{2} \beta _{1}\omega _{i}^{2}-n_{d0}\beta _{2}\omega _{r}^{2}e^{\alpha _{d}x} \\ &\quad{}+k^{2}\eta n_{d0}\beta _{2}\omega _{i}e^{\alpha _{d}x}+n_{d0}\beta _{2}\omega _{i}^{2}e^{\alpha _{d}x}=0, \end{aligned}$$
(24)
$$\begin{aligned} &k^{2}\lambda n_{d0}q_{0}^{2}\omega _{r}e^{2\alpha _{q}x+\alpha _{d}x}+B\lambda \omega _{r}^{3}-k^{2} \lambda \omega _{r}^{3}-2Bk^{2}\lambda \eta \omega _{r}\omega _{i} \\ &\quad{}+2k^{4}\lambda \eta \omega _{r}\omega _{i}-3B\lambda \omega _{r}\omega _{i}^{2}+3k^{2} \lambda \omega _{r}\omega _{i}^{2} \\ &\quad{}+k\lambda n_{d0}q_{0}^{2}\alpha _{d}\omega _{i}e^{2\alpha _{q}x+\alpha _{d}x} +k^{3}\lambda \eta n_{d0}q_{0}^{2}\alpha _{q}e^{2\alpha _{q}x+\alpha _{d}x} \\ &\quad{}+k\lambda n_{d0}q_{0}^{2}\alpha _{q}\omega _{i}e^{2\alpha _{q}x+\alpha _{d}x}-k^{2}B\eta \beta _{1}\omega _{r} \\ &\quad{}+k^{4}\eta \beta _{1}\omega _{r}-2B \beta _{1}\omega _{r}\omega _{i}+2k^{2} \beta _{1}\omega _{r}\omega _{i} \\ &\quad{}+kn_{d0}q_{0}^{2}\alpha _{d} \beta _{1}e^{2\alpha _{q}x+\alpha _{d}x} -k^{2}\eta n_{d0}\beta _{2}\omega _{r}e^{\alpha _{d}x} \\ &\quad{}-2n_{d0}\beta _{2}\omega _{r}\omega _{i}e^{\alpha _{d}x}=0. \end{aligned}$$
(25)

By solving the last two equations for ω r ≫ω i , the frequency ω r and the growth rate ω i are given by

$$\begin{aligned} \omega _{r} =&\frac{1}{2} \bigl( k^{2}B\lambda \eta -k^{4}\lambda \eta +B\beta _{1}-k^{2}\beta _{1}+n_{d0}\beta _{2}e^{\alpha _{d}x} \bigr) ^{-1} \\ &{}\times \bigl[ k\lambda n_{d0}q_{0}^{2}\alpha _{d}e^{2\alpha _{q}x+\alpha _{d}x}+k\lambda n_{d0}q_{0}^{2} \alpha _{q}e^{2\alpha _{q}x+\alpha _{d}x} \\ &{}- \bigl( \bigl( \bigl( k\lambda n_{d0}q_{0}^{2} \alpha _{d}e^{2\alpha _{q}x+\alpha _{d}x}+k\lambda n_{d0}q_{0}^{2} \alpha _{q}e^{2\alpha _{q}x+\alpha _{d}x} \bigr) ^{2} \\ &{}+4k^{2}n_{d0}q_{0}^{2}\beta _{1}e^{2\alpha _{q}x+\alpha _{d}x} \bigl(-k^{2}B\lambda \eta +k^{4}\lambda \eta -B\beta _{1} \\ &{}+k^{2}\beta _{1}-n_{d0}\beta _{2}e^{\alpha _{d}x} \bigr) \bigr) \bigr)^{-\frac{1}{2}} \bigr], \end{aligned}$$
(26)
$$\begin{aligned} \omega _{i} =&\frac{1}{2} \bigl( \bigl( B-k^{2} \bigr) \bigl( k^{2}\lambda \eta +\beta _{1} \bigr) +n_{d0}\beta _{2}e^{\alpha _{d}x} \bigr) ^{-3}A^{-\frac{1}{2}}k \\ &{}\times \bigl\{ -n_{d0}^{4}q_{0}^{2} \beta _{2}^{2}e^{2x(2\alpha _{q}+\alpha _{d})}\bigl(k^{2}\lambda ^{2}q_{0}^{2}e^{2\alpha _{q}x} ( \alpha _{d}+\alpha _{q} ) \\ &{}+\bigl(k^{2}\lambda \eta ( -\alpha _{d}+\alpha _{q} ) +2\alpha _{d}\beta _{1}\bigr)\beta _{2}\bigr)+k \bigl( -B+k^{2} \bigr) ^{3} \\ &{}\times \eta \beta _{1} \bigl( k^{2}\lambda \eta +\beta _{1} \bigr) ^{2}A^{\frac{1}{2}}+n_{d0}^{3} \bigl[k^{2}e^{3x ( \alpha _{d}+2\alpha _{q} ) } \\ &{}\times \bigl( -B+k^{2} \bigr) \lambda ^{4}q_{0}^{6} ( \alpha _{d}+\alpha _{q} ) ^{3}+k^{2}e^{3x\alpha _{d}+4x\alpha _{q}} \\ &{}\times \bigl( -B+k^{2} \bigr) \lambda ^{2}q_{0}^{4} ( \alpha _{d}+\alpha _{q} ) \bigl( 2k^{2}\eta \lambda -\beta _{1} \bigr) \beta _{2} \\ &{}-k\eta \beta _{2}^{3}e^{3x\alpha _{d}}A^{\frac{1}{2}}+q_{0}^{2} \beta _{2}^{2}e^{3x\alpha _{d}+2x\alpha _{q}}\bigl( \bigl( -B+k^{2} \bigr) \\ &{}\times \bigl(-2k^{4} \eta ^{2}\lambda ^{2} ( \alpha _{d}-2\alpha _{q} ) +3k^{2}\eta \lambda ( \alpha _{d}+\alpha _{q} ) \beta _{1} \\ &{}+6\alpha _{d}\beta _{1}^{2}\bigr)+k\lambda A^{\frac{1}{2}}\bigr)\bigr]+ \bigl( B-k^{2} \bigr) ^{2}n_{d0} \bigl( k^{2}\eta \lambda +\beta _{1} \bigr) \\ &{}\times \bigl[-k\eta e^{x\alpha _{d}} \bigl( k^{2}\eta \lambda +3 \beta _{1} \bigr) \beta _{2}A^{\frac{1}{2}}+q_{0}^{2}e^{x ( \alpha _{d}+2\alpha _{q} ) } \\ &{}\times \bigl(- \bigl( B-k^{2} \bigr) \bigl( k^{2}\eta \lambda +\beta _{1} \bigr) \bigl(k^{2}\eta \lambda \alpha _{q} \bigl( 2k^{2}\eta \lambda +\beta _{1} \bigr) \\ &{} +\alpha _{d}\beta _{1} \bigl( k^{2}\eta \lambda +2\beta _{1} \bigr) \bigr)+k^{3}\eta \lambda ^{2}A^{\frac{1}{2}}\bigr)\bigr] \\ &{}- \bigl( -B+k^{2} \bigr) n_{d0}^{2} \bigl[ -k \eta e^{2\alpha _{d}x}\bigl(2k^{2}\eta \lambda +3\beta _{1} \bigr)\beta _{2}^{2}A^{\frac{1}{2}} \\ &{}+k\lambda ^{2}q_{0}^{4}e^{2x ( \alpha _{d}+2\alpha _{q} ) } ( \alpha _{d}+\alpha _{q} ) \bigl(k^{3} \bigl( B-k^{2} \bigr) \eta \lambda \beta _{1} \\ &{}+2k \bigl( B-k^{2} \bigr) \beta _{1}^{2}+ \lambda \bigl(k^{5} \bigl( -B+k^{2} \bigr) \eta ^{2}\lambda \\ &{} + ( \alpha _{d}+\alpha _{q} ) A^{\frac{1}{2}}\bigr) \bigr)+q_{0}^{2}\beta _{2} \\ &{}\times e^{2x ( \alpha _{d}+\alpha _{q} ) }\bigl( \bigl( B-k^{2} \bigr) \alpha _{d} \bigl( k^{2}\eta \lambda +\beta _{1} \bigr) \\ &{}\times \bigl(k^{4}\lambda ^{2}\eta ^{2} -3 \beta _{1} \bigl( k^{2}\eta \lambda +2\beta _{1} \bigr) \bigr) \\ &{}+k\lambda \bigl(k \bigl( -B+k^{2} \bigr) \eta \alpha _{q}\bigl(k^{2}\eta \lambda +\beta _{1}\bigr) \bigl(5k^{2}\eta \lambda +3\beta _{1}\bigr) \\ &{}+\bigl(2k^{2}\eta \lambda +\beta _{1} \bigr)A^{\frac{1}{2}}\bigr)\bigr)\bigr]\bigr\} , \end{aligned}$$
(27)

where

$$\begin{aligned} A =&k^{2}n_{d0}q_{0}^{2}e^{x(2\alpha _{q}+\alpha _{d})} \bigl(-4 \bigl( B-k^{2} \bigr) \beta _{1} \bigl( k^{2}\lambda \eta +\beta _{1} \bigr) \\ &{}+n_{d0}e^{\alpha _{d}x} \bigl(\lambda ^{2}q_{0}^{2}e^{2\alpha _{q}x} ( \alpha _{d}+\alpha _{q} ) ^{2}-4\beta _{1}\beta _{2} \bigr) \bigr). \end{aligned}$$
(28)

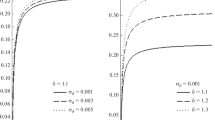
To make our theoretical results physically relevant, numerical calculations have been made using plasma parameters close to those values corresponding to typical dusty plasma, i.e., n d0(0)∼105 cm−3, n i0(0)∼109 cm−3, n e0(0)∼108 cm−3, T d ∼0.05 eV, T i ∼0.1 eV, T e ∼2 eV, a∼1 μm, m d ∼10−12 g∼1012 m i , respectively, as given in Zhang and Xue (2008). Both the frequency ω r and the growth rate ω i of the dust acoustic waves (DAW) in an unmagnetized inhomogeneous viscous dusty plasma consisting of extremely massive, micronsized, negatively charged dust fluid with nonthermal ions and electrons have been studied. The application of the linear normal mode analysis to the basic set of system fluid equations leads to the linear dispersion relation for low frequency waves in nonuniform dusty plasmas. To investigate the effects of nonthermality fraction of ions and electrons and dust kinematic viscosity coefficient on the instability of the (DAW), we proposed that all the inhomogeneity functions depend exponentially on space x. It is noticed that, the dispersion relation is dependent on dust kinematic viscosity coefficient, nonthermality of ions and electrons, inhomogeneity and non-adiabatic dust charge variation. The effect of parameters like the dust kinematic viscosity coefficient η, the fraction of nonthermality energetic population of electron-ion Γ, the temperature of ions σ i , the non-adiabatic dust charge variation λ and the carrier wave number k on the frequency ω r and growth rate ω i of the (DAW) mode are shown in Figs. 1, 2 and 3. The variation of ω r and ω i with the parameters η and Γ are shown in Fig. 1. It is founded that the increase of the kinematic viscosity coefficient η and the fraction of nonthermality energetic population of electron-ion Γ decreases the frequency ω r and the growth rate ω i . On the other hand, the variation of ω r and ω i with the parameters σ i and λ are shown in Fig. 2. It is emphasized that both the frequency ω r and the growth rate ω i decrease as σ i increases, while the increase of λ deceases the frequency ω r but increases the growth rate ω i . Finally, the increase of the parameter k decreases the frequency ω r but increases the growth rate ω i as depicted in Fig. 3.

Fig. 1
figure 1

The variation of ω r and ω i against η for different values of Γ for σ i =0.2, λ=50, k=6, x=0.2, z=2, μ=0.7, n d0=100000, α d =−4, α q =−5, α μ =−6

Full size image
Fig. 2
figure 2

The variation of ω r and ω i against σ i for different values of λ for α=0.6, Δ=0.2, k=6, η=0.01, x=0.2, z=2, μ=0.7, n d0=100000, α d =−4, α q =−5, α μ =−6

Full size image
Fig. 3
figure 3

The variation of ω r and ω i against x for different values of k for α=0.1, Δ=0.2, σ i =0.2, λ=100, η=0.6, z=2, μ=0.7, n d0=100000, α d =−4, α q =−5, α μ =−6

Full size image

In order to proceed further, we extend our investigation to include the characteristics of nonlinear waves (e.g. soliton and shock waves) of the plasma system under consideration.

4 Nonlinear analysis

4.1 KdV-Burgers equation

To study the nonlinear characteristics of the shock wave due to the viscosity, the reductive perturbation technique (Washimi and Taniuti 1966) has been used. In this section, we restrict our analysis to the case of homogeneous viscous dusty plasmas where the functions μ(x) and q(x,t) in the basic equations (1)–(5) are constants. According to the general method of reductive perturbation theory, we introduce the slow stretched coordinates

$$ \tau =\varepsilon ^{\frac{3}{2}}t,\qquad \xi =\varepsilon ^{\frac{1}{2}}(x- \tilde{\lambda}t),\qquad \eta =\varepsilon ^{\frac{1}{2}}\eta _{1}, $$
(29)

where ε is a small dimensionless expansion parameter measuring the strength of nonlinearity and \(\tilde{\lambda}\) is the wave speed. Expanding the physical quantities appearing in the basic equations and substituting into the basic equations, we finally obtain, after cumbersome of algebraic manipulations, the KdV-B equation as

$$ \frac{\partial \phi _{1}}{\partial \tau }+A\;\phi _{1}\frac{\partial \phi _{1}}{\partial \xi }+B\frac{\partial ^{3}\phi _{1}}{\partial \xi ^{3}} +C\frac{\partial ^{2}\phi _{1}}{\partial \xi ^{2}}=0, $$
(30)

where

$$\begin{aligned} &A =\frac{\tilde{\lambda}^{3}}{2q^{2}} \bigl(\mu _{i}- \mu _{e}\sigma _{i}^{2} \bigr)+\frac{3q}{2\tilde{\lambda}}, \\ &B =\frac{\tilde{\lambda}^{3}}{2q^{2}},\qquad C=-\frac{1}{2}\eta _{1}, \\ &\tilde{\lambda} =\sqrt{\frac{-q^{2}}{\mu _{e}(\theta -1)\sigma _{i}+\mu _{i}(\beta -1)}}. \end{aligned}$$
(31)

By using the co-moving coordinate system that is needed as χ=ξ−u 0 τ where u 0 is the velocity of the wave, and integrating with respect to the variable χ, the reduced KdV-B equation is

$$ \frac{d^{2}\phi _{1}}{d\chi ^{2}}-\frac{u_{0}}{B}\phi _{1}+\frac{A}{2B}\phi _{1}^{2}+\frac{C}{B}\frac{d\phi _{1}}{d\chi }=0. $$
(32)

Owing to the presence of the Burgers term \(\frac{C}{B}\frac{d\phi _{1}}{d\chi }\), (32) describes homogeneous and dissipative dusty plasmas. Particularly, if the Burgers coefficient C=0, the system of equations becomes conservative (i.e., \(\frac{dE}{d\chi }=0\)) and the total energy is

$$ \frac{1}{2} \biggl( \frac{d\phi _{1}}{d\chi } \biggr) ^{2}- \frac{u_{0}}{2B}\phi _{1}^{2}+\frac{A}{6B}\phi _{1}^{3}=E, $$
(33)

where the potential function V(ϕ 1) is given by

$$ V(\phi _{1})=-\frac{u_{0}}{2B}\phi _{1}^{2}+ \frac{A}{6B}\phi _{1}^{3}. $$
(34)

The existence of stable solitonic solution should satisfy the condition \(\frac{d^{2}V}{d\phi _{1}^{2}}<0\) at ϕ 1=0. In connection with (34), it is clear that this condition is satisfied and hence (32) has the following compressive stable solitonic solution

$$ \phi _{1}=\frac{3u_{0}}{A}\operatorname{sech}^{2} \biggl( \sqrt{\frac{u_{0}}{4B}}\chi \biggr) . $$
(35)

The behavior of the obtained solution is shown graphically in Fig. 4.

Fig. 4
figure 4

The variation of ϕ 1 against χ for different values of Γ for σ i =0.2, u 0=0.4, q=1

Full size image

If C≠0, the system of equations is dissipative and then the total energy E is not conserved. In this case, the exact solution of (32) can be constructed by means of different mathematical methods (Dutta et al. 2012; El-Hanbaly 2003; El-Hanbaly and Abdou 2006; El-Wakil et al. 2014; Mahmood and Ur-Rehman 2010). Among those, the tanh method has been proved to be a powerful mathematical technique for solving nonlinear partial differential equations (Malfliet and Hereman 1996).

Following the procedure of the tanh method, we consider the solution in the following form

$$ \phi _{1}=\sum_{n=0}^{N}a_{n} \tanh^{n}(\chi ), $$
(36)

where the coefficients a n and N should be determined. Balancing the nonlinear and dispersion terms in (32), we obtain N=2. Substituting (36) into (32) and equating to zero the different coefficients of different powers of tanh(χ) functions, one can write down the following solution of KdV-B equation

$$\begin{aligned} \phi _{1} =&\frac{u_{0}}{A}+\frac{8B}{A}+\frac{C^{2}}{25AB}+ \frac{12C}{5A}\tanh (\chi ) \\ &{}-\frac{12B}{A}\tanh^{2}(\chi ), \end{aligned}$$
(37)

or

$$\begin{aligned} \phi _{1} =&7\frac{1}{A} \biggl( u_{0}-4B+ \frac{C^{2}}{25B}+\frac{12C}{5}\tanh (\chi ) \\ &{}+12B\operatorname{sech}^{2}( \chi ) \biggr). \end{aligned}$$
(38)

It is obviously, this class of solution represents a particular combination of a solitary wave (\(\operatorname{sech}^{2}(\chi )\) term on the right hand side of (38)) with a Burgers shock wave (tanh(χ) term). The behavior of this solution is shown graphically in Fig. 5.

Fig. 5
figure 5

The variation of ϕ 1 against χ for different values of Γ for σ i =0.2, η 1=0.6, u 0=0.4, q=1

Full size image

5 Conclusion

The characteristics of linear and nonlinear dust acoustic waves in viscous dusty plasmas with nonthermal electrons and ions have been investigated. In the linear analysis, it is found that the combined influence of the dust kinematic viscosity coefficient η, the fraction of nonthermality energetic population of electron-ion Γ, the temperature of ions σ i , the non-adiabatic dust charge variation λ and the carrier wave number k can produce novel instabilities involving the DAWs. The given plasma parameters would modify the properties of linear dust acoustic in nonuniform plasma. So, we are hoping that forthcoming space missions and Hubble Space Telescope observations shall provide more observations that may lend support to our theoretical predictions.

On the other hand, the nonlinear analysis for the homogeneous dissipation arising from fluid viscosity dusty plasma is considered to investigate the propagation characteristics of finite amplitude shock wave. By means of reductive perturbation method, the fluid model reduces to KdV-B equation which is not integrable Hamiltonian system. This means that the energy of plasma system is not conserved due to Burgers term. In the absence of Burgers term the equation reduces to the integrable Hamiltonian KdV equation. By solving the obtained KdV-B equation, we succeed to distinguish some interesting classes of analytical solutions due to Burgers coefficient C. The compressive soliton solution exist when C=0 (Fig. 4). If C≠0, KdV-B equation is solved by using tanh method and exhibits a solution which is a particular combination of a solitary wave with a Burgers shock wave (Fig. 5). The real application of obtained results might be particularly interesting in the context of space plasma, particularly, the properties of linear and nonlinear DAWs that may propagate in cometary tails and mesospheric dusty plasma.