Keywords

1 Introduction

Investigation of ion-acoustic solitary waves is an interesting research problem in the field of plasma physics that has been extensively studied by numerous authors [1,2,3,4]. For the first time, Washimi and Taniuti [5] observed the distinctive behaviour of ion-acoustic solitary waves in plasma, which can be investigated using the Korteweg-de Vries (K-dV) equation. After that, ion-acoustic solitary waves in both magnetized and unmagnetized plasmas have been studied by a large number of researchers in different theoretical and experimental circumstances during the past few decades. There has been a lot of interest in the investigation of different types of nonlinear solitary waves in plasmas, like magneto-acoustic solitary waves, spherical and cylindrical-acoustic solitary waves, and lower-hybrid solitary waves [6,7,8,9]. A study of ion-acoustic solitary waves in magnetized negative ion plasma consisting of nonthermal electrons was carried out by Labany et al. [10]. They observed that the solitary waves are substantially influenced by the positive-to-negative ion mass ratio, the corresponding negative-to-positive ion density ratio, and the parameters of nonthermal electrons. For analysing ion-acoustic waves in a magnetized plasma, Zakharov and Kuznetsov developed the nonlinear equation known as the ZK equation. This ZK equation may be found in many branches of physics, such as fluid mechanics, astrophysics, solid state physics, and so on [11, 12]. It is most apparent in the subject of plasma physics. Using the extended tanh approach and the direct assumption method, Li et al. derived the ZK equation and got an exact travelling wave solution [13]. Taibany et al. [14] developed the ZK equation to investigate the IASWs in a magnetized multicomponent dusty plasma with negative ions. Recently, many researchers have been showing an interest in studying the impact of nonextensive electron distribution on IASWs in magnetized plasma. Mandi et al. [15] have investigated the effect of the q-nonextensivity of electrons on the characteristics of IASWs. Furthermore, the propagation of solitons in nonthermal plasma has generated much interest among researchers. Because of their practical significance, they continue to pique people's curiosity. Many studies in plasma physics, as well as complex plasma, have focused on ion-acoustic solitary waves and their properties in the field of nonthermal plasma. Pakzad [16] studied the behaviour of soliton structures in a three-component unmagnetized plasma containing cold ions, nonthermal electrons, and positrons. Dev et al. [17] studied the dust IASWs in a magnetized plasma in the presence of nonthermal electrons, positrons and relativistic thermal ions. They discovered that in the absence of nonthermal electron and positron populations, the plasma system behaves in the least nonlinear manner, but the system behaves in the most nonlinear manner when the populations of nonthermal electrons and positrons have the maximal value. In their investigation into three-dimensional ion-acoustic soliton structures, including warm ions, positrons, and nonthermal electrons, Chawla et al. [18] reveal that the presence of nonthermal electrons considerably impacts the amplitude and width of soliton pulses.

In this paper, the effects of nonthermal electrons, nonthermal positrons, and the influence of magnetic fields on the structure of three-dimensional nonlinear IASWs are investigated. We anticipate that the presence of nonthermal electrons and positrons will alter the characteristics of solitons as well as their existence regime.

2 Basic Model Equations

We consider a plasma model with constituent ions, nonthermal electrons and nonthermal positrons, where the magnetic field \(B_{0}\) is along the z-axis. The following normalized sets of ion continuity equations, momentum equations, and Poisson equations serve as the governing equations for the current plasma model:

$$\frac{{\partial n_{i} }}{\partial t} + \frac{{\partial \left( {n_{i} u} \right)}}{\partial x} + \frac{{\partial \left( {n_{i} v} \right)}}{\partial y} + \frac{{\partial \left( {n_{i} w} \right)}}{\partial z} = 0$$
(1)
$$\frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + w\frac{\partial u}{{\partial z}} = - \frac{\partial \phi }{{\partial x}} + \frac{{\Omega_{i} }}{{\omega_{pi} }}v$$
(2)
$$\frac{\partial v}{{\partial t}} + u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} + w\frac{\partial v}{{\partial z}} = - \frac{\partial \phi }{{\partial y}} - \frac{{\Omega_{i} }}{{\omega_{pi} }}u$$
(3)
$$\frac{\partial w}{{\partial t}} + u\frac{\partial w}{{\partial x}} + v\frac{\partial w}{{\partial y}} + w\frac{\partial w}{{\partial z}} = - \frac{\partial \phi }{{\partial z}}$$
(4)
$$\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi }}{{\partial y^{2} }} + \frac{{\partial^{2} \phi }}{{\partial z^{2} }} = n_{e} - \mu_{p} n_{p} - \mu_{i} n_{i}$$
(5)

The Boltzmann distributions [17] for nonthermal electrons and positrons are defined as

$$n_{e} = \left( {1 - \beta_{e} \phi + \beta_{e} \phi^{2} } \right)\exp \left( \phi \right)$$
(6)
$$n_{p} = \left( {1 + \sigma_{pe} \beta_{p} \phi + \sigma_{pe}^{2} \beta_{p} \phi^{2} } \right)\exp \left( { - \sigma_{pe} \phi } \right)$$
(7)

In the above expressions.

Also \(\mu_{p} = \frac{{n_{p0} }}{{n_{e0} }},\) \(\mu_{i} = \frac{{n_{i0} }}{{n_{e0} }}\) and \(\sigma_{pe} = \frac{{T_{e} }}{{T_{p} }}.\)

$$\beta_{e} = \frac{{4\alpha_{e} }}{{1 + 3\alpha_{e} }},\beta_{p} = \frac{{4\alpha_{p} }}{{1 + 3\alpha_{p} }}$$

here, \(\alpha_{e}\) is the nonthermal parameter for electrons and \(\alpha_{p}\) is the nonthermal parameter for positrons, which represent the population of energetic nonthermal electrons and positrons, respectively. \(T_{e}\) and \(T_{p}\) are the temperatures of electrons and positrons. In the above equations, the ion number densities \(n_{i}\) are normalized by \(n_{i0}\) and velocities \(\left( {u,v,w} \right)\) by the ion-acoustic speed \(C_{s} = \left( {T_{e} /m_{i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\), where \(m_{i}\) is the ion mass. Space coordinates \(\left( {x,y,z} \right)\) and time \(t\) are normalized in terms of Debye length \(\lambda_{D} = \left( {\varepsilon_{0} T_{e} /n_{i}^{0} e^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) and the inverse of plasma frequency \(\omega_{pi} = \left( {{{4\pi e^{2} n_{i}^{0} } \mathord{\left/ {\vphantom {{4\pi e^{2} n_{i}^{0} } {m_{i} }}} \right. \kern-\nulldelimiterspace} {m_{i} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) respectively. The electric potential \(\phi\) is normalized by \({{T_{e} } \mathord{\left/ {\vphantom {{T_{e} } e}} \right. \kern-\nulldelimiterspace} e}\), where e is the electronic charge. \(\Omega_{i}\) and \(\omega_{pi}\) are the ion-cyclotron frequency and plasma frequency.

3 Reductive Perturbation Method

To derive the ZK equation from the above basic set of equations, we used the reductive perturbation technique. The stretching coordinates [10, 19] are assume as

$$\xi = \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} x,\eta = \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} y,\zeta = \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {z - \lambda_{0} t} \right)\,{\text{and}}\,\tau = \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} t$$
(8)

where the symbol \(\varepsilon\) is the expansion parameter that measures the strength of nonlinearity and \(\lambda_{0}\) is the phase velocity of IASWs. We express the physical parameters in the power series expansion of \(\varepsilon\) in the following way:

$$\left. \begin{gathered} n_{i} = 1 + \varepsilon^{1} n^{1} + \varepsilon^{2} n^{2} + \varepsilon^{3} n^{3} + .... \hfill \\ u = \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} u^{1} + \varepsilon^{2} u^{2} + \varepsilon^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-\nulldelimiterspace} 2}}} u^{3} + .... \hfill \\ v = \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} v^{1} + \varepsilon^{2} v^{2} + \varepsilon^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-\nulldelimiterspace} 2}}} v^{3} + .... \hfill \\ w = 0 + \varepsilon^{1} w^{1} + \varepsilon^{2} w^{2} + \varepsilon^{3} w^{3} + .... \hfill \\ \phi = 0 + \varepsilon^{1} \phi^{1} + \varepsilon^{2} \phi^{2} + \varepsilon^{3} \phi^{3} + .... \hfill \\ \end{gathered} \right\}$$
(9)

We transform \(x\) and \(t\) by using the stretch coordinates as

$$\left. \begin{gathered} \frac{\partial }{\partial x} \equiv \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial }{\partial \xi },\frac{\partial }{\partial y} \equiv \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial }{\partial \eta },\frac{\partial }{\partial z} \equiv \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial }{\partial \zeta },\frac{\partial }{\partial t} \equiv - \lambda_{0} \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial }{\partial \zeta } + \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial }{\partial \tau } \hfill \\ \frac{{\partial^{2} }}{{\partial x^{2} }} \equiv \varepsilon \frac{{\partial^{2} }}{{\partial \xi^{2} }},\frac{{\partial^{2} }}{{\partial y^{2} }} \equiv \varepsilon \frac{{\partial^{2} }}{{\partial \eta^{2} }},\frac{{\partial^{2} }}{{\partial z^{2} }} \equiv \varepsilon \frac{{\partial^{2} }}{{\partial \zeta^{2} }} \hfill \\ \end{gathered} \right\}$$
(10)

Using (10), the transformation equations of (1)–(5) may be obtained as

$$- \lambda_{0} \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{{\partial n_{i} }}{\partial \zeta } + \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{{\partial n_{i} }}{\partial \tau } + \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{{\partial \left( {n_{i} u} \right)}}{\partial \xi } + \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{{\partial \left( {n_{i} v} \right)}}{\partial n} + \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{{\partial \left( {n_{i} w} \right)}}{\partial \zeta } = 0$$
(11)
$$- \lambda_{o} \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial u}{{\partial \zeta }} + \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial u}{{\partial \tau }} + u\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial u}{{\partial \xi }} + v\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial u}{{\partial \eta }} + w\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial u}{{\partial \zeta }} = - \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial \phi }{{\partial \xi }} + \frac{{\Omega_{i} }}{{\omega_{pi} }}v$$
(12)
$$- \lambda_{o} \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial v}{{\partial \zeta }} + \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial v}{{\partial \tau }} + u\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial v}{{\partial \xi }} + v\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial v}{{\partial \eta }} + w\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial v}{{\partial \zeta }} = - \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial \phi }{{\partial \eta }} + \frac{{\Omega_{i} }}{{\omega_{pi} }}u$$
(13)
$$- \lambda_{o} \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial w}{{\partial \zeta }} + \varepsilon^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial w}{{\partial \tau }} + u\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial w}{{\partial \xi }} + v\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial w}{{\partial \eta }} + w\varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial w}{{\partial \zeta }} = - \varepsilon^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{\partial \phi }{{\partial \zeta }}$$
(14)
$$\varepsilon \frac{{\partial^{2} \phi }}{{\partial \xi^{2} }} + \varepsilon \frac{{\partial^{2} \phi }}{{\partial \eta^{2} }} + \varepsilon \frac{{\partial^{2} \phi }}{{\partial \zeta^{2} }} = n_{e} - \mu_{p} n_{p} - \mu_{i} n_{i}$$
(15)

Now using (9) in the above equations and then collecting the lowest order terms.

in \(\varepsilon\), we get

$$\left. {\begin{array}{*{20}c} {n^{1} = \frac{{w^{1} }}{{\lambda_{0} }},} & {w^{1} = \frac{{\phi^{1} }}{{\lambda_{0} }},} \\ {u^{1} = - \frac{{\omega_{pi} }}{{\Omega_{i} }}\frac{{\partial \phi^{1} }}{\partial \eta },} & {\phi^{1} = \frac{{\mu_{i} n^{1} }}{{\left( {1 - \beta_{e} + \mu_{p} \sigma_{pe} - \beta_{p} \mu_{p} \sigma_{pe} } \right)}}} \\ {v^{1} = \frac{{\omega_{pi} }}{{\Omega_{i} }}\frac{{\partial \phi^{1} }}{\partial \xi },} & {} \\ \end{array} } \right\}$$
(16)

After solving for the first order perturbation terms, the dispersion relation of nonlinear IASWs is obtained as

$$\lambda_{0} = \sqrt {\frac{{\mu_{i} }}{{1 - \beta_{e} + \mu_{p} \sigma_{pe} - \beta_{p} \mu_{p} \sigma_{pe} }}}$$
(17)

Equation (17) represents the phase velocity of nonlinear IASWs.

The next higher order of \(\varepsilon\) gives

$$u^{2} = \frac{{\omega_{pi} \lambda_{0} }}{{\Omega_{i} }}\frac{{\partial v^{1} }}{\partial \zeta },$$
(18)
$$v^{2} = - \frac{{\omega_{pi} \lambda_{0} }}{{\Omega_{i} }}\frac{{\partial u^{1} }}{\partial \zeta },$$
(19)
$$\frac{{\partial n_{i}^{1} }}{\partial \tau } - \lambda_{0} \frac{{\partial n_{i}^{2} }}{\partial \zeta } + \frac{{\partial u^{2} }}{\partial \xi } + \frac{{\partial v^{2} }}{\partial \eta } + \frac{{\partial w^{2} }}{\partial \zeta } + \frac{{\partial (n_{i}^{1} w^{1} )}}{\partial \zeta } = 0,$$
(20)
$$\frac{{\partial w^{1} }}{\partial \tau } - \lambda_{0} \frac{{\partial w^{2} }}{\partial \zeta } + w^{1} \frac{{\partial w^{1} }}{\partial \zeta } + \frac{{\partial \phi^{2} }}{\partial \zeta } = 0,$$
(21)
$$\begin{aligned} & \frac{{\partial^{2} \phi^{1} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \phi^{1} }}{{\partial \eta^{2} }} + \frac{{\partial^{2} \phi^{1} }}{{\partial \zeta^{2} }} - \left( {1 - \beta_{e} + \mu_{p} \sigma_{pe} - \beta_{p} \mu_{p} \sigma_{pe} } \right)\phi^{2} \\ & - \frac{1}{2}\left( {1 - \sigma_{pe}^{2} \mu_{p} } \right)\left( {\phi^{1} } \right)^{2} + \mu_{i} n^{2} = 0, \\ \end{aligned}$$
(22)

Now, differentiating equation (22) w.r.t \(\zeta\), we get

$$\begin{aligned} & \frac{\partial }{\partial \zeta }\left( {\frac{{\partial^{2} \phi^{1} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \phi^{1} }}{{\partial \eta^{2} }}} \right) + \frac{{\partial^{3} \phi^{1} }}{{\partial \zeta^{3} }} - \left( {1 - \beta_{e} + \mu_{p} \sigma_{pe} - \beta_{p} \mu_{p} \sigma_{pe} } \right)\frac{{\partial \phi^{2} }}{\partial \zeta } \\ & - \left( {1 - \sigma_{pe}^{2} \mu_{p} } \right)\phi^{1} \frac{{\partial \phi^{1} }}{\partial \zeta } + \mu_{i} \frac{{\partial n^{2} }}{\partial \zeta } = 0. \\ \end{aligned}$$
(23)

Now, using the lowest order terms, the Eq. (23) can be written as

$$\frac{\partial }{\partial \zeta }\left( {\frac{{\partial^{2} \phi^{1} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \phi^{1} }}{{\partial \eta^{2} }}} \right) + \frac{{\partial^{3} \phi^{1} }}{{\partial \zeta^{3} }} - \frac{{\mu_{i} }}{{\lambda_{0}^{2} }}\frac{{\partial \phi^{2} }}{\partial \zeta } - \left( {1 - \sigma_{pe}^{2} \mu_{p} } \right)\phi^{1} \frac{{\partial \phi^{1} }}{\partial \zeta } + \mu_{i} \frac{{\partial n^{2} }}{\partial \zeta } = 0.$$
(24)

Now, eliminating the second order quantities from (20), (21) and (24), we obtain the ZK equation in terms of \(\phi^{1}\) as

$$\frac{{\partial \phi^{1} }}{\partial \tau } + A\phi^{1} \frac{{\partial \phi^{1} }}{\partial \zeta } + B\frac{{\partial^{3} \phi^{1} }}{{\partial \zeta^{3} }} + C\frac{\partial }{\partial \zeta }\left( {\frac{{\partial^{2} \phi^{1} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \phi^{1} }}{{\partial \eta^{2} }}} \right) = 0,$$
(25)

where the non-linear coefficient \(A\) is given by

$$A = \frac{2}{{\lambda_{0} }} - \frac{{\lambda_{0}^{3} }}{{2\mu_{i} }}\left( {1 - \sigma_{pe}^{2} \mu_{p} } \right).$$

\(B\) and \(C\) are the dispersive and higher order coefficients, expressed as

$$B = \frac{{\lambda_{0}^{3} }}{{2\mu_{i} }},\,{\text{and}}\,C = \frac{{\lambda_{0}^{3} }}{{2\mu_{i} }} + \frac{{\lambda_{0}^{3} }}{2}\frac{{\omega_{pi}^{2} }}{{\Omega_{i}^{2} }}.$$

4 Solution of ZK Equation

To analyse the Eq. (25), we use the \(tanh\) method. We consider the transformation \(\chi = \gamma \left( {l\xi + m\eta + n\zeta - U\tau } \right)\), where \(\phi \left( {\xi ,\eta ,\zeta ,\tau } \right) = \psi \left( \chi \right)\), we can use the following changes:

$$\begin{aligned} & \frac{\partial }{\partial \tau } \equiv - U\gamma \frac{d}{d\chi },\frac{\partial }{\partial \xi } \equiv l\gamma \frac{d}{d\chi },\frac{\partial }{\partial \eta } \equiv \gamma m\frac{d}{d\chi },\frac{\partial }{\partial \zeta } \equiv \gamma n\frac{d}{d\chi }, \\ & \frac{{\partial^{2} }}{{\partial \xi^{2} }} \equiv \gamma^{2} l^{2} \frac{{d^{2} }}{{d\chi^{2} }},\frac{{\partial^{2} }}{{\partial \eta^{2} }} \equiv \gamma^{2} m^{2} \frac{{d^{2} }}{{d\chi^{2} }},\frac{{\partial^{3} }}{{\partial \zeta^{3} }} \equiv \gamma^{3} n^{3} \frac{{d^{3} }}{{d\chi^{3} }} \\ \end{aligned}$$

Now the Eq. (25) becomes a reduced ordinary differential equation as

$$- U\gamma \frac{d\psi }{{d\chi }} + \frac{A\gamma n}{2}\frac{{d\psi^{2} }}{d\chi } + B\gamma^{3} n^{3} \frac{{d^{3} \psi }}{{d\chi^{3} }} + C\gamma n\frac{d}{d\chi }\left[ {\gamma^{2} \left( {l^{2} + m^{2} } \right)\frac{{d^{2} \psi }}{{d\chi^{2} }}} \right] = 0.$$
(26)

Integrating the above equation, we get

$$- U\psi + \frac{1}{2}An\psi^{2} + \gamma^{2} n\left[ {Bn^{2} + C\left( {l^{2} + m^{2} } \right)} \right]\frac{{d^{2} \psi }}{{d\chi^{2} }} = 0$$
(27)

To solve the above equation, we use the \(tanh\) method. Consider a new independent variable as:

\(z = \tan \left( \chi \right)\), where \(\psi \left( \chi \right) = w\left( z \right)\).

and we get.

\(\frac{{d^{2} }}{{d\chi^{2} }} = \left( {1 - z^{2} } \right)^{2} \frac{{d^{2} }}{{dz^{2} }} - 2z\left( {1 - z^{2} } \right)\frac{d}{dz}\).

Now the Eq. (27) becomes

$$\begin{aligned} & - Uw + \frac{1}{2}Anw^{2} + \gamma^{2} n\left( {Bn^{2} + C\left( {l^{2} + m^{2} } \right)} \right)\left( {1 - z^{2} } \right)^{2} \frac{{d^{2} w}}{{dz^{2} }} \\ & - 2\gamma^{2} n\left( {Bn^{2} + C\left( {l^{2} + m^{2} } \right)} \right)z\left( {1 - z^{2} } \right)\frac{dw}{{dz}} = 0. \\ \end{aligned}$$
(28)

In the tanh method the series solution of the Eq. (28) can be written as:

$$w(z) = \sum\limits_{i = 1}^{m} {a_{i} z^{i} }$$
(29)

In Eq. (29), the value of \(m\) can be obtained by balancing the highest order linear term with the nonlinear terms. On substitution of Eq. (29) into Eq. (28), we get \(m = 2\).

As a result, the solution \(w(z) = \sum\limits_{i = 1}^{m} {a_{i} z^{i} }\) is of the form

$$w\left( z \right) = a_{0} + a_{1} z + a_{2} z^{2} .$$
(30)

Now substituting \(w,\)\(\frac{dw}{{dz}},\)\(\frac{{d^{2} w}}{{dz^{2} }}\) from (30) into (28), then equating different coefficient of \(z\), we get.

\(a_{0} = - a_{2}\) and \(a_{1} = 0\).

Hence Eq. (30) reduce as

$$w\left( z \right) = a_{0} \left( {1 - z^{2} } \right).$$
(31)

Using (31) into (28) and equating the coefficients of \(z^{2}\), we get

$$a_{0} = \frac{{12\gamma^{2} \left[ {Bn^{2} + C\left( {l^{2} + m^{2} } \right)} \right]}}{A}.$$

And hence \(\gamma = \sqrt {\frac{U}{{4n\left( {Bn^{2} + C\left( {l^{2} + m^{2} } \right)} \right)}}} .\)

Using the values of the parameters, Eq. (31) provides a solution as

$$\phi = \phi_{m} {\text{sech}}^{2} \left( {\frac{\chi }{W}} \right).$$
(32)

Here, (32) represents the solution of the Eq. (25), where \(\phi_{m}\) and \(W\) are the amplitude and width of the soliton.

$${\text{Where}}\,\phi_{m} = \frac{3U}{{An}}$$
(33)

and

$$W = \sqrt {\frac{U}{{4n\left( {Bn^{2} + C\left( {l^{2} + m^{2} } \right)} \right)}}}.$$
(34)

5 Results and Discussion

For the study of soliton structures due to the existence of nonthermal components of electrons and positrons, we have plotted the variation of nonlinear coefficient \(A\) with electron-to-positron temperature ratio \(\left( {\sigma_{pe} } \right)\), positron-to-electron density ratio \(\left( {\mu_{p} } \right)\) and ion-to-electron density ratio \(\left( {\mu_{i} } \right)\) for different parameters of nonthermal electrons and positrons. The polarity (positive or negative) of the soliton structure completely depends on the sign of the nonlinear coefficient \(A\). The positive polarity (compressive soliton) structure exists for the positive value of the nonlinear coefficient and the negative polarity (rarefactive soliton) structure exists for the negative value of the nonlinear coefficient. Figure 1 shows that the nonlinearity of plasma increases with the electron-to-positron temperature ratio \(\left( {\sigma_{pe} } \right)\). The same result has been observed in Fig. 2, where the nonlinearity changes with the positron-to-electron density ratio \(\left( {\mu_{p} } \right)\). The variation of nonlinearity with ion-to-electron density ratio \(\left( {\mu_{i} } \right)\) in Fig. 3 shows the existence of rarefactive soliton structures. It can be seen from this graph that the sign of nonlinearity becomes negative after a certain value of \(\mu_{i}\). Therefore, the parameter \(\mu_{i}\) is very crucial to obtaining rarefactive soliton structures. The range of the parameter \(\mu_{i}\) for the existence of negative polarity can be obtained from Fig. 3b. Further, it is observed that, in all cases, the nonlinearity of plasma decreases as the parameters of nonthermal electrons and positrons are increased.

Fig. 1
figure 1

Variation of nonlinear coefficient against electron-to-positron temperature ratio \(\left( {\sigma_{pe} } \right)\) with \(\mu_{i} =\) 0.3 and \(\mu_{p} =\) 0.2. Blue line corresponds to \(\alpha_{e} = 0.01\), \(\alpha_{p} = 0.02\); black line corresponds to \(\alpha_{e} = 0.03\), \(\alpha_{p} = 0.04\); red line corresponds to \(\alpha_{e} = 0.05\), \(\alpha_{p} = 0.06\)

Full size image
Fig. 2
figure 2

Variation of nonlinear coefficient against positron-to-electron density ratio \(\left( {\mu_{p} } \right)\) with \(\sigma_{pe} = 0.1\) and \(\mu_{i} = 0.3\). Blue line corresponds to \(\alpha_{e} = 0.01\), \(\alpha_{p} = 0.02\); black line corresponds to \(\alpha_{e} = 0.03\), \(\alpha_{p} = 0.04\); red line corresponds to \(\alpha_{e} = 0.05\), \(\alpha_{p} = 0.06\)

Full size image
Fig. 3
figure 3

Variation of nonlinear coefficient against ion-to-electron density ratio \(\left( {\mu_{i} } \right)\) with \(\sigma_{pe} = 0.1\) and \(\mu_{p} = 0.2\). Blue line corresponds to \(\alpha_{e} = 0.01\), \(\alpha_{p} = 0.02\); black line corresponds to \(\alpha_{e} = 0.03\), \(\alpha_{p} = 0.04\); red line corresponds to \(\alpha_{e} = 0.05\), \(\alpha_{p} = 0.06\)

Full size image

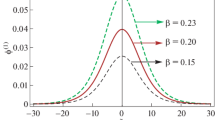
Figure 4 shows the change of the compressive soliton structure with \(\chi\) for different values of nonthermal parameters of electrons \(\left( {\alpha_{e} } \right)\) and positrons \(\left( {\alpha_{p} } \right)\). As in equation (34), it shows that the amplitude is the inverse of the nonlinear coefficient \(A\). As a result, as nonthermal parameters are increased, plasma nonlinearity decreases, and hence the amplitude of the soliton structure rises.

Fig. 4
figure 4

Variation of compressive soliton wave structure for different values of \(\alpha_{e}\) and \(\alpha_{p}\), with \(\mu_{i}\) = 0.3, \(\sigma_{pe} = 0.1\), \(\mu_{p}\) = 0.2, \(n\) = 0.6, \(U\) = 0.9, \(\Omega_{i}\) = 0.5 and \(\omega_{pi}\) = 1.4. Blue (dotted) curve corresponds to \(\alpha_{e}\) = 0.01 and \(\alpha_{p}\) = 0.03; black (solid) curve corresponds to \(\alpha_{e}\) = 0.04 and \(\alpha_{p}\) = 0.06; red (solid) curve corresponds to \(\alpha_{e}\) = 0.07 and \(\alpha_{p}\) = 0.09

Full size image

We have also shown the rarefactive soliton structure in Fig. 5 for different values of nonthermal parameters while keeping all other parameters fixed. The amplitude (width) of the solitons decreases (increases) with an increase in the values of \(\alpha_{e}\) and \(\alpha_{p}\).

Fig. 5
figure 5

Variation of rarefactive soliton structure for different values of \(\alpha_{e}\) and \(\alpha_{p}\), with \(\mu_{i}\) = 1.8, \(\mu_{p}\) = 0.2, \(\sigma_{pe} = 0.1\), \(n\) = 0.6, \(U\) = 0.9, \(\Omega_{i}\) = 0.5 and \(\omega_{pi}\) = 1.4. Blue (dotted) curve corresponds to \(\alpha_{e}\) = 0.01 and \(\alpha_{p}\) = 0.03; black (solid) curve corresponds to \(\alpha_{e}\) = 0.04 and \(\alpha_{p}\) = 0.06; red (solid) curve corresponds to \(\alpha_{e}\) = 0.07 and \(\alpha_{p}\) = 0.09

Full size image

A similar kind of variation in the soliton structure is observed in Fig. 6, when we change the positron-to-electron density ratio \(\left( {\mu_{p} } \right)\). This observation also provides an information about the change in amplitude and width when the value of \(\left( {\mu_{p} } \right)\) changes. Increase in the density ratio, enhances the amplitude of the soliton.

Fig. 6
figure 6

Variation of rarefactive soliton structure for different values of \(\mu_{p}\), with \(\mu_{i}\) = 1.8, \(\sigma_{pe} = 0.1\), \(n\) = 0.6, \(U\) = 0.9, \(\Omega_{i}\) = 0.5 and \(\omega_{pi}\) = 1.4, \(\alpha_{e} = 0.05\) and \(\alpha_{p} = 0.06\). Blue (dotted) curve corresponds to \(\mu_{p} = 0.1\); black (solid) curve corresponds to \(\mu_{p} = 0.5\) and; red (solid) curve corresponds to \(\mu_{p} = 0.9\)

Full size image

6 Conclusion

In the present work, we have studied the characteristics (amplitude and width) of nonlinear ion-acoustic solitary waves in a magnetically confined plasma under the influence of nonthermal electrons and positrons. We have determined the range of the parameters for the existence of both the positive and negative polarity soliton. We have noticed the following main results in our present study:

  1. 1.

    In our investigation, both the positive and negative polarity of soliton exist, whereas in the earlier study, this aspect was not covered by Chawla et al. [18].

  2. 2.

    The parameter ion-to-electron density ratio \(\left( {\mu_{i} } \right)\) is very crucial to getting two kinds of soliton structure. A very small change in this parameter, changes the polarity of the soliton structure.

  3. 3.

    We can obtained the parameter range for the existence of a negative polarity soliton from Fig. 3b.

We hope these results will be incredibly helpful in both space and laboratory plasmas, where solitary wave propagation is quite useful.