1 Introduction

Recently, there have been up-growing interests for researchers in understanding the non-linear features of electronegative plasmas (plasmas with significant amount of negative ions) (Berezhnoj et al. 2000; Franklin 2002; Mamun et al. 2010; Rahman et al. 2011; Plihon and Chabert 2011; Mannan and Mamun 2012). Electronegative plasmas (ENP) have attracted a great deal of attention not only because of their potential applications in microelectronic and photoelectronic industries (Lieberman and Lichtenberg 2005) but also because of their occurrence in both laboratory devices (Jacquinot et al. 1977; Weingarten et al. 2001; Ichiki et al. 2002) and space environments (Meige et al. 2007; Coates et al. 2007; Plihon and Chabert 2011). ENP are contaminated by solid impurities (dust). Therefore, ENP are also called dirty or dusty ENP (Kim and Merlino 2006; Merlino and Kim 2006; Mamun et al. 2009a).

The nonlinear features of the dust ion-acoustic (DIA) waves in ENP have been analyzed by many authors (Mamun et al. 2009a, 2009b, 2009c; Kim and Hershkowitz 2009; Rahman et al. 2011). Rahman et al. (2011) have studied the dust ion-acoustic solitary waves and their multi-dimensional instability in a magnetized dusty electronegative plasma with trapped negative ions. Sayed et al. (2008) studied dust ion-acoustic solitary waves in a dusty plasma with positive and negative ions. Mamun et al. (2010) investigated the effects of adiabaticity of electrons and negative ions on solitary waves and double layers in an electronegative plasma.

According to the various observations (Feldman et al. 1973; Formisano et al. 1973; Scudder et al. 1981; Marsch et al. 1982), the presence of super-thermal electron and ion structures is ubiquitous in a variety of astrophysical plasma environments. Due to the effect of external forces acting on the natural space environment plasmas or because of waveparticle interactions, super-thermal particles may arise. Plasmas with super-thermal electrons are normally characterized by a long tail in the high energy region. Such space plasmas can be modeled by generalized Lorentzian of kappa distribution, better than the Maxwellian distribution (Hasegawa et al. 1985; Thorne and Summers 1991; Summers and Thorne 1991,1994; Mace and Hellberg 1995). The velocity distribution functions in terms of Lorentzian or kappa distribution, was first given by Vasyliunas (1968). The velocity distribution function approaches a Maxwellian distribution for very large values of the spectral index (κ) but for low values of κ, they represent a hard spectrum with a strong non-Maxwellian tail. Kappa (superthermal) distribution has been used to analyze and interpret spacecraft data on the earth’s magnetospheric plasma sheet (Lui and Krimigis 1987), Jupiter (Leubner 1982) and Saturn (Armstrong et al. 1983). Solar wind plasmas, auroral zone plasmas, and magnetosphere (Scudder and Olbert 1979a, 1979b; Baluku and Hellberg 2008; Tribeche and Boubakour 2009; Pakzad 2011; Mannan et al. 2012; Ghosh et al. 2012a), are also examples of such plasmas where highly deviated velocity distribution functions are found to exist for the electron population. Super-thermal plasma behavior was also observed in various experimental fields such as laser matter interactions or plasma turbulence (Magni et al. 2005).

Several authors (Hellberg and Mace 2002; Podesta 2005; Abbasi and Pajouh 2007; Baluku and Hellberg 2008; Hellberg et al. 2009; Sultana et al. 2010; Baluku et al. 2010) have studied the effect of Landau damping on various plasma modes by using the kappa distribution. Many authors have considered such superthermal plasmas involving electrons, ions, and positrons (Eslami and Mottaghizadeh 2012; Runmoni et al. 2011; Pakzad 2011; El-Tantawy et al. 2011; Sabry et al. 2011; Bora et al. 2012). Eslami and Mottaghizadeh (2012) have studied the cylindrical ion-acoustic solitary waves in electronegative plasmas with superthermal electrons. They found that the solution supports only compressive solitary waves. Runmoni et al. (2011) have studied arbitrary amplitude dust ion acoustic solitary waves and double layers in a kappa distributed electron plasma by using Sagdeev’s pseudo-potential method.

Recently, Hussain et al. (2012) have studied the Korteweg-de Vries (K-dV) equation for electrostatic wave in an unmagnetized negative ion plasma with superthermal electrons by using reductive perturbation technique. This paper is concerned with ion-acoustic (IA) waves and has studied the basic properties of the IA solitary waves (SWs) by deriving the K-dV equation. This work is not concerned with the study of the SWs beyond the K-dV limit. El-Tantawy et al. (2012) have studied arbitrary amplitude IA SWs propagating in an ion plasma and have shown the existence of positive SWs only. They have used pseudo-potential approach to study the arbitrary amplitude SWs. Roy et al. (2012) have investigated arbitrary amplitude double layers in a four component dusty plasma with kappa distributed electron.

All of these previous studies (Eslami and Mottaghizadeh 2012; Runmoni et al. 2011; Pakzad 2011; El-Tantawy et al. 2011; Sabry et al. 2011; Bora et al. 2012) are limited to the study of the K-dV or Burger equation describing the solitary or shock waves which is not valid for a parametric regime corresponding to A=0 or A∼0 (where A is the coefficient of the nonlinear term of the K-dV or Burger equation, and A∼0 means here that A is not equal 0, but A is around 0). This is because, the latter gives rise to infinitely large amplitude structures which break down the validity of the reductive perturbation method (Washimi and Taniuti 1966). This means that to study finite amplitude SWs and DLs beyond this K-dV limit, one must resort the other type of nonlinear dynamical equation which can be valid for A∼0.

The technique of analyzing SWs and DLs, is Gardner approach which leads to a standard Gardner equation. From the analysis of standard Gardner equation, SW of permanent profile is found, which is known as Gardner soliton (GS) (Hossain et al. 2011; Mannan and Mamun 2011; Asaduzzaman and Mamun 2012; Ghosh et al. 2012a; Shuchy et al. 2012; Masud et al. 2013). Recently, many authors have successfully studied the nature of GS (Hossain et al. 2011; Mannan and Mamun 2011; Asaduzzaman and Mamun 2012; Ghosh et al. 2012a; Shuchy et al. 2012; Masud et al. 2013; Hasan et al. 2013), which is found to be more close to some critical parameter as well as near A=0.

El-Labany et al. (2012) have examined the solitons and double-layers of electron-acoustic waves in magnetized plasma. Akhter et al. (2013) have studied the effects of two temperature electrons on Gardner solitons and double layers in a nonthermal dusty electronegative plasma. But to the best of our knowledge no attempt has been taken to analyze GSs and DLs in dusty electronegative plasmas with kappa distributed electrons. Therefore, in our present work, we are going to analyze the DIA GSs and DLs in a dusty ENP system (consisting of positive and negative ions, kappa distributed electrons, and negatively charged static dust) by using Gardner approach. It allows us to study SWs at the vicinity of come critical parameter as well as near A=0, and investigate the basic properties of finite amplitude DIA GSs and DLs by the reductive perturbation method (Washimi and Taniuti 1966).

The manuscript is organized as follows. The model equations are provided in Sect. 2. The K-dV equation is derived in Sect. 3. The modified K-dV (mK-dV) equation is derived in Sect. 4. The standard Gardner (SG) equation is derived in Sect. 5. The numerical analysis is presented in Sect. 6. A brief discussion is finally given in Sect. 7.

2 Model equations

We consider a nonlinear propagation of the DIA waves in an unmagnetized dusty ENP containing inertial positive and negative ions, kappa distributed electrons, and negatively charged static dust. Thus, at equilibrium we have Z p n p0=Z n n n0+n e0+Z d n d0 where n p0, n n0, n e0, and n d0, are, respectively, positive ion, negative ion, kappa distributed electrons, and negative dust number density at equilibrium. Z p (Z n ) represents the charge state of positive (negative) ion.

The number density of kappa distributed electrons (Tribeche and Boubakour 2009; Pakzad 2011; Sultana et al. 2010), n e is given as

(1)

The nonlinear dynamics of these low-frequency (purely electrostatic) DIA waves in such a plasma system, whose phase speed is much smaller (larger) than the electron (ion) thermal speed is described by the normalized equations of the

(2)
(3)
(4)
(5)
(6)

where n s is the number density of the species s (s=p for positive ions, s=n for negative ions, s=e for kappa distributed electron) normalized by its equilibrium value n s0, u p (u n ) is the positive (negative) ion fluid speed normalized by C p =(Z p k B T e /m p )1/2, ϕ is the electrostatic wave potential normalized by k B T e /e, ρ is the normalized surface charge density, α=Z n m p /Z p m n , μ=n e0/Z p n p0, μ d =Z d n d0/Z p n p0, Z n n n0/Z p n p0=1−μ−μ d , k B is the Boltzmann constant, and e is the magnitude of the electron charge. The time variable t is normalized by \(\omega_{p}^{-1}=(m_{p}/4\pi n_{p0}Z_{p}^{2}e^{2})^{1/2}\), and the space variable x is normalized by λ Dm =(k B T e /4πn p0 Z p e 2)1/2.

We are interested in the propagation of a purely electrostatic perturbation mode on the time scale of the IA waves. Thus, the frequency (ω) of this perturbation mode is much higher than the dust-plasma-frequency (ω pd ), i.e. ω pd ≪ω. Therefore, dust are assumed to be stationary (Shukla and Silin 1992; Mamun and Shukla 2002a, 2002b).

3 Derivation of K-dV equation

To obtain the K-dV equation, we introduce the stretched coordinates (Washimi and Taniuti 1966):

(7)

where ϵ is a small parameter (0<ϵ<1) measuring the weakness of the dispersion, and V p (normalized by C p ) is the phase speed of the perturbation mode, and expand all the dependent variables (viz. n s , u s , ϕ, and ρ) in power series of ϵ:

(8)

Now, expressing (2)–(6) in terms of ζ and τ, and substituting (8) into the resulting equations [(2)–(6) expressed in terms of ζ and τ], one can easily develop different sets of equations in various powers of ϵ. To the lowest order in ϵ, one obtains

(9)
(10)
(11)

where ψ=ϕ (1), η=1−μ−μ d , \(c_{1}=\frac{\kappa-\frac{1}{2}}{\kappa-\frac{3}{2}}\). Equation (11) represents the linear dispersion relation for the DIA waves propagating in a dusty plasma under consideration. To the next higher order of ϵ, we obtain a set of equations, which, after using these equations, we obtain a equation of the form:

(12)

where

(13)
(14)

where

(15)

Equation (12) is the well-known K-dV equation describing the nonlinear propagation of the DIA waves in the dusty ENP system under consideration. The stationary SW solution of the K-dV equation (12) is obtained by transforming the independent variables to ξ=ζ−U 0 τ′ and τ′=τ, where U 0 is the speed of the SWs, and imposing the appropriate boundary conditions, viz. ψ→0, dψ/dξ→0, d 2 ψ/dξ 2→0 at ξ→±∞. Thus, one can express the stationary solitary wave solution of the K-dV equation (12) as

(16)

where the amplitude (ψ m ) and the width (Δ) are given by

(17)

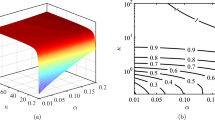
The general expressions for the coefficients B and A [by using (17)] are used to have some numerical appreciations of our results, viz. the SW height and width are numerically analyzed. It is clear from (17) that the solitary potential profile is positive (negative) if A>0 (A<0). Therefore, A(α=α c )=0, where α c is the critical value of α above (below) which the SWs with a negative (positive) potential exists, gives the value of α c . To find the parametric regimes for which the positive and negative solitary potential profiles exist, we have numerically analyzed A, and obtain A(α=α c )=0 surface plots. Figure 1 shows that α c , which is a function of μ, κ, and μ d , increases with μ and κ. Figure 2 shows the variation of α c with μ and μ d for κ=7.

Fig. 1
figure 1

The variation of α c [obtained from A(α=α c )=0] with μ and κ for μ d =0.3. Here, κ=5.5, κ=7, κ=10, κ=50, κ=100, denote the pink, dotted blue, dotted black, dotted red, and full black lines respectively

Full size image
Fig. 2
figure 2

The variation of α c [obtained from A(α=α c )=0] with μ and μ d for κ=7

Full size image

For typical dusty plasma parameters, we have the existence of the small amplitude solitary waves with a positive potential for α<α c , and with a negative potential for α>α c (as shown in Fig. 3).

Fig. 3
figure 3

Showing the K-dV soliton (positive and negative) for U 0=0.005, μ=0.4, κ=7, μ d =0.3, α=0.02 (for positive structure), and α=0.09 (for negative structure)

Full size image

4 Derivation of mK-dV equation

The K-dV equation is the result of the second order calculation of the ϵ. For plasmas with more than two species, there can arise a situation, where A vanishes at α=α c , and (12) fails to describe nonlinear evolution of perturbation. So higher order calculation is required at α=α c . From the third order calculation, which utilizes another set of stretched coordinate, a modified K-dV (mK-dV) equation is obtained to describe the nonlinear evolution near this critical parameter. The stretched coordinates for mK-dV equation is :

(18)

By using Eq. (18) in Eqs. (2)–(8), we find the same values of \(n_{n}^{(1)}\), \(u_{n}^{(1)}\), \(n_{p}^{(1)}\), \(u_{p}^{(1)}\), and V p as like as that of the K-dV. To the next higher order of ϵ, we obtain a set of equations, which, after using the values of \(n_{n}^{(1)}\), \(u_{n}^{(1)}\), \(n_{p}^{(1)}\), \(u_{p}^{(1)}\), and V p , can be simplified as

(19)
(20)
(21)
(22)

To the next higher order of ϵ, we obtain a set of equations, which, after using these equations, we obtain a equation of the form:

(23)

where D=BD 0, and

(24)
(25)

where

(26)

Equation (23) is known as mK-dV equation. As (12) do not contain any ψ 2 term, it is clear that (12) does not have any DL wave solution. The stationary localized solution of (23) is, therefore, directly given by

(27)

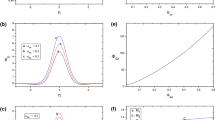
where the amplitude ψ m and the width Δ are given by \(\psi_{m}=\sqrt{6U_{0}/D}\) and \(\Delta=\sqrt{B/U_{0}}\). Figure 4 shows the variation of mK-dV solitons. From this figure it is clear that with the increasing values of κ, the amplitude (width) of the wave decreases (increases). Though mK-dV solitons have a finite value near α c , the mK-dV equation does not have any DLs solution. As we are interested in both SWs and DLs solution, we proceed into Gardner equation, which gives both SWs and DLs solutions.

Fig. 4
figure 4

Showing the mK-dV soliton for U 0=0.005, μ=0.4, μ d =0.3, and α=0.08. Here, κ=7, κ=10, κ=50, and κ=100, blue, pink, red, and black lines respectively

Full size image

5 Derivation of standard Gardner equation

It is obvious from (21) that A=0 since ψ≠0. One can find that A=0 at its critical value α=α c (which is a solution of A=0). So, for α around its critical value (α c ), A=A 0 can be expressed as

(28)

where |α−α c | is a small and dimensionless parameter, and can be taken as the expansion parameter ϵ, i.e. |α−α c |≃ϵ, and s=1 for α>α c and s=−1 for α<α c . So, ρ (2) can be expressed as

(29)

which, therefore, must be included in the third order Poisson’s equation. To the next higher order of ϵ, we obtain a set of equations:

(30)
(31)
(32)
(33)
(34)

where \(F_{n}=n_{n}^{(1)}u_{n}^{(2)}+n_{n}^{(2)}u_{n}^{(1)}+u_{n}^{(3)}\) and \(F_{p}=n_{p}^{(1)}u_{p}^{(2)}+n_{p}^{(2)}u_{p}^{(1)}+u_{p}^{(3)}\). Now, combining Eqs. (19)–(22) and (30)–(34), we obtain a equation of the form:

(35)

where p=sA α B.

Equation (35) is known as standard Gardner (SG) equation. It is often called mixed mK-dV (mmK-dV) equation, because it contains both ψ 2 term of K-dV and ψ 3 term of mK-dV. Equation (35) is valid for α near α c . It is important to note that if we neglect ψ 3 term, and put sA α =A, the SG equation reduces to a K-dV equation which can be derived by using a lower order stretching. However, in this K-dV equation, the nonlinear term vanishes at α=α c , is not valid near α=α c which makes soliton amplitude large enough to break down the validity of the reductive perturbation method. But the SG equation derived here is valid for α near α c .

6 Numerical analysis of SG equation

The exact analytical solution of (35) is not possible. Therefore, we have numerically solved (35), and have studied the effects of planar geometry on DIA-GSs and DIA-DLs.

The stationary SW solution of the SG equation is obtained by considering a moving frame (moving with speed U 0) ξ=ζ−U 0 τ, and imposing all the appropriate boundary conditions for the SW solution, including ψ→0, dψ/dξ→0, d 2 ψ/dξ 2→0 at ξ→±∞. These boundary conditions for the stationary Gardner soliton (GS) solution (Mannan and Mamun 2011) allow us to express the SG equation as

(36)

where

(37)
(38)

ψ m =−sA α /D 0, \(V_{0}=A_{\alpha}^{2}s^{2}B/6D_{0}\), and the width (Δ) of the Gardner solitons (GSs), is given by

(39)

We note that (36) represents a SW solution of (35). It is, therefore, obvious that, to have GSs we must have U 0<V 0, otherwise ψ m1,2 become imaginary. Figure 1 shows that α c , which is a function of μ, μ 1, μ 2, μ d and α, decreases with μ and increases with α. Therefore, for typical dusty plasma parameters, we have the existence of the small amplitude GSs with a positive potential for α<α c (shown in Fig. 5), and with a negative potential for α>α c (shown in Fig. 6).

Fig. 5
figure 5

The profile of positive GSs varying with α for U 0=0.006, μ=0.4, s=1, κ=7, and μ d =0.3

Full size image
Fig. 6
figure 6

The profile of negative GSs varying with α for U 0=0.006, μ=0.4, s=−1, κ=7, and μ d =0.3

Full size image

The stationary DL solution of the SG equation [i.e. (35)] is obtained by considering a moving frame (moving with speed U 0) ξ=ζ−U 0 τ, and imposing all the appropriate boundary conditions for the DL solution, including ψ→0, dψ/dξ→0, d 2 ψ/dξ 2→0 at ξ→−∞. These boundary conditions for the stationary DL solution (Mamun and Mannan 2011; Hossain and Mamun 2012) allow us to express the SG equation [i.e. (35)] as

(40)

where the amplitude (ψ m ) and the width (Δ) of the DLs, and U 0 are given by

(41)
(42)

It is clear from (40)–(42) that DLs exist if and only if D 0<0, i.e. α>α D , where α D , is represented by the D 0=0 surface plot shown in Fig. 7. Since B>0 and U 0>0, (40)–(42) indicate that the DLs are associated with negative potential if s=1, i.e. α>α c , and associated with positive potential if s=−1, i.e. α<α c . It is obvious from Fig. 7 that α D >α c which confirm us that DLs are associated with negative potential only (shown in Fig. 8). The parametric regimes for the existence of negative DLs are represented by Fig. 7, and DLs exist for parameters corresponding to any point above (D 0=0) surface plot. Figure 9 shows that with the increasing values of κ, the height of the DL increases but it becomes narrower.

Fig. 7
figure 7

Showing the parametric regime of α D for μ d =0.3, where κ=7, κ=10, κ=50, and κ=100, blue, pink, red, and black lines respectively

Full size image
Fig. 8
figure 8

Showing the DL structure varying with α for U 0=0.1, s=−1, μ=0.4, κ=7, and μ d =0.3

Full size image
Fig. 9
figure 9

Showing the DL structure varying with α for U 0=0.1, μ=0.4, α=0.69, s=−1, κ=7, μ d =0.3, where κ=7, κ=10, κ=50, and κ=100, blue, pink, red, and black lines respectively

Full size image

7 Discussion

We have considered the nonlinear propagation of DIA waves in a plasma system consisting of inertial positive and negative ions, super-thermal (kappa distributed) electrons, and negatively charged static dust. The reductive perturbation method has been employed in order to derive the SG equation which is valid beyond the K-dV limit (corresponding to the vanishing of the nonlinear coefficient of the K-dV equation, i.e. α∼α c in our present situation). The results, which have been found from the numerical solutions of the SG equation, can be pointed out as follows:

  1. 1.

    The GSs and DLs [represented by (36) and (40)], are found to be significantly different from the K-dV solitons which do not exist for α∼α c .

  2. 2.

    The dusty ENP system under consideration supports the finite amplitude GSs and DLs, whose basic features (polarity, amplitude, width, etc.) depend on the ratio of masses of two types of ions(α), electron densities(μ), static dust densities(μ d ), and spectral index(κ).

  3. 3.

    GSs are shown to exist around α=α c , and are found to be different from the K-dV solitons, which do not exist around α=α c . We note that α c =0.0639285 for μ=0.4, κ=7, and μ d =0.3.

  4. 4.

    It is found that at α<α c , positive GSs exist, whereas at α>α c , negative GSs exist.

  5. 5.

    It is also found that the magnitude of the amplitude of positive and negative GSs decreases with α and increases with U 0.

  6. 6.

    The width of positive and negative GSs decreases with α and U 0.

  7. 7.

    The DLs having large width and negative potential, exist for α>α D , and no positive DLs are formed. We note that α D =0.672725 for μ=0.4, κ=7, and μ d =0.3.

  8. 8.

    The magnitude of the amplitude of the DLs increases with the increase of α and U 0. The width of negative DLs increases with both of α and U 0.

  9. 9.

    The spectral index κ significantly changes the amplitude, width, and polarity of both SWs and DLs.

In our numerical analysis we have used a wide range of the plasma parameters (μ=0.1–0.9, μ d =0.1–0.5, κ=5–100 and α=0.01–0.1), are relevant to both space plasmas (Eslami and Mottaghizadeh 2012; Runmoni et al. 2011; Sayed et al. 2008; Pakzad 2011; El-Tantawy et al. 2011; Sabry et al. 2011; Bora et al. 2012; Lakhina et al. 2008; Sheridan et al. 1991).

It may be stressed here that the results of this investigation could be useful for understanding the nonlinear features of electrostatic disturbances in laboratory (Magni et al. 2005). It also will help to analyze and interpret spacecraft data on the earth’s magnetospheric plasma sheet (Lui and Krimigis 1987), Jupiter (Leubner 1982) and Saturn (Armstrong et al. 1983). Solar wind plasmas, auroral zone plasmas, and magnetosphere (Scudder and Olbert 1979a, 1979b; Baluku and Hellberg 2008; Tribeche and Boubakour 2009; Pakzad 2011; Mannan and Mamun 2012; Ghosh et al. 2012b), are also examples of such plasma model where highly deviated velocity distribution functions are found to exist for the electron population.

This paper should also help to understand the salient features of localized DIA waves in multicomponent laboratory and space dusty plasmas which are composed of the positive and negative ions, kappa distributed electrons and immobile charged dust grains. We note that observations (Coates et al. 2007) reveal the presence of both negative and positive ion populations in Titan’s ionosphere and our theoretical results for localized DIA waves may be relevant to the formation of structures in an organic-rich aerosol plasma of Titan. The present results could be applied for understanding of the nonlinear electrostatic structures in astrophysical environments, especially in interstellar medium where the superthermal electrons are expected to be present with a fraction of dust impurities.

It is well known that K-dV, mK-dV, or GS differ due to different kind of stretching coordinates that are used. The formation of different solitons due to the use of different stretchings and orders actually belong to different time scales. Therefore, we have shown the formation and variation of all the three kinds of nonlinear waves. If we neglect the higher order nonlinear term [viz. the term containing ψ 3], but would keep the lower order nonlinear term [viz. the term containing ψ 2], we would obtain the solitary structures that are due to the balance between nonlinearity (associated with ψ 2 only) and dispersion. Any space or laboratory situation can be described by any one or more of these wave structures.