1 Introduction

Structures made of the FG material are special structures and widely used in life such as construction industry, mechanical structures, air transport or a nuclear reactor. Variable thickness FGM shell helps to reduce the weight of structure and saves materials while ensuring load capacity; therefore, it is more and more popularly used in important industries. Study on nonlinear vibration and stability of FGM shell with variable thickness is necessary to make sure the structure works efficiently and reliably.

The nonlinear vibration and dynamic stability of FGM shell structure have been analyzed by several scientists. For instance, Loy et al. (1999, 2000) studied the natural frequencies of FG cylindrical shell subjected to mechanical load. Some influences of factors on natural frequencies of the structure were also examined. Sofiyev et al. (2003, 2013) presented nonlinear dynamic buckling analysis of FGM cylindrical and truncated conical shell subjected to impulsive and axial compressive load by using analytical method based on Love’s shell theory. Haddadpour et al. (2007), based on the Love shell theory and Galerkin method, investigated the free vibration of simply supported FGM circular cylinder shell with four different boundary conditions, and the nonlinear geometries of von Karman were taken into account. Matsunaga (2009) presented the vibration and stability analysis of FGM circular cylinder shell subjected to mechanical load based on the two-dimensional higher-order shear deformation theory (HSDT). Hamilton’s principle and power series expansion method were used to build the governing equation in this work. Bich and Nguyen (2012) based on improved Donnell shell theory and Volmir’s assumption to analyze the nonlinear vibration of FGM cylindrical shell subjected to mechanical load. The Galerkin method and the fourth-order Runge–Kutta method were employed to survey influences of FG material features, pre-loaded axial compression and dimensional ratios on the dynamical response of shells. Also based on the same theory, Avramov (2011) used the Galerkin method and harmonic balance method to study nonlinear vibration and stability of simply supported FGM cylindrical shells. Duc et al. (2014, 2015, 2014, 2015, 2016) studied nonlinear vibration, buckling and post-buckling of eccentrically stiffened S-FGM circular cylindrical shells surrounded by elastic foundations subjected to mechanical load in thermal environments. The Lekhnitsky’s smeared stiffener technique, the stress function and Galerkin method are employed to solve these problems. Wann (2015,) based on the first-order shear deformation theory (FSDT), Rayleigh Ritz method and variational approach, investigated the free vibration of FGM cylinder shells resting on the Pasternak elastic medium by using the analytical method. Malekzadeh et al. (2013) investigated the free vibration of rotating FGM truncated conical shells subjected to mechanical load with various boundary conditions. Dynamic equilibrium equations and motion equations of the shell were derived according to the FSDT. Nonlinear dynamic problems of imperfect double-curved shallow shells made of FGM and surrounded by elastic foundations have been solved by Duc et al. (2013, 2016). In this study, natural frequencies of the structures are calculated by using shear deformation shell theories, the Galerkin method and the fourth-order Runge–Kutta method. Also by using analytical method, nonlinear dynamics problem of cylindrical panels made of FGM and S-FGM has been solved by Quan et al. (2014, 2015). Alibeigloo et al. (2017) replied on elastic theories and differential quadrature method (DQM) to study the free vibration of simply supported sandwich FGM cylindrical shells. Using an analytical approach, Thanh et al. (2019) solved the nonlinear dynamic problems of imperfect FGM reinforced by carbon nanotube by using the Reddy’s FSDT, the Galerkin method and the fourth-order Runge–Kutta method. Also using analytical method, Phu et al. (2017, 2019) studied the nonlinear vibration of sandwich FGM and stiffened sandwich FGM cylindrical shell filled with fluid subjected to mechanical loads in thermal environment. The classical shell theory with geometrical nonlinearity in von Karman–Donnell sense and smeared stiffener technique were used to define motion equations of structure. Natural frequencies and dynamic responses of the shell were determined by using Galerkin’s method and Runge–Kutta method. By using the same approach, Dat et al. (2019) studied the nonlinear vibration of FGM elliptical cylindrical shells reinforced by carbon nanotube resting on elastic foundation subjected to thermal–mechanical load. Han et al. (2018) predicted free vibration of FGM thin cylinder shells filled inside with pressurized fluid based on Flügge shell theory. In governing equations, internal static pressure was regarded as the pre-stress term. On dynamic stability analysis of FGM shell, Huang et al. (2008, 2010a; b) solved nonlinear dynamic buckling problems of FGM cylindrical shells subjected to mechanical load based on Donnell shell theory and large deflection theory. Nonlinear dynamic responses of structure were obtained by applying energy method and the four-order Runge–Kutta method. The critical loads were determined according to Budiansky–Roth criterion. By the same method, Dung et al. (2015, 2017) focused on solving nonlinear dynamic buckling problems of stiffened FGM thin cylindrical shells surrounded by elastic foundations subjected to mechanical load in thermal environments. Recently, Zhang et al. (2019) focused on solving on dynamic buckling of FGM cylindrical shells under thermal shock based on the Hamiltonian principle. Nonlinear torsional buckling problems of sandwich FGM cylindrical shells with spiral stiffeners under torsion and thermal loads were solved by Nam et al. (2019).

Recently, there are some scientists interested in static and dynamic problems of variable thickness FGM cylindrical shell; for example, Sofiyev AH et al. (2002) analyzed dynamic buckling of variable thickness elastic cylindrical shell subjected to external pressure. The critical static and dynamics loads of the structure were found by using Galerkin's method and Ritz method. Ghannad et al. (2017, 2019) solved thermo-elastic problems of FGM cylindrical shells with variable thickness subjected to thermal–mechanical loads based on shear deformation theories. The distribution of displacement and stress in axial and radial direction were determined by using matched asymptotic method and finite element method (FEM). Selah et al. (2014) studied the mechanical responses of the variable thickness FGM truncated conical shell under asymmetric pressure using three dimensions elasticity theory and DQM. Using a semi-analytical approach based on the HSDT and multi-layer method, Jabbari and his co-workers examined thermo-elastic responses of FGM thick cylindrical Shell (2015) and truncated conical shell (2016) with the variable thickness subjected to thermal–mechanical load. Also, Kashkoli et al. (2018) studied the thermo-mechanical creep of thick variable thickness FGM-cylindrical pressure vessel under thermal–mechanical load. Shariyat et al. (2017) presented an investigation of the stresses and displacements of the variable thickness FGM cylindrical and truncated conical shells with different boundary conditions by using the FSDT. By using the Generalized DQM, the free vibration problems of singly-curved and doubly curved laminated composite shells with variable thickness were solved by Bacciocchi et al. (2016). Shariyat and Asgari (2013) used FEM replied on the third-order shear deformation theory and modified Budiansky’s criterion to present an analysis for thermal buckling and post-buckling of imperfect cylindrical shells with variable thickness made of bidirectional FGM.

According to the above reviews and the best author's knowledge, the nonlinear forced vibration and dynamic buckling behavior of variable thickness FGM cylindrical shells subjected to mechanical load are investigated for the first time. In the present article, by using the analytical approach based on the classical shell theory and von Kármán geometric nonlinearity, the governing equation of the variable thickness FGM cylindrical shell is derived. The obtained results of the present study are compared with other published works to demonstrate the accuracy and reliability of the present proposed method. Furthermore, the effects of the material, geometric parameters on responses of the structure are examined in detail.

2 Governing Equations

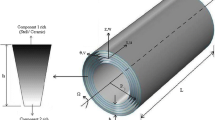
Consider a variable thickness FGM cylindrical shell with the length L and the radius R subjected to uniform external pressure q(t) and axial compression load p(t) (Fig. 1). Assume that the radius of shell are much larger than the thickness (R >  > h), thickness of the shell h can be determined as: \(h_{(x)} = ax + b\).

Fig. 1
figure 1

Variable thickness FGM cylindrical shell

Full size image

in which a = (h1-h0)/L; b = h0.

The effective properties of material can be expressed as follows:

$$ P(z) = P_{{\text{m}}} \cdot V_{{\text{m}}} (z) + P_{c} \cdot V_{c} (z) = P_{{\text{m}}} + \left( {P_{c} - P_{m} } \right)V_{c} (z) $$
(1)

in which Pm and Pc are material and ceramic properties, Vc and Vm are volume fractions of ceramic and metal constituent, respectively, and are related by Vc + Vm = 1.

Ceramic volume fractions in the structure are distributed as following law:

$$ {\text{V}}_{{\text{c}}} (z) = \left( {\frac{1}{2} + \frac{z}{{h_{\left( x \right)} }}} \right)^{k} $$
(2)

Poisson’s ratio is assumed to be constant (ν = constant).

According to the classical shell theory (Brush et al. 1975, Duc ND 2014) the strain–displacement relationship of the shells:

$$ \varepsilon_{ij} = \varepsilon_{ij}^{0} + zk_{ij} \,with\,(i \, j = \, xx, \, yy, \, xy) $$
(3)

in which

$$ \left\{ \begin{gathered} \varepsilon_{xx}^{0} = \frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} ;\varepsilon_{yy}^{0} = \frac{{\partial v_{0} }}{\partial y} - \frac{w}{R} + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} ;\gamma_{xy}^{0} = \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}} \hfill \\ k_{xx} = - \frac{{\partial^{2} w}}{{\partial x^{2} }};\,k_{yy} = - \frac{{\partial^{2} w}}{{\partial y^{2} }};\,k_{xy} = - 2\frac{{\partial^{2} w}}{\partial x\partial y} \hfill \\ \end{gathered} \right. $$
(4)

Applying Hooke’s law for the FGM shell subjected to mechanical load:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ \end{array} } \right\} = \frac{{E_{(z)} }}{{1 - \upsilon_{(z)}^{2} }}\left[ {\begin{array}{*{20}c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & {\left( {1 - \nu } \right)/2} \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\}\,or\,\left\{ \sigma \right\} = \left[ \Pi \right] \cdot \left\{ \varepsilon \right\} $$
(5)

Integrating Stress–Strain relationship through the thickness of the shell, we obtain the governing equations of the variable thickness FGM cylindrical shell:

$$ \left\{ {\begin{array}{*{20}c} {\left\{ {N_{ij} } \right\}} \\ {\left\{ {M_{ij} } \right\}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\left[ A \right]} & {\left[ B \right]} \\ {\left[ B \right]} & {\left[ D \right]} \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}c} {\left\{ {\varepsilon_{ij}^{0} } \right\}} \\ {\left\{ {k_{ij} } \right\}} \\ \end{array} } \right\}\,{\text{with}}\,\left( {i,j} \right) = (xx \, ,yy, \, xy) $$
(6)

in which

$$ \left\{ {\left[ A \right];\left[ B \right];\left[ D \right]} \right\} = \int\limits_{{ - h_{(x)} /2}}^{{h_{(x)} /2}} {\left[ \Pi \right]} .\left( {1,z,z^{2} } \right)dz $$
(7)

Equation (6) can be rewritten as follows:

$$ \left\{ \begin{gathered} N_{xx} \hfill \\ N_{yy} \hfill \\ N_{xy} \hfill \\ M_{xx} \hfill \\ M_{yy} \hfill \\ M_{xy} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{21} } & {A_{22} } & 0 \\ 0 & 0 & {A_{66} } \\ \end{array} } & {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & 0 \\ {B_{21} } & {B_{22} } & 0 \\ 0 & 0 & {B_{66} } \\ \end{array} } \\ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & 0 \\ {B_{21} } & {B_{22} } & 0 \\ 0 & 0 & {B_{66} } \\ \end{array} } & {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 \\ {D_{21} } & {D_{22} } & 0 \\ 0 & 0 & {D_{66} } \\ \end{array} } \\ \end{array} } \right] \cdot \left\{ \begin{gathered} \varepsilon_{xx}^{0} \hfill \\ \varepsilon_{yy}^{0} \hfill \\ \gamma_{xy}^{0} \hfill \\ k_{xx} \hfill \\ k_{yy} \hfill \\ k_{xy} \hfill \\ \end{gathered} \right\} $$
(8)

in which

$$ A_{11} = A_{22} = \frac{{E_{1} \cdot h_{\left( x \right)} }}{{1 - \nu^{2} }};A_{12} = A_{21} = \frac{{\nu \cdot E_{1} \cdot h_{\left( x \right)} }}{{1 - \nu^{2} }};\,B_{11} = B_{22} = \frac{{E_{2} \cdot h^{2}_{\left( x \right)} }}{{1 - \nu^{2} }};B_{12} = B_{21} = \frac{{\nu \cdot E_{2} \cdot h^{2}_{\left( x \right)} }}{{1 - \nu^{2} }}; $$
$$ D_{11} = D_{22} = \frac{{E_{3} \cdot h^{3}_{\left( x \right)} }}{{1 - \nu^{2} }};D_{12} = D_{21} = \frac{{\nu \cdot E_{3} \cdot h^{3}_{\left( x \right)} }}{{1 - \nu^{2} }};\,A_{66} = = \frac{{E_{1} \cdot h_{\left( x \right)} }}{{2\left( {1 + \nu } \right)}};B_{66} = \frac{{E_{2} \cdot h^{2}_{\left( x \right)} }}{{2\left( {1 + \nu } \right)}};D_{66} = \frac{{E_{2} \cdot h^{2}_{\left( x \right)} }}{{2\left( {1 + \nu } \right)}} $$

with:

$$ E_{1} = E_{{\text{m}}} + \frac{{E_{{\text{c}}} - E_{{\text{m}}} }}{(k + 1)};E_{2} = \frac{{\left( {E_{{\text{c}}} - E_{{\text{m}}} } \right)k}}{2(k + 1)(k + 2)}; \, E_{3} = \frac{{E_{{\text{m}}} }}{12} + \left( {E_{c} - E_{{\text{m}}} } \right)\left( {\frac{1}{k + 3} - \frac{1}{k + 2} + \frac{1}{4(k + 1)}} \right). $$

Internal force and moment resultants can be obtained from Eq. (7) as follows:

$$ \left\{ \begin{gathered} N_{xx} = A_{11} \left( {\varepsilon_{xx}^{0} + \upsilon \cdot \varepsilon_{yy}^{0} } \right) + B_{11} \left( {k_{xx} + \nu \cdot k_{yy} } \right) \hfill \\ N_{yy} = A_{11} \left( {\varepsilon_{yy}^{0} + \upsilon \cdot \varepsilon_{xx}^{0} } \right) + B_{11} \left( {k_{yy} + \nu \cdot k_{xx} } \right) \hfill \\ N_{xy} = A_{66} \cdot \gamma_{xy}^{0} + B_{66} \cdot k_{xy} \hfill \\ M_{xx} = B_{11} \left( {\varepsilon_{xx}^{0} + \nu \cdot \varepsilon_{yy}^{0} } \right) + D_{11} \left( {k_{xx} + \nu \cdot k_{yy} } \right) \hfill \\ M_{yy} = B_{11} \left( {\varepsilon_{yy}^{0} + \nu \cdot \varepsilon_{xx}^{0} } \right) + D_{11} \left( {k_{yy} + \nu \cdot k_{xx} } \right) \hfill \\ M_{xy} = B_{66} \cdot \gamma_{xy}^{0} + D_{66} \cdot k_{xy} \hfill \\ \end{gathered} \right. $$
(9)

Nonlinear motion equations of FGM cylindrical shell with variable thickness based on classical shell theory (Brush et al. 1975) are:

$$ \left\{ \begin{gathered} \frac{{\partial N_{{{\text{xx}}}} }}{\partial x} + \frac{{\partial N_{{{\text{xy}}}} }}{\partial y} = \rho_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} \hfill \\ \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{yy} }}{\partial y} = \rho_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} \hfill \\ \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} + N_{xx} \cdot \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{N_{y} }}{R} - p \cdot h(x)\frac{{\partial^{2} w}}{{\partial x^{2} }} + q = \rho_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon \rho_{1} \frac{\partial w}{{\partial t}} \hfill \\ \end{gathered} \right. $$
(10)

in which \(\rho_{1} = \left( {\rho_{m} + \frac{{\rho_{c} - \rho_{m} }}{k + 1}} \right)h_{(x)} = \rho_{1}^{*} h_{(x)}\)

Substituting Eq. (3) and Eq. in Eq. (10), we obtain:

$$ \left\{ \begin{gathered} L_{11} (u) + L_{12} (v) + L_{13} (w) + P_{1} (w) = \rho_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} \hfill \\ L_{21} (u) + L_{22} (v) + L_{23} (w) + P_{2} (w) = \rho_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} \hfill \\ L_{31} (u) + L_{32} (v) + L_{33} (w) + P_{3} (w) + P_{4} (u,w) + P_{5} (v,w) + q + p.h(x,y)\frac{{\partial^{2} w}}{{\partial x^{2} }} = \rho_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon \rho_{1} \frac{\partial w}{{\partial t}} \hfill \\ \end{gathered} \right. $$
(11)

in which

$$ L_{11} (u) = A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial A_{11} }}{\partial x}\frac{\partial u}{{\partial x}} + A_{66} \cdot \frac{{\partial^{2} u}}{{\partial y^{2} }};\,L_{12} (v) = A_{66} \cdot \frac{{\partial^{2} v}}{\partial x\partial y} + \nu \cdot \frac{{\partial A_{11} }}{\partial x}\frac{\partial v}{{\partial y}} + \nu \cdot A_{11} \frac{{\partial^{2} v}}{\partial x\partial y} $$
$$ L_{13} (w) = - B_{11} \frac{{\partial^{3} w}}{{\partial x^{3} }} - \nu \cdot B_{11} \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} - 2B_{66} \cdot \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} - \frac{{\partial B_{11} }}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} - \nu \cdot \frac{{\partial B_{11} }}{\partial x}\frac{{\partial^{2} w}}{{\partial y^{2} }} - \nu \cdot \frac{{\partial A_{11} }}{\partial x}\frac{w}{R} - \frac{1}{R}\nu \cdot A_{11} \frac{\partial w}{{\partial x}}; $$
$$ \begin{gathered} P_{1} ({\text{w}}) = \frac{1}{2}\frac{{\partial A_{11} }}{\partial x}\left( {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \nu .\left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right) + A_{11} \left( {\frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu .\frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{\partial x\partial y}} \right) + A_{66} .\left( {\frac{{\partial^{2} w}}{\partial x\partial y}\frac{\partial w}{{\partial y}} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right); \hfill \\ L_{21} (u) = \left( {A_{66} + A_{11} \nu } \right).\frac{{\partial^{2} u}}{\partial x\partial y} + \frac{{\partial A_{66} }}{\partial x}\frac{\partial u}{{\partial y}};\,L_{22} (v) = A_{66} .\frac{{\partial^{2} {\text{v}}}}{{\partial x^{2} }} + \frac{{\partial A_{66} }}{\partial x}\frac{{\partial {\text{v}}}}{\partial x} + A_{11} \frac{{\partial^{2} {\text{v}}}}{{\partial y^{2} }}; \hfill \\ \end{gathered} $$
$$ L_{23} (w) = - B_{11} \frac{{\partial^{3} w}}{{\partial y^{3} }} - \left( {\nu B_{11} + 2B_{66} } \right) \cdot \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} - 2\frac{{\partial B_{66} }}{\partial x} \cdot \frac{{\partial^{2} w}}{\partial x\partial y} - \frac{1}{R}A_{11} \frac{\partial w}{{\partial y}}; $$
$$ P_{2} (w) = A_{11} \left( {\frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{\partial x\partial y}} \right) + A_{66} \cdot \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{\partial w}{{\partial y}} + A_{66} \cdot \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial A_{66} }}{\partial x}\frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}}; $$
$$ I_{31} (u) = B_{11} \frac{{\partial^{3} u}}{{\partial x^{3} }} + \left( {2B_{66} + \nu \cdot B_{11} } \right)\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + 2\frac{{\partial B_{11} }}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} B_{11} }}{{\partial x^{2} }}\frac{\partial u}{{\partial x}} + 2\frac{{\partial B_{66} }}{\partial x}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{1}{R}\nu \cdot A_{11} \frac{\partial u}{{\partial x}}; $$
$$ L_{32} (v) = B_{11} \frac{{\partial^{3} v}}{{\partial y^{3} }} + \left( {2B_{66} + \nu \cdot B_{11} } \right)\frac{{\partial^{3} v}}{{\partial x^{2} \partial y}} + 2\nu \cdot \frac{{\partial B_{11} }}{\partial x}\frac{{\partial^{2} v}}{\partial x\partial y} + 2\frac{{\partial B_{66} }}{\partial x}\frac{{\partial^{2} v}}{\partial x\partial y} + \nu \frac{{\partial^{2} B_{11} }}{{\partial x^{2} }}\frac{\partial v}{{\partial y}} + \frac{1}{R}A_{11} \frac{\partial v}{{\partial y}}; $$
$$ \begin{aligned} L_{33} (w) = & - D_{11} \left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) - 2\left( {D_{11} \nu + 2D_{66} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} - 2\frac{{\partial D_{11} }}{\partial x}\left( {\frac{{\partial^{3} w}}{{\partial x^{3} }} + \nu \cdot \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}} \right) - \frac{{\partial^{2} D_{11} }}{{\partial x^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} - \nu \cdot \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) \\ & - \nu \cdot \frac{{\partial^{2} B_{11} }}{{\partial x^{2} }}\frac{w}{R} - \frac{1}{R}A_{11} \frac{w}{R} - \frac{2}{R}\nu \cdot \frac{{\partial B_{11} }}{\partial x}\frac{\partial w}{{\partial x}} - \frac{2}{R}\nu \cdot B_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{2}{R}B_{11} \frac{{\partial^{2} w}}{{\partial y^{2} }} - 4\frac{{\partial D_{66} }}{\partial x} \cdot \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}; \\ \end{aligned} $$
$$ \begin{aligned} P_{3} (w) = & \frac{1}{2R}A_{11} \left( {\left( {\frac{\partial w}{{\partial y}}} \right)^{2} + \nu \cdot \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right) - A_{11} \frac{w}{R}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} - \nu \cdot \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{1}{2}\frac{{\partial^{2} B_{11} }}{{\partial x^{2} }}\left( {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \nu \cdot \left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right) \\ & + 2\frac{{\partial B_{11} }}{\partial x}\left( {\frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \cdot \frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{\partial x\partial y}} \right) + B_{11} \left( {2\nu \cdot \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} + \frac{\partial w}{{\partial y}}\frac{{\partial^{3} w}}{{\partial y^{3} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{3} w}}{{\partial x^{3} }} + \nu \cdot \frac{\partial w}{{\partial y}}\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + \nu \frac{\partial w}{{\partial x}}\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}} \right) \\ & - 2B_{11} \nu \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\frac{{\partial B_{66} }}{\partial x}\left( {\frac{{\partial^{2} w}}{\partial x\partial y}\frac{\partial w}{{\partial y}} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + 2B_{66} .\left( {\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}\frac{\partial w}{{\partial y}} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} - \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}} \right); \\ \end{aligned} $$
$$ P_{4} (w) = \frac{1}{2}A_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \nu \cdot \left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right) + \frac{1}{2}A_{11} \frac{{\partial^{2} w}}{{\partial y^{2} }}\left( {\left( {\frac{\partial w}{{\partial y}}} \right)^{2} + \nu .\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right) + 2A_{66} \cdot \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{\partial x\partial y}; $$
$$ P_{5} (u,w) = A_{11} \frac{\partial u}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \cdot A_{11} \frac{\partial u}{{\partial x}}\frac{{\partial^{2} w}}{{\partial y^{2} }} + 2A_{66} \cdot \frac{\partial u}{{\partial y}}\frac{{\partial^{2} w}}{\partial x\partial y}; $$
$$ P_{6} (v,w) = A_{11} \frac{\partial v}{{\partial y}}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \cdot A_{11} \frac{\partial v}{{\partial y}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2A_{66} \cdot \frac{\partial v}{{\partial x}}\frac{{\partial^{2} w}}{\partial x\partial y} $$

Equations (11) can be used to investigate nonlinear vibration and dynamic stability of variable thickness FGM circular cylinder shell under mechanical load.

3 Solution Method

The present article considers a variable thickness FGM cylindrical shell with simply supported at both ends, under uniform external pressure q(t) and axial compression force p(t).

The boundary conditions are:

w = 0, Nxy = 0, Mxx = 0, Nxx = -p.h at x = 0 and x = L

Displacement components of the cylindrical shell can be expanded as:

$$ \left\{ \begin{gathered} u = U_{{{\text{mn}}}} (t)\cos \alpha x\,\sin \beta y; \hfill \\ v = V_{{{\text{mn}}}} (t)\sin \alpha x\,\cos \beta y; \hfill \\ w = W_{{{\text{mn}}}} (t)\sin \alpha x\,\sin \beta y. \hfill \\ \end{gathered} \right. $$
(12)

in which \(\alpha = \frac{{{\text{m}}\pi }}{L};\,\,\beta = \frac{{\text{n}}}{R}\). m, n—the half-waves number in x and y direction, respectively.

Substituting Eq. (12) in Eq. (11), then applying Galerkin procedure yields:

$$ \left\{ \begin{gathered} I_{11} U + I_{12} V + I_{13} W + R_{1} W^{2} = \rho_{1}^{**} \frac{{d^{2} U}}{{dt^{2} }} \hfill \\ I_{21} U + I_{22} V + I_{23} W + R_{2} W^{2} = \rho_{1}^{**} \frac{{d^{2} V}}{{dt^{2} }} \hfill \\ I_{31} U + I_{32} V + I_{33} W + R_{3} W^{2} + R_{4} W^{3} + R_{5} U \cdot W + R_{6} V \cdot W + \frac{{pm^{2} \pi^{3} (La + 2b)R}}{8L} \cdot W \hfill \\ + \frac{{4\delta_{n} \delta_{m} RLq}}{mn\pi } = \rho_{1}^{**} \frac{{d^{2} W}}{{dt^{2} }} + 2\varepsilon \rho_{1}^{**} \frac{dW}{{dt}} \hfill \\ \end{gathered} \right. $$
(13)

in which

$$ \rho_{1}^{**} = \frac{{\rho_{1}^{*} L\left( {La + 2b} \right)\pi R}}{8};\,\delta_{{\text{n}}} = \frac{{( - 1)^{n} - 1}}{2};\,\delta_{{\text{m}}} = \frac{{( - 1)^{m} - 1}}{2}; $$
$$ \begin{gathered} I_{11} = \frac{{E_{1} \pi \left( {(\nu - 1)n^{2} L^{2} - 2\pi^{2} R^{2} m^{2} } \right)(La + 2b)}}{{16RL(1 - \nu^{2} )}}; \hfill \\ I_{12} = I_{21} = \frac{{E_{1} m\pi^{2} n(La + 2b)}}{{16(1 - \nu^{2} )}}; \hfill \\ I_{13} = \frac{{E_{1} \nu m\pi^{2} (La + 2b)}}{{8(1 - \nu^{2} )}} - \frac{{E_{2} \Delta (\pi^{2} R^{2} m^{2} + L^{2} n^{2} \nu )}}{{24L^{2} Rm(1 - \nu^{2} )}} + \frac{{E_{2} n^{2} \Delta }}{24(1 + \nu )mR}; \hfill \\ \end{gathered} $$
$$ R_{1} = \frac{{2E_{1} \left( {2\pi^{2} R^{2} m^{2} - L^{2} n^{2} \nu } \right)\left( {La + 2b} \right)}}{{9L^{2} Rn\left( {\nu^{2} - 1} \right)}} - \frac{{E_{1} n(La + 2b)}}{{9\left( {1 + \nu } \right)R}};\,I_{22} = \frac{{E_{1} \pi \left( {La + 2b} \right)\left( {2L^{2} n^{2} - R^{2} m^{2} (\nu - 1)\pi^{2} } \right)}}{{16(\nu^{2} - 1)LR}}; $$
$$ \begin{gathered} I_{23} = - \frac{{E_{1} \pi Ln\left( {La + 2b} \right)}}{{8R\left( {1 - \nu^{2} } \right)}} + \frac{{E_{2} n\left( {3L^{4} a^{2} n^{2} - n^{2} \left( {R^{2} m^{2} \pi^{2} + L^{2} } \right)\left( {\Delta - 3L^{2} a^{2} } \right) + 3\left( {2\nu - 1} \right)m^{2} \pi^{2} L^{2} R^{2} a^{2} } \right)}}{{24(\nu^{2} - 1)R^{2} Lm^{2} \pi }}; \hfill \\ R_{2} = \frac{{2E_{1} \left( {2L^{2} n^{2} - \pi^{2} R^{2} m^{2} \nu } \right)(La + 2b)}}{{9R^{2} Lm\pi (\nu^{2} - 1)}} - \frac{{E_{1} m\pi (La + 2b)}}{9(1 + \nu ))L}; \hfill \\ \end{gathered} $$
$$ I_{31} = - \frac{{\nu E_{1} m\pi^{2} \left( {La + 2b} \right)}}{{8\left( {1 - \nu^{2} } \right)}} - \frac{{E_{2} \left( {m^{2} \pi^{2} R^{2} + L^{2} n^{2} \nu } \right)\left( {\Delta - 3L^{2} a^{2} } \right) - 3L^{2} a^{2} }}{{24L^{2} Rm\left( {\nu^{2} - 1} \right)}} + \frac{{E_{2} n^{2} \Delta }}{{24m\left( {1 + \nu } \right)R}}; $$
$$ I_{32} = \frac{{E_{1} Ln\pi (La + 2b)}}{{8R\left( {\nu^{2} - 1} \right)}} - \frac{{E_{2} L\left( {\Delta - 6L^{2} a^{2} } \right)n^{3} }}{{24m^{2} \pi R^{2} (\nu^{2} - 1)}} + \frac{{E_{2} n\Delta \pi }}{{24\left( {1 + \nu } \right)L}}; $$
$$ \begin{aligned} I_{33} = & \frac{{E_{1} L\left( {La + 2b} \right)\pi }}{{8R\left( {\nu^{2} - 1} \right)}} + \frac{{E_{2} \left[ {3L^{4} a^{2} n^{2} - \left( {\nu R^{2} m^{2} \pi^{2} + 2n^{2} L^{2} } \right)\left( {\Delta - 3L^{2} a^{2} } \right) - 6m^{2} \pi^{2} \left( {2R - 3} \right)\nu R^{2} L^{2} a^{2} } \right]}}{{12R^{2} L\pi m^{2} (\nu^{2} - 1)}} \\ & + \frac{{E_{3} \left( {La + 2b} \right)\left( {m^{4} \pi^{4} R^{2} \left[ {\left( {R^{2} m^{2} \pi^{2} + 2n^{2} L^{2} \nu } \right)\Delta^{*} - 3L^{2} R^{2} a^{2} } \right] + L^{4} n^{4} \left[ {m^{2} \pi^{2} \left( {\Delta^{*} + 6\nu R^{2} a^{2} } \right) - 3L^{2} a^{2} } \right]} \right)}}{{16\pi m^{2} (\nu^{2} - 1)R^{3} L^{3} }} \\ & - \frac{{E_{3} \pi (m^{2} \Delta^{*} \pi^{2} + 3L^{2} a^{2} )(La + 2b)}}{{8\left( {1 + \nu } \right)LR}}; \\ \end{aligned} $$
$$ \begin{aligned} R_{3} = & - \frac{{2E_{1} \left( {5L^{2} n^{2} - 3\pi^{2} R^{2} m^{2} \nu } \right)\left( {La + 2b} \right)}}{{9LR^{2} mn\pi (\nu^{2} - 1)}} + \frac{{8a^{2} E_{2} \left( {L^{2} n^{2} \nu - 11R^{2} m^{2} \pi^{2} } \right)}}{{27LRmn\pi (\nu^{2} - 1)}} \\ \frac{{4E_{2} \left[ {9\left( {R^{4} m^{4} \pi^{4} + L^{4} n^{4} } \right)m^{2} \pi^{2} \Delta^{*} - 4L^{2} a^{2} \left( {7R^{4} m^{4} \pi^{4} - 10L^{4} n^{4} } \right)} \right]}}{{81L^{3} R^{3} m^{3} \pi^{3} n(\nu^{2} - 1)}} + \frac{{4E_{2} n\nu (\left( {9m^{2} \pi^{2} \Delta^{*} - 44L^{2} a^{2} } \right)}}{{27LRm\pi (\nu^{2} - 1)}} \\ + \frac{{8E_{2} n\nu \left( {9m^{2} \Delta^{*} \pi^{2} - 34L^{2} a^{2} } \right)}}{{81LRm\pi (\nu^{2} - 1)}} + \frac{{16E_{2} a^{2} Ln}}{27Rm\pi (1 + \nu )} + \frac{{2E_{2} n(\left( {4L^{2} a^{2} - 9m^{2} \pi^{2} \Delta^{*} } \right)}}{81LRm\pi (1 + \nu )} \\ \end{aligned} $$
$$ R_{4} = \frac{{3E_{1} \pi \left( {\pi^{4} R^{4} m^{4} + 2L^{2} \pi^{2} R^{2} m^{2} n^{2} \nu + L^{4} n^{4} } \right)\left( {La + 2b} \right)}}{{256R^{3} L^{3} (\nu^{2} - 1)}} + \frac{{E_{1} m^{2} \pi^{3} n^{2} \left( {La + 2b} \right)}}{128L(1 + \nu )R} $$
$$ R_{5} = - \frac{{8E_{1} \left( {\pi^{2} R^{2} m^{2} + L^{2} n^{2} \nu } \right)\left( {La + 2b} \right)}}{{9L^{2} Rn(\nu^{2} - 1)}} + \frac{{2E_{1} n\left( {La + 2b} \right)}}{{9\left( {1 + \nu } \right)R}}; $$
$$ R_{6} = \frac{{8E_{1} \left( {\nu R^{2} m^{2} \pi^{2} + L^{2} n^{2} } \right)\left( {La + 2b} \right)}}{{9R^{2} Lm\pi \left( {1 - \nu^{2} } \right)}} + \frac{{2E_{1} m\pi \left( {La + 2b} \right)}}{{9L\left( {1 + \nu } \right)}}; $$
$$ \Delta = 2\pi^{2} m^{2} \left( {L^{2} a^{2} + 3Lab + 3b^{2} } \right) + 3L^{2} a^{2} ;\,\Delta^{*} = \left( {L^{2} a^{2} + 2Lab + 2b^{2} } \right) $$

According to Volmir’s assumption (Volmir 1972), by ignoring the inertial components along x and y axes (u <  < w, v <  < w), Eqs. (13) can be rewritten as:

$$ \left\{ \begin{gathered} I_{11} U + I_{12} V + I_{13} W + R_{1} W^{2} = 0 \hfill \\ I_{21} U + I_{22} V + I_{23} W + R_{2} W^{2} = 0 \hfill \\ I_{31} U + I_{32} V + I_{33} W + R_{3} W^{2} + R_{4} W^{3} + R_{5} U \cdot W + R_{6} V \cdot W + \frac{{pm^{2} \pi^{3} (La + 2b)R}}{8L} \cdot W \hfill \\ + \frac{{4\delta_{{\text{n}}} \delta_{{\text{m}}} RL}}{mn\pi }q = \rho_{1}^{**} \frac{{d^{2} W}}{{dt^{2} }} + 2\varepsilon \rho_{1}^{**} \frac{dW}{{dt}} \hfill \\ \end{gathered} \right. $$
(14)

From the first two equations of Eq. (14), we obtain Umn and Vmn in terms of Wmn then substituting in the third equation, we have

$$ \rho_{1}^{**} \frac{{d^{2} W}}{{dt^{2} }} + 2\varepsilon \rho_{1}^{**} \frac{dW}{{dt}} + a_{1} W + a_{2} W^{2} + a_{3} W^{3} - \frac{{pm^{2} \pi^{3} (La + 2b)R}}{8L} \cdot W - \frac{{4\delta_{{\text{n}}} \delta_{{\text{m}}} RL}}{mn\pi }q = 0 $$
(15)

in which

$$ a_{1} = - I_{33} - \frac{{I_{31} \left( {I_{12} I_{23} - I_{13} I_{22} } \right) + I_{32} \left( {I_{13} I_{21} - I_{11} I_{23} } \right)}}{{I_{11} I_{22} - I_{12} I_{21} }} $$
$$ a_{2} = - R_{3} - \frac{{R_{1} \left( {I_{32} I_{21} - I_{31} I_{22} } \right) + R_{2} \left( {I_{31} I_{12} - I_{32} I_{11} } \right) + R_{5} \left( {I_{12} I_{23} - I_{13} I_{22} } \right) + R_{6} \left( {I_{13} I_{21} - I_{11} I_{23} } \right)}}{{I_{11} I_{22} - I_{12} I_{21} }} $$
$$ a_{3} = - R_{4} - \frac{{R_{5} \left( {R_{2} I_{12} - R_{1} I_{22} } \right) + R_{6} \left( {R_{1} I_{21} - R_{2} I_{11} } \right)}}{{I_{11} I_{22} - I_{12} I_{21} }} $$

Assume that uniformly distributed pressure in the form q(t) = QsinΩt, Eq. (15) can be rewritten as:

$$ \left| {\begin{array}{*{20}c} {I_{11} + \rho_{1}^{**} \omega^{2} } & {I_{12} } & {I_{13} } \\ {I_{12} } & {I_{22} + \rho_{1}^{**} \omega^{2} } & {I_{23} } \\ {I_{31} } & {I_{32} } & {I_{33} + \rho_{1}^{**} \omega^{2} } \\ \end{array} } \right| = 0 $$
(16)

3.1 Nonlinear Dynamic Response Analysis

3.1.1 NATURAL Frequencies

Natural frequencies of variable thickness FGM shell can be determined from Eq. (13) by solving the equation:

$$ \left| {\begin{array}{*{20}c} {I_{11} + \rho_{1}^{**} \omega^{2} } & {I_{12} } & {I_{13} } \\ {I_{12} } & {I_{22} + \rho_{1}^{**} \omega^{2} } & {I_{23} } \\ {I_{31} } & {I_{32} } & {I_{33} + \rho_{1}^{**} \omega^{2} } \\ \end{array} } \right| = 0 $$
(17)

In other hand, natural frequencies of the structure can be obtained from Eq. (16) and expressed as:

$$ \omega_{0}^{{}} = \sqrt {\frac{{a_{1} - \frac{{pm^{2} \pi^{3} (La + 2b)R}}{8L}}}{{\rho_{1}^{**} }}} = \sqrt { - \frac{{I_{33} }}{{\rho_{1}^{**} }} - \frac{{I_{{{31}}} \left( {I_{{{12}}} I_{{{23}}} { - }I_{{{13}}} I_{{{22}}} } \right) + I_{{{32}}} \left( {I_{{{13}}} I_{{{21}}} { - }I_{{{11}}} I_{{{23}}} } \right)}}{{\rho_{1}^{**} \left( {I_{{{11}}} I_{{{22}}} { - }I_{{{12}}} I_{{{21}}} } \right)}} - \frac{{pm^{2} \pi^{3} (La + 2b)R}}{{8L\rho_{1}^{**} }}} $$
(18)

3.1.2 Nonlinear Dynamic Responses of the Variable Thickness Cylindrical Shell

Nonlinear dynamic responses of variable thickness cylindrical shells can be obtained from Eq. (16) by using Runge–Kutta method and shown in the numerical results.

3.2 Dynamic Stability Analysis

Analyze nonlinear dynamic stability of variable thickness FGM shell in two cases as follows:

  • Case 1 Variable thickness FGM cylindrical shell subjected to axial compression load in terms of time p = −c1t (c1-loading speed); q = 0.

  • Case 2 Variable thickness FGM shell under axial compression load p = constant and uniformly distributed pressure in terms of time q = c2t (c2- loading speed).

Solving Eq. (16) for each case, we obtain dynamic responses of the shell. Dynamic critical time tcr is obtained according to Budiansky–Roth criterion (Volmir, 1962), and dynamic critical loads can be determined as follows: pcr = c1tcr (case 1), qcr = c2tcr (case 2).

4 Validation

To verify the reliability of the proposed method, the obtained results of the present article are compared with results in the published work of Bich et al. (2012) and Loy et al. (1999). They studied on the vibration of FGM cylindrical shell made of stainless steel and nickel with material properties νc = νm = 0.31; Em = 207,788.109N/m2, ρm = 8166 kg/m3 and Ec = 205,098.109N/m2, ρc = 8900 kg/m3. Comparison results are shown in Table 1.

Table 1 Natural frequencies of FGM cylindrical shell (Hz)
Full size table

Besides that, natural frequencies (1/s) obtained in present paper are also compared with those in publication of Bich et al. (2012) for FGM cylinder shell made of ZrO2/Ti–6Al–4 V, material properties are: νc = νm = 0.2981; Em = 105,696.109N/m2, ρm = 4429 kg/m3, Ec = 154.109 N/m2, ρc = 5700 kg/m3. The comparison results are shown in Table 2.

Table 2 The comparison vibration frequency of constant thickness FGM shell (1/s)
Full size table

Moreover, the critical stress of the structures in present study was compared with results in publication of Huang et al. (2010) for FGM cylindrical shell made of ZrO2/Ti-6Al-4 V with material properties are: Em = 122.56 GPa; ρm = 4429 kg/m3; νm = 0.288; Ec = 244.27 GPa; ρc = 5700 kg/m3; νc = 0.288. Comparison results are shown in Table 3

Table 3 Critical stress of FGM cylindrical shell (Mpa)
Full size table

The comparisons show that results in the present paper are good agreement with those in the above literature. Therefore, the proposed method is completely accurate and reliable for solving the forced vibration and dynamic buckling problems of the FGM cylindrical shell with variable thickness.

5 Numerical Results

Consider a variable thickness FGM cylindrical shell made of aluminum and alumina with geometric dimensions: h1 = 0.006 m, h0 = 0.004 m, R/h0 = 200, L/R = 2. Material properties: Em = 70.109 N/m2, ρm = 2702 kg/m3 and Ec = 380.109 N/m2, ρc = 3800 kg/m3, νm = νc = 0.3. Assume that the shell is simply supported at both ends.

5.1 Nonlinear Vibration Analysis

5.1.1 Natural Vibration Frequencies

Natural frequencies of the shell are determined according to Eq. (18) and shown in Table 4. We can see that natural frequencies of structure depend on volume fraction (k) and vibration mode (m, n). In the present paper, the lowest natural frequency corresponding to vibration mode (m, n) = (1, 7).

Table 4 Natural frequencies of variable thickness FGM cylindrical shell (1/s)
Full size table

5.1.2 Nonlinear Dynamic Responses of Variable Thickness FGM Cylindrical Shell

Nonlinear dynamic responses of variable thickness FGM cylindrical shell can be obtained from Eq. (16) by using the fourth-order Runge–Kutta method. Figure 2 demonstrates the nonlinear dynamic responses of variable thickness FGM cylinder shell, simply supported at both ends and subjected to mechanical load. The effects of vibration mode on natural frequencies and nonlinear dynamic responses of variable thickness shell are shown in Table 4 and Fig. 3. We can see that, corresponding to the nonlinear vibration mode (m, n) = (1, 7), the nonlinear vibration amplitude of the shell is the greatest.

Fig. 2
figure 2

Nonlinear dynamic response of variable thickness FGM cylindrical shell

Full size image
Fig. 3
figure 3

Effect of vibration mode on response amplitude of the shell

Full size image

Nonlinear dynamic responses of variable thickness FGM shell with the various values of k are demonstrated in Fig. 4. The graph shows that vibration amplitude of the structure increases when value of k index increases. The cause of this phenomenon is that the value of k increases, the metal ratio in the structure increases, and therefore, the stiffness of the structure decreases and the amplitude of nonlinear dynamic response of the shell increases. The influences of excitation force intensity on the nonlinear dynamic response of the shell are shown in Fig. 5.

Fig. 4
figure 4

Effect of volume fraction (k) on the dynamic response of variable thickness cylindrical shell

Full size image
Fig. 5
figure 5

Effect of excitation force on nonlinear dynamic response of variable thickness cylindrical shell

Full size image

Influences of geometric dimensions on nonlinear dynamic responses of variable thickness FGM cylindrical shell are shown in Figs. 6, 7 and 8. The graphs show that the larger the L / R ratio (or R / h0 ratio) is, the greater the vibration amplitude of the shell get. In other words, the greater the length (or radius) of the structure is, the lower the stiffness of the structure is.

Fig. 6
figure 6

Influence of h1/h0 ratio on nonlinear dynamic responses of variable thickness cylindrical shell

Full size image
Fig. 7
figure 7

Influence of L/R ratio on nonlinear dynamic response of variable thickness cylindrical shell

Full size image
Fig. 8
figure 8

Influence of R/h0 ratio on the nonlinear dynamic responses of variable thickness cylindrical shell

Full size image

Nonlinear vibration characteristics of FGM cylindrical shell with variable thickness are investigated and presented in Figs. 9, 10, 11, 12 and 13.

Fig. 9
figure 9

Resonance phenomenon

Full size image
Fig. 10
figure 10

The harmonic beat phenomenon

Full size image
Fig. 11
figure 11

The dw/dt-w relationships

Full size image
Fig. 12
figure 12

The dw/dt -w relationship curves in cases of Ω >  > ω0

Full size image
Fig. 13
figure 13

The dw/dt -w relationship curves in case of very great excitation force intensity

Full size image

Resonance phenomenon will occur when the frequency of the excitation force is equal to the natural frequency of the shell Ω = ω0(1,7) = 502 (rad/s). Then nonlinear vibration amplitude of the shell will infinitely increase over time (Fig. 9).

When excitation frequency is close to the natural frequencies of the shell, the harmonic beat phenomenon will occur and shown in Fig. 10. The closer the excitation frequency is, the greater the dynamic responses amplitude and the vibration period are. The velocity–deflection relationships are closed curves shown in Fig. 11.

When frequencies of excitation force are far from natural frequencies of the shell (Ω >  > ω0), the deflection–velocity relationship becomes very complex curves (Fig. 12).

When increasing the intensity of excitation force to very great value, the velocity-deflection relationship becomes disturbed curves (Fig. 13).

5.2 Nonlinear Dynamics Stability of Variable Thickness FGM Shell

Case 1 Variable thickness FGM cylindrical shell subjected to axial compression load in terms of time p = -c1t (c1-loading speed); q = 0 (Fig. 14).

Fig. 14
figure 14

Nonlinear dynamic responses of variable thickness FGM shell

Full size image

The effects of volume fraction (index k) on nonlinear dynamic responses of variable thickness FGM shell are demonstrated in Fig. 15 and Table 5. We can see that when values of k increase, the critical load of structure decreases. This is reasonable because the higher the value of k is, the greater the metal volume fraction is, which lead to the stiffness of structure decrease and the stability capable of the shell decrease.

Fig. 15
figure 15

Nonlinear dynamic responses of the shell with various values of k

Full size image
Table 5 The critical load of FGM shell with various values of k (GPa)
Full size table

The effects of geometric parameters on the nonlinear dynamic response of the variable thickness FGM cylindrical shell are shown in Figs. 16, 17, and 18. It can be seen that the critical load of the structure increases when L/R (or R/h0) ratio increases (Fig. 16 and 17), which means the stability capacity of the shell will increase when the length (or radius) of structure increases.

Fig. 16
figure 16

Effect of L/R ratio on dynamic responses of variable thickness FGM shell

Full size image
Fig. 17
figure 17

Effect of R/h0 ratio on dynamic responses of variable thickness FGM shell

Full size image
Fig. 18
figure 18

Effects of h1/h0 ratio on dynamic response of the FGM shell

Full size image

The effect of h1/h0 ratio on the nonlinear dynamic response of the cylindrical shell is shown in Fig. 18. We can see that, with the increasing h1/h0 ratio, the dynamic critical load of structure also increases. The dynamic critical load of the shell reaches its maximum value when h1/h0 = 1.

Influences of loading speed on nonlinear dynamic response of the shell are shown in Fig. 19. The graph shows that the greater the loading speed is, the lower the critical time is and the greater the dynamic critical load is. That means, with the higher loading speed, the stability loss of the shell will occur faster and at the greater critical load.

Fig. 19
figure 19

Influence of loading speed on the dynamic response of the FGM shell

Full size image

Case 2 Variable thickness FGM cylindrical shell under axial compression load p = constant and uniformly distributed pressure in terms of time q = c2t (c2- loading speed).

The nonlinear dynamic responses of variable thickness FGM cylindrical shell, in this case, are demonstrated in Fig. 20, 21, 22, 23, 24 and 25.

Fig. 20
figure 20

Dynamic response of variable thickness FGM shell

Full size image
Fig. 21
figure 21

Dynamic response of variable thickness FGM shell with various k

Full size image
Fig. 22
figure 22

Effect of L/R ratio on the dynamic response of the shell

Full size image
Fig. 23
figure 23

Effect of R/h0 ratio on dynamic response of the shell

Full size image
Fig. 24
figure 24

Effects of h1/h0 ratio on the dynamic response of variable thickness FGM shell

Full size image
Fig. 25
figure 25

Dynamic response of the FGM shell with the various loading speed

Full size image

Effects of volume fraction index (k) on the dynamic response of variable thickness cylinder shell are shown in Fig. 21. We can see that the critical load will decrease with the increase in volume fraction index (k). In other words, the stability capacity of structure will decrease.

When L/R ratio increases, the dynamic critical loads of the shell decrease (Fig. 22). It means the greater the length of the structure is, the less the pressure-bearing capacity of the shell is.

Figure 23 shows the effect of R/h0 ratio on nonlinear dynamic responses of the shell. It can be seen that if the value of R/h0 ratio increases, dynamic critical pressure will increase. That means the bearing capacity of bigger shell will better than small one.

The effects of h1/h0 ratio on the nonlinear dynamic response of the shell are similar to those in case 1, and the critical load of cylindrical shell reaches a maximum value when h1/h0 = 1 (constant thickness FGM shell) (Fig. 24).

The effects of loading speed on the nonlinear dynamic response of the shell are shown in Fig. 25. The graph shows that the greater the loading speed is, the lower the critical time and the greater the critical pressure are. In other words, with the higher loading speed, the stability loss will occur faster and at the greater critical pressure.

6 Conclusions

By using an analytical approach, based on the thin shell theory, taking into account the nonlinear geometry of von Karman–Donnell, nonlinear vibration and stability problems of variable thickness FGM cylindrical shell are solved by using Galerkin method and the fourth-order Runge–Kutta method.

Some following conclusions can be drawn from the examined results:

  • Natural frequencies of variable thickness FGM shell depending on volume fraction index (k) and the vibration mode (m, n).

  • Geometric parameters of the shell (L, R, h1, h0) are factors effect on the nonlinear vibration amplitude of the structure. When geometric dimensions of the shell increase (L, R), dynamic responses amplitude of the shell will increase, which means the stiffness of structure decreases.

  • When the excitation frequency is greater than the natural frequency of the shell, the deflection–velocity relationships are closed curves. If the frequency and intensity of excitation force is very great, the deflection–velocity curves become very complex and disturbed curves

  • Volume fraction index (k) remarkably affects the dynamic critical load of the structure. The greater the volume fraction index is, the lower the critical load of the shell is. In other words, the metal-richer FGM shell will work less stability than ceramic-richer ones.

  • When the length (L) of cylindrical shell increases, the dynamic critical load in case of axial compression-bearing shell increases, but the critical load in case of external pressure-bearing shell decreases. That means, if the length of structure increase, the axial compression-bearing capacity of the shell increases but the external pressure-bearing capacity of the shell decreases.

  • If the value of loading speed increases, the stability loss of the shell will occur faster and at greater dynamic critical load.