Free and Forced Vibration Analysis of Moderately Thick Functionally Graded Doubly Curved Shell of Revolution by Using a Semi-Analytical Method

Abstract

This paper describes the free and forced vibration of the doubly curved shells of revolution made of functionally graded (FG) material and constrained by various boundary conditions using a convenient and efficient method based on the Jacobi–Ritz method. The theoretical formulation is established on the basis of the multi-segment partitioning technique and first-order shear deformation theory (FSDT). It is assumed that the material properties of the shell vary smoothly and gradually in the thickness direction according to a typical four-parameter power-law function. At both end positions of the shell, the artificial spring technique is introduced to model the corresponding boundary conditions. Similarly, the connective spring parameters are used to model the continuity conditions between the divided shells. The displacements and rotations of any point of the FG doubly curved shell of revolution including the boundary and connection positions are expanded in form of Jacobi orthogonal polynomials in the meridional direction and Fourier series in the circumferential direction. Then, the dynamic characteristics including natural frequency are easily obtained by the Ritz method. The accuracy and credibility of the present method for free and forced vibration analysis are evidenced through comparison with previous literature and the results of the finite element method (FEM). In addition, through numerical examples, some interesting results about the dynamic behaviors of FG doubly curved shells of revolution with various boundary conditions are investigated, which may be provided as reference data for future study.

1 Introduction

With a research history of more than 100 years, shell theory has been made and developed into a wide variety of classical and modern theories on the basis of various approximations and assumptions. The shell theory developed so far can be divided into two main theories: classical thin shell theory (CST) and shear strain shell theory (SDST). Many CSTs, such as Flügge's theory, Donner–Mushtari's theory, Reissner–Naghdi's linear shell theory, and Sanders' theory, are based on the first approximation of the Love–Kirchhoff hypothesis, which does not include the effect of transverse shear deformation. According to the literature (Leissa 1973), it can be found that most of the vibration analysis results based on the CSTs are very similar. While much studies have studied the vibrational properties of shells based on CSTs, there is also the view that CSTs have a large error in predicting the transverse deflections and natural frequencies of moderately thick shells or shells made materials with a high degree of anisotropy (Toorani and Lakis 2000). In order to accurately predict the dynamic behavior of moderately thick shells and to eliminate defects in CSTs, the so-called shear deformation shell theory (SDST) has been developed which takes into account the effects of shear strain and rotational inertia based on Love's fourth assumption. In SDST, the displacement of the shell can be extended in terms of shell thickness beyond the first order. In the case of first-order expansion, the theory is named FSDT (Qatu 2004). Since the purpose of this paper is to investigate the dynamic characteristics of moderately thick FG doubly curved shells of revolution, FSDT is employed to formulate the theoretical formula.

It is well known that doubly curved shells of revolution are widely used in structural and engineering applications, such as ship, aerospace, chemical industry and civil engineering, and so on (Zarastvand et al. 2021a, b; 2022a, b; Wang et al. 2017a; Asadijafari et al. 2021; Seilsepour et al. 2022; Rahmatnezhad et al. 2021). With the development of science and manufacturing technology, various composite materials are being newly developed, and FG material, a kind of composite material, is widely applied to structures in the aerospace industry due to its convenience in manufacturing and superior physical mechanics. In order to solve the problem of the free vibration of FG doubly curved shell of revolution, various numerical analysis methods and experimental results have been reported by many researchers. Wang et al. performed the analysis of free vibrations of doubly curved shells and panels made of FG material, laminated composite material, and FG reinforced carbon nanotubes material using the improved Fourier series method (Wang et al. 2017b, c) and semi-analytical methods (Wang et al. 2017d), and presented the frequency parameters and the corresponding mode shapes. Atteshamuddin and Yuwaraj (2021) analyzed static and free vibration of FG doubly curved shells using Hamilton's principle, which is further solved analytically using Navier's technique, which assumes unknown variables in a double triangular series. Li et al. (2019a, b) established an analytical model for free vibration analysis of FG doubly curved shells with uniform and un-uniform thickness by using the Ritz method and verified the accuracy of the presented formulation experimentally. Choe et al. (2018) studied the free vibration behavior of coupled FG doubly curved shell structures with general boundary conditions by the using unified Jacobi–Ritz method. Wang et al. (Zhao et al. 2019) performed a parameterization study for vibration behavior of FG porous doubly curved panels and shells of revolution by using a semi-analytical method. In this study, the admissible displacement functions are expanded as a modified Fourier series of a standard cosine Fourier series with the auxiliary functions. Alijani et al. (2011a, b) investigated geometrically nonlinear vibrations of FG doubly curved shells to be simply supported with movable edges by using a multi-modal energy approach and the Galerkin method. Based on Hamilton Principle and a higher-order shear deformation theory (HSDT), Wang et al. (2018) analyzed free vibration and static bending of FG graphene nanoplatelet reinforced composite doubly curved shallow shells with simply supported boundary conditions. Fares et al. (2018) established an improved layerwise theory for the bending and vibration responses of multi-layered FG doubly curved shells. Chorfi et al. (2010) investigated the nonlinear free vibration of the FG doubly curved shallow shell of the elliptical plan-form by using the p-version of the finite element method in conjunction with the blending function method. For analyzing the bending and free vibration of FG doubly curved shells subjected to uniform and sinusoidal loads, Rachid et al. (2022) developed a new formulated 2D and quasi-3D HSDT. By using the Navier method, Chen et al. (2017) analyzed the free vibration of the FG sandwich doubly curved shallow shells with simply supported conditions. Kumar and Kumar (2021) presented a mathematical model for free vibration analysis of eccentrically stiffened FG shallow shells taking into account the thermo-mechanical loads by using the Galerkin method. Jin et al. (2016) presented a unified solution for the vibration analysis of FG doubly curved shells with arbitrary boundary conditions by using the modified Fourier series method on the basis of the first-order shear deformation shell theory considering the effects of the deepness terms. Xie et al. (2020) developed a unified semi-analytic method for free vibration analysis of FG shells with arbitrary boundary conditions and in this method, displacements are expanded as power series and Fourier series in meridional and circumferential directions. Talebitooti and Anbardan (2019) analyzed the free vibration of FG generally doubly curved shells of revolution by using the Haar wavelet discretization approach. Tornabene et al. (2014) contributed to the study for free vibration analysis of FG shell using various shell theories and the Generalized Differential Quadrature (GDQ) method. Studies related to free vibration analysis of various FG shell structures such as conical, cylindrical, and spherical shells and their combined structures can also be found in the Refs. (Pang et al. 2018; Li et al. 2019; Wang et al. 2017, e; Liu et al. 2020; Qin et al. 2019; Chen et al. 2022; Xie et al. 2015; Kim et al. 2021; Qu et al. 2013; Heydarpour et al. 2014a, b; Heydarpour and Malekzadeh 2012, 2019).

Through the review of the above literature, it can be seen that the Rayleigh–Ritz method (Li et al. 2019a, b), GDQ (Tornabene and Viola 2009a, b; Tornabene et al. 2014; Malekzadeh and Heydarpour 2013; Malekzadeh et al. 2012; Heydarpour and Aghdam 2018) method, Fourier series method (Wang et al. 2017b, c) and numerical analysis method have been used for the vibration analysis of shell structures. And, we can know that most of the existing literature is focused on the free vibration analysis of doubly curved shells. However, in actual engineering, various dynamic forces are subjected to these structures along with the working conditions and environment, it is very important to study the forced vibration characteristics as well as free vibration of FG doubly curved shells of revolution. Thus, for analyzing the forced vibration of FG doubly curved shells of revolution with arbitrary boundary conditions, it is necessary to establish a unified numerical analysis method. This paper focuses on the forced vibration analysis of FG doubly curved shells of revolution using the unified Jacobi–Ritz method. Advantage of this method is that the calculation cost is reduced by using the penalty function and the Rayleigh–Ritz method and that the selection of the admissible displacement functions is generalized by using the Jacobi polynomials. The FG doubly curved shell of revolution is divided into its segments in the axial direction, and the displacements of individual shell segments are expressed by Jacobi polynomials along the axial direction. The boundary conditions and the continuity conditions of the shell are modeled by the penalty method, which is applied to the Ritz method to obtain the frequency parameters and mode shapes. The presented method is capable of investigating the dynamic behavior of various FG doubly curved shells of revolution structures with arbitrary boundary conditions. To identify the applicability and accuracy of the proposed method, numerical examples are given for dynamic behavior analysis of FG doubly curved shell of revolution with various boundary conditions, which may be provided as reference data for future study.

2 Theoretical Formulations

2.1 Description of the FG Doubly Curved Shell of Revolution

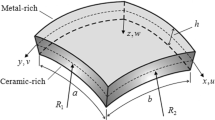
The geometric model and coordinate system of the FG doubly curved shell of revolution are shown in Fig. 1. The orthogonal curvilinear coordinate system (φ, θ, z) is fixed on the middle surface. The shell displacements in the meridional, circumferential and radial directions are expressed by u, v and w, respectively. The meridional angle φ refers to the angle formed by the external normal n to the reference surface and the axis of rotation Oz, or the geometric axis O₁z₁ of the meridian curve. The circumferential angle θ is the angle between the radius of the parallel circle and the x-axis. The horizontal radius is designated as R₀, and the radii of curvature in the meridional and circumferential directions are respectively represented by R_φ and R_θ. The doubly curved shell of revolution can be obtained by rotating the generatrix c₀c₁ around the axis of rotation z in the x–z plane. R_s is the offset distance of the rotation axis z with respect to the geometric central axis O₁z₁. h denotes the thickness of the shell. Due to the curvature characteristics, the engineering application will involve different doubly curved shells of revolution in shape. Thus, in this work, doubly curved shells of revolution with elliptical (Fig. 2a), paraboloidal (Fig. 2b), and hyperbolical (Fig. 2c) meridian curves are considered.

Fig. 1

Geometry and reference system of a doubly curved shell

Fig. 2

The geometric profile parameters of doubly curved shells of revolution: a elliptical shell, b paraboloidal shell, c hyperbolical shell

The geometric relationship of individual doubly curved shell structures is expressed as (Wang et al. 2017b; Li et al. 2019a; Jin et al. 2016):

(1). Elliptical shell, see Fig. 2a

$$R_{\varphi } (\varphi ) = \frac{{a_{e}^{2} b_{e}^{2} }}{{\sqrt {\left( {a_{e}^{2} \sin^{2} \varphi + b_{e}^{2} \cos^{2} \varphi } \right)^{3} } }}\;\;;\,\,R_{\theta } (\varphi ) = \frac{{a_{e}^{2} }}{{\sqrt {a_{e}^{2} \sin^{2} \varphi + b_{e}^{2} \cos^{2} \varphi } }}$$

(1a)

where a and b are the length of the semimajor and semiminor axes of the elliptic meridian, respectively. Specially,

$$L = \left( {\sqrt {a_{e}^{2} - R_{0}^{2} } - \sqrt {a_{e}^{2} - R_{1}^{2} } } \right)\frac{{b_{e} }}{{a_{e} }}$$

(1b)

$$\varphi_{0} = \arctan \left( {\frac{{b_{e} R_{0} }}{{a_{e} \sqrt {a_{e}^{2} - R_{0}^{2} } }}} \right),\,\,\,\varphi_{1} = \arctan \left( {\frac{{b_{e} R_{1} }}{{a_{e} \sqrt {a_{e}^{2} - R_{1}^{2} } }}} \right)$$

(1c)

(2). Paraboloidal shell, see Fig. 2b

$$R_{\varphi } (\varphi ) = \frac{k}{{2\cos^{3} \varphi }}\;\;;\,\,R_{\theta } (\varphi ) = \frac{k}{2\cos \varphi }$$

(2a)

where k is the characteristic parameter of the parabolic meridian. Specially,

$$k = \frac{{R_{1}^{2} - R_{0}^{2} }}{L}$$

(2b)

$$\varphi_{0} = \arctan \left( {\frac{{2R_{0} }}{k}} \right),\,\,\,\varphi_{1} = \arctan \left( {\frac{{2R_{1} }}{k}} \right)$$

(2c)

(3). Hyperbolical shell, see Fig. 2c

$$R_{\varphi } (\varphi ) = \frac{{ - a_{h}^{2} b_{h}^{2} }}{{\sqrt {\left( {a_{h}^{2} \sin^{2} \varphi - b_{h}^{2} \cos^{2} \varphi } \right)^{3} } }};\,\,R_{\theta } (\varphi ) = \frac{{a_{h}^{2} }}{{\sqrt {a_{h}^{2} \sin^{2} \varphi - b_{h}^{2} \cos^{2} \varphi } }} + \frac{{R_{s} }}{\sin \varphi }$$

(3a)

where a and b are the length of the semitransverse and semiconjugate axes of the hyperbolic meridian, respectively. R_s is the distance between the axis of rotation O₁z₁ and the geometric axis of the meridian Oz. Specially,

$$b_{h} = {{a_{h} L} \mathord{\left/ {\vphantom {{a_{h} L} {\left( {\sqrt {R_{0}^{2} - a_{h}^{2} } - \sqrt {R_{1}^{2} - a_{h}^{2} } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sqrt {R_{0}^{2} - a_{h}^{2} } - \sqrt {R_{1}^{2} - a_{h}^{2} } } \right)}}$$

(3b)

$$\varphi_{0} = \arctan \left( {\frac{{b_{h} \left( {R_{0} - R_{s} } \right)}}{{a_{h} \sqrt {\left( {R_{0} - R_{s} } \right)^{2} - a_{h}^{2} } }}} \right);\,\,\,\varphi_{1} = \arctan \left( {\frac{{b_{h} \left( {R_{1} - R_{s} } \right)}}{{a_{h} \sqrt {\left( {R_{1} - R_{s} } \right)^{2} - a_{h}^{2} } }}} \right)$$

(3c)

2.2 Material Properties

In this study, it is assumed that FG material is made by mixing ceramic and metal according to the uniform distribution law. When two materials are mixed and made according to a certain distribution rule, the material property parameters of FG material are expressed as (Li et al. 2019b; Tornabene and Viola 2009a; Chen et al. 2022):

$$E(z) = E_{m} + (E_{c} - E_{m} )V_{c} (z)$$

(4a)

$$\rho (z) = \rho_{m} + (\rho_{c} - \rho_{m} )V_{c} (z)$$

(4b)

$$\mu (z) = \mu_{m} + (\mu_{c} - \mu_{m} )V_{c} (z)$$

(4c)

where E, ρ and μ are Young's modulus, density, and Poisson's ratio, respectively. The subscripts m and c denote metals and ceramics, respectively. As can be seen from Eq. (4), the material property parameters change smoothly in the thickness direction z with the volume fraction V_c, where the volume fraction V_c follows two general four-parameter(a, b, c and p) power-law distributions:

$${\text{FGM}}_{{\text{I}}} \left( {a/b/c/p} \right):\,\,\,\,V_{c} (z) = \left[ {1 - a\left( {\frac{1}{2} + \frac{z}{h}} \right) + b\left( {\frac{1}{2} + \frac{z}{h}} \right)^{c} } \right]^{p}$$

(5a)

$${\text{FGM}}_{{{\text{II}}}} \left( {a/b/c/p} \right):\,\,\,\,V_{c} (z) = \left[ {1 - a\left( {\frac{1}{2} - \frac{z}{h}} \right) + b\left( {\frac{1}{2} - \frac{z}{h}} \right)^{c} } \right]^{p}$$

(5b)

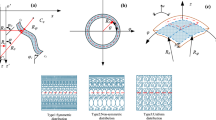
In which, h is thickness of doubly curved shell. Of the four parameters, the parameter p is called the power-law index. By setting the parameters a = 1 and b = 0 in Eq. (5), a classical volume fraction is obtained, and the corresponding volume fraction is shown in Fig. 3a. Also, Fig. 3b–d shows the changes in different volume fractions when parameters a, b, and c are randomly chosen. From Fig. 4, it can be clearly seen that the volume fraction changes symmetrically or asymmetrically according to the settings of parameters a, b, and c.

Fig. 3

Variations of the volume fraction V_C according to change of the power-law index p. a; FGM (a = 1/b = 0/c/p) b; FGM (a = 1/b = 1/c = 4/p), c; FGM (a = 1/b = 0.5/c = 2/p), d; FGM (a = 0/b = − 0.5/c = 2/p)

Fig. 4

Percentage error of the natural frequencies for the Jacobi parameters α and β. a elliptical shell, b paraboloidal shell, c hyperbolical shell

2.3 Energy Functional of Shell Segment

According to FSDT, the displacement field of the middle surface of the ξth segment of FG doubly curved shell of revolution is as follows (Wang et al. 2017b; Li et al. 2019a; Jin et al. 2016; Talebitooti and Shenaei Anbardan 2019; Xie et al. 2015):

$$\overline{U}_{\xi } \left( {\varphi ,\theta ,z,t} \right) = u_{\xi } \left( {\varphi ,\theta ,t} \right) + z\psi_{{\varphi_{\xi } }} \left( {\varphi ,\theta ,t} \right)$$

(6a)

$$\overline{V}_{\xi } \left( {\varphi ,\theta ,z,t} \right) = v_{\xi } \left( {\varphi ,\theta ,t} \right) + z\psi_{{\theta_{\xi } }} \left( {\varphi ,\theta ,t} \right)$$

(6b)

$$\overline{W}_{\xi } \left( {\varphi ,\theta ,z,t} \right) = w_{\xi } \left( {\varphi ,\theta ,t} \right)$$

(6c)

In Eq. (6), $\overline{U}_{\xi }$, $\overline{V}_{\xi }$ and $\overline{W}_{\xi }$ are the displacement fields of ξth segment of the FG doubly curved shell of revolution in φ, θ and z directions, respectively. And in the right-hand expression of Eq. (6), u_ξ, v_ξ and w_ξ denote translational displacement in φ, θ and z directions, $\psi_{{\varphi_{\xi } }}$ and $\psi_{{\theta_{\xi } }}$ denote the rotation of transverse normal about φ- and θ-axis, respectively. Based on the FSDT, under the assumption of small deformation and rotation, the nonzero strain components of composite laminated doubly curved shells of revolution according to the above displacement field are expressed as follows (Wang et al. 2017b; Li et al. 2019a; Jin et al. 2016; Talebitooti and Shenaei Anbardan 2019; Xie et al. 2015):

$$\varepsilon_{{\varphi_{\xi } }} = \varepsilon_{{\varphi_{\xi } }}^{0} + zk_{{\varphi_{\xi } }}^{0}$$

(7a)

$$\varepsilon_{{\theta_{\xi } }} = \varepsilon_{{\theta_{\xi } }}^{0} + zk_{{\theta_{\xi } }}^{0}$$

(7b)

$$\gamma_{{\varphi \theta_{\xi } }} = \gamma_{{\varphi \theta_{\xi } }}^{0} + zk_{{\varphi \theta_{\xi } }}^{0}$$

(7c)

$$\gamma_{{\varphi z_{\xi } }} = \gamma_{{\varphi z_{\xi } }}^{0}$$

(7d)

$$\gamma_{\theta z} = \gamma_{{\theta z_{\xi } }}^{0} \;$$

(7e)

where the strains are defined as(Wang et al. 2017b; Jin et al. 2016; Talebitooti and Shenaei Anbardan 2019):

$$\varepsilon_{{\varphi_{\xi } }}^{0} = \frac{1}{{R_{{\varphi_{\xi } }} }}\left( {\frac{{\partial u_{\xi } }}{{\partial \varphi_{\xi } }} + w_{\xi } } \right),$$

(8a)

$$\varepsilon_{{\theta_{\xi } }}^{0} = \frac{1}{{R_{{0_{\xi } }} }}\left( {\frac{{\partial v_{\xi } }}{{\partial \theta_{\xi } }} + u_{\xi } \cos \varphi + w_{\xi } \sin \varphi } \right),$$

(8b)

$$\gamma_{{\varphi \theta_{\xi } }}^{0} = \frac{1}{{R_{{\varphi_{\xi } }} }}\frac{{\partial v_{\xi } }}{{\partial \varphi_{\xi } }} + \frac{1}{{R_{{0_{\xi } }} }}\left( {\frac{{\partial u_{\xi } }}{{\partial \theta_{\xi } }} - v_{\xi } \cos \varphi } \right),$$

(8c)

$$\gamma_{{\varphi z_{\xi } }}^{0} = \frac{1}{{R_{{\varphi_{\xi } }} }}\left( {\frac{{\partial w_{\xi } }}{{\partial \varphi_{\xi } }} - u_{\xi } } \right) + \psi_{{\varphi_{\xi } }} ,$$

(8d)

$$\gamma_{{\theta z_{\xi } }}^{0} = \frac{1}{{R_{{0_{\xi } }} }}\left( {\frac{{\partial w_{\xi } }}{{\partial \theta_{\xi } }} - v_{\xi } \sin \varphi } \right) + \psi_{{\theta_{\xi } }} ,$$

(8e)

$$k_{{\varphi_{\xi } }} = \frac{1}{{R_{{\varphi_{\xi } }} }}\frac{{\partial \psi_{{\varphi_{\xi } }} }}{{\partial \varphi_{\xi } }},$$

(8f)

$$k_{{\theta_{\xi } }} = \frac{1}{{R_{{0_{\xi } }} }}\left( {\frac{{\partial \psi_{{\theta_{\xi } }} }}{{\partial \theta_{\xi } }} + \psi_{{\varphi_{\xi } }} \cos \varphi } \right),$$

(8g)

$$k_{{\varphi \theta_{\xi } }} = \frac{1}{{R_{{\varphi_{\xi } }} }}\frac{{\partial \psi_{{\theta_{\xi } }} }}{{\partial \varphi_{\xi } }} + \frac{1}{{R_{{0_{\xi } }} }}\left( {\frac{{\partial \psi_{{\varphi_{\xi } }} }}{{\partial \theta_{\xi } }} - \psi_{{\theta_{\xi } }} \cos \varphi } \right),$$

(8h)

According to Hooke’s law, the relationship between the stress and strain are obtained as (Wang et al. 2017b; Jin et al. 2016; Talebitooti and Shenaei Anbardan 2019):

$$\left\{ \begin{gathered} \sigma_{{\varphi_{\xi } }} \hfill \\ \sigma_{{\theta_{\xi } }} \hfill \\ \tau_{{\varphi \theta_{\xi } }} \hfill \\ \tau_{{\varphi z_{\xi } }} \hfill \\ \tau_{{\theta z_{\xi } }} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} \left( z \right)} & {Q_{12} \left( z \right)} & 0 & 0 & 0 \\ {Q_{12} \left( z \right)} & {Q_{11} \left( z \right)} & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} \left( z \right)} & 0 & 0 \\ 0 & 0 & 0 & {Q_{66} \left( z \right)} & 0 \\ 0 & 0 & 0 & 0 & {Q_{66} \left( z \right)} \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{{\varphi_{\xi } }} \hfill \\ \varepsilon_{{\theta_{\xi } }} \hfill \\ \gamma_{{\varphi \theta_{\xi } }} \hfill \\ \gamma_{{\varphi z_{\xi } }} \hfill \\ \gamma_{{\theta z_{\xi } }} \hfill \\ \end{gathered} \right\}$$

(9)

where $\sigma_{{\varphi_{\xi } }} ,\;\sigma_{{\theta_{\xi } }}$ are the normal stresses, $\tau_{{\varphi \theta_{\xi } }} ,\,\tau_{{\varphi z_{\xi } }} ,\tau_{{\theta z_{\xi } }}$ are the shear stresses of the ξth shell segment, and $\varepsilon_{{\varphi_{\xi } }} ,\;\varepsilon_{{\theta_{\xi } }}$ are the normal strain components, $\;\gamma_{{x\theta_{\xi } }} ,\,\,\gamma_{{\varphi z_{\xi } }} ,\,\gamma_{{\theta z_{\xi } }}$ are the shear strain components of the ξth shell segment, respectively. Q_ij(z) are the elastic constants, which are functions of thickness coordinate z and are defined as(Wang et al. 2017b; Jin et al. 2016; Talebitooti and Shenaei Anbardan 2019):

$$Q_{11} \left( z \right) = \frac{E\left( z \right)}{{1 - \mu^{2} \left( z \right)}}$$

(10a)

$$Q_{12} \left( z \right) = \frac{\mu \left( z \right)E\left( z \right)}{{1 - \mu^{2} \left( z \right)}}$$

(10b)

$$Q_{66}^{k} = \frac{E\left( z \right)}{{2\left[ {1 + \mu \left( z \right)} \right]}}$$

(10c)

The governing equations, which describe the relationship between the force and moment resultants and curvatures in the reference surface, are given in the following matrix form (Jin et al. 2016; Talebitooti and Shenaei Anbardan 2019):

$$\left[ {\begin{array}{*{20}c} {N_{{\varphi_{\xi } }} } \\ {N_{{\theta_{\xi } }} } \\ {N_{{\varphi \theta_{\xi } }} } \\ {N_{{\varphi \theta_{\xi } }} } \\ {M_{{\theta_{\xi } }} } \\ {M_{{\varphi \theta_{\xi } }} } \\ {Q_{{\varphi_{\xi } }} } \\ {Q_{{\theta_{\xi } }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 & 0 & 0 \\ {A_{12} } & {A_{11} } & 0 & {B_{12} } & {B_{11} } & 0 & 0 & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } & 0 & 0 \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 & 0 & 0 \\ {B_{12} } & {B_{11} } & 0 & {D_{12} } & {D_{11} } & 0 & 0 & 0 \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\kappa_{s} A_{66} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\kappa_{s} A_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{{\varphi_{\xi } }}^{0} } \\ {\varepsilon_{{\theta_{\xi } }}^{0} } \\ {\gamma_{{\varphi \theta_{\xi } }}^{0} } \\ {k_{\varphi } } \\ {k_{\theta } } \\ {k_{\varphi \theta } } \\ {\gamma_{\varphi z}^{0} } \\ {\gamma_{\theta z}^{0} } \\ \end{array} } \right]$$

(11)

where N_φξ, N_θξ and Nφ_θξ are the forces in-plane, M_φξ, M_θξ and Mφ_θξ are bending and twisting moments, and Q_φξ, Q_θξ are shear forces, respectively. κ_s is the shear correction factor. Where A_ij, B_ij, and D_ij(i,j = 1, 2 and 6) are tensile, tensile-bending coupling, and bending stiffness, respectively, defined as:

$$\left( {A_{ij} ,B_{ij} ,D_{ij} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,z^{2} } \right)Q_{ij} \left( z \right)dz} ,\,\,\,\,\,\,\,i,j = 1,2,6$$

(12)

The strain energy U_ξ of ξth segment in the FG doubly curved shell of revolution yields (Li et al. 2019a; Choe et al. 2018):

$$U_{\xi } = \frac{1}{2}\int\limits_{\varphi } {\int\limits_{\theta } {\left( \begin{gathered} N_{{\varphi_{\xi } }} \varepsilon_{{\varphi_{\xi } }}^{0} + N_{{\theta_{\xi } }} \varepsilon_{{\theta_{\xi } }}^{0} + N_{{\varphi \theta_{\xi } }} \gamma_{{\varphi \theta_{\xi } }}^{0} + M_{{\varphi_{\xi } }} k_{{\varphi_{\xi } }} + \hfill \\ M_{{\varphi_{\xi } }} k_{{\theta_{\xi } }} + M_{{\varphi \theta_{\xi } }} k_{{\varphi \theta_{\xi } }} + Q_{{\varphi_{\xi } }} \gamma_{{\varphi z_{\xi } }}^{0} + Q_{{\theta_{\xi } }} \gamma_{{\theta z_{\xi } }}^{0} \hfill \\ \end{gathered} \right)R_{{0_{\xi } }} R_{{\varphi_{\xi } }} d\theta d\varphi } }$$

(13)

The maximum kinetic energy of the shell segment can be defined as (Li et al. 2019a; Choe et al. 2018):

$$\begin{aligned} T_{\xi } & = \frac{1}{2}\iiint_{V} {\rho \left( z \right)}\left[ {\left( {\dot{\overline{U}}} \right)^{2} + \left( {\dot{\overline{V}}} \right)^{2} + \left( {\dot{\overline{W}}} \right)^{2} } \right]\left( {1 + \frac{z}{{R_{\varphi } }}} \right)\left( {1 + \frac{z}{{R_{\theta } }}} \right)R_{{0_{\xi } }} R_{{\varphi_{\xi } }} d\varphi d\theta dz \\ & = \frac{1}{2}\int\limits_{{\varphi_{0} }}^{{\varphi_{1} }} {\int\limits_{0}^{2\pi } {\left\{ {I_{0} \left[ {\left( {\dot{u}_{\xi } } \right)^{2} + \left( {\dot{v}_{\xi } } \right)^{2} + \left( {\dot{w}_{\xi } } \right)^{2} } \right] + 2I_{1} \left( {\dot{u}_{\xi } \dot{\psi }_{{\varphi_{\xi } }} + \dot{v}_{\xi } \dot{\psi }_{{\theta_{\xi } }} } \right) + I_{2} \left[ {\left( {\dot{\psi }_{{\varphi_{\xi } }} } \right)^{2} + \left( {\dot{\psi }_{{\theta_{\xi } }} } \right)^{2} } \right]} \right\}R_{{0_{\xi } }} R_{{\varphi_{\xi } }} d\theta d\varphi } } \\ \end{aligned}$$

(14)

where the dot above the displacement components represents differentiation with respect to time.

$$\left( {I_{0} ,I_{1} ,I_{2} } \right) = \int\limits_{ - h/2}^{h/2} {\rho \left( z \right)\left( {1 + \frac{z}{{R_{{\varphi_{\xi } }} }}} \right)\left( {1 + \frac{z}{{R_{{\theta_{\xi } }} }}} \right)\left( {1,\,z,\,z^{2} } \right)} dz$$

(15)

For the study of the dynamic characteristics of the FG doubly curved revolution shells, the work of external forces can be expressed as follows (Li et al. 2019a; Choe et al. 2018):

$$W_{\xi } = \frac{1}{2}\int\limits_{\varphi } {\int\limits_{\theta } {\left( {f_{{u_{\xi } }} u_{\xi } + f_{{v_{\xi } }} + f_{{w_{\xi } }} + m_{{\varphi_{\xi } }} \psi_{{\varphi_{\xi } }} + m_{{\theta_{\xi } }} \psi_{{\theta_{\xi } }} } \right)R_{{0_{\xi } }} R_{{\varphi_{\xi } }} d\theta d\varphi } }$$

(16)

2.4 Boundary and Continuity Conditions

In this analysis, the boundary and the continuity conditions of the FG doubly curved shell of revolution are modeled using the penalty method, where penalty parameters are defined by the stiffness values representing artificial translational and rotational springs (Wang et al. 2017b, c, d; Choe et al. 2018). In other words, the various boundary conditions of the doubly curved shells of revolution can be realized by appropriate penalty parameter values. The penalty parameter can represent various boundary conditions and continuity conditions of the doubly curved shell of revolution, permit the flexible selection of the admissible displacement functions, and the appropriate value of the penalty parameter ensures fast convergence of the solution. The potential energy stored in the boundary springs can be described as (Li et al. 2019a; Choe et al. 2018):

$$\begin{aligned} U_{b} & = \frac{1}{2}\int\limits_{0}^{2\pi } {\left( {k_{u,0} u^{2} + k_{v,0} v^{2} + k_{w,0} w^{2} + k_{\varphi ,0} \psi_{\varphi }^{2} + k_{\theta ,0} \psi_{\theta }^{2} } \right)_{{\varphi = \varphi_{0} }} R_{0} d\theta } \\ \,\,\,\,\,\,\, + \frac{1}{2}\int\limits_{0}^{2\pi } {\left( {k_{u,1} u^{2} + k_{v,1} v^{2} + k_{w,1} w^{2} + k_{\varphi ,1} \psi_{\varphi }^{2} + k_{\theta ,1} \psi_{\theta }^{2} } \right)_{{\varphi = \varphi_{1} }} R_{0} d\theta } \\ \end{aligned}$$

(17)

where k_ϕ,0(ϕ = u,v,w,φ,θ) and k_ϕ,1 denote the boundary spring stiffness of both ends of the doubly curved shell of revolution, respectively. That is, the boundary at both ends of the shell can be modeled as an arbitrary boundary condition according to the stiffness value of the artificial spring.

In the case of two adjacent shell segments at each shell component, the potential energy stored in the connective springs can be described as (Li et al. 2019a; Choe et al. 2018):

$$U_{{c_{\xi } }} = \frac{1}{2}\int\limits_{0}^{2\pi } {\left[ \begin{gathered} k_{uc} \left( {u_{\xi } - u_{\xi + 1} } \right)^{2} + k_{vc} \left( {v_{\xi } - v_{\xi + 1} } \right)^{2} + k_{wc} \left( {w_{\xi } - w_{\xi + 1} } \right)^{2} \hfill \\ + k_{\varphi c} \left( {\psi_{{\varphi_{\xi } }} - \psi_{{\varphi_{\xi + 1} }} } \right)^{2} + k_{\theta c} \left( {\psi_{{\theta_{\xi } }} - \psi_{{\theta_{\xi + 1} }} } \right)^{2} \hfill \\ \end{gathered} \right]_{\xi ,\xi + 1} R_{0} d\theta }$$

(18)

where k_uc, k_vc, k_wc, k_φc and k_θc denote the stiffnesses of the connective springs between the shell components, respectively. The superscripts, ξ and ξ + 1, represent the ξth and ξ + 1th shell segments. Therefore, the total potential energy reflecting boundary conditions and connective conditions can be expressed as

$$U_{BC} = U_{b} + \sum\limits_{\xi = 1}^{N - 1} {U_{{c_{\xi } }} }$$

(19)

Thus, the arbitrary boundary conditions are freely modeled in the present model by assigning the stiffnesses of the springs to the proper values.

2.5 Displacement Components and Solution Procedure

It is very important to select the suitable allowable displacement function for ensuring a stable convergence and accuracy of the solution. The displacement functions of the FG doubly curved shell of revolution can be flexibly selected by the penalty parameter, and fast convergence of the accurate solution can be ensured with the appropriate value of the penalty parameter. On the treatment of continuous boundary conditions, it makes the choice of the admissible function flexible to introduce the spring stiffness, which is the penalty parameter in nature (Wang et al. 2017b, c, d; Choe et al. 2018). The classical Jacobi polynomials (Choe et al. 2018; Heydarpour and Aghdam 2017), as we all know, are defined on the interval of $\phi \in [ - 1,1]$ and their recurrence formula $P_{i}^{(\alpha ,\beta )} (\phi )$ $P_{i}^{(\alpha ,\beta )} (\phi )$ of degree i is given by:

$$P_{0}^{(\alpha ,\beta )} (\phi ) = 1,\,\,P_{1}^{(\alpha ,\beta )} (\phi ) = \frac{\alpha + \beta + 2}{2}\phi - \frac{\alpha - \beta }{2}$$

(20)

$$\begin{aligned} P_{i}^{(\alpha ,\beta )} (\phi ) & = \frac{{{(}\alpha + \beta + 2i - 1)\left\{ {\alpha^{2} - \beta^{2} + \phi {(}\alpha + \beta + 2i)(\alpha + \beta + 2i - 2)} \right\}}}{{2i{(}\alpha + \beta + i)(\alpha + \beta + 2i - 2)}}P_{i - 1}^{(\alpha ,\beta )} (\phi ) \\ & \,\,\,\, - \frac{{{(}\alpha + i - 1)(\beta + i - 1)(\alpha + \beta + 2i)}}{{i{(}\alpha + \beta + i)(\alpha + \beta + 2i - 2)}}P_{i - 2}^{(\alpha ,\beta )} (\phi ) \\ \end{aligned}$$

(21)

where α,β >  − 1 and i = 2, 3…

The orthogonality condition for the classical Jacobi polynomials can be written as

$$\int\limits_{ - 1}^{1} {P_{j}^{(\alpha ,\beta )} (\phi )P_{k}^{(\alpha ,\beta )} (\phi )} w^{(\alpha ,\beta )} (\phi )d\phi = h_{k}$$

(22.a)

$$h_{k} = \left\{ \begin{gathered} \frac{{2^{\alpha + \beta + 1} }}{2k + \alpha + \beta + 1}\frac{\Gamma (k + \alpha + 1)\Gamma (k + \beta + 1)}{{\Gamma (k + \alpha + \beta + 1)k!}}\;\;,\;\;j = k \hfill \\ \;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;\;j \ne k \hfill \\ \end{gathered} \right.$$

(22.b)

where w^(α,β)(x) = (1-x)^α(1 + x)^β. The Jacoby polynomials are generalized orthonormal polynomials containing some orthonormal polynomials such as Legendre, Chebyshev, and Gegenbauer polynomials. For example, when α = β = -0.5, the Chebyshev polynomials of the first kind are obtained, whileα = β = 0.5 leads to the Chebyshev polynomials of the second kind. And when α = β = 0 is set, the Legendre polynomials are realized, while α = β provides the Gegenbauer polynomials. Therefore, in this paper, the allowable displacement function of the FG doubly curved shell of revolution is uniformly extended to the Jacobi polynomials regardless of the element shape and displacement type. The displacement functions of the shell segments can be written in the forms:

$$u_{\xi } = \sum\limits_{m = 0}^{M} {U_{m,\xi } P_{m}^{(\alpha ,\beta )} (\varphi_{\xi } )\cos (n\theta_{\xi } )e^{i\omega t} } ,$$

(23a)

$$v_{\xi } = \sum\limits_{m = 0}^{M} {V_{m,\xi } P_{m}^{(\alpha ,\beta )} (\varphi_{\xi } )\sin (n\theta_{\xi } )e^{i\omega t} ,\,}$$

(23b)

$$\,w_{\xi } = \sum\limits_{m = 0}^{M} {W_{m,\xi } P_{m}^{(\alpha ,\beta )} (\varphi_{\xi } )\cos (n\theta_{\xi } )e^{i\omega t} } ,$$

(23c)

$$\psi_{{\varphi_{\xi } }} = \sum\limits_{m = 0}^{M} {\Phi_{m,\xi } P_{m}^{(\alpha ,\beta )} (\varphi_{\xi } )\cos (n\theta_{\xi } )e^{i\omega t} } ,$$

(24d)

$$\psi_{{\theta_{\xi } }} = \sum\limits_{m = 0}^{M} {\Theta_{m,\xi } P_{m}^{(\alpha ,\beta )} (\varphi_{\xi } )\sin (n\theta_{\xi } )e^{i\omega t} }$$

(25e)

where U_m,ξ, V_m,ξ, W_m,ξ, Φ_m,ξ, and Θ_m,ξ are the corresponding Jacobi expanded coefficients; P_m^(α,β)(ϕ) are the mth order Jacobi polynomial for the displacement components in the meridional direction; ω is an angular frequency, t denotes time. The nonnegative integer n represents the circumferential wave number of the corresponding mode shape. M is the highest degree taken into admissible functions. In mathematics, the orthogonal Jacobi polynomials are defined on the interval ϕ ∈ [1-, 1]. Thus, for use of the Jacobi polynomials in the interval φ (for the ξ^th shell segment, φ ∈ [φ_ξ, φ_ξ+1]), should proceed with a linear transformation for each shell segment, i.e., φ = [(φ_ξ+1-φ_ξ)/2]ϕ + (φ_ξ+1 + φ_ξ)/2. The total Lagrangian energy functions (${\varvec{L}}$) of the FG doubly curved shell of revolution can be written in the forms:

$${\varvec{L}} = \sum\limits_{\xi = 1}^{N} {\left( {T_{\xi } - U_{\xi } + W_{\xi } } \right)} - U_{BC}$$

(24)

By using the Rayleigh–Ritz method, minimizing the total expression of the Lagrangian energy functional with respect to the undetermined coefficients;

$$\frac{\partial L}{{\partial \vartheta }} = 0\;\;\;\;\;\;\vartheta = U_{mn} ,\;V_{mn} ,\;W_{mn} ,{\kern 1pt} \psi_{\varphi mn} ,{\kern 1pt} \psi_{\theta mn}$$

(25)

By substituting Eqs. (13), (14), (16), (19) and Eq. (24) into Eq. (25), it can be summed up in a matrix form as follows:

$$\left( {{\mathbf{K}} - {\mathbf{M}}\omega^{2} } \right){\mathbf{A}} = {\mathbf{F}}$$

(26)

where, K, M and A represent the stiffness matrix, mass matrix, vector of the unknown coefficients for the shell and F is external force, respectively. By solving Eq. (26) the frequencies and the corresponding eigenvectors of the FG doubly curved shells of revolution can be easily obtained. The detailed expressions for the elements in these matrices can be found in “Appendix A”.

3 Numerical Results and Discussions

In this section, the study of the dynamic analysis of the FG doubly curved shells of revolution will be given by means of the MATLAB code compiled by ourselves in the MATLAB 15.0 platform. Some numerical examples are performed to verify the convergence, accuracy, and reliability of the present method. This section is organized as follows: Firstly, the convergence of the present method is examined through some numerical examples. Then, the accuracy of the present method is verified with the results of previous literature. On the basis of the accuracy verification of the presented method, some dynamic analysis results of FG doubly curved shells of revolution are presented. For the simplicity of study, it is assumed that the property parameters of FG material in all numerical examples of this paper are as follows (Li et al. 2019a, b; Talebitooti and Shenaei Anbardan 2019): E_m = 70Gpa, E_c = 168Gpa, ρ_m = 2707 kg/m³, ρ_c = 5700 kg/m³, μ_m = 0.3, μ_m = 0.3. In addition, unless otherwise mentioned, the geometric dimensions of FG doubly curved shells of revolution are set as follows; for elliptical shell: a_e = 1 m, b_e = 2 m, R₀ = 0.2 m, R₁ = a_e, for Paraboloidal shell: R₀ = 0.2 m, R₁ = 1 m, L = 1 m, R_s = 0, for hyperbolical shell: R₀ = 0.2 m, R₁ = 1 m, R_s = 4 m, L = 4 m, and thickness h = 0.05 m.

3.1 Convergence Study

In order to verify the convergence and accuracy of the presented method, some convergence studies are needed to study.

From the theoretical formulation, it can be seen that the Jacobi polynomial series can be expanded to infinite terms. However, the number of series terms must be truncated at an appropriate finite number by considering the effectiveness of computation and the accuracy of the solution. For this purpose, convergence studies are needed to establish the maximal order of series that should be used to obtain accurate results. Table 1 shows the change of frequency parameters of the FG doubly curved shells of revolution according to increases in the maximal order of the series of Jacobi polynomials. From Table 1, it can be clearly seen that the frequency parameters of shells steadily converge to a certain value as the maximal order M of the series of Jacobi polynomial increases. In particular, when M has a value of 8 or more, it can be seen that the frequency parameters of shells hardly change. Therefore, the maximal order of the series of Jacobi polynomial for all numerical examples is uniformly set as M = 8.

Table 1 Convergence of frequency parameters (Ω = ωR₁(ρ_c/E_c)^1/2)with the increasing of the degree M of the Jacobi polynomials (n = 1)

Table 2 shows the change of the natural frequencies with the increase in the number of shell segments. As can be seen from Table 2, the values of natural frequency converge steadily as the number of shell segments increases. It can also be seen that there is almost no change in the frequency value when the number of segments is four or more. Of course, in some cases (e.g. mode 1 for elliptical shells, mode 4 for parabolic shells, and modes 4 and 5 for hyperbolic shells), the frequency parameters converge more when the number of segments increases, however, the error is very small. it is clear that convergence to a more accurate solution as the number of segments increases, However, on the other hand, increases the computational cost. Therefore, in this paper, for simplicity of calculation, the number of shell segments is set as N = 4.

Table 2 Convergence and comparison of the frequency parameters(Ω = ωR₁(ρ_c/E_c)^1/2) with the increasing of the number of the shell segments (n = 1)

The percentage errors $\left( {\Omega_{\alpha ,\beta } - \Omega_{\alpha = 0,\beta = 0} } \right)/\Omega_{\alpha = 0,\beta = 0} \times 100$ of the solution for the Jacobi polynomials parameter, in the FG doubly curved rotation shell (FGM_I(a = 1/b = 0.5/c = 2/p = 1)), is shown in Fig. 4. The natural frequencies, where α = 0 and β = 0, are chosen as the reference value. From Fig. 4, it can be seen that changing the characteristic parameters α and β of the Jacobi polynomials does not affect the convergence of the solution, and the maximum value of the percentage error does not exceed 10^–5. Especially, in the case of the hyperbolical shell, the percentage error is the greatest, however, in this case, it does not exceed 2 × 10^–5 and it can be seen that even if α and β change, the frequency value hardly changes. Therefore, the characteristic parameters α and β of the Jacobi polynomials are set into α = β = 0.5 in the following numerical analysis.

Next, the convergence study is performed to establish boundary conditions. As mentioned in Sect. 2.4, boundary conditions can be set differently depending on the value of artificial spring stiffness. That is, to determine the boundary condition, the spring stiffness value corresponding to the boundary condition must be selected. Figure 5 shows the change characteristics of the frequency parameters of the FG doubly curved shell of revolution according to the increase of the spring stiffness value. The material of the shell is FGM_I and the parameters characterizing the distribution of the material are a = 1, b = 0, c = 0, p = 1. In addition, the case of the circumferential wave number n = 1 is investigated.

Fig. 5

Convergence of frequency parameters of the FG doubly curved shells of revolution on the boundary spring stiffness: a elliptical shell, b paraboloidal shell, c hyperbolical shell

As shown in Fig. 5, when the spring stiffness is less than 10⁶, the displacement is not greatly affected by the spring stiffness. Also, if it is larger than 10¹², it can be seen that there is little displacement. However, when the spring stiffness increases from 10⁶ to 10¹², the displacement also changes, and the change in displacement causes an increase in frequency.

Based on this, in order to simulate the clamp boundary condition, 10¹⁴ is assigned to the boundary spring stiffness and the stiffness value is set to 0 for the free boundary condition.

On the other hand, when the spring stiffness value increases from 10⁶ to 10¹², the frequency parameter changes significantly. Therefore, spring stiffness values can be set at intervals [10⁶, 10¹²] to model elastic boundary conditions. Table 3 shows the stiffness values of artificial springs for classical and elastic boundary conditions. For the convenience of presentation, classical boundary conditions such as clamped, free, simply supported and shear-diaphragm are as symbols C, F, SS and SD, respectively. Also, in this example, denoted as E₁, E₂ and E₃, three kinds of elastic boundary conditions are considered.

Table 3 The spring stiffness value corresponding to the boundary conditions

Through the convergence study on the boundary spring, it can be seen that when the artificial spring stiffness value is 10¹⁴, it can be regarded as a completely fixed case. Therefore, in Eq. (18), the value of the connecting spring stiffness, which characterizes the connective condition of the shell segments, is set to 10¹⁴.

3.2 Free Vibration Analysis of FG Doubly Curved Shell of Revolution

In the above subsection, calculation parameters such as the polynomial maximum order, polynomial parameters, and the value of the boundary spring stiffness are to be used in the dynamic analysis of the FG doubly curved shell of revolution were determined through convergence studies. In this subsection, the results of the free vibration analysis of the FG doubly curved shells of revolution will be reported. First, the accuracy of the current method for free vibration of the shell of revolution is verified through comparison with published literature. Tables 4, 5, 6 show the comparison results of frequency parameters of the FG doubly curved shells of revolution with different boundary conditions including classical and elastic boundary conditions. As shown in Tables 3, 4, 5, the results of the frequency parameters of the FG doubly curved shell of revolution by the current method agree very well with the results of the previous literature for all boundary conditions, and it can be seen that the current method has high accuracy for analyzing the free vibration of the FG doubly curved shells of revolution.

Table 4 Comparison of frequency parameters of a FG elliptical doubly curved shell of revolution

Table 5 Comparison of frequency parameters of a FG paraboloidal doubly curved shell of revolution

Table 6 Comparison of frequency parameters of a FG hyperbolical doubly curved shell of revolution

Based on the verification of the accuracy of the current method for the free vibration of the FG doubly curved shell of revolution, the next step will be to present the free vibration results such as the natural frequencies and mode shapes of the FG doubly curved shells of revolution according to several parameters through numerical examples. Tables 7, 8, 9 presents the first four natural frequencies of the FG doubly curved shells of revolution for different power-law index p under classical and elastic boundary conditions. The geometric dimensions of FG doubly curved shells of revolution are set as follows; for elliptical shell (Table 7): a_e = 1 m, b_e = 2 m, φ₀ = π/3, φ₁ = 2π/3, for Paraboloidal shell (Table 8): R₀ = 0.2 m, R₁ = 1 m, L = 1 m, R_s = 0, for hyperbolical shell (Table 9): a_h = 1 m, R₁ = 1 m, R_s = 2 m, C = 3 m, D = 4 m and For all types of shells, the thickness is the same, h = 0.05 m. The material of the shell is selected as FGM_I (a = 1/b = 0.5, c = 2/p).

Table 7 First four natural frequencies of the FG elliptical doubly curved shells of revolution with different boundary conditions

Table 8 First four natural frequencies of the FG paraboloidal doubly curved shells of revolution with different boundary conditions

Table 9 First four natural frequencies of the FG hyperbolical doubly curved shells of revolution with different boundary conditions

In Table 7, in the case of the classical boundary conditions, when the power-law index p increases, the natural frequencies of the FG elliptical doubly curved shell of revolution decrease. However, in the case of elastic boundary conditions, an interesting phenomenon is detected. In the case of the elastic boundary condition E₁, the natural frequencies are changed with a tendency similar to that of the classical boundary condition. However, in the case of elastic boundary conditions E₂ and E₃, if the power-law index p increases, the first natural frequency increases, but the frequency changes randomly in the remaining modes. This is because, in the case of elastic boundary conditions E₂ and E₃, when p increases, the stiffness of the shell corresponding to the mode shape changes randomly. It can be seen from Tables 8 and 9 that these phenomena also occur in paraboloidal and hyperbolical doubly curved shells of revolution.

To help the reader understand the free vibration characteristics of the FG doubly curved shells of revolution with different boundary conditions, Figs. 6, 7, 8 shows some of the shell modes corresponding to Tables 7, 8, 9.

Fig. 6

Mode shapes of the FG elliptical doubly-curved shells of revolution (p = 10); a C–C, b F–C, c E₁–E₁

Fig. 7

Mode shapes of the FG paraboloidal doubly curved shells of revolution (p = 10); a C–C, b F–C, c E₁–E₁

Fig. 8

Mode shapes of the FG hyperbolical doubly curved shells of revolution(p = 10); a C–C, b F–C, c E₁–E₁

3.3 Forced Vibration Analysis of FG Doubly Curved Shell of Revolution

In this section, studies on the forced vibration analysis of the FG doubly curved shells of revolution are conducted.

3.3.1 Steady-State Vibration Response

First, the steady-state vibration responses of the FG doubly curved shells of revolution under different external excitation forces are investigated. In this study, three common loads: point force, line force and surface forces are discussed. The diagrammatic sketch of three applied load types for the doubly curved shells of revolution is shown in Fig. 9.

Fig. 9

The diagrammatic sketch of three applied load types for the FG doubly curved shells of revolution; a Point force, b Line force, c Surface force

Figure 9a is in case of subject to the harmonic point force f_w applied at the Load Point A (φ_A = φ, θ_A = θ) in the thickness direction and vertical acting on the surface of the doubly curved shell of revolution. The point load in expressed as $f_{w} = \overline{f}_{w} \sin (\omega t)\delta (\varphi - \varphi_{A} )\delta (\theta - \theta_{A} )$, where the amplitude of the harmonic force is taken as $\overline{q}_{w} = 1N$ and $\omega$ is the frequency of the harmonic point force; $\delta (\varphi )$ is the Dirac delta function. The displacement response measured at Point B in the vertical direction is illustrated. The Fig. 7b is in the case of the axisymmetric line force $f_{u} = \overline{f}_{u} \sin (\omega t)\delta (\varphi - \varphi_{0} )$ are acted on the surface of the doubly curved shell of revolution, which is applied at the left end of doubly curved shell of revolution in the φ direction. The last case concerns the vibration responses of the doubly curved shell of revolution subjected to the normal distributed unit surface force f_w over the surface ([φ₁,φ₂], [θ₁, θ₂]).

Before investigating the forced vibration of the FG doubly curved shell of revolution, it is necessary to verify the accuracy of the presented method to analyze the steady-state vibration of the FG doubly curved shell of revolution. It is assumed that all shells compared have the property of FGM_I (a = 1/b = 0/c = 0/p = 1).The forced vibration parameters used for verification studies to analyze the steady-state vibration of the FG doubly curved shell of revolution are following: the Load Point A of concentrated point force; A(φ,θ) = (5π/12, 0), and detection point; B(φ,θ) = (π/4,0), concentrated point force; $f_{w} = \overline{f}_{w} \delta \left( {\varphi - \varphi_{A} } \right)\left( {\theta - \theta_{A} } \right)$, where $\overline{f}_{w} = - 1N$, $\Delta f = 1\,{\text{Hz}}$, and C–C boundary condition is selected. Due to the lack of prior literature on the steady-state vibration of the FG doubly curved shell of revolution, the comparisons are made with the results of the finite element analysis software ABAQUS. The comparison results are shown in Fig. 10. From Fig. 10, it can be seen that the steady-state vibration response by the current method agrees very well with the results of FEM regardless of the shape of the shell and it can be concluded that this method is a reasonable method for the steady-state vibration analysis of the FG doubly curved shells of revolution.

Fig. 10

The comparison of normal displacement of the FG doubly curved shell of revolution; a elliptical shell, b paraboloidal shell, c hyperbolical shell

Figure 11 presents the displacement-frequency characteristic of the FG double-curved shells of revolution with C–C boundary conditions under three types of load-point force, line force, and surface force. Forced vibration parameters are set as follows; for the elliptical and paraboloidal shell, the load point of point force: A(φ,θ) = (π/3, 0), Load position of line force: A(φ,θ) = ([π/3, 0], [π/4, π/3]), Load position of surface force: A(φ,θ) = ([π/6, π/3], [π/4, π/3]), for hyperbolical shell, Load point of point force: A(φ,θ) = (π/3, 0), Load position of line force: A(φ,θ) = ([π/3, 0], [π/4, π/3]), Load position of surface force: A(φ,θ) = ([π/4, π/3], [π/4, π/3]), for all shells, detection points are set as B(φ,θ) = (π/3,0) and B(φ,θ) = (π/4,0). And concentrated force:$f_{w} = \overline{f}_{w} \delta \left( {\varphi - \varphi_{A} } \right)\left( {\theta - \theta_{A} } \right)$, where $\overline{f}_{w} = - 1N$, $\Delta f = 1\,{\text{Hz}}$.

Fig. 11

The displacement-frequency characteristic of FG double-curved shell of revolution under three types of load; a elliptical shell, b paraboloidal shell, c hyperbolic shell

From Fig. 11, it can be seen that, for the same natural frequency, regardless of the detected point and the type of the shell, the displacement is the largest in the case of a point force and the smallest when a surface force is applied. It is obvious that this result occurs because the displacement due to the point force is greatest when the magnitude of the force is the same.

3.3.2 Transient Vibration Response

As the last part of this study, the methodology mentioned previously is applied to obtain the transient responses of the FG doubly curved shells of revolution subjected to different four shock loads, namely rectangular pulse, triangular pulse, half-sine pulse, and exponential pulse. The sketch of the load time domain curve is shown in Fig. 12.

Fig. 12

The sketch of load time domain curve. a Rectangular pulse; b Triangular pulse; c Half-sine pulse; d Exponential pulse

These load curves can be described by the following formulas:

$${\text{Rectangular pulse}}:\,\,\,\,f\left( t \right) = \left\{ {\begin{array}{*{20}c} {f_{t} } & {0 \le t \le \tau } \\ 0 & {t > \tau } \\ \end{array} } \right.$$

(27a)

$${\text{Triangular pulse}}:\,\,\,f\left( t \right) = \left\{ {\begin{array}{*{20}c} {\frac{2t}{\tau }f_{t} } & {0 \le t \le \frac{\tau }{2}} \\ {f_{t} - \frac{2}{\tau }\left( {t - \frac{\tau }{2}} \right)f_{t} } & {\frac{\tau }{2} \le t \le \tau } \\ 0 & {t > \tau } \\ \end{array} } \right.$$

(27b)

$${\text{Half}} - {\text{sine pulse}}:\,\,\,\,f\left( t \right) = \left\{ {\begin{array}{*{20}c} {f_{t} \sin \left( {\frac{\pi t}{\tau }} \right)} & {0 \le t \le \tau } \\ 0 & {t > \tau } \\ \end{array} } \right.$$

(27c)

$${\text{Exponential pulse}}:\,\,\,f\left( t \right) = \left\{ {\begin{array}{*{20}c} {f_{t} e^{ - \xi t} } & {0 \le t \le \tau } \\ 0 & {t > \tau } \\ \end{array} } \right.$$

(27d)

where f_t is the load amplitude; τ is the pulse width; t is the time variable.

As in all analysis problems, the accuracy of the proposed method must be verified in this study. Therefore, first, a study to verify the accuracy of the current method for transient response analysis is performed. As in the steady-state vibration analysis, the finite element analysis software ABAQUS is used in this verification study due to the lack of prior literature. The material properties, geometric dimensions, and forced vibration parameters of all shells are set the same as in the case of Fig. 10.

The calculation time t and calculation step Δt is set at 10 ms and 0.01 ms, respectively. Comparing the theoretical results with the results obtained by FEM, we can see that the theoretical results show a good agreement with the FEM results (Fig. 13). From the comparison result of Fig. 13, it can be confirmed that the current method is a reasonable method that has high accuracy not only in the steady-state vibration of the shell but also in the transient response analysis.

Fig. 13

The comparison of normal displacement response of the FG doubly curved shells of revolution with C–C boundary condition; a elliptical shell, b paraboloidal shell, c hyperbolic shell

After having investigated the accuracy of the present method on the transient vibration problems, the effects of different types of loads on the transient vibration responses of the FG doubly curved shells of revolution are presented (Fig. 14). The geometric and material parameters are the same as in Fig. 11. Point force is considered as the type of load. for all shells, Load point of point force: A(φ,θ) = (π/3, 0), detection points are set as B(φ,θ) = (π/3,0) and B(φ,θ) = (π/4,0). And concentrated force is $f_{w} = \overline{f}_{w} \delta \left( {\varphi - \varphi_{A} } \right)\left( {\theta - \theta_{A} } \right)$, where $\overline{f}_{w} = - 1N$, $\Delta f = 1\,\,{\text{Hz}}$. The calculation time t and calculation step Δt is set at 10 ms and 0.01 ms, respectively. As shown in Fig. 14, in all cases, the transient response characteristics for the rectangular pulse and exponential pulse appear very disordered. On the other hand, in the case of triangular pulse and half-sine pulse, the transient response characteristic decreases gently at first and then increases again in the vicinity of the intermediate position. This is because, due to the inertia after the load is applied, and after a certain period of time (half an hour according to the result), the displacement is maximized, and as the force is decreased, the displacement also decreases in the same way.

Fig. 14

The displacement response of doubly curved shells under different loads. a elliptical shell, b paraboloidal shell, c hyperbolic shell

In addition, it can be seen that the displacement of the rectangular pulse is always greater than the displacement of the exponential pulse and the displacement of the triangular pulse is always greater than the displacement of the half-sine pulse at the measurement position 1. However, at measurement position 2, the displacements of rectangular pulse and exponential pulse are almost the same, and the displacements of triangular pulse and half-sine pulse are almost the same. As such, when different impact loads are applied, the transient response characteristics are very different depending on the measurement points for the same FG doubly curved shell of revolution.

4 Conclusions

In this paper, a semi-analytic method for analyzing the forced vibrations of the FG doubly curved shells of revolution with elastic boundary conditions by using Jacobi polynomials is presented. The Jacobi polynomials are applied to generalize the choice of the allowable displacement function and the Rayleigh–Ritz method is used to get the formulation on the basis of the first-order shear deformation theory. The boundary spring technique is adopted to realize the kinematic compatibility and physical compatibility conditions at arbitrary boundary conditions and the continuity conditions at two adjacent segments were enforced by the penalty method. The studies of the convergence, accuracy and reliability for the FG doubly curved shells of revolution with various boundary conditions of the classical, elastic and their combinations are made. And the results show good agreement between the present method and the existing literature and FEM. Also, several numerical examples for the dynamic behavior of the laminated composite doubly curved shell of revolution with elastic boundary conditions are also presented. Moreover, some numerical parameter studies to analyze forced vibration of FG doubly curved shells of revolution are also carried out.

Appendix A: Detailed Expressions of the Matrices

The generalized mass and stiffness matrices of the FG doubly curved shell of revolution used in Eq. (26) are given as:

$${\mathbf{M}} = diag\left[ {{\mathbf{M}}_{1} ,{\mathbf{M}}_{2} , \cdot \cdot \cdot ,{\mathbf{M}}_{\xi } , \cdot \cdot \cdot ,{\mathbf{M}}_{N} } \right]$$

(28)

$${\mathbf{M}}_{\xi } = \int\limits_{{\varphi_{\xi } }}^{{\varphi_{\xi + 1} }} {\int\limits_{0}^{2\pi } {\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{\xi ,uu} } & 0 & 0 & {{\mathbf{M}}_{\xi ,u\varphi } } & 0 \\ 0 & {{\mathbf{M}}_{\xi ,vv} } & 0 & 0 & {{\mathbf{M}}_{\xi ,v\theta } } \\ 0 & 0 & {{\mathbf{M}}_{\xi ,ww} } & 0 & 0 \\ {{\mathbf{M}}_{\xi ,u\varphi } } & 0 & 0 & {{\mathbf{M}}_{\xi ,\varphi \varphi } } & 0 \\ 0 & {{\mathbf{M}}_{\xi ,v\theta } } & 0 & 0 & {{\mathbf{M}}_{\xi ,\theta \theta } } \\ \end{array} } \right]} } R_{\theta } d\varphi_{\xi } d\theta_{\xi }$$

(29)

$$\begin{gathered} {\mathbf{M}}_{\xi ,uu} = I_{0} {\mathbf{U}}^{T} {\mathbf{U}},\;\,\,\,\,{\mathbf{M}}_{\xi ,vv} = I_{0} {\mathbf{V}}^{T} {\mathbf{V}},\;\,\,\,\,{\mathbf{M}}_{\xi ,ww} = I_{0} {\mathbf{W}}^{T} {\mathbf{W}},\;\,\,\,{\mathbf{M}}_{\xi ,\varphi \varphi } = I_{2} {{\varvec{\Phi}}}^{T} {{\varvec{\Phi}}}, \hfill \\ {\mathbf{M}}_{\xi ,\theta \theta } = I_{2} {{\varvec{\Theta}}}^{T} {\mathbf{\Theta , }}\,\,\,\,{\mathbf{M}}_{\xi ,u\varphi } = I_{1} {\mathbf{U}}^{T} {{\varvec{\Phi}}},{\kern 1pt} {\kern 1pt} \,\,\,{\mathbf{M}}_{\xi ,v\theta } = I_{1} {\mathbf{V}}^{T} {{\varvec{\Theta}}} \hfill \\ \end{gathered}$$

(30)

$${\mathbf{U}} = {\mathbf{P}}_{m} \otimes {\mathbf{C}}_{n} ,\,\,{\mathbf{V}} = {\mathbf{P}}_{m} \otimes {\mathbf{S}}_{n} ,\,\,{\mathbf{W}} = {\mathbf{P}}_{m} \otimes {\mathbf{C}}_{n} ,\,\,\,{{\varvec{\Phi}}} = {\mathbf{P}}_{m} \otimes {\mathbf{C}}_{n} ,\,\,{{\varvec{\Theta}}} = {\mathbf{P}}_{m} \otimes {\mathbf{S}}_{n}$$

(31)

where

$${\mathbf{P}}_{m} = [P_{0}^{(\alpha ,\beta )} (\phi ),P_{1}^{(\alpha ,\beta )} (\phi ), \cdot \cdot \cdot ,P_{m}^{(\alpha ,\beta )} (\phi ), \cdot \cdot \cdot ,P_{M}^{(\alpha ,\beta )} (\phi )]$$

(32)

$${\mathbf{C}}_{n} = [\cos (0\theta_{\xi } ),\cos (1\theta_{\xi } ), \cdot \cdot \cdot \cos (n\theta_{\xi } ), \cdot \cdot \cdot ,\cos (N\theta_{\xi } )]$$

(33)

$${\mathbf{S}}_{n} = [\sin (0\theta_{\xi } ),\sin (1\theta_{\xi } ), \cdot \cdot \cdot \sin (n\theta_{\xi } ), \cdot \cdot \cdot ,\sin (N\theta_{\xi } )]$$

(34)

$${\mathbf{K}} = {\mathbf{K}}_{u} + {\mathbf{K}}_{b} + {\mathbf{K}}_{c}$$

(35)

$${\mathbf{K}}_{u} = diag\left[ {{\mathbf{K}}_{1} ,{\mathbf{K}}_{2} \cdot \cdot \cdot ,{\mathbf{K}}_{\xi } , \cdot \cdot \cdot ,{\mathbf{K}}_{N} } \right]$$

(36)

$${\mathbf{K}}_{\xi } = \int\limits_{{\varphi_{\xi } }}^{{\varphi_{\xi + 1} }} {\int\limits_{0}^{2\pi } {\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{\xi ,uu} } & {{\mathbf{K}}_{\xi ,uv} } & {{\mathbf{K}}_{\xi ,uw} } & {{\mathbf{K}}_{\xi ,u\varphi } } & {{\mathbf{K}}_{\xi ,u\theta } } \\ {{\mathbf{K}}_{\xi ,uv}^{T} } & {{\mathbf{K}}_{\xi ,vv} } & {{\mathbf{K}}_{\xi ,vw} } & {{\mathbf{K}}_{\xi ,v\varphi } } & {{\mathbf{K}}_{\xi ,v\theta } } \\ {{\mathbf{K}}_{\xi ,uw}^{T} } & {{\mathbf{K}}_{\xi ,vw}^{T} } & {{\mathbf{K}}_{\xi ,ww} } & {{\mathbf{K}}_{\xi ,w\varphi } } & {{\mathbf{K}}_{\xi ,w\theta } } \\ {{\mathbf{K}}_{\xi ,u\varphi }^{T} } & {{\mathbf{K}}_{\xi ,v\varphi }^{T} } & {{\mathbf{K}}_{\xi ,w\varphi }^{T} } & {{\mathbf{K}}_{\xi ,\varphi \varphi } } & {{\mathbf{K}}_{\xi ,\varphi \theta } } \\ {{\mathbf{K}}_{\xi ,u\theta }^{T} } & {{\mathbf{K}}_{\xi ,v\theta }^{T} } & {{\mathbf{K}}_{\xi ,w\theta }^{T} } & {{\mathbf{K}}_{\xi ,\varphi \theta }^{T} } & {{\mathbf{K}}_{\xi ,\theta \theta } } \\ \end{array} } \right]} } R_{\theta } d\varphi_{\xi } d\theta_{\xi }$$

(37)

$$\begin{gathered} {\mathbf{K}}_{\xi ,uu} = \frac{{A_{11} }}{{R_{\varphi }^{2} }}\frac{{\partial {\mathbf{U}}}}{\partial \varphi }^{T} \frac{{\partial {\mathbf{U}}}}{\partial \varphi } + \frac{{A_{22} }}{{R_{\theta }^{2} T_{\varphi }^{2} }}{\mathbf{U}}^{T} {\mathbf{U}} + \frac{{A_{66} }}{{R_{\theta }^{2} S_{\varphi }^{2} }}\frac{{\partial {\mathbf{U}}}}{\partial \theta }^{T} \frac{{\partial {\mathbf{U}}}}{\partial \theta } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{A_{12} }}{{R_{\varphi } R_{\theta } T_{\varphi } }}\left( {\frac{{\partial {\mathbf{U}}}}{\partial \varphi }^{T} {\mathbf{U}} + {\mathbf{U}}^{T} \frac{{\partial {\mathbf{U}}}}{\partial \varphi }} \right) + \frac{{\kappa_{s} A_{66} }}{{R_{\varphi }^{2} }}{\mathbf{U}}^{T} {\mathbf{U}} \hfill \\ \end{gathered}$$

(38)

$${\mathbf{K}}_{\xi ,uv} = \left( {\frac{{A_{{{22}}} C_{\varphi } }}{{R_{\theta }^{2} S_{\varphi }^{2} }}{\mathbf{U}} + \frac{{A_{12} }}{{R_{\varphi } R_{\theta } S_{\varphi } }}\frac{{\partial {\mathbf{U}}}}{\partial \varphi }} \right)^{T} \frac{{\partial {\mathbf{V}}}}{\partial \theta }\, + \frac{{A_{66} }}{{R_{\theta } S_{\varphi } }}\frac{{\partial {\mathbf{U}}^{T} }}{\partial \theta }{\mathbf{V}}_{1}$$

(39)

$${\mathbf{K}}_{\xi ,uw} = \left[ {\left( {\frac{{A_{11} }}{{R_{\varphi }^{2} }} + \frac{{A_{12} }}{{R_{\varphi } R_{\theta } }}} \right)\frac{{\partial {\mathbf{U}}}}{\partial \varphi } + \left( {\frac{{A_{22} }}{{R_{\theta }^{2} T_{\varphi } }} + \frac{{A_{12} }}{{R_{\varphi } R_{\theta } T_{\varphi } }}} \right){\mathbf{U}}} \right]^{T} {\mathbf{W}} - \frac{{\kappa_{s} A_{66} }}{{R_{\varphi }^{2} }}{\mathbf{U}}^{T} \frac{{\partial {\mathbf{W}}}}{\partial \varphi }$$

(40)

$$\begin{gathered} {\mathbf{K}}_{\xi ,u\varphi } = - \frac{{\kappa_{s} A_{66} }}{{R_{\varphi } }}{\mathbf{U}}^{T} {\mathbf{\Phi + }}\frac{{{\rm B}_{11} }}{{R_{\varphi }^{2} }}\frac{{\partial {\mathbf{U}}}}{\partial \varphi }^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi } + \frac{{B_{12} }}{{R_{\varphi } R_{\theta } T_{\varphi } }}\frac{{\partial {\mathbf{U}}}}{\partial \varphi }^{T} {{\varvec{\Phi}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{B_{12} }}{{R_{\varphi } R_{\theta } T_{\varphi } }}{\mathbf{U}}^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi } + \frac{{B_{22} }}{{R_{\theta }^{2} T_{\varphi }^{2} }}{\mathbf{U}}^{T} {{\varvec{\Phi}}} + \frac{{B_{66} }}{{R_{\theta }^{2} S_{\varphi }^{2} }}\frac{{\partial {\mathbf{U}}}}{\partial \theta }^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \theta } \hfill \\ \end{gathered}$$

(41)

$${\mathbf{K}}_{\xi ,u\theta } = \frac{{B_{12} }}{{R_{\varphi } R_{\theta } S_{\varphi } }}\frac{{\partial {\mathbf{U}}}}{\partial \varphi }^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta } + \frac{{B_{22} }}{{R_{\theta }^{2} T_{\varphi } S_{\varphi } }}{\mathbf{U}}^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta } + \frac{{B_{66} }}{{R_{\theta } S_{\varphi } }}\frac{{\partial {\mathbf{U}}}}{\partial \theta }^{T} {{\varvec{\Theta}}}_{1}$$

(42)

$${\mathbf{K}}_{\xi ,vv} = \frac{{A_{22} }}{{R_{\theta }^{2} S_{\varphi }^{2} }}\frac{{\partial {\mathbf{V}}}}{\partial \theta }^{T} \frac{{\partial {\mathbf{V}}}}{\partial \theta } + A_{66} {\mathbf{V}}_{1}^{T} {\mathbf{V}}_{1} + \frac{{\kappa_{s} A_{66} }}{{R_{\theta }^{2} }}{\mathbf{V}}^{T} {\mathbf{V}}$$

(43)

$${\mathbf{K}}_{\xi ,vw} = \left( {\frac{{A_{22} }}{{R_{\theta }^{2} S_{\varphi } }} + \frac{{A_{12} }}{{R_{\varphi } R_{\theta } S_{\varphi } }}} \right)\frac{{\partial {\mathbf{V}}}}{\partial \theta }^{T} {\mathbf{W}} - \frac{{\kappa_{s} A_{66} }}{{R_{\theta }^{2} S_{\varphi } }}{\mathbf{V}}^{T} \frac{{\partial {\mathbf{W}}}}{\partial \theta }$$

(44)

$${\mathbf{K}}_{\xi ,v\varphi } = \frac{{B_{12} }}{{R_{\varphi } R_{\theta } S_{\varphi } }}\frac{{\partial {\mathbf{V}}}}{\partial \theta }^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi } + \frac{{B_{22} }}{{R_{\theta }^{2} T_{\varphi } S_{\varphi } }}\frac{{\partial {\mathbf{V}}}}{\partial \theta }^{T} {{\varvec{\Phi}}} + \frac{{B_{66} }}{{R_{\theta } S_{\varphi } }}{\mathbf{V}}_{1}^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \theta }$$

(45)

$${\mathbf{K}}_{\xi ,v\theta } = - \frac{{\kappa_{s} A_{66} }}{{R_{\theta } }}{\mathbf{V}}^{T} {{\varvec{\Theta}}} + \frac{{B_{22} }}{{R_{\theta }^{2} S_{\varphi }^{2} }}\frac{{\partial {\mathbf{V}}}}{\partial \theta }^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta } + \frac{{B_{66} }}{{R_{\theta } S_{\varphi } }}{\mathbf{V}}_{1}^{T} {{\varvec{\Theta}}}_{1}$$

(46)

$${\mathbf{K}}_{\xi ,ww} = \left( {\frac{{A_{11} }}{{R_{\varphi }^{2} }} + \frac{{A_{22} }}{{R_{\theta }^{2} }} + \frac{{2A_{12} }}{{R_{\varphi } R_{\theta } }}} \right){\mathbf{W}}^{T} {\mathbf{W + }}\kappa_{s} A_{66} \left( {\frac{1}{{R_{\varphi }^{2} }}\frac{{\partial {\mathbf{W}}}}{\partial \varphi }^{T} \frac{{\partial {\mathbf{W}}}}{\partial \varphi } + \frac{1}{{R_{\theta }^{2} S_{\varphi }^{2} }}\frac{{\partial {\mathbf{W}}}}{\partial \theta }^{T} \frac{{\partial {\mathbf{W}}}}{\partial \theta }} \right)$$

(47)

$${\mathbf{K}}_{\xi ,w\varphi } = \frac{{\kappa_{s} A_{66} }}{{R_{\varphi } }}\frac{{\partial {\mathbf{W}}}}{\partial \varphi }^{T} {{\varvec{\Phi}}} + \frac{{B_{11} }}{{R_{\varphi }^{2} }}{\mathbf{W}}^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi }\, + \frac{{B_{12} }}{{R_{\varphi } R_{\theta } T_{\varphi } }}{\mathbf{W}}^{T} {{\varvec{\Phi}}}\, + \frac{{B_{12} }}{{R_{\varphi } R_{\theta } }}{\mathbf{W}}^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi }{\mathbf{ + }}\frac{{B_{22} }}{{R_{\theta }^{2} T_{\varphi } }}{\mathbf{W}}^{T} {{\varvec{\Phi}}}$$

(48)

$${\mathbf{K}}_{\xi ,w\theta } = \frac{{\kappa_{s} A_{66} }}{{R_{\theta } S_{\varphi } }}\frac{{\partial {\mathbf{W}}}}{\partial \theta }^{T} {{\varvec{\Theta}}} + \frac{{B_{12} }}{{R_{\varphi } R_{\theta } S_{\varphi } }}{\mathbf{W}}^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta } + \frac{{B_{22} }}{{R_{\theta }^{2} S_{\varphi } }}{\mathbf{W}}^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta }$$

(49)

$$\begin{gathered} {\mathbf{K}}_{\xi ,\varphi \varphi } = \kappa_{s} A_{66} {{\varvec{\Phi}}}^{T} {{\varvec{\Phi}}} + \frac{{D_{11} }}{{R_{\varphi }^{2} }}\frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi }^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi } + \frac{{D_{22} }}{{R_{\theta }^{2} T_{\varphi }^{2} }}{{\varvec{\Phi}}}^{T} {{\varvec{\Phi}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{D_{66} }}{{R_{\theta }^{2} S_{\varphi }^{2} }}\frac{{\partial {{\varvec{\Phi}}}}}{\partial \theta }^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \theta } + \frac{{D_{12} }}{{R_{\varphi } R_{\theta } T_{\varphi } }}\left( {{{\varvec{\Phi}}}^{T} \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi } + \frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi }^{T} {{\varvec{\Phi}}}} \right) \hfill \\ \end{gathered}$$

(50)

$${\mathbf{K}}_{\xi ,\varphi \theta } = \frac{{D_{22} }}{{R_{\theta }^{2} T_{\varphi } S_{\varphi } }}{{\varvec{\Phi}}}^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta } + \frac{{D_{66} }}{{R_{\theta } S_{\varphi } }}\frac{{\partial {{\varvec{\Phi}}}}}{\partial \theta }^{T} {{\varvec{\Theta}}}_{1} + \frac{{D_{12} }}{{R_{\varphi } R_{\theta } S_{\varphi } }}\frac{{\partial {{\varvec{\Phi}}}}}{\partial \varphi }^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta }$$

(51)

$${\mathbf{K}}_{\xi ,\theta \theta } = \kappa_{s} A_{66} {{\varvec{\Theta}}}^{T} {{\varvec{\Theta}}} + \frac{{D_{22} }}{{R_{\theta }^{2} S_{\varphi }^{2} }}\frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta }^{T} \frac{{\partial {{\varvec{\Theta}}}}}{\partial \theta } + D_{66} {{\varvec{\Theta}}}_{1}^{T} {{\varvec{\Theta}}}_{1}$$

(52)

where

$$C_{\varphi } = \cos (\varphi ),\,\,\,\,\,\,S_{\varphi } = \sin (\varphi ),\,\,\,\,\,\,T_{\varphi } = \tan (\varphi )$$

(53)

$${\mathbf{V}}_{1} = \frac{1}{{R_{\varphi } }}\frac{{\partial {\mathbf{V}}}}{\partial \varphi } - \frac{1}{{R_{\theta } T_{\varphi } }}{\mathbf{V,}}\,\,\,{{\varvec{\Theta}}}_{1} = \frac{1}{{R_{\varphi } }}\frac{{\partial {{\varvec{\Theta}}}}}{\partial \varphi } - \frac{1}{{R_{\theta } T_{\varphi } }}{{\varvec{\Theta}}}$$

(54)

$${\mathbf{K}}_{b} = diag\left[ {{\mathbf{K}}_{b0} ,0 \cdot \cdot \cdot ,{\mathbf{K}}_{b1} } \right]$$

(55)

$${\mathbf{K}}_{b0} = \int_{0}^{2\pi } {diag\left[ {{\mathbf{K}}_{b0,uu} ,{\mathbf{K}}_{b0,vv} ,{\mathbf{K}}_{b0,ww} ,{\mathbf{K}}_{b0,\varphi \varphi } ,{\mathbf{K}}_{b0,\theta \theta } } \right]_{{\varphi_{\xi } = \varphi_{0} }} R_{0} d\theta }$$

(56)

$$\begin{gathered} {\mathbf{K}}_{b0,uu} = k_{u0} {\mathbf{U}}^{T} {\mathbf{U,}}\,\,{\mathbf{K}}_{b0,vv} = k_{v0} {\mathbf{V}}^{T} {\mathbf{V}},\,\,{\mathbf{K}}_{b0,ww} = k_{w0} {\mathbf{W}}^{T} {\mathbf{W}}, \hfill \\ {\mathbf{K}}_{b0,\varphi \varphi } = k_{\varphi 0} {{\varvec{\Phi}}}^{T} {{\varvec{\Phi}}},\,\,{\mathbf{K}}_{b0,\theta \theta } = k_{\theta 0} {{\varvec{\Theta}}}^{T} {{\varvec{\Theta}}} \hfill \\ \end{gathered}$$

(57)

$${\mathbf{K}}_{b1} = \int_{0}^{2\pi } {diag\left[ {{\mathbf{K}}_{b1,uu} ,{\mathbf{K}}_{b1,vv} ,{\mathbf{K}}_{b1,ww} ,{\mathbf{K}}_{b1,\varphi \varphi } ,{\mathbf{K}}_{b1,\theta \theta } } \right]_{{\varphi_{\xi } = \varphi_{1} }} R_{0} d\theta }$$

(58)

$$\begin{gathered} {\mathbf{K}}_{b1,uu} = k_{u1} {\mathbf{U}}^{T} {\mathbf{U}},\,\,\,{\mathbf{K}}_{b1,vv} = k_{v1} {\mathbf{V}}^{T} {\mathbf{V}},\,\,{\mathbf{K}}_{b1,ww} = k_{w1} {\mathbf{W}}^{T} {\mathbf{W}}, \hfill \\ {\mathbf{K}}_{b1,\varphi \varphi } = k_{\varphi 1} {{\varvec{\Phi}}}^{T} {{\varvec{\Phi}}},\,\,{\mathbf{K}}_{b1,\theta \theta } = k_{\theta 1} {{\varvec{\Theta}}}^{T} {{\varvec{\Theta}}} \hfill \\ \end{gathered}$$

(59)

$${\mathbf{K}}_{c} = diag\left[ {{\mathbf{K}}_{c,1} ,{\mathbf{K}}_{c,2} , \cdot \cdot \cdot ,{\mathbf{K}}_{c,\xi } , \cdot \cdot \cdot ,{\mathbf{K}}_{c,N - 1} } \right]$$

(60)

$${\mathbf{K}}_{c,\xi } = \int\limits_{0}^{2\pi } {\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{c,\xi }^{11} } & {{\mathbf{K}}_{c,\xi }^{12} } \\ {{\mathbf{K}}_{c,\xi }^{12\,\,T} } & {{\mathbf{K}}_{c,\xi }^{22} } \\ \end{array} } \right]} R_{\theta } d\theta$$

(61)

$${\mathbf{K}}_{c,\xi }^{11} = diag\left[ {{\mathbf{K}}_{{u_{\xi } u_{\xi } }} ,{\mathbf{K}}_{{v_{\xi } v_{\xi } }} ,{\mathbf{K}}_{{w_{\xi } w_{\xi } }} {\mathbf{,K}}_{{\varphi_{\xi } \varphi_{\xi } }} {\mathbf{,K}}_{{\varphi_{\xi } \varphi_{\xi } }} } \right]$$

(62)

$${\mathbf{K}}_{c,\xi }^{12} = diag\left[ {{\mathbf{K}}_{{u_{\xi } u_{\xi + 1} }} ,{\mathbf{K}}_{{v_{\xi } v_{\xi + 1} }} ,{\mathbf{K}}_{{w_{\xi } w_{\xi + 1} }} {\mathbf{,K}}_{{\varphi_{\xi } \varphi_{\xi + 1} }} {\mathbf{,K}}_{{\varphi_{\xi } \varphi_{\xi + 1} }} } \right]$$

(63)

$${\mathbf{K}}_{c,\xi }^{22} = diag\left[ {{\mathbf{K}}_{{u_{\xi + 1} u_{\xi + 1} }} ,{\mathbf{K}}_{{v_{\xi + 1} v_{\xi + 1} }} ,{\mathbf{K}}_{{w_{\xi + 1} w_{\xi + 1} }} {\mathbf{,K}}_{{\varphi_{\xi + 1} \varphi_{\xi + 1} }} {\mathbf{,K}}_{{\varphi_{\xi + 1} \varphi_{\xi + 1} }} } \right]$$

(64)

$$\begin{gathered} {\mathbf{K}}_{{u_{\xi } u_{\xi } }} = k_{uc} {\mathbf{U}}_{\xi }^{T} {\mathbf{U}}_{\xi } ,\,\,\,{\mathbf{K}}_{{v_{\xi } v_{\xi } }} = k_{vc} {\mathbf{V}}_{\xi }^{T} {\mathbf{V}}_{\xi } ,\,\,\,{\mathbf{K}}_{{w_{\xi } w_{\xi } }} = k_{wc} {\mathbf{W}}_{\xi }^{T} {\mathbf{W}}_{\xi } , \hfill \\ {\mathbf{K}}_{{\varphi_{\xi } \varphi_{\xi } }} = k_{\varphi c} {{\varvec{\Phi}}}_{\xi }^{T} {{\varvec{\Phi}}}_{\xi } ,\,\,\,{\mathbf{K}}_{{\theta_{\xi } \theta_{\xi } }} = k_{\varphi c} {{\varvec{\Theta}}}_{\xi }^{T} {{\varvec{\Theta}}}_{\xi } \hfill \\ \end{gathered}$$

(65)

$$\begin{gathered} {\mathbf{K}}_{{u_{\xi } u_{\xi + 1} }} = k_{uc} {\mathbf{U}}_{\xi }^{T} {\mathbf{U}}_{\xi + 1} ,\,\,\,{\mathbf{K}}_{{v_{\xi } v_{\xi + 1} }} = k_{vc} {\mathbf{V}}_{\xi }^{T} {\mathbf{V}}_{\xi + 1} ,\,\,{\mathbf{K}}_{{w_{\xi } w_{\xi + 1} }} = k_{wc} {\mathbf{W}}_{\xi }^{T} {\mathbf{W}}_{\xi + 1} , \hfill \\ {\mathbf{K}}_{{\varphi_{\xi } \varphi_{\xi + 1} }} = k_{\varphi c} {{\varvec{\Phi}}}_{\xi }^{T} {{\varvec{\Phi}}}_{\xi + 1} ,\,\,\,{\mathbf{K}}_{{\theta_{\xi } \theta_{\xi + 1} }} = k_{\varphi c} {{\varvec{\Theta}}}_{\xi }^{T} {{\varvec{\Theta}}}_{\xi + 1} \hfill \\ \end{gathered}$$

(66)

$$\begin{gathered} {\mathbf{K}}_{{u_{\xi + 1} u_{\xi + 1} }} = k_{uc} {\mathbf{U}}_{\xi + 1}^{T} {\mathbf{U}}_{\xi + 1} ,\,\,\,{\mathbf{K}}_{{v_{\xi + 1} v_{\xi + 1} }} = k_{vc} {\mathbf{V}}_{\xi + 1}^{T} {\mathbf{V}}_{\xi + 1} ,\,\,\,{\mathbf{K}}_{{w_{\xi + 1} w_{\xi + 1} }} = k_{wc} {\mathbf{W}}_{\xi + 1}^{T} {\mathbf{W}}_{\xi + 1} , \hfill \\ {\mathbf{K}}_{{\varphi_{\xi + 1} \varphi_{\xi + 1} }} = k_{\varphi c} {{\varvec{\Phi}}}_{\xi + 1}^{T} {{\varvec{\Phi}}}_{\xi + 1} ,\,\,\,{\mathbf{K}}_{{\theta_{\xi + 1} \theta_{\xi + 1} }} = k_{\varphi c} {{\varvec{\Theta}}}_{\xi + 1}^{T} {{\varvec{\Theta}}}_{\xi + 1} \hfill \\ \end{gathered}$$

(67)