Nonlinear Dynamic Analysis of FGM Sandwich Shallow Shells with Variable Thickness of Layers

Abstract

This paper considers the application of the R-functions method to a new class of problems: the study of vibrations of sandwich FGM shallow shells with variable thickness of layers and complex shape. The core is fabricated of FGM, and the face sheets are made of metal. Mathematical formulation of the problem has been done in the framework of the refined shear deformation theory of the first order. To calculate the effective characteristics of the material, Voigt’s law was applied. Analytical expressions have been obtained for coefficients depended on thickness. These coefficients are to calculate the stress and moment resultants. Comparisons of the obtained results with known ones for a special case (bi-layered object) are carried out. Dynamic analysis is fulfilled for the shells and plates with parabolic thickness of layers and different constituent materials of FGM. Effect of materials and layers thickness on the natural frequencies and backbone curves of the shells is shown.

1 Introduction

Sandwich plates and shells are widely employed in many industries: aerospace, satellite, industrial construction, medicine, internal combustion engines and others. The manufacture of modern sandwich structures is often carried out from new advanced composite materials, called as functionally graded materials (FGM). It is connected with the following reasons. These materials provide lightness and strength of the construction and restrain a sharp change in the mechanical properties of the layers. Therefore, they prevent stress concentration, destruction and delamination of layers. Due to these reasons, the study of the static and dynamic behavior of FGM structures draws an attention of many researchers since the issue of FGM structures calculation is among the most important problems of modern mechanics. A huge number of works devoted to this problem and, in particular, to vibration of the sandwich plates and shells is known (Alijani and Amabili 2014; Swaminathan et al. 2015; Thai et al. 2014; Zenkour 2005; Bennoun et al. 2016; Li et al. 2008, Malekzaden and Ghaedsharaf 2014). New theory and models were developed (Thai et al. 2014; Bennoun et al. 2016) to study a nonlinear vibration of FG sandwich plates and shells. Recently, Birman and Kardomateas (2018) have been made a current analysis in research of sandwich FGM structures. Thai and Kim (2015) made a comprehensive analysis of different theories for studying FGM plates and shells. Authors analyze the theories used widely in the modeling FGM plates and shells: the classical plate theory, first- and higher-order shear deformation theories, simplified and mixed theories, which are equivalent to single-layer theories. The work of Thai et al. 2017 is devoted to wide-ranging review on the development of higher-order continuum models in predicting the behavior of small-scale structures. In particular, the finite element solutions for size-dependent analysis of beams and plates were also developed. Great interest for many modern engineering FGM sandwich structures leads to the development of new theories (Arshid et al. 2020). For example, in Arshid et al. (2020), the vibrational behavior of rectangular micro-scale sandwich plates resting on a visco-Pasternak foundation is studied by a novel quasi-3D hyperbolic shear deformation theory.

It should be noted that number of papers devoted to research of the nonlinear vibration of FGM sandwich shells with variable thickness is limited enough. Some reviewer of these works was presented in Tornabe et al. (2017). The authors employed several higher-order shear deformation theories, defined by a unified formulation in order to study FGM sandwich shell structures with variable thickness. The generalized differential quadrature method is used as numerical tool. Due to developed approach, the structural models can be considered as two-dimensional ones. It is one of the advantages of the proposed method.

Awrejcewicz et al. (2013) analyze geometrically nonlinear vibrations of single-layer shallow shells of variable thickness and complex shape using the R-functions theory (Rvachev 1982) and variational methods (RFM). The mathematical formulation of the problem is carried out within the framework of the classical theory. A distinctive feature of the proposed approach was also an original construction of approximate solutions to the nonlinear problem. Later in Awrejcewicz et al. (2015), Kurpa and Shmatko (2014), this approach was developed for multilayer shallow shells, provided that the layers had a variable thickness, but the total thickness was constant. The mathematical formulation is based on the first-order shear deformation theory of the shallow shells. These works have shown that this approach allows to study the dynamic behavior of shallow shells with an arbitrary shape of their plans and various types of boundary conditions.

In this article, we consider the issue of geometrically nonlinear vibrations of the FGM sandwich shallow shells, provided that the FGM core has a variable thickness. The method proposed in Awrejcewicz et al. (2015, Kurpa and Shmatko (2014), Kurpa et al. (2018), Awrejcewicz et al. 2018 is generalized to solve the problem under consideration. Software has been developed to implement RFM for the problem. Numerical results are presented for shallow shells with square and complex planform for parabolic law of changing layers thickness. Effect of the different parameter (gradient index, type of FGM, boundary conditions and others) on dynamic behavior of the structures is shown.

2 Formulation Problem

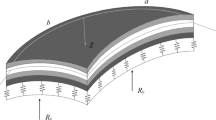
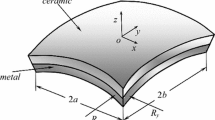
Consider a three-layered shallow shell with variable thickness of layers if total thickness is constant. Assume that face-sheet layers are made of metal and core is made of functionally graded materials. The layers are symmetric relative to the middle plane as it is shown in Fig. 4.1a and b. The functionally graded layer is made from a mixture of two phases (metal and ceramics). The effective material properties of the FGMs are calculated by power law (Voigt’s model). According to this model, elastic modulus E, Poisson’s ratio $\nu$ and the density $\rho$ of the composite are defined by the following relations

$$ E = \left( {E_{c} - E_{m} } \right)V_{c} + E_{m} ,\quad \nu = \left( {\nu_{c} - \nu_{m} } \right)V_{c} + \nu E_{m} ,\quad \rho = \left( {\rho_{c} - \rho_{m} } \right)V_{c} + \rho_{m} . $$

(4.1)

Fig. 4.1

Material variation along the thickness of FGM plate

Here, $E_{c} ,\nu_{c} ,\rho_{c}$ are elastic modulus, Poisson’s ratio and the density of ceramics relatively; $E_{m} ,\nu_{m} ,\rho_{m}$ are corresponding characteristics of metal. Fraction of ceramic $V_{c}$ and metal phases $V_{m}$ are related by formula

$$ V_{c} + V_{m} = 1. $$

(4.2)

Take into account that thickness of FGM layers changes symmetrically relative to the middle surface, let us present the expressions $V_{c}$ for the given case:

$$ \left\{ {\begin{array}{*{20}l} {V_{c} = 0,} \hfill & {z \in \left[ { - \frac{h}{2}, - h_{1} \left( {x,y} \right)} \right],} \hfill \\ {V_{c} = \left( {\frac{{z + h_{1} \left( {x,y} \right)}}{{h_{1} \left( {x,y} \right)}}} \right)^{p} ,} \hfill & {z \in \left[ { - h_{1} \left( {x,y} \right),0} \right],} \hfill \\ {V_{c} = \left( {\frac{{h_{1} \left( {x,y} \right) - z}}{{h_{1} \left( {x,y} \right)}}} \right)^{p} ,} \hfill & {z \in \left[ {0,h_{1} \left( {x,y} \right)} \right],} \hfill \\ {V_{c} = 0,} \hfill & {z \in \left[ {h_{1} \left( {x,y} \right),\frac{h}{2}} \right].} \hfill \\ \end{array} } \right. $$

(4.3)

In formula (4.3), index $p\left( {0 \le p < \infty } \right)$ denotes the volume fraction exponent (gradient index), z is the distance between a current point and the shell mid-surface. Note that if $h_{1} \left( {x,y} \right) = h/2$, then we have so-called bi-layered object.

Solution of the problem is carried out within the first-order shear deformation theory of shallow shells (FSDT).

According to this theory, the displacements components $u_{1} ,u_{2} ,u_{3}$ at a point $\left( {x,y,z} \right)$ are expressed as functions of the middle surface displacements $u,v$ and $w$ in the $Ox,Oy$ and $Oz$ directions and the independent rotations $\psi_{x} ,\psi_{y}$ of the transverse normal to middle surface about the $Oy$ and $Ox$ axes, respectively (Zenkour 2005, Bennoun et al. 2016, Li et al. 2008, Malekzaden and Ghaedsharaf 2014):

$$ u_{1} = u + z\psi_{x} ,\quad u_{2} = v + z\psi_{y} ,\quad u_{3} = w. $$

Strain components $\varepsilon = \left\{ {\varepsilon_{11} ;\varepsilon_{22} ;\varepsilon_{12} } \right\}^{{\text{T}}}$, $\chi = \left\{ {\chi_{11} ;\chi_{22} ;\chi_{12} } \right\}^{{\text{T}}}$ and $\gamma = \left\{ {\gamma_{yz} ;\gamma_{xz} } \right\}^{{\text{T}}}$, an arbitrary point of the shallow shell are:

$$ \begin{aligned} \varepsilon & = \left\{ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{12} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{,x} + \frac{w}{{R_{x} }} + \frac{1}{2}w_{,x}^{2} } \\ {v_{,y} + \frac{w}{{R_{y} }} + \frac{1}{2}w_{,y}^{2} } \\ {u_{,y} + v_{,x} + w_{,x} w_{,y} } \\ \end{array} } \right\},\chi = \left\{ {\begin{array}{*{20}c} {\chi_{11} } \\ {\chi_{22} } \\ {\chi_{12} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\psi_{{x^{\prime } x}} } \\ {\psi_{{y^{\prime } y}} } \\ {\psi_{{x^{\prime } y}} + \psi_{{y^{\prime } x}} } \\ \end{array} } \right\}, \\ \gamma & = \left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\psi_{y} + w_{,y} - \frac{v}{{R_{y} }}} \\ {\psi_{x} + w_{,x} - \frac{u}{{R_{x} }}} \\ \end{array} } \right\}. \\ \end{aligned} $$

In-plane force resultant vector $N = \left( {N_{11} ,N_{22} ,N_{12} } \right)^{{\text{T}}}$, bending and twisting moments resultant vector $M = \left( {M_{11} ,M_{22} ,M_{12} } \right)^{{\text{T}}}$ and transverse shear force resultant $Q = \left( {Q_{x} ,Q_{y} } \right)^{{\text{T}}}$ are calculated by integration along the Oz-axes and defined as:

$$ \begin{aligned} N & = \left[ A \right]\left\{ \varepsilon \right\} + \left[ B \right]\left\{ \chi \right\}, \\ M & = \left[ B \right]\left\{ \varepsilon \right\} + \left[ D \right]\left\{ \chi \right\}, \\ \end{aligned} $$

(4.5)

where

$$ \begin{aligned} \left[ A \right] & = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 \\ 0 & 0 & {A_{33} } \\ \end{array} } \right], \\ \left[ B \right] & = \left[ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & 0 \\ {B_{12} } & {B_{22} } & 0 \\ 0 & 0 & {B_{33} } \\ \end{array} } \right], \\ \left[ D \right] & = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 \\ {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {D_{33} } \\ \end{array} } \right]. \\ \end{aligned} $$

(4.6)

Elements $A_{ij} ,B_{ij} ,D_{ij}$ of the square matrices A, B and D in relations (4.5, 4.6) are calculated by formulas:

$$ \begin{aligned} A_{ij} & = \sum\limits_{r = 1}^{3} {\int\limits_{{z_{r} }}^{{z_{r + 1} }} {Q_{ij}^{\left( r \right)} {\text{d}}z,} } \\ B_{ij} & = \sum\limits_{r = 1}^{3} {\int\limits_{{z_{r} }}^{{z_{r + 1} }} {Q_{ij}^{\left( r \right)} z{\text{d}}z,} } \\ D_{ij} & = \sum\limits_{r = 1}^{3} {\int\limits_{{z_{r} }}^{{z_{r + 1} }} {Q_{ij}^{\left( r \right)} z^{2} {\text{d}}z,} } \\ \end{aligned} $$

(4.7)

where $z_{1} = - h/2,\quad z_{2} = - h_{1} \left( {x,y} \right),\quad z_{3} = h_{1} \left( {x,y} \right),\quad z_{4} = h/2$, $r = 1,2,3$ define a number of the layers. Values $Q_{ij}^{\left( r \right)} \left( {i,j = 1,2,3} \right)$ in formulas (4.7) are determined by the following expressions:

$$ Q_{11}^{\left( r \right)} = Q_{22}^{\left( r \right)} = \frac{{E^{\left( r \right)} }}{{1 - \left( {\nu^{\left( r \right)} } \right)^{2} }},Q_{12}^{\left( r \right)} = \frac{{\nu^{\left( r \right)} E^{\left( r \right)} }}{{1 - \left( {\nu^{\left( r \right)} } \right)^{2} }},Q_{66}^{\left( r \right)} = \frac{{E^{\left( r \right)} }}{{2\left( {1 + \nu^{\left( r \right)} } \right)}}. $$

(4.8)

Transverse shear force resultants $Q_{x}$, $Q_{y}$ are defined as:

$$ Q_{x} = K_{s}^{2} A_{33} \gamma_{xz} ,\quad Q_{y} = K_{s}^{2} A_{33} \gamma_{yz} , $$

(4.9)

where $K_{s}^{2}$ denotes the shear correction factor. In this paper, it is taken by $5/6$.

Further, we will consider materials with the same Poisson’s ratio for ceramics and metal, i.e., $\nu_{m} = \nu_{c}$. Then, elements $A_{ij} ,B_{ij} ,D_{ij}$ of matrices (6) $\left[ A \right],\left[ B \right],\left[ C \right]$ can be calculated in a direct way. Analytical expressions of these elements for shells with variable thickness of layers are obtained and presented below

$$ \begin{aligned} A_{11} & = \frac{1}{{1 - \nu^{2} }}\left( {E_{m} h + 2E_{cm} \frac{{h_{1} \left( {x,y} \right)}}{p + 1}} \right), {\varvec{B}}_{11} = 0, \\ D_{11} & = \frac{1}{{1 - \nu^{2} }}\left( {\frac{{E_{m} }}{12}h^{3} + 2E_{cm} h_{1}^{3} \left( {x,y} \right)\left( {\frac{1}{p + 1} - \frac{2}{p + 2} + \frac{1}{p + 3}} \right)} \right), \\ \end{aligned} $$

(4.10)

where $E_{cm}$ denotes the difference between $E_{c} ,E_{m}$, that is,

$$ E_{cm} = E_{c} - E_{m} . $$

Note that values

$$ \left\{ {A_{22} ,B_{22} ,D_{22} } \right\} = \left\{ {A_{11} ,B_{11} ,D_{11} } \right\}, $$

(4.11)

and values $A_{12} ,A_{66,} B_{12} ,B_{66,} D_{12} ,D_{66}$ are defined as:

$$ \begin{aligned} & \left\{ {A_{12} ,B_{12} ,D_{12} } \right\} = v\left\{ {A_{11} ,B_{11} ,D_{11} } \right\}, \\ & \left\{ {A_{66} ,B_{66} ,D_{66} } \right\} = \frac{1 - \nu }{2}\left\{ {A_{11} ,B_{11} ,D_{11} } \right\}. \\ \end{aligned} $$

(4.12)

The governing differential motion equations for a free vibration of shear deformable shallow shell can be presented as

$$ \begin{aligned} & \frac{{\partial N_{11} }}{\partial x} + \frac{{\partial N_{12} }}{\partial y} - \frac{{Q_{x} }}{{R_{x} }} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}; \\ & \frac{{\partial N_{22} }}{\partial y} + \frac{{\partial N_{12} }}{\partial x} - \frac{{Q_{y} }}{{R_{y} }} = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }}; \\ & \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + \frac{{N_{11} }}{{R_{x} }} + \frac{{N_{22} }}{{R_{y} }} + N_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + 2N_{12} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{22} \frac{{\partial^{2} w}}{{\partial y^{2} }} = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}; \\ \end{aligned} $$

(4.13)

$$ \begin{aligned} \frac{{\partial M_{11} }}{\partial x} + \frac{{\partial M_{12} }}{\partial y} - Q_{x} & = I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }}; \\ \frac{{\partial M_{22} }}{\partial y} + \frac{{\partial M_{12} }}{\partial x} - Q_{y} & = I_{2} \frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }}, \\ \end{aligned} $$

where

$$ \left( {I_{0} ,I_{1} ,I_{2} } \right) = \sum\limits_{r = 1}^{3} {\int\limits_{{z_{r} }}^{{z_{r + 1} }} {\left( \rho \right)_{r} } } \left( {1,z,z^{2} } \right)dz, $$

(4.14)

here $\left( \rho \right)_{r}$ is a mass density of the rth layer.

Analytical expressions of coefficients $I_{0} ,I_{1} ,I_{2}$ for shells provided that $\nu_{m} = \nu_{c}$ are presented below.

.

$$ \begin{aligned} I_{0} & = \rho_{m} h + 2\rho_{cm} \frac{{h_{1} \left( {x,y} \right)}}{p + 1},\quad \rho_{cm} = \rho_{c} - \rho_{m} , \\ I_{1} & = 0,I_{2} = \frac{{\rho_{m} }}{12}h^{3} + 2\rho_{cm} h_{1}^{3} \left( {x,y} \right)\left( {\frac{1}{p + 1} - \frac{2}{p + 2} + \frac{1}{p + 3}} \right). \\ \end{aligned} $$

(4.15)

3 Solution Method—Free Vibration Problem

To solve the formulated problem, we apply a variational method combined with the R-functions theory (RFM methods). Let us indicate the main steps of developed approach. First, we solve the linear vibration problem, applying Ritz’s method in order to find eigenfunctions. Solution of the linear vibration problem for laminated shells by RFM is described in works (Awrejcewicz et al. 2013, 2015, 2018; Rvachev 1982; Kurpa and Shmatko 2014; Kurpa et al. 2018, 2007). The main difference of the considered problem is dependence of the elements $A_{ij} ,B_{ij} ,D_{ij}$ on matrices (6) $\left[ A \right],\left[ B \right],\left[ C \right]$ of variables x and y. But due to an application of Ritz’s method, the variational formulation of the linear problem is formally the same and is reduced to finding the minimum of the total energy functional

$$ J = U_{s} - T, $$

(4.16)

here, strain energy $U_{s}$ can be written as

$$ U_{s} = \frac{1}{2}\int\limits_{\Omega } {N_{s}^{T} \varepsilon_{s} d\Omega ,} $$

(4.17)

where $N_{s}^{T} = \left\{ {N,M,\gamma } \right\},\quad \varepsilon_{s}^{T} = \left\{ {\varepsilon ,\chi ,\gamma } \right\}$_.

Kinetic energy T in (16) is defined as

$$ \begin{aligned} T & = \frac{1}{2}\int\limits_{\Omega } {I_{0} \left( {\dot{u}^{2} + \dot{v}^{2} + \dot{w}^{2} } \right)} + 2I_{1} \left( {\dot{u}\dot{\psi }_{x} + \dot{v}\dot{\psi }_{y} } \right)I_{2} \left( {\dot{\psi }_{x}^{2} + \dot{\psi }_{y}^{2} } \right)d\Omega , \\ I & = U\left( {u,v,w,\psi_{x} ,\psi_{y} } \right) - \lambda^{2} V\left( {u,v,w,\psi_{x} ,\psi_{y} } \right), \\ \end{aligned} $$

(4.18)

where $\lambda$ is a vibration frequency.

Now the expressions for $U$ and V in Eq. (4.16) are defined by relations:

$$ U = \frac{1}{2}\iint\limits_{\Omega } {N_{s}^{T} \varepsilon_{s} dxdy,} $$

(4.19)

$$ \begin{aligned} V & = \frac{1}{2}\iint\limits_{\Omega } {I_{0} \left( {u^{2} + v^{2} + w^{2} } \right)} \\ & \quad + 2I_{1} \left( {u\psi_{x} + v\psi_{y} } \right) + I_{2} \left( {\psi_{x}^{2} + \psi_{y}^{2} } \right)dxdy. \\ \end{aligned} $$

(4.20)

According to Ritz’ approach, unknown functions are presented as

$$ \begin{aligned} u & = \sum\limits_{i = 1}^{{N_{1} }} {a_{i} u_{i} ,} \quad v = \sum\limits_{{i = N_{1} + 1}}^{{N_{2} }} {a_{i} v_{i} ,} \quad w = \sum\limits_{{i = N_{2} + 1}}^{{N_{3} }} {a_{i} u_{i} ,} \\ \psi_{x} & = \sum\limits_{{i = N_{3} + 1}}^{N4} {a_{i} } \psi_{xi} ,\quad \psi_{y} = \sum\limits_{{i = N_{4} + 1}}^{N5} {a_{i} \psi_{yi} .} \\ \end{aligned} $$

(4.21)

Here, $\left\{ {u_{i} } \right\},\left\{ {v_{i} } \right\},\left\{ {w_{i} } \right\},\left\{ {\psi_{xi} } \right\},\left\{ {\psi_{yi} } \right\}$ are admissible functions that in case of a complex shape can be constructed by the R-functions theory (Rvachev 1982).

Coefficients of this expansion $\left\{ {a_{i} } \right\},i = \overline{{1,N_{5} }}$ is found from Ritz’s system

$$ \frac{\partial I}{{\partial a_{i} }} = 0,\quad i = \overline{{1,N_{5} }} . $$

To solve the nonlinear problem, the approach proposed by authors earlier and described in detail in (Awrejcewicz et al. 2015, 2018; Kurpa and Shmatko 2014; Kurpa et al. 2018) is used. Note that the obtained nonlinear differential equations of the second order are solved by Runge–Kutta method of the 7–8-th order.

4 Numerical Results

To verify an accuracy of the present results obtained by the proposed approach, we consider the solution of several test problems.

Problem 1

Simply supported square FG bi-layered plates are considered. The following material properties for metal and ceramic constituents are used (Li et al. 2008, Malekzaden and Ghaedsharaf 2014):

$$ \begin{aligned} & E_{m} = 70\;{\text{GPa}},E_{c} = 380\;{\text{GPa}},\rho_{m} = 2707\;{\text{kg}}/{\text{m}}^{3} , \\ & \rho_{c} = 3800\;{\text{kg}}/{\text{m}}^{3} ,\nu_{m} = 0.3,\nu_{c} = 0.3. \\ \end{aligned} $$

Comparison of non-dimensional natural frequency parameter $\varLambda = a^{2} \omega /h$ for different thickness-to-length ratio $h/a$, and material graded index (p) is shown in Table 4.1.

Table 4.1 Comparison of non-dimensional natural frequency of square FGM plate

Table 4.1 shows that results presented in Li et al. (2008), Malekzaden and Ghaedsharaf (2014) are in a good agreement with the obtained results.

Problem 2

Consider a three layer rectangular plate with layers of the variable thickness (Fig. 4.1). Layers arrangement is symmetric about the middle plane. The thickness of the middle layer (core) is varied.

$$ h_{1} \left( x \right) = - \left( {t_{1} + \frac{4}{{a^{2} }}\left( {t_{2} - t_{1} } \right)x^{2} } \right),\quad h_{2} \left( x \right) = - h_{1} \left( x \right). $$

(4.22)

If $t_{2} > t_{1}$, then middle layer has a form, as shown in Fig. 4.1a. If $t_{2} < t_{1}$, then form of the core is presented in Fig. 4.1b. If $t_{1} = t_{2}$, then we have three-layered plate with layers of constant thickness. But if $t_{1} = t_{2} = \frac{h}{2}$types, then plate is bi-layered. There are studied all cases in the paper. Three of FGMs for a core are considered: M1 is a mixture of ${\text{Al}}/{\text{ZrO}}_{2}$; M2 is a mixture of ${\text{Si}}_{3} {\text{N}}_{4} /{\text{SUS}}304$; M3 is a mixture of ${\text{Al}}_{2} {\text{O}}_{3} /{\text{Al}}$.

Mechanical properties of the constituent materials of the mixtures are taken from Alijani and Amabili (2014), Swaminathan et al. (2015) and presented in Table 4.2.

Table 4.2 Mechanical properties of the constituent materials

where $E_{0} = 1\;{\text{GPa}},\quad \rho_{0} = 1\;{\text{kg}}/{\text{m}}^{3}$.

Suppose that rectangular plate is clamped or simply supported along a whole border. Introduce the geometrical parameters $\alpha = \frac{{2t_{1} }}{h};\quad \beta = \frac{{2t_{2} }}{h}$. Let these parameters and ratio $\frac{a}{b}$ be varied, but the total thickness is constant and is equal to $\frac{h}{2a} = 0.1$. Two types of FGMs are taken ${\text{Al}}_{2} {\text{O}}_{3} /{\text{Al}}$ and ${\text{Si}}_{3} {\text{N}}_{4} /{\text{SUS}}304$.

Non-dimensional parameters of the natural frequency are defined as:

$$ \varLambda = a^{2} \omega \sqrt {\frac{{\rho_{c} }}{{E_{c} }}} /h. $$

(4.23)

Table 4.3 shows the results of non-dimensional fundamental frequency parameter for clamped rectangular sandwich plates with FGM core of the variable thickness.

Table 4.3 Effect of gradient index p on non-dimensional natural frequency of clamped rectangular plates ($\alpha = 0.4,\beta = 0.8$, Fig. 4.1a)

Figure 4.2 depicts the fundamental frequencies parameters for different values of gradient index p of two types of FGM simply supported sandwich rectangular plates for values $\alpha = 0.4,\beta = 0.8$ and different ratios a/b.

Fig. 4.2

Effect of gradient index p on non-dimensional natural frequency (23) for simply supported rectangular plates $\left( {\alpha = 0.4,\beta = 0.8} \right)$

Effect of parameters $\alpha$ and $\beta$ on behavior of the non-dimensional fundamental frequencies is shown in Fig. 4.3.

Fig. 4.3

Effect of parameters $\alpha = \frac{{2t_{1} }}{h},\beta = 1$ (Fig. 4.3a) and parameters $\beta = \frac{{2t_{2} }}{h}\alpha = 1$ (Fig. 4.3b) on non-dimensional natural frequency of rectangular plates $\left( {{\text{FGM}}\;{\text{is}}\;{\text{Si}}_{3} {\text{N}}_{4} /{\text{SUS}}304} \right)$

Note that for different ratio $\frac{b}{a}$ the frequencies are changing slightly, when the parameters $\alpha$ and $\beta$ vary from 0.2 to 1.

Problem 3

Vibration of the shallow shells with a complex planform. Let us consider the FGM sandwich shallow shells with a complex planform are shown in Fig. 4.4. Assume that thickness of layers is varied by parabolic law according to Eq. (4.22).

Fig. 4.4

Sandwich shallow shell and its planform

To construct a system of admissible functions, let us use the R-functions theory. Equation of the border is $\omega \left( {x,y} \right) = 0$. For the given domain function, $\omega \left( {x,y} \right)$ can be constructed as:

$$ \begin{aligned} & \omega \left( {x,y} \right) = \left( {f_{1} \wedge_{0} f_{2} } \right) \wedge_{0} \left( {f_{3} \vee_{0} f_{4} } \right) \wedge_{0} \left( {f_{5} \vee_{0} f_{6} } \right), \\ & f_{1} = \left( {a^{2} - x^{2} } \right)/2a,f_{2} = \left( {b^{2} - y^{2} } \right)/2b, \\ & f_{3} = \left( {b_{1} - y} \right) \ge 0;\quad f_{4} = \left( {a_{1} - x} \right) \ge 0; \\ & f_{5} = \left( {b_{2} - y} \right) \ge 0;\quad f_{6} = \left( {a_{2} - x} \right) \ge 0. \\ \end{aligned} $$

The signs $\wedge_{0}$ and $\vee_{0}$ define the R-operators: R-conjunction and R-disjunction relatively (Rvachev 1982). So, we have

$$ \begin{aligned} f_{1} \wedge_{0} f_{2} & = f_{1} + f_{2} - \sqrt {f_{1}^{2} + f_{2}^{2} } , \\ f_{3} \vee_{0} f_{4} & = f_{1} + f_{2} + \sqrt {f_{1}^{2} + f_{2}^{2} } . \\ \end{aligned} $$

For clamped shells, the system of admissible functions can be chosen in the following form:

$$ \begin{aligned} & u_{k} = \omega (x,y)\phi_{k}^{(u)} ,k = \overline{{1,N_{1} }} , \\ & v_{k} = \omega \left( {x,y} \right)\phi_{k}^{\left( v \right)} ,k = \overline{{N_{1} + 1,N_{2} }} , \\ & w_{k} = \omega \left( {x,y} \right)\phi_{k}^{\left( w \right)} ,k = \overline{{N_{2} + 1,N_{3} }} , \\ & \psi_{xk} = \omega \left( {x,y} \right)\phi_{k}^{{\left( {\psi_{x} } \right)}} ,k = \overline{{N_{3} + 1,N_{4} }} , \\ & \psi_{yk} = \omega \left( {x,y} \right)\phi_{k}^{{\left( {\psi_{y} } \right)}} ,k = \overline{{N_{4} + 1,N_{5} }} , \\ \end{aligned} $$

where $\phi_{k}^{\left( r \right)} ,r = u,v,w,\psi_{x} ,\psi_{y}$ are terms of some complete system functions $\varPhi_{i} ,i = 1,2,3,4,5$. System of power polynomials is taken for the given problem. Geometrical parameters for shell are put as:

$$ \begin{aligned} \frac{h}{2a} & = 0.1;\frac{b}{a} = 1,\frac{{a_{1} }}{2a} = 0.3;\frac{{b_{1} }}{2a} = 0.25;\frac{{a_{2} }}{2a} = - 0.3; \\ \frac{{b_{2} }}{2a} & = - 0.25;k_{1} = \frac{2a}{{R_{x} }} = 0.1;k_{2} = \frac{2a}{{R_{y} }} = 0.1. \\ \end{aligned} $$

Parameters $\alpha = \frac{{2t_{1} }}{h},\beta = \frac{{2t_{2} }}{h}$ and gradient index p vary. Non-dimensional parameters of the natural frequency are defined as:

$$ \varLambda = \left( {2a} \right)^{2} \omega \sqrt {\frac{{\rho_{c} }}{{E_{c} }}} /h. $$

(4.24)

Table 4.4 shows the influence of the gradient index on linear frequencies of the clamped plates and spherical shells for parabolic law (see Fig. 4.1a).

Table 4.4 Effect of gradient index p on non-dimensional natural frequencies (24) of clamped plate and spherical shell with complex shape $\left( {\alpha = \frac{{2t_{1} }}{h} = 0.4,\beta = \frac{{2t_{2} }}{h} = 0.8} \right)$; FGM is Si₃N₄ /SUS304

All natural frequencies $\Lambda_{i} \left( {i = 1,2,3,4} \right)$ are decreasing when gradient index p increases. The difference between frequencies of the plate and shallow spherical shell is not essential. It may be explained by boundary conditions and small curvatures of the shell.

Effect of the gradient index on the first four natural frequencies of the clamped spherical shells for different FGMs (M1-${\text{Al}}/{\text{ZrO}}_{2}$ and M2-${\text{Si}}_{3} {\text{N}}_{4} /{\text{SUS}}304$) is shown in Fig. 4.5. Parabolic law of thickness variation corresponds to Fig. 4.1b, parameters $\alpha = \frac{{2t_{1} }}{h} = 0.8;\beta = \frac{{2t_{2} }}{h} = 0.4$.

Fig. 4.5

Effect of gradient index p on non-dimensional natural frequencies (24) for clamped spherical shell with complex shape made of different material FGMs $\left( {\alpha = \frac{{2t_{1} }}{h} = 0.8,\beta = \frac{{2t_{2} }}{h} = 0.4} \right)$

As follows from Fig. 4.5, frequencies for core made of ${\text{Al}}/{\text{ZrO}}_{2}$ (M1) are decreasing, and they are increasing for FGM ${\text{Si}}_{3} {\text{N}}_{4} /{\text{SUS}}304$ (M2) if gradient index p increases.

Table 4.5 and Fig. 4.6 show an influence of boundary conditions on the natural frequencies while the gradient index is increasing. Two types of the mixed boundary conditions are considered: clamped simply supported and clamped-free. It is assumed that sides $y = \pm b$ are simply supported or free and remain part of the boundary is clamped. Values parameters $\alpha ,\beta$ are taken the following: $\alpha = 0.4,\beta = 0.8,$ Fig. 4.1a, FGMs is ${\text{Al}}/{\text{ZrO}}_{2}$.

Table 4.5 Effect of gradient index p on non-dimensional natural frequency (24) of spherical shell (Fig. 4.4) and different boundary condition for FGMs ${\text{Al}}/{\text{ZrO}}_{2}$ (M1)

Fig. 4.6

Effect of gradient index p on non-dimensional natural frequency parameter (24) of spherical shell (Fig. 4.4) with different boundary condition ($\alpha = \frac{{2t_{1} }}{h} = 0.4;$ $\beta = \frac{{2t_{2} }}{h} = 0.8;$ Fig. 4.1a)

Comparison analysis of the behavior of the natural frequency for different FGMs and mixed boundary conditions for values of parameters $\alpha = \frac{{2t_{1} }}{h} = 0.8,\beta = \frac{{2t_{2} }}{h} = 0.4$ (Fig. 4.1b) is presented in Table 4.6 and Fig. 4.7. It is observed that frequencies are essentially greater for material ${\text{Al}}/{\text{ZrO}}_{2}$ than for Si₃N₄ /SUS304.

Table 4.6 Effect of gradient index p on non-dimensional natural frequency parameter (24) of spherical shell with complex shape and different boundary condition made of different materials; FGM is $Si_{3} N_{4} /SUS304$ (M2) and ${\text{Al}}/{\text{ZrO}}_{2}$ (M1)

Fig. 4.7

Effect of gradient index p on non-dimensional natural frequency parameter (24) for spherical shell with complex shape and different boundary condition made of different FGM materials $\left( {\alpha = \frac{{2t_{1} }}{h} = 0.8;\beta = \frac{{2t_{2} }}{h} = 0.4} \right)$

Nonlinear behavior of the sandwich FGM spherical clamped shallow shells with planform drawn in Fig. 4.4 for different FG materials was studied for two values of the parameter $\alpha ,\;\beta$ $\alpha = \left( {0.4;0.8} \right);\beta = \left( {0.8;0.4} \right)$ and two values of the gradient index p = (0.5;2). The remain geometric parameters are the same with linear problem.

In Fig. 4.8, backbone curves are presented for case $\alpha = 0.4;\beta = 0.8$ that corresponds to Fig. 4.1a. The obtained results for ratio of nonlinear frequency to linear frequency for case $\alpha = 0.8;\beta = 0.4$ corresponding to Fig. 4.1b are shown in Fig. 4.9.

Fig. 4.8

Effect of gradient index and FGMs on nonlinear to linear frequency ratio of clamped spherical shells with variable thickness of layers defined by law (22) for values $\alpha = 0.4;\beta = 0.8$ and planform is shown in Fig. 4.4

Fig. 4.9

Effect of gradient index p and FGMs on nonlinear to linear frequency ratio of clamped spherical shells with variable thickness of layers defined by law (22) for values $\alpha = 0.4;\beta = 0.8$ and planform is shown in Fig. 4.4

From these plots, it follows that effect on backbone curves is more essential for layers arrangement corresponding to Fig. 4.1a. The ratio $\frac{{\omega_{N} }}{{\omega_{L} }}$ for FGM $Al/ZrO_{2}$ greater than for FGM Si3N4 /SUS304 in both the cases.

5 Conclusions

The linear and geometrically nonlinear free vibration of functionally graded shallow shells of sandwich type with a complex planform is investigated using the R-functions theory and variational methods. The considered shell consists of the layers of variable thickness that are symmetrical about the middle surface, but the total thickness is constant. The effective material properties are calculated according to the power law. Analytical expressions have been obtained for dependent on thickness coefficients needed for calculation of the stress and moment resultants.

The developed algorithm and corresponding software have been applied to plate and shallow shells with rectangular and complex planforms with different boundary conditions and various FGMs. As example, the parabolic law of the thickness change of layers has been considered. Effect of different parameters (form of the parabola, type of FGMs, boundary conditions, value of gradient index) on natural frequencies and response curves is shown.