Introduction

Micro-electro-mechanical systems (MEMS) due to their fast technological progress, remarkable performance, less power consumption, and accuracy are important devices for investigation to researchers. These devices owing to their ample potential significantly used in many applications such as resonators [1,2,3], switches [4, 5], actuators [6, 7] and sensors [8].

These devices typically consist of two electrodes of conducting materials: one is movable and the other is fixed. Structural members like micro/nanobeams and plates of various shapes are commonly used for the electrodes [9,10,11]. The applied voltage between the two electrodes leads to electrostatic force due to induced electrostatic charge. Moreover, when the gap between the electrodes is in submicron scale, the Casimir force in addition to the electrostatic force also contributes to the deflection of the movable electrode [12]. The deflection is resisted by restoring force (elastic force) from the movable electrode (structural members like microbeams, plates etc.). Apparently, the interaction between the electrostatic, Casimir and elastic forces determines the equilibrium/deflection of the beam. The natural frequencies of the microbeam are influenced by the deflected state of the beam [6, 13, 14]. Further, when the cumulative effort due to electrostatic and Casimir forces exceeds the resisting elastic force and reaches to a critical value, the movable electrode snaps down to the fixed electrode. The critical value of potential difference when the moveable electrodes collapse is known as the pull-in voltage [15, 16].

The deflection of electrostatically actuated microbeam frequently leads to mid-plane stretching in the beam, which results into axial load in the fixed–fixed microbeam [13]. This axial load can significantly change the pull-in voltage and natural frequencies, and thus, it is necessary to study the effect of mid-plane stretching (geometric non-linearity) while investigating the pull-in voltage and the free vibration characteristics of microbeam. The importance of considering the mid-plane stretching effect in order to investigate the performance of devices such as switches and resonators is also described in several literatures [13, 14, 17].

The micro-machining processes leads to existence of the residual stress in fixed–fixed microbeam of electrostatically actuated devices. The difference in coefficient of thermal expansion of beam and the other elements of MEMS devices is the main source for the residual stress [18]. It can significantly affect the pull-in voltage and frequency characteristics of the devices [19] and thus accurate information for the residual stress is important for the appropriate design of electrostatically actuated devices [20]. Various approaches are available in published work for the residual stress computation in micro-beam. For instance, the residual stress is evaluated based on natural frequency measurement of some lower mode shapes [21], from the data of frequency shift with variation in DC voltage [22] and using an analytical model fitted based on the measured deflection [23].

Several researchers investigated pull-in voltage and free vibration characteristics (dynamic characteristics) of microbeams considering the effects of residual stress. Abdel-Rahman et al. [13] investigated the pull-in voltage and free vibration characteristics of microbeam and depicted importance of the axial load due to mid-plane stretching and residual stress while estimating the pull-in voltage and for tuning the natural frequencies. Kuang and Chen [6] studied the free vibration characteristics of the shaped microbeam at deflected position in static equilibrium including the axial load due to residual stress. Jia et al. [24] and Jia et al. [14] conducted parametric study for micro-switches to display significant effect of the mid-plane stretching, residual stress and Casimir force on the pull-in voltage and natural frequencies. De Pasquale and Somà [22] experimentally obtained the dynamic characterisation of electrostatically actuated micro-structures with specific focus on the frequency shift due to residual stress. Further, the variation in temperature when the devices are in use also leads to axial stress in beams and in turn alters the frequency characteristics. The micro-resonators are considerably influenced by the temperature change during operation. Tilmans and Legtenberg [25] experimentally studied the influence of temperature on the resonance frequency of micro-resonators. Various techniques are proposed in published literature for reducing the temperature sensitivity of fixed–fixed beam resonators [26, 27].

The ability to tune the resonant frequency of electrostatically actuated devices is an important property for performance improvement of the devices such as micromechanical filters [28], mass sensor [29], temperature sensors [30] and so on. The frequency tuning is often implemented to enhance operational regime of the devices [31]. Various approaches for frequency tuning such as based on the adjustment in length of microstructure [32], deliberate introduction of axial stress by means of resistive heating of microstructure [1] and change of vibrating mass [33] are reported in published literature.

The significant decrease in gap size between the deformable electrode and fixed electrode needs consideration of fluctuation induced electromagnetic force for evaluating performance of the electrostatically actuated devices [34]. Based on the gap size in the device, the force is named as van der Waals (vdW) force or Casimir force in different operational regime [35, 36]. The origin of the vdW and Casimir force is related to a common source of current fluctuation in interacting macroscopic bodies [37]. The interaction results into the existence of electromagnetic field. The force resulting from the interaction is named as vdW force when retardation of electromagnetic interaction can be neglected owing to the gap size of the order of few nanometers, whereas the same interaction force when the retardation becomes substantial due to large gap size named as Casimir force [38]. These forces signify the same physical phenomenon in different operation regime and hence they can’t be taken into account at the same time for the design and analysis of the devices [39].

In some previous studies, pull-in voltage and free vibration characteristics of microbeam are investigated considering the effect of Casimir force [14, 24, 40]. Lin and Zhao [41] investigated non-linear behaviour of nanoscale electrostatic actuator incorporating influence of the Casimir force. It is to be noted that majority of reported works of MEMS devices on pull-in voltage and free vibration characteristics calculate the Casimir force based on the approximation of ideal conductor, which results into overestimation of the force. The results of Lifshitz [37] work specified the strong dependence of Casimir force on material properties. Further, the reported works on free vibration characteristics of MEMS devices incorporating the effect of the Casimir force do not addresses the tuning and stability characteristics of natural frequencies at deflected position of microbeam. These research gaps motivated the present work, wherein comprehensive investigations on the pull-in voltage and free vibration characteristics at deflected position of microbeam is presented incorporating the finite conductivity correction to the Casimir force. Furthermore, the free vibration characteristic for MEMS devices studied in present work provides detailed framework for the tuning and stability characteristics of microbeam at deflected position.

Theoretical Formulation

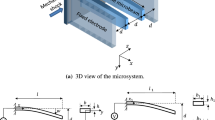
A fixed–fixed microbeam of length \(\widehat{L}\), suspended above a gate electrode with an initial separation distance \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g}\) (initial gap) is shown in Fig. 1. The microbeam is assumed to be of prismatic cross section and hence the beam has cross-sectional area \(\widehat{A}=\widehat{b}\widehat{h}\) and moment of inertia \(\widehat{I}=\frac{1}{12}\widehat{b}{\widehat{h}}^{3}\), where \(\widehat{b}\) and \(\widehat{h}\) denote the width and thickness of the beam. An applied driving voltage \(\widehat{V}\) between the microbeam and gate electrode (fixed electrode) initiates an attractive electrostatic force \({\widehat{F}}_{e}\). The combined action of the electrostatic force \({\widehat{F}}_{e}\) and Casimir force \({\widehat{F}}_{\text{Casimir}}\) governs the deflected position of the microbeam. The forces \({\widehat{F}}_{e}\) and \({\widehat{F}}_{Casimir}\) are non-linear function of gap between the deflected state of the beam and the gate electrode. The transverse deflection \(\widehat{u}\left(\widehat{x},\widehat{t}\right)\) of the microbeam under the effect of electrostatic force induced by driving voltage \(\widehat{V}\) and Casimir force can be stated based on Euler–Bernoulli beam equation as follows [42, 43]:

Fig. 1
figure 1

A Schematic drawing of fixed–fixed microbeam actuated by electrostatic force

Full size image
$$\widehat{E}\widehat{I}\frac{{\partial }^{4}\widehat{u}}{\partial {\widehat{x}}^{4}}+\widehat{\rho }\widehat{A}\frac{{\partial }^{2}\widehat{u}}{\partial {\widehat{t}}^{2}}+\widehat{c}\frac{\partial \widehat{u}}{\partial \widehat{t}}= \left[\frac{\widehat{E}\widehat{A}}{2\widehat{L}}\underset{0}{\overset{\widehat{L}}{\int }}{\left(\frac{\partial \widehat{u}}{\partial \widehat{x}}\right)}^{2}{\text{d}}\widehat{x}+\widehat{N}\right]\frac{{\partial }^{2}\widehat{u}}{\partial {\widehat{x}}^{2}}+{\widehat{F}}_{e}+{\widehat{F}}_{\text{Casimir}}$$
(1)

with the boundary conditions

$${\left.\frac{\partial \widehat{u}}{\partial \widehat{x}}\right|}_{\widehat{x}=0}= {\left.\frac{\partial \widehat{u}}{\partial \widehat{x}}\right|}_{\widehat{x}=\widehat{L}}={\left.\widehat{u}\right|}_{\widehat{x}=0}= {\left.\widehat{u}\right|}_{\widehat{x}=\widehat{L}}=0$$

where \(\widehat{x}\) and \(\widehat{t}\) represents the position along the microbeam length and time, respectively. The effective modulus and density of the beam are \(\widehat{E}\) and \(\widehat{\rho }\) , respectively. For narrow beams (\(\widehat{b}<5\widehat{h}\)), the \(\widehat{E}\) equals to Young’s modulus of the beam material \(E\), whereas for wide beams (\(\widehat{b}\ge 5\widehat{h}\)), the \(\widehat{E}\) is approximated to plate modulus \(E/(1-{\nu }^{2})\) [20], where \(\nu\) signifies the Poisson’s ratio. The manufacturing method of microbeam that is micro-fabrication process originates the residual stresses in fixed–fixed beam. The existence of residual stress yields axial force \(\widehat{N}\) in microbeam. Moreover, the microbeam is subjected to stretching (mid-plane stretching) owing to small finite deflection. The stretching also produces axial force, which is represented by integral term in right-hand side of (1). The microbeam vibrates in medium with viscous damping coefficient \(\widehat{c}\). The present work investigates the arrangement wherein the length and width of microbeam and fixed electrode are finite, however, substantially larger than gap between them. Therefore, even during pull-in, the ratio of microbeam deflection and length of the microbeam is very small (slope of the microbeam is very small). Hence, it confirms validity of the Euler–Bernoulli beam equation.

For parallel beam arrangement as shown in Fig. 1, the electrostatic force \({\widehat{F}}_{e}\)(accounting for fringing field correction) per unit length of the beam is as follows [44]:

$$\hat{F}_{e} = \frac{{\varepsilon _{0} \hat{b}\left( {\hat{V}_{{{\text{DC}}}} + \hat{V}_{{{\text{AC}}}} \cos \left( {\hat{\omega }_{f} \hat{t}} \right)} \right)^{2} }}{{2\left( {\hat{g} - \hat{u}} \right)^{2} }}\left( {1 + 0.65\frac{{\left( {\hat{g} - \hat{u}} \right)}}{{\hat{b}}}} \right)$$
(2)

where the vacuum permittivity \({\varepsilon }_{0}\)= 8.854 × 10−12C2N−1 m−2. The driving voltage \(\widehat{V}\) comprising of DC component \({\widehat{V}}_{\text{DC}}\) (polarisation voltage) and a small harmonic AC component \({\widehat{V}}_{\text{AC}}\cos\left({\widehat{\omega }}_{f}\widehat{t}\right)\), where, \({\widehat{V}}_{\text{AC}}\) and \({\widehat{\omega }}_{f}\) represent amplitude and driving frequency of the AC component.

For perfectly conducting parallel plates of infinitely long length and separated by distance \(\widehat{g}-\widehat{u}\), the Casimir force per unit length can be expressed as [35, 45]

$${\widehat{F}}_{c}^{0}=\frac{{\pi }^{2}{\bar{h}}{\bar{c}}\widehat{b}}{240{[\widehat{g}-\widehat{u}]}^{4}}$$
(3)

where \({\bar{h}}\) and \({\bar{c}}\) denote the Planck’s constant divided by 2π and the speed of the light, respectively. For such configurations wherein the length and width of microbeam and fixed electrode are finite, however, substantially larger than gap between them, the microbeam and fixed electrode can be approximated as plates of infinite length and hence Eq. (3) is suitable for calculating the Casimir force [12]. In addition, it is stated that correction for finite size of plates is insignificant [46]. Further, the expression for calculating the Casimir force is suitable for 20 nm or larger gap between the parallel plates [47]. For more realistic value of Casimir force, the Eq. (3) is corrected for accounting effect of the finite conductivity, temperature and surface roughness of interacting plate materials. Further, a common equation is unavailable which accounts for all the correction simultaneously [48].

The correction factor in terms of separation distance (\(\widehat{g}-\widehat{u}\)) between two parallel plates for accounting the finite conductivity of metal while computing the Casimir force is [49]

$${\eta }^{c}=1-\frac{16}{3}\frac{{\delta }_{0}}{\left[\widehat{g}-\widehat{u}\right]}+24\frac{{\delta }_{0}^{2}}{{\left[\widehat{g}-\widehat{u}\right]}^{2}}-\frac{640}{7}\left(1-\frac{{\pi }^{2}}{210}\right)\frac{{\delta }_{0}^{3}}{{\left[\widehat{g}-\widehat{u}\right]}^{3}}+\frac{2800}{9}\left(1-\frac{163 {\pi }^{2}}{7350}\right)\frac{{\delta }_{0}^{4}}{{\left[\widehat{g}-\widehat{u}\right]}^{4}}$$
(4)

where \({\delta }_{0}\) indicates the relative penetration depth of the electromagnetic zero-point oscillations into the metal. And \({\delta }_{0}=\frac{{\lambda }_{p}}{2\pi }\) where \({\lambda }_{p}\) denotes the effective plasma frequency of electrons. Bezerra et al. [50] investigated the applicability of Eq. (4) for three materials [aluminium (Al), gold (Au), copper (Cu)] and concluded that the Eq. (4) can be consistently used for separation distance (\(\widehat{g}-\widehat{u}\)) between two parallel plates more than \({\lambda }_{p}\). Further, The variation in optical data available from various sources yields small variation in magnitude of \({\lambda }_{p}\). However, the small variation in \({\lambda }_{p}\) leads to change in magnitude of estimated Casimir force by less than one percentage [49].

The approximate expression for roughness correction factor to the Casimir force with consideration of stochastic roughness of plates is [51]

$${\eta }^{r}=1+ 20{\left(\frac{\Delta }{\widehat{g}-\widehat{u} }\right)}^{2}+420{\left(\frac{\Delta }{\widehat{g}-\widehat{u} }\right)}^{4}$$
(5)

The dispersion and RMS (root mean square) values for the stochastic distribution of roughness are \(\Delta\) and \(\frac{\Delta }{\sqrt{3}}\) , respectively. The Eq. (5) states that with the increase in separation distance (\(\widehat{g}-\widehat{u}\)) between two parallel plates and decrease in RMS value of surface roughness, the correction factor to Casimir force decreases rapidly. The RMS value of 1.5 nm to 10.1 nm for silicon wafers with gold coating and from 2.6 to 10.3 nm for polysilicon microbeam is reported in published literatures [52, 53]. This confirms the possibility for attaining roughness value of the order of few nanometers through micro-fabrication processes. It is experimentally observed that maximum surface roughness correction to the Casimir force with gap spacing of 160 nm is 0.65% [46]. Moreover, maximum correction to the Casimir force for accounting the temperature effect is limited to 0.2% at temperature of 300°K with gap spacing less than 1 μm [12]. Thus, for theoretical formulation of MEMS, it is suitable to account only for the finite conductivity correction as a first approximation.

The expression for the Casimir force incorporating finite conductivity correction takes the following form:

$${\widehat{F}}_{C}={\eta }^{c}{\widehat{F}}_{c}^{0}$$
(6)

For representing (1) in suitable form following non-dimensional variables are implemented,

\(u=\frac{\widehat{u}}{\widehat{g}}\), \(x=\frac{\widehat{x}}{\widehat{L}}\) and \(t=\frac{\widehat{t}}{\widehat{T}}\), where time constant, \(\widehat{T}= \sqrt{\frac{\widehat{\rho }\widehat{A}{\widehat{L}}^{4}}{\widehat{E}\widehat{I}}}\)

Implementing the above variables along with expressions of the electrostatic force (2) and Casimir force (6) into governing Eq. (1), the following equation is obtained:

$$ \begin{aligned}{u}^{\prime\prime\prime\prime}&+\ddot{u}+c\dot{u}=\left(\alpha \underset{0}{\overset{1}{\int }}{{u}^{\prime 2}}{\text{d}}x+N\right){u}^{\prime\prime}+\frac{\beta {V}^{2}}{{\left(1-u\right)}^{2}}+f\frac{\beta {V}^{2}}{\left(1-u\right)}\\ &+ {\gamma }_{\text{Casimir}}\left[\frac{1}{{\left(1-u\right)}^{4}}-\frac{16\delta }{{3\left(1-u\right)}^{5}}+\frac{24{\delta }^{2}}{{\left(1-u\right)}^{6}}\right. \\&\quad \left. -\left(1-\frac{{\pi }^{2}}{210}\right)\frac{640{\delta }^{3}}{7{\left(1-u\right)}^{7}}+\left(1-\frac{163{\pi }^{2}}{7350}\right)\frac{2800{\delta }^{4}}{9{\left(1-u\right)}^{8}}\right]\end{aligned} $$
(7)

with the boundary conditions,

$${\left.u\right|}_{x=0}={\left.u\right|}_{x=1}={\left.u^{\prime}\right|}_{x=0}={\left.u^{\prime}\right|}_{x=1}=0$$

where \(\alpha =6{\left(\frac{\widehat{g}}{\widehat{h}}\right)}^{2}\), \(\beta =\frac{{\varepsilon }_{0}\widehat{b}{\widehat{L}}^{4}}{2{\widehat{g}}^{3}\widehat{E}\widehat{I}}\), \({\gamma }_{\text{Casimir}}=\frac{{\pi }^{2}{\bar{h}}{\bar{c}}\widehat{b}{\widehat{L}}^{4}}{240{\widehat{g}}^{5}\widehat{E}\widehat{I}}\), \(\delta =\frac{{\delta }_{0}}{\widehat{g}}\), \(N=\frac{\widehat{N}{\widehat{L}}^{2}}{\widehat{E}\widehat{I}}\), \(c=\frac{\widehat{c}{\widehat{L}}^{4}}{\widehat{E}\widehat{I}\widehat{T}}\), \(f=0.65\frac{\widehat{g}}{\widehat{b}}\), \(V={V}_{\text{DC}}+{V}_{\text{AC}}cos\left({\omega }_{f}t\right)\) and \({\omega }_{f}={\widehat{\omega }}_{f}\widehat{T}\).

The partial derivatives with respect to spatial coordinate \(x\) and time \(t\) in Eq. (7) are symbolised with superscript prime (') and dot above (˙). The parameters \(\alpha\) (mid-plane stretching), \({\gamma }_{Casimir}\) (Casimir force), \(N\) (axial load due to residual stress), \(f\)(fringing field) and \(\delta\) (finite conductivity) appearing in Eq. (7) are in non-dimensional form. However, in Eq. (7), the DC component \({V}_{\text{DC}}\) (polarisation voltage) and \({V}_{\text{AC}}\) (amplitude of ac component) of driving voltage are preserved in dimensional form.

Solution Using ROM

ROM for Static Analysis

The combined effect of the electrostatic force and Casimir force causes transverse deflection \(u\left(x,t\right)\) of fixed–fixed microbeam. The deflection can be approximated as follows:

$$u\left(x,t\right)= {u}_{s}\left(x\right)+{u}_{d}\left(x,t\right)$$
(8)

where \({u}_{s}\left(x\right)\) and \({u}_{d}\left(x,t\right)\) signify the static and dynamic components of the deflection, respectively. The \({u}_{s}\left(x\right)\) and \({u}_{d}\left(x,t\right)\) are induced by the DC and AC components of the driving voltage, respectively. All time-dependent and dynamic forcing terms of Eq. (7) are equated to zero and substituting (8) into (7) yields the following expression to determine the static response of microbeam:

$${u}_{s}^{\prime\prime\prime\prime}=\left(\alpha \underset{0}{\overset{1}{\int }}{{{u}_{s}}^{\prime 2}}{\text{d}}x+N\right){{u}_{s}}^{\prime\prime}+\frac{\beta {V}_{DC}^{2}}{{\left(1-{u}_{s}\right)}^{2}}+f\frac{\beta {V}_{DC}^{2}}{\left(1-{u}_{s}\right)}+ {\gamma }_{\text{Casimir}}\left[\frac{1}{{\left(1-{u}_{s}\right)}^{4}}-\frac{16\delta }{{3\left(1-{u}_{s}\right)}^{5}}+\frac{24{\delta }^{2}}{{\left(1-{u}_{s}\right)}^{6}}-\left(1-\frac{{\pi }^{2}}{210}\right)\frac{640{\delta }^{3}}{7{\left(1-{u}_{s}\right)}^{7}}+\left(1-\frac{163{\pi }^{2}}{7350}\right)\frac{2800{\delta }^{4}}{9{\left(1-{u}_{s}\right)}^{8}}\right]$$
(9)

The Eq. (9) represents two-point boundary value problem (BVP), where the voltage parameter in dimensionless form is represented by the term \(\beta {V}_{\text{DC}}^{2}\). The Galerkin discretisation technique is adopted in the present work for attaining ROM, to find the static component \({u}_{s}\left(x\right)\). Hence, the trial solution for static component of the transverse deflection is approximated as,

$$u_{s} \left( x \right) = \sum\limits_{{i = 1}}^{m} {a_{i} } \varphi _{i} \left( x \right)$$
(10)

where the scalar constant denoted by \({a}_{i}\) is to be evaluated. In Eq. (10), the spatial basis function designated by \({\varphi }_{i} (x)\) is the beam mode shapes. The mode shapes of the microbeam are normalised such that \({\int }_{0}^{1}{\varphi }_{i}^{2}dx\) and determined by solving the following expression [54]

$$\varphi ^{\prime\prime\prime\prime}{ = N}\varphi ^{\prime\prime}{\text{ + }}\omega ^{{\text{2}}} \varphi$$
(11)

with the boundary conditions

$${\left.\varphi \right|}_{x=0}={\left.\varphi \right|}_{x=1}={\left.{\varphi }^{\prime}\right|}_{x=0}={\left.{\varphi }{\prime}\right|}_{x=1}=0$$

For evaluating \({u}_{s}\left(x\right)\), ROM is found by substituting the trial solution (10) into (9), using Eq. (11) and orthogonality condition of \({\varphi }_{i}\), the resulting outcome is further multiplied by \({\varphi }_{n}\) and integrated between interval \(x=0\) to \(1\). The obtained ROM to evaluate \({u}_{s}\left(x\right)\), which represents set of non-linear algebraic equation, is as follows:

$${\omega }_{n}^{2}{a}_{n}=\left(\alpha \sum_{i,j,k=1}^{m}{a}_{i}{a}_{j}{a}_{k}{\int }_{0}^{1}{\varphi }_{i}^{\prime}{\varphi }_{j}^{\prime}{\text{d}}x{\int }_{0}^{1}{\varphi }_{k}^{\prime\prime}{\varphi }_{n}{\text{d}}x\right)+\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}\frac{1}{{\left(1-\sum_{i=1}^{m}{a}_{i}{\varphi }_{i}\right)}^{2}}{\varphi }_{n}{\text{d}}x+f\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}\frac{1}{\left(1-\sum_{i=1}^{m}{a}_{i}{\varphi }_{i}\right)}{\varphi }_{n}{\text{d}}x +\gamma \left[{\int }_{0}^{1}\frac{1}{{\left(1-\sum_{i=1}^{m}{a}_{i}{\varphi }_{i}\right)}^{4}}{\varphi }_{n}{\text{d}}x-\frac{16\delta }{3}{\int }_{0}^{1}\frac{1}{{\left(1-\sum_{i=1}^{m}{a}_{i}{\varphi }_{i}\right)}^{5}}{\varphi }_{n}{\text{d}}x+24{\delta }^{2}{\int }_{0}^{1}\frac{1}{{\left(1-\sum_{i=1}^{m}{a}_{i}{\varphi }_{i}\right)}^{6}}{\varphi }_{n}{\text{d}}x-\frac{640{\delta }^{3}}{7}\left(1-\frac{{\pi }^{2}}{210}\right){\int }_{0}^{1}\frac{1}{{\left(1-\sum_{i=1}^{m}{a}_{i}{\varphi }_{i}\right)}^{7}}{\varphi }_{n}{\text{d}}x+\frac{2800{\delta }^{4}}{9}\left(1-\frac{163{\pi }^{2}}{7350}\right){\int }_{0}^{1}\frac{1}{{\left(1-\sum_{i=1}^{m}{a}_{i}{\varphi }_{i}\right)}^{8}}{\varphi }_{n}{\text{d}}x\right]$$
(12)

where \(n\) = 1, 2…\(m\). The equation for mode shape \({\varphi }_{i}\) required for solving the Eq. (12) can be found from Eq. (11) is:

$$\varphi _{i} = \left( {\cosh _{{1i}} x - \cos \xi _{{3i}} x} \right) + \left[ {\frac{{\cos \xi _{{3i}} - \cosh \xi _{{1i}} }}{{\xi _{{3i}} \sinh \xi _{{1i}} - \xi _{{1i}} \sinh \xi _{{3i}} }}} \right]\left( {\xi _{{3i}} \sinh \xi _{{1i}} x - \xi _{{1i}} \sin \xi _{{3i}} x} \right)$$
(13)

The analytical solution of Eq. (11) yields characteristics equation as follows:

$$\omega - \omega \cos \xi _{3} \cosh \xi _{1} + \frac{N}{2}\sin \xi _{3} \sinh \xi _{1} = 0$$
(14)

where \({\xi }_{1}= \sqrt{\sqrt{\frac{{N}^{2}}{4}+{\omega }^{2}}+\frac{N}{2}}\) and \({\xi }_{3}= \sqrt{\sqrt{\frac{{N}^{2}}{4}+{\omega }^{2}}-\frac{N}{2}}.\)

The natural frequencies at undeflected position of microbeam denoted by \({\omega }_{i}\) including the influence of axial load can be obtained by solving the transcendental Eq. (14). The various integral terms consisting of \({\varphi }_{i}\) in Eq. (12) are evaluated numerically using trapezoidal integration method. The static deflection \({u}_{s}\left(x\right)\) is computed by solving the set of algebraic non-linear Eq. (12).

ROM for Free Vibration Characteristics

The linear free vibration characteristics at statically deflected position of microbeam are studied by establishing ROM. The natural frequencies at various deflected position of the beam vary owing to non-linearities emanated through electrostatic force, Casimir force and mid-plane stretching. The equation for analysing the free vibration of microbeam at deflected position is found by substituting Eq. (8) into (7), expanding forcing terms present in Eq. (7) about \({u}_{d}\left(x,t\right)=0\), using Eq. (9) of static deflection, ignoring damping and higher order terms and retaining only linear terms of \({u}_{d}\). The obtained expression for undamped free vibration of microbeam is,

$$u^{\prime\prime\prime\prime}_{d} + \ddot{u}_{d} = \left( {\alpha \int _{0}^{1} u^{\prime 2}_{s} {\text{d}}x + N} \right)u^{\prime\prime}_{d} \left( {2\alpha \int _{0}^{1} u^{\prime}_{s} u^{\prime}_{d} \,{\text{d}}x} \right)u^{\prime\prime}_{s} + 2\beta V_{{{\text{DC}}}}^{2} \frac{1}{{\left( {1 - u_{s} } \right)^{3} }}u_{d} + f\beta V_{{{\text{DC}}}}^{2} \frac{1}{{\left( {1 - u_{s} } \right)^{2} }}u_{d} + \gamma _{{{\text{Casimir}}}} \left[ {\frac{4}{{\left( {1 - u_{s} } \right)^{5} }} - \left( {\frac{{16\delta }}{3}} \right)\frac{5}{{\left( {1 - u_{s} } \right)^{6} }} + \left( {24\delta ^{2} } \right)\frac{6}{{\left( {1 - u_{s} } \right)^{7} }} - \left( {1 - \frac{{\pi ^{2} }}{{210}}} \right)\left( {\frac{{640\delta ^{3} }}{7}} \right)\frac{7}{{\left( {1 - u_{s} } \right)^{8} }} + \left( {1 - \frac{{163\pi ^{2} }}{{7350}}} \right)\left( {\frac{{2800\delta ^{4} }}{9}} \right)\frac{8}{{\left( {1 - u_{s} } \right)^{9} }}} \right]u_{d}$$
(15)

The separation of variables method is used for solving Eq. (15). For this, \({u}_{d}\left(x,t\right)\) is taken as,

$${u}_{d}\left(x,t\right)= {u}_{dt}\left(t\right){\varphi }_{df}\left(x\right)$$
(16)

The Eq. (16) of \({u}_{d}\left(x,t\right)\) is substituted in (15) and rearrangement results into two uncoupled ordinary differential equation. The uncouple differential equation in terms of spatial coordinate, which is also known as characteristic equation, provides natural frequencies and mode shapes at deflected position of microbeam. The equation is as follows:

$${\varphi }_{df}^{\prime\prime\prime\prime}-\left(\alpha {\int }_{0}^{1}{{u}_{s}^{\prime 2}}{\text{d}}x+N\right){\varphi }_{df}^{\prime\prime}-\left(2\alpha {\int }_{0}^{1}{u}_{s}^{\prime}{\varphi }_{df}^{\prime}{\text{d}}x\right){u}_{s}^{\prime\prime}-2\beta {V}_{\text{DC}}^{2}\frac{1}{{\left(1-{u}_{s}\right)}^{3}}{\varphi }_{df}-f\beta {V}_{\text{DC}}^{2}\frac{1}{{\left(1-{u}_{s}\right)}^{2}}{\varphi }_{df}-{\gamma }_{\text{Casimir}}\left[\frac{4}{{\left(1-{u}_{s}\right)}^{5}}-\left(\frac{16\delta }{3}\right)\frac{5}{{\left(1-{u}_{s}\right)}^{6}}+\left(24{\delta }^{2}\right)\frac{6}{{\left(1-{u}_{s}\right)}^{7}}-\left(1-\frac{{\pi }^{2}}{210}\right)\left(\frac{640{\delta }^{3}}{7}\right)\frac{7}{{\left(1-{u}_{s}\right)}^{8}}+\left(1-\frac{163{\pi }^{2}}{7350}\right)\left(\frac{2800{\delta }^{4}}{9}\right)\frac{8}{{\left(1-{u}_{s}\right)}^{9}}\right]{\varphi }_{df}-{\omega }_{df}^{2}{\varphi }_{df}=0$$
(17)

where natural frequencies and mode shapes at deflected state are denoted by \({\omega }_{df}\) and \(\varphi _{{df}}\) , respectively. The approximate solution to find ROM for studying the free vibration of microbeam is taken as,

$${\varphi }_{df}= \sum_{i=1}^{m}{b}_{i}{\varphi }_{i}$$
(18)

Substituting Eq. (18) into (17), making use of orthogonality relation of mode shapes, multiplying the outcome by \({\varphi }_{n}\) and integrating over beam length (between the interval \(x=0\) and \(x=1\)) yields expression of the ROM as

$${b}_{n}{\omega }_{n}^{2}- \sum_{i=1}^{m}{b}_{i}\left(\alpha {\int }_{0}^{1}{{u}_{s}^{\prime 2}}{\text{d}}x{\int }_{0}^{1}{\varphi }_{i}^{\prime\prime}{\varphi }_{n}{\text{d}}x+2\alpha {\int }_{0}^{1}{u}_{s}^{\prime}{\varphi }_{i}^{\prime}{\text{d}}x{\int }_{0}^{1}{u}_{s}^{\prime\prime}{\varphi }_{n}{\text{d}}x\right)-\sum_{i=1}^{m}{b}_{i}\left(2\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}\frac{1}{{\left(1-{u}_{s}\right)}^{3}}{\varphi }_{i}{\varphi }_{n}{\text{d}}x+f\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}\frac{1}{{\left(1-{u}_{s}\right)}^{2}}{\varphi }_{i}{\varphi }_{n}{\text{d}}x\right)-\sum_{i=1}^{m}{b}_{i}\left({\gamma }_{\text{Casimir}}{\int }_{0}^{1}\left[\frac{4}{{\left(1-{u}_{s}\right)}^{5}}-\left(\frac{16\delta }{3}\right)\frac{5}{{\left(1-{u}_{s}\right)}^{6}}+\left(24{\delta }^{2}\right)\frac{6}{{\left(1-{u}_{s}\right)}^{7}}-\left(1-\frac{{\pi }^{2}}{210}\right)\left(\frac{640{\delta }^{3}}{7}\right)\frac{7}{{\left(1-{u}_{s}\right)}^{8}}+\left(1-\frac{163{\pi }^{2}}{7350}\right)\left(\frac{2800{\delta }^{4}}{9}\right)\frac{8}{{\left(1-{u}_{s}\right)}^{9}}\right]{\varphi }_{i}{\varphi }_{n}{\text{d}}x\right)= {b}_{n}{\omega }_{df}^{2}$$
(19)

where \(n\) = 1, 2…\(m\). The Eq. (19) is solved using MATLAB software, which provides natural frequencies at various deflected position of microbeam.

Numerical Results and Discussion

Convergence Study and Validation

The convergence study for solution of the ROM up to five modes is depicted in Fig. 2. The geometric and material properties of microbeam used for the convergence study is given in Table 1 [14]. The Fig. 2 depicts normalised deflection at the mid-point (\({u}_{mid}\)) of the fixed–fixed beam versus \({V}_{DC}\). It can be observed from Fig. 2a that the results obtained for one and higher modes in ROM entirely overlaps, which signifies that one-mode ROM offers fully converged results for the microbeam. Gutschmidt [55] also concluded that single-mode approximation with the Galerkin method for discretisation of the BVP problem is adequate for predicting the pull-in voltage of microbeam device. The BVP problem of microbeam devices represented by Eq. (9) is evaluated using bvp4c solver of the MATLAB software [56] The solver requires a precise guess value for determining solution of the BVP. The results found from the single-mode ROM are supplied as the guess value for solving the BVP [19]. The Fig. 2a depicts that result of the BVP closely agrees with that of ROM results.

Fig. 2
figure 2

Variation of normalised transverse deflection at mid-point \(\left({u}_{mid}\right)\) with change in DC voltage \(({V}_{DC})\) for different magnitudes of axial force due to residual stress \(N\) for mid-plane stretching parameter \((\alpha )\) a \(\alpha\) = 3.7133 and b \(\alpha\) = 24

Full size image
Table 1 Geometric and material properties of micro-beam
Full size table

In Fig. 2a, the results of the \({u}_{\text{mid}}\) versus \({V}_{\text{DC}}\) are displayed for the microbeam with different values of tensile and compressive axial load due to the residual stress. The results for the case when \(N\)= 0 are compared with the results of Jia et al. [14]. The results of the present work agrees well with the results of Jia et al. [14]. The results in Fig. 2a are plotted for properties of the microbeam shown in Table 1, which gives mid-plane stretching parameter \(\alpha =\) 3.713. Further, Similar analysis is performed using the same microbeam properties, however, with the \(\widehat{g}\) = 3 μm, which gives mid-plane stretching parameter \(\alpha =\) 24. The result of the analysis with large value of mid-plane stretching parameter (\(\alpha =\) 24) is shown in Fig. 2b. The investigation with \(\alpha =\) 24 yields noteworthy results that, it is essential to take at least three modes in ROM for obtaining completely converged solution. Specifically, the combination of high mid-plane stretching and compressive residual stresses in microbeam demands for higher mode in ROM to find converged solution for pull-in voltage. In contrast for microbeam with low mid-plane stretching parameter, it can be observed from Fig. 2a that single mode offers sufficiently converged results irrespective of magnitude and nature of axial load.

Figure 3 shows comparison of results obtained in present work for the pull-in voltage through ROM considering the effect of Casimir force with results of Mousavi et al. [57]. In Fig. 3, validation is shown for both scenarios of with and without consideration of fringing field effect. The various dimensionless parameters used for the validation are also stated in the figure. Further comparison are depicted in Fig. 4 for validating the free vibration analysis of microbeam presented in current work. Figure 4a shows the comparison of the ratio of non-linear frequency at deformed state to that at undeformed state of the microbeam. The comparison of the results of current work with reported numerical and experimental results is depicted in Fig. 4a. Moreover, the comparison of the dimensional frequency at deformed state of the beam with the results of Jia et al. [24] incorporating the effect of Casimir force is depicted in Fig. 4b. It can be observed from validation study depicted in Figs. 3 and 4 that the results of present work closely agrees with the published experimental and numerical results [13, 14, 24, 25, 57]. This indicates the robustness of the solution obtained in the present work for pull-in voltage and frequencies of microbeam using the ROM.

Fig. 3
figure 3

Validation of results of current work for the pull-in voltage considering the effect of Casimir force

Full size image
Fig. 4
figure 4

Validation of results of current work for the linear free vibration of microbeam depicted in a by comparing the ratio of non-linear frequency at deformed state to that at undeformed state of the microbeam with reported numerical and experimental results and b through comparison with published numerical results for the dimensional frequency at deformed state of the beam with and without consideration of the effect of Casimir force

Full size image

Static Pull-in Instability Analysis

The mid-point deflection (\({u}_{\text{mid}}\)) of clamped–clamped microbeam subjected to combined effect of the electrostatic and Casimir force is investigated till the beam collapses to the fixed electrode (pull-in point). The results of (\({u}_{\text{mid}}\)) versus non-dimensional voltage parameter (\(\beta {V}_{\text{DC}}^{2}\)) are depicted in Fig. 5 for sole effect of the electrostatic force and for combined effect of the electrostatic and Casimir force. These results are plotted for tensile as well as compressive values of axial load due to residual stress. Moghimi Zand and Ahmadian [42] obtained identical relationship between the \({u}_{\text{mid}}\) and \(\beta {V}_{\text{DC}}^{2}\) while investigating the static characteristics of electrostatically actuated microbeam incorporating the effect of Casimir force. The results of the current work for one of the case when \(N\) = 0 is compared with the finite element method-based results of Moghimi Zand and Ahmadian [42]. The results of current work show good agreement with the reported results.

Fig. 5
figure 5

mid-point deflection (\({u}_{mid}\)) versus non-dimensional voltage parameter (\(\beta {V}_{DC}^{2}\)) for sole effect of electrostatic force and for combined effect of electrostatic and Casimir force

Full size image

The majority of the published works on microbeam estimates the Casimir force with the assumption of perfectly conducting parallel plates, hence results into overestimation of the force. It is important to note that in the present work, the Casimir force is estimated precisely by incorporating the correction for the finite conductivity. The results of (\({u}_{\text{mid}}\)) versus non-dimensional voltage parameter (\(\beta {V}_{\text{DC}}^{2}\)) are plotted for both the cases in Fig. 5. It can be observed from Fig. 5 that consideration of the finite conductivity correction to the Casimir force results in significant increase in pull-in voltage and mid-point deflection at pull-in compared to that with the approximation of perfect conductor for calculating the Casimir. The increase in the pull-in voltage is due to decrease in interaction force with consideration of correction for the finite conductivity while estimating the Casimir force.

The voltage parameter at pull-in \({(\beta {V}_{\text{DC}}^{2})}_{\text{PI}}\) versus Casimir force parameter \({\gamma }_{\text{Casimir}}\) depicted in Fig. 6 describes effect of the Casimir force. The results with filled symbols include the effect of the finite conductivity correction and with unfilled symbols neglect the finite conductivity correction while estimating the Casimir force. Fig. 6 shows that with the increase in \({\gamma }_{\text{Casimir}}\) , the \({(\beta {V}_{\text{DC}}^{2})}_{PI}\) decreases. The decrease in pull-in voltage is due to increases in the interaction force (Casimir force) with the increase in \({\gamma }_{\text{Casimir}}\). The results of \({(\beta {V}_{\text{DC}}^{2})}_{\text{PI}}\) versus \({\gamma }_{\text{Casimir}}\) in Fig. 6 are plotted for three values of axial load based on tensile and compressive nature of the residual stress. It can be observed from Fig. 6 that presence of tensile residual stress in microbeam results in high magnitude of pull-in voltage compared to beam with compressive residual stress. The capability of structures (microbeams) to resist external forces increases owing to the presence of tensile axial load and hence the pull-in voltage increases.

Fig. 6
figure 6

The effect of Casimir force on voltage parameter at pull-in \({(\beta {V}_{DC}^{2})}_{PI}\) depicted with filled symbols includes the effect of finite conductivity correction and with unfilled symbols neglects the finite conductivity correction while estimating the Casimir force

Full size image

The fringing field parameter \(f=0.65\frac{\widehat{g}}{\widehat{b}}\), which signifies that the effect of the fringing field mainly depends on gap between the deformable microbeam and fixed electrode (g) as well as on the width of microbeam (b). Hence, when g <  < b that is \(\frac{g}{b}\sim 0\), the effect of fringing field can be ignored. However, when gap between the deformable electrode and fixed electrode is nearly equal to width of the microbeam, the effect of fringing field becomes significant owing to the value of \(\frac{g}{b}\sim 1\). The substantial effect of the fringing field leads to decrease in pull-in voltage. The voltage parameter at pull-in \({(\beta {V}_{\text{DC}}^{2})}_{\text{PI}}\) versus Casimir force parameter \({\gamma }_{\text{Casimir}}\) , as presented in Fig. 7, plotted for \(f=\) 0 (neglecting fringing field effect) and \(f=\) 0.65 (accounting for fringing field effect) clearly explains the influence of the fringing field for electrostatically actuated microbeams.

Fig. 7
figure 7

The voltage parameter at pull-in \({(\beta {V}_{DC}^{2})}_{PI}\) versus Casimir force parameter \({\gamma }_{Casimir}\) for \(f=\) 0 (neglecting fringing field effect) and \(f=\) 0.65 (accounting for fringing field effect)

Full size image

Free Vibration Characteristics

Free vibration characteristics of the microbeam at statically deflected state are studied to find the behaviour of first natural frequency with applied voltage. ROM (19) is solved using different modes for studying the free vibration characteristics. BVP solution for linear free vibrations is also obtained by solving Eq. (17), for confirming the results of ROM. The results of the ROM and BVP solution are shown in Fig. 8. It can be observed from the figure that at least three modes are required for fully converged solution for the microbeam with high mid-plane stretching parameter in a similar manner to that of static analysis. Figure 8 shows variation of non-dimensional first natural frequency at deflected state \(({\omega }_{df})\) normalised with non-dimensional first natural frequency at undeformed state of the beam \(({\omega }_{1})\) versus \({V}_{\text{DC}}\) for two different cases. The result of the first case with α = 3.7131 is also compared with the results of Jia et al. [24] and Tilmans and Legtenberg [25]. The comparison shows good agreement between the results of present work and the reported results.

Fig. 8
figure 8

Conversion study for free vibration analysis of electrostatically actuated microbeam

Full size image

The variation of non-dimensional \(({\omega }_{df})\) versus non-dimensional voltage parameter \(\beta {V}_{\text{DC}}^{2}\) for two different value of mid-plane stretching parameter \(\alpha =\) 6 and \(\alpha =\) 24 is depicted in Fig. 9a and b, respectively. It is interesting to note that, the two different values of \(\alpha\) offer significantly distinct free vibration characteristics. Further, the variation of \({\omega }_{df}\) versus \(\beta {V}_{\text{DC}}^{2}\) in the Fig. 9 is shown for two distinct conditions, first neglecting influence of the Casimir force (i.e. for \(\gamma _{{{\text{casimir}}}}\) = 0) shown with open symbols and second incorporating influence of the Casimir force (i.e. for \(\gamma _{{{\text{casimir}}}}\) = 6) shown with solid symbols. It is to be noted that the Casimir force takes into account the correction for finite conductivity. The results depicted in Fig. 9 shows that neglect of the Casimir force results into larger value of \({\omega }_{df}\) for the beam with tensile force in both cases (i.e. \(\alpha =\) 6 and \(\alpha =\) 24). Further, Fig. 9a for \(\alpha =\) 6 (smaller mid-plane stretching), described that, except at very high value of compressive force, the variation of \({\omega }_{df}\) is monotonously decreasing. However, in case of \(\alpha =\) 24 (larger mid-plane stretching), except at high value of tensile force, the variation of \({\omega }_{df}\) is non-monotonous. The tunability of \({\omega }_{df}\) in the presence of compressive force increases significantly specifically for the microbeam with large mid-plane stretching parameter. This is evident for the case \(\alpha =\) 24 with \(N\)=  − 20 and \(N\)=  − 35 as shown in Fig. 9b. The \({\omega }_{df}\), for \(N\)=  − 35 incorporating the Casimir force at \(\beta {V}_{\text{DC}}^{2}\) = 0 equals to 9.19 increases to 23.19 at \(\beta {V}_{\text{DC}}^{2}\) = 46. However, the \({\omega }_{df}\) for \(N\)=  − 35 ignoring the Casimir force at \(\beta {V}_{\text{DC}}^{2}\) = 0 equals to 7.65 increases to 25.29 at \(\beta {V}_{\text{DC}}^{2}\) = 62. This shows that the \({\omega }_{df}\) for the microbeam can be tuned for more than two times incorporating effect of the Casimir force. Furthermore, it is interesting to note that the tunability of \({\omega }_{df}\) is overestimated when the effect of the Casimir force is ignored for the microbeam in the presence of high compressive force (refer Fig. 9a, b with \(N\)=  − 35).

Fig. 9
figure 9

The variation of \({\omega }_{df}\) versus \(\beta {V}_{DC}^{2}\) for distinct condition, first neglecting influence of the Casimir force (\({\gamma }_{casimir}\) = 0) shown with open symbols and second incorporating influence of the Casimir force (\({\gamma }_{casimir}\) = 6) shown with solid symbols for two different magnitudes of mid-plane stretching parameter \((\alpha )\) a \(\alpha\) = 6 and b \(\alpha\) = 24

Full size image

The nature of \({\omega }_{df}\) incorporating the effect of Casimir force can be explained with one-mode ROM. The expression for one-mode ROM can be obtained from Eq. (19) as follows:

$${\omega }_{df}^{2}-{\omega }_{1}^{2}=3\alpha {\left({\int }_{0}^{1}{{\varphi }_{1}^{\prime 2}}{\text{d}}x\right)}^{2}{a}_{1s}^{2}-\left(2\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{1}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{3}}{\text{d}}x+f\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{1}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{2}}{\text{d}}x\right)-{\gamma }_{\text{Casimir}}\left[{\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{4}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{5}}dx-\left(\frac{16\delta }{3}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{5}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{6}}{\text{d}}x+\left(24{\delta }^{2}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{6}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{7}}{\text{d}}x-\left(1-\frac{{\pi }^{2}}{210}\right)\left(\frac{640{\delta }^{3}}{7}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{7}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{8}}{\text{d}}x+\left(1-\frac{163{\pi }^{2}}{7350}\right)\left(\frac{2800{\delta }^{4}}{9}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{8}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{9}}{\text{d}}x\right]$$
(20)

The term \({\omega }_{df}^{2}-{\omega }_{1}^{2}\) in one-mode ROM (20) on the left side describes the difference of square of non-dimensional first natural frequency at deflected state and square of first natural frequency at undeformed state of the beam \(({\omega }_{1})\). The first term on the right side of one-mode ROM (20), \(3\alpha {\left({\int }_{0}^{1}{{\varphi }_{1}^{^{\prime}}}^{2}{\text{d}}x\right)}^{2}{a}_{1s}^{2}= {W}_{m}\) , describes rise in natural frequency owing to stretching of the mid-plane of the microbeam. The other two terms on the right-hand side of ROM (20) with negative sign, that is \(2\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{1}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{3}}{\text{d}}x+f\beta {V}_{\text{DC}}^{2}{\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{1}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{2}}{\text{d}}x= {W}_{\beta }\) and \({\gamma }_{\text{Casimir}}\left[{\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{4}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{5}}{\text{d}}x-\left(\frac{16\delta }{3}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{5}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{6}}{\text{d}}x+\left(24{\delta }^{2}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{6}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{7}}{\text{d}}x-\left(1-\frac{{\pi }^{2}}{210}\right)\left(\frac{640{\delta }^{3}}{7}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{7}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{8}}{\text{d}}x+\left(1-\frac{163{\pi }^{2}}{7350}\right)\left(\frac{2800{\delta }^{4}}{9}\right){\int }_{0}^{1}{{\varphi }_{1}}^{2}\frac{8}{{\left(1-{a}_{1s}{\varphi }_{1}\right)}^{9}}{\text{d}}x\right]= {W}_{\text{Casimir}}\) indicate decrement in natural frequency owing to the electrostatic force and Casimir force, respectively.

In Fig. 9b, the plots for \(N\) =  − 35 at \(\beta {V}_{\text{DC}}^{2}\) = 10 and 50 show that, the \({\omega }_{df}\) for both the conditions, that is, neglecting influence of the Casimir force (open symbols) and incorporating influence of the Casimir force (filled symbols), is more than \({\omega }_{1}\). This is because of dominance of the first term \({W}_{m}\) (restoring force due to mid-plane stretching) over the second term \({W}_{\beta }\) (due to electrostatic force) and the third term \({W}_{\text{Casimir}}\)(due to Casimir force). Further, the \({\omega }_{df}\) at \(\beta {V}_{\text{DC}}^{2}\) = 10 incorporating the Casimir force is more than that neglecting the Casimir force. This is owing to difference in \({W}_{m}\) and \({W}_{\beta }\) + \({W}_{\text{Casimir}}\) is more than the difference in \({W}_{m}\) and \({W}_{\beta }\). This signifies that the Casimir force is dominating the electrostatic force at \(\beta {V}_{\text{DC}}^{2}\) = 10. However, the \({\omega }_{df}\) at \(\beta {V}_{\text{DC}}^{2}\) = 50 neglecting the Casimir force is more than that incorporating the Casimir force. This is owing to difference in \({W}_{m}\) and \({W}_{\beta }\) is more than the difference in \({W}_{m}\) and \({W}_{\beta }\) + \({W}_{\text{Casimir}}\). This signifies that the electrostatic force is dominating the Casimir force at \(\beta {V}_{\text{DC}}^{2}\) = 50.

In Fig. 9b, the plots for \(N\) = 35 at \(\beta {V}_{\text{DC}}^{2}\) = 10 and 50 show that \({\omega }_{df}\) for both the conditions, that is, neglecting influence of the Casimir force (open symbols) and incorporating influence of the Casimir force (filled symbols), is less than \({\omega }_{1}\). This is because of dominance of the second term \({W}_{\beta }\) (due to electrostatic force) and the third term \({W}_{Casimir}\)(due to Casimir force) over the first term \({W}_{m}\) (restoring force due to mid-plane stretching). The plots for \(N\) = 35 clearly indicate that difference in \({\omega }_{df}\) and \({\omega }_{1}\) for the plot incorporating the Casimir force is more than that neglecting the Casimir force at \(\beta {V}_{\text{DC}}^{2}\) = 10 and 50. This is because the difference in \({W}_{m}\) and \({W}_{\beta }\) + \({W}_{\text{Casimir}}\) is more than the difference in \({W}_{m}\) and \({W}_{\beta }\). This signifies that Casimir force is dominating the electrostatic force at \(\beta {V}_{\text{DC}}^{2}\) = 10 and 50 for \(N\) = 35.

Frequency Stability Characteristics

Linear free vibration characteristic of microbeam at high mid-plane stretching parameter shown in Fig. 9b provides a required property for MEMS resonators such as frequency stability. The variation in temperature results into change in magnitude of axial stresses in microbeam, which alters the natural frequency. The variation of \({\omega }_{df}\) versus axial force \(N\) for compressive and tensile nature is shown in Fig. 10. It is important to note that the deviation range of \({\omega }_{df}\) due to variation in \(N\) at a particular value of \(\beta {V}_{\text{DC}}^{2}\) decreases as the applied voltage increases (Fig. 10). This signifies that impact of axial load \(N\) on \({\omega }_{df}\) decreases in comparison with \({\omega }_{1}\) (also refer Fig. 9b). Further, the values of non-dimensional first natural frequency for different values of \(N\) and \(\beta {V}_{\text{DC}}^{2}\) are given in Table 2 with and without considering the effect of the Casimir force. The Table 2 depicts that the variation range of first natural frequency ignoring influence of the Casimir force at undeformed state of the beam 22.729 corresponding to \(\beta {V}_{\text{DC}}^{2}\) = 0 decreases to 4.964 at \(\beta {V}_{\text{DC}}^{2}\) = 72, when the axial force varies force \(N\) =  − 35 to 35. In a similar manner, the variation range of first natural frequency incorporating influence of the Casimir force at undeformed state of the beam 20.992 corresponding to \(\beta {V}_{\text{DC}}^{2}\) = 0 decreases to 5.897 at \(\beta {V}_{\text{DC}}^{2}\) = 72, when the axial force varies force \(N\) =  − 35 to 35. Similar observation can also be seen for \(\beta {V}_{\text{DC}}^{2}\) equals to 36 and 52. This shows that impact of axial load \(N\) on \({\omega }_{df}\) decreases significantly at high value of \(\beta {V}_{\text{DC}}^{2}\) for microbeam with high mid-plane stretching parameter.

Fig. 10
figure 10

variation of \({\omega }_{df}\) versus axial force \(N\) for different magnitudes of voltage parameter \(\beta {V}_{DC}^{2}\) when \(\alpha =24\) and\({\gamma }_{Casimir}=6\)

Full size image
Table 2 Non-dimensional first natural frequency for different values of axial force and dimensionless voltage parameter
Full size table

The significantly less variation range or reduction in sensitivity of \({\omega }_{df}\) with change in axial force (owing to change in temperature) is a required property for design of the microbeam resonators. This signifies that the microbeam dimensions in resonator design should be decided in such a manner that it provides frequency stability characteristics similar to that depicted in Fig. 9b. Furthermore, the resonant frequency of the resonator should be the first natural frequency at deflected state \(({\omega }_{df})\) instead of first natural frequency at undeformed state of the beam \({(\omega }_{1})\). Bhushan et al. [19] reported similar conclusion while investigating the linear free vibration characteristics of nano-wire. However, while studying the linear free vibration characteristics, Bhushan et al. [19] neglected the effect of Casimir force and also the characteristics were not investigated for different values of mid-plane stretching. Fig. 9 in the present work represents the considerable influence of the Casimir force (applying correction for finite conductivity) as well as the effect of different values of mid-plane stretching parameter on the free vibration characteristics. The important observation of the present work provides useful information for the design of microbeam resonators.

Conclusions

In the present work, the static and dynamic characteristics of clamped–clamped microbeam subjected to electrostatic force and Casimir force are studied. The expressions for the electrostatic force and Casimir force take into account the correction for fringing field and the finite conductivity, respectively. The Galerkin-based reduced order model technique is adopted for obtaining non-linear algebraic equation from governing differential equations. The influence of the Casimir force on pull-in voltage and linear free vibrations is studied for microbeam under axial force. The current work shows effect of the Casimir force with and without correction for the finite conductivity on the pull-in voltage. The existence of the Casimir force leads to decrease in pull-in voltage and the reduction in pull-in voltage is significant for the microbeam with high axial compressive load. Further, the reduction in the pull-in voltage decreases with the inclusion of corrections for the finite conductivity to the Casimir force.

The study of Linear free vibration characteristics in the present work shows that microbeam with higher value of mid-plane stretching parameter provides significant frequency tunability specifically for microbeam with high compressive force. Further, the consideration of the Casimir force results into reduction in tunability value of resonant frequency. The resonant frequency can be tuned by more than two times for microbeams designed with appropriate combination of the axial load, mid-plane stretching and Casimir force parameters.

In case of microbeams with high mid-plane stretching parameter, the change in resonant frequency is marginal with variation in axial load at high voltage parameter. The stability of resonant frequency at high voltage parameter in microbeam is significantly affected by the Casimir force. The stability of resonant frequency while there is variation in axial load can be effectively applied in design of microbeam resonator. The results of current work on the static and dynamic characteristics of microbeam incorporating the Casimir force offer important information for MEMS designer.