1 Introduction

There is an emerging use of MEMS devices deploying electrically-actuated vibrating beams for several applications including inertial sensors (Zhoum 2014; Mo et al. 2014; Ghommem et al. 2010, 2013; Ghommem and Abdelkefi 2017a, b), bio-mass sensors (Bouchaala 2018; Bouchaala et al. 2016; Younis and Alsaleem 2009; Akbari et al. 2017), gas sensors (Bouchaala et al. 2016a, b; Nayfeh et al. 2010), microswitches (Samaali and Najar 2017; Samaali et al. 2011; Ramini et al. 2013) and RF filters (Ouakad and Younis 2014; Siavash and Ayazi 2005; Ouakad 2018) thanks to the significant progress in micromachining technology. One important matter that needs to be considered and assessed in the design of these microsystems is their reliability when exposed to mechanical shock and impact during fabrication, shipping, or operation in harsh environments. Numerous studies have reported failures in the operation of electrically-actuated microbeams when subject to mechanical shock (Srikar and Senturia 2002; Sundaram et al. 2011; Ibrahim and Younis 2009; Wagner et al. 2001). These failures take place through stiction and electric short circuits resulting from the collapse of the vibrating beams and hitting the fixed or movable electrodes. This is associated with the pull-in instability due to the combined effect of the electrostatic forcing and the mechanical shock. The occurrence of pull-in is undesired in many applications because it limits the safe operation range. The presence of mechanical shock can cause an early dynamic pull-in instability due to unexpected dynamic loading and impact imposed on the microbeam structure. As such, the analysis of electrically-actuated beams subject to mechanical shock have gained significant interest in the last few years (Jrad et al. 2016; Younis et al. 2006, 2007; Ibrahim and Younis 2009; Srikar and Senturia 2002; Sundaram et al. 2011; Askari and Tahani 2014; Ouakad 2015; Li et al. 2016; Zhoum 2014) to provide guidance in the design of robust MEMS devices in terms of resistance to mechanical shock or to investigate the possible exploitation of nonlinear phenomena for switching applications.

Many research groups studied the behavior of microbeam systems subject to combination of electrostatic force and mechanical shocks. They showed that these microbeam systems can be used to trigger a signal once receiving a mechanical shock to perform a preventive action (Samaali et al. 2011, 2014; Ramini et al. 2013; Younis et al. 2007; Dai and Wang 2015). These microswitches (or triggers) have gained a major focus since they replaced some complicated sensors while offering smaller size, lower cost, and improved performance. The use of these switches include airbag deployment in automobiles that functions when a sudden change in acceleration occurs. The same concept is exploited to protect electronic devices at free falling by triggering a signal that does an immediate action (Younis et al. 2006). The sensors used for the aforementioned applications belong to the category of “low-g sensors” (g stands for the gravitational constant). Ramini et al. (2013) conducted a theoretical investigation of an electrostatically-actuated resonant switch using a nonlinear single-degree-of-freedom model for earthquake detection. The microsystem was adjusted to operate near the dynamic pull-in bandwidth and being sensitive to low shock levels. Their study was complemented by an experimental investigation to demonstrate the capability of the proposed resonant switch to capture small levels of acceleration in the order of 0.02g. Jrad et al. (2016) proposed a new device comprising an electrostatically actuated cantilever microbeam attached to a tip mass and mounted on top of a compliant board or a printed circuit board. They developed a mathematical model of the proposed design and showed that it provides a great tunability when varying the DC and AC voltages and capability to detect a wide range of acceleration (from 0.33 to 200g).

The other shock threshold sensors category is the “high-g sensors”, which are expected to be sensitive only to high shock levels (the operation range is in the order of thousands of g) and are commonly used in military applications (Brown et al. 2001; Parkos et al. 2013; Raghunathan et al. 2010). On the other hand, the functionality of many electrically-actuated microsensors can be negatively affected by the mechanical shock (Ouakad 2015; Srikar and Senturia 2002; Sundaram et al. 2011; Wagner et al. 2001). To ensure the reliability of such sensors, mechanical shock effect needs to be avoided by implementing different designs that show more robustness in order to prevent the dynamic pull-in. Wagner et al. (2001) performed finite element analysis to optimize the reliability of MEMS accelerometer made of polysilicon cantilever beams with regards to shock loads arising during drop tests. Their optimal design was verified experimentally. Askari and Tahani (2014) developed a reduced-order model to analyze the impact of the mechanical shock on the dynamic pull-in instability of electrically-actuated clamped-clamped beams. The shock load is represented by a half-sine waveform with durations varying between 0.1 and 1 ms to simulate hard floor drop tests. They observed that setting the shock duration close to the natural period of the microbeam system speeds up the occurrence of the dynamic pull-in.

Ilyas et al. (2016) have recently implemented and tested a new design of a resonator made of a dual electrically-coupled cantilever microbeams. The coupled microsystem showed dynamic features that can be promising in various MEMS applications. In this work, we consider similar design while incorporating the effect of the mechanical shock, varying the electric actuation, and selecting different geometry properties. A nonlinear reduced-order model is developed to simulate the static and dynamic responses of microsystems composed of electrically-actuated single and dual beams. We verify the reduced-order model by comparing the results to those obtained from previous theoretical and experimental studies. The objective of the present study is twofold: (1) to assess the robustness of the microstructure to withstand different levels of shock loads and (2) to investigate the possible use of novel designs for switching applications.

2 Microsystem description and modeling

2.1 Equations of motion and boundary conditions

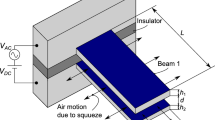
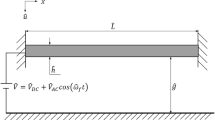
We consider a MEMS device consisting of two microbeams of different geometry and material properties placed at a gap distance d as shown in Fig. 1. Two fixed electrodes are arranged to be fully exposed to each microbeam (complete overlapping). The separation distance between the upper/lower microbeam and the top/bottom electrode is also d. This configuration enables to separately actuate each microbeam by deploying its respective fixed electrode (uncoupled actuation: single beam system) or applying a voltage among the two microbeams while deactivating the fixed electrodes (coupled actuation: dual beam system). We note that the microbeams are selected with different geometry properties to suit various applications. The microsystem is subject to mechanical shock transmitted via the fixed support of the microbeams. The shock force per unit length applied on each microbeam is represented by an impact acceleration pulse of a half-sine waveform (Srikar and Senturia 2002) which is expressed as:

$$\begin{aligned} F_{sh}=\rho b_i h_i a_0 {\mathrm {g}}(t), \end{aligned}$$
(1)

where \(\rho\) is the density, b denotes the width of the microbeam, h represents the thickness of the microbeam, and \(a_0\) is the amplitude of the shock (given in terms of units of the gravitational constant g). The subscript \(i=\{1,2\}\) refers to microbeam 1 and 2, respectively. The time-varying shock profile \({\mathrm {g}}(t)\) is given by:

$$\begin{aligned} {\mathrm {g}}(t)=\sin \left( \frac{\pi t}{T}\right) U(t)+\sin \left( \frac{\pi }{T}(t-T)\right) U(t-T), \end{aligned}$$
(2)

where T denotes the shock duration and U is the unit step function. It should be mentioned that half-sine shock profile is found to approximate well the shape of the actual shock pulse accelerations (Srikar and Senturia 2002).

Fig. 1
figure 1

Schematic of the electrically-actuated microbeams under mechanical shock

Full size image

Following Euler–Bernoulli beam assumptions, the equations of motion governing the transverse deflections \(w_i\) of the electrically-coupled microbeams subject to mechanical shock are given by Ilyas et al. (2016):

$$\rho b_1 h_1 \ddot{w}_1(x_1,t) + c_1 \dot{w}_1(x_1,t) + E I_{1} w_1^{''''}(x_1,t)= \frac{\epsilon b_1 (V_{DC}+v_{AC}(t))^2}{2(d-w_1(x_1,t)+w_2(x_1,t))^2} +\,\rho b_1 h_1 a_0 {\mathrm {g}}(t)$$
(3)
$$\rho b_2 h_2 \ddot{w}_2(x_2,t) + c_2 \dot{w}_2(x_2,t) + E I_{2} w_2^{''''}(x_2,t)= -\,\frac{\epsilon b_2 (V_{DC}+v_{AC}(t))^2}{2(d-w_1(x_2,t)+w_2(x_2,t))^2}U(x_2-\delta ) +\,\rho b_2 h_2 a_0 {\mathrm {g}}(t),$$
(4)

where E denotes the Young’s modulus, c is the damping coefficient, I is the beam’s cross sectional second moment of area, t is time, and x is the position along the microbeam length. The subscripts \(\{1,2\}\) refer to microbeam 1 and 2. Here, 1“\('\)” denotes the first derivative with respect to x and “\(^{.}\)” denotes the time derivative. The parameter \(\epsilon =8.85\times 10^{-12}\) C\(^2\) N\(^{-1}\) m\(^{-2}\) is the permittivity of the dielectric vacuum between the movable microbeam and the fixed electrode. \(V_{DC}\) and \(v_{AC}\) are the DC and AC voltages applied among the microbeams, respectively. The time-varying AC voltage is given by \(v_{AC}(t)=V_{AC} \cos (\Omega _e t )\) where \(V_{AC}\) is the voltage magnitude and \(\Omega _e\) is the excitation frequency. The unit step function U is introduced to account for the discontinuity of the electric field due to the difference in the microbeam lengths. The derivation steps of the equations of motion are shown in the “Appendix”.

The boundary conditions of these cantilever beams are given by:

At \(x_{1,2}=0\)

$$\begin{aligned} w_1=w_2=0 \quad \text{and} \quad w_1'=w_2'=0. \end{aligned}$$
(5)

At \(x_{1,2}=l_{1,2}\)

$$\begin{aligned} w_1''=w_2''=0 \quad \text{and} \quad w_1'''=w_2'''=0. \end{aligned}$$
(6)

Assuming the microbeams of rectangular cross section, the following parameters are used to nondimensionlize equations (1)–(6):

$$\begin{aligned} \hat{x_1}=\frac{x_1}{l_1}, \hat{w_1}=\frac{w_1}{d}, \hat{x_2}=\frac{x_2}{l_2}, \hat{w_2}=\frac{w_2}{d}, \hat{t}=\frac{t}{\tau }, \hat{T}=\frac{T}{\tau }, \tau = \sqrt{\frac{\rho b_1 h_1 l_1^4}{E I_1}} \\ \alpha =\frac{\epsilon b_1 l_1^4}{2 d^3 E I_1}, \beta = \left( \frac{l_2}{l_1}\right) ^4\left( \frac{h_1}{h_2}\right) ^2, \mu =\frac{c_1 l_1^4}{E I_1 \tau }, \eta =\frac{h_1}{h_2}\beta , \lambda =\frac{12 \rho a_0 l_1^4}{E d h_1^2}, \hat{\delta }=\frac{\delta }{l_2}. \end{aligned}$$
(7)

As for the dimensionless shock profile, it is obtained as:

$$\begin{aligned} {\hat{\mathrm {g}}}(\hat{t})=\sin \left( \frac{\pi \hat{t}}{\hat{T}}\right) U(\hat{t})+\sin \left( \frac{\pi }{\hat{T}}(\hat{t}-\hat{T})\right) U(\hat{t}-\hat{T}). \end{aligned}$$
(8)

Considering the defined dimensionless form, the governing equations can be rewritten:

$$\begin{aligned} \ddot{w}_1(x_1,t) + \mu \dot{w}_1(x_1,t) + w_1^{''''}(x_1,t) = \alpha \frac{ (V_{DC}+v_{AC}(t))^2}{(1-w_1(x_1,t)+w_2(x_1,t))^2}+\lambda {\mathrm {g}}(t) \end{aligned}$$
(9)
$$\begin{aligned} \beta \ddot{w}_2(x_2,t) + \eta \mu \dot{w}_2(x_2,t) + w_2^{''''}(x_2,t)&= -\,\beta \alpha \frac{ (V_{DC}+v_{AC}(t))^2}{(1-w_1(x_2,t)+w_2(x_2,t))^2}U(x_2-\delta ) \\&\quad+\,\beta \lambda {\mathrm {g}}(t). \end{aligned}$$
(10)

The parameter \(\lambda\) represents the dimensionless magnitude of the shock amplification. The parameter \(\beta\) indicates that the difference in the microbeams’ thickness introduces asymmetry in the electric actuation and their exposure to the mechanical shock. The thinner microbeam is expected to resist less to the electrostatic force and the mechanical shock.

Concerning the dimensionless boundary conditions, they are given as follows:

At \(x_{1,2}=0\)

$$\begin{aligned} w_1=w_2=0 \quad \text{and} \quad w_1'=w_2'=0. \end{aligned}$$
(11)

At \(x_{1,2}=1\)

$$\begin{aligned} w_1''=w_2''=0 \quad \text{and} \quad w_1'''=w_2'''=0. \end{aligned}$$
(12)

It should be noted that, in the rest of this study, the hats are dropped for the sake of simpler notation.

2.2 Nonlinear reduced-order modeling

To examine the dynamics of the electrically-coupled microbeams under mechanical shock, we derive the reduced-order model (ROM) using the Galerkin approach. This approach transforms the governing equations and boundary conditions given by Eqs. (9)–(12) into a set of ordinary differential equations which simulate the beam deflection. The deflections of the microbeams are expanded as follows Ilyas et al. (2016):

$$\begin{aligned} w_1(x_1,t)=\sum _{i=1}^{n} u_i^1(t)\phi _i(x_1) \end{aligned}$$
(13)
$$\begin{aligned} w_2(x_2,t)=\sum _{i=1}^{n} u_i^2(t)\phi _i(x_2), \end{aligned}$$
(14)

where the spatial function \(\phi _i(x)\) is the ith-linear normalized undamped mode shape of a cantilever beam and the time-varying functions \(u_i^1(t)\) and \(u_i^2(t)\) are the corresponding modal coordinates of the microbeams. Furthermore, n denotes the number of modes.

Next, we substitute Eqs. (13) and (14) into Eqs. (9) and (10), multiply the outcome by the mode shape \(\phi _j\), and integrate the resulting equations from 0 to 1 to obtain the ROM given by:

$$\begin{aligned}&\int _0^1 \phi _j(x_1)\left( \sum _{i=1}^{n} \ddot{u}_i^1(t)\phi _i(x_1) + \mu \sum _{i=1}^{n} \dot{u}_i^1(t)\phi _i(x_1) + \sum _{i=1}^{n} u_i^1(t)\phi _i''''(x_1)\right) dx_1 \\&\quad = \alpha (V_{DC}+v_{AC}(t))^2 \int _0^1 \frac{\phi _j(x_1)}{(1-\sum _{i=1}^{n} u_i^1(t)\phi _i(x_1)+\sum _{i=1}^{n} u_i^2(t)\phi _i(x_1))^2} dx_1 \\&\qquad +\,\lambda {\mathrm {g}}(t) \int _0^1 \phi _j(x_1) dx_1 \end{aligned}$$
(15)
$$\begin{aligned}&\int _0^1 \phi _j(x_2)\left( \beta \sum _{i=1}^{n} \ddot{u}_i^2(t)\phi _i(x_2) + \eta \mu \sum _{i=1}^{n} \dot{u}_i^2(t)\phi _i(x_2) + \sum _{i=1}^{n} u_i^2(t)\phi _i''''(x_2) \right) dx_2 \\&\quad = -\,\beta \alpha (V_{DC}+v_{AC}(t))^2 \int _0^1 \frac{\phi _j(x_2)}{(1-\sum _{i=1}^{n} u_i^1(t)\phi _i(x_2)+\sum _{i=1}^{n} u_i^2(t)\phi _i(x_2))^2}U(x_2-\delta ) dx_2 \\&\qquad +\,\beta \lambda {\mathrm {g}}(t) \int _0^1 \phi _j(x_2) dx_2 \end{aligned}$$
(16)

The obtained system of ordinary differential equations are numerically integrated using the Runge–Kutta method to simulate the dynamic response of the microsystem. We note that for the static analysis to determine the pull-in instability, the time-dependent terms arising from the inertia, the damping, the electric actuation (AC voltage), and the shock pulse acceleration in the ROM given by Eqs. (15) and (16) are dropped while substituting the time-varying modal coordinates \(u^{1}_i(t)\) and \(u^{2}_i(t)\) by unknown constants \(c^{1}_i\) and \(c^{2}_i\). We obtain instead the following system of nonlinear algebraic equations:

$$\begin{aligned} \int _0^1 \phi _j(x_1)\sum _{i=1}^{n} c_i^1\phi _i''''(x_1) dx_1 = \int _0^1 \frac{\alpha V_{DC}^2 \phi _j(x_1)}{(1-\sum _{i=1}^{n} c_i^1\phi _i(x_1)+\sum _{i=1}^{n} c_i^2\phi _i(x_1))^2} dx_1 \end{aligned}$$
(17)
$$\begin{aligned} \int _0^1 \phi _j(x_1)\sum _{i=1}^{n} c_i^2\phi _i''''(x_2) dx_2 = - \int _0^1 \frac{\beta \alpha V_{DC}^2 \phi _j(x_2)}{(1-\sum _{i=1}^{n} c_i^1\phi _i(x_2)+\sum _{i=1}^{n} c_i^2\phi _i(x_2))^2}U(x_2-\delta ) dx_2. \end{aligned}$$
(18)

The system of algebraic equations obtained for varying number of mode shapes are solved using the Newton–Raphson method.

In the present study, we consider microbeams of different geometric and material properties to investigate the static and dynamic behaviors under varying operating conditions (electric actuation and mechanical shock). The objective is to analyze numerically various microsystem designs so that the switches resulting from the pull-in instability can be activated at different shock levels based on the application of interest. The geometric and material properties of the microbeams under investigation are presented in Table 1. The case studies of electrically-actuated microbeams are summarized in Table 2. Some of these cases are selected to verify the predictive capability of the developed nonlinear reduced-order model.

Table 1 Geometric and material properties of the microbeams under investigation
Full size table
Table 2 Case studies under consideration
Full size table

3 Results and discussion

3.1 Static analysis: response to DC excitation

The microsystem is actuated by applying the electrostatic forcing and then we first analyze the static response and identify the critical DC voltage that leads to the pull-in instability onset; that is, the upper limit of the electrical potential at which the balance between the structural restoring force and electrostatic force is destroyed and the microbeam system collapses. We solve numerically the governing equations of the static problem given by Eqs. (17)–(18) while varying the value of the DC voltage. We first analyze the convergence behavior of the static response as the number of mode shapes is increased from 1 to 4. The results are shown in Fig. 2. Similar to the typical static response of electrostatic actuators, the curves show an increasing trend in the beam deflection as the DC voltage increases until reaching the pull-in instability. We note that only the stable branch of solutions is shown in Fig. 2. The use of three modes is observed to lead to an acceptable convergence of the static response of the coupled system. For the subsequent analysis, the same number of modes is considered.

Fig. 2
figure 2

Static response of the microsystem for varying number of modes (case study 1)

Full size image

To verify the numerical prediction of the developed reduced-order model given by Eqs. (17)–(18), we simulate the static response of the microbeam system under DC excitation using the finite element software ANSYS. A total of 1300 elements of rectangular type are used to build the regular mesh of finite element beam model. A convergence analysis is carried out to obtain invariant simulation results under mesh refinement. As shown in Fig. 3, the results obtained from the present model are in very good agreement with the numerical simulations based on the finite element model.

Fig. 3
figure 3

Static response to DC excitation for case study 1: comparison against numerical results obtained from finite element (FE) model in ANSYS

Full size image

Next, we use the reduced-order model to obtain the static response of the microsystem under DC actuation for all case studies reported in Table 2. The simulation results are displayed in Fig. 4. We note that the response corresponding to the coupled dual beam system is taken as the maximum relative distance between the two vibrating beams until the occurrence of pull-in (i.e., they touch each other). We observe that the dual beam resonator is more sensitive to DC actuation and the pull-in voltage is lower when compared to the single beam case (with fixed electrode). The relative distance between the two movable beams for the dual beam resonator is found the same as the displacement of the single beam system just before the occurrence of the pull-in. This distance is about 0.86 μm. The present results are in good agreement with those obtained numerically by Ilyas et al. (2016). The vertical dashed lines in Fig. 4a denote the experimental values of the pull-in voltage obtained by Ilyas et al. (2016) by varying the voltage against current using Keithley parameter analyzer. The numerical predictions of the static pull-in voltages are close to their experimental counterparts.

Fig. 4
figure 4

Static response to DC excitation for the different case studies (dual and single beam systems): comparison against previous works. The vertical dashed lines denote the experimental values of the pull-in voltage obtained by Ilyas et al. (2016)

Full size image

The static pull-in voltage of the single beam (uncoupled actuation) can be approximated by the following analytical expression Younis (2011):

$$\begin{aligned} V_{PI} = \sqrt{\frac{1.72}{\alpha }}. \end{aligned}$$
(19)

As for the dual beam case (coupled actuation) when considering identical beams (i.e., \(\beta =1\)), the static pull-in voltage can be approximated as Ilyas et al. (2016):

$$\begin{aligned} V_{PI} = \sqrt{\frac{0.868}{\alpha }}. \end{aligned}$$
(20)

Table 3 presents the values of the pull-in voltage obtained for all cases under investigation. The pull-in voltages obtained from the present study are compared to those reported in previous theoretical and experimental studies when considering similar beam configurations. A good agreement between the two sets of data is obtained. This demonstrates the capability of the current numerical model to predict accurately the static pull-in voltage. We note that the analytical formulas given by Eqs. (19) and (20) provide good approximation of the pull-in voltages for both single and dual beam cases. However, this is only valid when considering identical beams for the dual beam resonator and here comes the need for the numerical model to simulate any generic case. As expected, longer and/or thinner beam, being less stiff and having the tendency to bend more, leads to lower pull-in voltages. A reduction of 29–36% in the pull-in voltage is obtained when switching from the single beam case (uncoupled actuation) to dual beam case (coupled actuation). As such, dual beam microsystems seem to be more attractive for switching applications due to low power requirements to trigger the pull-in.

Table 3 Static pull-in voltages obtained for the cases under consideration (coupled and uncoupled actuation): comparison against previous theoretical and experimental studies
Full size table

We examine the effect of the DC voltage on the pull-in time (i.e., the switching time taken by the microbeam to touch the other fixed/movable electrode at the occurrence of the pull-in). We consider case studies 5 and 7 that correspond to single and dual beam configurations, respectively, to investigate the influence of the microsystem’s design on the switching time. The obtained results are shown in Fig. 5. Increasing the DC voltage beyond the pull-in voltage speeds up the snap-through of the beams. Clearly, the dual beam design enables a significant improvement in the switching time when compared to the single beam case. The dual beam system reduces the switching time by 35–45% for a DC voltage up to 1 V. These observations are consistent with the results reported by Ilyas et al. (2016) and show the potential use of dual beam resonators as MEMS switches which are expected to trigger quickly a signal in response to a mechanical shock to activate safety functionalities, such as airbag systems. This will be investigated in the next section when analyzing the dynamic response of the microsystem under mechanical shock.

Fig. 5
figure 5

Variations of the switching time with the DC voltage for the single and dual beam cases

Full size image

3.2 Natural frequencies under electrostatic forcing

Operating near resonance is recommended for several applications including resonant sensors and filters to amplify the microbeam motion and achieve higher output signal or to trigger the pull-in instability (e.g., microswitches). As such, we follow Younis (2011) to formulate the eigenvalue problem and evaluate the natural frequencies of the coupled system under electrostatic forcing. To do so, the deflections of the microbeams are split into a static component, resulting from the DC actuation, \(w^{s}_{1,2}(x_{1,2})\) and a dynamic component \(w^{d}_{1,2}(x_{1,2},t)\) :

$$\begin{aligned} w_{1,2}(x_{1,2},t) = w^{s}_{1,2}(x_{1,2}) + w^{d}_{1,2}(x_{1,2},t). \end{aligned}$$
(21)

Substituting Eq. (21) into Eqs. (9) and (10), dropping the damping and mechanical shock terms, linearizing the nonlinear electrostatic forcing around the static position, and the first-order terms in \(w^d_{1,2}\) results in the following linearized equation:

$$\begin{aligned} \ddot{w}^d_1(x_1,t) + (w_1^{d}(x_1,t))^{''''} = \frac{ 2\alpha V_{DC}^2}{(1-w_1^s(x_1)+w_2^s(x_1))^2}\left( {w}^d_1(x_1,t)-{w}^d_2(x_1,t)\right) \end{aligned}$$
(22)
$$\begin{aligned} \beta \ddot{w}^d_2(x_2,t) + (w_2^{d}(x_2,t))^{''''} =-\, \frac{ 2 \beta \alpha V_{DC}^2}{(1-w_1^s(x_2)+w_2^s(x_2))^2} \left( {w}^d_1(x_2,t)-{w}^d_2(x_2,t)\right) U(x_2-\delta ). \end{aligned}$$
(23)

To solve the eigenvalue problem associated with the above linearized equations and obtain the natural frequencies of the coupled system, we use again the Galerkin method and expand the dynamic components as:

$$\begin{aligned} w^d_{1,2}(x_{1,2},t)=\sum _{i=1}^{n} u_i^{1,2}(t)\phi _i(x_{1,2}). \end{aligned}$$
(24)

Substituting Eq. (24) into Eqs. (22)–(23), replacing the term \(\phi _i^{''''}\) by \(\omega _i^{2}\phi _i\), multiplying the outcome by \(\phi _j\), and integrating the resulting equations from 0 to 1, one obtains:

$$\begin{aligned} \ddot{u}_j^1 + \omega _j^2 u_j^1 = \sum _{i=1}^n\int _0^1\frac{ 2\alpha V_{DC}^2}{(1-w_1^s(x_1)+w_2^s(x_1))^2}\phi _i(x_{1})dx_1 \left( u_i^{1}(t)- u_i^{2}(t))\right) \end{aligned}$$
(25)
$$\begin{aligned} \beta \ddot{u}_j^2 + \omega _j^2 u_j^2 = - \sum _{i=1}^n\int _0^1\frac{ 2\beta \alpha V_{DC}^2}{(1-w_1^s(x_1)+w_2^s(x_1))^2}\phi _i(x_{2})U(x_2-\delta ) dx_2 \left( u_i^{1}(t)- u_i^{2}(t))\right) \end{aligned}$$
(26)

Equations (25) and (26) can be expressed in matrix form as follows:

$$\begin{aligned} \left( \begin{array}{c} \ddot{u}_1^1 \\ \ddot{u}_2^1 \\ \vdots \\ \ddot{u}_n^1 \\ \ddot{u}_1^2 \\ \ddot{u}_2^2 \\ \vdots \\ \ddot{u}_n^2 \\ \end{array} \right) +M \left( \begin{array}{c} u_1^1 \\ u_2^1 \\ \vdots \\ u_n^1 \\ u_1^2 \\ u_2^2 \\ \vdots \\ u_n^2 \\ \end{array} \right) =0, \end{aligned}$$
(27)

where M is \(2n\times 2n\) matrix and its constant coefficients are:

For \(i=1 \ldots n\) and \(j=1\ldots n\)

$$\begin{aligned} M_{i,j} = \delta _{i,j}\omega _i^2-\int _0^1\frac{ 2\alpha V_{DC}^2}{(1-w_1^s(x_1)+w_2^s(x_1))^2}\phi _j(x_{1})dx_1. \end{aligned}$$
(28)

For \(i=1 \ldots n\) and \(j=n+1\ldots 2n\)

$$\begin{aligned} M_{i,j} = \int _0^1\frac{ 2\alpha V_{DC}^2}{(1-w_1^s(x_1)+w_2^s(x_1))^2}\phi _j(x_{1})dx_1. \end{aligned}$$
(29)

For \(i=n+1 \ldots 2n\) and \(j=1\ldots n\)

$$\begin{aligned} M_{i,j} = \int _0^1\frac{ 2\alpha V_{DC}^2}{(1-w_1^s(x_2)+w_2^s(x_2))^2}\phi _j(x_{2})U(x_2-\delta ) dx_2. \end{aligned}$$
(30)

For \(i=n+1 \ldots 2n\) and \(j=n+1\ldots 2n\)

$$\begin{aligned} M_{i,j} = \delta _{i,j}\frac{1}{\beta }\omega _i^2-\int _0^1\frac{ 2\alpha V_{DC}^2}{(1-w_1^s(x_2)+w_2^s(x_2))^2}\phi _j(x_{2})U(x_2-\delta ) dx_2, \end{aligned}$$
(31)

where \(\delta _{i,j}=1\) if \(i=j\) otherwise 0. To compute the natural frequencies of the coupled system under DC excitation, we first determine the static deflections of the microbeams \(w_1^s\) and \(w_2^s\) by solving Eqs. (17) and (18), compute the coefficients \(M_{i,j}\) as given by Eqs. (28)–(31), and then calculate the eigenvalues of the matrix M. The natural frequencies are obtained by taking the square roots of these eigenvalues.

Fig. 6
figure 6

Variations of the natural frequency with the DC voltage for the different case studies (dual and single beam systems): comparison against previous works. Note that the results obtained by Ilyas et al. (2016) are originally reported in nondimensional form

Full size image

Figure 6 displays the variations of the natural frequencies with the DC voltage for the different cases under investigation. Some results as shown in Fig. 6a are compared to those obtained numerically by Ilyas et al. (2016). Again, a good agreement between the two sets of data is observed. Shorter and/or thicker beams result in higher natural frequencies as can be seen in Figure 6a, b while lower values are obtained when considering electrically-coupled beams in comparison to the single beam actuated by a fixed electrode. This indicates the possible use of dual beam resonators when lower operating frequency range is required.

3.3 Frequency-response: effect of electric actuation and microsystem design

We activate the AC excitation and examine the dynamic response of the microsystems for the cases under study. Figure 7 displays the frequency-responses of the microsystems for different AC and DC voltages near the primary resonance as identified in the previous section. The results are obtained by solving numerically the nonlinear reduced-order model given by Eqs. (15) and (16) for different excitation frequencies. We note that three modes are observed to be enough to obtain the convergence of the dynamic solutions. Figure 7a, b show that the increase in the DC voltage shifts the frequency-response curves to the left due to the softening effect of the electrostatic forcing. Clearly, varying the AC voltage affects significantly the frequency-response curves. As expected, increasing the AC voltage results in the amplification of the microbeam motion. For low AC and DC voltages, the system behavior is nearly-linear. For higher AC excitation, we observe the occurrence of dynamic pull-in bandwidth in the frequency-response curves; that is, only unstable solutions of the microbeam dynamics. For instance, the analysis of case study 1 (single beam) shows that the fold bifurcation (turning point) takes place at 2.38 MHz when setting the DC and AC voltages equal to 95 and 7 V, respectively (see Fig. 7a). Operating with an excitation frequency between 2.38 and 2.5 MHz results in the dynamic pull-in.

The frequency-response curves exhibit expanded pull-in bandwidth when operating the dual-beam systems near the primary resonance. Figure 7b shows that the pull-in bandwidth reaches 250 kHz when actuating the microbeams at a DC voltage of 60 V and an AC voltage of 5 V. As shown in Fig. 7c, d, the pull-in bandwidth increases from 5 to 17 kHz when shifting from the single beam to the dual beam system (case studies 5 and 7) while applying a DC voltage of 0.2 V and an AC voltage of 0.15 V for both cases. This presents an undesirable effect for the reliability of some MEMS devices, such as resonant sensors. However, this phenomenon can be deployed to design MEMS switches that are triggered by the presence of gas (Bouchaala et al. 2016a, b), biological mass (Younis and Alsaleem 2009; Bouchaala et al. 2016c), or actuated at or beyond a specific level of mechanical shock or acceleration (Younis et al. 2007; Askari and Tahani 2014; Ramini et al. 2013; Jrad et al. 2016).

The frequency-response curves of the dual beam system made of microbeams with different thickness shown in Fig. 8 exhibit two peaks near the natural frequencies related to each microbeam at low AC and DC voltages. Inspecting these frequency-response curves, we observe that higher amplitudes are obtained near the resonance frequency of the thinner microbeam being more flexible and then it is influenced more by the electrostatic coupling in comparison to the thicker microbeam. Higher electric actuation results in the expansion of the dynamic pull-in bandwidth in the frequency-response curves. This indicates that dual beam systems composed of nonidentical beams seem to enable more tunability for switching applications but less control on the safe operation frequency range for other microsystems which are expected to operate away from the pull-in instability.

Fig. 7
figure 7

Frequency-response curves of the microsystem for varying DC and AC voltages for the different case studies (dual and single beam systems). Results are shown near the primary resonance

Full size image
Fig. 8
figure 8

Frequency-response curves of the microsystem for varying AC voltages for case study 8 (dual beam system). Results are shown near the primary resonance

Full size image

3.4 Dynamic response under mechanical shock

Several research studies have reported failures in the operation of electrically-actuated MEMS resonators when undergoing mechanical shocks. As such, we simulate the response of different designs of resonators (as outlined in Tables 1, 2) under the combination of electrostatic forcing and mechanical shock. The objective of this study is twofold: to assess the robustness of the microstructure to withstand different levels of shock loads and to investigate the possible use of novel designs for switching applications.

The plotted curves in Fig. 9 show a linear decreasing trend in the dynamic pull-in voltage \(V_{DPI}\) for the single beam system (case study 1) when increasing the shock amplitude. The values of \(V_{DPI}\) are estimated by gradually increasing the applied DC voltage until the onset of the pull-in. The results are obtained for \(V_{AC}=0\) V and \(V_{AC}=6\) V and the shock duration T is set equal to 1 ms. High shock loading levels in the order of hundreds of thousands of g’s are required to reduce the pull-in voltage. The slopes are found equal to − 1.137 10\(^{-4}\) and − 0.8625 10\(^{-4}\) for \(V_{AC}=0\) V and \(V_{AC}=6\) V, respectively. We show also the time histories obtained for different shock amplitudes while keeping the DC and AC voltages equal to 50 and 6 V, respectively. Before reaching the critical value of the shock amplitude (\(a_0^c=419{,}000\)\(g\)), we observe an amplification of the time response once the microsystem undergoes the mechanical shock and then followed by the recovery to the original oscillations. For shock amplitudes higher than \(a_0^c\), the microbeam collapses and hits the fixed electrode.

Fig. 9
figure 9

Variations of the dynamic pull-in voltage with the amplitude of the mechanical shock (case study 1)

Full size image

To enhance the sensitivity of the microsystem to the mechanical shock, we consider thinner microbeams and analyze the dynamic response for case studies 5–8. It should be mentioned that case study 5 is similar to the one reported in Younis et al. (2006). The results are obtained when applying only DC voltage and mechanical shock with different pulse times (\(T=1\) ms and \(T=0.1\) ms), as presented in Fig. 10. The present numerical predictions of the dynamic pull-in voltages compare well with those obtained by Younis et al. (2006) using the Finite Element software ANSYS. Of interest, we observe that the dual beam is much less sensitive to the mechanical shock when compared to the single-beam case. Similar observations can be made even when considering microbeams of different thickness (case study 8). The simulation results indicate that dual-beam systems are more robust in terms of resistance to mechanical shock and provide a reliable design for the operation of MEMS devices in harsh environments characterized by high shock levels.

Fig. 10
figure 10

Variations of the dynamic pull-in voltage with the amplitude of the mechanical shock: a quasi-static (\(T=1\) ms) and b dynamic loading case (\(T=0.1\) ms). Results are compared to those reported by Younis et al. (2006).

Full size image

To examine the effect of the pulse time (shock duration) T on the dynamic response of the microbeam, we plot in Fig. 11 the time histories of the tip deflection under combined impact of DC actuation and shock load for \(T=1\) ms and \(T=0.1\) ms (case study 5). This figure shows the stable and unstable responses. The dynamic pull-in for this single microbeam without accounting for the effect of the mechanical shock is found equal to 0.6 V which is exactly equal to the value reported by Younis et al. (2006). The time histories depicted in Fig. 11 show that the dynamic pull-in voltage reduces to 0.37 and 0.29 V when setting the pulse time T equal to 1 and 0.1 ms, respectively. As observed by Younis et al. (2006) and Askari and Tahani (2014), setting the pulse time close to the natural period of the microbeam (\(T=0.1\) ms for the present microsystem) results in dynamic response while higher pulse time (\(T=1\) ms) leads to quasi-steady response. These results are consistent with those reported in Younis et al. (2006).

Fig. 11
figure 11

Stable and unstable time history of the tip: a quasi-static (\(T=1\) ms) and b dynamic loading case (\(T=0.1\) ms)

Full size image

Figures 9 and 10 show the possible tunability of switches (deploying single beams) with operation ranges varying from few hundreds to hundreds of thousands of g’s depending on the application of interest. For instance, microbeam systems sensitive to low g accelerations can be used for the detection of earthquake signals and the activation of other functionalities, such as alarm or a network of sensors for seismic activity recording (Ramini et al. 2013). Switches operating at high shock levels are commonly used for military purposes (Parkos et al. 2013; Raghunathan et al. 2010).

Next, we incorporate the AC actuation and depict in Fig. 12 the variations of the dynamic pull-in voltage with the shock amplitude for varying AC voltages (case study 8). The excitation frequency is set equal to 49.5 kHz and the shock pulse time is considered equal to 0.1 ms for all simulated cases. The dual beam system is found insensitive to mechanical shock up to a critical value. Beyond this value, the dynamic pull-in voltage decreases slightly when increasing the shock amplitude \(a_0\). For instance, a reduction of 25% in the dynamic pull-in voltage is observed when the microsystem is excited with an AC voltage of 0.05 V and undergoes a shock of magnitude 1000g. As such, the dual beam composed of electrically-actuated microbeams with different geometrical properties can be used for switching applications.

Fig. 12
figure 12

Variations of the dynamic pull-in voltage with the amplitude of the mechanical shock for different AC voltages (case study 8)

Full size image

We inspect the dynamic behavior of the microsystem under the mechanical shock when applying an AC voltage with different excitation frequencies. Following Jrad et al. (2016), we define the lowest detectable acceleration (LDA) as the minimum shock amplitude required to trigger the pull-in of the microbeam. Figure 13 displays the variations of LDA with the DC voltage for different AC voltages while varying the excitation frequency. The obtained results correspond to case study 5 (single beam case). As shown in Fig. 13a, setting the excitation frequency equal to 49.5 kHz (away from the natural frequency) results in linear decreasing trend in the variations of LDA with the DC voltage \(V_{DC}\). On the other hand, Fig. 13b shows that operating near the primary resonance (the excitation frequency is set equal to 79.2 kHz) affects significantly the slopes of the LDA-\(V_{DC}\) curves and leads to a sudden drop in the LDA values within a range of the DC voltage. This drop shows the weakness of the microstructure being excited within the dynamic pull-in bandwidth for this range of DC voltage. For instance, when applying an AC voltage of 0.05 V, we observe the occurrence of a local minimum of the LDA for \(V_{DC}=0.35\) V. Setting the AC voltage equal to 0.1 V results in zero LDA for \(V_{DC}\) ranging from 0.3 to 0.5 V. We notice that the range of the shock amplitudes is not affected by the excitation frequency. For the two cases, it varies between 0 and 800g. Figure 13b illustrates the impact of the AC harmonic load when operating near the primary resonance which gives rise to a nonlinear shock response of the microsystem when subject to varying electric loading. For instance, the finger-shaped curve observed in Fig. 13b when setting \(V_{AC}\) equal to 0.05 V is indicates the abrupt change in the sensitivity of the microsystem to the mechanical shock when reaching a critical value of the applied DC voltage. This behavior was not observed when setting the excitation frequency away from the natural frequency as shown in Fig. 13b. These observations are consistent with the numerical results reported by Jrad et al. (2016). However, it should be noted from Fig. 13 that the deployment of the electrically-actuated microsystem for switching applications would require less power when activating the AC excitation and selecting the frequency near the primary resonance.

Fig. 13
figure 13

Variations of the lowest detectable acceleration (LDA) with the DC voltage for different AC voltages (case study 5): a away from the primary resonance, b near the primary resonance

Full size image

4 Conclusions

In this work, we simulated the dynamic response of single and dual electrically-actuated microbeams under mechanical shock. The actuation of the single-beam system is made via a fixed electrode (uncoupled actuation) while the dual-beam system, composed of two movable microbeams, is actuated by applying a voltage among them (coupled actuation). The static analysis of the microsystems showed a significant reduction in the static pull-in voltage and switching time when considering the dual-beam system in comparison with the single-beam case. Furthermore, lower natural frequencies were obtained for electrically-coupled beams instead of single beams actuated by a fixed electrode. This indicates the possible use of dual beam resonators when lower operating frequency range is required. The simulation results compared well with those obtained from previously-published theoretical and experimental studies. The analysis of the frequency-response curves showed expanded dynamic pull-in bandwidth when operating the dual-beam system near the primary resonance. The present study revealed that the dual-beam systems withstand more to mechanical shock and then they are more suitable for the operation and reliability of MEMS devices in harsh environments characterized by high mechanical shock levels. On the other hand, single-beam systems were found more attractive for use as microswitches which are intended to trigger a signal once receiving a mechanical shock or abrupt change in acceleration to activate safety functionalities, such as airbag systems.