Introduction

In recent decades, orthotropic plates and shells are widely used as essential structural components in marine engineering applications which expose them to work under fluidic medium of varying temperature with unwanted intensity of high vibrations. Thus, the knowledge of the vibration characteristics of such structures under fluidic medium with temperature variation is important for their reliability evaluation. It becomes more interesting to understand the effect of temperature under fluidic medium when these structures contain various flaws in the form of holes and cracks. As per the literature, it is seen that researchers have analysed the vibration problems of intact plates in the presence of thermal and fluidic environments individually. However, the studies on analysis of cracked orthotropic plates including the effect of thermal environment and fluidic medium are insignificant. From the literature, it is observed that the presence of irregularities in a plate makes its dynamic behaviour drastically different from that of an intact one. To find the analytical solution of cracked thin plates, researchers have used the famous line spring model (LSM). This model was originally proposed by Rice and Levy [1], their concept of the LSM was based on Kirchhoff’s thin plate theory and they represented the partial crack as continuous line spring with stretching, bending and twisting compliances. Further, to simplify the line spring model, King [2] used linear algebraic equations rather than coupled integral equations and proposed a simplified line spring model. Zeng and Dai [3] employed simplified LSM in their modelling of a cracked rectangular plate to determine the stress intensity factors at the crack tips. Solecki [4] employed the Navier’s solution and finite Fourier transformation technique to construct an analytical model for vibration problem of cracked isotropic plates. Liew et al. [5] investigated the upper bound solutions for fundamental frequencies of plate using the Ritz method including the domain decomposition technique. Malhotra et al. [6] performed the frequency analysis of orthotropic plate using the Rayleigh–Ritz method. They studied the variation of fundamental frequency as affected by the fibre orientation for various boundary conditions and for various orthotropic materials. Using the LSM, the first approximate mathematical model for vibration problem of cracked isotropic plates is developed by Israr et al. [7], they used the relationship between bending and tensile stresses at far sides of the plate and at the crack area to introduce the effect of crack on governing equation of an isotropic plate. They studied the variation of crack length on the frequency response of plate for different boundary conditions. By extending the work of Israr et al. [7], a new model for a partially cracked rectangular isotropic plate with variably oriented crack is developed by Ismail and Cartmell [8]. It is concluded from their work that the natural frequencies of cracked plate decreases when crack length and its orientation increases. Taking the consideration of thermal effects, Joshi et al. [9, 10] have presented an analytical solution for buckling and vibration analysis of isotropic [9] and orthotropic [10] plate with surface and internal cracks. Soni et al. [11, 12] studied the effect of fluidic medium on vibration characteristics of cracked isotropic [11] and magneto-electro-elastic (MEE) [12] plates by incorporating the inertial effect of fluids forces on previously developed models. Recently Lai and Zhang [13] studied the buckling and vibration response of orthotropic and isotropic cracked plate under thermal effects using discrete singular convolution (DSC) method. They also proposed the relation for critical buckling temperature of cracked orthotropic and isotropic plate.

The fluid–structure interaction (FSI) problems have been receiving wide attention in current decades. In the literature, it is observed that the phenomenon of fluid–structure interaction significantly influences the vibration response of a structure. The first classical approach for FSI problem was given by Lamb [14]. He employed a hypothetical approach for computing the vibration response of a circular plate coupled with fluid. The created technique was based on the evaluation of rise in kinetic energy of surrounding fluid. Muthuveerappan et al. [15] employed the experimental technique to determine the fundamental frequencies of the intact cantilever plate submerged in water. They studied the effect of plate aspect ratio and thickness ratio on the fundamental frequencies of submerged plate. To determine the fundamental frequency of plate in water from the frequency of the plate in vacuum, Kwak [16] proposed an approximation for virtual added mass incremental factor using Rayleigh’s method. In the same way, to determine the fundamental frequencies of annular plate in contact with fluid, Amabili [17] used the virtual added mass approach of Kwak [16]. To study the vibration response of intact plates vibrating under fluid, Haddara and Cao [18] have given an approximate relation for the virtual added mass. Their results are investigated experimentally as well as analytically for different submergence levels and boundary conditions. Based on Sander’s shell theory and FEM technique, Kerboua et al. [19] developed an analytical model for free vibration problems of isotropic plate coupled with water. It has given the ease to study the plate–fluid interaction problems. Using the Mindlin’s plate hypothesis for deriving the model, Hosseini-Hashemi et al. [20] developed an analytical model for thick horizontal plates which are submerged in fluid partially and totally. Vibration problems of plates considering the effect of both crack and fluidic medium are found in few investigations (Refs. [21,22,23]). The effect of through-crack on the vibration characteristics of a circular plate coupled with fluid is shown in the analysis of perforated plates using the finite element method (FEM) by Liu et al. [21]. Similarly, the effect of fluidic medium and side crack on fundamental frequency of cracked circular and rectangular plates vibrating under water is given by Si et al. [22, 23] using the computational approach of FEM.

Similarly, for the effect of thermal environment on vibration problems of plates, it is seen that the presence of thermal stress decreases the stiffness of plate which results in the reduction of natural frequency. Yang and Shen [24] have given the results for natural frequency of FGM plates subjected to thermal environment. In their work, the effect of rise in temperature, boundary condition and volume fraction index are considered as input parameters and they presented the effect of these above parameters on frequency of plate using higher order theories. Jeyaraj et al. [25] worked on the computational approach-based ANSYS and SYSNOISE to find the acoustic response and vibration attributes of an isotropic plate under certain temperature variation. Continuing their work they further analysed both responses for a composite plate including internal material damping employing laminated plate theory [26]. The analysis of vibration problems being functionally graded plates exposed to thermal heating is stated by Li et al. [27]. Three-dimensional theory of elasticity to model the FGM plates in closeness of thermal environment is employed by them. Using the finite element method, Viola et al. [28] also practised on vibration analysis of cracked composite plate. Detailed study on vibration and buckling analyses of a functionally graded plate consists of internal discontinuities in form of cracks using FEM and first-order shear deformation (FSDT) theory is carried out by Natarajan et al. [29]. They showed the outcome of increment in crack length and temperature gradient on the natural frequency of the cracked plate.

The dynamics of vibrating structures submerged in fluid is a fundamental research problem and caters the wide engineering applications from aerodynamics to biosensors. Micro-machined plates are used as biosensors, micro-resonators, actuators, atomic force microscopes (AFMs), micro-switches, etc. It has been vastly accepted that the mechanical behaviours of small-scale structures are size dependent. It is found in the literature that as the structure dimensions diminish to the order of micro-/nano-scale, the effect of structure size plays a significant role in the correct examination of such structures. According to previous laboratory research, the classical continuum theory is unable to take account of size effects in the analysis of the behaviour of micro/nano structures. Thus, over the years, non-classical theories such as nonlocal theory, strain gradient theory and modified couple stress theory have been used by researchers to study the microstructures. Since these micro-sized structures often undergo dynamic loading and are regularly subjected to external environment such as thermal environment, knowledge of vibration characteristics become important to improve upon reliability of their design. In the recent literature on investigation of microstructures, it has been established that it alters the vibration response of plate structures [30,31,32,33,34,35,36]. Out of different theories which dominate the size effect on the analysis of the gradient elastic plates, among them, Mindlin and Eshel [37] proposed the strain gradient theory (SGT) to analyse the effect of microstructure. They (Ref. [37]) proposed a single length-scale parameter to catch size effect of microstructure in their expanded theory. Papargyri-Beskou and Beskos [38] established a sixth-order governing equilibrium equation of force and moment on gradient elastic plate. Extending their work, Papargyri-Beskou et al. [39] practised the principle of virtual work to draft the same problem for distinct possible boundary aspects. The bending analysis of a thin isotropic rectangular plate based on the second gradient theory is performed by Mousavi and Paavola [40]. In their developed model, they considered parameter of two length scale to capture size consequence and to make the model more competent. Akgöz and Civalek [41, 42] presented the analytical solutions for bending, vibration and buckling problems of micro-sized plates based on modified couple stress theory [41] and modified strain gradient theory [42]. In their work, they performed a detailed parametric study to demonstrate the effect of length-scale parameter, length-to-thickness ratio on buckling load, deflection, and fundamental frequencies of micro-plates. A new mathematical model for micro-plates based on the modified couple stress theory (MCST) is established by Tsiatas [43] and Tsiatas and Yiotis [44]. In their work, they examined distinct isotropic [43] and orthotropic [44] plates of numerous shapes and dimensions to figure out the effectiveness of their suggested model (MCST) in contrast with the Kirchhoff’s plate model. Extending their work, Tsiatas and Yiotis [45] also studied the static, dynamic and buckling analyses of orthotropic micro-plates based on MCST and nonlocal elasticity theory. Adopting the MCST of Tsiatas [43], Yin et al. [46] likewise worked on the vibration problems of micro-plates. In their research, they used a material-scale parameter to demonstrate the size outcome of microstructure. After evaluating the results for two distinct theories (MCST and CPT), they achieved that the results attained from MCST are always greater as compared to CPT. Ebrahimi and Barati [47] worked on buckling analysis of functionally graded (FG) nanobeams using nonlocal third-order shear deformation beam theory. They studied the thermal effects on buckling response of the nanobeams subjected to various types of thermal loading. Based on Euler–Bernoulli’s beam theory, Akgöz and Civalek [48] and Demir and Civalek [49] have investigated the buckling and bending behaviour of micro-beams for various types of boundary conditions. They (Ref. [48]) studied the effects of additional material length-scale parameters, material property variation function and slenderness ratio on the buckling response of FGM micro-beams and also compared the results for different non-classical theories. Extending the work of Ref. [48], Mercan and Civalek [50, 51] and Mercan et al. [52] have also analysed the buckling response of boron nitride nanotubes (BNNTs) [50], silicon carbide nanotubes (SiCNTs) [51] and nanowires (SiCNWs) [52] considering the size effect of microstructure using different size-dependent continuum theories. They determined their critical buckling load as affected by different geometrical quantities/parameters. Numanoglu et al. [53] investigated the longitudinal free vibration behaviours of nanorods based on Eringen’s nonlocal theory. Effects of nonlocal parameter, attachments, boundary conditions, and length on the natural frequencies of nanorods are studied in detail in their study. In the new governing equation of motion based on Hamilton’s principle, Gao and Zhang [54] used a material length scale steady to catch the size significance of microstructure. They also figure out that their outcomes for natural frequency achieved by the non-classical plate model (MCST) are greater than that of the classical plate model for thin plates. Most recently, Gupta et al. [55] produced an analytical model for vibration problem of a partially cracked thin isotropic and functionally graded cracked micro-plate using the LSM. They used classical plate theory (CPT) in conjunction with MCST and accomplished that their outcomes for fundamental frequencies are consistently higher for modified couple stress theory. Moreover, they demonstrated the significance of fibre orientation on vibration attributes of cracked orthotropic micro-plate [56].

It is well known from the literature (Ref. [57]) that the vibration response of a submerged micro-plate is extensively influenced by fluid loading due to its inertial effects. Also, in the case of a generally orthotropic micro-plate, the stiffness can be significantly altered by varying fibre orientation which is again reflected in the vibration response. Further, the vibration response is also dependent on the external environment such as thermal environment. Thus, the aim of the present work is to combine the research in these related areas and present comprehensive effect of microstructures, thermal environment, partial crack, surrounding fluid, fibre orientation on the vibration and deflection of the generally orthotropic micro-plate.

The present non-classical model extends the work of Refs. [56, 58] and narrows down the gap in the recently developing area of vibration analysis of cracked plates by addressing the following:

  1. 1.

    Vibration analysis of partially cracked orthotropic submerged plate based on the Kirchhoff’s thin plate theory as affected by the fibre orientation and thermal environment is proposed.

  2. 2.

    The proposed model is further extended for the case of orthotropic micro-plate with fibre orientation based on the non-classical modified couple stress theory.

  3. 3.

    The classical relation for central deflection of cracked orthotropic submerged plate which shows an important phenomenon of a shift in primary resonance due to fibre orientation, crack, temperature, and material length-scale parameter.

  4. 4.

    The effect of fibre orientation, level of submergence, temperature rise, material length-scale parameter, crack length and crack location on fundamental frequency as well as central deflection of cracked orthotropic submerged plate is studied in the presence of thermal environment for simply supported boundary condition.

  5. 5.

    The present work presents a comparison of classical plate theory and modified couple stress theory for vibration of partially cracked orthotropic micro-plate in the presence of thermal and fluidic environments.

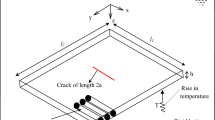
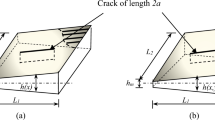
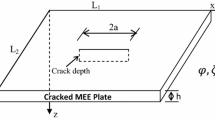
In the present study, an analytical model has been presented for cracked orthotropic rectangular plate in light of a non-classical approach. The moment equilibrium equations for cracked orthotropic plate are derived by taking the consideration of thermal environment and microstructure. The effect of crack is introduced in the form of additional membrane force and bending moment using the line spring model. The effect of fluidic medium is integrated in the model in the form of added virtual mass with the help of Bernoulli’s equation and velocity potential function. Figure 1 shows the plate configuration in which the in-plane dimensions of the plate are taken as L1 and L2 in x- and y-directions separately. The plate thickness is denoted by h. Figure 2a is the length of crack at plate centre and the depth of the crack is less than the thickness. d is the offset distance between plate centre and the crack centre along the x-axis. To study the effect of various parameters such as rise in temperature, crack length, crack location, fibre orientation, material length-scale parameter and level of submergence on fundamental frequency, SSSS (all sides simply supported) boundary condition is considered in the present work. The central deflection of the cracked plate has also been studied as affected by length of crack, location of crack, fibre orientation, temperature variation and material length-scale parameter. A comparison of these results with the classical plate theory has also been established.

Fig. 1
figure 1

a Partially cracked orthotropic submerged plate showing fibre orientation. b Plate configuration showing offset distance ‘d’

Full size image
Fig. 2
figure 2

Submerged orthotropic plate element showing moments and internal forces on the mid-plane

Full size image

Governing Equation

The governing differential equation of an intact and cracked orthotropic plate under influence of thermal environment and based on the approach of classical thin plate theory has been thoroughly treated in Refs. [9, 10], respectively. In this section, a new governing equation for a partially cracked orthotropic submerged plate with various fibre orientations subjected to thermal environment is derived based on a non-classical plate theory of elasticity. The assumptions considered in the derivation are customarily according to classical plate theory for thin plates (Refs. [56, 59]).

The constitutive relations for a thin orthotropic lamina considering the temperature gradient and fibre orientation have been obtained in Ref. [60]; based on the assumptions taken in the present study, such relations for an orthotropic lamina with uniform temperature rise can be given as

$$\left. \begin{aligned} {\rm E}_{x} &= \frac{{\sigma_{x} }}{{E_{x} }} - \vartheta_{y} \frac{{\sigma_{y} }}{{E_{y} }} - m_{x} \tau_{xy } + \alpha_{x} \Delta T \hfill \\ {\rm E}_{y} &= - \vartheta_{x} \frac{{\sigma_{x} }}{{E_{x} }} + \frac{{\sigma_{y} }}{{E_{y} }} - m_{y} \tau_{xy} + \alpha_{y} \Delta T \hfill \\ \gamma_{xy} &= - m_{x} \sigma_{x} - m_{y} \sigma_{y} + \frac{{\tau_{xy} }}{{G_{xy} }} + \alpha_{xy} \Delta T \hfill \\ \end{aligned} \right\},$$
(1)

where \({\mathcal{E}}_{x} , {\mathcal{E}}_{y} \;{\text{and}}\;\gamma_{xy}\) are the mid-plane strains. \(E_{x} , E_{y} , G_{xy} , \vartheta_{x}\) and \(\vartheta_{y}\) are the elastic constants. \(\alpha_{x}\), \(\alpha_{y}\) and \(\alpha_{xy}\) are the thermal expansion coefficients. The expressions for coefficient of thermal expansion can be stated as

$$\left. \begin{aligned} \alpha_{x} &= \alpha_{1} { \cos }^{2} \beta + \alpha_{2} { \sin }^{2} \beta \hfill \\ \alpha_{y} &= \alpha_{1} { \sin }^{2} \beta + \alpha_{2} { \cos }^{2} \beta \hfill \\ \alpha_{xy} &= \left( {2{ \sin }\beta { \cos }\beta } \right)\left( {\alpha_{1} - \alpha_{2} } \right) \hfill \\ \end{aligned} \right\},$$
(2)

where \(m_{x}\) and \(m_{y}\) are the coefficients of mutual influence which depends on the material elastic constants and fibre orientation angle and represents the coupling of the shear and normal stresses. The relations for the coefficients of mutual influence can be stated as [60]

$$\left. \begin{aligned} m_{x} = { \sin }2\beta \left\{ {\frac{{\vartheta_{x} }}{{E_{x} }} + \frac{1}{{E_{y} }} - \frac{1}{{2G_{xy} }} - \left( {{ \cos }^{2} \beta } \right)\left( {\frac{1}{{E_{x} }} + \frac{{2\vartheta_{x} }}{{E_{x} }} + \frac{1}{{E_{y} }} - \frac{1}{{G_{xy} }}} \right)} \right\} \hfill \\ m_{y} = { \sin }2\beta \left\{ {\frac{{\vartheta_{x} }}{{E_{x} }} + \frac{1}{{E_{y} }} - \frac{1}{{2G_{xy} }} - \left( {{ \sin }^{2} \beta } \right)\left( {\frac{1}{{E_{x} }} + \frac{{2\vartheta_{x} }}{{E_{x} }} + \frac{1}{{E_{y} }} - \frac{1}{{G_{xy} }}} \right)} \right\} \hfill \\ \end{aligned} \right\},$$
(3)

where \(m_{x}\) and \(m_{y}\) will vanish for fibre orientations \(\beta\) = 0° and \(\beta\) = 90° and, therefore, for the fibre orientations \(\beta\) = 0° and 90°, there is no extensional shear coupling [60]. For other than these fibre orientations, there exist six elasticity moduli: \(E_{1} , E_{2} , E_{x} , E_{y} , G_{12} , G_{xy}\). The representation of these elasticity constants can be found in Refs. [56, 60].

The mid-surface strains in the terms of transverse deflection can be stated as

$$\left. \begin{aligned} {\rm E}_{x} &= - z\frac{{\partial^{2} w}}{{\partial x^{2} }} \hfill \\ {\rm E}_{y} &= - z\frac{{\partial^{2} w}}{{\partial y^{2} }} \hfill \\ \tau_{xy} &= G_{xy} \left( { - 2z} \right)\frac{{\partial^{2} w}}{\partial x\partial y} \hfill \\ \end{aligned} \right\}.$$
(4)

Using Eqs. (1)–(4), the relationship for the normal stresses (\(\sigma_{x} , \sigma_{y}\)) and the in-plane shear stress (\(\tau_{xy}\)) can be written as

$$\sigma_{x} = \frac{\begin{aligned} \frac{{E_{x} }}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\left( { - z\frac{{\partial^{2} w}}{{\partial x^{2} }} - \vartheta_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( { - 2z\frac{{\partial^{2} w}}{\partial x\partial y} - m_{y} E_{y} z\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) \hfill \\ - \frac{{E_{x} }}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} \Delta T + m_{y} E_{y} \alpha_{y} \Delta T)}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)\Delta T} \right) \hfill \\ \end{aligned} }{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}},$$
(5)
$$\sigma_{y} = \frac{\begin{aligned} \frac{{E_{y} }}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\left( { - z\frac{{\partial^{2} w}}{{\partial y^{2} }} - \vartheta_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( { - 2z\frac{{\partial^{2} w}}{\partial x\partial y} - m_{x} E_{x} z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \hfill \\ - \frac{{E_{y} }}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} \Delta T + m_{x} E_{x} \alpha_{x} \Delta T )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)\Delta T} \right) \hfill \\ \end{aligned} }{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}},$$
(6)
$$\tau_{xy} = \frac{\begin{aligned} - 2z\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{1}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\left[ {m_{x} E_{x} \left( { - z\frac{{\partial^{2} w}}{{\partial x^{2} }} - \vartheta_{y} z\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + m_{y} E_{y} \left( { - z\frac{{\partial^{2} w}}{{\partial y^{2} }} - \vartheta_{x} z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right] \hfill \\ - \frac{{\Delta T\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}} \hfill \\ \end{aligned} }{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}}.$$
(7)

On integrating Eqs. (5)–(7) over the plate thickness, we obtain the expressions for bending and twisting moments as

$$\left. \begin{aligned} M_{x} = \mathop \int \limits_{ - h/2}^{h/2} \sigma_{x} z{\text{d}}z \hfill \\ M_{y} = \mathop \int \limits_{ - h/2}^{h/2} \sigma_{y} z{\text{d}}z \hfill \\ M_{xy} = \mathop \int \limits_{ - h/2}^{h/2} \tau_{xy} z{\text{d}}z \hfill \\ \end{aligned} \right\},$$
(8)
$$M_{x} = \frac{{ - D_{x} \left\{ {\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \vartheta_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2\frac{{\partial^{2} w}}{\partial x\partial y} + m_{y} E_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}} - M_{Tx} ,$$
(9)
$$M_{y} = \frac{{ - D_{y} \left\{ {\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \vartheta_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2\frac{{\partial^{2} w}}{\partial y\partial x} + m_{x} E_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} \,+\, m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} - M_{Ty} ,$$
(10)
$$M_{xy} = \frac{{ - \left\{ {\frac{{h^{3} }}{6}\frac{{\partial^{2} w}}{\partial x\partial y} + \left( {D_{x} m_{x} + \vartheta_{x} D_{y} m_{y} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {D_{y} m_{y} + \vartheta_{y} D_{x} m_{x} } \right)\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) \,+\, m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} - M_{Txy} ,$$
(11)

where

$$M_{Tx} = \mathop \int \limits_{ - h/2}^{h/2} \frac{{\frac{{E_{x} }}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} \Delta T + m_{y} E_{y} \alpha_{y} \Delta T)}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)\Delta T} \right)}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}}z{\text{d}}z,$$
$$M_{Ty} = \mathop \int \limits_{ - h/2}^{h/2} \frac{{\frac{{E_{y} }}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} \Delta T + m_{x} E_{x} \alpha_{x} \Delta T )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)\Delta T} \right)}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}}z{\text{d}}z,$$
$$M_{Txy} = \int\limits_{ - h/2}^{h/2} {\frac{{\frac{{\Delta T\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}}} z{\text{d}}z.$$

In the above equations, \(M_{x}\), \(M_{y}\) and \(M_{xy}\) are the internal bending and twisting moments and \(M_{Tx} ,\)\(M_{Ty}\) and \(M_{Txy}\) are bending and twisting moments due to thermal environment.

Consider a cracked orthotropic submerged plate element as shown in Fig. 2. The internal forces and bending moments acting on the mid-plane of the plate are considered as per Kirchhoff’s plate theory [59]. My*, Mx* and \(M_{xy*}\) = \(M_{yx*}\) denote the bending moments and twisting moments. \(M_{{-}\!\!\!{y}}\) represents the additional bending moment due to the crack (Refs. [61, 62]).

On resolving the internal forces along the z-direction and taking moment about x- and y-directions, we get the following equilibrium equations:

$$\sum F_{z} = 0,$$
$$\frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} = \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} + \Delta P - p_{z} ,$$
(12)

where Qx and Qy are the transverse forces. \(\rho h\frac{{\partial^{2} w}}{{\partial t^{2} }}\) denotes the inertia force of vibrating plate. \(\Delta P\) is the fluid dynamic pressure difference between the upper (\(P_{u}\)) and lower (\(P_{l}\)) surfaces of the plate. \(\rho\) and \(h\) are the density and thickness of plate and \(p_{z}\) represents the transverse load per unit area.

Taking moment equilibrium about the x- and y-axis one obtains

$$\frac{{\partial M_{y*} }}{\partial y} + \frac{{\partial M_{xy*} }}{\partial x} + \frac{{\partial M_{{-}\!\!\!{y}} }}{\partial y} = Q_{y} ,$$
(13)
$$\frac{{\partial M_{x*} }}{\partial x} + \frac{{\partial M_{yx*} }}{\partial y} = Q_{x} ,$$
(14)

where

$$M_{x*} = M_{x} + M_{x}^{l} ,$$
(15)
$$M_{y*} = M_{y} + M_{y}^{l} ,$$
(16)
$$M_{xy*} = M_{xy} + M_{xy}^{l} ,$$
(17)

where \(M_{y}^{l}\), \(M_{x}^{l}\) and \(M_{xy}^{l} = M_{yx}^{l}\) are the extra bending and twisting moments per unit length due to the effect of microstructure. The detailed description for Eqs. (15)–(17), addition of \(M_{x}^{l}\), \(M_{y}^{l}\) and \(M_{xy}^{l}\) to internal bending and twisting moments (\(M_{x}\), \(M_{y}\) and \(M_{xy}\)) based on the modified couple stress theory can be referred in Appendix A.

From Eqs. (12), (13) and (14), one obtains

$$\frac{{\partial^{2} M_{x*} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy*} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y*} }}{{\partial y^{2} }} + \frac{{\partial^{2} M_{{-}\!\!\!{y}}}}{{\partial y^{2} }} = \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} + \Delta P - p_{z } .$$
(18)

On expressing the bending and twisting moments of Eq. (18) in terms of transverse deflection from Eq. (8) to Eq. (11), the governing equation of cracked orthotropic micro-plate can be given as

$$\begin{aligned} &\frac{{(D_{x} + D^{lx} ) \left\{ {\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \vartheta_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + m_{y} E_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}} \hfill \\ &+ \frac{{2\left\{ {\frac{{h^{3} }}{6}\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \left( {(D_{x} + D^{lx} )m_{x} + \vartheta_{x} \left( {D_{y} + D^{ly} } \right)m_{y} } \right)\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + \left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} \left( {D_{x} + D^{lx} } \right)m_{x} } \right)\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}}} \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ &+ \frac{{(D_{y} + D^{ly} )\left\{ {\left( {\frac{{\partial^{4} w}}{{\partial y^{4} }} + \vartheta_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}} + m_{x} E_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &= - \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Delta P + p_{z} - \frac{{\partial^{2} M_{Tx} }}{{\partial x^{2} }} - \frac{{\partial^{2} M_{Ty} }}{{\partial y^{2} }} - \frac{{\partial^{2} M_{Txy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{{-}\!\!\!{y}} }}{{\partial y^{2} }}, \hfill \\ \end{aligned}$$
(19)

where \(D_{x} = \frac{{E_{x} h^{3} }}{{12\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\) and \(D_{y} = \frac{{E_{y} h^{3} }}{{12\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}\) are the flexural rigidities of an orthotropic plate in x- and y-directions and \(D_{x} = \frac{{E_{x} l^{2} h}}{{2\left( {1 + \vartheta_{x} } \right)}}\) and \(D_{y} = \frac{{E_{y} l^{2} h}}{{2\left( {1 + \vartheta_{y} } \right)}}\) are the additional flexural/bending rigidities due to the microstructure.

The in-plane forces considered for the cracked orthotropic plate are shown in Fig. 3. It is well known from the literature (Refs. [9, 10]) that the in-plane forces produced by the transverse deflection introduces non-linearity to the governing equation but does not affect the plate’s stiffness. In this present work, the in-plane forces induced only due to temperature variation are considered. Taking the summation of the in-plane forces along z-axis, we get

$$\sum F_{z} \left( {x,y} \right) = - N_{Tx} \frac{{\partial^{2} w}}{{\partial x^{2} }} - N_{Ty} \frac{{\partial^{2} w}}{{\partial y^{2} }} - 2N_{Txy} \frac{{\partial^{2} w}}{\partial x\partial y} - N_{{-}\!\!\!{y}} \frac{{\partial^{2} w}}{{\partial y^{2} }},$$
(20)
Fig. 3
figure 3

In-plane forces for the cracked orthotropic plate as affected by thermal environment

Full size image

where \(N_{Tx}\), \(N_{Ty}\) and \(N_{Txy}\) represent the in-plane compressive forces due to the uniform temperature rise of plate and \(N_{y}\) is the additional in-plane force due to the line crack [7, 9, 10]. On adding the in-plane forces given by Eq. (20) in Eq. (19), the governing equation of the cracked orthotropic plate considering the effect of couple stress, fibre orientation and thermal environment can be stated as

$$\begin{aligned} &\frac{{(D_{x} + D^{lx} ) \left\{ {\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \vartheta_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + m_{y} E_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}} \hfill \\ &+ \frac{{2\left\{ {\begin{array}{*{20}c} {\frac{{h^{3} }}{6}\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \left( {D^{lx} )m_{x} + \vartheta_{x} \left( {D_{y} + D^{ly} } \right)m_{y} } \right)\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + } \\ {\left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} \left( {D_{x} + D^{lx} } \right)m_{x} } \right)\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}}} \\ \end{array} } \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ &+ \frac{{(D_{y} + D^{ly} )\left\{ {\left( {\frac{{\partial^{4} w}}{{\partial y^{4} }} + \vartheta_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}} + m_{x} E_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &= - \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Delta P - \frac{{\partial^{2} M_{Tx} }}{{\partial x^{2} }} - \frac{{\partial^{2} M_{Ty} }}{{\partial y^{2} }} + \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }} - N_{Tx} \frac{{\partial^{2} w}}{{\partial x^{2} }} - N_{Ty} \frac{{\partial^{2} w}}{{\partial y^{2} }} - 2N_{Txy} \frac{{\partial^{2} w}}{\partial x\partial y} - N_{{-}\!\!\!{y}} \frac{{\partial^{2} w}}{{\partial y^{2} }} + P_{z} . \hfill \\ \end{aligned}$$
(21)

Crack Terms

The crack terms (\(m_{y}\) and \(r_{y}\)) are obtained using Line Spring Model (LSM) given by Rice and Levy [1]. The LSM can convert a complicated surface crack problem into a plane strain one and bring the net ligament stresses to the neutral plane of the plate and replacing the constraints due to the net ligament by some bending and membrane stresses on the crack location. Israr et al. [7] proposed the relationship of tensile and bending stresses at far edges of plate and at crack tips for an isotropic plate. These relations were further modified and applied to a specially orthotropic plate by Joshi et al. [63]. Extending their work Joshi et al. [9] have also derived the above relationship in the presence of temperature variation for the isotropic plates. Similar relations for the partially cracked orthotropic plate incorporating the moments and in-plane forces due to temperature variation and internal microstructure can be presented as

$$M_{{-}\!\!\!{y}} = - \frac{2a}{{3\left( {\frac{{\alpha_{bt} }}{6} + \alpha_{bb} } \right)\left( {3 + \vartheta_{x} } \right)\left( {1 - \vartheta_{x} } \right)h + 2a}}M_{y*} ,$$
(22)
$$N_{{-}\!\!\!{y}} = \frac{2a}{{\left( {6\alpha_{bt} + \alpha_{tt} } \right)\left( {1 - \vartheta_{x}^{2} } \right)h + 2a}}N_{Ty} ,$$
(23)

where the terms \(\alpha_{tt} , \alpha_{bb} , \alpha_{bt} = \alpha_{tb}\) are crack compliance coefficients for stretching, bending and tensile bending, respectively. These coefficients depend on crack depth (d) to thickness (h) ratio and vanish when d = 0. The required expressions for compliance coefficients as a function of crack depth to plate thickness ratio \(\left( {\delta = d/h} \right)\) can be written as (Ref. [7])

$$\begin{aligned} \alpha_{tt} = 1.154 \delta^{2} [1.98 \, - \, 0.54\delta + \, 18.65\delta ^{2} - \, 33.70 \delta^{3} + \, 99.26\delta^{4} - \, 211.90\delta^{5} + \, 436.84\delta^{6} \hfill \\ -\, 460.48 \delta^{7} + \, 289.98\delta^{8} ], \hfill \\ \end{aligned}$$
$$\begin{aligned} \alpha_{bb} = 1.154\delta^{2} [1.98 \, - \, 3.28 \delta + \, 14.43\delta^{2} - \, 31.26\delta^{3} + \, 63.56\delta^{4} - \, 103.36\delta^{5} + \, 147.52\delta^{6} \hfill \\ - \, 127.69\delta^{7} + \, 61.50\delta^{8} ], \hfill \\ \end{aligned}$$
$$\begin{aligned} \alpha_{bt} = \alpha_{tb} = 1.154 \delta^{2} [1.98 \, - \, 1.91\delta + \, 16.01 \delta^{2} - \, 34.84\delta^{3} + \, 83.93\delta^{4} - \, 153.65 \delta^{5} + \, 256.72 \delta^{6} \hfill \\ - \, 244.67 \delta^{7} + \, 133.55\delta^{8} ]. \hfill \\ \end{aligned}$$

It is to be noted that these above expressions for compliance coefficients are valid only for \(\left( {\delta = d/h} \right)\) values within the range 0.1–0.7 and in the present model, \(\delta\) is taken 0.6.

To introduce the effect of location of crack on frequency under thermal environment, the values of the above crack compliance coefficients is to be multiplied by a factor \(\left( {2/\sqrt {\pi \left( {\frac{\gamma }{\varGamma }} \right)} } \right){ \exp }\left( { - \left( {\frac{{\left( {\varGamma - \xi_{c} } \right)^{2} L_{1}^{2} }}{{\left( {\frac{\gamma }{\varGamma }} \right)}}} \right)} \right)\), here \(\xi_{c} \, = \,d/L_{ 1}\) is the eccentricity ratio, d is the offset distance between centre of the crack and centre of the plate, \(\gamma \, = \,(h/L_{ 1} )\) and \(\varGamma \, = \,(a/L_{1} )\). Similar treatment to introduce the effect of crack location can be found in the work of Bose et al. [64] and Gupta et al. [56, 61, 62]. Hence, the effect of change in crack location is taken into consideration by suitably modifying the crack compliance coefficients.

Fluid Terms

Consider a cracked plate element submerged in fluid horizontally as shown in Fig. 1. On expressing the velocity potential function in terms of Laplace equation and then using Bernoulli’s equation for the fluid dynamic pressure at fluid–plate interaction, we obtained the following expressions for the dynamic pressure acting on the plate’s upper surface (\(P_{u}\)) and lower surface (\(P_{l}\)) as [19] (the detailed derivation for fluid modelling can be referred from Appendix B)

$$P_{u} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + Ce^{{2\mu h_{1} }} }}{{1 - Ce^{{2\mu h_{1} }} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }},$$
(24)
$$P_{l} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + e^{{ - 2\mu h_{2} }} }}{{1 - e^{{ - 2\mu h_{2} }} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }},$$
(25)

where \(C = \frac{{g_{a} \mu - \omega^{2} }}{{g_{a} \mu - \omega^{2} }}\) in which \(\omega\) denotes the frequency of wave motion at free surface of fluid and \(g_{a}\) is the acceleration due to gravity. \(\rho_{f}\) is fluid density per unit volume and \(\mu\) is plane wavenumber which is taken as independent of boundary condition and it can be determined as \(\mu = \pi \sqrt {\frac{1}{{L_{1}^{2} }} + \frac{1}{{L_{2}^{2} }}}\) (Refs. [19, 11]). The approximate value of \(C\, = \, - 1\) is taken in the present work to avoid the influence of non-linearity on plate–fluid interface (Ref. [19]). Here \(\frac{{\partial^{2} w}}{{\partial t^{2} }}\) represents the inertia of the surrounding fluid that forces it to oscillate when the plate vibrates. \(h_{1}\) is the height of fluid above the surface of plate whereas \(h_{2}\) is the level of fluid below the plate surface.

For fully submerged plate, the net fluid dynamic pressure can be determined using Eqs. (18) and (19). The resulting fluid dynamic pressure difference \(\left( {\Delta P} \right)\) for the submerged plate can given as

$$\Delta P = P_{u} - P_{l} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + Ce^{{2\mu h_{1} }} }}{{1 - Ce^{{2\mu h_{1} }} }} - \frac{{1 + e^{{ - 2\mu h_{2} }} }}{{1 - e^{{ - 2\mu h_{2} }} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }},$$
(26)
$$\Delta P = m_{add} \frac{{\partial^{2} w}}{{\partial t^{2} }},$$
(27)

where \(m_{add} = - \frac{{\rho_{f} }}{\mu }\left[ {\frac{{1 + Ce^{{2\mu h_{1} }} }}{{1 - Ce^{{2\mu h_{1} }} }} - \frac{{1 + e^{{ - 2\mu h_{2} }} }}{{1 - e^{{ - 2\mu h_{2} }} }}} \right]\) is the additional virtual mass of submerged plate due to surrounding fluid. Thus, for the case of submerged plate vibrations, the mass of the plate is increased due to a layer of fluid vibrating with the plate. This added mass is referred to as virtual added mass.

On employing Eqs. (22), (23) and (27) in Eq. (21) and stating the moments \(M_{y}^{*}\) in terms of transverse deflection (\(w\)), from Eqs. (16) and (10) we get the required governing equation of motion of cracked orthotropic plate as

$$\begin{aligned} &\frac{{(D_{x} + D^{lx} ) \left\{ {\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \vartheta_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + m_{y} E_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}} \hfill \\ &+ \frac{{2\left\{ {\begin{array}{*{20}c} {\frac{{h^{3} }}{6}\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \left( {(D_{x} + D^{lx} )m_{x} + \vartheta_{x} \left( {D_{y} + D^{ly} } \right)m_{y} } \right)\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + } \\ {\left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} \left( {D_{x} + D^{lx} } \right)m_{x} } \right)\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}}} \\ \end{array} } \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ &+ \frac{{(D_{y} + D^{ly} )\left\{ {\left( {\frac{{\partial^{4} w}}{{\partial y^{4} }} + \vartheta_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}} + m_{x} E_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} = - \left( {\rho h + m_{\text{add}} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} \hfill \\ &+ \frac{2a}{{3\left( {\frac{{\alpha_{bt} }}{6} + \alpha_{bb} } \right)\left( {3 + \vartheta_{x} } \right)\left( {1 - \vartheta_{x} } \right)h + 2a}}\left[ {\frac{{(D_{y} + D^{ly} )\left\{ {\left( {\frac{{\partial^{4} w}}{{\partial y^{4} }} + \vartheta_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}} + m_{x} E_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} + \frac{{\partial^{4} M_{Ty} }}{{\partial y^{4} }}} \right] \hfill \\ &- N_{Tx} \frac{{\partial^{2} w}}{{\partial x^{2} }} - 2N_{Txy} \frac{{\partial^{2} w}}{\partial x\partial y} - \frac{{\left( {1 + 2a} \right)}}{{\left( {6\alpha_{bt} + \alpha_{tt} } \right)\left( {1 - \nu_{x}^{2} } \right)h + 2a}}N_{Ty} \frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\partial^{2} M_{Tx} }}{{\partial x^{2} }} - \frac{{\partial^{2} M_{Ty} }}{{\partial y^{2} }} + P_{z} . \hfill \\ \end{aligned}$$
(28)

Solution of Governing Equation

The presence of external environment-like rise in temperature has been included in the governing differential equation of cracked orthotropic submerged plate in the form of thermal bending moments and in-plane compressive forces. The present work restricts itself to the solution of governing equation for the case of uniformly heated plates (\(M_{Tx} = M_{Ty} = 0\)). Since, in majority of engineering applications thin plate structures having good thermal conductivity are used, there is a little temperature gradient along the plate thickness and they can be considered as uniformly heated plates. The constant in-plane compressive forces arising due to temperature are only considered for making the model geometrically linear. The modal functions which depend on the boundary conditions can be selected for the general solution of governing equation as

$$w\left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } A_{mn} X_{m } Y_{n} \emptyset_{mn} \left( t \right) .$$
(29)

In the above equation, \(X_{m } \;{\text{and}}\;Y_{n}\) are the modal functions which depend on the boundary conditions of the cracked plate under the fluidic medium, \(A_{mn}\) is arbitrary amplitude and \(\emptyset_{mn} \left( t \right)\) is the time-dependent modal term. The modal functions \(X_{m } \;{\text{and}}\;Y_{n}\) for the two boundary conditions considered in this work can be found from the literature (Refs. [7, 9, 10]). For uniform heating of the plate, the constant in-plane forces in terms of lateral deflection can be stated as [10]

$$\left. {\begin{array}{*{20}l} {N_{Tx} = \frac{{E_{x} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} + m_{y} E_{y} \alpha_{y} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)} \right)} \\ {N_{Ty} = \frac{{E_{y} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} + m_{x} E_{x} \alpha_{x} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} + \alpha_{x} \vartheta_{y} } \right)} \right)} \\ {N_{Txy} = \frac{{\Delta Th(\alpha_{xy} + m_{x} E_{x} (\alpha_{x} + \alpha_{y} + \vartheta_{y} ) + m_{y} E_{y} (\alpha_{y} + \alpha_{x} + \vartheta_{x} ))}}{{(1 - \vartheta_{x} \vartheta_{y} )}}} \\ \end{array} } \right\}.$$
(30)

On substituting Eqs. (29) and (30) in Eq. (28) and multiplying Eq. (28) by \(X_{m } Y_{n}\) and then integrating over whole plate area, the governing equation of submerged orthotropic cracked plate considering the thermal effects can be written as

$$\begin{aligned} &\left( {\rho h + m_{\text{add}} } \right)\mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } A_{mn} \int\limits_{0}^{L1} {\int\limits_{0}^{L2} {X_{m}^{2} Y_{n}^{2} {\text{d}}x{\text{d}}y\frac{{\partial^{2} \emptyset_{mn} \left( t \right)}}{{\partial t^{2} }}} } \hfill \\ &+ \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } A_{mn} \emptyset_{mn} \left( t \right)\int\limits_{0}^{L1} {\int\limits_{0}^{L2} {\left\{ {\frac{{(D_{x} + D^{lx} ) \left\{ {\left( {X_{m}^{iv} Y_{n} + \vartheta_{y} X_{m}^{ii} y_{n}^{ii} } \right) + \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2X_{m}^{iii} y_{n}^{i} + m_{y} E_{y} X_{m}^{ii} y_{n}^{ii} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}}} \right.} } \hfill \\ &+ \frac{{2\left\{ {\frac{{h^{3} }}{6}X_{m}^{ii} y_{n}^{ii} + \left( {(D_{x} + D^{lx} )m_{x} + \vartheta_{x} (D_{y} + D^{ly} )m_{y} } \right)X_{m}^{iii} y_{n}^{i} + \left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} (D_{x} + D^{lx} )m_{x} } \right)X_{m}^{i} y_{n}^{iii} } \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ &+ \frac{{(D_{y} + D^{ly} )\left\{ {\left( {Y_{n}^{iv} X_{m} + \vartheta_{x} X_{m}^{ii} y_{n}^{ii} } \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2X_{m}^{i} y_{n}^{iii} + m_{x} E_{x} X_{m}^{ii} y_{n}^{ii} } \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &- \frac{2a}{{3\left( {\frac{{\alpha_{bt} }}{6} + \alpha_{bb} } \right)\left( {3 + \vartheta_{x} } \right)\left( {1 - \vartheta_{x} } \right)h + 2a}}\frac{{\left( {D_{y} + D^{ly} } \right)\left\{ {\left( {Y_{n}^{iv} X_{m} + \vartheta_{x} X_{m}^{ii} y_{n}^{ii} } \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2X_{m}^{i} y_{n}^{iii} + m_{x} E_{x} X_{m}^{ii} y_{n}^{ii} } \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &+ \frac{{E_{x} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} + m_{y} E_{y} \alpha_{y} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)} \right)X_{m}^{ii} Y_{n} \hfill \\ &+ \left( {1 + \frac{2a}{{\left( {6\alpha_{bt} + \alpha_{tt} } \right)\left( {1 - \vartheta_{x}^{2} } \right)h + 2a}}} \right)\frac{{E_{y} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} + m_{x} E_{x} \alpha_{x} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)} \right)Y_{n}^{ii} X_{m} \hfill \\ &\left. { + 2\left( {\frac{{\Delta Th\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}} \right)X_{m}^{i} y_{n}^{i} } \right\}X_{m } Y_{n} {\text{d}}x{\text{d}}y = p_{z} . \hfill \\ \end{aligned}$$
(31)

On neglecting the point load \(p_{z}\) for free vibration analysis, Eq. (31) can be expressed in the form of famous Duffing equation as

$$M_{mn} \frac{{\partial^{2} \emptyset_{mn} \left( t \right)}}{{\partial t^{2} }} + K_{mn} \emptyset_{mn} \left( t \right) = 0,$$
(32)

where

$$M_{mn} = \left( {\rho h + m_{\text{add}} } \right)\mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } A_{mn} \int\limits_{0}^{L1} {\int\limits_{0}^{L2} {X_{m }^{2} Y_{n}^{2} {\text{d}}x{\text{d}}y} } ,$$
(33)
$$\begin{aligned} &K_{mn} = \sum\limits_{n = 1}^{\infty } {\sum\limits_{m = 1}^{\infty } {A_{mn} \emptyset_{mn} \left( t \right)} } \int\limits_{0}^{L1} {\int\limits_{0}^{L2} {\left\{ {\frac{{(D_{x} + D^{lx} ) \left\{ {\left( {X_{m}^{iv} Y_{n} + \vartheta_{y} X_{m}^{ii} y_{n}^{ii} } \right) + \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2X_{m}^{iii} y_{n}^{i} + m_{y} E_{y} X_{m}^{ii} y_{n}^{ii} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}}} \right.} } \hfill \\ &+ \frac{{2\left\{ {\frac{{h^{3} }}{6}X_{m}^{ii} y_{n}^{ii} + \left( {(D_{x} + D^{lx} )m_{x} + \vartheta_{x} \left( {D_{y + } D^{ly} } \right)m_{y} } \right)X_{m}^{iii} y_{n}^{i} + \left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} (D_{x} + D^{lx} )m_{x} } \right)X_{m}^{i} y_{n}^{iii} } \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ &+ \frac{{(D_{y} + D^{ly} )\left\{ {\left( {Y_{n}^{iv} X_{m} + \vartheta_{x} X_{m}^{ii} y_{n}^{ii} } \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2X_{m}^{i} y_{n}^{iii} + m_{x} E_{x} X_{m}^{ii} y_{n}^{ii} } \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &- \frac{2a}{{3\left( {\frac{{\alpha_{bt} }}{6} + \alpha_{bb} } \right)\left( {3 + \vartheta_{x} } \right)\left( {1 - \vartheta_{x} } \right)h + 2a}}\frac{{\left( {D_{y} + D^{ly} } \right)\left\{ {\left( {Y_{n}^{iv} X_{m} + \vartheta_{x} X_{m}^{ii} y_{n}^{ii} } \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2X_{m}^{i} y_{n}^{iii} + m_{x} E_{x} X_{m}^{ii} y_{n}^{ii} } \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &+ \frac{{E_{x} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} + m_{y} E_{y} \alpha_{y} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)} \right)X_{m}^{ii} Y_{n} \hfill \\ &+ \left( {1 + \frac{2a}{{\left( {6\alpha_{bt} + \alpha_{tt} } \right)\left( {1 - \vartheta_{x}^{2} } \right)h + 2a}}} \right)\frac{{E_{y} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} + m_{x} E_{x} \alpha_{x} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)} \right)Y_{n}^{ii} X_{m} \hfill \\ &\left. { + 2\left( {\frac{{\Delta Th\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}} \right)X_{m}^{i} y_{n}^{i} } \right\}X_{m } Y_{n} {\text{d}}x{\text{d}}y. \hfill \\ \end{aligned}$$
(34)

From Eq. (32), the fundamental frequency can be obtained as \(\omega_{mn}^{2} = K_{mn} /M_{mn}\).

Relation for Central Deflection of Plate

Consider a cracked orthotropic submerged plate with all sides simply supported, subjected to a lateral uniformly distributed dynamic load (Pz) harmonically varying with time. For a plate in the absence of thermal moments (\(M_{Tx} = M_{Ty} = M_{Txy} = 0\)) and the presence of constant in-plane forces (\(N_{Tx}\) and \(N_{Ty}\)) due to thermal environment only [Eq. (30)], the governing equation (28) becomes

$$\begin{aligned} &\frac{{(D_{x} + D^{lx} ) \left\{ {\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \vartheta_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + m_{y} E_{y} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}} \hfill \\ &+ \frac{{2\left\{ {\frac{{h^{3} }}{6}\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \left( {(D_{x} + D^{lx} )m_{x} + \vartheta_{x} \left( {D_{y} + D^{ly} } \right)m_{y} } \right)\frac{{\partial^{4} w}}{{\partial x^{3} \partial y}} + \left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} \left( {D_{x} + D^{lx} } \right)m_{x} } \right)\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}}} \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ &+ \frac{{(D_{y} + D^{ly} )\left\{ {\left( {\frac{{\partial^{4} w}}{{\partial y^{4} }} + \vartheta_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2\frac{{\partial^{4} w}}{{\partial y^{3} \partial x}} + m_{x} E_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &- \frac{2a}{{3\left( {\frac{{\alpha_{bt} }}{6} + \alpha_{bb} } \right)\left( {3 + \vartheta_{x} } \right)\left( {1 - \vartheta_{x} } \right)h + 2a}}\frac{{(D_{y} + D^{ly} )\left\{ {\left( {\frac{{\partial^{4} w}}{{\partial y^{4} }} + \vartheta_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {2\frac{{\partial^{3} w}}{{\partial y^{2} \partial x}} + m_{x} E_{x} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ &+ \frac{{E_{x} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} + m_{y} E_{y} \alpha_{y} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} \hfill \\ &+ \frac{{E_{y} \Delta Th}}{{\left( { 1 - \vartheta_{x} \vartheta_{y} } \right)}} \left( {1 + \frac{2a}{{\left( {6\alpha_{bt} + \alpha_{tt} } \right)\left( {1 - \vartheta_{x}^{2} } \right)h + 2a}}} \right)\left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} + m_{x} E_{x} \alpha_{x} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} \hfill \\ &+ 2\left( {\frac{{\Delta Th\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}} \right)\frac{{\partial^{2} w}}{\partial x\partial y} + \left( {\rho h + m_{\text{add}} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} = P_{z} . \hfill \\ \end{aligned}$$
(35)

Assuming the solution for lateral deflection as

$$w(x,y,t) = W_{mn} \sin \left( {\frac{m\pi x}{{L_{1} }}} \right)\sin \left( {\frac{n\pi y}{{L_{2} }}} \right)\sin \left( {\omega t} \right),$$
(36)

where \(\omega\) is the vibrational frequency. Now for the case of forced vibrations, the applied lateral dynamic load \(P_{z} = P_{z} (x,y,t)\) can be expressed as

$$P_{z} (x,y,t) = P_{mn} \sin \left( {\frac{m\pi x}{{L_{1} }}} \right)\sin \left( {\frac{n\pi y}{{L_{2} }}} \right)\sin \left( {\emptyset t} \right),$$
(37)

with \(\emptyset\) being the forcing frequency of the load. Substituting the general solution of lateral deflection \(\left( w \right)\) from Eq. (34) with \(\omega\) being replaced by \(\emptyset\) and the lateral dynamic load (\(P_{z}\)) from Eq. (35) into the governing equation (33) results in an expression for \(W_{mn}\). Thus, the classical relation for central deflection of cracked orthotropic submerged plate subjected to uniform heating can be proposed as

$$W_{mn} = \frac{{P_{mn} }}{{I - C - T - \left( {\rho h + m_{add} } \right) \emptyset^{2} }},$$
(38)

where

$$\begin{aligned} I &= \frac{{ - (D_{x} + D^{lx} )\pi^{4} \left\{ {\left( {\left( {\frac{m}{{L_{1} }}} \right)^{4} + \vartheta_{y} \left( {\frac{m}{{L_{1} }}} \right)^{2} \left( {\frac{n}{{L_{2} }}} \right)^{2} } \right) - \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2\left( {\frac{m}{{L_{1} }}} \right)^{3} \left( {\frac{n}{{L_{2} }}} \right) - m_{y} E_{y} \left( {\frac{m}{{L_{1} }}} \right)^{2} \left( {\frac{n}{{L_{2} }}} \right)^{2} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}} \hfill \\ &+ \frac{{ - 2\pi^{4} \left\{ {\begin{array}{*{20}c} {\frac{{h^{3} }}{6}\left( {\frac{m}{{L_{1} }}} \right)^{2} \left( {\frac{n}{{L_{2} }}} \right)^{2} - \left( {(D_{x} + D^{lx} )m_{x} + \vartheta_{x} \left( {D_{y} + D^{ly} } \right)m_{y} } \right)\left( {\frac{m}{{L_{1} }}} \right)^{3} \left( {\frac{n}{{L_{2} }}} \right)} \\ { - \left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} \left( {D_{x} + D^{lx} } \right)m_{x} } \right)\left( {\frac{m}{{L_{1} }}} \right)\left( {\frac{n}{{L_{2} }}} \right)^{3} } \\ \end{array} } \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ &+ \frac{{ - (D_{y} + D^{ly} )\pi^{4} \left\{ {\left( {\left( {\frac{n}{{L_{2} }}} \right)^{4} + \vartheta_{x} \left( {\frac{m}{{L_{1} }}} \right)^{2} \left( {\frac{n}{{L_{2} }}} \right)^{2} } \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( { - 2\left( {\frac{m}{{L_{1} }}} \right)\left( {\frac{n}{{L_{2} }}} \right)^{3} + m_{x} E_{x} \left( {\frac{m}{{L_{1} }}} \right)^{2} \left( {\frac{n}{{L_{2} }}} \right)^{2} } \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ C &= \frac{2a}{{3\left( {\frac{{\alpha_{bt} }}{6} + \alpha_{bb} } \right)\left( {3 + \vartheta_{x} } \right)\left( {1 - \vartheta_{x} } \right)h + 2a}}\frac{{(D_{y} + D^{ly} )\pi^{4} \left\{ {\begin{array}{*{20}c} {\left( {\left( {\frac{n}{{L_{2} }}} \right)^{4} + \vartheta_{x} \left( {\frac{m}{{L_{1} }}} \right)^{2} \left( {\frac{n}{{L_{2} }}} \right)^{2} } \right)} \\ { + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( {\begin{array}{*{20}c} { - 2\left( {\frac{m}{{L_{1} }}} \right)\left( {\frac{n}{{L_{2} }}} \right)^{3} } \\ { + m_{x} E_{x} \left( {\frac{m}{{L_{1} }}} \right)^{2} \left( {\frac{n}{{L_{2} }}} \right)^{2} } \\ \end{array} } \right)} \\ \end{array} } \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ T &= \pi^{2} \left[ {\frac{{E_{x} \Delta Th}}{{1 - \nu_{x} \nu_{y} }}\left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} + m_{y} E_{y} \alpha_{y} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)} \right)\left( {\frac{m}{{L_{1} }}} \right)^{2} + \frac{{E_{y} \Delta Th}}{{1 - \nu_{x} \nu_{y} }}\left( {1 + \frac{2a}{{\left( {6\alpha_{bt} + \alpha_{tt} } \right)\left( {1 - \vartheta_{x}^{2} } \right)h + 2a}}} \right)} \right. \hfill \\ &\left. {\left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} + m_{x} E_{x} \alpha_{x} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)} \right)\left( {\frac{n}{{L_{2} }}} \right)^{2} - 2\left( {\frac{{\Delta Th\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}} \right)\left( {\frac{m}{{L_{1} }}} \right)\left( {\frac{n}{{L_{2} }}} \right)} \right]. \hfill \\ \end{aligned}$$

For a special case of a square plate with side \(L_{1}\) and \(m = n = 1\), the central deflection \(W_{11}\) takes the form which clearly shows the presence of crack (\(C_{11}\)) and temperature (\(T_{11}\)) terms:

$$W_{11} = \frac{{P_{11} }}{{I_{11} - C_{11} - T_{11} - \left( {\rho h + m_{\text{add}} } \right) \emptyset^{2} }},$$
(39)

where

$$\begin{aligned} I_{11} = \frac{{ - (D_{x} + D^{lx} )\frac{{\pi^{4} }}{{L_{1}^{4} }} \left\{ {\left( {1 + \vartheta_{y} } \right) - \frac{{\left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} }}\left( {2 - m_{y} E_{y} } \right)} \right\}}}{{1 - \frac{{E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}}\left( {m_{x} + m_{y} \vartheta_{x} \frac{{E_{y} }}{{E_{x} }}} \right)}} \hfill \\ + \frac{{ - 2\frac{{\pi^{4} }}{{L_{1}^{4} }}\left\{ {\frac{{h^{3} }}{6} - \left( {(D_{x} + D^{lx} )m_{x} + \vartheta_{x} \left( {D_{y} + D^{ly} } \right)m_{y} } \right) - \left( {(D_{y} + D^{ly} )m_{y} + \vartheta_{y} \left( {D_{x} + D^{lx} } \right)m_{x} } \right)} \right\}}}{{\frac{1}{{G_{xy} }} - \frac{{m_{x} E_{x} \left( {\vartheta_{y} m_{y} + m_{x} } \right) + m_{y} E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}}} \hfill \\ + \frac{{ - (D_{y} + D^{ly} )\frac{{\pi^{4} }}{{L_{1}^{4} }}\left\{ {\left( {1 + \vartheta_{x} } \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( { - 2 + m_{x} E_{x} } \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ \frac{2a}{{3\left( {\frac{{\alpha_{bt} }}{6} + \alpha_{bb} } \right)\left( {3 + \vartheta_{x} } \right)\left( {1 - \vartheta_{x} } \right)h + 2a}}\frac{{(D_{y} + D^{ly} )\frac{{\pi^{4} }}{{L_{1}^{4} }}\left\{ {\left( {1 + \vartheta_{x} } \right) + \frac{{\left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} }}\left( { - 2 + m_{x} E_{x} } \right)} \right\}}}{{1 - \frac{{E_{y} \left( {\vartheta_{x} m_{x} + m_{y} } \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}}\left( {m_{y} + m_{x} \vartheta_{y} \frac{{E_{x} }}{{E_{y} }}} \right)}} \hfill \\ T_{11} = \frac{{\pi^{2} }}{{L_{1}^{2} }}\left[ {\frac{{E_{x} \Delta Th}}{{1 - \nu_{x} \nu_{y} }}\left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} + m_{y} E_{y} \alpha_{y} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)} \right)} \right. \hfill \\ + \frac{{E_{y} \Delta Th}}{{1 - \nu_{x} \nu_{y} }}\left( {1 + \frac{2a}{{\left( {6\alpha_{bt} + \alpha_{tt} } \right)\left( {1 - \vartheta_{x}^{2} } \right)h + 2a}}} \right)\left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} + m_{x} E_{x} \alpha_{x} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)} \right) \hfill \\ \left. { - 2\left( {\frac{{\Delta Th\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}} \right)} \right]. \hfill \\ \end{aligned}$$

The results for central deflection of a cracked orthotropic submerged plate without influence of thermal environment (∆T = 0), Eq. (39) can be expressed as

$$W_{11}^{\text{cracked}} = \frac{{P_{11} }}{{I_{11} - C_{11} - \left( {\rho h + m_{\text{add}} } \right) \emptyset^{2} }}.$$
(40)

Similarly, the result for central deflection of a uniformly heated intact orthotropic submerged plate without influence of any crack (a = 0), Eq. (39) can be expressed as

$$W_{11}^{\text{heated}} = \frac{{P_{11} }}{{I_{11} - T_{11}^{'} - \left( {\rho h + m_{\text{add}} } \right) \emptyset^{2} }},$$
(41)

where

$$\begin{aligned} T_{11}^{'} &= \frac{{\pi^{2} }}{{L_{1}^{2} }}\left[ {\frac{{E_{x} \Delta Th}}{{1 - \nu_{x} \nu_{y} }}\left( {\frac{{ \left( {\vartheta_{y} m_{y} + m_{x} } \right)(\alpha_{xy} + m_{y} E_{y} \alpha_{y} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{y}^{2} E_{y} } \right)}} + \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right)} \right)} \right. \\ &\quad+ \frac{{E_{y} \Delta Th}}{{1 - \nu_{x} \nu_{y} }}\left( {\frac{{ \left( {\vartheta_{x} m_{x} + m_{y} } \right)(\alpha_{xy} + m_{x} E_{x} \alpha_{x} )}}{{\left( {\frac{1}{{G_{xy} }} - m_{x}^{2} E_{x} } \right)}} + \left( {\alpha_{x} \vartheta_{x} + \alpha_{y} } \right)} \right) \\ &\quad \left. { - 2\left( {\frac{{\Delta Th\left( {\alpha_{xy} + m_{x} E_{x} \left( {\alpha_{x} + \alpha_{y} \vartheta_{y} } \right) + m_{y} E_{y} \left( {\alpha_{y} + \alpha_{x} \vartheta_{x} } \right)} \right)}}{{\left( {1 - \vartheta_{x} \vartheta_{y} } \right)}}} \right)} \right]. \\ \end{aligned}$$

The result for central deflection of an intact orthotropic submerged plate without influence of any crack (a = 0), thermal environment (∆T = 0) and fibre orientation (\(\beta\) = 0°), Eq. (39), can be expressed as

$$W_{11}^{\text{intact}} = \frac{{P_{11} }}{{\frac{{\pi^{4} }}{{L_{1}^{4} }}\left( {D_{x} + 2B + D_{y} } \right) - \emptyset^{2} \left( {\rho h + m_{\text{add}} } \right)}}.$$
(42)

The central deflection ratio \({{W_{11}^{\text{cracked}} } \mathord{\left/ {\vphantom {{W_{11}^{\text{cracked}} } {W_{11}^{\text{intact}} }}} \right. \kern-0pt} {W_{11}^{\text{intact}} }}\) can be obtained by dividing Eqs. (40) and (42) as

$$\frac{{W_{11}^{\text{cracked}} }}{{W_{11}^{\text{intact}} }} = \frac{{\frac{{\pi^{4} }}{{L_{1}^{4} }}\left( {D_{x} + 2B + D_{y} } \right) - \left( {\rho h + m_{\text{add}} } \right) \emptyset^{2} }}{{I_{11} - C_{11} - \left( {\rho h + m_{\text{add}} } \right) \emptyset^{2} }}$$
(43)

or

$$\frac{{W_{11}^{\text{cracked}} }}{{W_{11}^{\text{intact}} }} = \frac{{\left( {\emptyset /\omega } \right)^{2} }}{{\frac{{L_{1}^{4} \left( {I_{11} - C_{11} } \right)}}{{\pi^{4} \left( {D_{x} + 2B + D_{y} } \right)}} - \left( {\emptyset /\omega } \right)^{2} }},$$
(44)

where \(\omega = \sqrt {\frac{{\frac{{\pi^{4} }}{{L_{1}^{4} }}\left( {D_{x} + 2B + D_{y} } \right)}}{{\left( {\rho h + m_{\text{add}} } \right)}}}\) is the natural frequency of intact orthotropic submerged plate.

Similarly, the central deflection ratio \(W_{11}^{\text{heated}} /W_{11}^{\text{intact}}\) can be obtained by dividing Eqs. (41) and (42) as

$$\frac{{W_{11}^{\text{heated}} }}{{W_{11}^{\text{intact}} }} = \frac{{1 - \left( {\emptyset /\omega } \right)^{2} }}{{\frac{{L_{1}^{4} \left( {I_{11} - T_{11}^{'} } \right)}}{{\pi^{4} \left( {D_{x} + 2B + D_{y} } \right)}} - \left( {\emptyset /\omega } \right)^{2} }}.$$
(45)

Results and Discussion

In this section, new results for fundamental frequency and central deflection of a cracked orthotropic submerged plate as affected by crack length (\(a\)), crack location (\(\xi_{c}\)), fibre orientation \(\left( \beta \right)\), level of submergence (\(h_{1} /L_{1}\)), rise in temperature (ΔT) and microstructure (\(l\)) are presented for SSSS boundary condition. The orthotropic plate under consideration is made up of Boron Epoxy; the material properties are considered same as that used in Refs. [10, 56]: Ex = 208 × 109 Pa, Ey = 18.9 × 109 Pa, \(\vartheta_{1} \, = \,0. 2 3\), \(\vartheta_{2} \, = \,0.0 20 8\), G12 = 5.7 × 109 Pa and ρ = 2000 kg/m3. The coefficients of thermal expansion taken are \(\alpha_{x} = 7.10{\text{e}} - 06/^{ \circ } {\text{C}}\) and \(\alpha_{y} = 2.3{\text{e}} - 05/^{ \circ } {\text{C}}\). The fluid density is 1000 kg m−3. The dimensions of reservoir tank are 5 m × 5 m × 5 m. The depth of crack is 0.006 m and the plate thickness is 0.01 m throughout this work. The plate dimensions are taken as L1 = L2 = 1 m. As the literature lacks in the results for orthotropic submerged plate, validation of the present model is done with the cracked orthotropic plate in vacuum medium. Table 1 represents the results for frequency parameter of an intact and cracked orthotropic plate for various fibre orientations and length-scale parameters. The material constants of plate for this validation (Table 1) are taken from Ref. [56]. Results in Table 1 shows that the present outcomes are in exact agreement with the existing results which verifies the correctness of the proposed model.

Table 1 Comparison of frequency parameter for intact and cracked orthotropic plate in vacuum
Full size table

To compare the effect of level of submergence (fluidic medium), the present model is applied for a partially cracked isotropic submerged plate and the compared results for fundamental frequency parameter are shown in Table 2. The material constants and plate dimensions for results in Table 2 are taken from Ref. [11]. Again, the results are in exact agreement with the existing results which indicates that the proposed model deduces to the model developed by Ref. [11] when applied for an isotropic plate. In the absence of fluidic medium, the results for fundamental frequency of especially orthotropic cracked plate as affected by thermal environment can be found in the literature (Ref. [10]). The present model reduces to the one presented by Ref [10] when applied for a cracked orthotropic plate in the absence of fluidic medium with fibre orientation at 0° and 90°. Therefore, such validation is omitted here.

Table 2 Comparison of fundamental frequency parameter \(\left( {\omega_{mn} L_{1}^{4} \sqrt {\rho h/D} } \right)\) for cracked isotropic plate as a function of fluid level and half crack length. (l = 0, ΔT = 0)
Full size table

Figure 4 shows new results for the variation in fundamental frequency of intact and cracked orthotropic plates with fibre orientations (\(\beta\) = 0–90°) and temperature (\(\Delta T\) = 0–8 °C) for two different surrounding mediums (vacuum and fluid). It is well known that, for a square intact orthotropic plate, the fundamental frequency increases gradually from fibre orientation 0° to 45° (maximum) and is symmetric for 45°–90°. A similar trend is seen in the present results for an intact orthotropic plate (Fig. 4a, c), for both the surrounding mediums when the fibres are oriented from 0° to 90°. But in case of the cracked plate (Fig. 4b, d), it is observed that, due to presence of crack, the pattern of frequency variation for various fibre orientations is not symmetrical about 45°. This is because the crack under consideration is parallel to either edges of the plate and for every fibre orientation the stiffness is differently affected. In Fig. 4b, d it is clearly seen that stiffness is least affected when fibres are at 0° and most when fibres are at 90°, i.e. crack is across the fibres which satisfies one’s physical understanding. Literature shows that the rise in temperature of cracked isotropic plate reduces its frequency (Ref. [9]). Such a reduction in frequency is due to decrease in stiffness which is also observed to be valid for cracked orthotropic plate in both the vacuum and fluid medium in present case. It is interesting to see from Fig. 4a–d that with every fibre orientation, the reduction in frequency with uniform rise in temperature (∆T = 0–8 °C) is different. It is noted that the reduction in frequency at 45° of fibre orientation is less when compared to 0° and 90° for both intact and cracked orthotropic plates, it is due to the thermal stresses induced for a given temperature at 45° fibre orientation is less as compared to 0 and 90° and hence the reduction in the stiffness due to temperature is lesser at 45°.

Fig. 4
figure 4

Fundamental frequency (rad/s) as affected by temperature (ΔT) for various fibre orientations (β°) (l = 0.001 m, for in fluid—h1/L1= 0.1)

Full size image

Again it is also observed from Fig. 4a, b (in vacuum) and Fig. 4c, d (in fluid) that the frequencies are reduced in fluidic medium as compared to plate in vacuum. This is because of the virtual added mass (\(m_{\text{add}}\)) due to surrounding fluid which increases the overall mass (\(M_{mn}\)) of coupled system as shown in Eq. (33), thus validating one’s physical understanding. Similar type of variation in frequencies due to fluidic medium is also evident in the works of Ref. [11] for isotropic plates thereby validating the present variations for orthotropic plate.

By employing the modified couple stress theory, the variation in fundamental frequency of an intact and cracked orthotropic plate with internal length-scale parameter (l) is shown in Fig. 5. It is seen that for a given fibre orientation angle as the material length-scale parameter increases (l = 0–0.003 m) the fundamental frequency also increases, such increase in frequency is due to the contribution of microstructure to the flexural rigidity of the plate. It can be noted that classical plate theory under-predicts the frequency in the case of a micro-plate and the difference in both the theories is noticeable. Figure 5c, d shows such variation is observed to be valid for the case of intact and cracked orthotropic submerged plates also. Therefore, the consideration of microstructure in terms of material length-scale parameter is significant. It is important to mention that the frequency decreases due to the presence of crack whereas it increases when the internal length-scale parameter is considered. From Figs. 4 and 5 it is found that the effect of variation in temperature and length-scale parameter on fundamental frequency for a given fibre orientation is same for submerged plate as well as plate in vacuum. Such similarity is due to the assumption that the rise in temperature and length-scale parameter does not affect the virtual added mass (\(m_{\text{add}}\)).

Fig. 5
figure 5

Fundamental frequency (rad/s) for intact and cracked orthotropic plate as affected by material length-scale parameter l (m) for various fibre orientations (β) (ΔT = 2 °C, for in fluid—h1/L1= 0.1)

Full size image

The comparison of variation in fundamental frequency as affected by temperature and internal length-scale parameter for various level of submergence is shown in Fig. 6 for a fixed fibre orientation (\(\beta\) = 45°). It is observed from Fig. 6a–d that for a given temperature difference and length-scale parameter, as the plate goes deeper into the fluid tank, i.e. with the increase in depth of submergence, the frequency of the plate decreases for both intact and cracked plates. This is due to the resistance offered by the fluid medium in the form of dynamic pressure to the vibratory motion of plate. As the submerged plate goes deep into the fluid, the mass of fluid layer vibrating with the plate increases thereby increasing the virtual added mass or the total mass of the coupled system. Such a phenomenon of variation in frequency is also found in Refs. [20, 11] for intact and cracked isotropic plates, respectively. It is seen from Fig. 6a, b that for a given level of submergence, as the temperature of plate is increased from \(\Delta T\) = 0–20 °C, the frequency is decreased, which is again due to the decrease in the thermal stiffness of the plate which further reduces the overall plate’s stiffness. It is interesting to see from Fig. 6b that for the cracked plate at a fixed level of submergence, the reduction in frequency as affected by temperature variation is found to be more when compared to intact plate (Fig. 6a). The reason behind such reduction in frequency is for an intact plate, decrease in stiffness is only due to thermal stress but for a cracked plate, it is due to thermal stresses as well as due to effect of crack. This interaction between the crack and temperature is clearly shown by the third term in the expression for plate’s stiffness [Eq. (34)]. Thus, it is concluded that the presence of thermal environment and crack in an orthotropic plate can severely affect the fundamental frequency of plate. Again, it is seen from Fig. 6c, d that for a given level of submergence as the internal length-scale parameter increases (l = 0–0.003 m), the fundamental frequency also increases due to the effect of microstructure.

Fig. 6
figure 6

Fundamental Frequency (rad/s) of an intact and cracked orthotropic submerged plate as affected by temperature (ΔT) and internal length-scale parameter (l) for different level of submergence (β = 45°, for cracked—a = 0.05 m)

Full size image

From Fig. 7a, b, it is observed that for a given length-scale parameter, the fundamental frequency decreases with the increase in temperature (ΔT = 0–20 °C). It is found that for higher values of length-scale parameter (l = 0.01), the effect of increase in temperature on frequency reduces; this is because of the substantial contribution of material length-scale parameter to the stiffness.

Fig. 7
figure 7

Fundamental frequency (rad/s) of orthotropic submerged plate as affected by temperature (ΔT) and internal length-scale parameter l (m) (β = 45°, h1/L1= 0.1)

Full size image

Tables 3 and 4 show the results for fundamental frequency as a function of crack location and temperature variation for cracked plate vibrating in vacuum and fluid, respectively. Plate dimension considered are L1 = L2 = 1 m for both the tables and all the results are obtained for SSSS boundary condition. The crack length is kept constant at a = 0.2 m and internal material length-scale parameter at \(l\) = 0.001 m. It is seen from both the tables that as the crack moves away from the centre the fundamental frequency increases, this is because the crack at centre of the plate affects the stiffness to maximum as compare to other locations. A similar phenomenon was seen in Ref. [56] in the absence of thermal environment. Thus, it can be concluded that for the case of thermal environment also, the crack at the centre affects the fundamental frequency more when compared to crack at any other location. Again, it is seen that the crack location affects the stiffness most for the fibre orientation 90° (crack across the fibres) and least for 0° (crack parallel to the fibres). It is because the crack is parallel to either edges of the plate and with every orientation of fibre plate’s stiffness is differently affected. From Tables 3 and 4, it is also found that the effect of crack locations on fundamental frequency for a given temperature and fibre orientation is same for submerged plate and plate in vacuum. This is due to the assumption that the crack terms do not affect the virtual added mass (\(m_{\text{add}}\)) of plate.

Table 3 Fundamental frequency for a cracked orthotropic plate as affected by crack location and temperature variation for different fibre orientation in vacuum (a = 0.2 m, l = 0.001 m)
Full size table
Table 4 Fundamental frequency for a cracked orthotropic submerged plate as affected by crack location and temperature variation for different fibre orientation (a = 0.2 m, l = 0.001 m, h1/l1 = 0.1)
Full size table

Figure 7 represents the variation of ratio of deflection of cracked plate to intact orthotropic plate. To investigate the primary resonance, the ratio of forcing frequency to fundamental frequency of intact plate based on strain gradient theory is varied from 0.92 to 1.04. It is interesting to note that the presence of crack shifts the primary resonance and it takes place well below \(\emptyset /\omega = 1\). This is due to the reduction in plate’s stiffness due to centrally located crack. Similarly, the effect of fibre orientation and crack location on deflection of cracked plate is shown in Figs. 9 and 10, respectively. The results for variation of deflection ratio of heated intact plate to intact plate with respect to the ratio of forcing frequency and fundamental frequency are shown in Fig. 11. With the rise in temperature of plate, it is known that the fundamental frequencies decrease; such a fact seen in the literature is validated from the results of Fig. 11. As expected, the rise of temperature decreases the fundamental frequency of plate thereby increasing the deflection. The shift in primary resonance can be ascribed to the decrease in plate’s stiffness due to temperature rise. Figure 12 shows the ratio of deflections \(W_{11}^{\text{cracked}} /W_{11}^{\text{intact}}\) versus \(\left( {\emptyset /\omega } \right)^{2}\) for various values of length scale of microstructure (l). It is seen that increasing values of l result in shifting the primary resonance position of the classical case (\(\emptyset /\omega = 1\)) to higher values of (\(\emptyset /\omega\)). The shift in primary resonance can be attributed to the increase in stiffness due to internal length scale of microstructure. Thus, it can be concluded that the primary resonance occurs at higher values of forcing frequency (\(\emptyset\)). As per the authors’ knowledge, Figs. 8, 9, 10, 11 and 12 along with Eqs. (38–45) present first time the effect of crack length, crack location, fibre orientation, temperature and length scale of microstructure on deflection and primary resonance of cracked orthotropic submerged plate.

Fig. 8
figure 8

Central deflection ratio Wcracked11 /Wintact11 versus the normalized operational frequency (\(\emptyset\)/ω)2 for various values of crack length (a) in metres. (ΔT = 0, β = 0°, l = 0 m)

Full size image
Fig. 9
figure 9

Central deflection ratio Wcracked11 /Wintact11 versus the normalized operational frequency (\(\emptyset\)/ω)2 for various values of fibres angle (β°) (ΔT = 0, a = 0.01 m, l = 0 m)

Full size image
Fig. 10
figure 10

Central deflection ratio Wcracked11 /Wintact11 versus the normalized operational frequency (\(\emptyset\)/ω)2 for various values of crack location (ξc) (a = 0.2 m, ΔT = 0, β = 0°, l = 0 m)

Full size image
Fig. 11
figure 11

Central deflection ratio Wheated11 /Wintact11 versus the normalized operational frequency (\(\emptyset\)/ω)2 for various values of temperature ΔT. (a = 0 m, β = 0°, l = 0 m)

Full size image
Fig. 12
figure 12

Central deflection ratio Wcracked11 /Wintact11 versus the normalized operational frequency (\(\emptyset\)/ω)2 for various values of internal material length-scale parameter (l) in metres. (ΔT = 0, a = 0.01 m, β = 0°, z = 0 m)

Full size image

Conclusions

Micro-sized structures such as micro-plate have recently emerged as promising frequency sensing devices. In practice, these micro-plates are often operated under different surroundings such as fluidic medium and thermal environment. For, e.g. a micro-plate when used as a bio-sensor needs to interact with biological particles in natural fluid–thermal environment. When these micro-plates are used as frequency sensing devices, they usually undergo dynamic loading and when submerged in fluidic medium they also bear fluid inertial loads. Due to such dynamic loading, micro-plates are prone to develop flaws such as cracks, this is in line with one’s physical understanding and hence, it is necessary to predetermine its characteristics at the design level.

To cater the above problem, on the basis of classical plate theory and modified couple stress theory, vibration and deflection analyses of submerged orthotropic micro-plate with arbitrarily located crack are investigated in the presence of thermal environment. For this purpose, the governing differential equation is derived following the equilibrium principle and analytically solved for the simply supported boundary condition. A classical relation for central deflection of cracked plate affected by forcing frequency, crack length and its location, temperature, material length-scale parameter and fibre environment is also deduced in the present work.

The effects of crack length, crack location, fibre orientation, level of submergence, material length-scale parameter and thermal environment are examined in detail for boron-epoxy orthotropic micro-plate. It is established that the fundamental frequency of plate decreases by the presence of crack and thermal environment and this decrease in frequency is further intensified by presence of surrounding fluid medium in the present study. It is further observed that the presence of centrally located crack affects the frequency differently for each fibre orientation. It is because the crack is assumed to be parallel to either edge of the plate and with every orientation of fibre plate’s stiffness is differently affected. Another important conclusion is that with the increase in temperature variation the reduction in frequency at 45° of fibre orientation is less as compared to 0 and 90° for both intact and cracked orthotropic plate. It is known from the strength point of view that 45° fibre orientation makes the plate stronger and the present work proves this to be true for orthotropic micro-plate in the presence of partial crack, fluid and thermal environment. Few results are presented in tabular and graphical form to show the comparative differences between the results obtained by classical plate theory and modified couple stress theory.

The rise in temperature and increase in crack length shifts the resonance to lower values of forcing frequency whereas the increase in fibre orientation and length-scale parameter shift the resonance to higher values. It is also seen that as the crack moves away from centre the resonance also shifts to higher values of forcing frequency, this is because the crack at centre of plate affects the frequency to maximum as compared to other locations.