1 Introduction

Micro and nano electromechanical systems (MEMS and NEMS) are gaining considerable attention of many researchers due to their advantages and technological developments. Structural elements of microns and sub-microns scale, such as plates and beams are used in devices like micro and nano-mirrors, micro switches and nano-switches, micro actuators and nano-actuators (Moeenfard and Ahmadian 2012; Sadeghian et al. 2007; Lin and Zhao 2005; Kuang and Chen 2004; Soroush et al. 2010). There are many applications of these devices in various fields such as automobile, biomedical and electronics.

A typical arrangement of electrostatically actuated device is comprised of deformable structure suspended above a fixed electrode. An applied voltage between the two members when increases beyond a certain point, elastic force which restores the deformable structure to its original position cannot balance applied electrostatic force and the deformable structure collapses on to the fixed electrode. This instability is described as ‘pull-in instability’ and is a significant phenomenon related with electrostatically actuated devices. (Abdel-Rahman et al. 2002; Joglekar and Pawaskar 2011; Tahani and Askari 2014). The study of pull-in instability with very less gap between deformable structure and fixed electrode requires consideration of intermolecular forces at nano scale (Yang et al. 2008). At such scale, the functions of MEMS and NEMS devices are significantly influenced by intermolecular forces (Mousavi et al. 2013). In addition, free vibration characteristics offer an important information for the design of electrostatically actuated devices with better performance (Jia et al. 2010). It is also helpful to determine residual stress by identifying the important dynamic parameter like natural frequencies (Soma and Ballestra 2009). Further, it should be noted that the axial force due to residual stress is a significant parameter which influences the pull-in instability and free vibration characteristics of electrostatically driven devices (Sadeghian et al. 2007; De Pasquale and Soma 2010).

At submicrometer scale, there is necessity to consider fluctuation induced electromagnetic forces for evaluating the operational factors of MEMS and NEMS (Gusso and Delben 2008). Based on the operative regime, these forces are recognised with different names such as van der Waals (vdW) force, Casimir-Polder force and more commonly, Casimir forces (Rodriguez et al. 2011). Both these forces initiate from the same source associated with fluctuating currents in macroscopic bodies were first recognised by Lifshitz (1956). The fluctuating currents between interacting bodies induce the electromagnetic field. At very small separation of a few nanometres, one can neglect retardation of electromagnetic interaction and the resulting interaction is termed as vdW force, while at larger distance where the retardation becomes significant, the same force is termed as Casimir force (Svetovoy and Palasantzas 2015). The vdW force and Casimir force cannot be considered at the same time as they define common physical phenomenon at different regime (Batra et al. 2008). Various studies investigating the effect of intermolecular forces on pull-in instability and free vibration of electrostatically actuated devices are available (Ramezani et al. 2007; Jia et al. 2011; Batra et al. 2008).

Internal axial stress or residual stress is commonly developed in fixed–fixed beam structures due to micro machining processes, variation of temperature during application of device and mismatch of thermal expansion coefficient of materials used for beam and other elements of device (Elata and Abu-Salih 2005; Tilmans and Legtenberg 1994). Several methods are described in literature for measurement of residual stress in micro-beam such as using frequency shift with changes in DC voltage, from best fit of modelled and measured deflection curves and based on measured natural frequencies of the lowest few Eigen modes (De Pasquale and Soma 2010; Baker et al. 2002; Tung et al. 2013). The MEMS and NEMS resonators are greatly influenced by change in temperature during application. The change in temperature develops axial stress which in turn alters the frequency characteristics of resonators. The effect of axial stress on frequency characteristics is investigated for micro/nano resonators through various experimental and theoretical studies (De Pasquale and Soma 2010; Bhushan et al. 2011). Temperature sensitivity can be reduced in fixed–fixed beam resonators with different approaches discussed in published literature (Melamud et al. 2007; Salvia et al. 2010).

Resonance frequency tuning is a required property to improve performance of MEMS and NEMS devices such as energy harvesters (De Pasquale and Soma 2010), mass sensor (Ilic et al. 2004), pressure sensor (Southworth et al. 2009) etc. The resonant frequency tuning of mechanical structure of these devices is normally adopted to increase operative regime (Pandey 2013). In order to tune the frequency characteristics of these devices, internal axial stress can be developed intentionally in the micro/nano-beams. The internal axial stress is introduced using resistive heating for tuning resonant frequency characteristics (Syms 1998). The tensile stress is made adjustable through large scale chip bending to obtain exceptionally high frequency tunability, which allows to use the resonators as variable frequency reference (Verbridge et al. 2007).

In some of the previous studies, effect of intermolecular forces are investigated; however the effect of axial force was not considered (Lin and Zhao 2005; Yang et al. 2008; Mousavi et al. 2013; Dequesnes et al. 2004). Some studies consider the effect of axial force while dealing with geometric nonlinearity (Jia et al. 2010, 2011). To the best of authors’ knowledge, no earlier work in open literature is reported which discusses the effect of vdW force on resonant frequency stability and frequency tuning characteristics of nano-beam. The objective of the current work is to study the effect of vdW force on pull-in parameter and free vibration characteristics for beam under axial load. The reduced order model (ROM) is obtained for static analysis and linear free vibration characteristics to study the effect of vdW force on pull-in instability, resonant frequency tuning as well as frequency stability characteristics for electrostatically actuated beam.

2 Theoretical formulation

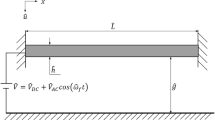
Shown in Fig. 1 is electrostatically actuated beam with fixed–fixed end condition. The beam of length \(\hat{L}\), width \(\hat{b}\) and thickness \(\hat{h}\) is suspended above a fixed electrode plate with an initial gap \(\hat{g}\). This arrangement functions as a parallel plate capacitor when potential difference is applied between the beam and fixed electrode. The applied voltage between beam and fixed electrode results in an electrostatic force \(\hat{F}_{e}\). The combined effect of electrostatic force and vdW force \(\hat{F}_{3}\) causes the beam to deflect towards fixed electrode. It is observed that the results from continuum model agree well with molecular dynamic simulation results for nanostructure (Dequesnes et al. 2004; Ouakad and Younis 2010). Therefore in the current study, Euler–Bernoulli beam theory is used instead of molecular dynamic approach for modelling nano-beam including vdW force. The governing equations for displacement \(\hat{y}\left( {\hat{x},\hat{t}} \right)\) of clamped–clamped beam is as follows (Zand and Ahmadian 2010; Rasekh et al. 2010):

$$\widehat{E}\widehat{I}\frac{{\partial^{4} \widehat{y}}}{{\partial \widehat{x}^{4} }} + \widehat{\rho }\widehat{A}\frac{{\partial^{2} \widehat{y}}}{{\partial \widehat{t}^{2} }} + \widehat{c}\frac{{\partial \widehat{y}}}{{\partial \widehat{t}}} = \left[ {\frac{{\widehat{E}\widehat{A}}}{{2\widehat{L}}}\mathop \int \nolimits_{0}^{{\widehat{L}}} \left( {\frac{{\partial \widehat{y}}}{{\partial \widehat{x}}}} \right)^{2} d\widehat{x} + \widehat{N}} \right]\frac{{\partial^{2} \widehat{y}}}{{\partial \widehat{x}^{2} }} + \widehat{F}_{e} + \widehat{F}_{3}$$
(1)

the boundary conditions used for the above equation are:

$$\left. {\frac{{\partial \widehat{y}}}{{\partial \widehat{x}}}} \right|_{{\widehat{x} = 0}} = \left. {\frac{{\partial \widehat{y}}}{{\partial \widehat{x}}}} \right|_{{\widehat{x} = \widehat{L}}} = \left. {\widehat{y}} \right|_{{\widehat{x} = 0}} = \left. {\widehat{y}} \right|_{{\widehat{x} = \widehat{L}}} = 0$$

where, \(\widehat{A}\), \(\widehat{I}\), \(\widehat{E}\) and \(\widehat{\rho }\) are cross section area, moment of inertia about the neutral axis, effective modulus and density of the beam respectively. In case of narrow beams (\(\widehat{b}\) < 5 \(\widehat{h}\)) the effective modulus \(\widehat{E} = E\)(Young’s modulus) whereas for wide beams (\(\widehat{b}\) ≥ 5 \(\widehat{h}\)), the effective modulus \(\widehat{E} = E/\left( {1 - \nu^{2} } \right)\), where \(\nu\) represents the Poisson’s ratio. \(\widehat{N}\) is the axial force due to residual stresses of the beam. The beam is subjected to viscous damping with a damping coefficient \(\widehat{c}\). The integral term in the governing Eq. (1) takes into account the non-linear mid-plane stretching of the beam. \(\widehat{F}_{e}\) is the electrostatic force per unit length of the beam due to an applied voltage \(\widehat{V}\). For parallel beam configuration and considering first order fringing field correction, the \(\widehat{F}_{e}\) is given as (Huang et al. 2001)

$$\widehat{F}_{e} = \frac{{\varepsilon_{0} \widehat{b}\left( {\widehat{V}_{DC} + \widehat{V}_{AC} \cos \left( {\widehat{\omega }_{f} \widehat{t}} \right)} \right)^{2} }}{{2\left( {\widehat{g} - \widehat{y}} \right)^{2} }}\left( {1 + 0.65\frac{{\left( {\widehat{g} - \widehat{y}} \right)}}{{\widehat{b}}}} \right)$$
(2)

where, \(\varepsilon_{0}\) is permittivity of vacuum. Applied voltage \(\widehat{V}\) consists of DC component \(\widehat{V}_{DC}\) superimposed to an AC harmonics of amplitude \(\widehat{V}_{AC}\) and excitation frequency \(\widehat{\omega }_{f} .\)

Fig. 1
figure 1

Schematic diagram of fixed–fixed electrostatically actuated beam

Full size image

When the separation between two parallel plates is typically smaller than 20 nm (Serry et al. 1995), the vdW force per unit length of the beam as a function of separation distance is (Israelachvili 1992)

$$\widehat{F}_{3} = \frac{{\overline{A} \widehat{b}}}{{6\pi \left[ {\widehat{g} - \widehat{y}} \right]^{3} }}$$
(3)

where, \(\overline{A}\) is the Hamaker constant which takes into account the material properties of the plates.

For convenience, Eq. (1) is expressed in terms of dimensionless variables as,\(y = \frac{{\widehat{y}}}{{\widehat{g}}}\), \(x = \frac{{\widehat{x}}}{{\widehat{L}}}\) and \(t = \frac{{\widehat{t}}}{{\widehat{T}}}\), where, time constant, \(\widehat{T} = \sqrt {\frac{{\widehat{\rho }\widehat{A}\widehat{L}^{4} }}{{\widehat{E}\widehat{I}}}}.\)

Substituting dimensionless variables and Eqs. (2) and (3) into (1), the obtained governing equation is,

$$y^{\prime\prime\prime\prime} + {\ddot{y}} + c\dot{y} = \left({\alpha \int_{0}^{1} {y^{\prime 2} dx + N}} \right)y^{\prime\prime} + \frac{{\beta V^{2}}}{{\left({1 - y} \right)^{2}}} + f\frac{{\beta V^{2}}}{{\left({1 - y} \right)}} + \frac{{\gamma_{3}}}{{\left({1 - y} \right)^{3}}}$$
(4)

Note that in Eq. (4), \(V = V_{DC} + V_{AC} cos\left( {\omega_{f} t} \right)\) and \(\omega_{f} = \widehat{\omega }_{f} \widehat{T}\).

The dimensionless forms of the boundary conditions are:

$$\left. y \right|_{x = 0} = \left. y \right|_{x = 1} = \left. {y^{\prime}} \right|_{x = 0} = \left. {y^{\prime}} \right|_{x = 1} = 0$$

The various dimensionless parameters appearing in Eq. (4) are as follows:where, \(\alpha = 6\left( {\frac{{\widehat{g}}}{{\widehat{h}}}} \right)^{2}\), \(\beta = \frac{{\varepsilon_{0} \widehat{b}\widehat{L}^{4} }}{{2\widehat{g}^{3} \widehat{E}\widehat{I}}}\), \(\gamma_{3} = \frac{{\overline{A} \widehat{b}\widehat{L}^{4} }}{{6\pi \widehat{g}^{4} \widehat{E}\widehat{I}}}\), \(N = \frac{{\widehat{N}\widehat{L}^{2} }}{{\widehat{E}\widehat{I}}}\), \(c = \frac{{\widehat{c}\widehat{L}^{4} }}{{\widehat{E}\widehat{I}\widehat{T}}}\), \(f = 0.65\frac{{\widehat{g}}}{{\widehat{b}}}\).

The superscript prime and over dot indicate the partial derivatives with respect to spatial coordinate \(x\) and time \(t\) respectively. In Eq. (4), the applied voltage (\(V\)) is in dimensional form and the \(\gamma_{3}\) represents dimensionless vdW force parameter.

3 Solution using ROM

3.1 ROM for static analysis

ROM based on Galerkin method is used to discretise the governing differential equation for static and linear free vibration analysis of nano-beam. The overall deflection of the beam \(y \left( {x,t} \right)\) is assumed as consisting of static component \(y_{s} \left( x \right)\) due to DC voltage together with vdW force and dynamic component \(y_{d} \left( {x,t} \right)\) due to the AC voltage that is \(y\left( {x,t} \right) = y_{s} \left( x \right) + y_{d} \left( {x,t} \right)\). All time derivative terms and variable forcing terms are set to zero in Eq. (4) yielding equation to simulate the static behavior as,

$$y^{\prime\prime\prime\prime}_{s} = \left({\alpha \int_{0}^{1} {y_{s}^{\prime 2} dx + N}} \right)y_{s}^{\prime\prime} + \frac{{\beta V_{DC}^{2}}}{{\left({1 - y_{s}} \right)^{2}}} + f\frac{{\beta V_{DC}^{2}}}{{\left({1 - y_{s}} \right)}} + \frac{{\gamma_{3}}}{{\left({1 - y_{s}} \right)^{3}}}$$
(5)

In Eq. (5), \(\beta V_{DC}^{2}\) represents dimensionless voltage parameter. To develop the ROM based on Galerkin method, the linear undamped normalised mode shape \(\emptyset_{i}\) of straight beam is used as spatial basis function. Hence, the solution of Eq. (5) is assumed as,

$$y_{s} \left( x \right) = \mathop \sum \limits_{i = 1}^{m} a_{i} \emptyset_{i} \left( x \right)$$
(6)

where, \(a_{i}\) is scalar constant to be evaluated. The modes \(\emptyset_{i} \left( x \right)\) are normalised such that \(\int_{0}^{1} {\emptyset_{i}^{2} dx}\) = 1 and determined from the equation (Bokaian 1988)

$$\emptyset^{\prime\prime\prime\prime} = N\emptyset^{\prime\prime} + \omega^{2} \emptyset$$
(7)

the boundary conditions for above equation are

$$\left. \emptyset \right|_{x = 0} = \left. \emptyset \right|_{x = 1} = \left. {\emptyset^{\prime}} \right|_{x = 0} = \left. {\emptyset^{\prime}} \right|_{x = 1} = 0$$

To analyse the static behavior, the ROM is obtained by substituting Eqs. (6) into (5), using condition for orthogonality of mode shape and the Eq. (7), multiplying it with \(\emptyset_{n}\) and integrated over the beam length. The ROM—representing set of algebraic non-linear equations—obtained is as follows:

$$\begin{aligned} \omega_{n}^{2} a_{n} & = \left( {\alpha \mathop \sum \limits_{i,j,k = 1}^{m} a_{i} a_{j} a_{k} \mathop \int \nolimits_{0}^{1} \emptyset_{i}^{'} \emptyset_{j}^{'} dx\mathop \int \nolimits_{0}^{1} \emptyset_{k}^{''} \emptyset_{n} dx} \right) + \beta V_{DC}^{2} \mathop \int \nolimits_{0}^{1} \frac{1}{{\left( {1 - \mathop \sum \nolimits_{i = 1}^{m} a_{i} \emptyset_{i} } \right)^{2} }}\emptyset_{n} dx \\ & \quad + f\beta V_{DC}^{2} \mathop \smallint \limits_{0}^{1} \frac{1}{{\left( {1 - \mathop \sum \nolimits_{i = 1}^{m} a_{i} \emptyset_{i} } \right)}}\emptyset_{n} dx + \gamma_{3} \mathop \int \nolimits_{0}^{1} \frac{1}{{\left( {1 - \mathop \sum \nolimits_{i = 1}^{m} a_{i} \emptyset_{i} } \right)^{3} }}\emptyset_{n} dx \\ \end{aligned}$$
(8)

where, n = 1, 2…m. The static deflection of the beam is obtained from solution of Eq. (8) using MATLAB software. In Eq. (8), the mode shape \(\emptyset_{i}\) can be obtained from Eq. (7). The analytical solution of Eq. (7) provides characteristic equation to obtain natural frequencies at undeflected state under axial load as

$$\omega - \omega { \cos }\lambda_{3} { \cosh }\lambda_{1} + \frac{N}{2}{ \sin }\lambda_{3} { \sinh }\lambda_{1} = 0$$
(9)

where, \(\lambda_{1} = \sqrt {\sqrt {\frac{{N^{2} }}{4} + \omega^{2} } + \frac{N}{2}}\) and \(\lambda_{3} = \sqrt {\sqrt {\frac{{N^{2} }}{4} + \omega^{2} } - \frac{N}{2}}\).

The solution of (7) also provides expression for the mode shape \(\emptyset_{i}\) as,

$$\emptyset_{i} = \left( {{ \cosh }\lambda_{1i} x - { \cos }\lambda_{3i} x} \right) + \left[ {\frac{{{ \cos }\lambda_{3i} - { \cosh }\lambda_{1i} }}{{\lambda_{3i} { \sinh }\lambda_{1i} - \lambda_{1i} { \sinh }\lambda_{3i} }}} \right]\left( {\lambda_{3i} { \sinh }\lambda_{1i} x - \lambda_{1i} { \sin }\lambda_{3i} x} \right)$$
(10)

where, equations for the \(\lambda_{1i}\) and \(\lambda_{3i}\) are same as mentioned above for \(\lambda_{1}\) and \(\lambda_{3}\) respectively, corresponding to \(\omega_{i}\) (ith natural frequency of the beam) obtained by solving transcendental Eq. (9). Single mode ROM is used for static analysis as it gives sufficiently accurate result (Tahani and Askari 2014; Bhushan et al. 2011; Ouakad and Younis 2010). The single mode ROM resulting from Eq. (8) by substituting \(m\) = 1 is,

$$\begin{aligned} \omega_{1}^{2} a_{1} + \alpha \left({\int_{0}^{1} {\emptyset_{1}^{\prime 2} dx}} \right)^{2} a_{1}^{3} & = \beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1} \frac{1}{{\left({1 - a_{1} \emptyset_{1}} \right)^{2}}}dx} + f\beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1} \frac{1}{{\left({1 - a_{1} \emptyset_{1}} \right)}}dx} \\ & \quad + \gamma_{3} \int_{0}^{1} {\emptyset_{1} \frac{1}{{\left({1 - a_{1} \emptyset_{1}} \right)^{3}}}dx} \\ \end{aligned}$$
(11)

Equation (11) is solved iteratively for \(a_{1}\) till the pull-in is occurred. Note that integrals \(\int_{0}^{1} {\emptyset_{1} \frac{1}{{\left( {1 - a_{1} \emptyset_{1} } \right)^{2} }}dx}\), \(\int_{0}^{1} {\emptyset_{1} \frac{1}{{\left( {1 - a_{1} \emptyset_{1} } \right)}}dx}\) and \(\int_{0}^{1} {\emptyset_{1} \frac{1}{{\left( {1 - a_{1} \emptyset_{1} } \right)^{3} }}dx}\) are estimated numerically for each iteration.

3.2 ROM for free vibration characteristics

ROM is also obtained to analyse the linear free vibration about its static equilibrium position at deflected state of the beam. For this, deflection of the beam is assumed as consisting of static component \(y_{s} \left( x \right)\) and dynamic component \(y_{d} \left( {x,t} \right)\). Hence, the solution of Eq. (4) is assumed as,

$$y\left( {x,t} \right) = y_{s} \left( x \right) + y_{d} \left( {x,t} \right)$$
(12)

The static component of deflection \(y_{s} \left( x \right)\) is decided by electrostatic actuation due to DC voltage together with vdW force, while the dynamic component \(y_{d} \left( {x,t} \right)\) is due to the AC voltage. It is assumed that magnitude of dynamic component of deflection \(y_{d} \left( {x,t} \right)\) and AC voltage is very small compared to magnitude of \(y_{s} \left( x \right)\) and DC voltage respectively. The linear equation of motion for free vibration at the deflected state is obtained by substituting Eqs. (12) into (4), expanding the forcing terms of Eq. (4) about \(y_{d} \left( {x,t} \right) = 0\), incorporating static deflection Eq. (5), then neglecting the terms of higher order, damping, forcing and retaining linear terms in \(y_{d}\) only.

The obtained free vibration equation is,

$$\begin{aligned} y_{d}^{\prime\prime\prime\prime} + {\ddot{y}}_{d} &= \left({\alpha \int_{0}^{1} {y_{s}^{\prime 2} dx + N}} \right)y_{d}^{\prime\prime} + \left({2\alpha \int_{0}^{1} {y_{s}^{\prime} y_{d}^{\prime} dx}} \right)y_{s}^{\prime\prime} + 2\beta V_{DC}^{2} \frac{1}{{\left({1 - y_{s}} \right)^{3}}}y_{d} \hfill \\ & \qquad + f\beta V_{Dc}^{2} \frac{1}{{\left({1 - y_{s}} \right)^{2}}}y_{d} + 3\gamma_{3} \frac{1}{{\left({1 - y_{s}} \right)^{4}}}y_{d} \hfill \\ \end{aligned}$$
(13)

The solution of (13) is obtained by separation of variables method. For this, \(y_{d} \left( {x,t} \right)\) is expressed as

$$y_{d} \left( {x,t} \right) = y_{dt} \left( t \right)\emptyset_{df} \left( x \right)$$
(14)

Substituting Eqs. (14) into (13) and rearranging yields two uncoupled ordinary differential equation. Differential equation in spatial coordinate gives natural frequencies and mode shapes at deflected state. The differential equation in spatial coordinate is,

$$\begin{aligned} \emptyset_{df}^{\prime\prime\prime\prime} - \left({\alpha \int_{0}^{1} {y_{s}^{\prime 2} dx + N}} \right)\emptyset_{df}^{\prime\prime} &- \left({2\alpha \int_{0}^{1} {y_{s}^{\prime} \emptyset_{df}^{\prime} dx}} \right)y_{s}^{\prime\prime} - 2\beta V_{DC}^{2} \frac{1}{{\left({1 - y_{s}} \right)^{3}}}\emptyset_{df} - f\beta V_{DC}^{2} \frac{1}{{\left({1 - y_{s}} \right)^{2}}}\emptyset_{df} \hfill \\ & - 3\gamma_{3} \frac{1}{{\left({1 - y_{s}} \right)^{4}}}\emptyset_{df} - \omega_{df}^{2} \emptyset_{df} = 0 \hfill \\ \end{aligned}$$
(15)

Equation (15) is a characteristics equation, where \(\omega_{df}\) and \(\emptyset_{df}\) are natural frequency and mode shape at deflected state respectively. To obtain the ROM, the solution of (15) is assumed as

$$\emptyset_{df} = \mathop \sum \limits_{i = 1}^{m} b_{i} \emptyset_{i}$$
(16)

Substituting Eqs. (16) into (15), using the condition for orthogonality of mode shape, then by multiplying the result with \(\emptyset_{n}\) and integrating over the beam domain yields ROM as,

$$\begin{aligned} &b_{n} \omega_{n}^{2} - \sum\limits_{i = 1}^{m} {b_{i}} \left({\alpha \int_{0}^{1} {y_{s}^{\prime 2} dx} \int_{0}^{1} {\emptyset_{i}^{\prime\prime}} \emptyset_{n} dx + 2\alpha \int_{0}^{1} {y_{s}^{\prime}} \emptyset_{i}^{\prime} dx\int_{0}^{1} {y_{s}^{\prime\prime}} \emptyset_{n} dx} \right) \\ & \quad - \sum\limits_{i = 1}^{m} {b_{i} \left({2\beta V_{DC}^{2} \int_{0}^{1} {\frac{1}{{\left({1 - y_{s}} \right)^{3}}}\emptyset_{i}} \emptyset_{n} dx + f\beta V_{DC}^{2} \int_{0}^{1} {\frac{1}{{\left({1 - y_{s}} \right)^{2}}}\emptyset_{i} \emptyset_{n} dx}} \right)} \\ & \quad - \sum\limits_{i = 1}^{m} {b_{i} \left({3\gamma_{3} \int_{0}^{1} {\frac{1}{{\left({1 - y_{s}} \right)^{4}}}\emptyset_{i} \emptyset_{n} dx}} \right) = b_{n} \omega_{df}^{2}} \\ \end{aligned}$$
(17)

where, n = 1, 2…m. Equation (17) provides natural frequencies and mode shapes of undamped free vibration at deflected state. Equation (17) is solved using MATLAB software for free vibration analysis with single mode ROM. The single mode ROM obtained from (17) by substituting \(m\) = 1 is,

$$\begin{aligned} \omega_{df}^{2} - \omega_{1}^{2} & = 3\alpha \left({\int_{0}^{1} {\emptyset_{1}^{\prime 2} dx}} \right)^{2} a_{1s}^{2} \\ & \quad - \left({2\beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left({1 - a_{1s} \emptyset_{1}} \right)^{3}}}dx} + f\beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left({1 - a_{1s} \emptyset_{1}} \right)^{2}}}dx}} \right) \\ & \quad - 3\gamma_{3} \int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left({1 - a_{1s} \emptyset_{1}} \right)^{4}}}dx} \\ \end{aligned}$$
(18)

where, \(\omega_{df}\) and \(\omega_{1 }\) are first natural frequencies at deflected state \(y_{s} \left( x \right) = a_{1s} \emptyset_{1}\) and undeflected state respectively. Equation (18) is solved iteratively for \(a_{1s}\) till the pull in is occurred. Note that here also integrals \(\int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left( {1 - a_{1s} \emptyset_{1} } \right)^{3} }}dx}\), \(\int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left( {1 - a_{1s} \emptyset_{1} } \right)^{2} }}dx}\) and \(\int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left( {1 - a_{1s} \emptyset_{1} } \right)^{4} }}dx}\) are estimated numerically for each iteration.

4 Numerical results and discussion

4.1 Result validation

The validation of present methodology is shown in Fig. 2a for pull-in voltage against the differential quadrature method (DQM) based numerical results of Mousavi et al. (2013) for various values of \(\gamma_{3}\) and with the experimental results of Tilmans and Legtenberg (1994) in Fig. 2b for the ratio of dimensionless first natural frequency at deflected state \(\omega_{df}\) and at un-deflected state \(\omega_{1}\) versus applied voltage V DC . Further comparisons are shown in Tables 1 and 2 with the published numerical results of Kuang and Chen (2004) and Tahani and Askari (2014) as well as with the experimental results of Tilmans and Legtenberg (1994). The geometric and material properties of the beam for the comparison shown in Table 1 and Fig. 2b are as follows: \(\widehat{b}\) = 100 µm, \(\widehat{h}\) = 1.5 µm, \(\widehat{E}\) = 151 GPa, and \(\nu\) = 0.3 (Tilmans and Legtenberg 1994). The validation shown in Table 2 is with the following properties of the beam: \(\widehat{L}\) = 5 µm, \(\widehat{b}\) = 1 µm, \(\widehat{h}\) = 100 nm, \(\widehat{E}\) = 80 GPa, and \(\nu\) = 0.42 (Tahani and Askari 2014). The Excellent agreement between present and published numerical and experimental results found in all the cases mentioned above, shows robustness of the present model for micro/nano beam.

Fig. 2
figure 2

Comparison of a voltage parameter at pull-in \(\left( {\beta V_{DC}^{2} } \right)_{PI}\) versus non-dimensional van der Waals force parameter \(\gamma_{3}\) for \(N = 0\) and \(\alpha = 0\) b ratio of dimensionless first natural frequency at deflected state \(\omega_{df}\) and at un-deflected state \(\omega_{1}\) versus applied voltage VDC

Full size image
Table 1 Comparison of pull-in voltage with the measured and calculated results for \(g\) = 1.18 µm
Full size table
Table 2 Comparison of pull-in voltage results for various values of axial-stress \(\sigma_{r}\) incorporating vdW force
Full size table

4.2 Static pull-in instability analysis

The static deflection of the beam subject to electrostatic and vdW force is studied till pull-in instability point. The relationship between voltage parameter \(\beta V_{DC}^{2}\) and mid-point deflection \(y_{mid}\) of the beam when mid-plane stretching parameter \(\alpha\) = 30 and vdW force parameter \(\gamma_{3}\) = 10 is shown in Fig. 3a. The results are obtained for various values of axial force representing tensile to compressive. Also comparison of the results with and without vdW force is shown the figure. Zand and Ahmadian (2010) reported the similar behavior between the voltage parameter and mid-point deflection for different values of \(\gamma_{3}\). Zand and Ahmadian (2010) obtained the solution using finite element method. It is interesting to note that neglecting vdW force results in considerable higher pull-in voltage specifically at high axial compressive force. The difference becomes smaller as the axial force changes to tensile from compressive.

Fig. 3
figure 3

a Variation of voltage parameter \(\beta V_{DC}^{2}\) with mid-point deflection \(y_{mid}\) for two different situations, one ignoring the effect vdW force (i.e. for \(\gamma_{3} = 0\)) depicted with hollow symbols and the other considering the effect vdW force (i.e. for \(\gamma_{3} = 10\)) depicted with filled symbols, for values of axial force varying from compressive to tensile, where \(N_{buc }\) is dimensionless buckling load b Variation of electrostatic force \(F_{\beta }\), electrostatic force along with vdW force \(F_{\beta } + F_{vdW}\) and elastic restoring force \(F_{r}\) with mid-point deflection \(y_{mid}\) for \(\beta V_{DC}^{2}\) = 30

Full size image

The effect of vdW force under axial load is explained with a parametric study using single mode ROM. Single mode ROM Eq. (11) is consisting of three parts. The first part due to electrostatic actuation force including first order fringing field correction \(F_{\beta } = \beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1} \frac{1}{{\left( {1 - a_{1} \emptyset_{1} } \right)^{2} }}dx} + f\beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1} \frac{1}{{\left( {1 - a_{1} \emptyset_{1} } \right)}}dx},\) second part due to vdW force \(F_{vdW} = \gamma_{3} \int_{0}^{1} {\emptyset_{1} \frac{1}{{\left( {1 - a_{1} \emptyset_{1} } \right)^{3} }}dx}\) and third part due to elastic restoring forces \(F_{r} = \omega_{1}^{2} a_{1} + \alpha \left( {\int_{0}^{1} {\emptyset_{1}^{2} dx} } \right)^{2} a_{1}^{3}\).

Figure 3b shows the relationship of \(F_{r}\), \(F_{\beta } + F_{vdW}\) and \(F_{\beta }\) versus mid- point deflection \(y_{mid}\) for three values of axial force at \(\beta V_{DC}^{2}\) = 30 (shown with dashed line in Fig. 3a). The curves of \(F_{r}\) and \(F_{\beta }\) intersect at two points when mid-point deflection varies from 0 to 1. These intersections of curves—depicted with unfilled symbols—are static solution neglecting vdW force. Similarly, intersections of curves \(F_{r}\) and \(F_{\beta } + F_{vdW}\)—depicted with filled symbols—provide static solution considering the vdW force. \(F_{r}\) and \(F_{\beta }\) curves intersect first at lower value of mid-point deflection is stable solution and the second intersection at higher value of mid-point deflection is unstable solutions. Likewise, there are stable and unstable solutions from the intersections of curves \(F_{r}\) and \(F_{\beta } + F_{vdW}\). It can be seen that there is negligible difference in \(F_{\beta }\) curves for different value of axial force and the same can also be observed for \(F_{\beta } + F_{vdW}\) curves. This is due to non-dependency of \(F_{\beta }\) and \(F_{vdW}\) directly on axial force. \(F_{r}\) increases as axial force becomes tensile from compressive because first natural frequency of undeflected beam \(\omega_{1}\) increases with axial force (refer Table 3). \(F_{r}\) and \(F_{\beta }\) curves intersect first at lower value of mid-point deflection, therefore stable solution decreases with increase in value of axial force at a particular value of voltage parameter. \(F_{\beta } + F_{vdW}\) curves are always above the \(F_{\beta }\) curves when mid-point deflection increases from 0 to 1 and hence, stable solution considering vdW force is always at higher value of mid-point deflection than that of stable solution neglecting vdW forces.

Table 3 Dimensionless first natural frequency \(\left( {\omega_{1} } \right)\) normalised with dimensionless first natural frequency at zero axial force (\(\omega_{01}\)) for normalised axial force varying from compressive to tensile
Full size table

The effect of vdW force on voltage parameter at pull-in \(\left( {\beta V_{DC}^{2} } \right)_{PI}\) and mid-point deflection at pull-in \((y_{mid} )_{PI}\) of fixed–fixed nano-beam is presented in Figs. 4 and 5 respectively for different values of axial force. It can be seen from Fig. 4 that with increase in \(\gamma_{3}\), the voltage parameter at pull-in decreases. The increase in \(\gamma_{3}\) specifies the increase in vdW force (increase in interaction force), which in turn leads to decrease in pull-in voltage. When the separation distance of the beam and fixed electrode is very much less than width of the beam (g ≪ b), the influence of fringing field can be ignored. Hence, \(\frac{g}{b}\sim0\) indicates that the effect of fringing field is neglected. However, when the separation distance of the beam and fixed electrode is comparable to beam width, it is important to take into account the effect of fringing field as with the increase in \(\frac{g}{b}\), the effect of fringing field becomes stronger, thus affecting the pull-into occur at lower applied voltage. The results presented for voltage parameter at pull-in are without and with consideration of fringing field effect in Fig. 4a, b respectively.

Fig. 4
figure 4

Effect of vdW force on voltage parameter at pull-in \(\left( {\beta V_{DC}^{2} } \right)_{PI}\) considering different values of axial force for mid-plane stretching parameter \(\alpha\) = 30

Full size image
Fig. 5
figure 5

Effect of vdW force on mid-point deflection at pull-in \(\left( {y_{mid} } \right)_{PI}\) considering different values of axial force for \(\alpha\) = 30

Full size image

Figure 5 shows that the mid-point deflection at pull-in decreases with increase in \(\gamma_{3}\). The effect of axial load on pull-in parameters \(\left( {\beta V_{DC}^{2} } \right)_{PI}\) and \((y_{mid} )_{PI}\) of fixed–fixed nano-beam for different values of \(\gamma_{3}\) is shown in Figs. 6 and 7 respectively. The effect of vdW force on mid-point deflection of fixed–fixed beam at pull-in \((y_{mid} )_{PI}\) is presented in Fig. 5. As discussed earlier, the increase in \(\gamma_{3}\) indicates the increase in interaction force (i.e. vdW force), causes the pull-into occur earlier and hence mid-point deflection at pull-in decreases, which can be observed from Fig. 5. It can also be concluded that as the tensile axial load induces in the beam, the structure’s capacity to resist the applied forces increases. As a result, the deflection at pull-in decreases (Figs. 5, 7) and pull-in voltage increases (Fig. 6). It is observed from Figs. 6 and 7 that presence of high axial compressive force leads to significant decrease in pull-in voltage and increase in the mid-point deflection of the fixed–fixed nano-beam. The results of the current work for \(N = 0\) is compared with the results of Tahani and Askari (2014) in Figs. 4 and 6. The result of the present work shows good agreement with the reported results. Note that Tahani and Askari (2014) obtained the solution using single mode ROM.

Fig. 6
figure 6

Effect of axial force on voltage parameter at pull-in \(\left( {\beta V_{DC}^{2} } \right)_{PI}\) for different values of \(\gamma_{3}\) and \(\alpha = 30\)

Full size image
Fig. 7
figure 7

Effect of axial force on mid-point deflection at pull-in \(\left( {y_{mid} } \right)_{PI}\) for different values of \(\gamma_{3}\) and \(\alpha = 30\)

Full size image

4.3 Free vibration characteristics

Linear free vibration at deflected position of the beam is analysed to obtain the variation of first natural frequency versus voltage parameter. Figure 8 shows the variation of dimensionless first natural frequency at deflected state of the beam \(\left( {\omega_{df} } \right)\) with applied V DC for two different situations, one ignoring the effect vdW force (i.e. for \(\gamma_{3}\) = 0) depicted with hollow symbols and the other considering the effect vdW force (i.e. for \(\gamma_{3}\) = 10) depicted with filled symbols. The general behavior of \(\omega_{df}\) is non-monotonous except at high tensile force. It is interesting to note that, neglecting vdW force results in higher value of \(\omega_{df}\) for tensile force. However, the difference is more pronounced at higher voltage parameter. Moreover, with compressive force, the tunability of \(\omega_{df}\) increases remarkably. It is evident from Fig. 8 that neglecting vdW force for the beam with high compressive force results in overestimation of tunability value of \(\omega_{df}\). For compressive force equals to −0.9 \(N_{buc}\) considering vdW force, \(\omega_{df}\) of the beam for \(\beta V_{DC}^{2}\) = 0 is 13.58 and at \(\beta V_{DC}^{2}\) = 36 it reaches to 25.95. While neglecting vdW force, \(\omega_{df}\) of the beam for \(\beta V_{DC}^{2}\) = 0 is 7.1914 and at \(\beta V_{DC}^{2}\) = 54 it reaches to 28.56.

Fig. 8
figure 8

Variation of dimensionless first natural frequency at deflected state of the beam \(\left( {\omega_{df} } \right)\) with applied V DC for two different situations, one ignoring the effect vdW force (i.e. for \(\gamma_{3} = 0\)) depicted with hollow symbols and the other considering the effect vdW force (i.e. for \(\gamma_{3} = 10\)) depicted with filled symbols when \(\alpha = 30\)

Full size image

The behavior of \(\omega_{df}\) considering vdW force can be described using single mode ROM. Left hand side of the single mode ROM Eq. (18) represents difference of the square of first dimensionless natural frequency at statically deflected position of the beam and square of first dimensionless natural frequency of undeflected beam. Right side of the Eq. (18) consists of three terms. First term defined as \(W_{m} = 3\alpha \left({\int_{0}^{1} {\emptyset_{1}^{\prime 2} dx}} \right)^{2} a_{1s}^{2}\) represents increase in natural frequency due to mid-plane stretching, the second term \(W_{\beta } = 2\beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left( {1 - a_{1s} \emptyset_{1} } \right)^{3} }}dx} + f\beta V_{DC}^{2} \int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left( {1 - a_{1s} \emptyset_{1} } \right)^{2} }}dx}\) and the third term \(W_{vdW } = 3\gamma_{3} \int_{0}^{1} {\emptyset_{1}^{2} \frac{1}{{\left( {1 - a_{1s} \emptyset_{1} } \right)^{4} }}dx}\) with negative sign represent decrease in natural frequency due to electrostatic force and vdW force respectively.

Figure 9a, b show the variation of parameters \(W_{m}\), \(W_{\beta }\), and \(W_{\beta } + W_{vdW }\) as a function of mid-point deflection \(y_{mid}\) for axial force equals to −0.9 \(N_{buc}\) and 0.9 \(N_{buc}\) respectively. These curves are plotted for \(\beta V_{DC}^{2}\) = 9 and \(\beta V_{DC}^{2}\) = 45. The curves of \(W_{m}\) and \(W_{\beta }\) as well as curves of \(W_{m}\) and \(W_{\beta } + W_{vdW }\) intersect at two points. The \(y_{mid}\) solutions are depicted in Fig. 9a for both \(\beta V_{DC}^{2}\) = 9 and \(\beta V_{DC}^{2}\) = 45, which lie between first and second intersection of curves \(W_{m}\) and \(W_{\beta }\), and between these intersection points \(W_{m}\) is always above \(W_{\beta }\). In a similar manner, \(y_{mid}\) solutions for both \(\beta V_{DC}^{2}\) = 9 and \(\beta V_{DC}^{2}\) = 45 also lie between the first and second intersection of curves \(W_{m}\) and \(W_{\beta } + W_{vdW }\), and between these intersection points \(W_{m}\) is always above \(W_{\beta } + W_{vdW }\). This indicates the dominance of non-linearity due to mid-plane stretching over electrostatic force and vdW force. Therefore, \(\omega_{df}\) is greater than \(\omega_{1}\) for both values of \(\beta V_{DC}^{2}\) (refer Fig. 8 for \(N\) = −0.9 \(N_{buc}\)). From the \(y_{mid}\) solution depicted in Fig. 9a, it can be seen that difference in parameters \(W_{m}\) and \(W_{\beta }\) is less than \(W_{m}\) and \(W_{\beta } + W_{vdW }\) for \(\beta V_{DC}^{2}\) = 9. This indicates the dominance of vdW force over electrostatic force. Therefore at \(\beta V_{DC}^{2}\) = 9, \(\omega_{df}\) considering vdW force is more than that neglecting vdW force. While at \(\beta V_{DC}^{2}\) = 45 difference in parameters \(W_{m}\) and \(W_{\beta }\) is more than \(W_{m}\) and \(W_{\beta } + W_{vdW }\), which indicates the dominance of electrostatic force over vdW force, Hence, \(\omega_{df}\) considering vdW force is less than that neglecting vdW force.

Fig. 9
figure 9

Variation of parameters \(W_{m}\), \(W_{\beta }\) and \(W_{\beta } + W_{vdW }\) with mid-point deflection \(y_{mid}\) for a compressive axial force (−0.9 \(N_{buc}\)) and b tensile axial force (0.9 \(N_{buc} )\) when \(\alpha = 30\)

Full size image

In Fig. 9b, the \(y_{mid}\) solutions are depicted for \(\beta V_{DC}^{2}\) = 9 and \(\beta V_{DC}^{2}\) = 45 with axial force equals to 0.9 \(N_{buc}\). In this case, both \(y_{mid}\) solutions lie before the first intersection of curves \(W_{m}\) and \(W_{\beta }\), and in this region \(W_{\beta }\) remains above \(W_{m}\). In a similar manner, both \(y_{mid}\) solutions considering vdW force also lie before the first intersection of curves \(W_{m}\) and \(W_{\beta } + W_{vdW }\), where \(W_{\beta } + W_{vdW }\) remains above \(W_{m}\). This indicates the dominance of electrostatic and vdW force over mid-plane stretching. Therefore, \(\omega_{df}\) is less than \(\omega_{1}\) for both voltage parameters (refer Fig. 8 for \(N\) = 0.9 \(N_{buc}\)). The magnified view of detail at ‘A’ shows that difference in parameters \(W_{m}\) and \(W_{\beta }\) is less than \(W_{m}\) and \(W_{\beta } + W_{vdW }\) for \(y_{mid}\) solutions depicted for \(\beta V_{DC}^{2}\) = 9 and \(\beta V_{DC}^{2}\) = 45. This indicates the dominance of vdW force over electrostatic force. Therefore, difference between \(\omega_{df}\) and \(\omega_{1}\) considering vdW force is higher than ignoring vdW force. Hence, \(\omega_{df}\) considering vdW force is less than that ignoring vdW force. In this case, \(\omega_{df}\) decreases monotonously with an increase in \(\beta V_{DC}^{2}\).

While Fig. 8 shows variation in \(\omega_{df}\) with applied V DC for \(\gamma_{3} = 0\) and \(\gamma_{3} = 10\) at five different values of N, Fig. 10a shows the variation in \(\omega_{df}\) with applied V DC for \(N\) = −0.9 \(N_{buc}\) and five different values of \(\gamma_{3}\). It is found from Fig. 10a that the tunability of \(\omega_{df}\) decreases with increase in value of \(\gamma_{3}\). Figure 10b shows the effect of mid plane stretching parameter on \(\omega_{df}\) for \(N\) = −0.9 \(N_{buc}\). It is found from Fig. 10b that the tunability of \(\omega_{df}\) increases with increase in value of \(\alpha\). These results indicate that frequency can be tuned to some hundred percent with proper combination of \(\alpha\) and \(\gamma_{3}\). The same can be observed from Fig. 10b for value of \(\alpha\) = 40 and \(\gamma_{3}\) = 10. Further as described earlier, Fig. 10a shows that the increase in \(\gamma_{3}\) (increase in vdW force) strengthen the pulling forces which result in the decrease in pull-in voltage, whereas, Fig. 10b shows that the increase in α (due to increase in gap between beam and fixed electrodes) in turn decreases the electrostatic force which delays the pull-in and hence pull-in voltage increases.

Fig. 10
figure 10

Variation of dimensionless natural frequency at deflected state \(\omega_{df}\) for a different values of \(\gamma_{3}\) and b different values of \(\alpha\)

Full size image

4.4 Frequency stability characteristics

Figure 11 shows the relationship of \(\omega_{df}\) with variation of axial force ranging from compressive to tensile. The change in temperature develops axial stresses which result in change in natural frequency as described earlier (refer Table 3). Note that the range of deviation of \(\omega_{df}\) owing to change in axial load N at specific value of V DC reduces as the applied DC voltage increases (Fig. 11). This indicates that sensitivity of \(\omega_{df}\) to axial load reduces at deflected position of the beam in relation to undeflected position of the beam (also refer Fig. 8). Moreover, Fig. 11 shows that frequency stability is observed at \(\beta V_{DC}^{2}\) = 63 without considering vdW force, but it is interesting to note that the frequency stability is achieved at \(\beta V_{DC}^{2}\) = 45 considering vdW force. This important observation shows that ignoring vdW force may lead to wrong estimation voltage parameter at which frequency stability can be achieved.

Fig. 11
figure 11

Relationship of dimensionless natural frequency at deflected state \(\omega_{df}\) with axial force ranging from compressive to tensile for different values of voltage parameter \(\beta V_{DC}^{2}\) when \(\alpha = 30\), \(\gamma_{3} = 10\)

Full size image

Similar to discussion for static analysis and frequency characteristic mentioned in previous sections, here also frequency stability is explained with single mode ROM (18). Figure 12 shows relationship of parameters \(\omega_{1}^{2} + W_{m}\) and \(W_{\beta } + W_{vdW }\) versus mid-point deflection. These curves are plotted for various combinations of voltage parameter and axial force. Single mode ROM (18) gives square of \(\omega_{df}\) equals to difference of parameter \(\omega_{1}^{2} + W_{m}\) and \(W_{\beta } + W_{vdW }\). The parameter \(\omega_{1}^{2} + W_{m}\) is independent of DC voltage and depends on axial force. Therefore, there are two curves for the parameter related to different values of axial force. The parameter \(W_{\beta } + W_{vdW }\) does not depend on axial force directly. Hence, there are three curves for the parameter related to different values of voltage parameter. It can be observed from the Fig. 12 that the difference in parameters \(\omega_{1}^{2} + W_{m}\) and \(W_{\beta } + W_{vdW }\) decreases as voltage parameter increases for variation in axial force. As shown in Fig. 12 difference in these parameters is very less when \(\beta V_{DC}^{2}\) = 45 for the study with beam under vdW force. This indicates that for \(\beta V_{DC}^{2}\) = 45, change in \(\omega_{df}\) is insignificant with change in axial force.

Fig. 12
figure 12

Variation of parameters \(\omega_{1}^{2} + W_{m}\) and \(W_{\beta } + W_{vdW }\) with mid-point deflection \(y_{mid}\) for various combination of voltage parameter and axial force when \(\alpha = 30\), \(\gamma_{3} = 10\)

Full size image

The stability of natural frequency at deflected state of beam with change in temperature is an important consideration in nano-beam oscillators design. The dimensions of the beam should be selected in such a way that first natural frequency in deflected state of the beam is the desired resonant frequency instead of first natural frequency of the straight beam. Similar observation were reported by Bhushan et al. (2011) while studying the frequency stability characteristic ignoring vdW force. As shown in Fig. 11, there is significant influence of vdW force on frequency stability characteristics. The appropriate voltage parameter is to be found from (11) and (18) to design beam which gives high frequency stability under variation of temperature.

5 Conclusions

In this study, the two-point boundary value problem of clamped–clamped nano-beam subject to the electrostatic force and van der Waals force is investigated. The modelling of the electrostatic force takes into consideration the effect of fringing field. The obtained governing equation is nonlinear as a result of the geometric nonlinearity due to mid-plane stretching, and also due to inherent nonlinearity of electrostatic force and van der Waals force. The governing nonlinear differential equation is converted to non-linear algebraic equation using Galerkin based reduced order model. The effect of van der Waals force on static pull-in instability and free vibration characteristics of beams under axial force is investigated. The detailed investigations of the problem is deliberated by means of the single mode ROM which represents the single degree of freedom equation.

The presence of van der Waals force reduces pull-in voltage and pull-in displacement. The reduction in the pull-in parameters due to van der Waals force is considerable for beam with high axial compressive force. The pull-in voltage decreases and mid-point deflection at pull-in increases as the tensile force becomes compressive. The existence of high compressive force increases tunability of natural frequency at deflected state of beam. However, this higher tunability of resonance frequency at high compressive force decreases when effect of van der Waals force is taken into account. In case of nano beam under high axial compressive initial stress along with suitable combination of mid-plane stretching and van der Waals force parameters, frequency can be tuned for some hundred percent.

With variation in axial force, minimal frequency variation is observed at high value of voltage parameter. The presence of van der Waals force reduces the magnitude of voltage parameter at which frequency stability can be obtained. This stability of natural frequency with variation of axial force can be successfully employed in the design of oscillators. The results of the current study provide useful information for design of nano-beam oscillators, which is considered to be vital in understanding the application.