1 Introduction

The Micro/Nano-Electro-Mechanical Systems (MEMS/NEMS) have various unique advantages such as small size, high precision and low power consumption. Among MEMS/NEMS, the micro/nanobeam system is one of the most studied in the literature, and the applications such as switches and non-volatile memories have been found in these systems (Brown 1998; Charlot et al. 2008; Intaraprasonk and Fan 2011; Jang et al. 2008; Roodenburg et al. 2009; Rueckes et al. 2000). The micro/nanobeams can also be driven to vibration by an Alternating Current (AC) voltage, and the obtained micro/nano-resonators can be used as mass sensors, temperature sensors, transmitters and receivers (Burg et al. 2007; Chaste et al. 2012; Chiu et al. 2008; Eltaher et al. 2016; Hopcroft et al. 2007; Kivi et al. 2015; Kwon et al. 2008; Mohanty 2005; Peng et al. 2006; Southworth et al. 2010; Wang and Arash 2014; Yang et al. 2006).

Theoretical and experimental studies on the primary resonance frequency of the micro/nano-resonator have been conducted in the literature, and the evolutions of resonance frequency with the applied AC voltage and a biased DC (direct current) voltage have been largely reported (Jia et al. 2012; Jonsson et al. 2004; Kuang and Chen 2004; Tilmans and Legtenberg 1994). The dynamic behavior of the micro/nano-resonator have also been reported, and the frequency response curves of linear, hardening, and softening characteristics have been observed in the experiments (Almog et al. 2007; Alsaleem et al. 2009; Badzey et al. 2004; Carr et al. 1999; Evoy et al. 1999; Mestrom et al. 2008; Ruzziconi et al. 2013; Tilmans and Legtenberg 1994; Zook et al. 1992) as well as predicted from the theoretical investigations (Caruntu and Knecht 2011; Caruntu et al. 2013; Caruntu and Martinez 2014; Farokhi and Ghayesh 2015a, b; Gui et al. 1998; Kacem et al. 2011; Kim and Lee 2013; Ouakad and Younis 2010; Rhoads et al. 2006; Ruzziconi et al. 2013).

Careful literature review indicates that most of the work is concerned with the micro/nano-resonator biased by a DC voltage. Caruntu and Knecht (2011), Caruntu et al. (2013), and Caruntu and Martinez (2014) studied theoretically a non-biased cantilever-type micro-resonator, and the dynamic pull-in near the primary resonance regime was found. Moreover, most work is conducted at a certain level of the applied voltages, and one characteristic feature of the dynamic behavior is observed or predicted. Studies concerned with characterizing the dynamic behavior of the micro/nano-resonator at different levels of the applied voltages and determining the parameters which govern the dynamic behavior characteristics are limited.

In this paper, we extend the earlier work to study the dynamic behavior of the non-biased micro-resonator at different levels of AC voltage. The remaining parts of the paper are organized as follows. Section 2 is devoted to the beam model formulation. In Sect. 3, the methods of multiple scales and long-time integration are presented to obtain respectively the steady-state frequency response and the transient response of the microbeam from the beam model. Various effects on the dynamic behavior of the microbeam are investigated in Sect. 4, including the effects of mid-plane stretching, fringing field, damping, and boundary conditions. A design diagram in terms of AC voltage amplitude and mid-plane stretching parameter is also developed, indicating the domains of different characteristic features of the dynamic behavior. Finally, a general conclusion is given in Sect. 5.

2 Model formulation

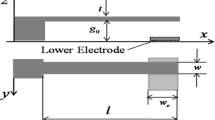
The situation envisaged is that of an electrically actuated rectangular microbeam of length L, width b and thickness h, as depicted in Fig. 1. Suppose that the displacements u x , u y and u z of any point in the beam only depend on x- and z-coordinate, and u y is equal to 0, i.e., no displacement along y-coordinate. Further suppose that the studied microbeam is thin (h ≪ L), then the Euler–Bernoulli beam theory can be applied as:

$$u_{x} (x,z,t) = u(x,t) - z\frac{\partial w}{\partial x}(x,t)$$
(1a)
$$u_{z} (x,z,t) = w(x,t)$$
(1b)

where t is time, u and w are respectively the axial (along x-coordinate) and transverse (along z) displacements of a point on the mid-plane of the beam. The von Karman nonlinear strain is used to account for the geometric nonlinearity due to mid-plane stretching. Therefore, the only nonzero strain component from Eq. (1) is (Reddy 2011):

$$\varepsilon_{xx} = \frac{{\partial u_{x} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial u_{z} }}{\partial x}} \right)^{2} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2}$$
(2)

Considering Eq. (2), we calculate the variation δU elas of the elastic strain energy as:

$$\delta U_{elas} = \int_{0}^{L} {\int_{S} {\left( {\underline{\underline{\sigma }} :\delta \underline{\underline{\varepsilon }} } \right)} \, ds \, dx}$$
$$\begin{aligned} = - \int_{0}^{L} {\frac{\partial N(x,t)}{\partial x}\delta u \, dx} - \int_{0}^{L} {\left( {\frac{{\partial^{2} M(x,t)}}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {N(x,t)\frac{\partial w}{\partial x}} \right)} \right)\delta w \, dx} \\ \quad + \left. {N(x,t)\delta u} \right|_{x = 0}^{L} + \left. {\left( {\frac{\partial M(x,t)}{\partial x} + N(x,t)\frac{\partial w}{\partial x}} \right)\delta w} \right|_{x = 0}^{L} - \left. {M(x,t)\frac{\partial \delta w}{\partial x}} \right|_{x = 0}^{L} \\ \end{aligned}$$
(3)

where ∫ S ds is the integral over the cross section, i.e., the y–z plane in Fig. 1; the axial force N and the bending moment M are defined as follows:

$$N = \int_{S} {\sigma_{xx} ds}$$
(4a)
$$M = \int_{S} {z\sigma_{xx} ds}$$
(4b)

The variation δE k of the kinetic energy is calculated with the aid of Eq. (1) as:

$$\delta E_{k} = \int_{0}^{L} {\int_{S} {\rho \left( {\frac{{\partial u_{x} }}{\partial t}\frac{{\partial \delta u_{x} }}{\partial t} + \frac{{\partial u_{z} }}{\partial t}\frac{{\partial \delta u_{z} }}{\partial t}} \right)ds} \, dx}$$
$$= \int_{0}^{L} {\left( {\rho S\left( {\frac{\partial u}{\partial t}\frac{\partial \delta u}{\partial t} + \frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}} \right) + \rho I\left( {\frac{{\partial^{2} w}}{\partial x\partial t}\frac{{\partial^{2} \delta w}}{\partial x\partial t}} \right)} \right)dx}$$
(5)

where ρ is the mass density, S (=bh) is the cross-sectional area, and I (=bh 3/12) is the second moment of area.

Fig. 1
figure 1

Clamped–clamped microbeam actuated by alternating current voltage. The arrow indicates the direction of the induced distributed electrostatic force

Full size image

The variation δW ext of the work done by the external forces is:

$$\delta W_{ext} = \int_{0}^{L} {\left( {f_{damp} + f_{elec} } \right)\delta w \, dx}$$
(6)

where f damp and f elec are respectively the viscous damping force and the electrostatic force per unit length. We can estimate f damp as:

$$f_{damp} = - c_{d} \frac{\partial w}{\partial t}$$
(7)

with c d being the damping coefficient per unit length. Considering a small gap (≪ beam length) between the beam and the electrode, we can regard the beam and the electrode as a parallel-plate capacitor. To further consider the fringing fields at the edges of the microbeam, Palmer’s formula (Palmer 1937) is used, and the electrostatic force f elec is calculated as (Caruntu and Knecht 2011; Gupta 1997):

$$f_{elec} = \frac{1}{2}\frac{{\varepsilon_{0} b\left( {V_{AC} \cos (\omega t)} \right)^{2} }}{{(g_{0} - w)^{2} }}\left( {1 + 0.65\frac{{g_{0} - w}}{b}} \right)$$
(8)

where ε 0 (=\(8.8542 \times 10^{ - 12} {\text{ F}} \cdot {\text{m}}^{ - 1}\)) is the vacuum permittivity, b is the beam width, g 0 is the initial gap between the beam and the rigid electrode, as shown in Fig. 1, and V AC is the amplitude of the applied AC voltage with the angular velocity ω. It is noted that Palmer’s formula is only valid for wide microbeams, i.e., b > 5 h and b > 10g 0 (Caruntu and Knecht 2011). When the beam is narrow, more complicated formulae such as (Batra et al. 2006; van der Meijs and Fokkema 1984) should be used.

Introducing Eqs. (3), (5) and (6) into the following Hamilton’s principle

$$\int_{0}^{{t_{1} }} {\left( {\delta E_{k} + \delta W_{ext} - \delta U_{elas} } \right)dt = 0}$$
(9)

and integrating the result by parts with respect to t and x, we arrive at:

$$\begin{aligned} \int_{0}^{{t_{1} }} {\int_{0}^{L} {\left( {\frac{\partial N}{\partial x} - \rho S\frac{{\partial^{2} u}}{{\partial t^{2} }}} \right)\delta u \, dx \, dt} } \hfill \\ \quad + \int_{0}^{{t_{1} }} {\int_{0}^{L} {\left( {\frac{{\partial^{2} M}}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {N\frac{\partial w}{\partial x}} \right) + f_{damp} + f_{elec} -\, \rho S\frac{{\partial^{2} w}}{{\partial t^{2} }} + \rho I\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right)\delta w \, dx \, dt} } \hfill \\ \quad + \int_{0}^{{t_{1} }} {\left( { - N\delta u - \left( {\frac{\partial M}{\partial x} + N\frac{\partial w}{\partial x} + \rho I\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}} \right)\delta w + M\frac{\partial \delta w}{\partial x}} \right)_{x = 0}^{L} dt} \hfill \\ \quad + \int_{0}^{L} {\left( {\rho S\frac{\partial u}{\partial t}\delta u + \rho S\frac{\partial w}{\partial t}\delta w + \rho I\frac{{\partial^{2} w}}{\partial x\partial t}\frac{\partial \delta w}{\partial x}} \right)_{t = 0}^{{t_{1} }} \, dx = 0} \hfill \\ \end{aligned}$$
(10)

The following governing equations can be obtained from Eqs. (7), (8) and (10):

$$\delta u:\frac{\partial N}{\partial x} - \rho S\frac{{\partial^{2} u}}{{\partial t^{2} }} = 0$$
(11a)
$$\delta w:\frac{{\partial^{2} M}}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {N\frac{\partial w}{\partial x}} \right) - \rho S\frac{{\partial^{2} w}}{{\partial t^{2} }} + \rho I\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} - c_{d} \frac{\partial w}{\partial t} + \frac{1}{2}\frac{{\varepsilon_{0} b\left( {V_{AC} \cos (\omega t)} \right)^{2} }}{{(g_{0} - w)^{2} }}\left( {1 + 0.65\frac{{g_{0} - w}}{b}} \right) = 0$$
(11b)

Since the studied microbeam is thin (thickness ≪ length), the axial displacement u and the beam curvature \(\frac{{\partial^{2} w}}{{\partial x^{2} }}\) are quite small and negligible with respect to the transverse displacement w. As a result, we neglect the axial inertia term \(\rho S\frac{{\partial^{2} u}}{{\partial t^{2} }}\) and the rotational inertia term \(\rho I\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}\) in Eq. (11), and obtain:

$$\delta u:\frac{\partial N}{\partial x} = 0$$
(12a)
$$\begin{aligned} \delta w:\frac{{\partial^{2} M}}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left( {N\frac{\partial w}{\partial x}} \right) - \rho S\frac{{\partial^{2} w}}{{\partial t^{2} }} - c_{d} \frac{\partial w}{\partial t} \hfill \\ \quad { + }\frac{1}{2}\frac{{\varepsilon_{0} b\left( {V_{AC} \cos (\omega t)} \right)^{2} }}{{(g_{0} - w)^{2} }}\left( {1 + 0.65\frac{{g_{0} - w}}{b}} \right) = 0 \hfill \\ \end{aligned}$$
(12b)

with Eqs. (12a), (12b) can be reduced to:

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} + N\frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho S\frac{{\partial^{2} w}}{{\partial t^{2} }} - c_{d} \frac{\partial w}{\partial t} + \frac{1}{2}\frac{{\varepsilon_{0} b\left( {V_{AC} \cos (\omega t)} \right)^{2} }}{{(g_{0} - w)^{2} }}\left( {1 + 0.65\frac{{g_{0} - w}}{b}} \right) = 0$$
(13)

Suppose that the beam material is elastically isotropic with Young’s modulus E and Poisson’s ratio ν. Then the 1D constitutive relation becomes:

$$\sigma_{xx} = E^{*} \varepsilon_{xx}$$
(14)

where E * is the effective Young’s modulus. We take E * = E/(1 − ν 2) for the wide microbeam studied here. When the beam is narrow, E * = E. Introducing Eqs. (2) and (14) into Eq. (4), we have:

$$N = E^{*} S\left( {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right)$$
(15a)
$$M = - E^{*} I\frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(15b)

Equation (12a) shows that the axial force N is constant along x-coordinate. Using Eq. (15a), we estimate N as the following average value:

$$N = \frac{{E^{*} S}}{2L}\left( {\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} dx} } \right)$$
(16)

To obtain Eq. (16), we have used the boundary conditions of clamped–clamped beam, i.e., u(0) = u(L) = 0. Introducing Eqs. (15b) and (16) into Eq. (13), we obtain:

$$\rho S\frac{{\partial^{2} w}}{{\partial t^{2} }} + c_{d} \frac{\partial w}{\partial t} + E^{*} I\frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{E^{*} S}}{2L}\left( {\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} dx} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} = \frac{1}{2}\frac{{\varepsilon_{0} b\left( {V_{AC} \cos (\omega t)} \right)^{2} }}{{(g_{0} - w)^{2} }}\left( {1 + 0.65\frac{{g_{0} - w}}{b}} \right)$$
(17)

Considering the dimensionless quantities in Table 1, we rewrite Eq. (17) in the following dimensionless form:

$$\frac{{\partial^{2} \overline{w} }}{{\partial \overline{t}^{2} }} + \overline{{c_{d} }} \frac{{\partial \overline{w} }}{{\partial \overline{t} }} + \frac{{\partial^{4} \overline{w} }}{{\partial \overline{x}^{4} }} - \alpha \left( {\int_{0}^{1} {\left( {\frac{{\partial \overline{w} }}{{\partial \overline{x} }}} \right)^{2} d\overline{x} } } \right)\frac{{\partial^{2} \overline{w} }}{{\partial \overline{x}^{2} }} = \left( {\overline{{V_{AC} }} \cos (\overline{\omega } \overline{t} )} \right)^{2} \left( {\frac{1}{{\left( {1 - \overline{w} } \right)^{2} }} + \frac{\beta }{{\left( {1 - \overline{w} } \right)}}} \right)$$
(18)

In Eq. (18), the 4th term on the left-hand-side with a stretching parameter α represents the effect of mid-plane stretching, which stiffens the microbeam. The dimensionless boundary conditions of the clamped–clamped microbeam are:

$$\delta \overline{w} :\overline{w} (0,\overline{t} ) = 0,\quad \overline{w} (1,\overline{t} ) = 0$$
(19a)
$$\frac{{\partial \delta \overline{w} }}{{\partial \overline{x} }}:\frac{{\partial \overline{w} }}{{\partial \overline{x} }}(0,\overline{t} ) = 0,\quad \frac{{\partial \overline{w} }}{{\partial \overline{x} }}(1,\overline{t} ) = 0$$
(19b)
Table 1 Dimensionless quantities adopted in the study
Full size table

3 Solution methodology

3.1 Method of multiple scales

The micro-resonator is usually vibrating at low amplitude with small damping effect. In this case, the method of multiple scales can be used (Caruntu and Knecht 2011; Ouakad and Younis 2010). Considering low vibration amplitude, small damping, and weak nonlinearity, we expand the electrostatic force around \(\overline{w} = 0\) in Eq. (18), and further set the electrostatic force, damping and mid-plane stretching terms to a slow scale by multiplying them by a small bookkeeping parameter ξ:

$$\begin{aligned} \frac{{\partial^{2} \overline{w} }}{{\partial \overline{t}^{2} }} + \xi \overline{{c_{d} }} \frac{{\partial \overline{w} }}{{\partial \overline{t} }} + \frac{{\partial^{4} \overline{w} }}{{\partial \overline{x}^{4} }} - \xi \alpha \left( {\int_{0}^{1} {\left( {\frac{{\partial \overline{w} }}{{\partial \overline{x} }}} \right)^{2} d\overline{x} } } \right)\frac{{\partial^{2} \overline{w} }}{{\partial \overline{x}^{2} }} \hfill \\ = \xi \left( {\overline{{V_{AC} }} \cos (\overline{\omega } \overline{t} )} \right)^{2} \left( {1 + \beta + \left( {2 + \beta } \right)\overline{w} + \left( {3 + \beta } \right)\overline{w}^{2} + \left( {4 + \beta } \right)\overline{w}^{3} } \right) \hfill \\ \end{aligned}$$
(20)

Introducing the first-order expansion of the dimensionless deflection \(\overline{w}\) as:

$$\overline{w} = \overline{w}_{0} (\overline{x} ,T_{0} ,T_{1} ) + \xi \overline{w}_{1} (\overline{x} ,T_{0} ,T_{1} )$$
(21)

with T 0 (=\(\overline{t}\)) being the fast time scale and T 1 (=\(\xi \overline{t}\)) being the slow time scale, we derive the following time derivatives from Eq. (21):

$$\frac{{\partial \overline{w} }}{{\partial \overline{t} }} = \frac{{\partial \overline{w}_{0} }}{{\partial T_{0} }} + \left( {\frac{{\partial \overline{w}_{0} }}{{\partial T_{1} }} + \frac{{\partial \overline{w}_{1} }}{{\partial T_{0} }}} \right)\xi + \frac{{\partial \overline{w}_{1} }}{{\partial T_{1} }}\xi^{2}$$
(22a)
$$\frac{{\partial^{2} \overline{w} }}{{\partial \overline{t}^{2} }} = \frac{{\partial^{2} \overline{w}_{0} }}{{\partial T_{0}^{2} }} + \left( {2\frac{{\partial^{2} \overline{w}_{0} }}{{\partial T_{0} \partial T_{1} }} + \frac{{\partial^{2} \overline{w}_{1} }}{{\partial T_{0}^{2} }}} \right)\xi + \left( {\frac{{\partial^{2} \overline{w}_{0} }}{{\partial T_{1}^{2} }} + 2\frac{{\partial^{2} \overline{w}_{1} }}{{\partial T_{0} \partial T_{1} }}} \right)\xi^{2} + \frac{{\partial^{2} \overline{w}_{1} }}{{\partial T_{1}^{2} }}\xi^{3}$$
(22b)

By introducing Eqs. (21) and (22) into Eqs. (19) and (20), and equating the like powers of ξ, we obtain:

Order ξ 0:

$$\frac{{\partial^{2} \overline{w}_{0} }}{{\partial T_{0}^{2} }} + \frac{{\partial^{4} \overline{w}_{0} }}{{\partial \overline{x}^{4} }} = 0$$
(23a)
$$\overline{w}_{0} (0,T_{0} ,T_{1} ) = 0, \, \overline{w}_{0} (1,T_{0} ,T_{1} ) = 0, \, \frac{{\partial \overline{w}_{0} }}{{\partial \overline{x} }}(0,T_{0} ,T_{1} ) = 0, \, \frac{{\partial \overline{w}_{0} }}{{\partial \overline{x} }}(1,T_{0} ,T_{1} ) = 0$$
(23b)

Order ξ 1:

$$\begin{aligned} \frac{{\partial^{2} \overline{w}_{1} }}{{\partial T_{0}^{2} }} + \frac{{\partial^{4} \overline{w}_{1} }}{{\partial \overline{x}^{4} }} & = - 2\frac{{\partial^{2} \overline{w}_{0} }}{{\partial T_{0} \partial T_{1} }} - \overline{{c_{d} }} \frac{{\partial \overline{w}_{0} }}{{\partial T_{0} }} + \alpha \left( {\int_{0}^{1} {\left( {\frac{{\partial \overline{w}_{0} }}{{\partial \overline{x} }}} \right)^{2} d\overline{x} } } \right)\frac{{\partial^{2} \overline{w}_{0} }}{{\partial \overline{x}^{2} }} \\ \quad + \left( {\overline{{V_{AC} }} \cos (\overline{\omega } T_{0} )} \right)^{2} \left( {1 + \beta + \left( {2 + \beta } \right)\overline{w}_{0} + \left( {3 + \beta } \right)\overline{w}_{0}^{2} + \left( {4 + \beta } \right)\overline{w}_{0}^{3} } \right) \\ \end{aligned}$$
(24a)
$$\overline{w}_{1} (0,T_{0} ,T_{1} ) = 0, \, \overline{w}_{1} (1,T_{0} ,T_{1} ) = 0, \, \frac{{\partial \overline{w}_{1} }}{{\partial \overline{x} }}(0,T_{0} ,T_{1} ) = 0, \, \frac{{\partial \overline{w}_{1} }}{{\partial \overline{x} }}(1,T_{0} ,T_{1} ) = 0$$
(24b)

Suppose that the solution to Eq. (23) is:

$$\overline{w}_{0} = \phi_{j} (\overline{x} )\left( {A(T_{1} )e^{{i\omega_{j} T_{0} }} + A^{*} (T_{1} )e^{{ - i\omega_{j} T_{0} }} } \right)$$
(25)

where A is a coefficient depending on the slow time scale T 1 and A * is its complex conjugate; ϕ j (j = 1, 2, …, n) is the jth linear undamped vibration mode of the clamped–clamped beam, being:

$$\phi_{j} (\overline{x} ) = C_{j} \left( {\cosh (\lambda_{j} \overline{x} ) - \cos (\lambda_{j} \overline{x} ) - \frac{{\sinh (\lambda_{j} ) + \sin (\lambda_{j} )}}{{\cosh (\lambda_{j} ) - \cos (\lambda_{j} )}}\left( {\sinh (\lambda_{j} \overline{x} ) - \sin (\lambda_{j} \overline{x} )} \right)} \right)$$
(26)

where C j is a constant satisfying \(\mathop {\hbox{max} }\limits_{{\overline{x} \in [0,1]}} \left| {\phi_{j} (\overline{x} )} \right| = 1\), and λ j is a frequency parameter satisfying cosh (λ j ) cos (λ j ) = 1. λ j is related to the resonance angular frequency ω j by: ω j  = λ 2 j . The micro-resonator usually works near the primary resonance regime, so we only consider the first vibration mode here, i.e., j = 1 in Eq. (25). The square of the applied voltage can be expressed as:

$$\left( {\overline{{V_{AC} }} \cos (\overline{\omega } T_{0} )} \right)^{2} = \frac{1}{2}\overline{{V_{AC} }}^{2} + \frac{1}{2}\overline{{V_{AC} }}^{2} \cos (2\overline{\omega } T_{0} )$$
(27)

Equation (27) shows that the microbeam vibrates at a frequency of \(2\overline{\omega }\). To indicate the nearness of \(2\overline{\omega }\) to the primary resonance frequency ω 1, a detuning parameter δ is introduced as:

$$2\overline{\omega } = \omega_{1} + \xi \delta$$
(28)

with Eqs. (28), (27) can be rewritten as:

$$\left( {\overline{{V_{AC} }} \cos (\overline{\omega } T_{0} )} \right)^{2} = \frac{1}{2}\overline{{V_{AC} }}^{2} + \frac{1}{4}\overline{{V_{AC} }}^{2} \left( {e^{{i(\omega_{1} T_{0} + T_{1} \delta )}} + e^{{ - i(\omega_{1} T_{0} + T_{1} \delta )}} } \right)$$
(29)

By introducing Eqs. (25) and (29) into the right-hand-side of Eq. (24a), we have:

$$\begin{aligned} \frac{{\partial^{2} \overline{w}_{1} }}{{\partial T_{0}^{2} }} + \frac{{\partial^{4} \overline{w}_{1} }}{{\partial \overline{x}^{4} }} & = c_{0} + \left( {c_{1} e^{{i\omega_{1} T_{0} }} + c_{1}^{*} e^{{ - i\omega_{1} T_{0} }} } \right) + \left( {c_{2} e^{{i(2\omega_{1} T_{0} )}} + c_{2}^{*} e^{{ - i(2\omega_{1} T_{0} )}} } \right) \\ \quad + \left( {c_{3} e^{{i(3\omega_{1} T_{0} )}} + c_{3}^{*} e^{{ - i(3\omega_{1} T_{0} )}} } \right) + \left( {c_{4} e^{{i(4\omega_{1} T_{0} )}} + c_{4}^{*} e^{{ - i(4\omega_{1} T_{0} )}} } \right) \\ \end{aligned}$$
(30)

with c 0 ~ c 4 being coefficients and \(c_{1}^{*} \sim c_{4}^{*}\) being the complex conjugates of c 1 ~ c 4. c 1 is calculated as:

$$\begin{aligned} c_{1} & = - 2i\omega_{1} \phi_{1} \frac{dA}{{dT_{1} }} - i\overline{{c_{d} }} \omega_{1} \phi_{1} A + 3\alpha \phi_{1}^{{\prime \prime }} \left( {\int_{0}^{1} {\left( {\phi_{1}^{{\prime \prime }} } \right)^{2} d\overline{x} } } \right)A^{2} A^{*} + \frac{1}{2}\left( {2 + \beta } \right)\overline{{V_{AC} }}^{2} \phi_{1} A \\ \quad + \frac{3}{2}\left( {4 + \beta } \right)\overline{{V_{AC} }}^{2} \phi_{1}^{3} A^{2} A^{*} + \frac{1}{4}\left( {1 + \beta } \right)\overline{{V_{AC} }}^{2} e^{{iT_{1} \delta }} + \frac{1}{2}\left( {3 + \beta } \right)\overline{{V_{AC} }}^{2} \phi_{1}^{2} AA^{*} e^{{iT_{1} \delta }} \\ \quad + \frac{1}{4}\left( {3 + \beta } \right)\overline{{V_{AC} }}^{2} \phi_{1}^{2} A^{2} e^{{ - iT_{1} \delta }} \\ \end{aligned}$$
(31)

where a superimposed apostrophe denotes a derivative with respect to the normalized coordinate \(\overline{x}\). The solvability condition states that the right-hand-side of Eq. (30) must be orthogonal to any solution of Eq. (23), which is expressed in Eq. (25) with j = 1 (Caruntu and Knecht 2011). Then we have:

$$c_{1} \phi_{1} = 0$$
(32)

Introducing Eq. (31) into Eq. (32) and integrating the result from \(\overline{x} = 0\) to 1, we obtain:

$$\begin{aligned} - 2i\omega_{1} m_{2} \frac{dA}{{dT_{1} }} - i\overline{{c_{d} }} \omega_{1} m_{2} A + 3\alpha s_{1} A^{2} A^{*} + \frac{1}{2}\left( {2 + \beta } \right)\overline{{V_{AC} }}^{2} m_{2} A + \frac{3}{2}\left( {4 + \beta } \right)\overline{{V_{AC} }}^{2} m_{4} A^{2} A^{*} \hfill \\ \quad + \frac{1}{4}\left( {1 + \beta } \right)\overline{{V_{AC} }}^{2} m_{1} e^{{iT_{1} \delta }} + \frac{1}{2}\left( {3 + \beta } \right)\overline{{V_{AC} }}^{2} m_{3} AA^{*} e^{{iT_{1} \delta }} + \frac{1}{4}\left( {3 + \beta } \right)\overline{{V_{AC} }}^{2} m_{3} A^{2} e^{{ - iT_{1} \delta }} = 0 \hfill \\ \end{aligned}$$
(33)

where the parameters are given below:

$$\begin{aligned} m_{1} = \int_{0}^{1} {\phi_{1} } d\overline{x} , \, m_{2} = \int_{0}^{1} {\phi_{1}^{2} } d\overline{x} , \, m_{3} = \int_{0}^{1} {\phi_{1}^{3} } d\overline{x} , \, m_{4} = \int_{0}^{1} {\phi_{1}^{4} } d\overline{x} \hfill \\ s_{1} = \left( {\int_{0}^{1} {\left( {\phi_{1} '} \right)^{2} d\overline{x} } } \right)\left( {\int_{0}^{1} {\phi_{1} \phi_{1} ''d\overline{x} } } \right) \hfill \\ \end{aligned}$$
(34)

Express A(T 1) in the following polar form:

$$A(T_{1} ) = \frac{1}{2}a(T_{1} )e^{{i\theta (T_{1} )}}$$
(35)

It can be derived from Eqs. (25) and (35) that a is the vibration amplitude. The time derivative can be obtained from Eq. (35) as:

$$\frac{dA}{{dT_{1} }} = \frac{1}{2}\left( {\frac{da}{{dT_{1} }}e^{i\theta } + a\frac{d\theta }{{dT_{1} }}ie^{i\theta } } \right)$$
(36)

Introducing Eqs. (35) and (36) into Eq. (33), separating the real and imaginary parts, and after several calculations we obtain:

$$\frac{da}{{dT_{1} }} = - \frac{{\overline{{c_{d} }} }}{2}a + \left( {\frac{{m_{1} }}{{4m_{2} \omega_{1} }}\left( {1 + \beta } \right) + \frac{{m_{3} }}{{16m_{2} \omega_{1} }}\left( {3 + \beta } \right)a^{2} } \right)\overline{{V_{AC} }}^{2} \sin (T_{1} \delta - \theta )$$
(37a)
$$\begin{aligned} a\frac{d\theta }{{dT_{1} }} & = - \frac{1}{{4\omega_{1} }}\left( {2 + \beta } \right)\overline{{V_{AC} }}^{2} a - \frac{{3\alpha s_{1} }}{{8m_{2} \omega_{1} }}a^{3} - \frac{{3m_{4} }}{{16m_{2} \omega_{1} }}\left( {4 + \beta } \right)\overline{{V_{AC} }}^{2} a^{3} \\ \quad - \left( {\frac{{m_{1} }}{{4m_{2} \omega_{1} }}\left( {1 + \beta } \right) + \frac{{3m_{3} }}{{16m_{2} \omega_{1} }}\left( {3 + \beta } \right)a^{2} } \right)\overline{{V_{AC} }}^{2} \cos (T_{1} \delta - \theta ) \\ \end{aligned}$$
(37b)

With the phase lag γ:

$$\gamma = T_{1} \delta - \theta$$
(38)

Equation (37) can be rewritten as:

$$\frac{da}{{dT_{1} }} = - \frac{{\overline{{c_{d} }} }}{2}a + \left( {\frac{{m_{1} }}{{4m_{2} \omega_{1} }}\left( {1 + \beta } \right) + \frac{{m_{3} }}{{16m_{2} \omega_{1} }}\left( {3 + \beta } \right)a^{2} } \right)\overline{{V_{AC} }}^{2} \sin \gamma$$
(39a)
$$\begin{aligned} a\frac{d\gamma }{{dT_{1} }} & = a\delta + \frac{1}{{4\omega_{1} }}\left( {2 + \beta } \right)\overline{{V_{AC} }}^{2} a + \frac{{3\alpha s_{1} }}{{8m_{2} \omega_{1} }}a^{3} + \frac{{3m_{4} }}{{16m_{2} \omega_{1} }}\left( {4 + \beta } \right)\overline{{V_{AC} }}^{2} a^{3} \\ \quad + \left( {\frac{{m_{1} }}{{4m_{2} \omega_{1} }}\left( {1 + \beta } \right) + \frac{{3m_{3} }}{{16m_{2} \omega_{1} }}\left( {3 + \beta } \right)a^{2} } \right)\overline{{V_{AC} }}^{2} \cos \gamma \\ \end{aligned}$$
(39b)

When the response of the microbeam becomes steady, we have \(\frac{da}{{dT_{1} }} = 0\) and \(\frac{d\gamma }{{dT_{1} }} = 0\). In this case, Eq. (39) can be reduced to:

$$\left( {\frac{{m_{1} }}{{4m_{2} \omega_{1} }}\left( {1 + \beta } \right) + \frac{{m_{3} }}{{16m_{2} \omega_{1} }}\left( {3 + \beta } \right)a^{2} } \right)\overline{{V_{AC} }}^{2} \sin \gamma = \frac{{\overline{{c_{d} }} }}{2}a$$
(40a)
$$\begin{aligned} \left( {\frac{{m_{1} }}{{4m_{2} \omega_{1} }}\left( {1 + \beta } \right) + \frac{{3m_{3} }}{{16m_{2} \omega_{1} }}\left( {3 + \beta } \right)a^{2} } \right)\overline{{V_{AC} }}^{2} \cos \gamma & = - a\delta - \frac{1}{{4\omega_{1} }}\left( {2 + \beta } \right)\overline{{V_{AC} }}^{2} a \\ \quad - \frac{{3\alpha s_{1} }}{{8m_{2} \omega_{1} }}a^{3} - \frac{{3m_{4} }}{{16m_{2} \omega_{1} }}\left( {4 + \beta } \right)\overline{{V_{AC} }}^{2} a^{3} \\ \end{aligned}$$
(40b)

Combining Eqs. (40a) and (40b), we have:

$$\begin{aligned} b_{1}^{2} b_{3}^{2} a^{10} + \left( {2b_{1}^{2} b_{3} b_{4} + 2b_{1} b_{2} b_{3}^{2} - 9b_{1}^{4} b_{6}^{2} } \right)a^{8} \hfill \\ \quad + \left( {b_{1}^{2} b_{4}^{2} + 4b_{1} b_{2} b_{3} b_{4} + b_{2}^{2} b_{3}^{2} + 9b_{1}^{2} b_{5}^{2} - 24b_{1}^{3} b_{2} b_{6}^{2} } \right)a^{6} \hfill \\ \quad + \left( {2b_{1} b_{2} b_{4}^{2} + 2b_{2}^{2} b_{3} b_{4} + 6b_{1} b_{2} b_{5}^{2} - 22b_{1}^{2} b_{2}^{2} b_{6}^{2} } \right)a^{4} \hfill \\ \quad + \left( {b_{2}^{2} b_{4}^{2} + b_{2}^{2} b_{5}^{2} - 8b_{1} b_{2}^{3} b_{6}^{2} } \right)a^{2} - b_{2}^{4} b_{6}^{2} = 0 \hfill \\ \end{aligned}$$
(41a)
$$\gamma = arccos\left( { - \frac{{\left( {b_{4} a + b_{3} a^{3} } \right)}}{{b_{6} \left( {b_{2} + 3b_{1} a^{2} } \right)}}} \right)$$
(41b)

where the coefficients b 1 ~ b 6 are:

$$\begin{aligned} b_{1} & = \frac{{m_{3} }}{{16m_{2} \omega_{1} }}\left( {3 + \beta } \right), \, b_{2} = \frac{{m_{1} }}{{4m_{2} \omega_{1} }}\left( {1 + \beta } \right), \, b_{3} = \frac{{3\alpha s_{1} }}{{8m_{2} \omega_{1} }} + \frac{{3m_{4} }}{{16m_{2} \omega_{1} }}\left( {4 + \beta } \right)\overline{{V_{AC} }}^{2} \\ b_{4} & = \delta + \frac{1}{{4\omega_{1} }}\left( {2 + \beta } \right)\overline{{V_{AC} }}^{2} , \, b_{5} = \frac{{\overline{{c_{d} }} }}{2}, \, b_{6} = \overline{{V_{AC} }}^{2} \\ \end{aligned}$$
(42)

To study the damping effect, a quality factor Q is commonly used, which is related to the dimensionless damping coefficient \(\overline{{c_{d} }}\) by (Nayfeh et al. 2007):

$$\overline{{c_{d} }} = \frac{{\omega_{1} }}{Q}$$
(43)

By solving Eq. (41a) at different levels of the detuning parameter δ, we can obtain the steady-state frequency response of the microbeam, i.e., the evolution of the maximum deflection (normalized as the dimensionless vibration amplitude a) with the applied angular frequency (normalized as \(\overline{\omega }\), calculated from Eq. (28) with ξ = 1).

To analyze the stability of each point (δ 0, a 0) on the frequency response curve, we take the following procedures: by introducing δ = δ 0 and a = a 0 into Eq. (41b) and solving the resulting equation, we obtain the phase lag γ 0; further introducing γ 0 and a 0 into the following Jacobian matrix J a of Eq. (39):

$$J_{a} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \left( {da/dT_{1} } \right)}}{\partial a}} & {\frac{{\partial \left( {da/dT_{1} } \right)}}{\partial \gamma }} \\ {\frac{{\partial \left( {d\gamma /dT_{1} } \right)}}{\partial a}} & {\frac{{\partial \left( {d\gamma /dT_{1} } \right)}}{\partial \gamma }} \\ \end{array} } \right]$$
$$= \left[ {\begin{array}{*{20}c} { - b_{5} + 2b_{1} b_{6} a\sin \gamma } & {\left( {b_{2} + b_{1} a^{2} } \right)b_{6} \cos \gamma } \\ {2b_{3} a - \left( {\frac{{b_{2} }}{{a^{2} }} - 3b_{1} } \right)b_{6} \cos \gamma } & { - \left( {\frac{{b_{2} }}{a} + 3b_{1} a} \right)b_{6} \sin \gamma } \\ \end{array} } \right]$$
(44)

we calculate the eigenvalues of J a . If the real parts of all the eigenvalues are negative, the point (δ 0, a 0) is stable; otherwise, it is unstable.

3.2 Long-time integration

To validate the steady-state frequency response obtained from the analytical model given in Eq. (41a), we solve the governing equation Eq. (18) with the boundary conditions of Eq. (19) to obtain the time evolution of the beam deflection at each frequency. To do so, the Galerkin decomposition of the dimensionless deflection \(\overline{w}\) is used (Jia et al. 2012; Kim and Lee 2013; Ouakad and Younis 2010; Rhoads et al. 2006; Ruzziconi et al. 2013):

$$\overline{w} = \sum\limits_{j = 1}^{n} {q_{j} (\overline{t} )\phi_{j} (\overline{x} )}$$
(45)

where ϕ j (j = 1, 2, …, n) is the jth linear undamped vibration mode of the straight clamped–clamped beam, which has already been given in Eq. (26), and q j is its generalized coordinate. Multiplying Eq. (18) by \(\left( {1 - \overline{w} } \right)^{2}\), introducing Eq. (45), and further multiplying the result by ϕ i (i = 1, 2, …, n) and integrating from \(\overline{x} = 0\) to 1, we obtain the following n-degree-of-freedom reduced-order model:

$$\begin{aligned} \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right){\ddot{q}}_{i} - 2\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{k} {\ddot{q}}_{j} } } + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{l} q_{k} {\ddot{q}}_{j} } } } \hfill \\ \quad + \overline{{c_{d} }} \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right)\dot{q}_{i} - 2\overline{{c_{d} }} \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{k} \dot{q}_{j} } } + \overline{{c_{d} }} \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{l} q_{k} \dot{q}_{j} } } } \, \hfill \\ \quad + \lambda_{i}^{4} \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right)q_{i} - 2\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)\lambda_{j}^{4} q_{k} q_{j} } } + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)\lambda_{j}^{4} q_{l} q_{k} q_{j} } } } \hfill \\ \quad - \alpha \left( {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k}^{{\prime }} \phi_{j}^{{\prime }} d\overline{x} } } \right)q_{k} q_{j} } } } \right)\left( {\sum\limits_{j = 1}^{n} {\left( {\int_{0}^{1} {\phi_{j}^{{\prime \prime }} \phi_{i} \, d\overline{x} } } \right)q_{j} } } \right. \hfill \\ \left. {\quad - 2\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j}^{{\prime \prime }} \phi_{i} \, d\overline{x} } } \right)q_{k} q_{j} } } + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j}^{{\prime \prime }} \phi_{i} \, d\overline{x} } } \right)q_{l} q_{k} q_{j} } } } } \right) \hfill \\ \quad = \left( {\overline{{V_{AC} }} \cos (\overline{\omega } \overline{t} )} \right)^{2} \left( {\left( {1 + \beta } \right)\int_{0}^{1} {\phi_{i} \, d\overline{x} } - \beta \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right)q_{i} } \right) \hfill \\ \quad {\text{for }}i = 1, \, 2, \ldots , \, n \hfill \\ \end{aligned}$$
(46)

with an over dot denoting a derivative with respect to the normalized time \(\overline{t}\). Introducing the following variables:

$$q_{i0} = q_{i}$$
(47a)
$$q_{i1} = \dot{q}_{i}$$
(47b)

where i = 1, 2, …, n, we have:

$$\dot{q}_{i0} = q_{i1}$$
(48a)
$$\dot{q}_{i1} = {\ddot{q}}_{i}$$
(48b)

Further introducing Eqs. (47) and (48b) into Eq. (46), we obtain:

$$\begin{aligned} \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right)\dot{q}_{i1} - 2\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{k0} \dot{q}_{j1} } } + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{l0} q_{k0} \dot{q}_{j1} } } } \hfill \\ \quad + \overline{{c_{d} }} \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right)q_{i1} - 2\overline{{c_{d} }} \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{k0} q_{j1} } } + \overline{{c_{d} }} \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)q_{l0} q_{k0} q_{j1} } } } \hfill \\ \quad + \lambda_{i}^{4} \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right)q_{i0} - 2\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)\lambda_{j}^{4} q_{k0} q_{j0} } } + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j} \phi_{i} \, d\overline{x} } } \right)\lambda_{j}^{4} q_{l0} q_{k0} q_{j0} } } } \hfill \\ \quad - \alpha \left( {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k}^{{\prime }} \phi_{j}^{{\prime }} d\overline{x} } } \right)q_{k0} q_{j0} } } } \right)\left( {\sum\limits_{j = 1}^{n} {\left( {\int_{0}^{1} {\phi_{j}^{{\prime \prime }} \phi_{i} \, d\overline{x} } } \right)q_{j0} } } \right. \hfill \\ \left. {\quad - 2\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\left( {\int_{0}^{1} {\phi_{k} \phi_{j}^{{\prime \prime }} \phi_{i} \, d\overline{x} } } \right)q_{k0} q_{j0} } } + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {\left( {\int_{0}^{1} {\phi_{l} \phi_{k} \phi_{j}^{{\prime \prime }} \phi_{i} \, d\overline{x} } } \right)q_{l0} q_{k0} q_{j0} } } } } \right) \hfill \\ \quad = \left( {\overline{{V_{AC} }} \cos (\overline{\omega } \overline{t} )} \right)^{2} \left( {\left( {1 + \beta } \right)\int_{0}^{1} {\phi_{i} \, d\overline{x} } - \beta \left( {\int_{0}^{1} {\phi_{i}^{2} d\overline{x} } } \right)q_{i0} } \right) \hfill \\ \quad {\text{for }}i = 1, \, 2, \, \ldots , \, n \hfill \\ \end{aligned}$$
(49)

Equations (48a) and (49) are 2n first-order differential equations. With the initial deflection and velocity equal to zero (q i0 = q i1 = 0 at \(\overline{t} = 0\)), we solve Eqs. (48a) and (49) using the commercial software Matlab. The function ode45 based on an explicit Runge–Kutta method is adopted. To obtain a steady-state solution, we solve the equations over a long period of time, i.e., \(\overline{t} = 0\) ~ 2000, so-called the long-time integration. It is shown in the literature that the reduced-order model using five modes can accurately describe the dynamic behavior of microbeams (Caruntu and Martinez 2014; Ouakad and Younis 2010). Therefore, we take the first five vibration modes in this study, i.e., taking n = 5 in Eq. (45).

4 Results and discussions

4.1 Effects of applied AC voltage and mid-plane stretching

Let us consider an electrically actuated microbeam system described in Table 2. Two levels of initial gap between the microbeam and the rigid electrode are taken into account in this table, i.e., large gap of 5 μm and small one of 0.5 μm. With the aid of Tables 1 and 2, we obtain the following dimensionless quantities: \(\overline{{V_{AC} }} = 0\sim4\) for both large and small gaps, stretching parameter α = 1.5 for large gap and 0.015 for small gap. Introducing the values of \(\overline{{V_{AC} }}\) and α into Eq. (41a) and taking the fringing field parameter β = 0 (no fringing field effect) and quality factor Q = 1000 (using Eq. (43) to obtain the dimensionless damping coefficient \(\overline{{c_{d} }}\)), we solve the resulting equation at different levels of the detuning parameter δ, and obtain the frequency response of the microbeam. The typical results are shown in Figs. 2 and 3.

Table 2 Values of the dimensional quantities for an electrically actuated microbeam system
Full size table
Fig. 2
figure 2

Frequency response at different levels of AC voltage amplitude: a \(\overline{{V_{AC} }} = 0.2\), b \(\overline{{V_{AC} }} = 0.6\) and c \(\overline{{V_{AC} }} = 2\). Stretching parameter α = 1.5. SN1 and SN2 are saddle-node bifurcation points. Solid and dashed lines are respectively the stable and unstable responses

Full size image
Fig. 3
figure 3

Frequency response at different levels of AC voltage amplitude: a \(\overline{{V_{AC} }} = 0.4\), b \(\overline{{V_{AC} }} = 0.6\) and c \(\overline{{V_{AC} }} = 0.7\). Stretching parameter α = 0.015. Solid and dashed lines are respectively the stable and unstable responses

Full size image

Figure 2 is for the large initial gap of 5 μm, which corresponds to a large stretching parameter of 1.5. It is seen from the figure that the dynamic behavior of the microbeam depends on the normalized AC voltage amplitude \(\overline{{V_{AC} }}\). When \(\overline{{V_{AC} }}\) is small (e.g., 0.2 in Fig. 2a), the linear frequency response is observed with the maximum deflection changing gradually with the frequency of the applied AC voltage. When \(\overline{{V_{AC} }}\) becomes larger (0.6 in Fig. 2b), the microbeam exhibits the frequency response of hardening characteristic. With the increase of the applied frequency, the maximum deflection increases gradually until reaching the first saddle-node bifurcation point SN1, where the deflection drops (SN1 → ① in Fig. 2b). During the decrease of the applied frequency, the maximum deflection increases gradually until the second saddle-node bifurcation point SN2, where it jumps (SN2 → ②). In the remainder of this paper, such a characteristic frequency response associated with the hardening effect on the microbeam will be named “hardening frequency response”. When \(\overline{{V_{AC} }}\) is large (e.g., 2 in Fig. 2c), near the primary resonance regime, a transient dimensionless deflection reaching 1 is predicted by the long-time integration. This indicates that the beam deflection equals to the initial gap between the beam and the electrode, so the microbeam has collapsed onto the rigid electrode. Such behavior is called the dynamic pull-in instability.

Reducing the initial gap between the microbeam and the rigid electrode can reduce the actuation voltage for the microbeam. Figure 3 shows the case of a small initial gap of 0.5 μm, which corresponds to a small stretching parameter of 0.015. Different from the case of a large stretching parameter in Fig. 2, the hardening frequency response is not observed in Fig. 3. The microbeam exhibits the linear frequency response at small levels of \(\overline{{V_{AC} }}\), as shown in Figs. 3a, b; while at large levels of \(\overline{{V_{AC} }}\), it exhibits the dynamic pull-in behavior, as shown in Fig. 3c.

It is noted for Figs. 2 and 3 that the results from the analytical model given in Eq. (41a) agree well with those from the numerical simulations using long-time integration, except when there is dynamic pull-in behavior. The analytical model cannot capture the dynamic pull-in (Caruntu and Knecht 2011).

Figures 2 and 3 show that the dynamic behavior of the microbeam highly depends on the normalized AC voltage amplitude \(\overline{{V_{AC} }}\) and the stretching parameter α. To define the levels of \(\overline{{V_{AC} }}\) and α at which the microbeam exhibits the characteristic dynamic behavior, we solve Eq. (41a) at different levels of \(\overline{{V_{AC} }}\) (0–4) and α (0.0006–6) and mark the characteristic feature of the obtained frequency response in a diagram in terms of \(\overline{{V_{AC} }}\) and α, as shown in Fig. 4. The dynamic pull-in behavior is also marked in the figure by the predictions from the long-time integration.

Fig. 4
figure 4

Design diagram identifying the dynamic behavior of a clamped–clamped microbeam under alternating current voltage. The inset shows the minimum allowable stretching parameter α c  = 0.03 for the existence of hardening frequency response

Full size image

Figure 4 shows that when \(\overline{{V_{AC} }}\) is low, the microbeam exhibits the linear frequency response. At low levels of \(\overline{{V_{AC} }}\), the beam deflection is small, and as a result, the mid-plane stretching is insignificant. With the increase of \(\overline{{V_{AC} }}\), the beam deflection increases, and the mid-plane stretching (leading to a hardening effect on the microbeam) becomes more significant. Consequently, the microbeam exhibits a hardening frequency response. At high levels of \(\overline{{V_{AC} }}\), the beam deflection becomes large. So the beam can be close to the rigid electrode. In this case, it may collapse onto the electrode, i.e., dynamic pull-in. On the other hand, high actuating voltage leads to a large electrostatic force, which results in a softening effect on the microbeam (Jia et al. 2012). So the microbeam may also exhibit a frequency response of softening characteristic. However, it is seen from Fig. 4 that the softening frequency response is suppressed and the dynamic pull-in is dominant. This is different from the case of the microbeam biased by a DC voltage. In the case of a DC-biased microbeam, the softening frequency response can be observed at high levels of DC voltage (Mestrom et al. 2008).

The inset of Fig. 4 also shows that the stretching parameter α should be large enough for the existence of the hardening frequency response. In fact, α quantifies the effect of mid-plane stretching; i.e., by increasing α, the mid-plane stretching becomes more significant, which leads to the stiffening of the microbeam. The expression in Table 1 indicates that in order to control α, we can adjust the beam thickness h and/or the initial gap g 0 between the beam and the electrode.

4.2 Effects of fringing field and damping

The fringing field effect due to the finite size of the beam width b is described by a fringing field parameter β, whose expression can be found from Table 1 as 0.65g 0/b with g 0 being the initial gap between the beam and the rigid electrode. For the proper application of Palmer’s formula to estimate the electrostatic force, the microbeam system must satisfy the inequality b > 10g 0 (Caruntu and Knecht 2011). In this case, β varies between 0 and 0.065. Using Eqs. (41a) and (43) with Tables 1 and 2, we obtain the frequency responses at different levels of β (0–0.065), as depicted in Fig. 5. It is seen from the figure that the effect of β at the studied level is negligible.

Fig. 5
figure 5

Frequency response at different levels of fringing field parameter β: a for stretching parameter α = 1.5 and b for α = 0.015. In both figures, \(\overline{{V_{AC} }} = 0.6\), quality factor Q = 1000. Solid and dashed lines are respectively the stable and unstable responses

Full size image

The frequency responses of the microbeam at different levels of quality factor Q are shown in Fig. 6. To obtain this figure, Tables 1 and 2 and Eqs. (41a) and (43) are used. Figure 6a indicates that increasing Q strengthens the hardening effect. Q is inversely proportional to the dimensionless damping coefficient \(\overline{{c_{d} }}\) (see Eq. (43)). So increasing Q reduces the damping effect (\(\overline{{c_{d} }}\) decreases), which results in an increase of the beam deflection. Therefore, the hardening effect due to mid-plane stretching becomes more significant. Figure 6b further indicates that Q influences the minimum allowable stretching parameter for the existence of hardening frequency response: when Q = 1000, the stretching parameter α should be larger than 0.03 to observe the hardening frequency response (refer to Fig. 4); however, when Q = 3000, hardening frequency response is observed at α = 0.015 (<0.03) in Fig. 6b. Using the analytical model (Eq. (41a) and the long-time integration presented in Sect. 3.2, we obtain the minimum allowable stretching parameter α c at different levels of quality factor Q, as shown in Fig. 7. Increasing Q strengthens the hardening effect, so α c decreases with the increase of Q.

Fig. 6
figure 6

Frequency response at different levels of quality factor Q: a for stretching parameter α = 1.5 and b for α = 0.015. In both figures, \(\overline{{V_{AC} }} = 0.4\), fringing field parameter β = 0 (no fringing field effect). Solid and dashed lines are respectively the stable and unstable responses

Full size image
Fig. 7
figure 7

Minimum allowable stretching parameter α c for the existence of hardening frequency response: effect of quality factor Q

Full size image

4.3 Effects of boundary conditions

The microbeam investigated in the previous Sects. 4.1 and 4.2 is clamped at both ends. The beam can also be subjected to other boundary conditions such as simply-supported and cantilever, as shown in Fig. 8. This subsection is devoted to studying the effects of boundary conditions on the dynamic behavior of the microbeam.

Fig. 8
figure 8

Microbeam under different boundary conditions: a simply-supported and b cantilever

Full size image

Figure 8a shows a simply-supported microbeam. Its axial displacements at the two beam ends are the same as those of the clamped–clamped beam, i.e., u(0) = u(L) = 0. Therefore, the axial force expressed in Eq. (16) for the clamped–clamped beam can also be used for the simply-supported beam. As a result, the same governing equation Eq. (18) can be used. By taking the first linear undamped vibration mode ϕ 1 of simply-supported beam:

$$\phi_{1} (\overline{x} ) = \sin (\pi \overline{x} )$$
(50)

with the frequency parameter λ 1 = π, and following the similar procedure to the one adopted in Sect. 3.1, we obtain the same expression as Eq. (41a) to study the frequency response of the simply-supported beam.

A cantilever-type microbeam anchored at one end is shown in Fig. 8b. The axial force at the free end of the beam is zero, i.e., N(L, t) = 0. Then from Eq. (12a) we have:

$$N(x,t) = 0$$
(51)

With Eqs. (51) and (15b), Eq. (13) can be reduced to:

$$\rho S\frac{{\partial^{2} w}}{{\partial t^{2} }} + c_{d} \frac{\partial w}{\partial t} + E^{*} I\frac{{\partial^{4} w}}{{\partial x^{4} }} = \frac{1}{2}\frac{{\varepsilon_{0} b\left( {V_{AC} \cos (\omega t)} \right)^{2} }}{{(g_{0} - w)^{2} }}\left( {1 + 0.65\frac{{g_{0} - w}}{b}} \right)$$
(52)

Introducing the quantities in Table 1, we rewrite Eq. (52) in the following dimensionless form:

$$\frac{{\partial^{2} \overline{w} }}{{\partial \overline{t}^{2} }} + \overline{{c_{d} }} \frac{{\partial \overline{w} }}{{\partial \overline{t} }} + \frac{{\partial^{4} \overline{w} }}{{\partial \overline{x}^{4} }} = \left( {\overline{{V_{AC} }} \cos (\overline{\omega } \overline{t} )} \right)^{2} \left( {\frac{1}{{\left( {1 - \overline{w} } \right)^{2} }} + \frac{\beta }{{\left( {1 - \overline{w} } \right)}}} \right)$$
(53)

The mid-plane stretching term does not exist in Eq. (53) because there is no axial force in the cantilever (refer to Eq. (51)). Therefore, the cantilever-type microbeam cannot exhibit the hardening frequency response. Taking the first linear undamped vibration mode ϕ 1 of cantilever:

$$\phi_{1} (\overline{x} ) = C_{1} \left( {\cosh (\lambda_{1} \overline{x} ) - \cos (\lambda_{1} \overline{x} ) - \frac{{\sinh (\lambda_{1} ) - \sin (\lambda_{1} )}}{{\cosh (\lambda_{1} ) + \cos (\lambda_{1} )}}\left( {\sinh (\lambda_{1} \overline{x} ) - \sin (\lambda_{1} \overline{x} )} \right)} \right)$$
(54)

with C 1 satisfying \(\mathop {\hbox{max} }\limits_{{\overline{x} \in [0,1]}} \left| {\phi_{1} (\overline{x} )} \right| = 1\) and λ 1 satisfying cosh (λ 1) cos (λ 1) = −1, and following the procedures in Sect. 3.1, we obtain a similar expression to Eq. (41a). The only difference is that the coefficient b 3 in Eq. (41a) is modified to be \(\frac{{3m_{4} }}{{8m_{2} \omega_{1} }}\left( {4 + \beta } \right)\overline{{V_{AC} }}^{2}\).

Using Tables 1 and 2 and Eqs. (41a) and (43), and taking the fringing field parameter β = 0, quality factor Q = 1000, we obtain the frequency responses of the microbeam under different boundary conditions. The results of the cantilever-type microbeam are depicted in Fig. 9. As predicted, the cantilever cannot exhibit the hardening frequency response. At low levels of \(\overline{{V_{AC} }}\), the linear frequency response is observed (see \(\overline{{V_{AC} }} = 0.05\) in Fig. 9); while at high levels (e.g., \(\overline{{V_{AC} }} = 0.11\)), the dynamic pull-in near the primary resonance frequency is predicted by the long-time integration.

Fig. 9
figure 9

Frequency response of cantilever-type microbeam at different levels of AC voltage amplitude

Full size image

The frequency responses of simply-supported and clamped–clamped microbeams are compared in Fig. 10. It is found from Fig. 10a that the hardening effect in the simply-supported beam is more significant than that in the clamped–clamped beam. Moreover, Fig. 10b shows that compared with the clamped–clamped beam, the simply-supported one is prone to pull-in. The reduced rotation at the two ends of the clamped–clamped microbeam makes it more difficult to bend, and as a result, the dynamic pull-in is hindered. The beam deflection is also reduced, which weakens the hardening effect due to mid-plane stretching.

Fig. 10
figure 10

Frequency response of simply-supported and clamped–clamped microbeams: a for \(\alpha = 1.5, \, \overline{{V_{AC} }} = 0.2\) and b for \(\alpha = 0.015, \, \overline{{V_{AC} }} = 0.3\). Solid and dashed lines are respectively the stable and unstable responses

Full size image

Using Tables 1 and 2, Eq. (41a), and the long-time integration in Sect. 3.2, we draw the design diagram for the simply-supported microbeam in Fig. 11. The figure is analogous to Fig. 4 of the clamped–clamped microbeam. However, smaller voltage input \(\overline{{V_{AC} }}\) is required to induce the dynamic pull-in and the hardening frequency response in the simply-supported beam. Moreover, the insets in Figs. 4 and 11 show that the simply-supported beam has a smaller minimum allowable stretching parameter α c for the existence of hardening frequency response. The stiffer fixation as observed in the clamped–clamped fixation versus the simply-supported case weakens the hardening effect and makes it more difficult to actuate the beam. Consequently, higher α c (stronger hardening effect) and higher \(\overline{{V_{AC} }}\) (larger electrostatic force) are needed for the clamped–clamped beam.

Fig. 11
figure 11

Design diagram identifying the dynamic behavior of an electrically actuated simply-supported microbeam. The inset depicts the minimum allowable stretching parameter α c  = 0.01 for the existence of hardening frequency response

Full size image

5 Conclusions

The dynamic behavior of a microbeam under various levels of AC (alternating current) voltage is investigated. The beam model is developed using Euler–Bernoulli beam theory. The mid-plane stretching, fringing field and damping effects are all taken into account in the model formulation. The transient response and the steady-state frequency response of the microbeam under different boundary conditions are derived from the beam model respectively by the method of multiple scales and the long-time integration.

Our results reveal that unlike the microbeam biased by a DC voltage, the non-biased microbeam does not exhibit the softening frequency response. Our results also reveal that the characteristic feature of the dynamic behavior of the non-biased microbeam highly depends on the applied AC voltage and the mid-plane stretching parameter α, which can be altered by the beam thickness and the initial gap between the beam and the rigid electrode. A diagram in terms of α and AC voltage amplitude is developed to show the domains of characteristic dynamic behaviors. The diagram provides some basic guidelines for designing the micro-resonators. Furthermore, our results real that damping and boundary conditions have significant effects on the dynamic behavior of the microbeam, while the effect of fringing field is negligible.