1 Introduction

Artificial intelligence is the development of traditional control methods or learning methods. In recent years, artificial intelligence methods have been extensively studied and applied [1,2,3,4,5,6]. The support vector machine (SVM) is proposed based on the principle of statistical learning theory and Vapnik–Chervonenkis (VC) dimensional theory, which is a promising machine learning approach that has been adopted in classification and regression [7, 8]. The adoption of the kernel trick can extend the algorithm for use in nonlinear cases. The basic idea of the SVM is to construct a hyperplane that can partition the samples from different classes with minimum generalization error by maximizing the margin. Compared with other supervised learning methods, it has many strong points, such as being with sparse solution constructed by ‘support vectors’, having generalization error minimization, and needing only a small-scale dataset. It has become one of the most powerful tools for pattern classification and regression [9].

To improve the performance of the standard SVM, many modified methods were proposed. Jayadeva et al. [10] proposed a twin SVM (TSVM) by seeking two nonparallel bound functions, and each one is close to one class of samples and as far as possible from the other. The TSVM can increase the computational speed by solving two small-size quadratic programming problems (QPPs) rather than a large one as in the standard SVM. Later, Peng [11] extended this strategy to regression applications, resulting in the twin support vector regression (TSVR); the target of the regression problem is to get the relationship between inputs and their corresponding outputs. Solving the SVM is based on QPP problems subject to linear inequality constraints, which is with heavy computational costs. Suyken et al. [12, 13] proposed the least squares SVM (LS-SVM) for large-scale dataset problems. It follows a similar spirit as that of the SVM except for the constraints being linear equalities, which can reduce the computational complexity significantly. The \(\nu\)-support vector regression (\(\nu\)-SVR) [14] extends the standard SVR via enforcing a fraction of the data samples to lie inside an \(\epsilon\) tube, and minimizing the width of the tube by introducing a parameter \(\nu\). Inspired by the \(\nu\) -SVR and combined with the concept of pinball loss [15,16,17,18]. Xu [19] proposed asymmetric \(\nu\)-twin support vector regression (Asy-\(\nu\)-TSVR), which is a kind of twin SVR suitable for dealing with asymmetric noise. However, these methods only take into account the empirical risk minimization rather than the structural risk minimization, which will produce the overfitting problem. To overcome the overfitting problem, Shao et al. [20] introduced regularization terms into the objective functions of TSVR. Recently, Rastogi et al. proposed a \(\nu\)-twin support vector machine-based regression method (\(\nu\)-TWSVR) [21]: the regularization terms and the insensitive bound values \(\epsilon\) in the method were all added into the objective functions to minimize the risks, which can adjust the values of \(\epsilon\) automatically. However, in the methods mentioned above, such as TSVR and \(\nu\)-TWSVR, all of the training samples are considered as having the same status and are given the same penalties, which may degrade the performance due to the influence of noise. Therefore, it is useful to give the training samples different weights depending on their importance. Xu et al. [22] proposed the K-nearest neighbor (KNN)-based weighted twin support vector regression, in which the local information of data was used for improving the prediction accuracy. KNN-based methods are suitable for regression situations with clustered samples but not for time series due to the nature of the KNN.

In this paper, a novel TSVR-based regression model termed WTWTSVR is proposed. Some of the features of the proposed WTWTSVR are as follows.

  1. 1.

    The prior information of the training samples is incorporated into the proposed algorithm. A weight matrix is introduced into the quadratic empirical risks term, and a weight vector is introduced into the first-degree empirical risks term to reduce the influence of outliers.

  2. 2.

    Wavelet transform theory is adopted to calculate the weight matrix, which is a new angle for preprocessing samples. Wavelet transform is a kind of time-frequency representation for signals, and the proposed method based on the wavelet theory is suitable for dealing with time series samples due to the character of the wavelet transform.

  3. 3.

    The proposed model also takes into account the regularization terms and the insensitive bound values \(\epsilon\) as penalty terms. The effectiveness of our WTWTSVR is demonstrated by experiments on artificial datasets and benchmark datasets. The numerical results show that the proposed algorithm has better generalization ability than traditional ones.

This paper is organized as follows: Sect. 2 briefly describes TSVR and \(\nu\)-TWSVR. Section 3 proposes our WTWTSVR. Experimental results are described in Sect. 4 to investigate the validity of our proposed algorithm, and Sect. 5 ends the paper with concluding remarks.

2 Brief introduction to TSVR and \(\nu\)-TWSVR

In this section, the linear TSVR and \(\nu\)-TWSVR algorithms are described briefly. Nonlinear cases can be solved by Kernel methods. Given a training set \(T=\{(x_{1},y_{1}),(x_{2},y_{2}),\ldots ,(x_{m},y_{m})\}\), where \(x_{i}\in \mathfrak {R}^{n}\) and \(y_{i}\in \mathfrak {R}\), \(i=1,2,\ldots ,m\). Then the output vector of the training data can be denoted as \(Y=(y_{1},y_{2},\ldots ,y_{m})^{T}\in \mathfrak {R}^{m}\) and the input matrix as \(A=(A_{1},A_{2},\ldots ,A_{m})^{T}\in \mathfrak {R}^{m\times n}\), and the ith row \(A_{i}=(x_{i1},x_{i2},\ldots ,x_{in})^{T}\) is the ith training sample. We let e and I be a ones vector and an identity matrix of appropriate dimensions, respectively.

2.1 Twin support vector regression (TSVR)

TSVR proposed by Peng [11] is an efficient regression method with low computational costs compared with SVR [23, 24]. TSVR has two \(\epsilon\)-insensitive bounds: the down-bound is denoted as \(f_{1}(x)=w_{1}^{T}x+b_{1}\) , the up-bound is denoted as \(f_{2}(x)=w_{2}^{T}x+b_{2}\), and the regressor f(x) can be obtained by taking the mean of the two bound functions, i.e.

$$\begin{aligned} f(x)= & {} \frac{1}{2}(f_{1}(x)+f_{2}(x))\nonumber \\= & {} \frac{1}{2}(w_{1}+w_{2})^{T}x+\frac{1}{2} (b_{1}+b_{2})\text {.} \end{aligned}$$
(1)

The two \(\epsilon\)-insensitive bound functions can be obtained by solving the following pair of QPPs:

$$\begin{aligned} \begin{array}{l} \underset{w_{1},b_{1},\xi _{1}}{\min }\frac{1}{2}\left\| Y-e\epsilon _{1}-(Aw_{1}+eb_{1})\right\| ^{2}+C_{1}e^{T}\xi _{1} \\ s.t.\text { }Y-(Aw_{1}+eb_{1})\ge e\epsilon _{1}-\xi _{1},\text { }\xi _{1}\ge 0\text {,} \end{array} \end{aligned}$$
(2)

and

$$\begin{aligned} \begin{array}{l} \underset{w_{2},b_{2},\xi _{2}}{\min }\frac{1}{2}\left\| Y+e\epsilon _{2}-(Aw_{2}+eb_{2})\right\| ^{2}+C_{2}e^{T}\xi _{2} \\ s.t.\text { }(Aw_{2}+eb_{2})-Y\ge e\epsilon _{2}-\xi _{2},\text { }\xi _{2}\ge 0\text {,} \end{array} \end{aligned}$$
(3)

where \(\epsilon _{1},\epsilon _{2}\ge 0\) are insensitive parameters, which are introduced to construct the \(\epsilon\)-insensitive zone, ‘\(\epsilon\) tube’. \(\xi _{1}\) and \(\xi _{2}\) are slack vectors to measure the errors of samples outside the ‘\(\epsilon\) tube’. \(C_{1},C_{2}>0\) are parameters used to make the trade-off between the fitting errors and the slack errors. After introducing the Lagrangian functions of (2) and (3), and considering the corresponding Karush–Kuhn–Tucker (KKT) optimality conditions, the dual QPPs can be obtained as

$$\begin{aligned} \begin{array}{l} \underset{\alpha }{\min }\frac{1}{2}\alpha ^{T}G(G^{T}G)^{-1}G^{T}\alpha -f_{1}^{T}G\left( G^{T}G\right) ^{-1}G^{T}\alpha +f_{1}^{T}\alpha \\ s.t.\text { }0e\le \alpha \le C_{1}e, \end{array} \end{aligned}$$
(4)

and

$$\begin{aligned} \begin{array}{ll} \underset{\beta }{\min } &{} \frac{1}{2}\beta ^{T}G(G^{T}G)^{-1}G^{T}\beta +f_{2}^{T}G(G^{T}G)^{-1}G^{T}\beta -f_{2}^{T}\beta \\ s.t. &{} 0e\le \beta \le C_{2}e, \end{array} \end{aligned}$$
(5)

where \(G=[A\)e], \(f_{1}=Y-e\epsilon _{1}\), \(f_{2}=Y+e\epsilon _{2}\), and \(\alpha ,\beta \in \mathfrak {R}^{m}\) are Lagrangian multiplies vectors.

After solving the dual QPPs (4) and (5), we can get solutions \(\alpha\) and \(\beta\), and then the regression parameters can be obtained as \(\left[ w_{1}^{T},b_{1}\right] ^{T}=(G^{T}G)^{-1}G^{T}(f_{1}-\alpha )\) and \(\left[ w_{2}^{T},b_{2}\right] ^{T}=(G^{T}G)^{-1}G^{T}(f_{2}+\beta )\).

2.2 \(\nu\)-Twin support vector regression (\(\nu\)-TWSVR)

Rastogi proposed a modification of TSVR. Similar to the TSVR model, \(\nu\)-TWSVR also solves a pair of optimization problems (6) and (7):

$$\begin{aligned} \begin{array}{ll} \underset{w_{1},b_{1},\xi _{1},\epsilon _{1}}{\min } &{} \frac{1}{2}\left\| Y-(Aw_{1}+eb_{1})\right\| ^{2}+\frac{1}{2} c_{1}(w_{1}^{T}w_{1}+b_{1}^{2})\\ &{}\quad +c_{2}\left( v_{1}\epsilon _{1}+\frac{1}{m}e^{T}\xi _{1}\right) \\ s.t. &{} \begin{array}{l} Y-(Aw_{1}+eb_{1})\ge -\epsilon _{1}e-\xi _{1} \\ \xi _{1}\ge 0e,\epsilon _{1}\ge 0, \end{array} \end{array} \end{aligned}$$
(6)

and

$$\begin{aligned} \begin{array}{ll} \underset{w_{2},b_{2},\xi _{2},\epsilon _{2}}{\min } &{} \frac{1}{2}\left\| Y-(Aw_{2}+eb_{2})\right\| ^{2}+\frac{1}{2} c_{3}(w_{2}^{T}w_{2}+b_{2}^{2})\\ &{}\quad +c_{4}\left( v_{2}\epsilon _{2}+\frac{1}{m}e^{T}\xi _{2}\right) \\ s.t. &{} \begin{array}{l} (Aw_{2}+eb_{2})-Y\ge -\epsilon _{2}e-\xi _{2} \\ \xi _{2}\ge 0e,\epsilon _{2}\ge 0, \end{array} \end{array} \end{aligned}$$
(7)

where \(v_{1},v_{2},c_{1},c_{2},c_{3},c_{4}>0\) are user-specified parameters, and \(\epsilon _{1},\epsilon _{2},\xi _{1}\), and \(\xi _{2}\) are the same as in TSVR. Different from the TSVR model, the insensitive parameters \(\epsilon _{1}\) and \(\epsilon _{2}\) are not given parameters but are optimized. After introducing the Lagrangian functions of (6) and (7), and considering the KKT conditions, the dual QPPs can be obtained as

$$\begin{aligned} \begin{array}{cc} \underset{\alpha }{\min } &{} \frac{1}{2}\alpha ^{T}G(G^{T}G+c_{1}I)^{-1}G^{T}\alpha -Y^{T}G(G^{T}G+c_{1}I)^{-1}G^{T}\alpha +Y^{T}\alpha \\ s.t. &{} \begin{array}{c} 0e\le \alpha \le \frac{c_{2}}{m}e, \\ e^{T}\alpha \le c_{2}v_{1}, \end{array} \end{array} \end{aligned}$$
(8)

and

$$\begin{aligned} \begin{array}{cc} \underset{\alpha }{\min } &{} \frac{1}{2}\beta ^{T}G(G^{T}G+c_{3}I)^{-1}G^{T}\beta +Y^{T}G(G^{T}G+c_{3}I)^{-1}G^{T}\beta -Y^{T}\beta \\ s.t. &{} \begin{array}{c} 0e\le \beta \le \frac{c_{4}}{m}e, \\ e^{T}\beta \le c_{4}v_{2}, \end{array} \end{array} \end{aligned}$$
(9)

where \(G=[A\)e] and \(\alpha ,\beta \in \mathfrak {R}^{m}\) are Lagrangian multiplies vectors.

After solving the dual QPPs (8) and (9), we can get solutions \(\alpha\) and \(\beta\), and then the regression parameters can be obtained as \(\left[ w_{1}^{T},b_{1}\right] ^{T}=(c_{1}I+G^{T}G)^{-1}G^{T}(Y-\alpha )\), \(\left[ w_{2}^{T},b_{2}\right] ^{T}=(c_{3}I+G^{T}G)^{-1}G^{T}(Y+\beta )\). Then, the regressor f(x) can be obtained by taking the mean of the two bound functions: \(f(x)=\frac{1}{2} (f_{1}(x)+f_{2}(x))=\frac{1}{2}(w_{1}+w_{2})^{T}x+\frac{1}{2}(b_{1}+b_{2}).\)

3 Wavelet transform-based weighted \(\nu\)-twin support vector regression

In this section, a novel wavelet transform-based weighted \(\nu\)-TSVR is presented. Similar to the \(\nu\)-TWSVR model, the WTWTSVR is constructed by two nonparallel hyperplanes, down-bound \(f_{1}(x)\), and up-bound \(f_{2}(x)\); each hyperplane determines the \(\epsilon\)-insensitive bound regressor, and the end regressor is \(f(x)=\frac{1}{2} (f_{1}(x)+f_{2}(x))\).

3.1 Linear wavelet transform-based weighted \(\nu\)-TSVR

Linear WTWTSVR also solves a pair of optimization problems, which are described as follows:

$$\begin{aligned}&\begin{array}{ll} \underset{w_{1},b_{1},\xi _{1},\epsilon _{1}}{\min } &{} \frac{1}{2} (Y-(Aw_{1}+eb_{1}))^{T}D(Y-(Aw_{1}+eb_{1}))\\ &{}\quad +\frac{1}{2} c_{1}(w_{1}^{T}w_{1}+b_{1}^{2})+c_{2}\left( v_{1}\epsilon _{1}+\frac{1}{m}d^{T}\xi _{1}\right) \\ \text {s.t.} &{} \begin{array}{cc} Y-(Aw_{1}+eb_{1})\ge -\epsilon _{1}e-\xi _{1} &{} \begin{array}{cc} \xi _{1}\ge 0e &{} \epsilon _{1}\ge 0 \end{array} \end{array} , \end{array} \end{aligned}$$
(10)
$$\begin{aligned}&\begin{array}{ll} \underset{w_{2},b_{2},\xi _{2},\epsilon _{2}}{\min } &{} \frac{1}{2} (Y-(Aw_{2}+eb_{2}))^{T}D(Y-(Aw_{2}+eb_{2}))\\ &{}\quad +\frac{1}{2} c_{3}(w_{2}^{T}w_{2}+b_{2}^{2})+c_{4}\left( v_{2}\epsilon _{2}+\frac{1}{m}d^{T}\xi _{2}\right) \\ \text {s.t.} &{} \begin{array}{cc} (Aw_{2}+eb_{2})-Y\ge -\epsilon _{2}e-\xi _{2} &{} \begin{array}{cc} \xi _{2}\ge 0e &{} \epsilon _{2}\ge 0 \end{array} \end{array} , \end{array} \end{aligned}$$
(11)

where \(v_{1},v_{2},c_{1},c_{2},c_{3},c_{4}>0\) are parameters chosen a priori by the user, \(\epsilon _{1}\) and \(\epsilon _{2}\) are insensitive parameters, \(\xi _{1}\) and \(\xi _{2}\) are slack vectors to measure the errors of samples outside the ‘\(\epsilon\) tube’, and m is the number of training points. \(d\in \mathfrak {R}^{m}\) is a weighting vector, and the diagonal matrix \(D=diag(d)\in \mathfrak {R}^{m\times m}\) is a weighting matrix, which will be discussed later. Note that when \(D=I\) and \(d=e\), the proposed WTWTSVR will be degraded to \(\nu\)-TWSVR, and thus the WTWTSVR is the extension of \(\nu\)-TWSVR.

The first term in the objective function of (10) is the sum of weighted squared distances from training points to the down-bound function. The second term is a regularization term, which can make \(f_{1}(x)\) as smooth as possible. The third term aims to make the \(\epsilon\) tube as narrow as possible and minimize the sum of errors of the points to lower than the down-bound \(f_{1}(x)\), which brings the possibility of overfitting the training points. The ratio of three penalty terms in the objective function of (10) can be adjusted by the choice of \(c_{1},c_{2},v_{1}\). For the optimization problem (11), we have similar illustrations.

To solve the optimization problems (10) and (11), their dual problems must be derived. Now the Lagrangian function for the problem (10) is introduced as follows:

$$\begin{aligned}&L\left( w_{1},b_{1},\xi _{1},\epsilon _{1},\alpha ,\beta ,\gamma \right) \nonumber \\&\quad = \frac{1}{2}(Y-(Aw_{1}+eb_{1}))^{T}D(Y-(Aw_{1}+eb_{1})) \nonumber \\&\qquad +\,\frac{1}{2}c_{1}(w_{1}^{T}w_{1}+b_{1}^{2})+c_{2}\left( v_{1}\epsilon _{1}+\frac{ 1}{m}d^{T}\xi _{1}\right) \nonumber \\&\qquad -\,\alpha ^{T}(Y-(Aw_{1}+eb_{1})+\epsilon _{1}e+\xi _{1}) \nonumber \\&\qquad -\,\beta ^{T}\xi _{1}-\gamma \epsilon _{1}, \end{aligned}$$
(12)

where \(\alpha =(\alpha _{1},\alpha _{2},\ldots ,\alpha _{m})^{T}\) , \(\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{m})^{T}\), and \(\gamma\) are nonnegative Lagrangian multipliers. The KTT optimality conditions are given by

$$\begin{aligned}&\frac{\partial L}{\partial w_{1}} =-A^{T}D(Y-(Aw_{1}+eb_{1}))+c_{1}w_{1}+A^{T}\alpha =0, \end{aligned}$$
(13)
$$\begin{aligned}&\frac{\partial L}{\partial b_{1}} =-e^{T}D(Y-(Aw_{1}+eb_{1}))+c_{1}b_{1}+e^{T}\alpha =0, \end{aligned}$$
(14)
$$\begin{aligned}&\frac{\partial L}{\partial \xi _{1}}=\frac{c_{2}}{m}d-\alpha -\beta =0, \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\partial L}{\partial \epsilon _{1}}=c_{2}v_{1}-e^{T}\alpha -\gamma =0, \end{aligned}$$
(16)
$$\begin{aligned}&\begin{array}{cc} Y-(Aw_{1}+eb_{1})\ge -\epsilon _{1}e-\xi _{1},&\begin{array}{cc} \xi _{1}\ge 0,&\epsilon _{1}\ge 0, \end{array} \end{array} \end{aligned}$$
(17)
$$\begin{aligned}&\alpha ^{T(}Y-(Aw_{1}+eb_{1})+\epsilon _{1}e+\xi _{1})=0, \end{aligned}$$
(18)
$$\begin{aligned}&\begin{array}{cc} \beta ^{T}\xi _{1}=0,&\gamma \epsilon _{1}=0 \end{array} , \end{aligned}$$
(19)
$$\begin{aligned}&\begin{array}{ccc} \alpha \ge 0e,&\beta \ge 0e,&\gamma \ge 0. \end{array} \end{aligned}$$
(20)

It follows from (15), (16), and (20) that the following is true:

$$\begin{aligned}&0e\le \alpha \le \frac{c_{2}}{m}d, \\&\quad e^{T}\alpha \le c_{2}v_{1}. \end{aligned}$$

Defining \(G=[ \begin{array}{cc} A&e \end{array} ]\) and \(u_{1}=[ \begin{array}{cc} w_{1}^{T}&b_{1} \end{array} ]^{T}\), and combining (13) and (14) would result in the equation

$$\begin{aligned} -G^{T}DY+(G^{T}DG+c_{1}I)u_{1}+G^{T}\alpha =0, \end{aligned}$$

from which the following can be determined:

$$\begin{aligned} u_{1}=(G^{T}DG+c_{1}I)^{-1}G^{T}(DY-\alpha ). \end{aligned}$$

After substituting the value of \(u_{1}\) into (12), and using the above KTT optimality conditions, the dual problem of the proposed method can obtained as follows:

$$\begin{aligned} \max \limits _{\alpha }L =&\max \limits _{\alpha }\frac{1}{2} (Y-Gu_{1})^{T}D(Y-Gu_{1})\nonumber \\&+\,\frac{1}{2}c_{1}u_{1}^{T}u_{1}+c_{2}v_{1}\epsilon _{1}+\frac{c_{2}}{m}d^{T}\xi _{1} \nonumber \\&-\,\alpha ^{T}\left( Y-Gu_{1}+\epsilon _{1}e+\xi \right) -\beta ^{T}\xi _{1}-\gamma \epsilon _{1} \nonumber \\ =&\max \limits _{\alpha }\frac{1}{2}(Y^{T}D-u_{1}^{T}G^{T}D)(Y-Gu_{1})\nonumber \\&+\,\frac{1 }{2}c_{1}u_{1}^{T}u_{1}-\alpha ^{T}Y+\alpha ^{T}Gu_{1} \nonumber \\ =&\max \limits _{\alpha }\frac{1}{2}Y^{T}DY-\frac{1}{2}u_{1}^{T}G^{T}DY-\frac{ 1}{2}Y^{T}DGu_{1}\nonumber \\&+\,\frac{1}{2}u_{1}^{T}(G^{T}DG+c_{1}I)u_{1}+\alpha ^{T}Gu_{1}-\alpha ^{T}Y \nonumber \\ =&\max \limits _{\alpha }\frac{1}{2}Y^{T}DY-\frac{1}{2}u_{1}^{T}G^{T}DY-\frac{ 1}{2}Y^{T}DGu_{1}\nonumber \\&+\,\frac{1}{2}u_{1}^{T}G^{T}DY-\frac{1}{2}u_{1}^{T}G^{T} \alpha -\alpha ^{T}Y+\alpha ^{T}Gu_{1} \nonumber \\ =&\max \limits _{\alpha }\left( -\frac{1}{2}Y^{T}DG+\frac{1}{2}\alpha ^{T}G\right) u_{1}-\alpha ^{T}Y \nonumber \\ =&\max \limits _{\alpha }\left( -\frac{1}{2}Y^{T}DG+\frac{1}{2}\alpha ^{T}G\right) \nonumber \\&\quad \times \,(G^{T}DG+c_{1}I)^{-1}G^{T}(DY-\alpha )-\alpha ^{T}Y \end{aligned}$$
(21)

Note that \(D=D^{T}\) and the terms that are not related to \(\alpha\) [such as the term \(\frac{1}{2}Y^{T}DY\) in (21)] are omitted; this does not affect the maximization process. The dual problem of (12) can be expressed as

$$\begin{aligned}&\min \frac{1}{2}\alpha ^{T}G(G^{T}DG+c_{1}I)^{-1}G^{T}\alpha -Y^{T}\nonumber \\&\quad DG(G^{T}DG+c_{1}I)^{-1}G^{T}\alpha +Y^{T}\alpha \nonumber \\&s.t.0e\le \alpha \le \frac{c_{2}}{m}d, \nonumber \\&e^{T}\alpha \le c_{2}v_{1}. \end{aligned}$$
(22)

Similarly, the dual problem of (11) is deduced as

$$\begin{aligned}&\min \frac{1}{2}\lambda ^{T}G(G^{T}DG+c_{3}I)^{-1}G^{T}\lambda +Y^{T}\nonumber \\&\quad DG(G^{T}DG+c_{3}I)^{-1}G^{T}\lambda -Y^{T}\lambda \nonumber \\&s.t.0e\le \lambda \le \frac{c_{4}}{m}d, \nonumber \\&e^{T}\lambda \le c_{4}v_{2}, \end{aligned}$$
(23)

and

$$\begin{aligned} u_{2}=[w_{2}^{T}\text { }b_{2}]^{T}=(G^{T}DG+c_{3}I)^{-1}G^{T}(DY+\lambda ). \end{aligned}$$

Thus, the down-bound \(f_{1}(x)=w_{1}^{T}x+b_{1}\) and the up-bound \(f_{2}(x)=w_{2}^{T}x+b_{2}\) are obtained to calculate the regressor \(f(x)= \frac{1}{2}(f_{1}(x)+f_{2}(x))\).

3.2 Nonlinear wavelet transform-based weighted \(\nu\)-TSVR

The SVR can be used to solve linear regression problems. A line/plane/hyperplane can be adopted to regress the relationship between inputs and outputs by training samples. Unfortunately, the line/plane/hyperplane is only suitable for linear problems. The adoption of kernel mapping can extend the algorithm to nonlinear cases, which are the majority of cases in the real world based on Vapnik’s theory [7]. The kernel trick is adopted to map the input into a higher-dimensional feature space. The following kernel-generated functions are considered: down-bound \(f_{1}(x)=K(x^{T},A^{T})w_{1}+b_{1}\) and up-bound \(f_{2}(x)=K(x^{T},A^{T})w_{2}\)\(+b_{2}\), where K is an appropriately chosen kernel. Therefore, the end regressor is \(f(x)=\frac{1}{2}(f_{1}(x)+f_{2}(x))\). The corresponding optimization problems can be described as follows:

$$\begin{aligned}&\begin{array}{ll} \underset{w_{1},b_{1},\xi _{1},\epsilon _{1}}{\min } &{} \begin{array}{l} \frac{1}{2}(Y-(K(A,A^{T})w_{1}+eb_{1}))^{T}D(Y-(K(A,A^{T})w_{1}+eb_{1})) \\ \quad +\frac{1}{2}c_{1}(w_{1}^{T}w_{1}+b_{1}^{2})+c_{2}(v_{1}\epsilon _{1}+\frac{1 }{m}d^{T}\xi _{1}) \end{array} \\ \text {s.t.} &{} \begin{array}{cc} Y-(K(A,A^{T})w_{1}+eb_{1})\ge -\epsilon _{1}e-\xi _{1} &{} \begin{array}{cc} \xi _{1}\ge 0e &{} \epsilon _{1}\ge 0 \end{array} \end{array} , \end{array} \end{aligned}$$
(24)
$$\begin{aligned}&\begin{array}{ll} \underset{w_{2},b_{2},\xi _{2},\epsilon _{2}}{\min } &{} \begin{array}{l} \frac{1}{2}(Y-(K(A,A^{T})w_{2}+eb_{2}))^{T}D(Y-(K(A,A^{T})w_{2}+eb_{2})) \\ \quad +\frac{1}{2}c_{3}(w_{2}^{T}w_{2}+b_{2}^{2})+c_{4}(v_{2}\epsilon _{2}+\frac{1 }{m}d^{T}\xi _{2}) \end{array} \\ \text {s.t.} &{} \begin{array}{cc} (K(A,A^{T})w_{2}+eb_{2})-Y\ge -\epsilon _{2}e-\xi _{2} &{} \begin{array}{cc} \xi _{2}\ge 0e &{} \epsilon _{2}\ge 0 \end{array} \end{array} . \end{array} \end{aligned}$$
(25)

We define the Lagrangian function for the QPP problem (24) as

$$\begin{aligned}&L\left( w_{1},b_{1},\xi _{1},\epsilon _{1},\alpha ,\beta ,\gamma \right) \nonumber \\&\quad = \frac{1}{2}(Y-(K(A,A^{T})w_{1}+eb_{1}))^{T}\nonumber \\&\qquad \times \, D(Y-(K(A,A^{T})w_{1}+eb_{1})) \nonumber \\&\qquad +\,\frac{1}{2}c_{1}(w_{1}^{T}w_{1}+b_{1}^{2})+c_{2}\left( v_{1}\epsilon _{1}+\frac{ 1}{m}d^{T}\xi _{1}\right) \nonumber \\&\qquad -\,\alpha ^{T}(Y-(K(A,A^{T})w_{1}+eb_{1})+\epsilon _{1}e+\xi _{1})\nonumber \\&\qquad -\,\beta ^{T}\xi _{1}-\gamma \epsilon _{1}, \end{aligned}$$
(26)

where \(\alpha =(\alpha _{1},\alpha _{2},\ldots ,\alpha _{m})^{T}\) , \(\beta =(\beta _{1},\beta _{2},\ldots ,\beta _{m})^{T}\), and \(\gamma\) are nonnegative Lagrangian multipliers. The KTT optimality conditions are given by

$$\begin{aligned}&\frac{\partial L}{\partial w_{1}} =-K(A,A^{T})^{T}D(Y-(K(A,A^{T})w_{1}+eb_{1}))\nonumber \\&\quad +c_{1}w_{1}+K(A,A^{T})^{T} \alpha =0, \end{aligned}$$
(27)
$$\begin{aligned}&\frac{\partial L}{\partial b_{1}} =-e^{T}D(Y-(K(A,A^{T})w_{1}+eb_{1}))\nonumber \\&\quad +c_{1}b_{1}+e^{T}\alpha =0, \end{aligned}$$
(28)
$$\begin{aligned}&\frac{\partial L}{\partial \xi _{1}}=\frac{c_{2}}{m}d-\alpha -\beta =0, \end{aligned}$$
(29)
$$\begin{aligned}&\frac{\partial L}{\partial \epsilon _{1}}=c_{2}v_{1}-e^{T}\alpha -\gamma =0, \end{aligned}$$
(30)
$$\begin{aligned}&\begin{array}{cc} Y-(K(A,A^{T})w_{1}+eb_{1})\ge -\epsilon _{1}e-\xi _{1},&\begin{array}{cc} \xi _{1}\ge 0,&\epsilon _{1}\ge 0, \end{array} \end{array} \end{aligned}$$
(31)
$$\begin{aligned}&\alpha ^{T(}Y-(K(A,A^{T})w_{1}+eb_{1})+\epsilon _{1}e+\xi _{1})=0, \end{aligned}$$
(32)
$$\begin{aligned}&\begin{array}{cc} \beta ^{T}\xi _{1}=0,&\gamma \epsilon _{1}=0 \end{array} , \end{aligned}$$
(33)
$$\begin{aligned}&\begin{array}{ccc} \alpha \ge 0e,&\beta \ge 0e,&\gamma \ge 0. \end{array} \end{aligned}$$
(34)

Defining \(H=[ \begin{array}{cc} K(A,A^{T})&e \end{array} ]\) and \(u_{1}=[ \begin{array}{cc} w_{1}^{T}&b_{1} \end{array} ]^{T}\), and then combining (27) and (28) would result in the following equation:

$$\begin{aligned} -H^{T}DY+(H^{T}DH+c_{1}I)u_{1}+H^{T}\alpha =0. \end{aligned}$$

Thus, we have

$$\begin{aligned} u_{1}=(H^{T}DH+c_{1}I)^{-1}G^{T}(DY-\alpha ). \end{aligned}$$
(35)

By replacing \(w_{1}\) and \(b_{1}\) in (26) by (35), and applying the above KTT optimality conditions, the dual problem can be obtained as follows:

$$\begin{aligned}&\min \frac{1}{2}\alpha ^{T}H(H^{T}DH+c_{1}I)^{-1}H^{T}\alpha \nonumber \\&\qquad -Y^{T}DH(H^{T}DH+c_{1}I)^{-1}H^{T}\alpha +Y^{T}\alpha \nonumber \\&s.t.0e\le \alpha \le \frac{c_{2}}{m}d, \nonumber \\&e^{T}\alpha \le c_{2}v_{1}. \end{aligned}$$
(36)

Similarly, the dual problem of (25) can be expressed by

$$\begin{aligned}&\min \frac{1}{2}\lambda ^{T}H(H^{T}DH+c_{3}I)^{-1}H^{T}\lambda \nonumber \\&\quad +Y^{T}DH(H^{T}DH+c_{3}I)^{-1}G^{T}\lambda -Y^{T}\lambda \nonumber \\&s.t.0e\le \lambda \le \frac{c_{4}}{m}d, \nonumber \\&e^{T}\lambda \le c_{4}v_{2}, \end{aligned}$$
(37)

and we can have

$$\begin{aligned} u_{2}=[ \begin{array}{cc} w_{2}^{T}&b_{2} \end{array} ]^{T}=(H^{T}DH+c_{3}I)^{-1}G^{T}(DY+\lambda ). \end{aligned}$$
(38)

3.3 Determination of weighting parameters by wavelet transform

The parameters mentioned in the first subsection, \(d\in \mathfrak {R}^{m}\) and \(D\in \mathfrak {R}^{m\times m}\)\(( D=diag(d))\), are the weighting vector and matrix, respectively. They should be determined beforehand according to the importance of training data. By direct observation of the objective functions of TSVR and \(\nu\)-TWSVR, it is easy to see that all of the samples have the same penalties, which may reduce the performance of the regressors due to the impact of data with too much noise. Instinctively, different training samples should be given different weights; a larger given weight means that the sample is more important. Motivated by this idea and noting that the Gaussian function can reflect this trend, the weighting parameter \(d\left( =[d_{1},d_{2},\ldots ,d_{m}]^{T}\right)\) is determined by the Gaussian function described as follows:

$$\begin{aligned} d=E\exp \left( -\left| Y-\hat{Y}\right| ^{2}/\sigma ^{2}\right) , \end{aligned}$$
(39)

where E is the amplitude, \(\sigma\) represents the standard deviation, and the selection of E and \(\sigma\) is determined by the statistical characteristics of training data and is usually adjusted by experiments. The inappropriate selection of E and \(\sigma\) makes (39) unable to reflect the statistical characteristics of training data and reduces the regression performance. \(\hat{Y}(=[\hat{y_{1}},\hat{y_{2}},\ldots ,\hat{y_{m}} ]^{T})\) is the estimation value vector of output \(Y(=[y_{1},y_{m},\ldots ,y_{m}]^{T})\). Any time series filter can be used to calculate \(\hat{Y}\), but the wavelet filter is applicable to short-term signal processing, which is characteristic of most actual time series signals. Wavelet transform is a transform analysis method. It inherits and develops the idea of short-time Fourier transform localization, and overcomes the shortcomings of window size not changing with frequency. It can provide a time-frequency window that changes with frequency. It is a relatively ideal tool for time-frequency analysis and processing signals. Therefore, wavelet filtering is adopted to calculate \(\hat{Y}\) by three stages, as described below.

  1. 1.

    Wavelet transform may be considered a form of time-frequency representation for signals, and thus are related to harmonic analysis. Discrete wavelet transforms (DWT) use discrete-time filter banks. The DWT of a signal in the l-th decomposition step \(x_{l}^{a}(n)\) is calculated by a series of filters. The samples are passed through a low-pass filter with impulse response \(\phi (t)\) resulting in the approximation coefficients \(x_{l+1}^{a}\), and through a high-pass filter with impulse response \(\psi (t)\) resulting in the detail coefficients \(x_{l+1}^{d}\).

    $$\begin{aligned} x_{l+1}^{a}(n)= & {} \sum _{k}\phi (k-2n)x_{l}^{a}(k) \end{aligned}$$
    (40)
    $$\begin{aligned} x_{l+1}^{d}(n)= & {} \sum _{k}\psi (k-2n)x_{l}^{a}(k) \end{aligned}$$
    (41)

    The approximation coefficients \(x_{l+1}^{a}\) can be decomposed further to get \(x_{l+2}^{a}\) and \(x_{l+2}^{d}\). This process of decomposition is represented as a binary tree, as illustrated in Fig. 1a.

  2. 2.

    The obtained l groups of decomposed sequence (\(x_{1}^{d},x_{2}^{d},\ldots ,x_{l}^{d},x_{l}^{a}\)) after l steps of decomposition are processed by an appropriate algorithm to remove noise. In this paper, the high frequency part of the frequency domain signal is directly zeroed as denoising algorithm. Then the denoised sequence (\(x_{1}^{d\prime },x_{2}^{d\prime },\ldots ,x_{l}^{d\prime },x_{l}^{a\prime }\)) is obtained.

  3. 3.

    In this stage, the estimation value of output \(\hat{y}\) is reconstructed by the denoised sequence (\(x_{1}^{d\prime },x_{2}^{d\prime },\ldots ,x_{l}^{d\prime },x_{l}^{a\prime }\)).

    $$\begin{aligned} x_{l-1}^{a\prime }(n)=\sum _{k}\phi (n-2k)x_{l}^{a\prime }(k)+\sum _{k}\psi (n-2k)x_{l}^{d\prime }(k) \end{aligned}$$
    (42)

    This process of reconstruction is carried on further, and after l steps of reconstruction the estimation value of output \(\hat{Y}\) can be obtained, i.e., \(\hat{Y}=x_{0}^{a\prime }\). We next substitute \(\hat{Y}\) into (39), and then the weighting vector d and matrix D can be calculated. The process of signal decomposition and reconstruction is illustrated in Fig. 1.

Fig. 1
figure 1

Wavelet transform-based signal processing. a Decomposition process, and b reconstruction process

Full size image

The wavelet decomposition layers l can affect the performance of denoising. Usually, too many decomposition layers will result in serious loss of signal information. After denoising, the signal-to-noise ratio may decrease and the computational complexity will increase. If the number of decomposition layers is too small, the denoising effect is not ideal and the signal-to-noise ratio is not improved much. The general decomposition layers are determined by empirical methods.

3.4 Algorithm summary and discussion

In this subsection, we illustrate the proposed WTWTSVR algorithm.

Algorithm 1: Wavelet transform-based weighted \(\nu\)-twin support vector regression.

Input: Training data input matrix A; training data output vector Y; the appropriate parameters \(c_{1}, c_{2}, c_{3}, c_{4}\), \(\nu _{1}\) and \(\nu _{2}\) , in (24) and (25); Gaussian function parameters E, \(\sigma ^{2}\) in (39).

Output: The regression function f(x).

Process:

  1. 1.

    Preprocess Y by the wavelet transform method described in subsection (3.3) and get \(\hat{Y}\). Calculate d by (39).

  2. 2.

    By calculating the QPP problems in Eqs. (36) and (37), we can get \(\alpha\) and \(\lambda\), respectively.

  3. 3.

    Calculate \(u_{1}\) and \(u_{2}\) by (35) and (38), respectively.

  4. 4.

    Compute \(f(x)=\frac{1}{2}(w_{1}+w_{2})^{T}x+\frac{1}{2}(b_{1}+b_{2}).\)

The computation complexity of the proposed algorithm is mainly determined by the computations of a pair of QPPs and a pair of inverse matrices. If the number of training samples is l, then the training complexity of dual QPPs of the proposed algorithm is about O(2\(l^{3}\)) while the training complexity of the traditional SVR is about O(8\(l^{3}\)), which implies that the training speed of SVR is about four times slower than that of the proposed algorithm. Furthermore, a pair of inverse matrices with the size \((l+1)(l+1)\) in QPPs have the same computational cost O(\(l^{3}\)). During the training process, it is good to cache the inverse matrices with some memory cost in order to avoid repeated computations. In addition, the proposed algorithm contains the wavelet transform weighted matrix, and a Db-3 wavelet with a length of 6 is used in this paper; then, the complexity of the wavelet transform is less than 12l. By comparing with the computations of QPPs and the inverse matrix, the complexity of computing the wavelet matrix can be ignored. Therefore, the computation complexity of the proposed algorithm is about O(3\(l^{3}\)).

We mention that weights are inserted into both quadratic and first-degree terms in the proposed method, which is significantly different from previous works [22, 25]. The weights adopted in [22, 25] are only inserted into the quadratic term. Intuitively, the WTWTSVR can make full use of the prior information of training samples. The weight matrix and weight vector, which represent the distance of noised samples and its ‘real position,’ can reflect the prior information of the training samples. The larger weight is given to samples with smaller noise and the smaller weight is given to samples with larger noise. The adding of the weight matrix and weight vector to the objective function can reduce the impact of noise and outliers.

The weight calculation method given in [22] is also used to make use of the prior information of training data. One of the differences between the WTWTSVR and the method proposed in [22] lies in the calculation method of weights. In [22], the K-nearest neighbor (KNN) algorithm is adopted. In the algorithm, the KNN is adopted to calculate the penalty weights of samples. The idea of the KNN is that a sample point x is important if it has a larger number of K-nearest neighbors, whereas it is not important if it is an outlier that has a small number of K-nearest neighbors. We can see that the KNN algorithm is suitable for dealing with clustered samples but not time series. The wavelet transform theory adopted in our proposed algorithm is a new angle for preprocessing samples. Wavelet transform is a kind of time-frequency representation for signals, and the proposed method based on the wavelet theory is suitable for dealing with time series samples.

4 Experimental results

In this section, some experiments are made to examine the performance of our proposed WTWTSVR. WTWTSVR is compared with TSVR [11], \(\nu\)-TWSVR [21], Asy-\(\nu\)-TSVR [19], KNNUPWTSVR [26], and WL-\(\epsilon\)-TSVR [25] using three artificial datasets and eight benchmark datasets. The computer simulations are implemented in a Matlab R2014a environment on a PC with an Intel Core i5 processor (3.3 GHz) with 8 GB RAM. In this paper, the Gaussian nonlinear kernel is adopted for all of the datasets, that is

$$\begin{aligned} K(a^{T},b^{T})=exp\left( -\frac{\left\| a-b\right\| ^{2}}{e}\right) , \end{aligned}$$
(43)

where e determines the width of the Gaussian function. The choice of parameters is essential for the performance of algorithms. In this paper, parameter values are chosen by the grid search method from the set of values \(\{10^{i}|i=-4,-3,\ldots ,5\}\). In order to degrade the computational complexity of parameter selection, let \(C_{1}=C_{2}=C\) and \(\epsilon _{1}=\epsilon _{2}=\epsilon\) in TSVR; \(C_{1}=C_{2}=C\) and \(\nu _{1}=\nu _{2}=\nu\) in Asy- \(\nu\)-TSVR; and \(c_{1}=c_{3}\), \(c_{2}=c_{4}\), and \(\nu _{1}=\nu _{2}=\nu\) in \(\nu -\)TWSVR and the proposed WTWTSVR.

The performance of our proposed WTWTSVR and the three other methods are evaluated by selected criteria. The number of testing samples is denoted by l, \(y_{i}\) denotes the real value of a testing sample point \(x_{i}\), \(\bar{y }=\sum _{i}\frac{1}{l}y_{i}\) is the mean value of \(y_{1},y_{2},\ldots ,y_{l}\), and \(\hat{y}_{i}\) denotes the predicted value of \(x_{i}\). The criteria are specified as follows.

SSE::

Sum squared error of testing samples, defined as SSE = \(\sum _{i=1}^{l}(y_{i}-\hat{y}_{i})^{2}\).

SST::

Sum squared deviation of testing samples, defined as SST = \(\sum _{i=1}^{l}(y_{i}-\bar{y}_{i})^{2}\).

SSR::

Sum squared deviation that can be explained by the estimator, defined as SSR = \(\sum _{i=1}^{l}(\hat{y}_{i}-\bar{y}_{i})^{2}\).

SSE represents the fitting precision, but too small of an SSE value may mean overfitting of the regressor due to the fitting of noise. SST represents the variance of the testing samples, and SSR reflects the explanation ability of the regressor.

SSE/SST::

Ratio between sum squared error and sum squared deviation of testing samples, defined as SSE/SST=\(\sum _{i=1}^{l}(y_{i}-\hat{y} _{i})^{2}/(y_{i}-\bar{y}_{i})^{2}\).

SSR/SST::

Ratio between interpretable sum squared deviation and real sum squared deviation of testing samples, defined as SSR/SST=\(\sum _{i=1}^{l}( \hat{y}_{i}-\bar{y}_{i})^{2}/\sum _{i=1}^{l}(y_{i}-\bar{y}_{i})^{2}\).

In most cases, a small SSE/SST represents good agreement between estimations and real values; however, too small of an SSE/SST also probably means overfitting of the regressor. SSR/SST is the variance ratio of estimated data over sample data; if SSR/SST = 1, the estimated data share the same variance as training samples.

4.1 Experiments on artificial datasets

To demonstrate the performance of the proposed algorithm on artificial datasets, consider three noised functions for approximation denoted as \(y=f(x)+n\), where the noise \(n{}^{\sim }N(0,\varsigma ^{2})\ \)is Gaussian additive noise with mean zero, and variance \(\varsigma ^{2}\) is \(0.1^{2}\) and \(0.2^{2}\), respectively. Set the number of training points to be 300. The Db-3 wavelet used in WTWTSVR is selected to denoise the training data and the number of decomposition layers is 5. Five algorithms (TSVR [11] , \(\nu\)-TWSVR [21], Asy-\(\nu\)-TSVR [19], KNNUPWTSVR [26], and WL-\(\epsilon\)-TSVR [25]) are adopted for performance comparisons with the proposed WTWTSVR.

Figure 2 shows the one-run approximation functions obtained by the six algorithms.

The selection of parameters can be seen in Table 1. The adopted functions for regression are defined as follows.

Function 1::

\(f(x)=\frac{\sin x}{x}\).

Function 2::

\(f(x)=x^{2/3}\).

Function 3::

\(f(x)=\frac{4}{\left| x\right| +2}+\cos (2x)+\sin (3x).\)

To avoid biased comparisons, for each case, ten independent groups of noised samples are generated randomly, and the number of training points and testing points are all set to 300. Testing data is selected randomly under a uniform distribution and is assumed to be noise-free. Other settings can be seen in Table 1.

Fig. 2
figure 2

Performance of WTWTSVR on a Function 1 with noise \(\varsigma =0.1\), b Function 1 with noise \(\varsigma =0.2\), c Function 2 with noise \(\varsigma =0.1\), d Function 2 with noise \(\varsigma =0.2\), e Function 3 with noise \(\varsigma =0.1\), and f Function 3 with noise \(\varsigma =0.2\)

Full size image

The average results are summarized in Table 2. In the numerical value columns, the first column shows the mean value of ten testing results, and the second column represents the plus or minus the standard deviation. Obviously, the proposed WTWTSVR obtains the lowest testing errors compared with TSVR, Asy-\(\nu\)-TSVR, \(\nu\)-TWSVR, KNNUPWTSVR, and WL-\(\epsilon\)-TSVR, and it gets the smallest SSE and SSE/SST values. Although the SSR/SST value of WTWTSVR is not the largest, it is close to that obtained by other algorithms. From the comparisons of the six algorithms, we can see that the proposed WTWTSVR has better performance in most criteria.

Table 1 Parameter selection for the six algorithms on artificial datasets with different variance of Gaussian noises
Full size table
Table 2 Performance comparison of algorithms on artificial datasets with different variance of Gaussian noises
Full size table

Figure 3 shows the impact of variance \(\sigma ^{2}\) in (39) on the performance index SSE. The x coordinate is \(\sigma ^{2}\), and the y coordinate is the SSE value. The function for approximation is Function 1, and the Gaussian additive noise is with mean zero, and variance \(\varsigma ^{2}=0.1^{2}\) or \(0.2^{2}\). The result is averaged by 500 independent tests. We can see that the variance \(\sigma ^{2}\) of the Gaussian function for weighting has a great influence on the regression performance of WTWTSVR. The curve is convex, and for fixed noise, optimal \(\sigma ^{2}\) can be obtained. The parameter \(\sigma ^{2}\) determines the width of the Gaussian function. A large \(\sigma ^{2}\) leads to a fat Gaussian curve and similar weights for samples, while a small \(\sigma ^{2}\) leads to a narrow Gaussian curve and largely different weights for samples. Therefore, the value of \(\sigma ^{2}\) determines the impact of different samples, and the curve in Fig. 3 decreases sharply and increases slowly.

Fig. 3
figure 3

SSE value over \(\sigma ^{2}\) of Gaussian function. a\(\varsigma =0.1\), and b\(\varsigma =0.2\)

Full size image

The selection of the kernel function is important for the performance of regression algorithms. In order to test the effect of kernel functions, we study the performance of six kernel functions for artificial datasets. Function 1 includes the Gaussian kernel adopted in the proposed method. The function expressions and performance are listed in Table 3. It is easy to see that the Gaussian kernel achieves the best results.

Table 3 Comparisons of WTWTSVR on Function 1 using different kernel functions
Full size table

To test the effect of weighting parameter D, experiments on the SSE value of regression of artificial functions are conducted. Table 4 shows the results of tests for noise variances \(\varsigma ^{2}\) of \(0.1^{2}\) and \(0.2^{2}\). The first row in the table represents the performance of the proposed WTWTSVR (with D), and the second row shows that of the same algorithm except when setting D as an identity matrix (\(D=\mathbf {1}\)). The selected parameters can be seen in Table 1. It is seen that the SSE values of WTWTSVR are low when introducing the weighting parameter D calculated by the wavelet transform method; this verifies the effectiveness of adding the weighting parameter D.

Table 4 SSE value of regression of artificial functions
Full size table

To test the sensitivity of parameter selection on WTWTSVR regression performance, we study the influence of parameters \(c_{1},c_{2},\nu ,E,\)and \(\sigma ^{2}\) on SSE for artificial datasets with Function 1 with noise variance \(\sigma ^{2}=0.1^{2}\). From Figure 4 we can see that the SSE curves show convexity, i.e., with the increase in a parameter, performance value first decrease and then increase, which ensures that the optimal value can be found. However, the sensitivities to the change in parameter values are different. The performance is sensitive to \(c_{1},E\), and \(\sigma ^{2}\), but not to \(c_{2}\) and \(\nu\).

Fig. 4
figure 4

The influence of parameters \(c_{1},c_{2},\nu ,E\), and \(\sigma ^{2}\) on SSE for artificial datasets with Function 1 with noise variance \(\sigma ^{2}=0.1 ^{2}\)

Full size image

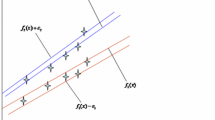
To test the robustness of the proposed algorithm to outliers, we verified the performance of the proposed method on Function 1 with Gaussian additive noise, and with mean zero and variance \(\varsigma ^{2}=0.1^{2}\). Figure 5 shows that the prediction performance of the proposed method is satisfying (see the blue line); SSE, SSE/SST, and SSR/SST values were 0.1678, 0.0058, and 0.9601, respectively. By comparing with the results in Table 2, it can be concluded that the performance of the proposed method with outliers is still better than that of the competitive algorithms with no outliers.

Fig. 5
figure 5

Regression performance of WTWTSVR on noised Function 1 with outliers

Full size image

4.2 Experiments on benchmark datasets

To further evaluate the performance of the proposed algorithm, experiments on benchmark datasets from the UCI machine learning repository [27] are conducted. The selected datasets are all time series. For all of the real-word examples considered in this paper, the original data is normalized as \(\tilde{s}_{i}=(s_{i}-s_{\min })/(s_{\max }-s_{\min })\), where \(s_{i}\) is the input value of the ith sample, \(\tilde{s}_{i}\) is its corresponding normalized value, and \(s_{\min }\) and \(s_{\max }\) denote the minimum and maximum values, respectively. The selection of parameters can be seen in Table 5. Table 6 show the performance of the six algorithms for the following benchmark datasets.

Energy: Energy use prediction of appliances. This dataset studies the energy use of appliances in a low-energy building based on 29 attributes, such as temperature and humidity conditions, averaged for 10-min periods. The number of instances is 19,735. We choose 1000 instances, including 500 training samples and 500 test samples with 22 attributes (dimensions of input) for regression and testing, respectively.

PM2.5: Beijing PM2.5 data. This dataset aims to predict the hourly PM2.5 concentration data at the US embassy in Beijing. 43,824 instances and 13 attributes, such as dew point, temperature, and wind speed, are included; and 1000 instances and four attributes are adopted in our experiments.

AirQuality: Air quality. The dataset contains hourly averaged responses from an array of five metal oxide chemical sensors. 822 instances and nine attributes are adopted.

DowJones: Dow Jones index. This dataset predicts the Dow Jones index value; 720 instances and four attributes are adopted in our experiments.

Istanbul1/2/4/8 is dataset of the Istanbul stock exchange; 536 samples with one, two, four, and eight attributes (input dimensions) are adopted independently.

Odd-numbered samples are selected as training data, while even-numbered samples are selected as test data; thus the number of the training data and test data are the same. The number (m) and dimension (n) of samples are listed in Table 6. In order to not destroy the time series characteristic of the data, one-shot experiments but not cross-validation experiments are conducted. From Table 6 we can see that our proposed WTWTSVR outperforms the other five algorithms. On most datasets, the WTWTSVR obtains the smallest SSE and SSE/SST values. Only on Istanbul1 does our WTWTSVR have the second smallest value. For SSR/SST criteria, WTWTSVR achieves the second or the third values close to 1 on Energy to DowJones , and achieves the closest value to 1 on Istanbul1 to Istanbul8. We can also see from Table 6 that the SSE value decreases with increasing input dimension, i.e., more input information leads to more accurate estimation. Based on the above analysis, it can be concluded that the performance of algorithms depends not only on the algorithm itself and the statistical characteristics of the data but also on the choice of parameters. The experimental results verify the effectiveness of training data preprocessing by the wavelet transform method, which can utilize the prior information of samples. The experimental results also show that the introduction of weighting parameters into both quadratic and first-degree empirical risk terms can improve the performance of the model.

Table 5 Parameter selection for the six algorithms on benchmark datasets
Full size table
Table 6 Performance comparison of the six algorithms on benchmark datasets
Full size table

4.3 Statistical analysis of experimental results

Nonparametric statistical tests are carried out to validate the experimental performance results of the proposed algorithm. The Friedman test [28] ranks the algorithms over six artificial datasets and eight real datasets. The Friedman test uses alpha = 0.05, and is distributed according to chi-square with 5 degrees of freedom. The Friedman statistic is 42.04 and 43.01 with p values of 5.7845e−8 and 3.6806e−8 for SSE and SSE/SST, respectively. The average ranks obtained by the six algorithms for SSE and SSE/SST are shown in Table 7. We can see that the average SSE and SSE/SST ranks of the WTWTSVR are lower than those of other algorithms. This shows the superiority of the proposed algorithm, which achieves better performance. In order to check the significant differences between the algorithms, the p-value is calculated through the Bonferroni–Dunn nonparametric test by computing multiple pairwise comparisons. The test assumes that the performances of two algorithms are significantly different if their average ranks differ by at least some critical value [28]. Table 8 lists the p values of the Bonferroni–Dunn test for the SSE criteria and SSE/SST ranking results obtained by the Friedman procedure. The null hypothesis of these tests is that there is no difference between the result distributions. From Table 8 we can see that the p values are very small, which means that the WTWTSVR is quite different from other methods, and therefore confirms the superiority of our method.

From the above analysis, we can conclude that the proposed WTWTSVR can actually improve the performance. The introduction of the weighting parameters into both quadratic and first-degree empirical risk terms are feasible and effective, and the preprocessing of training data by the wavelet transform method can utilize the prior information of samples. It should be noticed that wavelet theory is a powerful denoising tool for a time series signal. Therefore, the proposed method is suitable for dealing with time series datasets. If we deal with non-series samples by the proposed WTWTSVR, performance may be decreased. Additionally, the proposed model is suitable for small sample size datasets, and a large number of training samples will bring about tremendous computational cost.

Table 7 Algorithms’ average rankings for SSE and SSE/SST
Full size table
Table 8 p value from Bonferroni–Dunn tests for SSE and SSE/SST, with comparisons to the proposed WTWTSVR
Full size table

5 Conclusions

In this paper, a novel wavelet transform-based weighted \(\nu\)-twin support vector regression (WTWTSVR) is proposed. Unlike the cases in TSVR and \(\nu\) -TWSVR, samples in different positions in the proposed WTWTSVR model are given by different weights according to the distance between samples, and results are preprocessed by the wavelet transform. Computational comparisons between WTWTSVR and other existing methods are performed on artificial and benchmark datasets to show the better performance of the WTWTSVR, which demonstrates the effectiveness of the proposed method. Furthermore, since one of the theoretical bases of the proposed method is wavelet theory, which is a powerful denoising tool for time series signals, the proposed method is suitable for dealing with time series datasets. If we deal with non-series samples using the proposed WTWTSVR, performance may be decreased. Additionally, SVR is suitable for small sample size datasets, and a large number of training samples will bring about tremendous computational cost. Furthermore, one can notice that the precision of preprocessing and the selection of variance \(\sigma ^{2}\) of the Gaussian function can affect the performance of WTWTSVR. Therefore, for future work, study of parameter selection and the method of preprocessing should be carried out.