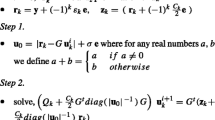1 Introduction

Support vector machines (SVMs), being computationally powerful tools for pattern classification and regression [1–3], have been successfully applied to a variety of real-world problems [5–7]. Regards to support vector classification, there exist some classical methods such as C-support vector classification (C-SVC) [2, 4], least square support vector classification (LS-SVC) [8], etc. The basic idea of all of these classifiers is to find the decision function by maximizing the margin between two parallel hyperplanes. Recently, some nonparallel hyperplane classifiers such as generalized eigenvalue proximal support vector machine (GEPSVM) and twin support vector machine (TWSVM) were proposed in [9, 10]. TWSVM seeks two nonparallel proximal hyperplanes such that each hyperplane is closest to one of two classes and as far as possible from the other class. A fundamental difference between TWSVM and C-SVC is that TWSVM solves two smaller sized quadratic programming problems (QPPs), whereas C-SVC solves one larger QPP. This makes TWSVM work faster than C-SVC. In addition, TWSVM is excellent at dealing with the “Cross Planes” dataset. Thus, the methods of constructing the nonparallel hyperplanes have been studied extensively [11–17].

Regards to the support vector regression, there exist some corresponding methods such as ε-support vector regression (ε-SVR), least square support vector regression (LS-SVR) [8, 18], etc. For linear ε-SVR, its primal problem can be understood in the following way: finds a linear function f(x) such that, on the one hand, more training samples locate in the ε-intensive tube between f(x) − ε and f(x) + ε, on the other hand, the function f(x) is as flat as possible, leading to introduce the regularization term. Thus, the structural risk minimization principle is implemented. Linear LS-SVR works in a similar way. Different from ε-SVR and LS-SVR, Peng [19] proposed a regressor in the spirit of TWSVM, termed as twin support vector regression (TSVR). The formulation of TSVR is in the spirit of TWSVM via two nonparallel planes and also solves two smaller sized QPPs, whereas the classical SVR solves one larger QPP. Experimental results in [19] showed the effectiveness of TSVR over ε-SVR in terms of both generalization performance and training time. Thus, TSVR has been studied in [20–24].

It is well known that one significant advantage of ε-SVR is the implementation of the structural risk minimization principle [25]. However, only the empirical risk is considered in the primal problems of TSVR. In addition, we noticed that the matrix \({(G^{\top}G)^{-1}}\) appears in the dual problems derived from the primal problems of TSVR. So, the extra condition that \({G^{\top}G}\) is nonsingular, must be assumed. This is not perfect from the theoretical point of view although it has been handled by modifying the dual problems technically and elegantly.

In this study, we proposes another regressor in the spirit of TWSVM, named ε-twin support vector regression (ε-TSVR). Similar to TSVR, linear ε-TSVR constructs two nonparallel ε-insensitive proximal functions by solving two smaller QPPs. However, there are differences as the following: (1) The main difference is that, in the primal problems of TSVR, the empirical risk is minimized, whereas, in our ε-TSVR, the structural risk is minimized by adding a regularization term. Similar to ε-SVR, the minimization of this term requires that two functions are as flat as possible. (2) The dual problems of our primal problems can be derived without any extra assumption and need not to be modified any more. We think that our method is more rigorous and complete than TSVR from theoretical point of view. (3) In order to shorten training time, an effective successive overrelaxation (SOR) technique is applied to our ε-TSVR. The preliminary experiments show that our ε-TSVR is not only faster, but also has better generalization.

This study is organized as follows. Section 2 briefly dwells on the standard ε-SVR, LS-SVR, and TSVR. Section 3 proposes our ε-TSVR, and the SOR technique is used to solve the optimization problems in ε-TSVR. Experimental results are described in Sect. 4 and concluding remarks are given in Sect. 5.

2 Background

Consider the following regression problem, suppose that the training set is denoted by (A, Y), where A is a l × n matrix and the i-th row \(A_i\in R^n\) represents the i-th training sample, \(i=1,2,\ldots,l. \) Let \(Y=(y_{1};y_{2};\ldots;y_{l})\) denotes the response vector of training sample, where \(y_{i}\in R. \) Here, we briefly describe some methods that are closely related to our method, including ε-SVR, LS-SVR and TSVR. For simplicity, we only consider the linear regression problems.

2.1 ε-Support vector regression

Linear ε-SVR [3, 25–27] searches for an optimal linear regression function

$$ f(x)=w^{\top}x+b, $$
(1)

where \(w\in R^n\) and \(b\in R. \) To measure the empirical risk, the ε-intensive loss function

$$ R_{\text emp}^{\varepsilon}[f]=\frac{1}{l}\sum_{i=1}^{l}|y_{i}-f(x_{i})|_{\varepsilon}, $$
(2)

is used, where \(|y_{i}-f(x_{i})|_{\varepsilon}=\max\{0,|y_{i}-f(x_{i})|-\varepsilon\}. \) By introducing the regularization term \(\frac{1}{2}||w||^2\) and the slack variables ξ,  \(\xi ^{*}, \) the primal problem of ε-SVR can be expressed as

$$ \begin{array}{lll} \underset{w,b,\xi,\xi^{*}}{\min}&\frac{1}{2}||w||^2+ C (e^{\top}\xi+e^{\top}\xi^{*}),\\ \hbox{s.t. } & Y-(Aw+eb)\leq \varepsilon e+\xi,\quad\xi\geq 0, \\ &(Aw+eb)-Y\leq \varepsilon e+\xi^{*},\quad\xi^{*}\geq 0, \end{array} $$
(3)

where C > 0 is a parameter determining the trade-off between the empirical risk and the regularization term. Note that a small \(\frac{1}{2} \|w\|^2\) corresponds to the linear function (1) that is flat [25, 26]. In the case of support vector classification, the structural risk minimization principle is implemented by this regularization term \(\frac{1}{2} \|w\|^2. \) In the case of support vector regression, this term is also added to minimize the structural risk.

2.2 Least squares support vector regression

Similar to ε-SVR, linear LS-SVR [8, 18] also searches for an optimal linear regression function

$$ f(x)=w^{\top}x+b, $$
(4)

and the following loss function is used to measure the empirical risk

$$ R_{\text emp}[f]=\frac{1}{l}\sum_{i=1}^{l}(y_{i}-f(x_{i}))^{2}. $$
(5)

By adding the regularization term \(\frac{1}{2}||w||^2\) and the slack variable ξ, the primal problem can be expressed as

$$ \begin{array}{lll} \underset{w,b,\xi}{\min}&\frac{1}{2}||w||^2 + \frac{C}{2}\xi^{\top}\xi,\\ \hbox{s.t. }& Y-(Aw+eb)=\xi, \end{array} $$
(6)

where C > 0 is a parameter.

2.3 Twin support vector regression

Different from ε-SVR and LS-SVR, linear TSVR seeks a pair of up-bound and down-bound functions

$$ f_{1}(x)=w_{1}^{\top}x+b_{1}\quad \hbox{ and}\quad f_{2}(x)=w_{2}^{\top}x+b_{2}, $$
(7)

where \(w_{1}\in R^n,\,w_{2}\in R^n,\,b_{1}\in R\,{\text {and}}\,b_{2}\in R. \) Here, the empirical risks are measured by:

$$ R_{\text emp}^{\varepsilon_1}[f_{1}]=\sum_{i=1}^{l}\max\{0, (y_{i}-f_{1}(x_{i})-\varepsilon_1)^{2}\} +c_{1}\sum_{i=1}^{l}\max\{0, -(y_{i}-f_{1}(x_{i})-\varepsilon_1)\} $$
(8)

and

$$ R_{\text emp}^{\varepsilon_2}[f_{2}]=\sum_{i=1}^{l}\max\{0, (f_{2}(x_{i})-y_{i}-\varepsilon_2)^{2}\}+c_{2}\sum_{i=1}^{l}\max\{0, -(f_{2}(x_{i})-y_{i}-\varepsilon_2)\} $$
(9)

where c 1 > 0 and c 2 > 0 are parameters. By introducing the slack variable ξ,  \(\xi ^{*}, \) η and \(\eta ^{*}, \) the primal problems are expressed as

$$ \begin{array}{ll} \underset{w_{1},b_{1},\xi,\xi^{*}}{\min}& \frac{1}{2}\xi^{*\top}\xi^{*} +c_{1}e^{\top}\xi,\\ \hbox{s.t. } & Y-(Aw_{1}+eb_{1}) \geq \varepsilon_{1}e-\xi,\quad\xi \geq 0, \\ & Y-(Aw_{1}+eb_{1})=\varepsilon_{1}e+\xi^{*}, \end{array} $$
(10)

and

$$ \begin{array}{ll} \underset{w_{2},b_{2},\eta,\eta^{*}}{\min}& \frac{1}{2}\eta^{*\top}\eta^{*} +c_{2}e^{\top}\eta,\\ \hbox{s.t. } & (Aw_{2}+eb_{2})-Y\geq \varepsilon_{2}e-\eta,\quad\eta \geq 0, \\ & (Aw_{2}+eb_{2})-Y=\varepsilon_{2}e+\eta^{*}. \end{array} $$
(11)

Their dual problems are

$$ \begin{array}{ll} \underset{\alpha}{\max}& -\frac{1}{2}\alpha^{\top} G(G^{\top}G)^{-1}G^{\top}\alpha+f^{\top}G(G^{\top}G)^{-1}G^{\top}\alpha-f^{\top}\alpha\\ \hbox{s.t. }& 0 \leq \alpha \leq c_{1}e. \end{array} $$
(12)

and

$$ \begin{array}{ll} \underset{\gamma}{\max}& -\frac{1}{2}\gamma^{\top} G(G^{\top}G)^{-1}G^{\top}\gamma-h^{\top}G(G^{\top}G)^{-1}G^{\top}\gamma+h^{\top}\gamma\\ \hbox{s.t. }& 0 \leq \gamma \leq c_{2}e. \end{array} $$
(13)

respectively when \({G^{\top}G}\) is positive definite, where \(G=[A\quad e],\,f =Y-e\varepsilon_{1}\) and \(h=Y+e\varepsilon_{2}. \)

In order to deal with the case when \({G^{\top}G}\) is singular and avoid the possible ill-conditioning, the above dual problems are modified artificially as:

$$ \begin{array}{ll} \underset{\alpha}{\max} &-\frac{1}{2}\alpha^{\top} G(G^{\top}G+\sigma I)^{-1}G^{\top}\alpha+f^{\top}G(G^{\top}G+\sigma I)^{-1}G^{\top}\alpha-f^{\top}\alpha\\ \hbox{s.t. }& 0 \leq \alpha \leq c_{1}e. \end{array} $$
(14)

and

$$ \begin{array}{ll} \underset{\gamma}{\max}& -\frac{1}{2}\gamma^{\top} G(G^{\top}G+\sigma I)^{-1}G^{\top}\gamma-h^{\top}G(G^{\top}G+\sigma I)^{-1}G^{\top}\gamma+h^{\top}\gamma\\ \hbox{s.t. }& 0 \leq \gamma \leq c_{2}e. \end{array} $$
(15)

by adding a term σI, where σ is a small positive scalar, and I is an identity matrix of appropriate dimensions.

The augmented vectors can be obtained from the solution α and γ of (14) and (15) by

$$ v_1= (G^{\top}G+\sigma I)^{-1}G^{\top}(f-\alpha), $$
(16)

and

$$ v_2=(G^{\top}G+\sigma I)^{-1}G^{\top}(h+\gamma), $$
(17)

where v 1 = [w 1  b 1], v 2 = [w 2  b 2].

3 ε-Twin support vector regression

3.1 Linear ε-TSVR

Following the idea of TWSVM and TSVR, in this section, we introduce a novel approach that we have termed as ε-twin support vector regression (ε-TSVR). As mentioned earlier, ε-TSVR also finds two ε-insensitive proximal linear functions:

$$ f_{1}(x)=w_{1}^{\top}x+b_{1}\quad \hbox{ and}\quad f_{2}(x)=w_{2}^{\top}x+b_{2}. $$
(18)

Here, the empirical risks are measured by:

$$ R_{\text emp}^{\varepsilon_1}[f_{1}]=\sum_{i=1}^{l}\max\{0,(y_{i}-f_{1}(x_{i}))^{2}\}+ c_{1}\sum_{i=1}^{l}\max\{0,-(y_{i}-f_{1}(x_{i})+\varepsilon_1)\} $$
(19)

and

$$ R_{\text emp}^{\varepsilon_2}[f_{2}]=\sum_{i=1}^{l}\max\{0,(f_{2}(x_{i}) -y_{i})^{2}\}+c_{2}\sum_{i=1}^{l} \max\{0,-(f_{2}(x_{i})-y_{i}+\varepsilon_2)\} $$
(20)

where c 1 > 0 and c 2 > 0 are parameters, and \(\sum\nolimits_{{i = 1}}^{l} {\max \{ 0, - (y_{i} - f_{1} (x_{i} ) + \varepsilon _{1} )\} } \) and \(\sum\nolimits_{{i = 1}}^{l} {\max \{ 0, - (f_{2} (x_{i} ) - y_{i} + \varepsilon _{2} )\} } \) are the one-side ε-insensitive loss function [25].

By introducing the regularization terms \(\frac{1}{2}(w_{1}^{\top}w_{1}+b_{1}^{2})\) and \(\frac{1}{2}(w_{2}^{\top}w_{2}+b_{1}^{2}), \) the slack variables ξ,  \(\xi ^{*}, \) η and \(\eta ^{*}, \) the primal problems can be expressed as

$$ \begin{array}{lll} \underset{w_{1},b_{1},\xi,\xi^{*}}{\min}& \frac{1}{2}c_{3}(w_{1}^{\top}w_{1}+b_{1}^{2})+\frac{1}{2} \xi^{*\top}\xi^{*}+c_{1}e^{\top}\xi,\\ \hbox{s.t. } & Y-(Aw_{1}+eb_{1})=\xi^{*}, \\ & Y-(Aw_{1}+eb_{1}) \geq -\varepsilon_{1}e-\xi,\quad\xi \geq 0, \end{array} $$
(21)

and

$$ \begin{array}{lll} \underset{w_{2},b_{2},\eta,\eta^{*}}{\min}& \frac{1}{2}c_{4}(w_{2}^{\top}w_{2}+b_{2}^{2}) +\frac{1}{2}\eta^{*\top}\eta^{*}+c_{2}e^{\top}\eta,\\ \hbox{s.t. } & (Aw_{2}+eb_{2})-Y=\eta^{*}, \\ & (Aw_{2}+eb_{2})-Y \geq -\varepsilon_{2}e-\eta,\quad\eta \geq 0, \end{array} $$
(22)

where c 1, c 2, c 1, ε1 and ε2 are positive parameters.

Now, we discuss the difference between the primal problems of TSVR and our ε-TSVR, by comparing problem (10) and problem (21).

  1. 1.

    The main difference is that there is an extra regularization term \(\frac{1}{2}c_{3}(\|w_{1}\|^2+b_{1}^{2})\) in (21). Now, we show that the structural risk is minimized in (21) due to this term. Remind the primal problem of ε-SVR, where the structural risk minimization is implemented by minimizing the regularization term \(\frac{1}{2} \|w\|^2\) and a small \(\|w\|^2\) corresponds to the linear function (1) that is flat. In fact, by introducing the transformation from R n to R n+1: \({\bf x}=\left[\begin{array}{c} x \\ 1 \end{array} \right], \) the functions \({f_1(x)=w_{1}^{\top}x+b_{1}}\) can be expressed as:

    $$ {\bf w_{1}}^{\top}{\bf x}=[w_{1}^{\top},b_{1}]\left[\begin{array}{c} x \\ 1 \end{array} \right] $$
    (23)

    showing that the flatness of the linear function f 1(x) in the x-space can be measured by \(\|w_1\|^2 + b_1^2. \) So, it is easy to see that the minimization of \(\|w_1\|^2+b_1^2\) requires that the linear function (23) is as flat as possible in x-space. Thus, the structural risk minimization principle is implemented. Note that the corresponding extra regularization term was proposed in our TBSVM [15] for classification problems. Peng [22] also added a similar regularization term in TSVR.

  2. 2.

    Except the regularization term \(\frac{1}{2}c_{3}(\|w_{1}\|^2+b_{1}^{2}), \) the other terms in (21) are different from (10) just because we choose the empirical risk (19) in ε-TSVR, whereas the empirical risk (8) is used in TSVR. Figure 1 gives the geometric interpretation of linear TSVR and ε-TSVR formulations for an example.

Fig. 1
figure 1

The geometric interpretation for TSVR (a), ε-TSVR (b)

Full size image

In order to get the solutions to problems (21) and (22), we need to derive their dual problems. The Lagrangian of the problem (21) is given by

$$ \begin{aligned} L(w_{1},b_{1},\xi,\alpha,\beta)&=\frac{1}{2}(Y-(Aw_{1}+eb_{1}))^{\top}(Y-(Aw_{1}+eb_{1}))\\ &\quad +\frac{1}{2}c_{3}(\|w_{1}\|^{2}+b_{1}^{2})+c_{1}e^{\top}\xi-\alpha^{\top} (Y-(Aw_{1}+eb_{1})+\varepsilon_{1}e+\xi) -\beta^{\top}\xi, \end{aligned} $$
(24)

where \(\alpha=(\alpha_{1},\ldots,\alpha_{l})\) and \(\beta=(\beta_{1},\ldots,\beta_{l})\) are the vectors of Lagrange multipliers. The Karush-Kuhn-Tucker (K.K.T.) condition for w 1, b 1, ξ and α, β are given by:

$$ -A^{\top}(Y-Aw_{1}-eb_{1})+c_{3}w_{1}+A^{\top}\alpha=0, $$
(25)
$$ -e^{\top}(Y-Aw_{1}+eb_{1})+c_{3}b_{1}+e^{\top}\alpha=0, $$
(26)
$$ c_{1}e-\beta-\alpha=0, $$
(27)
$$ Y-(Aw_{1}+eb_{1}) \geq -\varepsilon_{1}e-\xi,\quad\xi \geq 0, $$
(28)
$$ \alpha^{\top}(Y-(Aw_{1}+eb_{1})+\varepsilon_{1}e+\xi)=0,\quad\beta^{\top}\xi=0, $$
(29)
$$ \alpha \geq 0,\, \beta \geq 0. $$
(30)

Since β ≥ 0, from the (27) we have

$$ 0\leq \alpha \leq c_{1}e. $$
(31)

Obviously, (25)–(26) imply that

$$ -\left[ \begin{array}{cc} A^{\top}\\ e^{\top}\\ \end{array} \right]Y + \left(\left[ \begin{array}{cc} A^{\top}\\ e^{\top}\\ \end{array} \right] [A\quad e]+c_{3}I \right)\left[ \begin{array}{cc} w_{1}\\ b_{1}\\ \end{array} \right]+\left[ \begin{array}{cc} A^{\top}\\ e^{\top}\\ \end{array} \right]\alpha=0. $$
(32)

Defining \({G=[A\quad e],\,v_{1}=[w_{1}^{\top}\, b_{1}]^{\top}, }\) the Eq. (32) can be rewritten as:

$$ -G^{\top}Y + (G^{\top}G+c_{3}I)v_{1}+G^{\top}\alpha=0, $$
(33)

or

$$ v_{1}=(G^{\top}G+c_{3}I)^{-1}G^{\top}(Y-\alpha). $$
(34)

Then putting (34) into the Lagrangian and using the above K.K.T. conditions, we obtain the dual problem of the problem (21):

$$ \begin{array}{ll} \underset{\alpha}{\max}& -\frac{1}{2}\alpha^{\top}G(G^{\top}G+c_{3}I)^{-1}G^{\top} \alpha^{\top}+Y^{\top}G(G^{\top}G+c_{3}I)^{-1}G^{\top}\alpha -(e^{\top}\varepsilon_{1}+Y^{\top})\alpha\\ \hbox{s.t.\ }& 0\leq \alpha \leq c_{1}e, \end{array} $$
(35)

It is easy to see that the formulation of the problem (35) is similar to that of the problem (12) when the parameter c 3 in (35) is replaced by σ. However, σ in (12) is just a fixed small positive number, so the structural risk minimization principle can not be reflected completely as c 3 does. The experimental results in Sect. 4 will show that adjusting the value of c 3 can improve the classification accuracy indeed.

In the same way, the dual of the problem (22) is obtained:

$$ \begin{array}{ll} \underset{\gamma}{\max}& -\frac{1}{2}\gamma^{\top}G(G^{\top}G+c_{4}I)^{-1}G^{\top} \gamma^{\top}-Y^{\top}G(G^{\top}G+c_{4}I)^{-1}G^{\top}\gamma+(Y^{\top}-e^{\top} \varepsilon_{2})\gamma\\ \hbox{s.t. }& 0\leq \gamma \leq c_{2}e, \end{array} $$
(36)

where γ is the Lagrange multiplier. The augmented vector \({v_{2}=[w_{2}^{\top}\quad b_{2}]^{\top}}\) is given by

$$ v_{2}=(G^{\top}G+c_{4}I)^{-1}G^{\top}(Y+\gamma). $$
(37)

Once the solutions (w 1, b 1) and (w 2, b 2) of the problems (21) and (22) are obtained from the solutions of (35) and (36), the two proximal functions f 1(x) and f 2(x) are obtained. Then the estimated regressor is constructed as follows

$$ f(x)=\frac{1}{2}(f_{1}(x)+f_{2}(x))=\frac{1}{2}(w_{1} +w_{2})^{\top}x+\frac{1}{2}(b_{1}+b_{2}). $$
(38)

3.2 Kernel ε-TSVR

In order to extend our results to nonlinear regressors, consider the following two ε-insensitive proximal functions:

$$ f_{1}(x)=K(x^{\top},A^{\top})u_{1}+b_{1} \quad \hbox{and}\quad f_{2}(x)=K(x^{\top},A^{\top})u_{2}+b_{2}, $$
(39)

where K is an appropriately chosen kernel. We construct the primal problems:

$$ \begin{array}{lll} \underset{u_{1},b_{1},\xi}{\min}& \frac{1}{2}c_{3}(u_{1}^{\top}u_{1}+b_{1}^{2})+\frac{1}{2}\xi^{\top}\xi^{*}+c_{1}e^{\top}\xi,\\ \hbox{s.t. } & Y-(K(A,A^{\top})u_{1}+eb_{1}) \geq-\varepsilon_{1}e-\xi,\quad\xi \geq 0,\\ & Y-(K(A,A^{\top})u_{1}+eb_{1})=\xi^{*}, \end{array} $$
(40)

and

$$ \begin{array}{lll} \underset{u_{2},b_{2},\eta}{\min}& \frac{1}{2}c_{4}(u_{2}^{\top}u_{2}+b_{2}^{2})+\frac{1}{2} \eta^{\top}\eta^{*}+c_{2}e^{\top}\eta,\\ \hbox{s.t. } & (K(A,A^{\top})u_{1}+eb_{1})-Y \geq -\varepsilon_{2}e-\eta,\quad\eta \geq 0, \\ & (K(A,A^{\top})u_{2}+eb_{2})-Y=\eta^{*}. \end{array} $$
(41)

where c 1,  c 2,  c 3 and c 4 are positive parameters. In a similar way, we obtain their dual problems as the following:

$$ \begin{array}{ll} \underset{\alpha}{\max}& -\frac{1}{2}\alpha^{\top}H(H^{\top}H+c_{3}I)^{-1}H^{\top} \alpha^{\top}-(e^{\top}\varepsilon_{1}+Y^{\top})\alpha+Y^{\top}H(H^{\top}H +c_{3}I)^{-1}H^{\top}\alpha\\ \hbox{s.t. } & 0\leq \alpha \leq c_{1}e. \end{array} $$
(42)

and

$$ \begin{array}{ll} \underset{\gamma}{\max}& -\frac{1}{2}\gamma^{\top}H(H^{\top}H+c_{4}I)^{-1}H^{\top} \gamma^{\top}+(Y^{\top}-e^{\top}\varepsilon_{2})\gamma-Y^{\top}H(H^{\top}H+c_{4}I)^{-1}H^{\top}\gamma\\ \hbox{s.t. } & 0\leq \gamma \leq c_{2}e, \end{array} $$
(43)

where \({H=[K(A,A^{\top})\quad e]. }\) Then the augmented vector \({v_1=[u_1^{\top}\quad b_1]^{\top}}\) and \({v_{2}=[u_{2}^{\top}\quad b_{2}]^{\top}}\) are given by

$$ v_{1}=(H^{\top}H+c_{3}I)^{-1}H^{\top}(Y-\alpha), $$
(44)

and

$$ v_{2}=(H^{\top}H+c_{4}I)^{-1}H^{\top}(Y+\gamma). $$
(45)

Once the solutions (u 1,b 1) and (u 2,b 2) of the problems (40) and (41) are obtained from the solution of (42) and (43), the two functions f 1(x) and f 2(x) are obtained. Then the estimated regressor is constructed as follows

$$ f(x)=\frac{1}{2}(f_{1}(x)+f_{2}(x))=\frac{1}{2}(u_{1}^{\top}+u_{2}^{\top}) K(A,x)+\frac{1}{2}(b_{1}+b_{2}). $$
(46)

3.3 A fast ε-TSVR solver–successive overrelaxation technique

In our ε-TSVR, there are four strictly convex quadratic problems to be solved: (35), (36), (42), (43). It is easy to see that these problems can be rewritten as the following unified form:

$$ \begin{array}{cc} \underset{\alpha}{\max} & {\text d}\alpha-\frac{1}{2}\alpha^{\top}Q\alpha,\\ \hbox{s.t. } & \alpha \in S=\{0\leq \alpha \leq ce\}, \end{array} $$
(47)

where Q is positive definite. For example, the above problem becomes the problem (35), when \({Q=G(G^{\top}G+c_{3}I)^{-1}G^{\top},\quad c=c_1}\) and \(d=Y^{\top}Q-(e^{\top}\varepsilon_{1}+Y^{\top}). \) Because the problem (35) entails the inversion of a possibly massive m × m matrix, to reduce the complexity of computation, we make immediate use of the Sherman–Morrison–Woodbury formula [28] for matrix inversion as used in [13, 14, 16, 29], which results in: \((c_3I+G^{\top}G)^{-1} =\frac{1}{c_3}(I-G^{\top}(c_3I+GG^{\top})^{-1} G). \)

The above problem (47) can be solved efficiently by the following successive overrelaxation (SOR) technique, see [15, 30].

Algorithm 3.1

Choose \(t\in(0,2). \) Start with any \(\alpha^{0}\in R^{n}. \) Having αi compute αi+1 as follows

$$ \alpha^{i+1}=(\alpha^{i}-tE^{-1}(Q\alpha^{i}-d+L (\alpha^{i+1}-\alpha^{i})))_{\sharp}, $$
(48)

until ||αi+1 − αi|| is less than some prescribed tolerance, where the nonzero elements of \(L\in R^{m\times m}\) constitute the strictly lower triangular part of the symmetric matrix Q, and the nonzero elements of \(E\in R^{m\times m}\) constitute the diagonal of Q.

SOR has been proved that this algorithm converges linearly to a solution. It should be pointed out that we also improve the original TSVR by applying the SOR technique to solve the problems (12) and (13). The experimental results in the following section will show that the SOR technique has remarkable acceleration effect on both our ε-TSVR and TSVR.

3.4 Comparison with TPISVR

We mentioned that our ε-TSVR is motivated by the TSVR. And different from only empirical risk is implemented in TSVR, a regularization term is added in ε-TSVR. Similar to ε-TSVR, TPISVR [23] also introduced a regularization term in its primal problems. Now, we show some comparisons of our ε-TSVR with TPISVR. The primal problems of linear TPISVR can be expressed as

$$ \begin{array}{ll} \underset{w_{1},b_{1},\xi}{\min}&\frac{1}{2}||w_{1}||^{2}+ \frac{\nu_1}{l}e^{\top}(Aw_{1}+eb_{1})+\frac{c_1}{l}e^{\top}\xi,\\ \hbox{s.t. } & Y-(Aw_{1}+eb_{1}) \geq -\xi,\quad\xi \geq 0, \end{array} $$
(49)

and

$$ \begin{array}{ll} \underset{w_{2},b_{2},\eta}{\min}&\frac{1}{2}||w_{2}||^{2} +\frac{\nu_2}{l}e^{\top}(Aw_{1}+eb_{1})+\frac{c_2}{l}e^{\top}\eta,\\ \hbox{s.t. } & Y-(Aw_{1}+eb_{1}) \leq \eta,\quad\eta \geq 0, \end{array} $$
(50)

where c 1, c 2, ν1 and ν2 are positive parameters. From the above two QPPs, we can see that our ε-TSVR derives the similar characteristics as TPISVR, such as both of them has the same decisions and also loses the sparsity. However, by comparing the formulations of our ε-TSVR and TPISVR, we can see that both the objective functions and the constraints are differences, and Fig. 1a, b show the geometric interpretations of the TSVR (TPISVR) and our ε-TSVR, respectively. From Fig. 1, we can see that the two algorithms have some differences in geometric interpretations. TPISVR constructs a pair of up-bound and down-bound functions, while our ε-TSVR constructs a pair of ε-insensitive proximal functions. In addition, in our ε-TSVR, only have the boundary constraints, this strategy makes SOR can be used for our ε-TSVR (and TSVR), which obtains the less learning cost than TPISVR. But in our ε-TSVR, the parameters have no meaning of bounds of the fractions of SVs and margin errors as in TPISVR.

4 Experimental results

In this section, some experiments are made to demonstrate the performance of our ε-TSVR compared with the TSVR, ε-SVR, and LS-SVR on several datasets, including two type artificial datasets and nine benchmark datasets. All methods are implemented in Matlab 7.0 [31] environment on a PC with an Intel P4 processor (2.9 GHz) with 1 GB RAM. ε-SVR and LS-SVR are solved by the optimization toolbox: QP and LS-SVMlab in Matlab [31, 32] respectively. Our ε-TSVR and TSVR are solved by SOR technique. The values of the parameters in four methods are obtained through searching in the range 2−8–28 by tuning a set comprising of random 10 % of the dataset. In our experiments, we set c 1 = c 2, c 3 = c 4 and ε1 = ε2, to degrade the computational complexity of parameter selection.

4.1 Performance criteria

In order to evaluate the performance of the algorithms, some evaluation criteria [19, 33, 34] commonly used should be introduced firstly. Without loss of generality, let l be the number of training samples and denote m as the number of testing samples, \(\hat{y}_{i}\) as the prediction value of y i , and \(\bar{y}=\frac{1}{m}\sum\nolimits_{i}y_{i}\) as the average value of \(y_1,\ldots,y_m. \) Then the definitions of some criteria are stated in Table 1.

Table 1 Performance metrics and their calculations
Full size table

4.2 Artificial datasets

In order to compare our ε-TSVR with TSVR, ε-SVR, LS-SVR, we choose the same artificial datasets to the ones in [19] and [35]. Firstly, consider the function: \(y=x^{\frac{2}{3}}.\) To effectively reflect the performance of the methods, training samples are polluted by Gaussian noises with zero means and 0.2 standard deviation, i.e. we have the following training samples (x i , y i ):

$$ y_i=x_i^{\frac{2}{3}}+\xi_i,\quad x\sim U[-2, 2],\;\xi_i\sim N(0,0.2^2), $$
(51)

where U[a, b] represents the uniformly random variable in [a, b] and \(N(\bar{a}, \bar{b}^{2})\) represents the Gaussian random variable with means \(\bar{a}\) and \(\bar{b}\) standard deviation, respectively. To avoid biased comparisons, ten independent groups of noisy samples are generated randomly using Matlab toolbox, which consists of 200 training samples and 200 none noise test samples.

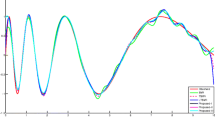
Figure 2a–d illustrate the estimated functions obtained by these four methods, respectively. It can be observed that our ε-TSVR obtain the best approximation among four methods. The results of the performance criteria are listed in Table 2. Our ε-TSVR derives the smallest SSE, NMSE and the largest R 2 among the four methods. This indicates the statistical information in the training dataset is well presented by our ε-TSVR with fairly small regression errors. Besides, Table 2 also compares the training CPU time for these four methods. It can be seen that ε-TSVR is the fastest learning method, indicating that SOR technique can improve the training speed.

Fig. 2
figure 2

Predictions of our ε-TSVR, TSVR, ε-SVR and LS-SVR on \(y=x^{\frac{2}{3}}\) function

Full size image
Table 2 Result comparisons of our ε-TSVR, TSVR, ε-SVR and LS-SVR on datasets (51) and (52)
Full size table

Furthermore, we generate the datasets by the sinc function that is polluted by Gaussian noises with zero means and 0.2 standard deviation. We have the training samples (x i , y i ):

$$ y_{i}=\frac{\sin(x_{i})}{x_{i}}+\xi_{i},\quad x\sim U[-4\pi, 4\pi],\;\xi_{i}\sim N(0,0.2^{2}). $$
(52)

Our dataset consists of 252 training samples and 503 test samples. Figure 3a–d illustrate the estimated functions obtained by four methods and Table 2 lists the corresponding performances. These results also show the superiority of our method.

Fig. 3
figure 3

Predictions of our ε-TSVR, TSVR, ε-SVR and LS-SVR on Sinc function

Full size image

4.3 UCI datasets

For further evaluation, we test nine benchmark datasets: the Motorcycle [36], Diabetes, Boston housing, Auto-Mpg, Machine CPU, Servo, Concrete Compressive Strength, Auto price, and Wisconsin breast cancer datasets [37], which are commonly used in testing machine learning algorithms. More detailed description can be found in Table 3.

Table 3 The description for real datasets
Full size table

Because the two datasets “Motorcycle” and “Diabetes” have smaller number of samples and features, the criterions leave-one-out are used on them. Figure 4 shows the regression comparison of our ε-TSVR, TSVR, ε-SVR and LS-SVR on the “Motorcycle” dataset. Table 4 lists the learning results of these four methods on the Motorcycle and Diabetes datsets. It can be seen that our ε-TSVR outperforms the other three methods. For instance, our ε-TSVR obtains the largest R 2 and the smallest NMSE among the four methods. As for the computation time, although LS-SVR spends on the least CPU time, our ε-TSVR needs far less CPU time than ε-SVR, indicating that ε-TSVR is an efficient algorithm for regression.

Fig. 4
figure 4

Predictions of ε-TSVR, TSVR, ε-SVR and LS-SVR on the “Motorcycle” dataset

Full size image
Table 4 Result comparisons of ε-TSVR, TSVR, ε-SVR and LS-SVR on Motorcycle and Diabetes datasets
Full size table

For the other seven datasets, the criterions “NMSE”, “R 2” and “MAPE” are used. Table 5 shows the testing results of the proposed ε-TSVR, TSVR, ε-SVR and LS-SVR on these seven datasets. The results in Table 5 are similar with that appeared in Table 4 and therefore confirm the superiority of our method further. Table 6 lists the best parameters selected by ε-TSVR and TSVR on the above UCI datasets. It can be seen that the c 3 and c 4 vary and are usually not take a smaller value in our ε-TSVR, while σ is a fixed small positive scalar in TSVR. This implies that the regularization terms in our ε-TSVR are useful.

Table 5 Result comparisons of ε-TSVR, TSVR, ε-SVR and LS-SVR on UCI datasets
Full size table
Table 6 The best parameters of ε-TSVR and TSVR on UCI datasets
Full size table

5 Conclusions

For regression problems, an improved version ε-TSVR based on TSVR is proposed in this study. The main contribution is that the structural risk minimization principle is implemented by adding the regularization term in the primal problems of our ε-TSVR. This embodies the marrow of statistical learning theory. The parameters c 3 and c 4 introduced are the weights between the regularization term and the empirical risk, so they can be chosen flexibly. In addition, the application of SOR technique is also an excellent contribution, since it speeds up the training procedure. Computational comparisons between our ε-TSVR and other methods including TSVR, ε-SVR, and LS-SVR have been made on several datasets, indicating that our ε-TSVR is not only faster, but also shows better generalization. We believe that its nice generalization mainly comes from the fact that the parameters c 3 and c 4 are adjusted properly. Our ε-TSVR Matlab codes can be downloaded from: http://math.cau.edu.cn/dengnaiyang.html.

It should be pointed out that as does the TWSVM, our ε-TSVR also loses sparsity, so it is interesting to find a sparsity algorithm for our ε-TSVR. Note that, for LS-SVR, there are some relevant improvements such as the work in [38, 39]. May be they are useful references in further study. Besides, the parameters selection is a practical problem and should be addressed in the future too.