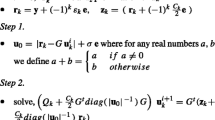A ν-twin support vector machine based regression with automatic accuracy control

Abstract

This paper presents an efficient ν-Twin Support Vector Machine Based Regression Model with Automatic Accuracy Control (ν-TWSVR). This ν-TWSVR model is motivated by the celebrated ν-SVR model (Schlkoff et al. 1998) and recently introduced 𝜖-TSVR model (Shao et al., Neural Comput Applic 23(1):175–185, 2013). The ν-TSVR model can automatically optimize the parameters 𝜖 ₁ and 𝜖 ₂ according to the structure of the data such that at most certain specified fraction ν ₁(respectively ν ₂) of data points contribute to the errors in up (respectively down) bound regressor. The ν-TWSVR formulation constructs a pair of optimization problems which are mathematically derived from a related ν-TWSVM formulation (Peng, Neural Netw 23(3):365–372, 2010) and making use of an important result of Bi and Bennett (Neurocomputing 55(1):79–108, 2003). The experimental results on artificial and UCI benchmark datasets show the efficacy of the proposed model in practice.

1 Introduction

The last decade has witnessed the evolution of Support Vector Machines (SVMs) as a powerful paradigm for pattern classification and regression [1–4, 15]. SVMs emerged from the research in statistical learning theory on how to regulate the trade off between structural complexity and empirical risk. SVM classifiers attempt to reduce generalization error by maximizing the margin between two separating hyperplanes [1–4].

Support Vector Regression (SVR) is a technique for handling regression problem which is similar in principle to SVM. The standard 𝜖-SVR is an 𝜖-insensitive model which sets an epsilon tube around the data points. The data points outside the epsilon tube contribute to the errors which are penalized in the objective function via a user specified parameter. Therefore, an appropriate choice of 𝜖 should be supplied beforehand in order to meet the desired accuracy. Bi and Bennett [5] have developed a geometric framework for SVR showing that it can be related to an appropriate SVM problem. This result of Bi and Bennett [5] is very significant as it allows to explore the possibilities of deriving new regression models corresponding to existing classification models.

Twin Support Vector Machine(TWSVM) [6] is a novel binary classification method that determines two non-parallel hyperplanes, each of them are proximal to its own class and has at least unit distance from the opposite class. TWSVM is faster than SVM as it solves two related SVM-type problems each of which is smaller than the conventional SVM. The ν-TWSVM [11] model modifies the TWSVM formulation. It finds a pair of the non-parallel hyperplanes, each of them are proximal to its own class and is as far as possible from the points of opposite class.

In an attempt to extend twin methodology to the regression problem, Peng [7] proposed a novel algorithm which he termed as Twin Support Vector Machine for Regression (TSVR). However in a recent paper, Khemchandani et al. [8] observed that the model of Peng [7] is not in the true spirit of twin methodology. They [8] presented a new twin support vector machine based regression and termed it as TWSVR model. It is interesting to note that the TWSVR model can be derived mathematically using an important result of Bi and Bennett [5] together with the TWSVM formulation. Later, Shao et al.[9] presented another twin model for regression termed as 𝜖-TSVR. The formulation of the 𝜖-TSVR [9] is different from that of Peng [7] and is justified on the basis of different empirical risk functionals. Later, Xu et al. [14] proposed the K-nearest neighbor-based weighted twin support vector regression by using the local information present in the samples for improving the prediction accuracy.

In this paper, we have proposed a novel ν-TWSVM based regression formulation termed as ν-TWSVR. Some of the important features of ν-TWSVR are as follows.

• (i) The proposed ν-TWSVR model automatically adjusts the values of 𝜖 ₁ and 𝜖 ₂ in order to achieve the desired accuracy level to the data in hand.

• (ii) It provides an efficient way to control the fraction of errors and support vectors by adjusting the values of 𝜖 ₁ and 𝜖 ₂ via the user specified parameters ν ₁ and ν ₂.

• (iii) The proposed ν-TWSVR formulation is in the true spirit of ν-TWSVM [11]. Thus, the two QPPs in the formulation of ν-TWSVR can be mathematically derived using an important result of Bi and Bennett [5].

• (iv) As a consequence of our derivation, it can be shown that the 𝜖-TSVR formulation of Shao et al. [9] is also in the true spirit of twin methodology and can be derived using Bi and Bennett approach [5].

• (v) The experimental results on artificial and UCI-benchmark real world datasets show that ν-TWSVR outperforms 𝜖-TSVR model in practice.

The rest of this paper is organized as follows. Section 2 introduces notations used in the paper and briefly describes ν-SVR model [10]. Section 3 discusses the linear ν-TWSVM [11] while Section 4 briefly describes 𝜖-TSVR [9]. Section 5 proposes the linear ν-Twin Support Vector Machine Based Regression(ν-TWSVR) and its extension for the non-linear case. Section 6 describes the experimental results while Section 7 is devoted to the conclusions.

2 Support vector regression models

2.1 𝜖-support vector regression

Let the training samples be denoted by a set of l row vectors A = (A ₁, A ₂,...,A _l ) where the i ^th sample A _i = (A _i1, A _i2,...,A _{i n} ) is in the n-dimensional real space $\mathbb {R}^{n}$. Also let Y = (y ₁, y ₂,...,y _l ) denote the response vector of training samples where $y_{i} \in \mathbb {R}$. Let ξ = (ξ ₁, ξ ₂,..,ξ _l ) and $\xi ^{*} = (\xi ^{*}_{1},\xi ^{*}_{2},..,\xi ^{*}_{l})$ be l dimensional vector which will be used to denote the errors and e is column vector of ‘ones’ of appropriate dimension.

Linear 𝜖-SVR finds a linear function f(x) = w ^T x + b, where $w \in \mathbb {R}^{n}$ and $b \in \mathbb {R}$. It minimizes the 𝜖-insensitive loss function with a regularization term $\frac {1}{2}\Arrowvert w \Arrowvert ^{2}$ which makes the function f(x) as flat as possible. The 𝜖-insensitive loss function ignores the error up to 𝜖. The Support Vector Regression(SVR) solves following optimization problem

$$\begin{array}{@{}rcl@{}} &&\min\limits_{_{w,b,\xi ,\xi^{*}}} ~ ~ \frac{1}{2}\Arrowvert w \Arrowvert^{2} + C \sum\limits_{i=1}^{l} (\xi_{i} + \xi_{i}^{*})\\ && \hbox{subject to,} \\ && y_{i} - (A_{i}w +b) \leq \epsilon+ \xi_{i}, (i=1,2,..,l), \\ && (A_{i}w +b) -y_{i} \leq \epsilon +\xi_{i}^{*}, (i=1,2,..,l ), \\ && \xi_{i}\geq0 , ~ \xi_{i}^{*}\geq0 ~~, (i=1,2,..,l) , \end{array} $$

(1)

where C > 0 is the user specified parameter that balances the trade off between the fitting error and the flatness of the function.

2.2 Support vector regression with automatic accuracy control

In 𝜖-SVR, a good choice of 𝜖 should be specified beforehand in order to meet desired level of accuracy. A bad choice of 𝜖 can lead to poor accuracy. In [10] author proposes Support Vector Regression with Automatic Accuracy Control (ν−SVR) which automatically minimizes the size of 𝜖-tube and adjusts the accuracy level according to the data in hand. For the linear case ν-SVR solves the following optimization problem

$$\begin{array}{@{}rcl@{}} \min\limits_{_{w,b,\epsilon,\xi_{1} ,\xi_{2}}} ~ ~ \frac{1}{2}\Arrowvert w \Arrowvert^{2} + C\left( v.\epsilon + \frac{1}{l}\sum\limits_{i=1}^{l} (\xi_{i} + \xi_{i}^{*})\right)\\ & \hbox{subject to,}\\ & y_{i} - (A_{i}w +b) \leq \epsilon+ \xi_{i}, (i=1,2,..,l), \\ & (A_{i}w +b) -y_{i} \leq \epsilon +\xi_{i}^{*}, (i=1,2,..,l), \\ & \xi_{i}\geq 0 , ~ \xi_{i}^{*}\geq 0 ~~, (i=1,2,..,l) . \end{array} $$

(2)

The tube size 𝜖 is traded off against the model complexity and slack variables via a constant ν ≥ 0. Using the K.K.T. optimality conditions, the Wolfe dual of the optimization problem (2) is obtained as follows

$$\begin{array}{@{}rcl@{}} &&\min\limits_{\alpha ,\alpha^{*}}~~ \frac{1}{2}\sum\limits_{i=1}^{l}\sum\limits_{j=1}^{l} (\alpha^{*}_{i} -\alpha_{i})(\alpha^{*}_{j} -\alpha_{j}) {A_{i}^{T}}A_{j}-\sum\limits_{i=1}^{l} y_{i}(\alpha^{*}_{i} -\alpha_{i}) \\ && \hbox{subject to,} \\ && \displaystyle\sum\limits_{i=1}^{l} (\alpha^{*}_{i} - \alpha_{i}) = 0 ~,~~~ \sum\limits_{i=1}^{l} (\alpha^{*}_{i} + \alpha_{i}) \leq C\nu, \\ &&0\leq \alpha_{i} \leq \frac{C}{l}~,~~~~~0\leq \alpha^{*}_{i} \leq \frac{C}{l}. \end{array} $$

(3)

After finding the optimal values of α and α ^∗, the estimated regressor for the test point x is given by

$$\begin{array}{@{}rcl@{}} f(x) = \sum\limits^{l}_{i=1}(\alpha^{*}_{i} - \alpha_{i}){A_{i}^{T}}x + b. \end{array} $$

3 A ν-twin support vector machine for classification

Peng [11] proposed a modification of TWSVM, termed as ν-TWSVM and introduced the two new parameters ν ₁ and ν ₂ instead of the trade-off parameters c ₁ and c ₂ of TWSVM. Similar to the ν-SVM [12], the parameters ν ₁ and ν ₂ in the ν-TWSVM controls the bounds on the number of support vectors and the margin errors. ν−Twin Support Vector Machine (ν-TWSVM) modifies the optimization problem of TWSVM as follows

(ν-TWSVM-1):

$$\begin{array}{@{}rcl@{}} \min\limits_{_{w_{1},b_{1},\rho_{+},\xi_{1}}} ~ ~ \frac{1}{2}||Aw_{1}+e_{1}b_{1}||_{2} - v_{1}\rho_{+} + \frac{1}{l_{2}}{e_{2}^{T}} \xi_{1} \\ & \text{subject to,} \\ & - (Bw_{1}+e_{2}b_{1}) \geq e_{2}\rho_{+} -\xi_{1}, \\ & \xi_{1} \geq 0 ,~ \rho_{+}\geq0, \end{array} $$

(4)

and

(ν-TWSVM-2):

$$\begin{array}{@{}rcl@{}} \min\limits_{_{w_{2},b_{2},\rho_{-},\xi_{2}}} ~ ~ \frac{1}{2}||Bw_{2}+e_{2}b_{2}||_{2} - v_{2}\rho_{-} + \frac{1}{l_{1}}{e_{1}^{T}} \xi_{2} \\ & \text{subject to,} \\ & (Aw_{1}+e_{1}b_{1}) \geq e_{1}\rho_{-} -\xi_{2}, \\ & \xi_{2} \geq 0 , ~ \rho_{-} \geq0 , \end{array} $$

(5)

where A and B are (l ₁×n) and (l ₂×n) matrices representing data points belonging to class +1 (positive) and class -1 (negative) respectively. Here ξ ₁ and ξ ₂ are l-dimensional error vector. The introduction of the variables ρ ₊ and ρ ₋ provides an efficient way to control the number of support vectors in TWSVM. In practice rather than solving the primal optimization problems (4) and (5), we solve their respective Wolfe duals by using the K.K.T. optimality conditions.

4 An 𝜖-twin support vector machine for regression

On the lines of TWSVM, 𝜖-Twin Support Vector Machine for Regression(𝜖-TSVR) [9] also finds two 𝜖-insensitive proximal functions $f_{1}(x) = {w_{1}^{T}}x+b_{1}$ and $f_{2}(x) = {w_{2}^{T}}x + b_{2}$, which are obtained by solving following pairs of optimization problems

$$\begin{array}{@{}rcl@{}} \text{(\(\epsilon\)-TSVR-1)}\\ \min\limits_{w_{1} ,b_{1},\xi}&\frac{c_{3}}{2}\left( ||w_{1}||^{2}+{b_{1}^{2}}\right) +\frac{1}{2}||(Y-(Aw_{1}+eb_{1})||^{2} \\& + c_{1}e^{T}\xi \\ &\text{subject to,} \\ & Y -(Aw_{1}+eb_{1}) \geq -\epsilon_{1}e- \xi ,~~ \xi \geq 0 , \end{array} $$

(6)

and

$$\begin{array}{@{}rcl@{}} \text{~~(\(\epsilon\)-TSVR-2)}\\ \min\limits_{w_{2} ,b_{2},\eta} & \frac{c_{4}}{2}\left( ||w_{2}||^{2}+{b_{2}^{2}}\right) +\frac{1}{2}||(Y-(Aw_{2}+eb_{2})||^{2} \\&+ c_{2}e^{T}\eta \\ &\text{subject to,} & \\ & (Aw_{2}+eb_{2})-Y \geq -\epsilon_{2}e - \eta, ~~ \eta \geq 0 , \end{array} $$

(7)

where parameters 𝜖 ₁, 𝜖 ₂, c ₁, c ₂, c ₃ and c ₄ are user supplied positive numbers. Defining $G = \left [\begin {array}{cc} \textit {A} ,& \textit {e} \\ \end {array}\right ]$ and using the K.K.T optimality conditions, the Wolfe dual of (𝜖-TSVR-1) can be obtained as follows

(Dual 𝜖-TSVR-1):

$$\begin{array}{@{}rcl@{}} &&\min\limits_{\alpha}~~\frac{1}{2}\alpha^{T}G(c_{3}I+G^{T}G)^{-1}G^{T}\alpha\\&&-Y^{T}G(G^{T}G+c_{3}I)^{-1}G^{T}\alpha+ (e^{T}\epsilon_{1} + Y^{T})\alpha \\ &&\text{subject to,} ~~~0\leq \alpha \leq c_{1}e, \end{array} $$

(8)

where α is vector of Lagrangian multipliers.

The Wolfe dual of the optimization problem (𝜖-TSVR-2) is obtained as

(Dual 𝜖-TSVR-2):

$$\begin{array}{@{}rcl@{}} \min\limits_{\gamma}~~\frac{1}{2}\gamma^{T}G(c_{4}I+G^{T}G)^{-1}G^{T}\gamma + Y^{T}G(G^{T}G+\\ & c_{4}I)^{-1}G^{T}\gamma - (Y^{T}-e^{T}\epsilon_{2})\gamma \\ & \text{subject to ,} ~~~0\leq \gamma \leq c_{2}e , \end{array} $$

(9)

where γ is vector of Lagrange multipliers.

After solving the optimization problems (8) and (9), the augmented vector $v_{1} = \left [\begin {array}{cc} w_{1} \\ b_{1} \end {array}\right ]$and $v_{2} = \left [\begin {array}{cc} w_{2} \\ b_{2} \end {array}\right ]$are obtained as

$$\begin{array}{@{}rcl@{}} v_{1} = (c_{3}I+G^{T}G)^{-1} G^{T}(Y-\alpha ), \end{array} $$

(10)

and

$$\begin{array}{@{}rcl@{}} v_{2} = (c_{4}I+G^{T}G)^{-1} G^{T}(Y+\lambda). \end{array} $$

(11)

The final regressor is then obtained by

$$\begin{array}{@{}rcl@{}} f\!(x) \,=\, \frac{1}{2}(f_{1}(x)\,+\,f_{2}(x)) \,=\, \frac{1}{2}(w_{1}\,+\,w_{2})^{T}x\,+\, \frac{1}{2}(b_{1}\,+\,b_{2}). \end{array} $$

(12)

For the non-linear case, the 𝜖-TSVR considers following kernel generated surfaces

$$\begin{array}{@{}rcl@{}} f_{1}(x) = K(x^{T},A^{T})u_{1}+b_{1}, \end{array} $$

(13)

and

$$\begin{array}{@{}rcl@{}} f_{2}(x) = K(x^{T},A^{T})u_{2} + b_{2}, \end{array} $$

which are obtained by solving following pairs of QPPs

(Kernel 𝜖−TSVR-1):

$$\begin{array}{@{}rcl@{}} \min\limits_{u_{1} ,b_{1},\xi} &\frac{c_{3}}{2}\left( ||u_{1}||^{2}+{b_{1}^{2}}\right) +\frac{1}{2}||(Y-(K (A,A^{T})u_{1}+eb_{1})||^{2} \\& + c_{1}e^{T}\xi \\ & \text{subject to,} \\ & Y -(K(A,A^{T})u_{1}+eb_{1}) \geq -\epsilon_{1}e- \xi ,~~ \xi \geq 0, \end{array} $$

(14)

and

(Kernel 𝜖−TSVR-2):

$$\begin{array}{@{}rcl@{}} \min\limits_{u_{2} ,b_{2},\eta} & \frac{c_{4}}{2}\left( ||u_{2}||^{2}+{b_{2}^{2}}\right) +\frac{1}{2}||(Y-(K(A,A^{T})u_{2}+eb_{2})||^{2} \\&+ c_{2}e^{T}\eta \\ &\text{subject to,} & \\ & (K(A,A^{T})u_{2}+eb_{2})-Y \geq -\epsilon_{2}e - \eta, ~~ \eta \geq 0. \end{array} $$

(15)

Similar to the linear case, the (Kernel 𝜖−TSVR-1) and (Kernel 𝜖−TSVR-2) are solved in their dual forms using the K.K.T. optimality conditions.

5 ν-TWSVM based regression

Similar to 𝜖-SVR model, in TWSVR model also, a good choice of 𝜖 ₁ and 𝜖 ₂ should be supplied beforehand in order to meet the desired accuracy. A bad choice of 𝜖 ₁ and 𝜖 ₂ could lead to poor results. The ν-TWSVM based Regression (ν-TWSVR ) finds the optimal choices of 𝜖 ₁ and 𝜖 ₂ by trading off the values of 𝜖 ₁ and 𝜖 ₂ in the two respective optimization problems via the user specified parameters ν ₁ and ν ₂. The value of ν ₁ (respectively ν ₂) specifies an upper bound on the fraction of points allowed to contribute to the error ξ (respectively η) and specifies a lower bound on the number of support vectors for up (respectively down) bound function.

5.1 Linear ν-TWSVM based regression

Similar to the TSVR model, ν-TWSVR also solves a pair of optimization problems which are as follows

(ν-TWSVR-1):

$$\begin{array}{@{}rcl@{}} \min\limits_{w_{1} ,b_{1},\epsilon_{1},\xi} & \frac{c_{1}}{2}\left( ||w_{1}||^{2}+{b_{1}^{2}}\right) +\frac{1}{2}||(Y-(Aw_{1}+eb_{1})||^{2} \\ & +~c_{2}(\nu_{1}\epsilon_{1}+\frac{1}{l}e^{T}\xi)\\ &\text{subject to,} & \\ & Y-(Aw_{1}+eb_{1}) \geq -\epsilon_{1}e-\xi,\\ & \xi \geq 0 , \epsilon_{1} \geq 0 , \end{array} $$

(16)

and

(ν-TWSVR-2):

$$\begin{array}{@{}rcl@{}} \min\limits_{w_{2} ,b_{2},\epsilon_{2},\eta} &\frac{c_{3}}{2}\left( ||w_{2}||^{2}+{b_{2}^{2}}\right) +\frac{1}{2}||(Y-(Aw_{2}+eb_{2})||^{2} \\& +c_{4}\left( \nu_{2}\epsilon_{2}+\frac{1}{l}e^{T}\eta\right)\\& \text{subject to,} & \\ &(Aw_{2}+eb_{2})-Y \geq -\epsilon_{2}e-\eta,\\ &\eta \geq 0 , \epsilon_{2} \geq 0, \end{array} $$

(17)

where ν ₁, ν ₂, c ₁, c ₂, c ₃ and c ₄ are user specified positive parameters.

In the above optimization problems, the size of 𝜖 ₁ (respectively 𝜖 ₂) tubes is traded off against the model complexity and other terms via positive parameters ν ₁ (respectively ν ₂) which allows them to automatically adjust according to the structure of data. Preposition-1 gives a theoretical interpretations of parameters ν ₁ and ν ₂. The derivation of the above formulation of ν-TWSVR from an appropriately constructed ν-TWSVM classification problem is given in Appendix B. This derivation is based on the work of Bi and Bennett [5] and Khemchandani et al. [8].

In order to get the solution of optimization problems (16) and (17), we derive their dual problems. We first consider (ν-TWSVR-1) and its corresponding Lagrangian function

$$\begin{array}{@{}rcl@{}} &&L(w_{1},b_{1},\epsilon_{1},\xi,\alpha,\beta,\gamma)= \frac{c_{1}}{2}\left( ||w_{1}||^{2}+{b_{1}^{2}}\right)\\ &&+\frac{1}{2}||(Y-(Aw_{1}+eb_{1})||^{2} +c_{2}\left( \nu_{1}\epsilon_{1}+\frac{1}{l}e^{T}\xi\right) \\&&+\alpha^{T}(-Y+(Aw_{1}+eb_{1})-e\epsilon_{1}-\xi)- \beta^{T}\xi -\gamma\epsilon_{1}~, \end{array} $$

(18)

where α = (α ₁, α ₂,...,α _l ),β = (β ₁, β ₂,...,β _l ) and γ are Lagrange multipliers. The K.K.T. optimality conditions are given by

$$\begin{array}{@{}rcl@{}} &&\frac{\partial L}{\partial w_{1}} = -A^{T}(Y\,-\,(Aw_{1}+eb_{1}))\! +\! c_{1}w_{1}+A^{T}\alpha = 0, \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} &&\frac{\partial L}{\partial b_{1}}= -e^{T}(Y-(Aw_{1}+eb_{1})) + c_{1}b + e^{T}\alpha =0, \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} &&\frac{\partial L}{\partial \xi}=\frac{c_{2}}{l}e -\alpha -\beta =0, \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} &&\frac{\partial L}{\partial \epsilon_{1}}=c_{2}\nu_{1} -e^{T}\alpha-\gamma = 0, \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} &&Y-(Aw_{1}+eb_{1}) \geq -e\epsilon_{1}-\xi ~, \xi \geq 0, \epsilon_{1} \geq 0, \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} &&\alpha^{T}(Y-(Aw_{1}+eb_{1})+e\epsilon_{1}+\xi)=0,\ \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} &&\beta^{T}\xi = 0 , \gamma\epsilon_{1} =0, \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} &&\alpha \geq 0 ,\beta \geq 0 , \gamma \geq 0. \end{array} $$

(26)

Since β ≥ 0, therefore from (21) and (26) we have

$$\begin{array}{@{}rcl@{}} 0 \leq \alpha \leq \frac{c_{2}}{l}e. \end{array} $$

(27)

Also, since γ ≥ 0, so (22) would lead to

$$\begin{array}{@{}rcl@{}} e^{T}\alpha \leq c_{2}\nu_{1} . \end{array} $$

(28)

Consider $G = \left [\begin {array}{cc} \textit {A} ,& \textit {e} \\ \end {array}\right ]$ and $v_{1} = \left [\begin {array}{cc} w_{1} \\ b_{1} \end {array}\right ]$. Then combining (19) and (20) would result in following equation

$$\begin{array}{@{}rcl@{}} -G^{T}Y+(G^{T}G+ c_{1}I)v_{1}+G^{T}\alpha =0 , \end{array} $$

(29)

or

$$\begin{array}{@{}rcl@{}} v_{1} = (c_{1}I+G^{T}G)^{-1} G^{T}(Y-\alpha). \end{array} $$

(30)

After substituting the value of v ₁ in (18) and using the above K.K.T optimality conditions the dual problem of the (ν-TWSVR-1) can be obtained as

(Dual ν-TWSVR-1):

$$\begin{array}{@{}rcl@{}} &&\min\limits_{\alpha} \frac{1}{2}\alpha^{T}G(c_{1}I+G^{T}G)^{-1}G^{T}\alpha \\ && -Y^{T}G(c_{1}I+G^{T}G)^{-1}G^{T}\alpha +Y^{T}\alpha \\ &&\text{subject to,}\\ && 0 \leq \alpha \leq \frac{c_{2} }{l}e, \\ && e^{T}\alpha\leq c_{2}\nu_{1}. \end{array} $$

(31)

In a similar way, the dual of the problem (ν-TWSVR-2) can be obtained as

(Dual ν-TWSVR-2):

$$\begin{array}{@{}rcl@{}} &&\min\limits_{\lambda} \frac{1}{2}\lambda^{T}G(c_{3}I+G^{T}G)^{-1}G^{T}\lambda \\ &&+ ~Y^{T}G(c_{3}I+G^{T}G)^{-1}G^{T}\lambda -Y^{T}\lambda \\ &&\text{subject to.} \\&& 0 \leq \lambda \leq \frac{c_{4}}{l}e, \\ && e^{T}\lambda\leq c_{4}\nu_{2} , \end{array} $$

(32)

where λ is the vector of the Lagrange multipliers. The augmented vector $v_{2} = \left [\begin {array}{cc} w_{2} \\ b_{2} \end {array}\right ]$ is given by

$$\begin{array}{@{}rcl@{}} v_{2} = (c_{3}I+G^{T}G)^{-1} G^{T}(Y+\lambda). \end{array} $$

(33)

After obtaining the solution of the dual problems (31) and (32), the decision variables v ₁ and v ₂ can be obtained by using (30) and (33) respectively. For the given $x \in \mathbb {R}^{n}$, the estimated regressor is obtained as follows

$$\begin{array}{@{}rcl@{}} f(x) = \frac{1}{2}(f_{1}(x)+f_{2}(x)) = \frac{1}{2}(w_{1}\,+\,w_{2})^{T}x\!+ \frac{1}{2}(b_{1}+b_{2}). \end{array} $$

5.2 ν-TWSVM based regression for non-linear case

For finding the non-linear regressor, the ν-TWSVR considers the following kernel generated functions

$$\begin{array}{@{}rcl@{}} f_{1}(x) = K(x^{T},A^{T})u_{1}+b_{1} ,\\ \text{and~~} f_{2}(x) = K(x^{T},A^{T})u_{2} + b_{2}, \end{array} $$

where K is an appropriately chosen kernel function. For the non-linear case, the Kernel ν-TWSVR-1 and Kernel ν-TWSVR-2 can be formulated as

(Kernel ν-TWSVR-1):

$$\begin{array}{@{}rcl@{}} &&\min\limits_{u_{1},b_{1},\epsilon_{1},\xi}\frac{c_{1}}{2}(||u_{1}||^{2}+{b_{1}^{2}}) +\frac{1}{2}||(Y\,-\,(K(A,A^{T})u_{1}+eb_{1})||^{2} \\ &&+c_{2}(\nu_{1}\epsilon_{1}+\frac{1}{l}e^{T}\xi)\\ &&\text{subject to,} ~~~\\ &&Y-(K(A,A^{T})u_{1}+eb_{1}) \geq -\epsilon_{1}e - \xi,\\ &&\xi \geq 0 ~ , ~ \epsilon_{1} \geq 0, \end{array} $$

(34)

and

(Kernel ν-TWSVR-2):

$$\begin{array}{@{}rcl@{}} &&\min\limits_{u_{2},b_{2},\epsilon_{2},\eta} ~\frac{c_{3}}{2}(||u_{2}||^{2}+{b_{2}^{2}}) +\!\frac{1}{2}||(Y\,-\,(K(A,A^{T})u_{2}+eb_{2})||^{2} \\ &&+c_{4}\left( \nu_{2}\epsilon_{2}+\frac{1}{l}e^{T}\eta\right)\\ &&\text{subject to,} ~~~\\ &&(K(A,A^{T})u_{2}+eb_{2})-Y \geq -\epsilon_{2}e-\eta\\ &&\eta \geq 0 ~ ,~~\epsilon_{2} \geq 0. \end{array} $$

(35)

Working on the lines similar to the linear case, the dual problems corresponding to the primal optimization problems (Kernel- ν-TWSVR-1) and (Kernel- ν-TWSVR-2) can be obtained as

$$\begin{array}{@{}rcl@{}} &&\min\limits_{\alpha} \frac{1}{2}\alpha^{T}H(c_{1}I+H^{T}H)^{-1}H^{T}\alpha \\ & &-Y^{T}H(c_{1}I+H^{T}H)^{-1}H^{T}\alpha + Y^{T}\alpha \\ &&\text{subject to,} \\&&0 \leq \alpha \leq \frac{c_{2} }{l}e , \\ & &e^{T}\alpha\leq c_{2}\nu_{1} , \end{array} $$

(36)

and

$$\begin{array}{@{}rcl@{}} &&\min\limits_{\lambda} \frac{1}{2}\lambda^{T}H(c_{3}I+H^{T}H)^{-1}H^{T}\lambda \\ &&+Y^{T}H(c_{3}I+H^{T}H)^{-1}H^{T}\lambda -Y^{T}\lambda \\ &&\text{subject to,}\\ && 0 \leq \lambda \leq \frac{c_{4}}{l}e, \\ & & e^{T}\lambda\leq c_{4}\nu_{2}, \end{array} $$

(37)

respectively.

Here H= $\left [\begin {array}{cc} K(A,A^{T}), & e \\ \end {array}\right ]$ and the augmented vectors $v_{1} = \left [\begin {array}{cc} w_{1} \\ b_{1} \end {array}\right ]$ and $v_{2} = \left [\begin {array}{cc} w_{2} \\ b_{2} \end {array}\right ]$ are given as

$$\begin{array}{@{}rcl@{}} v_{1} = (c_{1}I+H^{T}H)^{-1} H^{T}(Y-\alpha), \end{array} $$

(38)

and

$$\begin{array}{@{}rcl@{}} v_{2} = (c_{3}I+H^{T}H)^{-1} H^{T}(Y+\lambda). \end{array} $$

(39)

For a given value $x \in \mathbb {R}^{n}$, the estimated regressor is obtained as

$$\begin{array}{@{}rcl@{}} f(x) &=& \frac{1}{2}(f_{1}(x)+f_{2}(x)) \\ &=& \frac{1}{2}(u_{1}+u_{2})^{T}K(A,x)+ \frac{1}{2}(b_{1}+b_{2}). \end{array} $$

Proposition 1

Suppose ν-TWSVR is applied on a dataset which results 𝜖 ₁ (respectively 𝜖 ₂ ) > 0, then following statements hold.

• (a) v ₁ (respectively v ₂ ) is an upper bound on fraction of error ξ(respectively η).

• (b) v ₁ (respectively v ₂ ) is a lower bound on fraction of support vectors for up bound (respectively down bound) regressor.

Proof

The proof of the proposition is described in Appendix A. □

Remark 1

ν ₁(respectively ν ₂) can be used to control the number of points allowed to contribute to errors. Furthermore, it has been experimentally observed that if ν ₁(respectively ν ₂) > 1 then 𝜖 ₁(respectively 𝜖 ₂)= 0. For ν ₁(respectively ν ₂) < 1, it can still happen that 𝜖 ₁(respectively 𝜖 ₂)= 0 if the data is noise free.

6 Experimental results

This section experimentally verifies claims made in this paper. To show the efficacy of our proposed algorithm, we have considered artificial and UCI-benchmark datasets [13]. We have also compared the proposed algorithm with 𝜖-TSVR and shown that the proposed algorithm outperforms it in practice. All the simulations have been performed in Matlab 12.0 environment (http://in.mathworks.com/) on Intel XEON processor with 16.0 GB RAM. Throughout these experiments we have used the RBF kernel $exp\left (\frac {-||x-y||^{2}}{q}\right )$ where q is the kernel parameter.

One of the issues with the 𝜖-TSVR model is that it involves a large number of parameters which should be tunned in order to meet the desired accuracy level. To reduce the computational complexities of parameter selection involved in 𝜖-TSVR, we have set c ₁ = c ₂, c ₃ = c ₄ and 𝜖 ₁ = 𝜖 ₂. We have also set c ₁ = c ₃, c ₂ = c ₄ and ν ₁ = ν ₂ for the proposed method for all kinds of experiments. For artificial datasets, we have considered two type of synthetic training dataset (x _i , y _i ) for i = 1,2,..,l as follow

Type 1 :

$$\begin{array}{@{}rcl@{}} y_{i} = \frac{sin(x_{i})}{x_{i}} + \xi_{i} ~~\xi_{i}\sim N(0,\sigma) ~~,~~ x_{i} \in U[-4\pi ,4\pi]. \end{array} $$

Type 2 :

$$\begin{array}{@{}rcl@{}} y_{i} = x_{i}^{\frac{2}{3}} + \xi_{i} ~~\xi_{i}\sim N(0,\sigma)~~,~x_{i} \in U[-2 ,2]. \end{array} $$

Table 1 list the different performance metrics for a regression model where $y^{\prime }_{i}$ is the predicted value of y _i and $\overline {y}$ denotes the mean of y _i for i = 1 , 2 ,...l.

Table 1 Performance metrics and their calculations

To avoid the biased comparison, ten independent groups of noisy samples are generated randomly using the Matlab toolbox for synthetic datasets which consists of 100 training samples and 655 non-noise testing samples. For artificial datasets, we have also solved the primal problem of ν-TWSVR as we have to retrieve the value of 𝜖 ₁ and 𝜖 ₂.

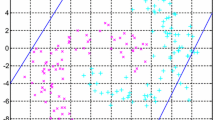
Figure 1 shows the performance of ν-TWSVR for different values of ν on Type 1 and Type 2 synthetic datasets. In the figures, the size of 𝜖 ₁ and 𝜖 ₂ tubes decreases as the value of ν increases. For ν = 0.9, the 𝜖-tubes almost vanish. Figure 2 shows the performance of ν-TWSVR on Type 1 and Type 2 synthetic datasets for the different noise coefficients σ = 0.01, σ = 0.2 and σ = 0.5. It can be easily seen that for the fixed value of ν = 0.01, the tube width automatically adjust for the different value of σ. Figures 3a and 4a show the plot of ν versus 𝜖 ₁ and 𝜖 ₂ for the Type 1 and Type 2 synthetic datasets respectively. It is evident that as value of ν increases, the value of 𝜖 ₁ and 𝜖 ₂ decreases. In view of the proposition (1), it can be inferred that as the value of ν increases, the proposed method reduces the size of one sided 𝜖-tube in order to control the number of points lying outside the 𝜖-tubes. Figures 3b and 4b show that for a fixed value of ν, the size of one sided 𝜖-tubes increases as more noise is introduced in the data for Type 1 and Type 2 datasets respectively. It can be also seen that RMSE increases as the more noises is added in the data. Figure 5a and b show the plot of ν versus fraction of support vectors and errors for up and down bound regressor on the Type 1 synthetic dataset respectively. Figure 6a and b show the plot of ν versus fraction of support vectors and errors for up and down bound regressor on the Type 2 synthetic dataset respectively. It verifies claims made in Preposition-1. Figure 7a and b show the plot of fraction of support vectors and errors versus l o g ₂ c ₂ and l o g ₂ c ₄ for up bound and down bound regressor receptively for the Type 1 synthetic dataset. It can be observed that the bounds specified in Proposition 1 get loser as the value of c ₁ and c ₂ increases.

Fig. 1

Performance of ν-TWSVR (a) for ν = 0.01 on Type 1 dataset (b) for ν = 0.01 on Type 2 dataset (c) for ν = 0.1 on Type 1 dataset (d) for ν = 0.1 on Type 2 dataset (e) for ν = 0.9 on Type 1 dataset and (f) for ν = 0.9 on Type 2 dataset

Fig. 2

Performance of ν-TWSVR (a) for σ = 0.01 on Type 1 dataset (b) for σ = 0.01 on Type 2 dataset (c) for σ = 0.2 on Type 1 dataset (d) for σ = 0.2 on Type 2 dataset (e) for σ = 0.5 on Type 1 dataset and (f) for σ = 0.5 on Type 2 dataset for fixed value of ν = 0.01

Fig. 3

a ν-TWSVR for different value of ν, b ν-TWSVR for different value of σ on Type 1 dataset

Fig. 4

a ν-TWSVR for different value of ν, b ν-TWSVR for different value of σ on Type 2 dataset

Fig. 5

Plot of ν versus fraction of support vectors and fraction of errors (a) for up bound regressor and (b) for down bound regressor on Type 1 dataset

Fig. 6

Plot of ν versus fraction of support vectors and fraction of errors (a) for up bound regressor and (b) for down bound regressor on Type 2 dataset

Fig. 7

a Plot of fraction of support vectors and fraction of errors versus log c ₁ for up bound regressor. b Plot of fraction of support vectors and fraction of errors versus log c ₂

Figure 8 shows the performance of 𝜖-TSVR for the fixed value of 𝜖 ₁ = 0.2 and 𝜖 ₂ = 0.2 for the noise coefficient σ = 0 and σ = 0.5. It can been seen that the 𝜖-TSVR performs well for σ = 0 but as the noise increases it fails to predict accurately. So in the case of 𝜖- TWSVR, a good choice of 𝜖 ₁ and 𝜖 ₂ should be supplied beforehand in order to have accurate result which is not the case of ν-TWSVR.

Fig. 8

Performance of 𝜖-TSVR for (a) σ = 0 and (b) σ = 0.5 for 𝜖 = 0.2

For further evaluation, we test six UCI benchmark datasets namely, Boston Housing, Auto-Price, Machine-CPU, Servo, Concrete CS. These datasets are commonly used in testing machine learning algorithms. For all datasets, feature vectors were normalized in the [ −1, 1]. Tables 2 and 3 show the performance of the proposed algorithm on different values of ν on synthetic datasets Type 1 and Type 2 for the noise coefficient σ = 0.5. Tables 4 and 5 show the results of the proposed algorithm on Servo and Machine-CPU datasets for different value of ν. In these tables following abbreviations are used.

Table 2 Result on synthetic dataset type 1

Table 3 Result on synthetic dataset type 2

Table 4 Result on servo dataset

Table 5 Result on machine CPU dataset

SV1 ::

Number of Support Vectors for up bound Regressor.

SV2 ::

Number of Support Vectors for down bound Regressor.

Error1 ::

Number of points lying outside of the one sided 𝜖 ₁ tube for up bound regressor.

Error2 ::

Number of points lying outside of the 𝜖 ₂ tube for down bound regressor.

The numerical results of the tables verify the claim made in the Preposition-1. These tables also show how the size of one sided 𝜖-tubes decrease as the value of ν increases, which further affect the values of SSE, SSE/SST and SSR/SST.

To compare the proposed algorithm with 𝜖-TSVR, we have downloaded the code of 𝜖-TSVR from http://www.optimal-group.org/Resource. We have tunned the parameters of 𝜖-TSVR and proposed method through the set of values { 2ⁱ|i = −9,−8,... ,10 } by tuning a set comprising of random 10 % of the dataset.

Table 6 lists the mean of SSE/SST and SSR/SST of the the proposed method with the 𝜖-TSVR on five different UCI-benchmark datasets. For these datasets the ten-fold cross validation method was used to report the results. It can be easily observed that the proposed method outperform the 𝜖-TSVR in practice. Table 7 lists our findings about the best value of parameters for the 𝜖-TSVR and ν-TWSVR for the above mentioned UCI-datasets.

Table 6 Comparision of proposed ν-TWSVR with 𝜖-TSVR on UCI datasets

Table 7 Tunned parameters of 𝜖-TSVR and ν-TWSVR

7 Conclusions

In this paper, we have proposed a ν-Twin Support Vector Machine Based Regression Model (ν-TWSVR) which is capable of automatically optimizing the parameters 𝜖 ₁ and 𝜖 ₂ appearing in the recently proposed 𝜖-TSVR model of Shao et al. [9]. It has been proved mathematically that the parameters ν ₁ and ν ₂ can be used for controlling the fraction of data points which contribute to the errors and support vectors. It has also been shown experimentally that ν-TWSVR outperforms 𝜖-TSVR as it automatically adjusts the parameter 𝜖 ₁(𝜖 ₂) according to noise present in the data.

The optimization problems appearing in the ν-TWSVR formulation have been derived by employing an important result of Bi and Bennett [5] which connects a regression problem to an appropriately constructed classification problem. This development also gives a mathematical justification to the 𝜖-TSVR formulation and thereby establishes that similar to TWSVR formulation [8], the 𝜖-TSVR formulation is also in the true spirit of TWSVM methodology.

Appendices

Appendix A

Proposition 1

Suppose ν-TWSVR is applied on a dataset which results 𝜖 ₁ (respectively 𝜖 ₂ ) > 0, then following statements hold.

• (a) v ₁ (respectively v ₂ ) is an upper bound on fraction of error ξ(respectively η).

• (b) v ₁ (respectively v ₂ ) is a lower bound on fraction of support vectors for up bound (respectively down bound) regressor.

Proof

• (a) Using the KKT conditions (21) and (25) for up bound regressor, we can find that for ξ _i > 0, β _i = 0 and $\alpha _{i} = \frac {c_{2}}{l}$. Since from (22) and (26), e ^T α≤c ₂ v ₁, so there may exist at most l v ₁ points for which ξ _i ≠0. In the similar way using the K.K.T. optimality conditions for down bound regressor we can prove that there are at most l v ₂ points for which η _i ≠0.

• (b) Using the KKT conditions (22) and (25) for 𝜖 ₁≠0 we find that γ = 0. This implies that e ^T α = c ₂ v ₁.

  Since $0 \leq \alpha _{i} \leq \frac {c_{2}}{l}$ so there must be at least l v ₁ points for which α _i ≠0. In similar way using the K.K.T conditions for down bound regressor we can prove that there are at least l v ₂ points for which λ _i ≠0 .

□

Appendix B: ν-TWSVR via ν-TWSVM

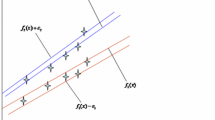
Bi and Bennett [5] have shown the equivalence between a given regression problem and an appropriately constructed classification problem. They have shown that for a given regression training set (A,Y), a regressor y = w ^T x + b is an 𝜖-insensitive regressor if and only if the set D ⁺ and D ⁻ locate on different sides of n+1 dimensional hyperplane w ^T x−y + b = 0 respectively where

$$\begin{array}{@{}rcl@{}} D^{+} = \{(A_{i},y_{i}+\epsilon),i=1,2,...,l\}\\ D^{-} = \{(A_{i},y_{i}-\epsilon),i=1,2,...,l\}. \end{array} $$

In veiw of this result of Bi and Bennett [5], the regression problem is equivalent to the classification problem of sets D ⁺ and D ⁻ in R ⁿ⁺¹. If we use the TWSVM methodology [6] for the classification of these two sets D ⁺ and D ⁻ then we can find TWSVM based Regression [8]. It is relevant to mention here that the classification of set D ⁺ and D ⁻ is a special case of classification where we have following privilege informations.

• (a) D ⁺ and D ⁻ classes are symmetric in nature and have equal number of sample points.

• (b) Points in the class D ⁺ and D ⁻ are separated by the distance 2𝜖.

These privileged informations must be exploited for the better classification as better classification of the set D ⁺ and D ⁻ will eventually lead to better regressor. The classification of the set D ⁺ and D ⁻ in R ⁿ⁺¹ using ν-TWSVM results into following QPPs

$$\begin{array}{@{}rcl@{}} \underset{(w_{1},\eta_{1},b_{1},\rho_{+})}{Min} & \frac{c_{1}}{2}\left( ||w_{1}||^{2}\,+\, {\eta_{1}^{2}} + {b_{1}^{2}}\right) \,+\,\frac{1}{2}||Aw_{1}\,+\,\eta_{1}(Y+\epsilon e)\,+\,eb_{1}||^{2} \\ & - c_{2}v_{1}\rho_{+} \ \\ \text{subject to,} & \\ &(Aw_{1}+\eta_{1}(Y-\epsilon e)+eb_{1})+\rho_{+}e \leq 0,\\ ~&\rho_{+} \geq 0, \end{array} $$

(40)

and

$$\begin{array}{@{}rcl@{}} &&{}\underset{(w_{2},\eta_{2},b_{2},\rho_{-})} { Min} \frac{c_{3}}{2}\left( ||w_{2}||^{2}+ {\eta_{2}^{2}}+{b_{2}^{2}} \right) +\frac{1}{2}||Aw_{2}\\ & &+\eta_{2}(Y-\epsilon e)+eb_{2}||^{2} -c_{4}v_{2} \rho_{-} \\ &\text{subject to,} & \\ && (Aw_{2}+\eta_{2}(Y+\epsilon e)+eb_{2})-\rho_{-}e \geq 0, \\ &&\qquad\qquad\rho_{-} \geq 0 . \\ \end{array} $$

(41)

Let us first consider the problem (40). Here we note that η ₁≠0 and therefore, without loss of generality, we can assume that η ₁ > 0. The constraint of (40) can be rewriteen as

$$\left[-A\!\left( \frac{-w_{1}}{\eta_{1}}\right) \,+\, (Y\!-\epsilon e) \!-e\left( \frac{-b}{\eta_{1}}\right)\right] + \frac{\rho_{+}e}{\eta_{1}} \leq 0 ,\,\, \rho_{+} \geq 0$$

On replacing w ₁:=−w ₁/η ₁, b ₁:=−b ₁/η ₁ and noting that η ₁≥0, (40) reduces to

$$\begin{array}{@{}rcl@{}} \underset{(w_{1},b_{1},\rho_{+})}{Min} \frac{1}{2}||w_{1}||^{2}+{b_{1}^{2}} +||(Y+\epsilon e) \,-\,(Aw_{1}+eb_{1})||^{2} - c_{2}v_{1}\rho_{+} \\ &\text{subject to,} \\ & Aw_{1} + eb_{1} +\epsilon e \geq Y + \frac{\rho_{+}e}{\eta_{1}}, \\ & \rho_{+} \geq 0 . \end{array} $$

(42)

Next, if we replace e b ₁: = e b ₁−𝜖 e in (42) then it reduces to

$$\begin{array}{@{}rcl@{}} \underset{(w_{1},b_{1},\rho_{+})}{Min} \frac{1}{2}||w_{1}||^{2}+{b_{1}^{2}} +||Y \!-(Aw_{1}+eb_{1})||^{2} \,-\, c_{2}v_{1}\rho_{+} \\ &\text{subject to,} \\ & Aw_{1} + eb_{1} \geq Y -\left( 2\epsilon e-\frac{\rho_{+}e}{\eta_{1}}\right) \\ & \rho_{+} \geq 0 . \end{array} $$

(43)

Let $\left (2e\epsilon -\frac {\rho _{+}}{\eta _{1}}\right ):=e\epsilon _{1}$ then it will reduce to

$$\begin{array}{@{}rcl@{}} \underset{w_{1} ,b_{1},\epsilon_{1}}{Min } & \frac{1}{2}||w_{1}||^{2}+{b_{1}^{2}} +\frac{1}{2}||(Y-(Aw_{1}+eb_{1})||^{2} \\& +c_{2}v_{1}\epsilon_{1} \\ \text{subject to,} & (Aw_{1}+eb_{1}) -Y\geq -\epsilon_{1} e. \end{array} $$

(44)

In the similar manner, assuming η ₂ > 0 and using the replacement w ₂:=−w ₂/η ₂, b ₂:=−b ₂/η ₂, problem (41) can be written as

$$\begin{array}{@{}rcl@{}} \underset {(w_{2},b_{2},\rho_{-})}{Min} \frac{1}{2}||w_{2}||^{2}+{b_{2}^{2}} +\frac{1}{2}||(Y-\epsilon e) \,-\,(Aw_{2}+eb_{2})||^{2} -c_{4}v_{2}\rho_{-} \\ & \text{~~ subject to,}, \\ & (Aw_{2}+eb_{2})-\epsilon e \leq Y -\frac{\rho_{-}}{\eta_{2}}e, \\ &\rho_{-} \geq 0 . \end{array} $$

If we replace e b ₂: = e b ₂ + 𝜖 e and $(2e\epsilon -\frac {\rho _{-}}{\eta _{2}}):=e\epsilon _{2}$ then problems reduces to

$$\begin{array}{@{}rcl@{}} \underset{w_{2} ,b_{2},\epsilon_{2}}{Min } & \frac{1}{2}||w_{2}||^{2}+{b_{2}^{2}} +\frac{1}{2}||(Y-(Aw_{2}+eb_{2})||^{2} \\&& +c_{4}v_{1}\epsilon_{2} \\ \text{subject to,} & Y-(Aw_{2}+eb_{2})\geq -\epsilon_{2}e. \end{array} $$

(45)

Looking at problems (44) and (45 ) we observe that our approach is valid provided we can show that $\epsilon _{1}=(2\epsilon -\frac {2\rho _{+}}{\eta _{1}}) \geq 0$ and $\epsilon _{2} = (2\epsilon -\frac {2\rho _{-}}{\eta _{2}}) \geq 0$. We can prove this assertion as follow.

As the first hyperplane w ^T x + η ₁ y + b ₁ = 0 is the least square fit for the class D ⁺ so there certainly exists an index j such that

$$\begin{array}{@{}rcl@{}} \eta_{1}(y_{j}+\epsilon) +{w_{1}^{T}}x_{j}+b_{1} \geq 0. \end{array} $$

(46)

Also from (40),

$$\begin{array}{@{}rcl@{}} \eta_{1}(y_{i}-\epsilon) +{w_{1}^{T}}x_{j}+b_{1}+\rho_{+} \leq 0,~~\text{for all \textit{i}} \end{array} $$

(47)

In particular, taking (47) for j we get

$$\begin{array}{@{}rcl@{}} \eta_{1}(y_{j}-\epsilon) +{w_{1}^{T}}x_{j}+b_{1} + \rho_{+} \leq 0, \\ \text{i.e.~~} -\eta_{1}(y_{j}-\epsilon) -{w_{1}^{T}}x_{j}-b_{1}-\rho_{+} \geq 0 \end{array} $$

(48)

Adding (47) and (48) we get $\epsilon _{1} = \left (2\epsilon -\frac {\rho _{+}}{\eta _{1}}\right ) \geq 0$. Similarly we can prove that $\epsilon _{2} = \left (2\epsilon -\frac {\rho _{-}}{\eta _{2}}\right ) \geq 0$.

Remark 2

The above proof can be appropriately modified to show that 𝜖-TSVR formulation of Shao et al. [9] also follows from Bi and Bennett [5] results and TWSVM methodology.