1 Introduction

The support vector machine (SVM) approach, motivated by VC dimensional theory and statistical learning theory [20], is a promising machine learning technique. Compared with other machine learning approaches like artificial neural networks [18], SVM gains many advantages. First, SVM solves a QPP, assuring that once an optimal solution is obtained, it is the unique (global) solution. Second, SVM derives a sparse and robust solution by maximizing the margin between the two classes. Third, SVM implements the structural risk minimization principle rather than the empirical risk minimization principle, which minimizes the upper bound of the generalization error [22]. At present, SVM has been successfully applied into various aspects ranging from machine learning, data mining to knowledge discovery [24].

However, one of the main challenges for the standard SVM is the high computational complexity. The training cost of O(l 3), where l is the total size of training data, is expensive. To further improve the computational speed of SVM, Jayadeva et al. [8] proposed a twin support vector machine (TSVM) for the binary classification data in the spirit of the proximal SVM [5–7]. TSVM generates two nonparallel hyper-planes by solving two smaller-sized QPPs such that each hyper-plane is closer to one class and as far as possible from the other. The strategy of solving two smaller-sized QPPs rather than a single large one makes the learning speed of TSVM approximately four times faster than that of the standard SVM. At present, TSVM has become one of the popular methods because of its low computational complexity. Many variants of TSVM have been proposed in [9, 11, 17, 19, 23, 26]. Certainly, algorithms mentioned above are suitable for the classification problems. For the regression problem, Peng proposed an efficient TSVR [16].

It is well known that the same effects on the bound functions are considered to the training samples in TSVR. However the local information among samples is ignored in TSVR. To enhance the prediction accuracy, Xu et al. proposed a weighted TSVR [25], where different penalty coefficients are given to the samples dissatisfying constraint depending on their different positions. In addition, Cheng et al. proposed a localized support vector machine (LSVM), where different penalty coefficients are given to the training samples dissatisfying the constraint depending on the similarities to the testing samples. Certainly the similarity is measured by K-nearest neighbor method. A point x is important if it has a larger number of K-nearest neighbors [3, 12, 28], whereas it is not important if it is an outlier. Motivated by the above studies, a K-nearest neighbor-based weighted TSVR (KNNWTSVR) is proposed in this paper [14], where different weights are proposed to give each training sample depending on their local information. Specifically, major weights are proposed to give the samples if they have more K-nearest neighbors. Whereas minor weights are given to the samples with a smaller number of K-nearest neighbors. Certainly our proposed algorithm only explored the relation among the training samples, and different weights are proposed to give each training sample, which is significantly different from LSVM. In addition, to further increase the computational speed of KNNWTSVR, a successive over relaxation method is employed to solve the QPPs, therefore we named it as SOR KNNWTSVR.

The effectiveness of the proposed algorithm is demonstrated by the experiments on eight benchmark datasets. The numerical results show that our proposed algorithms KNNWTSVR and SOR KNNWTSVR achieve nearly the same testing errors in all datasets. Moreover, they produce lower testing errors than SVR and TSVR for most cases. We can also find that SOR KNNWTSVR costs the least running time for almost all datasets. Finally we apply the new methods to predicting the content of protein by the spectral features of wheat. Compared with other algorithms, our proposed algorithms also yield lower prediction errors.

The paper is organized as follows. Section 2 outlines SVR and TSVR. A K-nearest neighbor-based weighted TSVR is proposed in Sect. 3, which includes the linear and nonlinear cases. A successive overrelaxation method for the KNNWTSVR is given in Sect. 4. Section 5 performs experiments on eight benchmark datasets and a real data experiment to investigate the effectiveness of the proposed algorithm. The last section contains the conclusions.

2 Related works

In this section, we give a brief description of the SVR and TSVR. Given a training set T={(x 1,y 1),(x 2,y 2),…,(x n ,y n )}, where x i ∈R d and y i ∈R. For the sake of conciseness, let matrix A=(x 1;x 2;⋯;x n ) and matrix Y=(y 1;y 2;⋯;y n ).

2.1 Support vector regression

The nonlinear SVR seeks to find a regression function f(x)=w T ϕ(x)+b in a high dimensional feature space tolerating the small error in fitting the given data points. This can be achieved by utilizing the ϵ-insensitive loss function that sets an ϵ-insensitive “tube” around the data, within which errors are discarded. The nonlinear SVR can be obtained by resolving the following QPP,

$$\begin{aligned} \min_{w, b, \xi, \xi^{*}} ~~& \frac{1}{2}\|w\|^{2}+ c\cdot\bigl(e^{T} \xi+e^{T}\xi^{*}\bigr) \\ \mbox{s.t.} ~~&\bigl(\phi^{T}(A)w+eb\bigr)-Y\leq e\epsilon+\xi, \\ ~~&Y-\bigl(\phi^{T}(A)w+eb\bigr)\leq e\epsilon+\xi^{*}, \\ ~~&\xi\geq0e, \quad \xi^{*}\geq0e, \end{aligned}$$
(1)

where c is a parameter chosen a priori, which weights the tradeoff between the fitting error and flatness of the regression function, ξ and ξ ∗ are the slack vectors reflecting whether the samples locate into the ϵ-tube or not, e is the vector of ones of appropriate dimensions [25].

By introducing the Lagrangian multiplies α and α ∗, we can derive the dual problem of the QPP (1) as follows,

$$\begin{aligned} \max_{\alpha, \alpha^{*}} ~~&-\frac{1}{2} \bigl(\alpha^{*}-\alpha\bigr)^{T}K\bigl(A,A^{T} \bigr) \bigl(\alpha^{*}-\alpha\bigr) \\ ~~&\quad {} +Y^{T}\bigl( \alpha^{*}-\alpha\bigr) +\epsilon e^{T}\bigl( \alpha^{*}+\alpha\bigr) \\ \mbox{s.t.} ~~&e^{T}\bigl(\alpha^{*}-\alpha\bigr)=0, \\ ~~&0e\leq\alpha, \quad \alpha^{*}\leq ce. \end{aligned}$$
(2)

Once the QPP (2) is resolved, we can achieve its solution \(\alpha^{(*)}=(\alpha_{1}, \alpha_{1}^{*}, \alpha_{2}, \alpha_{2}^{*}, \ldots, \alpha_{n}, \alpha_{n}^{*})\) and threshold b, and then obtain the regression function,

$$\begin{aligned} f(x)=\sum_{i=1}^{n} \bigl(\alpha_{i}^{*}-\alpha_{i} \bigr) K(x_{i},x)+b. \end{aligned}$$
(3)

Here K(x i ,x)=(ϕ(x i )⋅ϕ(x)) represents a kernel function which gives the dot product in the high dimensional feature space.

2.2 Twin support vector regression

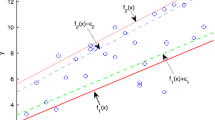
To further improve the computational speed, an efficient TSVM for the regression problem, termed as TSVR, was proposed in [16, 25]. TSVR generates an ϵ-insensitive down-bound function \(f_{1}(x)=w_{1}^{T}x+b_{1}\) and an ϵ-insensitive up-bound function \(f_{2}(x)=w_{2}^{T}x+b_{2}\). TSVR is illustrated in Fig. 1.

Fig. 1
figure 1

Illustration of the TSVR

Full size image

The final regressor f(x) is decided by the mean of these two bound functions, i.e.,

$$ \begin{aligned}[b] f(x)&=\frac{1}{2}\bigl(f_{1}(x)+f_{2}(x) \bigr) \\ &=\frac{1}{2}(w_{1}+w_{2})^{T}x+ \frac{1}{2}(b_{1}+b_{2}). \end{aligned} $$
(4)

TSVR is obtained by solving the following pair of QPPs,

$$\begin{aligned} \min_{w_{1},b_{1},\xi} ~~&\frac{1}{2} \bigl\| Y-e\epsilon_{1}-(Aw_{1}+eb_{1}) \bigr\| ^{2}+c_{1}e^{T}\xi \\ \mbox{s.t.} ~~&Y-(Aw_{1}+eb_{1})\geq e \epsilon_{1}-\xi, \\ ~~&\xi\geq0e, \end{aligned}$$
(5)

and

$$\begin{aligned} \min_{w_{2},b_{2},\eta} ~~&\frac{1}{2} \bigl\| Y+e\epsilon_{2}-(Aw_{2}+eb_{2}) \bigr\| ^{2}+c_{2}e^{T}\eta \\ \mbox{s.t.} ~~&(Aw_{2}+eb_{2})-Y\geq e\epsilon_{2}- \eta, \\ ~~&\eta\geq0e, \end{aligned}$$
(6)

where c 1, c 2, ϵ 1 and ϵ 2 are parameters chosen a priori, ξ and η are slack vectors. By introducing the Lagrangian multipliers α and β, we derive their dual problems as follows,

$$\begin{aligned} \max_{\alpha} ~~&-\frac{1}{2} \alpha^{T}G\bigl(G^{T}G\bigr)^{-1}G^{T} \alpha \\ ~~&\quad {}+g^{T}G\bigl(G^{T}G\bigr)^{-1}G^{T} \alpha-g^{T}\alpha \\ \mbox{s.t.} ~~& 0 e \leq\alpha\leq c_{1}e, \end{aligned}$$
(7)

and

$$\begin{aligned} \max_{\beta} ~~&-\frac{1}{2} \beta^{T}G\bigl(G^{T}G\bigr)^{-1}G^{T} \beta \\ ~~&\quad {}-h^{T}G\bigl(G^{T}G\bigr)^{-1}G^{T} \beta+h^{T}\beta \\ \mbox{s.t.} ~~& 0 e \leq\beta\leq c_{2}e, \end{aligned}$$
(8)

where G=[A e], g=Y−eϵ 1, and h=Y+eϵ 2.

Once the dual problems (7) and (8) are solved, we can get vectors w 1,b 1 and w 2,b 2 as follows,

$$\begin{aligned} \left[ \begin{array}{c} w_{1}\\ b_{1} \end{array} \right]=\bigl(G^{T}G \bigr)^{-1}G^{T}(g-\alpha), \end{aligned}$$
(9)

and

$$\begin{aligned} \left[ \begin{array}{c} w_{2}\\ b_{2} \end{array} \right]=\bigl(G^{T}G \bigr)^{-1}G^{T}(h+\beta). \end{aligned}$$
(10)

For the nonlinear case, TSVR resolves the following pair of QPPs,

$$\begin{aligned} \min_{w_{1},b_{1},\xi} ~~&\frac{1}{2} \bigl\| Y-e\epsilon_{1}-\bigl(K\bigl(A, A^{T}\bigr)w_{1}+eb_{1} \bigr)\bigr\| ^{2} +c_{1}e^{T}\xi \\ \\ \mbox{s.t.} ~~&Y-\bigl(K\bigl(A, A^{T}\bigr)w_{1}+eb_{1} \bigr)\geq e\epsilon_{1}-\xi, \\ ~~&\xi\geq0e, \end{aligned}$$
(11)

and

$$\begin{aligned} \min_{w_{2},b_{2},\eta} ~~&\frac{1}{2} \bigl\| Y+e\epsilon_{2}-\bigl(K\bigl(A, A^{T}\bigr)w_{2}+eb_{2} \bigr)\bigr\| ^{2} +c_{2}e^{T}\eta \\ \\ \mbox{s.t.} ~~&K\bigl(A, A^{T}\bigr)w_{2}+eb_{2}-Y \geq e\epsilon_{2}-\eta, \\ ~~&\eta\geq0e. \end{aligned}$$
(12)

Similarly, we can derive the dual formulations of QPPs (11) and (12) as follows,

$$\begin{aligned} \max_{\alpha} ~~&-\frac{1}{2} \alpha^{T}H\bigl(H^{T}H\bigr)^{-1}H^{T} \alpha \\ ~~&\quad {}+g^{T}H\bigl(H^{T}H\bigr)^{-1}H^{T} \alpha-g^{T}\alpha \\ \mbox{s.t.} ~~& 0 e \leq\alpha\leq c_{1}e, \end{aligned}$$
(13)

and

$$\begin{aligned} \max_{\beta} ~~&-\frac{1}{2} \beta^{T}H\bigl(H^{T}H\bigr)^{-1}H^{T} \beta \\ ~~&\quad {}-h^{T}H\bigl(H^{T}H\bigr)^{-1}H^{T} \beta+h^{T}\beta \\ \mbox{s.t.} ~~& 0 e \leq\beta\leq c_{2}e, \end{aligned}$$
(14)

where H=[K(A,A T) e], g=Y−eϵ 1, and h=Y+eϵ 2.

Once the dual QPPs (13) and (14) are resolved, we can get vectors w 1,b 1 and w 2,b 2 as follows,

$$\begin{aligned} \left[ \begin{array}{c} w_{1}\\ b_{1} \end{array} \right]=\bigl(H^{T}H \bigr)^{-1}H^{T}(g-\alpha), \end{aligned}$$
(15)

and

$$\begin{aligned} \left[ \begin{array}{c} w_{2}\\ b_{2} \end{array} \right]=\bigl(H^{T}H \bigr)^{-1}H^{T}(h+\beta). \end{aligned}$$
(16)

Note that TSVR is comprised of a pair of QPPs such that each QPP determines one of up- or down-bound functions by using only one group of constraints compared with the standard SVR. Hence, TSVR resolves two smaller-sized QPPs rather than a single large one, which implies that TSVR works approximately four times faster than the standard SVR in theory. However, the information among samples are not exploited in TSVR, and some priori knowledge are ignored, which reduces the generalization performance of TSVR to a certain degree.

3 K-nearest neighbor-based weighted twin support vector regression

In this section, we first present the concept of K-nearest neighbor [12], and then propose a K-nearest neighbor-based weighted TSVR. The weight of each training sample varies according to its local information.

3.1 K-nearest neighbor method

Given l data points x 1,x 2,…,x l , where x i ∈R n from the underlying submanifold M, one can build a nearest neighbor graph G to model the local geometrical structure of M. For each data point x i , we find its k nearest neighbors and put an edge between x i and its neighbors. Let \(N(x_{i}) = \{x_{i}^{1}, x_{i}^{2}, \ldots, x_{i}^{k} \}\) be the set of its K-nearest neighbors. Thus, the weight matrix of G can be defined as follows:

$$\begin{aligned} W_{i,j} = \left\{ \begin{array}{l@{\quad}l} 1,& \mbox{if } x_{i} \mbox{ is $k$-nearest neighbors of } x_{j} \\ & \quad \mbox{or }x_{j} \mbox{ is $k$-nearest neighbors of }x_{i},\\ 0,& \mbox{otherwise}. \end{array} \right. \end{aligned}$$
(17)

The nearest neighbor graph G with weight matrix W characterizes the local geometry of the data manifold. It has been frequently used in manifold based learning techniques.

To embody the importance of a point, we introduce a new variable \(d_{i}=\sum_{j=1}^{l}W_{ij}\) (i=1,2,…,l) for each sample. A larger value d i denotes the i-th sample possesses more neighbors, which implies that the i-th sample is important. According to this principle, we present the following weighted algorithm.

3.2 Linear case

In TSVR, all samples are equally weighted. This implies that samples will play the same roles on the bound functions no matter whether they are important or not. Before presenting the new algorithm, we first modify the original TSVR, and it is illustrated in Fig. 2. As we can learn that it degrades into the original SVR when f 1(x)=f 2(x). It is well known that different samples have different effects on the bound functions. A point x is more important if it owns a great number of K-nearest neighbors. Motivated by the above studies, a K-nearest neighbor-based weighted TSVR is proposed in this section, where different weights are proposed to give each sample depending on their local information.

Fig. 2
figure 2

Illustration of the modified TSVR

Full size image
$$\begin{aligned} \min_{w_1,b_1,\xi} ~~&\frac{1}{2} \bigl(Y-(A w_1+e b_1)\bigr)^{T}D\bigl(Y-(A w_1+e b_1)\bigr) \\ ~~&\quad {} +c_{1}e^{T}\xi \\ \mbox{s.t.} ~~&Y-(A w_1+e b_1)\geq- \epsilon_{1}e-\xi, \\ ~~&\xi\geq0, \end{aligned}$$
(18)

and

$$\begin{aligned} \min_{w_2,b_2,\eta} ~~&\frac{1}{2} \bigl(Y-(A w_2+e b_2)\bigr)^{T}D\bigl(Y-(A w_2+e b_2)\bigr) \\ ~~&\quad {} +c_{2}e^{T}\eta \\ \mbox{s.t.} ~~&(A w_2+e b_2)-Y\geq- \epsilon_{2}e-\eta, \\ ~~&\eta\geq0, \end{aligned}$$
(19)

where c 1,c 2>0,ε 1, ε 2≥0 are parameters chosen a priori. D=diag(d 1,d 2,…,d l ) is a weighted diagonal matrix, and \(d_{i}=\sum_{j=1}^{l}W_{ij}\). The larger value d i is, the more important the i-th sample is. Then it is more reasonable to give it a major weight.

Note that there are two terms in the objective function of (18). The first term is the sum of squared distances from the shifted function f 1(x) to the training points. Moreover different weights are given to each training sample depending on their local information. This is significantly different from the LSVM. In the second term, slack vector ξ i is introduced to measure the error whether the distance from the down bound function to the sample is smaller than ϵ 1. However, the second term in the objective function of the LSVM [2] means that different penalties are given to the training samples depending on the similarity to the test examples. The similarity is captured by a weighted function σ. Certainly the weighted penalties are only given to the training samples dissatisfying the constraint.

To resolve (18), we first introduce the following Lagrangian function,

$$\begin{aligned} L =&\frac{1}{2}\bigl(Y-(A w_1+e b_1) \bigr)^{T}D\bigl(Y-(A w_1+e b_1) \bigr)+c_{1}e^{T}\xi \\ &{}-\alpha^{T}\bigl(Y-(Aw_1+eb_1)+ \epsilon_{1}e+\xi\bigr)-\beta^{T}\xi, \end{aligned}$$
(20)

where α,β≥0 are Lagrangian multipliers. Differentiating the Lagrangian function with respect to w 1,b 1 and ξ yields the following Karush-Kuhn-Tucker (KKT) conditions:

$$\begin{aligned} &\frac{\partial L}{\partial w_1}=-A^{T}D(Y-A w_1-e b_1)+A^{T}\alpha=0, \end{aligned}$$
(21)
$$\begin{aligned} &\frac{\partial L}{\partial b_1}=-e^{T}D(Y-A w_1-e b_1)+e^{T}\alpha=0, \end{aligned}$$
(22)
$$\begin{aligned} &\frac{\partial L}{\partial\xi}=c_1 e-\alpha-\beta=0, \end{aligned}$$
(23)
$$\begin{aligned} &\alpha^{T}\bigl(Y-(A w_1+e b_1)+ \epsilon_{1}e+\xi\bigr)=0, \end{aligned}$$
(24)
$$\begin{aligned} &\beta^{T}\xi=0. \end{aligned}$$
(25)

Combining (21) and (22), we can achieve

$$\begin{aligned} -\left[ \begin{array}{c} A^{T}\\ e^{T} \end{array} \right]D(Y-Aw_{1}-eb_{1})+ \left[ \begin{array}{c} A^{T}\\ e^{T} \end{array} \right]\alpha=0. \end{aligned}$$
(26)

Define

$$\begin{aligned} G=[A \quad e], \qquad u_1=\bigl[w_{1}^{T} \quad b_1\bigr]^{T}, \end{aligned}$$
(27)

then we have

$$\begin{aligned} -G^{T}D(Y-G u_1)+G^{T}\alpha=0, \end{aligned}$$
(28)

i.e.

$$\begin{aligned} u_1=\bigl(G^{T}D G\bigr)^{-1}G^{T}(D Y-\alpha). \end{aligned}$$
(29)

Finally, the dual formulation of (18) can be derived as

$$\begin{aligned} \max_{\alpha} ~~&-\frac{1}{2} \alpha^{T}G\bigl(G^{T}D G\bigr)^{-1}G^{T} \alpha-Y^{T}\alpha-\epsilon_{1}e^{T}\alpha \\ ~~&\quad {} +Y^{T}D G\bigl(G^{T}D G\bigr)^{-1}G^{T} \alpha +\frac{1}{2}Y^{T}D Y \\ ~~&\quad {}-\frac{1}{2}Y^{T}D G \bigl(G^{T}D G\bigr)^{-1}G^{T}D Y \\ \mbox{s.t.} ~~&0 \leq\alpha\leq c_{1}e, \end{aligned}$$
(30)

where \(\frac{1}{2}Y^{T}D Y-\frac{1}{2}Y^{T}D G(G^{T}D G)^{-1}G^{T}D Y\) is a constant for the variable α, we may discard it and resolve the following simplified QPP,

$$\begin{aligned} \min_{\alpha} ~~&\frac{1}{2} \alpha^{T}G\bigl(G^{T}D G\bigr)^{-1}G^{T} \alpha+Y^{T}\alpha+\epsilon_{1}e^{T}\alpha \\ ~~&\quad {} -Y^{T}D G\bigl(G^{T}D G\bigr)^{-1}G^{T} \alpha \\ \mbox{s.t.} ~~&0 \leq\alpha\leq c_{1}e. \end{aligned}$$
(31)

Similarly, the dual formulation of (19) can be derived as follows,

$$\begin{aligned} \min_{\gamma} ~~&\frac{1}{2} \gamma^{T}G\bigl(G^{T}D G\bigr)^{-1}G^{T} \gamma+\epsilon_{2}e^{T}\gamma \\ ~~&\quad {} +Y^{T}D G \bigl(G^{T}D G\bigr)^{-1}G^{T}\gamma-Y^{T} \gamma \\ \mbox{s.t.} ~~&0 \leq\gamma\leq c_{2}e. \end{aligned}$$
(32)

Notice that G T DG is always positive semidefinite, it is possible that it may not be well conditioned in some situations. To overcome this ill-conditioning case, we introduce a regularization term δI, where δ is a very small positive number, such as δ=1e−7. Then (29) is modified to

$$\begin{aligned} \mu_{1}=\bigl(G^{T}D G+\sigma I \bigr)^{-1}G^{T}(D Y-\alpha). \end{aligned}$$
(33)

Similarly, μ 2 is modified to

$$\begin{aligned} \mu_{2}=\bigl[w_{2}^{T} \quad b_2\bigr]^{T}=\bigl(G^{T}D G+\sigma I \bigr)^{-1}G^{T}(D Y+\gamma). \end{aligned}$$
(34)

Once the vectors μ 1 and μ 2 are known from (33) and (34), the up- and down-bound functions can be obtained. The end regressor is decided by the mean of these two functions,

$$\begin{aligned} f(x) =&\frac{1}{2}\bigl(f_{1}(x)+f_{2}(x) \bigr) \\ =&\frac{1}{2}(w_{1}+w_{2})^{T}x+ \frac{1}{2}(b_{1}+b_{2}). \end{aligned}$$
(35)

3.3 Nonlinear case

In this subsection, we extend the linear KNNWTSVR to the nonlinear case using the kernel trick. The input data are mapped into a high dimensional feature space by some nonlinear kernel functions. In the feature space, a linear regression function is implemented which corresponds to a nonlinear regression function in the input space [10],

$$\begin{aligned} \min_{w_1,b_1,\xi} ~~&\frac{1}{2} \bigl(Y-\bigl(K\bigl(A,A^{T}\bigr) w_1+e b_1 \bigr)\bigr)^{T} \\ ~~&\quad {} \times D\bigl(Y-\bigl(K\bigl(A,A^{T}\bigr) w_1+e b_1\bigr)\bigr)+c_{1}e^{T}\xi \\ \mbox{s.t.} ~~&Y-\bigl(K\bigl(A,A^{T}\bigr) w_1+e b_1\bigr)\geq-\epsilon_{1}e-\xi, \\ ~~&\xi\geq0, \end{aligned}$$
(36)

and

$$\begin{aligned} \min_{w_2,b_2,\eta} ~~&\frac{1}{2} \bigl(Y-\bigl(K\bigl(A,A^{T}\bigr) w_2+e b_2 \bigr)\bigr)^{T} \\ ~~&\quad {}\times D\bigl(Y-\bigl(K\bigl(A,A^{T}\bigr) w_2+e b_2\bigr)\bigr)+c_{2}e^{T}\eta \\ \mbox{s.t.} ~~&\bigl(K\bigl(A,A^{T}\bigr) w_2+e b_2\bigr)-Y\geq-\epsilon_{2}e-\eta, \\ ~~&\eta\geq0, \end{aligned}$$
(37)

where c 1,c 2>0 and ε 1,ε 2≥0 are parameters chosen a priori. D=diag(d 1,d 2,…,d l ) is a weighted diagonal matrix, and \(d_{i}=\sum_{j=1}^{l}W_{ij}\). To resolve the QPP (36), we first introduce the following Lagrangian function,

$$\begin{aligned} L =&\frac{1}{2}\bigl(Y-\bigl(K\bigl(A,A^{T}\bigr) w_1+e b_1\bigr)\bigr)^{T} \\ & {}\times D\bigl(Y-\bigl(K \bigl(A,A^{T}\bigr) w_1+e b_1\bigr) \bigr)+c_{1}e^{T}\xi \\ &{}-\alpha^{T}\bigl(Y-\bigl(K\bigl(A,A^{T}\bigr) w_1+eb_1\bigr)+\epsilon_{1}e+\xi\bigr)- \beta^{T}\xi, \end{aligned}$$
(38)

where α,β≥0 are Lagrangian multipliers. Differentiating the Lagrangian function with respect to w 1,b 1 and ξ yields the following KKT conditions,

$$\begin{aligned} &\frac{\partial L}{\partial w_1}=-K\bigl(A,A^{T}\bigr)^{T}D \bigl(Y-K\bigl(A,A^{T}\bigr) w_1-e b_1\bigr) \\ &\hphantom{\frac{\partial L}{\partial w_1}=} {} +K \bigl(A,A^{T}\bigr)^{T}\alpha=0, \end{aligned}$$
(39)
$$\begin{aligned} &\frac{\partial L}{\partial b_1}=-e^{T}D\bigl(Y-K\bigl(A,A^{T} \bigr) w_1-e b_1\bigr)+e^{T}\alpha=0, \end{aligned}$$
(40)
$$\begin{aligned} &\frac{\partial L}{\partial\xi}=c_1 e-\alpha-\beta=0, \end{aligned}$$
(41)
$$\begin{aligned} &\alpha^{T}\bigl(Y-\bigl(K\bigl(A,A^{T}\bigr) w_1+e b_1\bigr)+\epsilon_{1}e+\xi\bigr)=0, \end{aligned}$$
(42)
$$\begin{aligned} &\beta^{T}\xi=0. \end{aligned}$$
(43)

Combining Eqs. (39) and (40), we get

$$\begin{aligned} &-\left[ \begin{array}{c} K(A,A^{T})^{T}\\ e^{T} \end{array} \right]D\bigl(Y-K\bigl(A,A^{T} \bigr)w_{1}-eb_{1}\bigr) \\ &\quad {}+\left[ \begin{array}{c} K(A,A^{T})^{T}\\ e^{T} \end{array} \right] \alpha=0. \end{aligned}$$
(44)

Define

$$\begin{aligned} H=\bigl[K\bigl(A,A^{T}\bigr) \quad e\bigr] \quad \mbox{and} \quad u_{1}=\bigl[w_{1}^{T} \quad b_1 \bigr]^{T}, \end{aligned}$$
(45)

we can then get

$$\begin{aligned} -H^{T}D(Y-H u_1)+H^{T}\alpha=0. \end{aligned}$$
(46)

We further get

$$\begin{aligned} u_1=\bigl(H^{T}D H\bigr)^{-1}H^{T}(D Y-\alpha). \end{aligned}$$
(47)

Finally, the dual formulation of (36) can be derived as follows,

$$\begin{aligned} \max_{\alpha} ~~&-\frac{1}{2} \alpha^{T}H\bigl(H^{T}D G\bigr)^{-1}H^{T} \alpha -Y^{T}\alpha-\epsilon_{1}e^{T}\alpha \\ ~~&\quad {} +Y^{T}D H\bigl(H^{T}D H\bigr)^{-1}H^{T} \alpha+\frac{1}{2}Y^{T}D Y \\ ~~&\quad {}-\frac{1}{2}Y^{T}D H \bigl(H^{T}D H\bigr)^{-1}H^{T}D Y \\ \mbox{s.t.} ~~&0 \leq\alpha\leq c_{1}e. \end{aligned}$$
(48)

Since \(\frac{1}{2}Y^{T}D Y-\frac{1}{2}Y^{T}D H(H^{T}D H)^{-1}H^{T}D Y\) is a constant for the variable α, we can discard it and resolve the following dual formulation,

$$\begin{aligned} \min_{\alpha} ~~&\frac{1}{2} \alpha^{T}H\bigl(H^{T}D H\bigr)^{-1}H^{T} \alpha+Y^{T}\alpha+\epsilon_{1}e^{T}\alpha \\ ~~&\quad {} -Y^{T}D H\bigl(H^{T}D H\bigr)^{-1}H^{T} \alpha \\ \mbox{s.t.} ~~&0 \leq\alpha\leq c_{1}e. \end{aligned}$$
(49)

Similarly, we can derive the following dual formulation of (37) as follows,

$$\begin{aligned} \min_{\gamma} ~~&\frac{1}{2} \gamma^{T}H\bigl(H^{T}D H\bigr)^{-1}H^{T} \gamma+\epsilon_{2}e^{T}\gamma \\ ~~&\quad {} +Y^{T}D H \bigl(H^{T}D H\bigr)^{-1}H^{T}\gamma-Y^{T} \gamma \\ \mbox{s.t.} ~~&0 \leq\gamma\leq c_{2}e. \end{aligned}$$
(50)

Once the dual QPPs (49) and (50) are solved, we can get vectors μ 1 and μ 2 for the ill-condition case,

$$\begin{aligned} \mu_1=\bigl(H^{T}D H+\sigma I \bigr)^{-1}H^{T}(D Y-\alpha), \end{aligned}$$
(51)

and

$$\begin{aligned} \mu_2=\bigl[w_{2}^{T} \quad b_2\bigr]^{T}=\bigl(H^{T}D H+\sigma I \bigr)^{-1}H^{T}(D Y+\gamma). \end{aligned}$$
(52)

Finally, we can achieve the end regressor for the nonlinear case as follows,

$$\begin{aligned} f(x) =&\frac{1}{2}\bigl(f_1(x)+f_2(x) \bigr) \\ =&\frac{1}{2}(w_{1}+w_{2})^{T}K(A,x)+ \frac{1}{2}(b_{1}+b_{2}). \end{aligned}$$
(53)

3.4 Computational complexity analysis

The computational complexity is discussed in this subsection. Suppose there are l training samples. From the QPP (2) we can know that SVR resolves a larger-sized QPP with two inequality constraints and an equality constraint. However TSVR resolves a pair of smaller-sized QPPs, each of which has only one inequality constraint. So TSVR works approximately 4 times faster than SVR in theory. In the following we discuss the computational complexity of our proposed KNNWTSVR. The main computational process in our algorithm involves two steps:

(1) K-nearest neighbors graph. Using O(l 2log(l)) for all the l training points to compute the weight matrix W [1].

(2) Optimization of our KNNWTSVR. KNNWTSVR has the similar dual formulation to the TSVR, then KNNWTSVR spends nearly the same running time as TSVR does. It means that the KNNWTSVR does not improve the computational complexity.

4 Successive overrelaxation approach

In this subsection, we discuss the implementation of KNNWTSVR. Successive overrelaxation is an iterative procedure that employs the Gauss-Seidel iterations with the extrapolation factor t∈(0,2) to accelerate the solving of the QPPs with linear convergence [13].

We can easily rewrite QPPs (31), (32), (49) and (50) into the following unified form,

$$\begin{aligned} \min_{\alpha} ~~&\frac{1}{2} \alpha^{T}Q\alpha+d\alpha \\ \mbox{s.t.} ~~&\alpha\in S=\{0\leq\alpha\leq ce\}. \end{aligned}$$
(54)

We take the dual formulation (31) for example, it can be rewritten in the above unified form, where Q=G(G T DG+σI)−1 G T and d=Y T+ϵ 1 e T−Y T DQ.

A necessary and sufficient optimality condition for (31) is the following gradient projection optimality condition,

$$\begin{aligned} \alpha=\bigl(\alpha-t_{1}D_{1}^{-1}(Q\alpha+Y+ \epsilon_{1}e-Q D Y)\bigr)_{*}, \end{aligned}$$
(55)

where (⋅)∗ denotes the 2-norm projection on the feasible region S, that is

$$\begin{aligned} \bigl((\alpha)_{*}\bigr)_{i}= \begin{cases}0, & \alpha_{i}\leq0, \\ \alpha_{i}, & 0\leq\alpha_{i}\leq c_{1}, \\ c_{1}, & \alpha_{i}\geq c_{1}. \end{cases} \end{aligned}$$
(56)

Define Q=L+D 1+L T, where L∈R l×l constitutes the strictly lower triangular part of the symmetric matrix of Q, and the nonzero elements of D 1 constitute the diagonal of Q. We can split the matrix Q into the sum of two matrices B and C as follows:

$$\begin{aligned} Q=t_{1}^{-1}D_{1}(B+C), \end{aligned}$$
(57)

where

$$\begin{aligned} B=I+t_{1}D_{1}^{-1}L, \end{aligned}$$
(58)
$$\begin{aligned} C=(t_{1}-1)I+t_{1}D_{1}^{-1}L^{T}, \end{aligned}$$
(59)

where 0<t 1<2, I is an identity matrix of appreciate dimensions. The matrix B+C is positive semidefinite, and matrix B−C is positive definite. Finally we can derive the following iterative formula,

$$\begin{aligned} \alpha_{r+1} =&\bigl(\alpha_{r+1}-B\alpha_{r+1}-C \alpha_{r}+t_{1}D_{1}^{-1}(Y+ \epsilon_{1}e \\ &{}-Q DY)\bigr)_{*}. \end{aligned}$$
(60)

Similarly, we can obtain the other iterative formula,

$$\begin{aligned} \gamma_{r+1} =&\bigl(\gamma_{r+1}-B\gamma_{r+1}-C \gamma_{r} \\ &{}+t_{2}D_{1}^{-1}( \epsilon_{2}e+Q DY-Y)\bigr)_{*}. \end{aligned}$$
(61)

The flowchart of SOR KNNWTSVR is described as follows:

SOR KNNWTSVR algorithm

Input: The matrix Q and vector d.

1. Select parameters t 1,t 2∈(0,2), and initialize α 0,γ 0∈R l;

2. Compute α and γ as following formulation \(\alpha_{r+1}=(\alpha_{r}-t_{1}D_{1}^{-1}(Q\alpha+Y+\epsilon_{1}e-Q DY+L(\alpha_{r+1}-\alpha_{r})))_{*}\) and \(\gamma_{r+1}=(\gamma_{r}-t_{2}D_{1}^{-1}(Q\gamma-Y+\epsilon_{2}e+Q DY+L(\gamma_{r+1}-\gamma_{r})))_{*}\). Where Q=G(G T DG+σI)−1 G T. Define Q=L+D 1+L T, where L∈R l×l is a strictly lower triangular matrix, and D 1∈R l×l is a diagonal matrix.

3. Compute ∥α r+1−α r ∥ and ∥γ r+1−γ r ∥ until they are less than some prescribed tolerance.

Output: the optimal values of α and γ.

It is well known that the successive overrelaxation method is linear convergence, but other iterative methods, e.g., Newton iteration, and so on, are quadratic convergence. So the successive overrelaxation method is employed to accelerate the speed of KNNWTSVR.

5 Numerical experiments

We conduct two kinds of experiments including eight benchmark datasets from the UCI machine learning repositoryFootnote 1 and a real dataset to investigate the effectiveness of our KNNWTSVR. All experiments are carried out in Matlab 7.9 (R2009b) on Windows XP running on a PC with system configuration Intel(R) Core(TM) 2 Duo CPU E7500 (2.93 GHz) with 3.00 GB of RAM.

5.1 Evaluation criteria

To evaluate the performance of our proposed algorithm, the evaluation criteria are specified before presenting the experimental results. The total number of testing samples is denoted by m, while y i denotes the real-value of a sample point x i , \(\hat{y}_{i}\) denotes the predicted value of x i , and \(\bar{y}=\sum_{i=1}^{m}y_{i}\) is the mean of y 1,y 2,…,y m . We use the following criteria for algorithm evaluation [16, 22].

MAE: Mean absolute error, defined as

$$\begin{aligned} \mathit{MAE}= \frac{1}{m}\sum_{i=1}^{m}|y_{i}- \hat{y}_{i}|. \end{aligned}$$
(62)

MAE is also a popular deviation measurement between the real and predicted values.

RMSE: Root mean squared error, defined as

$$\begin{aligned} \mathit{RMSE}= \sqrt{\frac{1}{m}\sum _{i=1}^{m}(y_{i}-\hat{y}_{i})^{2}}. \end{aligned}$$
(63)

SSE/SST: Ratio between sum of squared error and sum of squared deviation of testing samples, defined as

$$\begin{aligned} \mathit{SSE}/\mathit{SST}={\sum_{i=1}^{m}(y_{i}- \hat{y}_{i})^{2}}\bigg/{\sum _{i=1}^{m}(y_{i}-\bar{y}_{i})^{2}}. \end{aligned}$$
(64)

SSR/SSE: Ratio between interpretable sum of squared deviation and real sum of squared deviation of testing samples, defined as

$$\begin{aligned} \mathit{SSR}/\mathit{SSE}=\sum_{i=1}^{m}( \hat{y}_{i}-\bar{y}_{i})^{2}\bigg/{\sum _{i=1}^{m}(y_{i}-\hat{y}_{i})^{2}}. \end{aligned}$$
(65)

In most cases, small SSE/SST means there is good agreement between the estimates and the real values, and decreasing SSE/SST is usually accompanied by an increase in SSR/SST. However, an extremely small value for SSE/SST is in fact not good, for it probably means that the regressor is over-fitting the data.

5.2 Parameters selection

We know that the kernel function and its parameters in SVM have great effects on the experimental results [4]. In our experiments, we only consider the Gaussian kernel function k(x i ,x j )=exp(−∥x i −x j ∥2/γ 2) for these datasets as it is often employed and yields great generalization performance. We choose optimal values for the parameters by the grid search method. The optimal Gaussian kernel parameter γ was selected over the range {2i∣i=−3,−2,…,9}. The optimal values of parameter c in all algorithms were searched from set {2i∣i=−3,−2,…,8}. The parameter ε in all algorithms was searched from the set \(\{\frac{i}{10} \mid i=1, 2, \ldots, 9\}\). The parameter t in our proposed algorithm ranged from the set {0.25,0.5,0.75,1,1.25,1.5,1.75}.

5.3 Experiments on benchmark datasets

In this section, we performed experiments on eight benchmark datasets, they are Diabetes, Pyrim, Con.s, Machine cpu, Triazines, Auto-mpg, Auto-price, and Chwirut. For each experiment, we use 5-fold cross-validation to evaluate the performance of four algorithms, i.e., KNNWTSVR, SOR KNNWTSVR, TSVR and SVR. That is to say, the dataset is split randomly into five subsets, and one of those sets is reserved as a test set. This process is repeated five times, and the average value of five testing results is used as the performance measure. We test the validity of the proposed algorithm from both testing errors and computational time aspects.

The performance comparisons of four algorithms are summed in Table 1. In error items, the first item denotes the mean value of five times testing results, and the second item stands for plus or minus the standard deviation. Time denotes the mean value of time taken by five experiments, and each experimental time consists of training time and testing time.

Table 1 Performance comparisons of four algorithms with Gaussian kernel function on eight benchmark datasets
Full size table

From the perspective of prediction error, we can find that KNNWTSVR and SOR KNNWTSVR yield nearly the same testing errors on eight benchmark datasets. Moreover they are lower than that produced by SVR and TSVR for most cases.

In terms of computational time, our SOR KNNWTSVR costs the least running time among four algorithms for most cases. The next is our KNNWTSVR. However SVR costs the most computational time. The main reason lies in that SVR resolves a larger-sized QPP, but three other algorithms resolves a pair of smaller-sized QPP. Although the TSVR works four times faster than SVR in theory, sometimes more than four times, as we can learn from the datasets Machine cpu, Triazines, Auto-mpg, Auto-pric, and Chwirut. The possible reason is that there is an equality constraint in the dual formulation (2) of SVR, but only an inequality constraint in the dual formulation of TSVR, our KNNWTSVR, and SOR KNNWTSVR.

Generally speaking, as the size of the training dataset increases, our SOR KNNWTSVR has more obvious advantages in computational time.

5.4 Experiment on a real dataset

In this real data experiment, there are 210 wheat samples from all over China. The protein content of wheat ranges from 9.83 % to 20.26 %. They are provided by Heilongjiang research institute of agricultural science. Each sample has 1193 spectral features. They were scanned in transmission mode using a commercial spectrometer MATRIX-I. Samples were acquired in a rectangular quartz cuvette of 1-mm path length with air as reference at room temperature (20–24 °C). The reference spectrum was subtracted from the sample spectra to remove background noise. The rectangular quartz cuvette was cleaned after each sample was scanned to minimize cross-contamination [27].

In this high dimensional data experiment, we predict the content of protein using 1193 spectral features of wheat. The prediction errors of four algorithms are summed in Table 2.

Table 2 Performance comparisons of four algorithms with Gaussian kernel function on wheat dataset
Full size table

From Table 2, we can learn that SOR KNNWTSVR yields lowest prediction error (0.799 %) among four algorithms. The prediction error (0.866 %) of KNNWTSVR follows. The errors produced by them are lower than that produced by SVR (1.171 %) and TSVR (0.955 %). The main reason is that SOR KNNWTSVR and KNNWTSVR consider the local information among samples, and different weights are proposed to give the samples depending on their local information. But in SVR and TSVR, all samples are equally weighted. In addition, to further improve the prediction accuracy, we can incorporate feature selection into our proposed algorithms. The first step is to reduce the dimensions of training samples [15, 21], and then predict the content of protein by the reduced spectral features of wheat.

In terms of computational time, SVR costs the most running time (21.885 s) among four algorithms. TSVR and KNNWTSVR cost nearly the same computational time, and they are slightly higher than that of SOR KNNWTSVR. Moreover, we can further find that TSVR, KNNWTSVR and SOR KNNWTSVR work more than four times faster than SVR. The possible reason is that only one inequality constraint is included in the dual formulations of them, but two constraints including an equality and an inequality constraints in SVR.

6 Conclusion

A K-nearest neighbor-based weighted TSVR is proposed in this paper, and the local information among samples is exploited in the model. The KNN method is employed to count the number d i of neighbors for each sample. The larger value d i denotes the i-th sample has a great number of K-nearest neighbors, and more important for the i-th sample. So a major weight is proposed to give the i-th sample. In contrast, a minor weight is given to the samples with a smaller number of k-nearest neighbors. Moreover successive overrelaxation method is used to further improve the speed of KNNWTSVR. Experimental results on eight benchmark datasets and a real dataset demonstrate the validity of our proposed algorithms. Our SOR KNNWTSVR not only yields lower testing error but also costs the least running time. How to incorporate the feature selection into our proposed algorithms when addressing the high dimensional data is our future research.