Rényi holographic dark energy model with two IR cutoffs in Marder type universe

Abstract

In the study of Saez–Ballester scalar tensor theory (Saez and Ballester in Phys Lett A 113:467, 1986), we examine the cosmic expansion phenomenon using the Rényi holographic dark energy (RHDE) with spatially homogeneous and anisotropic Marder type space time. Using a metric potential relationship, we find the solution to the field equations. Using Hubble and Granda–Oliveros horizon as IR cutoffs, we have derived the equation of state parameter (EoS) ($\omega _{de}$), RHDE energy density ($\rho _{de}$) and matter energy density ($\rho _{m}$), RHDE density parameter ($\Omega _{de}$), and Om-diagnostic. In this study, these parameters are plotted against the redshift (z). For three different choices of n and $\delta$, the EoS parameter exhibits quintom-like behavior for both IR cutoffs. Further, looking into the $\omega _{de}-\omega _{de}'$ plane and stability of the DE model by using a metric perturbation method. It has been found that quintom-like behavior and freezing region explain the Universe’s accelerating rate of growth.

1 Introduction

General relativity(GR) describes the theory of gravitation in terms of geometry, and is one of the most aesthetically pleasing structures of theoretical physics. GR has been modified several times (Capozziello and Laurentis [1], Dimitrijevic et al. [2, 3]) to incorporate desirable physical properties. Broadly speaking, scalar tensor theories are generalizations of GR, in which the metric can be produced by a scalar gravitational field and non-gravitational field (matter). Gravitation theory with a scalar field can be divided into two categories. In the first category, we consider a scalar field whose dimension is $\frac{1}{G}$. It was initially suggested by Brans and Dicke (Brans and Dicke [4]). The Scalar tensor theory in [4] is based on Mach’s principle with assumption of cosmic scalar field and large distribution of matter in motion with interaction of inertial masses of elementary particles. By varying the coupling function ${ w}$, we determine the strength of the coupling among the gravitational field and the scalar field. In curving space time, non-gravitational fields form the scalar gravitational field $\phi$. In the second category, solving the dark matter problem is simpler when using a scalar tensor theory of gravity. This is done by coupling a dimensionless scalar field with the metric. The weak field is described by this coupling. Even though the scalar field is dimensionless, there is an antigravity regime, which describes the weak fields satisfactorily as proposed by Saez and Ballester [5]. The Friedmann-Roberson-Walker flat Universe could be solved by this theory because it solves the missing matter problem. The Scalar tensor theory of SBT is based on the following field equations [5].

$$\begin{aligned} R_{uv}-\frac{1}{2}Rg_{uv}-{ w}\phi ^{r} \left( \phi _{,u}\phi _{,v}-\frac{1}{2}g_{uv} \phi _{,\kappa }\phi ^{,\kappa }\right) =-8\pi T_{uv}, \end{aligned}$$

(1)

and

$$\begin{aligned} 2\phi ^{r}\phi _{;u} ^{,u}+r\phi ^{r-1}\phi _{,\kappa }\phi ^{,\kappa }=0, \end{aligned}$$

(2)

where $R_{uv}$ is the Ricci tensor, R is the scalar curvature, $g_{uv}$ is the metric potential, ${ w}$ is the dimensionless constant, r is a constant, $T_{uv},\, \phi$ describes the energy momentum tensor and scalar field successively. Furthermore, a mathematical equation for energy conservation

$$\begin{aligned} T^{uv}~_{;v}=0, \end{aligned}$$

(3)

is a aftermath of the field Eqs. (1) and (2). Scalar–tensor theories have been studied in the context of cosmological models for decades. Specifically, Shaikh et al. [6] have present an analysis of the behavior of a cosmological model in the presence of matter and a modified Ricci dark energy for homogeneous hyper surfaces in SBT of gravity. SBT of gravitation has been examined by Sharma et al. [7] with cosmological models in the transit of heat flow and perfect fluid. A model of bulk viscous string in SBT of gravity has been investigated by Mishra and Dua [8]. In Bianchi type-I Universe with perfect fluid content and bilinearly varying deceleration parameter (DP), Mishra and Chand [9] have investigated their dynamical nature. Axially symmetric domain walls cosmology has been studied by Ahmad and Tade [10] in SBT of gravity. In SBT of gravity, Garg et al. [11] have studied generalized ghost pilgrim dark energy. In [12], Mishra and Dua have investigated a model of Bianchi type-I with varying DP in SBT of gravity. In a SBT of gravitation, Naidu et al. [13] have examined dynamical behavior of Kaluza-Klein FRW type dark energy cosmological models. Singh and Singh [14], Santhi and Naidu [15] and some recent studies have looked at the stabilization of extra dimensions and the RHDE model in scalar tensor theories.

It is evident from cosmological observations that the Universe is expanding rapidly. It has been observed from numerous observational studies that our cosmos is characterized by both a rapid inflation at the beginning of its history and a rapid expansion later (Miller et al. [16]; Riess et al. [17]; Perlmutter et al. [18]; Fedeli et al. [19]). It is believed that this is due to the presence of an unidentified source of energy with enormous negative pressure known as dark energy (Nojiri and Odintsov [20]; Bamba et al. [21]). Dark energy and dark matter are two mysterious components of our Universe (Amendola et al. [22]). The amount of dark matter in the Universe is around $25\%$ of its total energy density, whose nature is unknown to us. Another element of our Universe is dark energy. Due to dark energy, the Universe is currently accelerating and contributes around $70\%$ of the Universe’s energy density. Further investigation of its exact nature remains to be done. In spite of its incredible success, the standard cosmology has been insufficient for addressing certain significant problems, especially in searching for the most suitable candidate for dark energy. In addressing certain significant problems, the cosmic constant is the simplest candidate for dark energy, but it faces two serious theoretical problems like fine-tuning and the coincidence problem (Amendola [23]; Malquarti et al. [24]). To resolve this issue, there are two possibilities: dynamical dark energy is introduced into the right-hand side of the Einstein field equations within the framework of GR and modified gravity theories are introduced into left-hand side of the Einstein equations. A family of scalar fields belong to the first approach, including quintessence (Ratra and Peebles [25]), phantom (Caldwell [26]), tachyon (Padmanabhan [27]), K-essence (Armendariz-Picon et al. [28]), as well as others were put forward to describe accelerated expansion as dark energy candidates. Another way to understand the expansion of the Universe is through modified theories of gravity, that includes f(R) gravity (Capozzielo [29]), f(R, T) (Harko et al. [30]), here, R is the scalar curvature and T is the trace of the energy momentum tensor and Brans–Dicke ([4]), Saez–Ballester ([5]) scalar tensor theories of gravity.

The dark energy models that are included in the first approach to a scalar field family are also included (as described above). There has been considerable interest in solving the dark energy puzzle with HDE, which has some quantum gravity properties. To study the DE scenario, Li [31] has proposed HDE. There are many properties of the HDE that align with quantum gravity as well as with the holographic principle (Susskind [32]; Gong et al. [33]; Nojiri and Odintsov [34]; Li et al. [35]) that states a physical system’s degrees of freedom scale with its bounding surface, rather than its volume. Several examinations have been carried out on the HDE model, including $\rho _{de} \propto \Lambda ^4,$ whereas the relationship between the IR cut-off L, UV cut-off $\Lambda$, and the entropy S is $\Lambda ^3\,L^3\le (S)^{\frac{3}{4}}$. Hence, the energy density of the HDE model is given by the IR cut-offs and the entropy. Based on Bekenstein-Hawking entropy, HDE is defined as $S =\frac{A}{4G},$ with $A = 4\pi L^2,$ density is $\rho _{de} = \frac{3d^2}{8\pi G} L^{-2}$, where G is gravitational constant, d is a numerical constant. In the literature, IR-cutoffs have been discussed as conformal Universe age, Ricci scalar radius, particle horizon, event horizon, ultraviolet, Hubble horizon, Granda–Oliveros (GO) and infrared cutoff (Guo et al. [36]; Granda and Oliveros [37]; Wei and Cai [38]; Granda and Oliveros [39]; Drepanou et al. [40]; Luciano and Saridakis [41]). As a result of a newly developed HDE model, the Universe is expanding at an accelerated rate and current observational data support the transition from the deceleration phase $(q>0)$ to the acceleration phase $(q<0)$.

Several generalized entropy models of gravity and cosmology have been developed due to the long-range aspects of gravity and the unknown nature of space time. Examples are Tsallis HDE (Tsallis and Cirto [42]; Tavayef et al. [43]), Sharma-Mittal HDE (Jahromi et al. [44]) and RHDE model (Moradpour et al. [46]). THDE models are based on the Tsallis generalized entropy, which is not stable at classical levels [42,43,44, 46], although SMHDE is classically stable when the cosmos is not interacting. RHDE is more stable as there is no interaction between sectors of the cosmos (Moradpour et al. [46]). The RHDE model has been examined by Sharma and Dubey [47], taking three different parametrizations of the dark energy and dark matter interaction term in FLRW Universe. In GR, Prasanthi and Aditya [48] have investigated anisotropic RHDE models. Using the Rényi entropy in the flat FLRW Universe, Golanbari et al. [49] investigated the entropy modifying HDE model. In the D-dimensional fractal Universe, Maity and Debnath [50] discussed HDE models based on Sharma-Mittal, Renyi and Tsallis. RHDE in Brans Dicke cosmology has recently been examined by Sharma and Dubey [51]. In other modified gravity theories, the RHDE has been discussed [52,53,54,55]. According to the earlier study, we analyze the HDE by applying the new entropy formalism: RHDE with the Hubble and GO horizons as IR cutoffs.

We have focused our attention on the Marder type cosmological model with Hubble, GO horizons as IR cutoffs in the context of SBT of gravity. Our paper is structured as follows: In Sect. 2, we discuss the model’s mathematical formalism. In Sect. 3, we study the RHDE model with cosmological behavior. In Sect. 4, we investigate stability analysis. In Sect. 5, we discuss Om diagnostic and Kinematic tests in Sect. 6. The outcomes of our model are discussed in the final section.

2 Model mathematical formalism

The Universe’s early and modern epochs are represented by spatially homogeneous and isotropic FRW models that are widely accepted in cosmology. Cosmic Background Explorers, Wilkinson Microwave Anisotropy Probe (WMAP), and Planks collaboration confirm the existence of an anisotropic stage that progresses to an isotropic stage. Given this, it might be beneficial to investigate models of Universe with an anisotropic background when analyzing dark energy. In spite of the present situation on large scales, the existing cosmos appears relatively isotropic, Ellis and Callum [56] found that the early and very late Universes could be anisotropic. An anisotropic Universe’s physical qualities change depending on the direction from which they are measured. In order to obtain a realistic picture of the Universe in its early stages, cosmological models that are spatially homogeneous and anisotropic play a vital role in characterizing the large-scale behavior of the cosmos. The current Universe shows some anisotropic behavior according to WMAP’s data (Komatsu et al. [57]). Marder space-time has some characteristics for explaining the formation of galaxies during the early stages of the Universe evolution (Kilinc [58]). As the Marder line element is a homogeneous and anisotropic space-time, it helps us understand the anisotropy at the beginning of the Universe and provides transition from anisotropy to isotropy, thus motivating us to consider such a space-time. Also, by using the transformation $t\rightarrow \int p_{1}(t)dt$, one can reduce the Marder space-time to the Bianchi type-I model, which further reduces to the FRW Universe. Hence, we classify the line element accordingly if anisotropy at later times or at early stages of the Universe (Sharif and Kausar [59]). Thus, Marder space-time not only facilitates us to study about anisotropic Universe, but also the isotropic one. Within the context of GR, such models have gained a lot of attention. We preferred the Marder’s space-time in Einstein’s GR and scalar tensor theories, because it is a homogeneous and anisotropic space-time (a better metric to explain anisotropy at the beginning of the Universe) and provides transition from anisotropic to isotropic. We consider the spatially homogeneous and anisotropic Marder type space time form as follows (Marder [60])

$$\begin{aligned} ds^2=p_1^2(t) dx^2+p_2^2(t)dy^2+p_3^2(t)dz^2-p_1^2(t)dt^2, \end{aligned}$$

(4)

where $p_1$, $p_2$ and $p_3$ are functions of time t only.

In this analysis we will explore how physical parameters influence the formulation of field equations for the Marder type space time given by Eq. (4). Some of the authors who have studied Marder space time with various energy momentum tensors are Singh and Abdussattar [61], Prakash [62], Roy and Chatterjee [63], Mukherjee [64], Aygün et al. [65], Ali and Aygün [66], Aygün et al. [67] and Ali et al. [68], Pawar and Panpatte [69], Pawar and Solanke [70], Aygün [71], Aygün et al. [72, 73] and Aktas et al. [74]. The investigation of the magnetized string distribution in the Marder Universe with the cosmological term in f(R, T) theory done by Kömürcü and Aktas [75]. Wet dark fluid model in Marder space time which is anisotropic and homogeneous has recently been constructed by Pawar et al. [76]. Recently, bulk viscous string cosmological model in a modified theory of gravity has been studied by Santhi et al., [77]. Viscous holographic dark energy cosmological model in Marder space-time has been investigated by Santhi et al., [78]. Very recently, Marder space-time with Tsallis holographic dark energy has been studied by Santhi and Naidu [79]. Dark energy and pressureless matter are assumed to be the distribution of matter, respectively as

$$\begin{aligned} T_{uv}=T'_{uv}+{{\overline{T}}_{uv}}, \end{aligned}$$

(5)

where $T'_{uv}$, ${\overline{T}}_{uv}$, are energy momentum tensors for pressure-less dark matter and RHDE respectively. These are given by

$$\begin{aligned} {{\overline{T}}_{uv}}&=\left( \rho _{de}+p_{de}\right) U_u U_v+p_{de}g_{uv}, \end{aligned}$$

(6)

$$\begin{aligned}{} \& \quad T'_{uv}&=\rho _m U_u U_v, \end{aligned}$$

(7)

where $\rho _{de}$, $p_{de}$ & $\rho _m$ are energy density, pressure of dark energy and energy density of matter respectively and $U_u=(0,0,0, -p_{1})$ is the four velocity vector. Also, $\omega _{de}=\frac{p_{de}}{\rho _{de}}$ is the EoS parameter of dark energy.

Now with the help of Eq. (5), the field Eqs. (1) and (2) for the metric in Eq. (4) can be written as

$$\begin{aligned} \frac{1}{p_1^2}\left( \frac{\ddot{p}_{2}}{p_2}+\frac{\ddot{p_3}}{p_3}+\frac{\dot{p_2}\dot{p_3}}{p_2p_3}-\frac{\dot{p_1}\dot{p_2}}{p_1p_2}-\frac{\dot{p_1}\dot{p_3}}{p_1p_3}\right) -\frac{ { w}\phi ^r \dot{\phi }^2}{2p_1^2}=&-8\pi \omega _{de}\rho _{de}, \end{aligned}$$

(8)

$$\begin{aligned} \frac{1}{p_1^2}\left( \frac{\ddot{p_1}}{p_1}+\frac{\ddot{p_3}}{p_3}-\frac{\dot{p_1}^2}{p_1^2}\right) -\frac{{ w}\phi ^r \dot{\phi }^2}{2p_1^2}=&-8\pi \omega _{de}\rho _{de}, \end{aligned}$$

(9)

$$\begin{aligned} \frac{1}{p_1^2}\left( \frac{\ddot{p_1}}{p_1}+\frac{\ddot{p_2}}{p_2}-\frac{\dot{p_1}^2}{p_1^2}\right) -\frac{{ w}\phi ^r \dot{\phi }^2}{2p_1^2}=&-8\pi \omega _{de}\rho _{de}, \end{aligned}$$

(10)

$$\begin{aligned} \frac{1}{p_1^2}\left( \frac{\dot{p_1}\dot{p_2}}{p_1p_2}+\frac{\dot{p_2}\dot{p_3}}{p_2p_3}+\frac{\dot{p_3}\dot{p_1}}{p_3p_1}\right) +\frac{{ w}\phi ^r \dot{\phi }^2}{2p_1^2}=&8\pi (\rho _m+\rho _{de}), \end{aligned}$$

(11)

$$\begin{aligned}{} \& \quad \ddot{\phi }+\dot{\phi }\left( \frac{2\dot{p_1}}{p_1}+\frac{\dot{p_2}}{p_2}+\frac{\dot{p_3}}{p_3}\right) +\frac{r\dot{\phi }^2}{2\phi }=&0. \end{aligned}$$

(12)

Similarly, by using the conservation equation, the following equation can be found:

$$\begin{aligned} \dot{\rho }_{m}+\dot{\rho }_{de}+3\left( \frac{2\dot{p_1}}{p_1}+\frac{\dot{p_2}}{p_2} +\frac{\dot{p_3}}{p_3}\right) \left( \rho _{m}+\rho _{de}+\omega _{de}\rho _{de}\right) =0. \end{aligned}$$

(13)

Throughout the article, the overhead dot indicates differentiation with respect to cosmic time (t). There are seven unknown variables in the field Eqs. (8)–(12):  $p_1$, $p_2$, $p_3$, $\phi$, $\rho _{m}$, $\rho _{de}$ and $\omega _{de}$. For the above equations to be solved, we need some conditions. A relationship between the metric potentials can be obtained by assuming a proportionality between the expansion scalar $\theta$ and shear scalar $\sigma$ (Collins et al. [80]). That is

$$\begin{aligned} p_1=(p_2p_3)^{n}. \end{aligned}$$

(14)

The space time is anisotropic and $n\ne 1$ maintains that. From Eqs. (9) and (10), we get

$$\begin{aligned} \frac{\ddot{p_2}}{p_2}-\frac{\ddot{p_3}}{p_3}=0. \end{aligned}$$

(15)

From Eqs. (8) and (10), we obtain

$$\begin{aligned} \frac{\ddot{p_3}}{p_3}-\frac{\ddot{p_1}}{p_1}+\frac{\dot{p_2}\dot{p_3}}{p_2p_3} -\frac{\dot{p_2}\dot{p_1}}{p_2p_1}-\frac{\dot{p_1}\dot{p_3}}{p_1p_3}+\frac{\dot{p_1}^2}{p_1^2}=0. \end{aligned}$$

(16)

From Eqs. (14) and (16), we obtain a new equation

$$\begin{aligned} \frac{\ddot{p_2}}{p_2}+\frac{\dot{p_2}\dot{p_3}}{p_2p_3}=0. \end{aligned}$$

(17)

For the sake of simplicity, we apply the following substitutions,

$$\begin{aligned} p_2=\sqrt{\mu \alpha }~~\text {and}~~p_3=\sqrt{\frac{\mu }{\alpha }}, \end{aligned}$$

(18)

where $\mu$ & $\alpha$ are functions of time.

From Eqs. (15) and (18), we get

$$\begin{aligned} \frac{d}{dt}\left( \frac{\mu }{\alpha }\dot{\alpha }\right) =0. \end{aligned}$$

(19)

From Eqs. (17) and (18), we get

$$\begin{aligned} \frac{d}{dt}\left[ \mu \left( \frac{\dot{\mu }}{\mu }+\frac{\dot{\alpha }}{\alpha }\right) \right] =0. \end{aligned}$$

(20)

Integrating Eq. (19), we get

$$\begin{aligned} \frac{\mu }{\alpha }\dot{\alpha }=k_1, \end{aligned}$$

(21)

where $k_1$ is constant of integration.

From Eqs. (20) and (21), we obtain

$$\begin{aligned} \frac{d}{dt}\left( \dot{\mu }+k_1\right) =0. \end{aligned}$$

(22)

Integrating Eq. (22), we get

$$\begin{aligned} \mu =k_3t+k_4, \end{aligned}$$

(23)

where $k_3=k_2-k_1$ and $k_4$ are integration constants. Therefore, from Eqs. (14) and (23), we obtain one of the metric potentials as

$$\begin{aligned} p_1=\left( k_3t+k_4\right) ^n. \end{aligned}$$

(24)

Now solving Eq. (21), we get

$$\begin{aligned} \alpha =k_5\left( k_3t+k_4\right) ^{k_6}, \end{aligned}$$

(25)

where $k_5>1$ and $k_6=\frac{k_1}{k_3}$ are positive integration constants. In the same manner, we get the remaining metric potentials from the Eqs. (18), (23) and (25) as

$$\begin{aligned} p_2=k_7\left( k_3t+k_4\right) ^{\frac{1+k_6}{2}}~~\text {and}~~ p_3=k_8\left( k_3t+k_4\right) ^{\frac{1-k_6}{2}}, \end{aligned}$$

(26)

where $k_7=\sqrt{k_5}$ and $k_8=\sqrt{\frac{1}{k_5}}$ are positive integration constants. Substituting $p_1, p_2$ and $p_3$ values in Eq. (12), we find that

$$\begin{aligned} \phi =\left[ \frac{k_{10}(r+2)}{2}-\frac{k_9(r+2)}{4k_3n\left( k_3t+k_4\right) ^{2n}}\right] ^{\frac{2}{r+2}}, \end{aligned}$$

(27)

where the constants $k_9$ and $k_{10}$ are constants of integration.

Now, the metric in Eq. (4) can be rewritten as

$$\begin{aligned}{} & {} ds^2=\left( k_3t+k_4\right) ^{2n} dx^2+\left( k_7\left( k_3t+k_4\right) ^{\frac{1+k_6}{2}}\right) ^2dy^2\nonumber \\{} & {} \qquad +\left( k_8\left( k_3t+k_4\right) ^{\frac{1-k_6}{2}}\right) ^2dz^2-\left( k_3t+k_4\right) ^{2n}dt^2. \end{aligned}$$

(28)

In Marder space time Volume (V), average scaling factor (a(t)), anisotropic parameter $(\mathcal {A}_h)$, Hubble parameter (H), expansion scalar $(\theta )$, shear-scalar $(\sigma ^2)$ and deceleration parameter (DP) (q) is defined as

$$\begin{aligned} V&= \left( k_3t+k_4\right) ^{2n+1}, \end{aligned}$$

(29)

$$\begin{aligned}&a(t)=\left( k_3t+k_4\right) ^{\frac{2n+1}{3}}, \end{aligned}$$

(30)

$$\begin{aligned}&H=\frac{k_3 (2n+1)}{3\left( k_3t+k_4\right) }, \end{aligned}$$

(31)

$$\begin{aligned}&\theta =\frac{k_3 (2n+1)}{\left( k_3t+k_4\right) ^{n+1}}, \end{aligned}$$

(32)

$$\begin{aligned}&\sigma ^2=\frac{k_3^2\left( 4n^2+3k_6^2-4n+1\right) }{12\left( k_3t+k_4\right) ^{2n+2}}, \end{aligned}$$

(33)

$$\begin{aligned}&\mathcal {A}_h=\frac{\left( 4n-1\right) ^2+3k_6^2}{2(2n+1)^2}, \end{aligned}$$

(34)

$$\begin{aligned}&~~~ \& ~~~ q=\frac{2-2n}{2n+1}. \end{aligned}$$

(35)

From Eqs. (29)–(33), we observed that, the Volume and average scaling factor increases exponentially with time. This illustrates growth of the Universe with time. Also, the parameters H, $\theta$ an $\sigma ^2$ are diminishing. At $t=\frac{-k_4}{k_3}$, volume vanishes and the other parameters tend to infinity. The non zero value of $\mathcal {A}_h$ indicates that Marder type cosmological models are anisotropic in nature. In cosmic expansion, the parameter q quantifies expansion of the Universe. As a result of this, it indicates deceleration (if q is positive) or acceleration (if q is negative), while the marginal inflation occurs at $q=0$ and $q=-1$, the current Universe shows de-Sitter expansion. Based on the analysis of the model, it is concluded that accelerated inflation occurs for $-1\le q<0$, and super exponential inflation for $q < -1$. Depending on the sign of H and q, we classify model of Universe as: For $H<0$, we have contracting and decelerating Universe for $q>0$ and contracting and accelerating Universe for $q<0$. For $H>0$, we have expanding and decelerating Universe at $q>0$, expanding and accelerating Universe for $q<0$, expanding with zero deceleration at $q=0$. For $H=0$, $q=0$ we obtain a static Universe. From Eq. (35), we can observe that the DP is independent of time and takes negative values for $H > 0$, $n>1$ indicates the accelerating expansion of the Universe. Berman [81], Kumar and Singh [82], Samanta [83], Santhi et al. [84], Bishi et al. [85], Santhi and Naidu [15, 86], Samanta and Mishra [87] etc., authors have found time-independent deceleration parameter in there literature.

Galaxies emit light with different wavelengths when they move relative to us. An essentially dimensionless quantity known as redshift describes the ratio between the wavelength change and the wavelength emitted by the light.

Scale factor a(t) is related to redshift z as

$$\begin{aligned} z=\frac{a_0}{a}-1. \end{aligned}$$

(36)

In order to get the complete details of the Universe, we have to express parameters of cosmology in terms of z. One can write the cosmic time t in terms of redshift z as

$$\begin{aligned} t(z)=\frac{\bigg (\bigg (\frac{a_0}{1+z}\bigg )^\frac{3}{2n+1}-k_4\bigg )}{k_3}. \end{aligned}$$

(37)

3 RHDE model with cosmological behavior

Recent investigations of gravitational cosmological incidences have used an enhanced version of the DE model using the Rényi entropy [45, 46]. It is possible to think about a system with $\mathfrak {W}$ outcomes having a probability $\mathfrak {i}^{\mathfrak {th}}$ in order to obtain a $\mathfrak {P_i}$ outcome and fulfil the condition $\sum _{\mathfrak {i}=1}^{\mathfrak {W}}\mathfrak {P_i}=1$. We define Tsallis and Rényi entropies as

$$\begin{aligned} \mathfrak {S_R}=\frac{1}{\delta } \ln \sum _{\mathfrak {i}=1}^{\mathfrak {W}}\mathfrak {P_i}^{1-\delta }, \end{aligned}$$

(38)

$$\begin{aligned} \mathfrak {S_T}=\frac{1}{\delta } \ln \sum _{\mathfrak {i}=1}^{\mathfrak {W}}\mathfrak {P_i}^{1-\delta }-\mathfrak {P_i}, \end{aligned}$$

(39)

where $\delta \equiv 1-\mathfrak {U}$, where $\mathfrak {U}$ represents a real number. These two equations together form

$$\begin{aligned} \mathfrak {S_R}=\frac{1}{\delta } \ln \left( 1+\delta \mathfrak {S_T}\right) . \end{aligned}$$

(40)

It is demonstrated that $\mathfrak {S_R}$ exhibits the class of entropy functions that are most general for homogeneous systems. This following formula is used to determine the Bekenstein entropy of a system in mathematical terms: $\mathfrak {S_T}=\frac{\mathfrak {A}}{4}$, where $\mathfrak {A}=4 \pi \mathfrak {L}^2$ and $\mathfrak {L}$ is a change in IR cut off. Here, we have use Rényi entropy as:

$$\begin{aligned} \mathfrak {S_R}=\frac{1}{\delta }\ln \left( \frac{\delta }{4}\mathfrak {A}+1\right) =\frac{1}{\delta }\ln \left( \pi \delta \mathfrak {L}^2+1\right) . \end{aligned}$$

(41)

The gravitational field is strong enough for the construction of the Universe with a small amount of dark energy and dark matter for $\delta <1$. Moreover, the gravitational field becomes weaker for $\delta >1$, which requires a large quantity of dark energy and dark matter. Assuming $\rho _{de} dV \propto T dS$, the Rényi HDE density becomes

$$\begin{aligned} \rho _{de}=\frac{3d^2}{8\pi \mathfrak {L}^2}\left( 1+\pi \delta \mathfrak {L}^2\right) ^{-1}. \end{aligned}$$

(42)

3.1 RHDE model with hubble horizon cutoff

In our analysis, we have used Hubble horizon as IR cutoff. Choosing $\mathfrak {L}=H^{-1}$ and $8\pi =1$, we obtain RHDE density as

$$\begin{aligned} \rho _{de}=\frac{3d^2H^2}{1+\pi \delta H^{-2}}. \end{aligned}$$

(43)

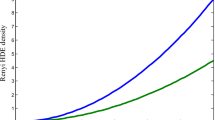
From Eqs. (31), (36) and (43), we obtain energy density of RHDE ($\rho _{de}$) as

$$\begin{aligned} \rho _{de}=\frac{d^2k_3^4(2n+1)^4}{3\bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}}\left( k_3^2(2n+1)^2+9\pi \delta \bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}}\right) }. \end{aligned}$$

(44)

The energy density of matter ($\rho _{m}$) is given by

$$\begin{aligned} \left. \begin{aligned} \rho _{m}&=\frac{1}{96 \pi \bigg (\frac{a_0}{1+z}\bigg )^{\frac{18n+12}{2n+1}} k_3^2 (2n+1)^2+864 \pi \delta \bigg (\frac{a_0}{1+z}\bigg )^{\frac{18n+18}{2n+1}}}\\&\times \Bigg (12 n k_3^4 \bigg (\frac{a_0}{1+z}\bigg )^{\frac{12n+6}{2n+1}} (2n+1)^2\\&+108 \pi \delta n k_3^2 \bigg (\frac{a_0}{1+z}\bigg )^{\frac{12n+12}{2n+1}}+3 k_3^4 \bigg (\frac{a_0}{1+z}\bigg )^{\frac{12n+6}{2n+1}} (2n+1)^2\\&+27 \pi \delta \bigg (\frac{a_0}{1+z}\bigg )^{\frac{12n+12}{2n+1}} k_3^2\\&-3k_3^4 k_6^2 \bigg (\frac{a_0}{1+z}\bigg )^{\frac{12n+6}{2n+1}}(2n+1)^2-27 \pi \delta k_3^2 k_6^2 \bigg (\frac{a_0}{1+z}\bigg )^{\frac{12n+12}{2n+1}}\\&+6{ w}k_9^2 k_3^2 (2n+1)^2 \bigg (\frac{a_0}{1+z}\bigg )^\frac{6}{2n+1}\\&+54{ w}k_9^2 \pi \delta \bigg (\frac{a_0}{1+z}\bigg )^\frac{12}{2n+1}-32 \pi \bigg (\frac{a_0}{1+z}\bigg )^{\frac{18n+6}{2n+1}} d^2 k_3^4 (2n+1)^4 \Bigg ). \end{aligned}\right\} \end{aligned}$$

(45)

The EoS parameter $\omega _{de}$ is given by

$$\begin{aligned} \left. \begin{aligned} \omega _{de}=&\frac{-3}{8 d^2 \pi k_3^4 (2n+1)^4}\times \Bigg (\Bigg (k_3^2 (k_6^2-4n-1)\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-6n}{2n+1}}\\&-2\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-18n-6}{2n+1}}{ w}k_9^2\Bigg )\times \\&\Bigg (\bigg (\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2 }{k^2_3 4}+(n+\frac{1}{2})^2\bigg )k_3^2\\&+\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )k_4}{2}+\frac{9 \pi \delta k_4^2}{4}\Bigg )\bigg (\frac{a_0}{1+z}\bigg )^\frac{6}{2n+1}\Bigg ). \end{aligned}\right\} \end{aligned}$$

(46)

Fig. 1

RHDE Energy density $\rho _{de}$ $({\textrm{kg}}\,{\textrm{m}}^{-1}{\textrm{s}}^{-2})$ against redshift (z)

Fig. 2

Matter Energy density $\rho _{m}$ $({\textrm{kg}}\,{\textrm{m}}^{-1}{\textrm{s}}^{-2})$ against redshift (z)

Fig. 3

EoS parameter $(\omega _{de})$ against redshift (z)

Fig. 4

$\omega _{de}-\omega _{de}'$ plane

The $\omega _{de}'$ is given by

$$\begin{aligned} \left. \begin{aligned} \omega _{de}'=&\frac{9}{4\pi d^2 k_3^4(2n+1)^5}\\&\times \Bigg (\Bigg (k_3^2 (k_6^2-4n-1)\Bigg (\Bigg (\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{k^2_3 4}\\&+\bigg (n+\frac{1}{2}\bigg )^2\Bigg )k_3^2\\&+\frac{9 \pi \delta k_4^2}{4}\\&+\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}} -k_4\bigg )k_4}{2}\Bigg )\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6n-6}{2n+1}}\\&+k_3^2 (k_6^2-4n-1)\bigg (\bigg (\frac{9 \pi \delta (n-2) \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{4k_3^2}\\&-\frac{1}{4}+n^3-\frac{3n}{4}\bigg )k_3^2+\frac{9 \pi \delta k_4^2 (n-2)}{4}\\&+\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )k_4 (n-2)}{2}\bigg )\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-6n}{2n+1}}\\&-4 k_9^2 { w}\bigg (\bigg (n+\frac{1}{2}\bigg )\bigg (\bigg (\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{k^2_3 4}\\&+\bigg (n+\frac{1}{2}\bigg )^2\bigg )k_3^2+\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )k_4}{2}\\&+\frac{9 \pi \delta k_4^2}{4}\bigg )\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-18n}{2n+1}}\\&+\bigg (\bigg (\frac{9 \pi \delta (n-2) \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{k^2_3 4}-\frac{1}{4}\\&+n^3-\frac{3n}{4}\bigg )\frac{\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-18n}{2n+1}}}{2}k_3^2\\&+\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )k_4 (n-2)}{2}\\&+\frac{9 \pi \delta k_4^2 (n-2)}{4}\bigg )\bigg )\bigg )\bigg (\frac{a_0}{1+z}\bigg )^\frac{6}{2n+1}\Bigg ). \end{aligned}\right\} \end{aligned}$$

(47)

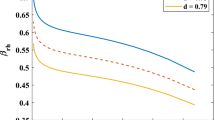
Using Eqs. (31), (36) and (44), we obtain the density parameter of RHDE as

$$\begin{aligned} \Omega _{de}=\frac{d^2 k_3^2 (2n+1)^2}{9 \pi \delta k_4^2+18 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg ) k_4+\bigg (\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{k_3^2} +4 \bigg (n+\frac{1}{2}\bigg )^2\bigg )k_3^2}. \end{aligned}$$

(48)

3.2 RHDE model with Granda–Oliveros cutoff

Here, we consider Granda–Oliveros (GO) horizon cutoff for RHDE model $L=\left( \mu _1 H^2+\mu _2 \dot{H}\right) ^{\frac{-1}{2}}$. This cutoff scale has been presented by Granda and Oliveros [37, 39] for defining the famous cosmological problem of causality and cosmic coincidence. Using GO cutoff in Eq. (42) and $8\pi =1$, we obtain

$$\begin{aligned} \rho _{de}=3d^2\left( \mu _1 H^2+\mu _2 \dot{H}\right) \left( 1+\frac{\pi \delta }{\left( \mu _1 H^2+\mu _2 \dot{H}\right) }\right) ^{-1}. \end{aligned}$$

(49)

From Eqs. (31) and (49), the energy density of RHDE $\rho _{de}$ is given by

$$\begin{aligned} \rho _{de}=\frac{d^2k_3^4(2n+1)^2\left( 2n\mu _1+\mu _1-3\mu _2\right) ^2}{3\bigg (\frac{a_0}{1+z}\bigg )^\frac{6}{2n+1} \Big (k_3^2(2n+1)\left( 2n\mu _1+\mu _1-3\mu _2\right) +9\pi \delta \left( \frac{a_0}{1+z}\right) ^\frac{6}{2n+1}\Big )}. \end{aligned}$$

(50)

The energy density of matter $\rho _{m}$ is given by

$$\begin{aligned} \left. \begin{aligned} \rho _{m}=&\frac{1}{96 \pi \bigg (\frac{a_0}{1+z}\bigg )^{\frac{18n+12}{2n+1}}\big (k_3^2 (2n+1) (2n \mu _1+\mu _1-3 \mu _2)+9 \pi \delta \bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}}\big )}\times \Bigg ( (4n+1-k_6^2)\bigg (\frac{a_0}{1+z}\bigg )^{\frac{12n+6}{2n+1}}\\&3 k_3^2\Big (k_3^2 (2n+1)(2n \mu _1+\mu _1-3 \mu _2)\\&+9 \pi \delta \bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}}\Big )+6 { w}k_9^2 \bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}} \Big (k_3^2 (2n+1) (2n \mu _1\\&+\mu _1-3 \mu _2)+9 \pi \delta \bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}}\Big )\\&-32 \pi d^2\big (k_3^2 (2n+1) (2n \mu _1+\mu _1-3 \mu _2)\big )^2 \pi \bigg (\frac{a_0}{1+z}\bigg )^{\frac{18n+6}{2n+1}}\Bigg ). \end{aligned}\right\} \end{aligned}$$

(51)

The EoS parameter $\omega _{de}$ is given by

$$\begin{aligned} \left. \begin{aligned} \omega _{de}=&\frac{-27}{32 \bigg (d^2 \pi k_3^4 (2n+1)^2 \bigg (2\mu _1n+\mu _1-3 \mu _2\bigg )^2\bigg )}\\&\times \Bigg (\Bigg (\bigg (\frac{4 n^2 \mu _1}{9}+\bigg (\frac{4 \mu _1}{9}-\frac{2 \mu _2}{3}\bigg )n\\&+\frac{\pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{k_3^2} +\frac{\mu _1}{9}-\frac{\mu _2}{3}\bigg )k_3^2\\&+2 \delta k_4 \pi \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )+\delta k_4^2 \pi \Bigg )\times \\&\bigg (k_3^2\bigg (k_6^2-4n-1\bigg ) \bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-6n}{2n+1}}\\&-2\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-18n}{2n+1}}{ w}k_9^2\bigg )\bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}} \Bigg ). \end{aligned}\right\} \end{aligned}$$

(52)

Fig. 5

RHDE Energy density $\rho _{de}$ $( {\textrm{kg}}\,{\textrm{m}}^{-1}{\textrm{s}}^{-2})$ against redshift (z)

Fig. 6

Matter Energy density $\rho _{m}$ $({\textrm{kg}}\,{\textrm{m}}^{-1}{\textrm{s}}^{-2})$ against redshift (z)

The $\omega _{de}'$ is given by

$$\begin{aligned} \left. \begin{aligned} \omega _{de}'=&\frac{81}{16 d^2 k_3^4 (2n+1)^3 \bigg (2\mu _1n+\mu _1-3\mu _2\bigg )^2 \pi k_3}\\&\times \Bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{6}{2n+1}}\bigg ((k_6^2-4n-1)k_3^3\\&\bigg (\bigg (\frac{4 n^2 \mu _1}{9}+\bigg (\frac{4 \mu _1}{9}-\frac{2 \mu _2}{3}\bigg )n+\frac{\pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{k_3^2}\\&+\frac{\mu _1}{9}-\frac{\mu _2}{3}\bigg )k_3^2+2 \delta k_4 \pi \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )\\&+ \pi \delta \pi k_4^2\bigg )(1+n)\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6n-6}{2n+1}}\\&-6\bigg (n+\frac{1}{3}\bigg )k_3 { w}\bigg (\bigg (\frac{4 n^2 \mu _1}{9}+\bigg (\frac{4 \mu _1}{9}-\frac{2 \mu _2}{3}\bigg )n\\&+t^2 \pi \delta +\frac{\mu _1}{9}-\frac{\mu _2}{3}\bigg )k_3^2\\&+2 \delta k_4 \pi \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )+ \pi \delta \pi k_4^2\bigg )\\&k_9^2\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-18n-6}{2n+1}}-2\bigg (\bigg (\frac{2 n^2 \mu _1}{9}+\bigg (\frac{2 \mu _1}{9}-\frac{ \mu _2}{3}\bigg )n\\&+\frac{\pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{k_3^2} +\frac{\mu _1}{18}-\frac{\mu _2}{6}\bigg )k_3^2\\&+2 \delta k_4 \pi \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )+ \pi \delta \pi k_4^2\bigg )\\&\bigg (k_3^2\big (k_6^2-4n-1\big )\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-6n}{2n+1}}\\&-2\bigg (\frac{a_0}{1+z}\bigg )^{\frac{-6-18n}{2n+1}}{ w}k_9^2\bigg )k_3\bigg )\Bigg ). \end{aligned}\right\} \end{aligned}$$

(53)

Fig. 7

EoS parameter $(\omega _{de})$ against redshift (z)

Fig. 8

$\omega _{de}-\omega _{de}'$ plane

Using Eqs. (31), (36) and (50), we obtain the density parameter of RHDE as

$$\begin{aligned} \Omega _{de}=\frac{\bigg (d^2 k_3^4 \big (2 \mu _1 n+\mu _1-3 \mu _2\big )^2 \bigg (\frac{a_0}{1+z}\bigg )^\frac{6}{2n+1}\bigg )}{\Bigg (k_3^2 \big (\frac{a_0}{1+z}\big )^2 \bigg (\bigg (\bigg (n+\frac{1}{2}\bigg )^2\mu _1+\frac{9 \pi \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )^2}{4k_3^2}-\frac{3 n \mu _2}{2}-\frac{3\mu _2}{4}\bigg )k_3^2+\frac{9 \pi k_4 \delta \bigg (\bigg (\frac{a_0}{1+z}\bigg )^{\frac{3}{2n+1}}-k_4\bigg )}{2}+\frac{9 \pi \delta k_4^2}{4}\bigg )\Bigg )}. \end{aligned}$$

(54)

Fig. 9

Density parameter $(\Omega _{de})$ against redshift (z)

Fig. 10

Density parameter $(\Omega _{de})$ against redshift (z)

In this section, we deal with the characteristics of the fundamental quantities of the Universe, such as RHDE’s energy density ($\rho _{de}$), energy density of matter ($\rho _{m}$), EoS parameter ($\omega _{de}$), and density parameter ($\Omega _{de}$). In defining a density parameter, one has to take into account the relation among the critical density ($\rho _{c}=\frac{3H^2}{8 \pi }$) and the observed density ($\rho _{de}$) of the Marder Universe. In our model, the physical parameters are chosen to be constants with the following choices: $k_3=6.35$,  $k_4=9.33,$ $H_0=0.53$, $k_6=3$, $k_9=5$, ${ w}=10.36$, $\mu _1=0.15,$ $\mu _2=0.84.$ $n=0.410,\,0.411,\,0.412$,   $\delta =0.021,\,0.025,\,0.030$ , $d=0.0015,$ $c_0=0.1$, $a_0=5000000$, $c_2=0.25$, $c_1=0.15$. By taking different values of n and $\delta$ for Hubble and GO horizon cutoffs, while keeping the other parameters as it is. We have plotted RHDE energy density $(\rho _{de})$, matter energy density $(\rho _{m})$ and density parameter ($\Omega _{de}$) against the redshift (z) as shown in Figs. 1, 2, 5 and 6,9 and 10 respectively. It is observed that, for various values of $\delta$ and n the graphs of $\rho _{de}$, $\rho _{m}$ and $\Omega _{de}$ show a positive and decreasing behavior towards redshift (z). This reflects that our Universe is expanding at an accelerated rate.

3.3 EoS parameter ($\omega _{de}$):

In the RHDE model, the EoS parameter $\omega _{de}$ is calculated as $\frac{p_{de}}{\rho _{de}}$. The EoS parameter provides the most effective explanation for the expansion of the Universe (Amendola and Tsujikawa [88]). Also, the accelerated and decelerated phases of the cosmos can be categorized with the help of EoS parameter. The following eras are the phases of dominate dark energy: (i) $\omega _{de}=1$ $\Rightarrow$ stiff fluid, (ii) $0<\omega _{de}<\frac{1}{3}$ $\Rightarrow$ radiation dominated phase,(iii) $\omega _{de}>1$ $\Rightarrow$ Ekpyrotic phase, (iv) $\omega _{de}=0$ $\Rightarrow$ non-relativistic matter, (v) $-1<\omega _{de}<\frac{-1}{3}$ $\Rightarrow$ quintessence, (vi) $\omega _{de}=-1$ $\Rightarrow$ cosmological constant, (vii) $\omega _{de}<-1$ $\Rightarrow$ phantom. We investigated the evolution of EoS parameter $\omega _{de}$ against redshift (z) with different values of $\delta$ and n for Hubble, GO horizon cutoff as shown in Figs. 3 and 7 respectively. It is observed from Figs. 3 and 7 that the EoS parameter begins from the quintessence phase and transits to the phantom region passing through the vacuum dominated era (phantom divide line $\omega _{de} =-1$) of the Universe for all the values of $\delta$ and n. As a result, the Universe has a quintom like nature and the path of the EoS parameter of RHDE-H and GO models are in accordance with the results of the Planck collaboration (2018). Planck collaboration data (2018) by Aghanim et al. [89] gives limits for EoS parameter as

$$\begin{aligned}{} & {} \omega _{de}=-1.56_{-0.48}^{+0.60} (Planck + TT + lo{ w}E)\\{} & {} \omega _{de}=-1.58_{-0.41}^{+0.52} (Planck + TT, EE + lo{ w}E)\\{} & {} \omega _{de}=-1.57_{-0.40}^{+0.50} (Planck + TT, TE, EE + lo{ w}E+lensing) \\{} & {} \omega _{de}=-1.04_{-0.10}^{+0.10}\\{} & {} \quad (Planck + TT, TE, EE + lo{ w}E+lensing+BAO). \end{aligned}$$

3.4 Analysis of the $\omega _{de}-\omega _{de}'$ pair

Many dark energy models have been developed over the years to elucidate the accelerated expansion of the Cosmos. Phase plane evaluation as proposed by Caldwell and Linder [90] is one of the most useful tools in separating dark energy models. The derivative of the EoS parameter $\omega _{de}$ with respect to $\ln a$ is referred as $\omega _{de}'$. Besides, $\omega _{de}-\omega _{de}'$ plane can be divided into two parts which are known as thawing $(\omega _{de}<0,\,\, \omega _{de}'>0)$ and freezing $(\omega _{de}< 0,\,\, \omega _{de}'< 0)$ regions. In freezing regions, cosmic expansion occurs at an accelerated rate compared with thawing regions. As shown in Figs. 4, 5, 6, 7 and 8, $\omega _{de}-\omega _{de}'$ planes corresponding to Hubble, GO horizons with different values of $\delta$ and n. It is observed that they lie in the freezing region $(\omega _{de}<0,\,\, \omega _{de}'<0 )$ for all values of $\delta$ and n. The $\omega _{de}-\omega _{de}'$ plane corresponding to Hubble, GO horizon cutoffs with different values for $\delta$ and n, fits closely with observational data (Ade et al. [91]; Hinshaw et al. [92]):

$$\begin{aligned}{} & {} \omega _{de}=-1.13_{-0.25}^{+0.24}, \omega _{de}'<1.32 (Planck + WP + BAO)\\{} & {} \omega _{de}=-1.34_{-0.18}^{+0.18}, \omega _{de}'\\{} & {} \quad =0.85\pm 0.7 (WMAP + eCAMB+BAO+H_0) \\{} & {} \omega _{de}=-1.17_{-0.12}^{+0.13}, \omega _{de}'\\{} & {} \quad =0.85_{-0.49}^{+0.50} (WMAP+eCAMB+BAO+H_0+SNe). \end{aligned}$$

4 Stability analysis

Our Analysis is based on perturbation technique to ensure the stability of the exact or approximated background solution. Perturbations of the fields of the gravitational system is compared to the background evolutionary solution (Chen and Kao [93], Sharma et al. [94]). In this work our focus will be on the stability of the background solution under perturbations of the metric. All the three expansion factors $a_1$, $a_2$ and $a_3$ will be considered for possible perturbations through this method.

$$\begin{aligned} a_{\nu }\rightarrow a_{B_\nu }+\delta a_{\nu }=a_{B_\nu } \bigg (1+a_{b_\nu }\bigg ). \end{aligned}$$

(55)

For convenience, we will be focusing on the inputs $\delta b_\nu$, in place of $\delta a_\nu$. Hence, the volume scale factor can be perturbed as $V_B=\prod _{\nu =1}^{3} a_\nu$, directional Hubble factors $\theta _\nu =\frac{\dot{a_\nu }}{a_\nu }$ as well as the average Hubble factor $\theta =\sum _{\nu =1}^{3}=\frac{\theta _\nu }{3}=\frac{\dot{V}}{3V}$. As a result, the following can be demonstrated as

$$V \to V_{B} + V_{B} \sum\limits_{\nu } \delta b_{\nu } ,\theta _{\nu } \to \theta _{{B_{\nu } }} + \sum\limits_{\nu } \delta b_{\nu } ,\theta \to \theta _{B} + \frac{1}{3}\sum\limits_{\nu } \delta b_{\nu } .$$

(56)

The metric perturbations seem to be $\delta b_\nu$ and it obeys the following equations at linear orders in $\delta b_\nu$

$$\begin{aligned}{} & {} \sum _\nu \delta \ddot{b}_\nu +2 \sum _\nu \theta _{B_\nu } \delta \dot{b_\nu }=0. \end{aligned}$$

(57)

$$\begin{aligned}{} & {} \delta \ddot{b_\nu }+\frac{\dot{V_B}}{V_B} \delta \dot{b_\nu }+\sum _{\nu _1}\delta \dot{b_{\nu _1}}\theta _{B_\nu }=0. \end{aligned}$$

(58)

$$\begin{aligned}{} & {} \sum \delta \dot{b_\nu }=0. \end{aligned}$$

(59)

We can easily calculate the following information from the above three equations

$$\begin{aligned} \delta \ddot{b_\nu }+\frac{\dot{V_B}}{V_B} \delta \dot{b_\nu }=0. \end{aligned}$$

(60)

where $V_B$ is the background volume scale factor. In our case, $V_B$ is given by

$$\begin{aligned} V_B=\bigg (tk_3+k_4\bigg )^{2n+1}. \end{aligned}$$

(61)

According to Eqs. (60) and (61), the metric perturbation is

$$\begin{aligned} \delta b_\nu =c_2-\frac{c_1}{2n k_3 \bigg (t k_3+k_4\bigg )^{2n}}, \end{aligned}$$

(62)

the constants $c_1$ and $c_2$ represent integration constants. Hence, the actual fluctuations for each expansion factor $\delta a_{\nu }=a_{B_\nu } \delta b_{\nu }$ are expressed as

$$\begin{aligned}{} & {} \delta a_{\nu }=c_2\bigg (t k_3+k_4\bigg )^{\frac{2n+1}{3}}-\frac{c_1 }{2n k_3 \bigg (t k_3+k_4\bigg )^{\frac{4n-1}{3}}}. \end{aligned}$$

(63)

$$\begin{aligned}{} & {} \delta a_{\nu }=c_2\bigg (\frac{a_{0}}{1+z}\bigg )-\frac{c_1 \bigg (\frac{a_{0}}{1+z}\bigg )^{\frac{1-4n}{2n+1}}}{2n k_3 }. \end{aligned}$$

(64)

According to Eq. (64), the $\delta a_\nu$ approaches to zero as $z\rightarrow \infty$, i.e.,  $\delta a_{\nu } \rightarrow 0$. As a result, the solution to the background problem is stable in the presence of the metric perturbation.

Fig. 11

Om(z) against redshift (z)

5 Om-diagnostic

In separating the Universe into its various phases, Sahni et al. [95] developed the Om-diagnostic, which complements the state-finder parameters, allowing for the interpretation of the current matter density contrast to Om(z) within the context of various models of the Universe. In addition, it is a geometric diagnostic that explicitly considers the Hubble parameter (H) and redshift (z).

Let us define the Om diagnostic function as follows:

$$\begin{aligned} \text {Om}(z)=\frac{H^2(z)-H^2_0}{H^2_0((1+z)^3-1)}. \end{aligned}$$

(65)

Here, $H_0$ represents the current value of the Hubble parameter. By analyzing the first derivative of the scale factor, the Om(z) function is easier to reconstruct than state-finder parameters. Dynamical dark energy on the basis of the fact that they are distinct from the cosmological constant, the slope of Om(z), with or without regard to the matter density. It could be said that the constant behavior of Om(z) with respect to z demonstrates that dark energy is the cosmological constant $(\Lambda CDM)$. According to the positive slope of Om(z), dark energy behaves like a phantom $(\omega _{de}<-1)$, while the negative slope means that dark energy behaves like a quintessence $(0>\omega _{de}>-1)$. We plotted Om(z) versus redshift (z) in Fig. 11. We observe that the slope of Om(z) is positive, so that the Om-diagnostic indicates a phantom region.

6 Kinematical tests

One can extend phenomenological analysis to arbitrary redshifts by using the formula in Eq. (29). For our obtained model, we derive kinematical relations such as the look-back time, luminosity distance, angular diameter distance, and distance modulus.

• Look-Back time: In astronomy, the look-back time is the point in the past when a distant object emits its light. Based on the dynamics of the Universe, light (the look back time $\triangle t=t_0-t$) was emitted a long time ago. The radiation travel time for a photon emitted by a source at instant t and received at $t_0$ is

  $$\begin{aligned} \triangle t= \int _{a}^{a_0}\frac{da}{\dot{a}}, \end{aligned}$$

  (66)

  where $a_0$ is the present scale factor of the Universe. The scale factor a(t) corresponds to $a_0$ for a given redshift z as

  $$\begin{aligned} 1+z=\frac{a_0}{a}=\left( \frac{k_3t_0+k_4}{k_3t+k_4}\right) ^{\frac{2n+1}{3}}. \end{aligned}$$

  (67)

  The above equation provides

  $$\begin{aligned} H_0 (t_0-t)=\frac{2n+1}{3}\left[ 1-(1+z)^{\frac{-3}{2n+1}}\right] . \end{aligned}$$

  (68)

  It is believed that at the present time, $H_0$ is Hubble’s constant, which is approximately in the range 50 to $100 kms^{-1} Mpc^{-1}$. In this regard, the Hubble constant’s reciprocal is known as the Hubble time $T_H$ $i.e., T_H=H_0^{-1}$, where $T_H$ is measured in s and $H_0$ in $s^{-1}$. Limit $z \rightarrow \infty$ in Eq. (68), the age of the Universe (extrapolated from the Big Bang) is

  $$\begin{aligned} t_0=\frac{(2n+1)H_0^{-1}}{3}=\frac{(2n+1)T_H}{3}\simeq \frac{2}{3}T_H. \end{aligned}$$

  (69)

• Luminosity Distance: In order to determine a light source’s luminosity distance, you need to divide the total energy flux L by the total apparent luminosity l, $\left( d^2_L=\frac{L}{(4\pi l)}\right)$. The luminosity distance is calculated by generalizing the inverse square law of brightness from static Euclidean space to a curved space by using the expression (Waga [96]):

  $$\begin{aligned} d_L=c_0\left( 1+z\right) r_1(z). \end{aligned}$$

  (70)

  The radial coordinate distance of an object is $r_1(z)$, and is as expressed

  $$\begin{aligned} r_1(z)=\int _{t}^{t_0}\frac{dt}{a}. \end{aligned}$$

  (71)

  From (29), (70) and (71), we get

  $$\begin{aligned} d_L=\frac{3c_0^{\frac{3}{n+1}}}{k_3(2-2n)}\left( \frac{k_3 (2n+1)}{3 H_0}\right) ^{\frac{2-2n}{3}}\left[ (1+z)-(1+z)^{\frac{3}{2n+1} }\right] . \end{aligned}$$

  (72)

• Angular diameter distance: According to Hogg [97] and Rudra [98], at a proper distance $(r_1(z))$ D relative to $t_0$, the angular diameter of a light source is defined as follows:

  $$\begin{aligned} \delta =\frac{D(1+z)^2}{d_L}. \end{aligned}$$

  (73)

  In order to calculate diameter distance, we need to divide the diameter of the source by the angular diameter (in radians), so we shall define the diameter distance $d_A$ as,

  $$\begin{aligned} d_A=\frac{D}{\delta }=d_L(1+z)^{-2}. \end{aligned}$$

  (74)

  For our model the angular diameter distance $d_A$ is given by

  $$\begin{aligned}{} & {} d_A=\frac{3c_0^{\frac{3}{n+1}}}{k_3(2-2n)}\left( \frac{k_3 (2n+1)}{3 H_0}\right) ^{\frac{2-2n}{3}}\nonumber \\{} & {} \quad \left[ (1+z)^{-1}-(1+z)^{\frac{1-4n}{2n+1} }\right] . \end{aligned}$$

  (75)

• Distance Modulus: The distance modulus $D_M$ is given by

  $$\begin{aligned} \begin{aligned} D_M&=5 \log (d_L)+25\\&=5\log \left( \frac{3c_0^{\frac{3}{n+1}}}{k_3(2-2n)}\left( \frac{k_3 (2n+1)}{3 H_0}\right) ^{\frac{2-2n}{3}}\left[ (1+z)-(1+z)^{\frac{3}{2n+1} }\right] \right) +25. \end{aligned} \end{aligned}$$

  (76)

  In Figs. 12, 13 and 14 we have plotted luminosity distance $(d_L)$, angular diameter $(d_A)$ and distance modules $(D_M)$ versus redshift (z) respectively. It is observed that the trajectories of luminosity distance $(d_L)$, angular diameter $(d_A)$ and distance modules $(D_M)$ are varying in positive region, which indicates that these results are more compatible with recent observations. Also, we observe that for different values of n the trajectories of $d_{L}$, $d_{A}$ & $D_{M}$ are decreasing with decreases of redshift i.e.,  decreases as time increases which is nearly equally to present observational data.

Fig. 12

Plot of luminosity distance $(d_L)$ against redshift (z)

Fig. 13

Plot of angular diameter $(d_A)$ against redshift (z)

Fig. 14

Plot of distance modulus $(D_M)$ against redshift (z)

In this work, we have examined the RHDE model with SBT by using spatially homogeneous and anisotropic Marder type space time. To the best of our knowledge, this is the first time that RHDE with SBT in an anisotropic background like Marder type Universe. Indeed, all previous studies are framed in the standard homogeneous and isotropic FRW Universe. In this sense, all the results obtained in the present analysis are novel, as they account for anisotropic effects in the evolution of the Universe. By assuming the Hubble radius as an IR cutoff, we have investigated some cosmological quantities like the RHDE energy density ($\rho _{de}$), matter energy density ($\rho _{m}$), EoS $(\omega _{de})$, $\omega _{de}-\omega _{de}'$ plane, RHDE density parameter ($\Omega _{de}$), stability analysis through perturbation, Om-diagnostic, and kinematical tests, which are functions of the redshift (z). In this study, these parameters are plotted against the redshift (z) and discussed their agreement with recent findings. For three various numbers of n and $\delta$, the EoS parameter exhibits quintom-like behavior for both IR cut-offs. We then look into the $\omega _{de}-\omega _{de}'$ plane and stability of the dark energy model by using a metric perturbation method. It has been found that quintom-like behavior and freezing region explain the Universe’s accelerating rate of growth. Among the main advantages over other descriptions of dark energy, we have shown that our model correctly reproduces the current accelerating phase of the cosmos. Now, we present a comparative analysis of our work with the recent works on this RHDE which is given below:

Maity and Debnath [50] have investigated Tsallis, Rényi and Sharma-Mittal holographic and new agegraphic dark energy models in D-dimensional fractal Universe. We noticed that the EoS parameter of our model is consistent and $\omega _{de}-\omega _{de}'$ plane is inconsistent with the results of Maity and Debnath ([50]). Sharma and Dubey [51] have investigated Rényi holographic dark energy with Hubble horizon cutoff in the Brans Dicke cosmology. We observe that our EoS parameter is consistent for RHDE with Hubble horizon cutoff. Jawad et al. [52] have explored Tsallis, Rényi and Sharma-Mittal holographic dark energy models in Loop Quantum Cosmology with Hubble horizon cutoff. We observe that our EoS parameter is consistent, $\omega _{de}-\omega _{de}'$ plane have quite opposite behavior for RHDE with Hubble horizon cutoff. Younas et al. [99] have investigated cosmological implications of the generalized entropy based holographic dark energy models in dynamical Chern-Simons modified gravity with Hubble horizon cutoff. We noticed that the EoS parameter is consistent and $\omega _{de}-\omega _{de}'$ plane have opposite behavior for RHDE with Hubble horizon cutoff. Iqbal and Jawad [100] have discussed Tsallis, Rényi and Sharma-Mittal holographic dark energy models in DGP brane-world with Hubble horizon cutoff. We noticed that the EoS parameter of RHDE with Hubble horizon cutoff is consistent the results of Iqbal and Jawad [100], whereas $\omega _{de}-\omega _{de}'$ plane of RHDE with Hubble horizon cutoff has opposite behavior. Luciano [101] has studied Saez–Ballester gravity in Kantowski-Sachs Universe filled up with BHDE and dark matter by assuming the Hubble radius as an IR cutoff and also investigated both the cases of non-interacting and interacting dark energy scenarios. We observe that BHDE $\rho _{de}$ for the non-interacting model varies in positive regions and is consistent with our results. The behavior of BHDE EoS parameter for both non-interacting and interacting is consistent with our results. Also, the behavior of BHDE $\omega _{de}-\omega _{de}'$ plane for both non-interacting and interacting are consistent with the results. The stability of both non-interacting and interacting models are unstable whereas in our case we have obtained the stable behavior.

7 Conclusion

In this work, we discuss some of the possible consequences of RHDE model with Marder type space time with two IR cutoffs: Hubble horizon $L=\frac{1}{H}$ and GO horizon $L=\big (\mu _1 H^2+\mu _2 \dot{H}\big )^{\frac{-1}{2}}$ cutoffs, in the framework of SBT of gravitation. For this purpose, we have analyzed cosmological features associated with both the IR cutoffs including energy density of RHDE ($\rho _{de}$), energy density of matter ($\rho _{m}$), EoS parameter $(\omega _{de})$, $\omega _{de}-\omega _{de}'$ plane, density parameter of RHDE ($\Omega _{de}$), Om-diagnostic, stability analysis and kinematical tests. Briefly, we summarize our results:

The obtained model (28) is anisotropic and expanding with passage of time t. For both IR cutoffs ($i.e., \text {Hubble and GO}$) energy density of matter ($\rho _{m}$) and energy density of RHDE ($\rho _{de}$) are positive throughout evolution of the Universe. It is shown that in both IR cutoffs, the path of the EoS parameter ($\omega _{de}$) displays the evolution from the quintessence to the phantom region of the Universe, $\omega _{de}-\omega _{de}'$ plane lies in freezing region and the Om-diagnostic gives phantom region. It is also observed that both IR cutoffs have a positive density parameter of RHDE ($\Omega _{de}$) throughout the evolution. Using perturbation analysis, we have examined the stability of the DE model and found that RHDE demonstrates a greater stability during cosmic evolution. Therefore model (28) is stable. It is also tested kinematically with the findings of look-back time $(\triangle t)$, luminosity distance $(d_L)$, angular diameter distance $(d_A)$, and distance modulus $(D_M)$.