Viscous holographic dark energy cosmological model in general relativity

Abstract

In this article, we analyze Marder-type space-time in the framework of general relativity theory, with viscous holographic dark energy. To solve the field equations, we use the shear scalar $(\sigma )$ is proportional to the expansion scalar $(\theta )$ which leads to a relation between metric potentials and hybrid expansion law (HEL) proposed by Akarsu et al. (J Cosmol Astropart Phys 01:022, 2014). Also, we determine the cosmological parameters, namely the deceleration parameter(q), jerk parameter (j), statefinder parameters $(r-s)$, equation of state parameter ($\omega _{\text {de}}$) and $\omega _{\text {de}}-\omega '_{\text {de}}$ plane for the obtained model. The derived model supports the accelerating behavior of the Universe along with the null, weak and dominant energy conditions that are obeyed by violating strong energy condition as per the present accelerated expansion.

1 Introduction

Researchers are always keen to study the early evolution of the Universe. Current cosmological observations have revealed that our current Universe is experiencing rapid expansion. The main reason for this cosmic acceleration is an exotic force with tremendous negative pressure called ‘dark energy’(DE). Dark energy which is defined as the exotic negative pressure causing the accelerated expansion of the Universe [1, 2] is attracting the attention of several researchers in recent years. The cosmological analysis of these observations suggests that the Universe consists of about 70% DE, 30% dust matter (cold dark matter plus baryons), and negligible radiation. It is a widely accepted idea that dark energy leads to the ultimate-rapid expansion of the Universe. However, the nature of such a DE is still a source of debate. Several theoretical models have been proposed to explain this late-time acceleration of the Universe. The most obvious theoretical candidate for DE is the cosmological constant [3], which has the equation of state (EoS) $\omega _{\text {de}}=-1$. However, it suffers from a cosmological constant (CC) problem (fine-tuning problem) and a cosmic coincidence problem [4,5,6]. Both of these problems are related to DE density. Two ways have been suggested to explain this mysterious concept. One way is to construct dark energy models, and the other one is to modify the geometrical part of Einstein’s field equations which is known as modified gravity theory to study the corresponding anisotropic dark energy cosmological models. In the literature, various kinds of research on DE patterns have appeared to explain this mysterious concept of DE. In particular, Arun et al. [7] have discussed reviews of the different possible candidates for DM including exotic candidates and their possible detection and, also, cover the different models for DE and the possibility of unified models for DM and DE. Significant dynamical DE models among them are scalar field models such as quintessence [8], Phantom [9], tachyon field [10], quintom [11], Chaplygin gas [12], $k-$essence [13, 14], agegraphic dark energy [15, 16] and holographic DE model [17] have been proposed to explain the nature of DE phenomenon.

Among the various dynamic dark energy models, in particular, the HDE model has become a convenient technique in recent times to study the dark energy mystery. In recent years, considerable interest has been noticed in the study of the holographic dark energy (HDE) model to explain the recent phase transition of the Universe as well as a viable candidate to explain the problems of modern cosmology. The HDE models explain the recent accelerated expansion as well as the coincidence problem of the Universe [18, 19]. The concept of HDE is based on the holographic principle proposed by ’t Hooft [20] and found its roots in the quantum field theory. According to the holographic principle, the short-distance (ultraviolet) cut-off is related to the long-distance (infrared) cut-off L due to a limit determined by the formation of the black hole [17]. The infrared (IR) cut-off is relevant to the large-scale structure, and the UV cut-off is relevant to the vacuum energy of the cosmos, i.e.,  Hubble horizon, particle horizon, event horizon, Ricci scalar, etc. In the development of the holographic principle, this is crucial if a black hole forms and then evaporates [21]. When the vacuum energy of a black hole is less than the mass of the black hole, the IR cut-off L is chosen by saturating the inequality, resulting in the obtained vacuum energy being known as holographic dark energy (HDE) [22]. However, the HDE event horizon model is not compatible with the age of some old high redshift objects [23]. To avoid this problem, a new HDE model was proposed by Granda and Oliveros [24] which contains a new IR cut-off and the local quantities of the Hubble and the time derivative of the Hubble scale. Recently, Hatkar et al. [25] have discussed viscous holographic dark energy in Brans–Dicke theory of gravitation. Very recently, Singh and Srivastava [26] have studied new holographic dark energy model with bulk viscosity in f(R, T) gravity.

Universe evolution involves a sequence of dissipative processes. Bulk viscosity, shear viscosity, and heat transport are included in these processes. To be more realistic, the perfect fluid Universe is just an approximation of the viscous Universe. Misner [27] was the first to use the viscosity concept in cosmology. The origin of the bulk viscosity in a physical system can be traced to deviations from the local thermodynamic equilibrium [28, 29]. In a cosmological fluid, the bulk viscosity arises at any time when a fluid expands ( or contracts) too rapidly so that the system does not have enough time to restore the local thermodynamic equilibrium [30]. In Weinberg [31], the theoretical concept of bulk viscosity in cosmology has been discussed which provides insight into the nature of bulk viscosity. Within the context of early inflation, it has been known since a long time ago that an imperfect fluid with bulk viscosity can produce an accelerated expansion without the need for a cosmological constant or some other inflationary scalar field [32, 33]. An accelerating Universe can be achieved with the right viscosity coefficient. At the late time, since we do not know the nature of the Universe’s contents (dark matter and dark energy components) very clearly, the bulk viscosity is reasonable and can play a role as a dark energy candidate. Therefore, it is natural to consider the bulk viscosity in an accelerating Universe. It has been shown that inflation and recent acceleration can be explained using the viscous behavior of the Universe and play an important role in the phase transition of the Universe [34,35,36,37,38,39,40,41]. The concept of viscous DE has been discussed extensively in the literature [42,43,44]. Feng and Li [45] have shown that the age problem of the Ricci dark energy can be alleviated using the bulk viscosity, and Chakraborty and Chattopadhyay have studied in ref [46] cosmology of a generalized version of holographic dark energy in the presence of bulk viscosity and its inflationary dynamics through slow roll parameters in the general theory of relativity. Several authors worked on the general theory of relativity with different metrics [47,48,49,50]. (We have simply mentioned a few of them.)

The small anisotropies observed in the cosmological observations such as microwave background radiation (Dunkley et al. [51]) and large-scale structures (Tegmark et al. [52]) indicate that a pure Friedmann–Robertson–Walker model could not explain all the properties of the Universe. It is therefore natural to consider anisotropic cosmological models which are useful to describe the early Universe. Anisotropic Universe means the physical properties of the Universe have different values when measured in different directions. However, in the early stages of the evolution of the Universe, it is generally accepted that the Universe is homogeneous and anisotropic. For this reason, homogeneous and anisotropic models must be studied. We prefer the Marder-type space-time in a scalar–tensor theory because it is a homogeneous and anisotropic space-time (a nice metric to explain anisotropy at the beginning of the Universe) and provides a transition from anisotropic to isotropic. Using $t\rightarrow \int A(t) \textrm{d}t$ coordinate transformation, Marder-type Universe transforms to Bianchi type I Universe model. Bianchi-type models are anisotropic and spatially homogeneous and have been extensively used to investigate cosmological models to describe the early stages of the evolution of the Universe in the presence of various physical distributions of matter. This indicates that these models are more a realistic picture of past eras in the history of the Universe. Recently, the investigation of the magnetized string distribution in the Marder-type Universe with the cosmological term in f(R, T) theory was done by Cihan Kömürcü and Aktas [53]. Some other authors have discussed this Marder-type cosmological model given in the literature [54,55,56,57,58,59].

By the above works, we focus our attention on the Marder-type cosmological model with viscous holographic dark energy (VHDE) in the framework of the general theory of relativity. This paper is organized as follows: In Sect. 2, we obtain metric and field equations. In Sect. 3, we derive the solution of the Marder-type models. In Sect. 4, we investigate the cosmological parameters and their physical discussion is presented. We summarize the results in the last section.

2 Metric and field equations

We consider the spatially homogeneous and anisotropic Marder-type space-time is as follows

$$\begin{aligned} \text {d}s^2=b_{1}^{2} \text {d}x^2+b_{2}^{2}\text {d}y^2+b_{3}^{2}\text {d}z^2-b_{1}^{2}\text {d}t^2, \end{aligned}$$

(1)

where $b_{1}$, $b_{2}$ and $b_{3}$ are functions of time t only. As our intention is to study the behavior of physical parameters which are useful in finding the solution of the field equations for Marder-type space-time given by Eq. (1).

• The volume V and average scale factor a(t) of the Marder-type space-time are defined as

  $$\begin{aligned} V = [a(t)]^3 =b^{2}_{1}b_{2}b_{3}. \end{aligned}$$

  (2)

• The anisotropic parameter ${\mathcal {A}}_h$ is given by

  $$\begin{aligned} {\mathcal {A}}_h=\frac{1}{3}\sum _{i=1}^{3}\left( \frac{H_i-H}{H}\right) ^2, \end{aligned}$$

  (3)

  where $H_1=\frac{\dot{b_{1}}}{b_{1}}$,  $H_2=\frac{\dot{b_{2}}}{b_{2}}$,  $H_3=\frac{\dot{b_{3}}}{b_{3}}$ are directional Hubble’s parameters and $H=\frac{{\dot{a}}}{a}$ is the Hubble’s parameter. Here and after an overhead dot denotes differentiation with respect to cosmic time t.

• The expansion scalar $(\theta )$ is given by

  $$\begin{aligned} \theta =u^i;_i=\frac{1}{b_{1}}\left( \frac{2\dot{b_{1}}}{b_{1}}+\frac{\dot{b_{2}}}{b_{2}}+\frac{\dot{b_{3}}}{b_{3}}\right) . \end{aligned}$$

  (4)

• The shear scalar $(\sigma ^2)$ is given by

  $$\begin{aligned} \sigma ^2=\frac{1}{2}\left( \sum _{i=1}^{3}H_i^2-\frac{\theta ^2}{3}\right) . \end{aligned}$$

  (5)

The field equations of Einstein general theory of relativity are

$$\begin{aligned} G_{ij}=- T_{ij}, \end{aligned}$$

(6)

where $G_{ij}=R_{ij}-\frac{1}{2}Rg_{ij}$ is an Einstein tensor, and $T_{ij}$ is the energy–momentum tensor. Also, the conservation equation is given by

$$\begin{aligned} T^{ij}~ _{;j}=0. \end{aligned}$$

(7)

The energy–momentum tensor for a viscous holographic dark energy is taken as,

$$\begin{aligned} T_{ij}=T_{ij}^m+T_{ij}^h. \end{aligned}$$

(8)

Here $T_{ij}^{m}$ and $T_{ij}^{h}$ represent matter and viscous holographic dark energy tensors given by

$$\begin{aligned} T_{ij}^h= & {} \left( {\bar{P}}_h+\rho _h\right) U_i^hU_j^h+{\bar{P}}_hg_{ij}, \end{aligned}$$

(9)

$$\begin{aligned}{} \& \quad T_{ij}^m= & {} \rho _m U_i^m U_j^m, \end{aligned}$$

(10)

where $\rho _m$ is the energy density of the matter, ${\bar{P}}_h$ and $\rho _h$, respectively, represent the pressure and energy density of the viscous holographic dark energy; $U_i$ denotes the co-moving velocity vector of the matter and viscous holographic dark energy satisfying $U_i U^i=-1$. VHDE pressure satisfies the relation ${\bar{P}}_h=P_h-3\zeta H$ with $\zeta =\zeta _0+\zeta _1H$, where $\zeta _0$ and $\zeta _1$ are positive constants, and H is the Hubble parameter.

Now with the help of Eq. (8), the field Eq. (6) for the metric in Eq. (1) can be written as

$$\begin{aligned} \frac{1}{b_{1}^2}\left( \frac{\ddot{b_{2}}}{b_{2}}+\frac{\ddot{b_{3}}}{b_{3}}+\frac{\dot{b_{2}}\dot{b_{3}}}{b_{2}b_{3}}-\frac{\dot{b_{1}}\dot{b_{2}}}{b_{1}b_{2}}-\frac{\dot{b_{1}}\dot{b_{3}}}{b_{1}b_{3}}\right) =&-{\bar{P}}_h, \end{aligned}$$

(11)

$$\begin{aligned} \frac{1}{b_{1}^2}\left( \frac{\ddot{b_{1}}}{b_{1}}+\frac{\ddot{b_{3}}}{b_{3}}-\frac{\dot{b_{1}}^2}{b_{1}^2}\right) =&-{\bar{P}}_h, \end{aligned}$$

(12)

$$\begin{aligned} \frac{1}{b_{1}^2}\left( \frac{\ddot{b_{1}}}{b_{1}}+\frac{\ddot{b_{2}}}{b_{2}}-\frac{\dot{b_{1}}^2}{b_{1}^2}\right) =&-{\bar{P}}_h, \end{aligned}$$

(13)

$$\begin{aligned}{} \& \quad \frac{1}{b_{1}^2}\left( \frac{\dot{b_{1}}\dot{b_{2}}}{b_{1}b_{2}}+\frac{\dot{b_{2}}\dot{b_{3}}}{b_{2}b_{3}}+\frac{\dot{b_{3}}\dot{b_{1}}}{b_{3}b_{1}}\right) =&\rho _{m}+\rho _{h}. \end{aligned}$$

(14)

Also, the energy conservation equation leads to

$$\begin{aligned} {\dot{\rho }}_{m}+\left( \frac{\dot{b_{1}}}{b_{1}}+\frac{\dot{b_{2}}}{b_{2}}+\frac{\dot{b_{3}}}{b_{3}}\right) \rho _{m}=&0, \end{aligned}$$

(15)

$$\begin{aligned}{} \& \quad {\dot{\rho }}_{h}+\left( \frac{\dot{b_{1}}}{b_{1}}+\frac{\dot{b_{2}}}{b_{2}}+\frac{\dot{b_{3}}}{b_{3}}\right) \left( \rho _{h}+{\bar{P}}_h\right) =&0. \end{aligned}$$

(16)

3 Solution of the field equations

The field Eqs. (11)–(14) are a system of four independent equations with six unknown variables:  $b_{1}$, $b_{2}$, $b_{3}$, $\rho _{h}$, $\rho _{m}$ and ${\bar{P}}_{h}$. Therefore, we consider the following additional conditions to solve the above set of equations:

• The shear scalar $(\sigma )$ is proportional to the expansion scalar $(\theta )$, which leads to a relationship between the metric potentials (Collins et al. [60]). That is

  $$\begin{aligned} b_{1}=(b_{2}b_{3})^{n}, \end{aligned}$$

  (17)

  where $n\ne 1$ is a positive constant and preserves the anisotropic character of the space-time.

• We consider hybrid expansion law (HEL) of the scale factor a(t), given by (Akarsu et al. [61])

  $$\begin{aligned} a(t)=t^{\nu }e^{t\mu }, \end{aligned}$$

  (18)

  where $\nu$ and $\mu$ are positive constants. The above form of the scale factor is more generalized as it is the product of both exponential and power functions of cosmic time t. The main purpose of choosing this scale factor is that the smooth transition from the early deceleration phase to the late time inflation of the Universe can be observed in the model. Also, this preferred average scale factor leads to a time-dependent deceleration parameter. Santhi et al. [62, 63], Mishra et al. [64], Yadav et al. [65], Santhi et al. [66], Singh et al. [67], Santhi and Naidu [68], Yadav et al. [69] are some of the authors who have investigated various DE models in different theories by taking this HEL.

From Eqs. (12) and (13), we have

$$\begin{aligned} b_{2}=\gamma _1^2b_{3}, \end{aligned}$$

(19)

where $\gamma _1^2\ne 1$ is a positive constant.

Now from Eqs. (2), (17), (18) and (19), we obtain the metric potentials as

$$\begin{aligned} b_{1}&=\left( t^\nu e^{t\mu }\right) ^{\frac{3n}{n+1}}\,\,\,, \end{aligned}$$

(20)

$$\begin{aligned} b_{2}&=\gamma _1\left( t^\nu e^{t\mu }\right) ^{\frac{3}{2n+2}}\,\,\,, \end{aligned}$$

(21)

$$\begin{aligned}{} \& \quad b_{3}&=\frac{\left( t^\nu e^{t\mu }\right) ^{\frac{3}{2n+2}}}{\gamma _1}\,\,\,. \end{aligned}$$

(22)

The energy density of the matter is given by

$$\begin{aligned} \rho _{{m}}=\kappa _1 \left( t^\nu e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}, \end{aligned}$$

(23)

where $\kappa _1$ is an integration constant.

The energy density of the viscous holographic dark energy is given by

$$\begin{aligned} \rho _{{h}}=\frac{-4 (n+1)^2 \kappa _1 t^2\left( t^\nu e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}+36 \left( t^\nu e^{t\mu }\right) ^{\frac{-6n}{n+1}} \left( \mu _{{1}}t+\nu _{{1}}\right) ^2 \left( \frac{1}{4}+n\right) }{4 \left( n+1\right) ^2 t^2}. \end{aligned}$$

(24)

The pressure of the viscous holographic dark energy is given by

$$\begin{aligned} {\bar{P}}_{{h}}=\frac{2\left( t^\nu e^{t\mu }\right) ^{\frac{-6n}{n+1}}\left( \left( \frac{3n}{2}-\frac{15}{8}\right) \nu ^2+\left( n^2+\left( 3\mu t+2\right) n-\frac{15}{4}t \mu +1\right) \nu +\frac{3}{2}t^2 \left( n-\frac{5}{4}\right) \mu ^2\right) }{\left( n+1\right) ^2 t^2}. \end{aligned}$$

(25)

The bulk viscosity is given by

$$\begin{aligned} \zeta =\left( \mu \zeta _1+\zeta _0\right) +\zeta _1\frac{\nu }{t}. \end{aligned}$$

(26)

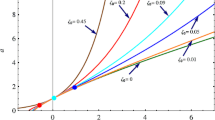
In all the discussions and graphical representations of our Marder VHDE cosmological model, we constraint the following constants: $\nu =0.44,\,0.55,\,0.66$; $\mu =0.055,\,0.065,\,0.075$; $\kappa _1=0.1$; $n=0.011$; $\zeta _0=0.025$; $\zeta _1=0.95$. The nature of the energy density of matter ($\rho _{m}$) and the energy density of VHDE ($\rho _{{h}}$) versus cosmic time (t) is plotted in Figs. 1 and 2. We can observe that the trajectories of the energy density of matter ($\rho _{m}$) and energy density of VHDE ($\rho _{{h}}$) vary in the positive region and decrease with time (t) for different values of $\nu$ and $\mu$, which indicates the expansion of the Universe. Also, from Fig. 3, we can observe that the total pressure (p) is negative and increasing with time (t) for different values of $\nu$ and $\mu$. However, the negative pressure indicates the phenomenon of the accelerated expansion of the Universe, and thus, Fig. 3 indicates the acceleration of the Universe. From Fig. 4, we observe that the trajectories of bulk viscosity are varying in the positive region and decreasing against cosmic time t.

Fig. 1

Plot of energy density of matter versus cosmic time t (Gyr)

Fig. 2

Plot of energy density of VHDE versus cosmic time t (Gyr)

Fig. 3

Plot of total pressure of VHDE versus cosmic time t (Gyr)

Fig. 4

Plot of bulk viscosity of VHDE versus cosmic time t (Gyr)

Now, the metric (1) can be written as

$$\begin{aligned} ds^2= & {} \left( t^\nu e^{t\mu }\right) ^{\frac{6n}{n+1}} dx^2+\left( \gamma _1\left( t^\nu e^{t\mu }\right) ^{\frac{3}{2n+2}}\right) ^2dy^2\nonumber \\{} & {} +\left( \frac{\left( t^\nu e^{t\mu }\right) ^{\frac{3}{2n+2}}}{\gamma _1}\right) ^2dz^2-\left( t^\nu e^{t\mu }\right) ^{\frac{6n}{n+2}}dt^2. \end{aligned}$$

(27)

Thus, the metric (27) represents a spatially homogeneous and anisotropic Marder-type VHDE cosmological model in general relativity with the following properties along with the physical parameters given in the next sections which are important in the discussion of cosmology.

• The volume (V), average scale factor (a(t)), mean Hubble parameter (H), expansion scalar $(\theta )$ of the Marder-type space-time are given by

  $$\begin{aligned} V&= \left( t^{3\nu } e^{t3\mu }\right) , \quad \end{aligned}$$

  (28)
  $$\begin{aligned} a(t)&=\left( t^{\nu } e^{t\mu }\right) , \end{aligned}$$

  (29)
  $$\begin{aligned} H&=\mu +\frac{\nu }{t}, \end{aligned}$$

  (30)
  $$\begin{aligned}{} \& \quad \theta&=3\left( \mu +\frac{\nu }{t}\right) \left( t^{\nu } e^{t\mu }\right) ^{\frac{-3n}{n+1}}. \end{aligned}$$

  (31)

• The shear scalar $(\sigma ^2)$ is given by

  $$\begin{aligned} \sigma ^2=\frac{3 \left( -\left( n+1\right) ^2\left( t^{\nu } e^{t\mu }\right) ^{\frac{-6n}{n+1}}+3n^2+\frac{3}{2}\right) \left( \mu +\frac{\nu }{t}\right) ^2 }{2 \left( n+1\right) ^2}. \end{aligned}$$

  (32)

• The anisotropic parameter ${\mathcal {A}}_h$ is given by

  $$\begin{aligned} {\mathcal {A}}_h=\frac{\left( 2n-1\right) ^2}{2(n+1)^2}. \end{aligned}$$

  (33)

From Eq. (33), we observe that ${\mathcal {A}}_h\ne 0$, which represents the Marder-type cosmological model is always anisotropic throughout the evolution of the Universe except $n=\frac{1}{2}$. We have plotted volume (V) versus cosmic time (t) in Fig. 5, and we observe that the trajectory of the volume is monotonically increasing against cosmic time (t), which indicates the spatial volume (V) increases exponentially and shows the spatial expansion of the Universe. Also, it can be observed from Eqs. (28)–(32), at the initial epoch (i.e.,  at $t=0$), the spatial volume (V) and the average scale factor a(t) become zero and increase with the cosmic time, which indicates the volume of an expanding Universe. It is also observed that the Hubble parameter H and shear scalar ($\sigma$) diverge at the initial epoch and attain constant value at late times, whereas the expansion scalar ($\theta$) of the model vanishes at late times and diverges at the initial epoch. The plot of the expansion scalar $(\theta )$ and Hubble’s parameter (H) is given in Fig. 6. It can be seen that both are decreasing functions of time and become constant at late times. Thus, it is concluded from these observations that the model starts its expansion with zero volume and it continues to expand up to an infinitely large volume concerning cosmic time (t).

Fig. 5

Plot of volume V versus cosmic time t (Gyr)

Fig. 6

Plot of Hubble parameter and expansion scalar versus cosmic time t (Gyr)

4 Some other important cosmological parameters

Here, we examine expanding behavior of the Universe through well-known cosmological parameters like deceleration parameter (q), jerk parameter (j), EoS parameter ($\omega _{\text {de}}$), squared sound speed $(v_s^2)$, energy conditions, density parameters, i.e.,  $\Omega _{m},\,\, \Omega _{\text {vhde}}\,\, \& \,\,\Omega$ and cosmological planes such as $(r-s)$, $(r-q)$, & $\omega _{\text {de}}-\omega '_{\text {de}}$ for constructed anisotropic VHDE model.

• Deceleration Parameter: As we know that cosmography is efficient as it permits to test of any cosmological model which does not contradict the cosmological principles. The modification of the general theory of relativity evidently changes the dependence of scale factor a(t), but it does not affect the relation between the kinematical characteristics. The dynamics of the Universe are described by Einstein’s equations. It is also observed that if a is constant, the scaling factor is proportional to time t, and the deceleration term is zero, when the Hubble term is constant the DP is also constant and equal to $-1$. In most of the cases, the deceleration term changes with time. The cosmological models may change whether they expand or contract or accelerate or decelerate. This means that both the Hubble parameter and the DP can change the sign during evolution. As we believe that we live in an expanding Universe and the nature of the Universe varies with the following conditions:

  • (a) $H>0$, $q>0$ $\Rightarrow$ Expanding and decelerating Universe.

  • (b) $H>0$, $q<0$ $\Rightarrow$ Expanding and accelerating Universe.

  • (c) $H>0$, $q=0$ $\Rightarrow$ Expanding Universe with zero deceleration.

  The deceleration parameter is given by

  $$\begin{aligned} q=\frac{d}{dt}\left( \frac{1}{H}\right) -1=\frac{\nu }{(\nu +\mu t)^2}-1. \end{aligned}$$

  (34)

  It is a dimensionless quantity that measures the rate of the cosmos’ expansion. It indicates decelerated expansion, depending on its sign (in case of positive sign) or accelerated expansion (in case of negative sign), whereas the marginal inflation occurs at $q=0$ and $q=-1$ current Universe shows de-Sitter expansion. The model shows accelerated expansion for $-1\le q < 0$ and a super-exponential expansion for $q < -1$. We have plotted the deceleration parameter (q) versus cosmic time (t) in Fig. 7 and we observe that the trajectories of the deceleration parameter give a nice transaction from early deceleration to the present accelerated phase for three different values of $\nu$ and $\mu$. The present value of the deceleration parameter (q) for our obtained model is $q\approx -0.6939, -0.7373$ and $-0.7703$ which is consistent with the astrophysical observational data given by Cunha [70] (SNIa), Xu et al. [71] $(SN Ia + BAO + H(z))$, Santos et al. [72] $(SN Ia + BAO/CMB + H(z))$, Haridasu et al. [73] $(CC + SN Ia + BAO + R18)$ as follows:

  $$\begin{aligned} q= & {} -0.73\qquad \qquad (SN Ia),\\ q= & {} -0.658_{-0.057}^{+0.061} \qquad (SN Ia + BAO + H(z)),\\ q= & {} -0.54_{-0.05}^{+0.07} \qquad (SN Ia + BAO/CMB + H(z)), \\ \& q= & {} -0.57_{-0.05}^{+0.05}\qquad (CC + SN Ia + BAO + R18). \end{aligned}$$

• Jerk Parameter: Jerk parameter in cosmology is defined as the dimensionless third derivative of scale factor with respect to time and is given by

  $$\begin{aligned} j=\frac{\dddot{a}}{aH^3} = 1-\frac{3\nu }{(\nu + \mu t)^2}+\frac{2\nu }{(\nu + \mu t)^3}. \end{aligned}$$

  (35)

  In modern cosmology, the general assumption is the jerk parameter can describe the transition of the Universe from the decelerating to accelerating phase. This transition of the Universe arises for various models with a positive value of the jerk parameter and negative value of the deceleration parameter (Chiba and Nakamura [74]; Visser [75]).

  Here, we have plotted the graph for the jerk parameter with respect to cosmic time(t) as shown in Fig. 8a and b for three different values of $\nu$ and $\mu$. We can observe that the trajectories of the jerk parameter vary in the positive region throughout the evolution and finally equal to one. This shows that our model is consistent with the recent observations (i.e. $\Lambda$CDM model has a constant jerk parameter and is equal to unity). Also, we observe that the nature of the jerk parameter completely depends on $\nu$ and $\mu$.

• Statefinder diagnostics: To differentiate many candidates of dark energy, Sahni et al. [76] proposed a new geometrical diagnostic named the statefinder pair $\{r, s\}$, where r is generated from the scale factor a(t) and its derivatives with respect to the cosmic time (t) up to the third order and s is a simple combination of r and the deceleration parameter q. The statefinder parameters are given as,

  $$\begin{aligned} r= & {} \frac{\dddot{a}}{aH^3} = 1-\frac{3\nu }{(\nu + \mu t)^2}+\frac{2\nu }{(\mu + \mu t)^3}; \quad \nonumber \\ s= & {} \frac{r-1}{3(q-\frac{1}{2})} =\frac{2(2\nu -3\nu (\nu +\mu t))}{3(2\nu -3(\nu +\mu t)^3)}. \end{aligned}$$

  (36)

  Due to their total dependence on the scale factor these parameters have geometrical diagnostic. The statefinder diagnostic is a useful tool in modern-day cosmology and is being used to serve the purpose of distinguishing different dark energy models [77,78,79]. In this setup, different trajectories in $r-s$ and $r-q$ planes define the temporal evolution for various dark energy models. Using this pair one can describe the well-known regions as follows: $(r, s)=(1, 0)$ indicates $\Lambda$CDM limit, $(r, s)=(1, 1)$ shows CDM limit, while $s > 0$ and $r < 1$ represent the region of phantom and quintessence dark energy eras. In the $r-s$ and $r-q$ planes, the departure of any dark energy model from these fixed points is analyzed. The plots of diagnostic pairs (r, s) and (r, q) for our model are shown in Figs. 9 and 10. From Fig. 9, we observe that the statefinder parameter curve passes the point, $(r,s)=(1,0)$, which corresponds to the $\Lambda$CDM model. The $r-s$ plane also provides the regions of Chaplygin gas $(r>1, s<0)$, quintessence and phantom $(r<1, s>0)$ eras. Figure 10 demonstrates the evolution of our model with $r-q$ plane. In this diagnostic plane, the dotted line in the middle depicts the evolution of the standard $\Lambda$CDM cosmological model and also divides the plane into two equal halves where the quintessence dark energy model exists in the lower half, while the Chaplygin gas dark energy models exist in the upper half. Also, it can be seen that the profile starts from the region $q>0$ and $r>1$, which corresponds to the SCDM Universe then followed by the region $r<1$ and $q<0$ and finally approaches to the de-Sitter phase ($i.e., r=1, q=-1$).

• EoS Parameter: To obtain EoS parameter we will use the following equation

  $$\begin{aligned} \omega _{\text {de}}=\frac{{\bar{P}}_h}{\rho _{h}}. \end{aligned}$$

  (37)

  Here, ${\bar{P}}_h$ and $\rho _{h}$ represent pressure and DE density of VHDE, respectively. EoS parameter is used to categorize the decelerated and accelerated phases of the Universe. The DE-dominated phase has following eras:

  • (i) $\omega _{\text {de}}=0$ corresponds to non-relativistic matter.

  • (ii) $-1<\omega _{\text {de}}<\frac{-1}{3}$ quintessence.

  • (iii) $\omega _{\text {de}}=-1$ cosmological constant.

  • (iv) $\omega _{\text {de}}<-1$ phantom.

  From 37, the EoS parameter of the model as

  $$\begin{aligned} \omega _{\text {de}}=\frac{-\left( 8\left( \left( \frac{3n}{2}-\frac{18}{8}\right) \nu ^2+\left( 3\left( n-\frac{5}{4}\right) \mu t+\left( n+1\right) ^2\right) \nu +\frac{3}{2}\left( n-\frac{5}{4}\right) \mu ^2 t^2\right) \left( t^\nu e^{t\mu }\right) ^{\frac{3}{n+1}} \right) }{\left( -36\left( \mu t+\nu \right) ^2 \left( t\nu e^{t\mu }\right) ^{\frac{3}{n+1}} \left( n+\frac{1}{4}\right) +4\kappa _1\left( n+1\right) ^2 t^2 \right) }. \end{aligned}$$

  (38)

  The EoS parameter of the VHDE model (27) is given in Eq. (38). In Fig. 11, we investigate the evolution of the EoS parameter $\omega _{\text {de}}$ in terms of cosmic time t with different values of $\nu$ and $\mu$ for model (27). The trajectories of the EoS parameter for model (27) are started from the quintessence phase and turn toward the phantom region by crossing vacuum dominated era (phantom divide line $\omega _{\text {de}}=-1$) of the Universe for all the values of $\nu$ and $\mu$. This is called quintom-like nature of the Universe for our obtained model. It can be seen that the results for the EoS parameter of our obtained model are consistent with the 2018 Planck collaboration data (Aghanim et al., [80]), where the limits on the EoS parameter are given as follows:

  $$\begin{aligned} \omega _{\text {de}}= & {} -1.56_{-0.48}^{+0.60}\qquad (Planck + TT + lowE),\\ \omega _{\text {de}}= & {} -1.58_{-0.41}^{+0.52}\qquad (Planck + TT, EE + lowE),\\ \omega _{\text {de}}= & {} -1.57_{-0.40}^{+0.50}\qquad (Planck + TT, TE, EE + lowE+lensing), \\ \& \omega _{\text {de}}= & {} -1.04_{-0.10}^{+0.10}\qquad (Planck + TT, TE, EE + lowE+lensing+BAO). \end{aligned}$$

• $\omega _{\text {de}}-\omega _{\text {de}}'$ plane: The $\omega _{\text {de}}-\omega _{\text {de}}'$ plane analysis is used to study the dynamical properties of dark energy models which is first proposed by [81], where $(')$ prime indicates derivative with respect to $\ln a$. This approach has been applied on the quintessence model which leads to two types of its planes, i.e.,  the area belongs to the region $(\omega _{\text {de}}<0,\,\, \omega _{\text {de}}'>0)$ corresponds to the thawing region, while the area under the region $(\omega _{\text {de}}<0,\,\, \omega _{\text {de}}'<0)$ implies the freezing region. By taking the derivative of Eq. (38) with respect to $\ln a$, we obtain the expression for $\omega _{\text {de}}'$ as

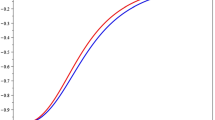
  $$\begin{aligned}{} & {} \omega _{\text {de}}'=\frac{{\mathcal {N}}}{16\left( \left( n+1\right) \left( -9\left( \mu t +\nu \right) ^2 \left( \frac{1}{4}+n\right) \left( t^\nu e^{t\mu }\right) ^{\frac{3}{n+1}}+\kappa _1 (n+1)^2 t^2\right) ^2t\right) }. \nonumber \\{} & {} \left. \begin{aligned} \text {where} \quad&{\mathcal {N}}={\mathcal {N}}_{11}+{\mathcal {N}}_{12}+{\mathcal {N}}_{13}+{\mathcal {N}}_{14},\,\, \text {where} \\&{\mathcal {N}}_{11}=-192 e^{t\mu }\bigg (\left( \left( \frac{3n}{2}-\frac{15}{8}\right) \nu +\left( n+1\right) ^2\right) \nu ^2 t^{2+6\nu }\\&\quad +\bigg (\nu \left( \left( \frac{9n}{2}-\frac{45}{8}\right) \nu \right. \\&\left. \quad + \left( n+1\right) ^2\right) \\&t^{6\nu +3}+\frac{9}{2}\left( t^{6\nu +4}\nu +t^{6\nu +5}\mu \right) \left( n-\frac{5}{4}\right) \mu \bigg )\mu \bigg )\\&{\mathcal {N}}_{12}=\left( n+\frac{1}{2}\right) \left( n+1\right) ^2 \kappa _1 \left( t^{\nu }e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}\\&\quad +\eta 3 \nu ^2\bigg (\left( 5n^2-\frac{25n}{4}\right) \nu +\left( n^2+\frac{3n}{2}-\frac{5}{8}\right) \\&\left( n+1\right) \bigg ) \mu ^2 t^{2+6\nu }+\eta \nu \left( \left( 15n^2-\frac{75n}{4}\right) \nu \right. \\&\left. \quad +\left( n^2+\frac{3n}{2}-\frac{5}{8}\right) \left( n+1\right) \right) \mu ^3 t^{6\nu +3}\\&+3\eta \nu ^2\mu t^{1+6\nu }\bigg (\bigg (\frac{5n^2}{2}-\frac{25n}{8}\bigg )\nu ^2\\&\quad +\left( n^2+\frac{3n}{2}-\frac{5}{8}\right) \left( n+1\right) \nu \bigg )+3\eta \nu ^2\mu t^{1+6\nu }\frac{1}{9}\left( n+1\right) ^3\\&+\eta \frac{15}{2}\nu n\left( n-\frac{5}{4}\right) \mu ^4 t^{4+6\nu }+\eta \frac{3n}{2}\left( n-\frac{5}{4}\right) \mu ^5 t^{5+6\nu }\\&\quad +\left( \left( \frac{3n}{2}-\frac{15}{8}\right) \nu +\left( n+1\right) ^2\right) \\&\nu ^3t^{6\nu }\left( n\nu +\frac{n}{3}+\frac{1}{3}\right) \\&{\mathcal {N}}_{13}=192\bigg (\left( \frac{3n^2}{2}\frac{15n}{8}\right) \nu ^3\\&\quad +\bigg (\frac{-5}{8}+n^3 +\left( \frac{9t\mu }{2}+\frac{5}{2}\right) n^2\\&\quad +\left( \frac{-45t^2\mu ^2}{8}+\frac{7t\mu }{8}+1\right) n\\&-\frac{5t\mu }{8}+\frac{1}{3}\bigg )\nu +\frac{3n}{2}\left( n-\frac{5}{4}\right) \mu ^3 t^3\bigg )\\&{\mathcal {N}}_{14}=\left( -9\left( \mu t+\nu \right) ^2\left( \frac{1}{4}+n\right) \left( t^{\nu }e^{t\mu }\right) ^{\frac{6}{n+1}}\right. \\&\left. \quad +\left( t^{\nu }e^{t\mu }\right) ^{\frac{3}{n+1}}t^2 \kappa _1 \left( n+1\right) ^2\right) \\&\eta =1728 e^{6t\mu } \left( \frac{1}{4}+n\right) \left( t^{\nu }e^{t\mu }\right) ^{\frac{-6n}{n+1}} \end{aligned}\right\} \end{aligned}$$

  (39)

  From Fig. 12, we observe that the trajectories of $\omega _{\text {de}}-\omega _{\text {de}}'$ plane vary in the freezing region for all values of $\nu$ and $\mu$. Observational data suggest that the expansion of the Universe in the freezing region is relatively accelerating. It is concluded that $\omega _{\text {de}}-\omega _{\text {de}}'$ plane analysis for the present scenario gives consistent results with the accelerated expansion of the Universe. The evolution of trajectories of $\omega _{\text {de}}-\omega _{\text {de}}'$ plane confirms that there is more acceleration of the cosmic expansion and our models remain in freezing region $(\omega _{\text {de}}<0, \omega _{\text {de}}'<0)$ which obeys the following observational data (Ade et al., [82]; Hinshaw et al., [83]).

  $$\begin{aligned} \omega _{\text {de}}= & {} -1.13_{-0.25}^{+0.24}, \\ \omega _{\text {de}}'< & {} 1.32\text {(Planck + WP + BAO)},\\ \omega _{\text {de}}= & {} -1.34_{-0.18}^{+0.18},\\ \omega _{\text {de}}'= & {} 0.85\pm 0.7 \text {(WMAP + eCAMB+BAO}+H_0),\\ \omega _{\text {de}}= & {} -1.17_{-0.12}^{+0.13},\\ \omega _{\text {de}}'= & {} 0.85_{-0.49}^{+0.50} \text {(WMAP+eCAMB+BAO}+H_0+\text {SNe}). \end{aligned}$$

• Squared speed of sound: We now consider and study an important quantity considered in cosmology in order to check the stability of any DE model and it is known as the squared speed of sound, it is denoted with $v_s^2$ and this parameter is useful in discussing the stability of DE models depends upon its sign. The models with $v_s^2>0$ are stable, whereas models with $v_s^2<0$ are unstable. The squared speed of the sound is defined as follows:

  $$\begin{aligned} \left. \begin{aligned} v_s^2&=\frac{\dot{{\bar{P}}}_{h}}{{\dot{\rho }}_{h}}=\frac{{\mathcal {N}}_2}{{\mathcal {N}}_3}.\\ {\mathcal {N}}_2&= \left( \frac{3n^2}{2}-\frac{15n}{8}\right) \nu ^3+\left( \frac{9n}{2}\left( n-\frac{5}{4}\right) \mu t\right. \\&\left. \qquad +\left( n^2+\frac{3n}{2}-\frac{5}{8}\right) (n+1)\right) \nu ^2 12\left( t^{\nu }e^{t\mu }\right) ^{\frac{-6n}{n+1}}\\&\quad +12\left( t^{\nu }e^{t\mu }\right) ^{\frac{-6n}{n+1}}\left( \frac{9n}{2}\left( n-\frac{5}{4}\right) \mu ^2 t^2\right. \\&\left. \qquad +\left( n^2+\frac{3n}{2}-\frac{5}{8}\right) (n+1)\mu t+\frac{(n+1)^3}{3}\right) \nu \\&\qquad +\frac{3n}{2}\left( n-\frac{5}{4}\right) \mu ^3 t^3\\ {\mathcal {N}}_3&=(-1)6\left( \mu t+\nu \right) \kappa _1\left( n+1\right) ^2t^2\left( n+\frac{1}{2}\right) \left( t^{\nu }e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}\\&\qquad -54 \left( \mu t+\nu \right) \left( \frac{1}{4}+n\right) \bigg (\bigg (t^2\mu ^2+2t\mu \nu +\nu ^2\\&\quad +\frac{\nu }{3}\bigg )n+\frac{\nu }{3}\bigg )\left( t^{\nu }e^{t\mu }\right) ^{\frac{-6n}{n+1}} \end{aligned}\right\} . \end{aligned}$$

  (40)

  squared speed of sound expression for model (27) is given in Eq. (40). In Fig. 13, we analyze the squared speed of sound for model (27) in terms of cosmic time t for different values of $\nu$ and $\mu$. It is observed that the trajectories of $v_s^2$ are in the negative region for all values of $\nu$ and $\mu$, which give unstable behavior of the Universe.

• Energy conditions: There are various types of energy conditions(EC’s) at the astrophysical level and cosmological level, which came from Raychaudhuri equations [84]. Generally, in the study of energy conditions, the energy–momentum tensor plays a vital role, so, in the present discussion, we have defined energy–momentum tensor in terms of normal pressure ${\bar{P}}_h$ and normal energy density $\rho _{h}$; thereby, all four EC’s can be written as, null energy condition(NEC), weak energy condition(WEC), dominant energy condition(DEC) and strong energy condition(SEC). The main purpose of these energy conditions is to check the expansion of the Universe. Several authors have worked on these energy conditions, particularly Salti et al. [85], Sahoo et al. [86], Hegazy and Rahaman [87], Kumar and Singh [88], Bhar et al. [89], Mishra et al. [90, 91], Aziz et al. [92], Mollah and Singh [93]. These conditions put extra constraints on the viability of the constructed cosmological model and are defined as

  • WEC: $\rho _{h}\ge 0$

  • NEC: $\rho _{h}+{\bar{P}}_h\ge 0$

  • DEC: $\rho _{h}-{\bar{P}}_h\ge 0$

  • SEC: $\rho _{h}+3{\bar{P}}_h\ge 0$

  Here, WEC, NEC, DEC and SEC denote weak energy condition, null energy condition, dominant energy condition and strong energy condition, respectively. For the constructed model, we have examined the behavior of these energy conditions, as shown in Fig. 14. It is observed that WEC, NEC and DEC are well satisfied throughout the cosmic evolution, whereas SEC is violated at late times, which represents an accelerating Universe. Also, we have observed that the DEC dominates the NEC, and for the obtained model, this is an interesting observation.

• Density parameters: Generally, most of the authors suggest that the total density parameter is approximately equal to 1 i.e. $\Omega \approx 1$. It is still important to know whether $\Omega$ is greater than 1, less than 1 or exactly equal to 1 as it reveals the ultimate destiny of the Universe. If $\Omega >1$, the Universe is closed, and eventually, it will stop its expansion and recollapse. If $\Omega <1$, then the Universe is open and will continue to expand forever, if $\Omega =1$ then the Universe is flat and has enough material to stop the expansion, but it is not enough to recollapse it. The expression for dimensionless density parameters is defined as

  $$\begin{aligned} \Omega _{\text {vhde}}&=\frac{\rho _{h}}{3H^2}, \nonumber \\ \Omega _{m}&=\frac{\rho _{m}}{3H^2},\nonumber \\ \& \quad \Omega&=\Omega _{\text {vhde}}+\Omega _{m} . \end{aligned}$$

  (41)

  The density parameter of VHDE, matter and total density for model (27) is, respectively, given by

  $$\begin{aligned} \Omega _{\text {vhde}}&=\frac{-4 (n+1)^2 \kappa _1 t^2\left( t^\nu e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}+36 \left( t^\nu e^{t\mu }\right) ^{\frac{-6n}{n+1}} \left( \mu _{{1}}t+\nu _{{1}}\right) ^2 \left( \frac{1}{4}+n\right) }{12 \left( n+1\right) ^2 t^2 \left( \mu +\frac{\nu }{t}\right) ^2}, \end{aligned}$$

  (42)
  $$\begin{aligned} \Omega _{m}&=\frac{\kappa _1 \left( t^\nu e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}}{3\left( \mu +\frac{\nu }{t}\right) ^2}. \end{aligned}$$

  (43)
  $$\begin{aligned} \Omega&=\frac{-4 (n+1)^2 \kappa _1 t^2\left( t^\nu e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}+36 \left( t^\nu e^{t\mu }\right) ^{\frac{-6n}{n+1}} \left( \mu _{{1}}t+\nu _{{1}}\right) ^2 \left( \frac{1}{4}+n\right) }{12 \left( n+1\right) ^2 t^2 \left( \mu +\frac{\nu }{t}\right) ^2}+\frac{\kappa _1 \left( t^\nu e^{t\mu }\right) ^{\frac{-6n-3}{n+1}}}{3\left( \mu +\frac{\nu }{t}\right) ^2}. \end{aligned}$$

  (44)

  From Fig. 15, we analyze the behavior of the density parameter of VHDE ($\Omega _{\text {vhde}}$), matter ($\Omega _{m}$) and total density ($\Omega$) against cosmic time t for model (27), for the different values of $\nu$ and $\mu$, respectively. We observe that the trajectory of density parameters of VHDE ($\Omega _{\text {vhde}}$), matter ($\Omega _{m}$) and total density ($\Omega$) for model (27) is positive and decreasing against cosmic time and approaches to a value less than one at late time and also we observe that for this model (27), the total density ($\Omega$) initially dominates both VHDE and matter density parameters.

Fig. 7

Plot of deceleration parameter of VHDE versus cosmic time t (Gyr)

Fig. 8

Plot of jerk parameter versus cosmic time t (Gyr)

Fig. 9

Plot of $r-s$ plane

Fig. 10

Plot of $q-r$ plane

Fig. 11

Plot of EoS parameter versus cosmic time t (Gyr)

Fig. 12

Plot of $\omega _{\text {de}}-\omega _{\text {de}}'$ plane

Fig. 13

Plot of squared speed of sound versus cosmic time t (Gyr)

Fig. 14

Plot of energy conditions versus cosmic time t (Gyr)

Fig. 15

Plot of density parameters versus cosmic time t (Gyr)

5 Conclusions

In this paper, we have studied the viscous holographic dark energy model with Marder-type space-time in the framework of Einstein’s general theory of gravity. The field equations of viscous holographic dark energy have been solved by using hybrid expansion law, which is a combination of power and exponential functions, which leads to a varying deceleration parameter. We have investigated well-known cosmological parameters such as deceleration parameter (q), jerk parameter (j), EoS parameter $(\omega _{\text {de}})$, $\omega _{\text {de}}-\omega _{\text {de}}'$ plane, $r-s$ plane, $r-q$ plane, squared speed of sound and density parameters $\left( i.e., \Omega _{m},\,\,\, \Omega _{\text {vhde}}\,\,\, \& \,\,\, \Omega \,\,\, \right)$. The following are conclusions:

The model is free from initial singularity and the model starts its expansion with zero volume and it continues to expand up to infinitely large volume concerning cosmic time. In fact, this leads to inflation of the Universe. It is observed that the dynamical parameters of our model diverge at the initial epoch and attain constant volume at late times. The average anisotropy parameter $(A_h)$ is constant and does not vanish $(i.e.,\, A_h \ne 0)$, and hence, our model is anisotropic throughout the evolution of the Universe. The DP for our constructed model (27) gives a nice transaction from the early deceleration to the present accelerated phase for three different values of $\nu$ and $\mu$ which is shown in Fig. 7. It can be seen that from (34), the present value $(i.e.,\, \text {at}\,\,t_0=13.8Gyr)$ of DP is obtained as $-0.73$ for $\nu =0.55$, $\mu =0.065$, which matches the modern observational data of SNeIa and indicates the present value of DP lies within the range $-1\le q<0$  ($i.e.q\approx -0.73$ at $t_0=13.8Gyr$). We observe that the jerk parameter and statefinder parameters are time dependent and it can be seen that the value of the jerk parameter is positive throughout the evolution. Here, we plotted the graph of the jerk parameter with respect to cosmic time(t) as shown in Fig. 8a and b for three different values of $\nu$ and $\mu$. We can observe that the trajectories of the jerk parameter vary in the positive region throughout the evolution and finally equal to one. This shows that our model is consistent with the recent observations (i.e., $\Lambda$CDM model has a constant jerk parameter and is equal to unity). The $r-s$ plane corresponding to our model (27) is shown in Fig. 9. It is observed that the constructed model of the Universe starts evolving from quintessence and phantom regions and then reaches the $\Lambda CDM$ model $(r=1,s=0)$ and finally passing through the Chaplygin gas region. Figure 10 shows the time evolution of the $r-q$ trajectories in the $r-q$ plane. Here, the signature change from positive to negative in q clearly explains the phase transition of the Universe. We observe that initially, the VHDE model approaches to the SCDM model and de-Sitter phase of the Universe in future. The energy density of matter $\rho _{m}$ and energy density of VHDE are always positive and decrease with cosmic time t (Ref Figs. 1 and 2). However, the total pressure (p) of the model is negative and increases with cosmic time (t) (Ref Fig. 3). The negative value of pressure could contribute to the present accelerated expansion of the Universe. From Fig. 4, we observe that the trajectories of bulk viscosity are varying in the positive region and decreasing against cosmic time t. The evolution of EoS parameter $(\omega _{\text {de}})$ has also been observed graphically. It shows that $\omega _{\text {de}}$ evolves from the quintessence phase to the phantom phase by crossing vacuum dominated era (phantom divide line $\omega _{\text {de}}=-1$) of the Universe for all the values of $\nu$ and $\mu$. This is called quintom-like behavior of the Universe. We study $\omega _{\text {de}}-\omega _{\text {de}}'$ plane for different values of $\nu$ and $\mu$ as given in Fig. 12. From Fig. 12, we observe that the trajectories of $\omega _{\text {de}}-\omega _{\text {de}}'$ plane vary the in freezing region for all values of $\nu$ and $\mu$, and such feature of the model is in good agreement with observational data. We analyze the squared speed of sound for model (27) graphically against cosmic time(t) in Fig. 13 for different values of $\nu$ and $\mu$. It is observed that the trajectories of $v_s^2$ are in the negative region for all values of $\nu$ and $\mu$, which give unstable behavior of the Universe. All the energy conditions except SEC are well satisfied throughout the evolution of the Universe. SEC is violated at late times in our model due to negative pressure. It is observed that the density parameters of VHDE ($\Omega _{\text {vhde}}$), matter ($\Omega _{m}$) and total density ($\Omega$) of the model (27) are positive and decreasing against cosmic time and approaches to a number less than one at late times and also we observe that for this VHDE model, the total density ($\Omega$) initially dominates both VHDE and matter density parameters.

Finally, we may conclude that all the above results of the obtained model are in good agreement with the recent cosmological observations.