1 Introduction

Recent cosmological observations (Riess et al. 1998; Perlmutter et al. 1999; Spergel et al. 2003; Tegmark et al. 2004; Eisenstein et al. 2005; Kessler et al. 2009) indicate that the universe is spatially flat and has an accelerated expansion. These observations lead to a matter called dark energy (DE) which has large negative pressure. The DE can be explained in terms of cosmological constant (\(\wedge\)), which acts like a perfect fluid with an equation of state, satisfying the observational data so far. However, these involve the problems of fine tuning and cosmic coincidence. The simplest candidate for DE is the cosmological constant with equation of state parameter \(\omega = - 1\), since it fits the observational data well, but it needs to be extremely fine-tuned to satisfy the present value of DE Copeland et al. (2006). To solve cosmological constant problem at present epoch, \(\wedge\) with a dynamical character is preferred over a constant \(\wedge\), especially a time dependent \(\wedge\) which has decreased slowly from its large initial value to reach its present small value (Overduin and Cooperstocket 1998). To further investigate the properties of DE, many dynamical DE models have been proposed, such as quintessence, phantom Caldwell (2003), tachyon Padmanabhan and Choudhary (2002); Bagla et al. (2003), dilatonic ghost condensate Gasperini et al. (2001), quartessence Leon and Saridakis (2010), and so forth.

The nature of DE can also be studied according to some basic quantum gravitational principles, for example, holographic dark energy principle. According to this principle, the degrees of freedom in a bounded system should be finite and do not scale by it volume but with its boundary era. Cohen et al. (1999) found that for a system with infrared (long distance) cut-off scale L and ultraviolet (short distance) cut-off scale \(\wedge\) without decaying into a black hole, the quantum vacuum energy should be less than or equal to the mass of a black hole, i.e., \(L^3\rho _\wedge \le LM_p^2\) . Here, \(\rho _\wedge\) is the vacuum energy density and \(M_p=(8\pi G)^{-\frac{1}{2}}\) is the reduced Plank mass. Using this idea in cosmology, one can take L which satisfies this inequality with \(\rho _\wedge\) as DE density. The holographic principle is considered as another alternative to the solution of the DE problem. This principle was first put forwarded by G.’t Hooft (1993) in the context of black hole physics. According to the holographic principle, the entropy of a system scales not with its volume, but with its surface area Li (2004). In the cosmological context, Fischler and Susskind (1998) have proposed a new version of the holographic principle, viz., at any time during cosmological evolution, the gravitational entropy within a closed surface should not be always larger than the particle entropy that passes through the past light-cone of that surface. In the context of the DE problem, though the holographic principle proposes a relation between the holographic DE density \(\rho _\wedge\) and the Hubble parameter H as \(\rho _\wedge =H^2,\) it does not contribute to the present accelerated expansion of the universe. Granda and Oliveros (2008) proposed a holographic density of the form \(\rho _\wedge \cong \alpha H^2+\beta \dot{H}\), where H is the Hubble parameter and \(\alpha\) and \(\beta\) are constants which must satisfy the restrictions imposed by the current observational data. They showed that this new model of DE represents the accelerated expansion of the universe and is consistent with the current observational data. Moreover, Granda and Oliveros (2009) studied the corresponding between the quintessence, tachyon, k-essence, and dilaton DE models with this holographic DE model in the flat FRW universe. There exist many cosmological versions of holographic principle in literature (Setare 2006a, b, 2007a, b; Mubasher et al. 2009). Esther and Lowe (1999) found that this principle can be replaced by generalized second law of thermodynamics (GSLT) for time-dependent backgrounds. This is similar to the cosmological holographic principle given by Fischler and Susskind (1998) for an isotropic open and flat universe with fixed equation of state. Spatially homogeneous and anisotropic cosmological models play a significant role in the description of large scale behavior of the universe and such models have been widely studied by many authors in search of relativistic picture of the early universe. Anisotropic Bianchi type-I, Bianchi type-III, and Bianchi type-V dark energy models with the usual perfect fluid have also been extensively studied in the literature (Adhav 2011a, b; Pradhan et al. 2011; Akarsu and Kilinc 2010; Yadav and Yadav 2011; Kumar and Yadav 2011; Yadav and Saha 2012; Reddy et al. 2013; Samanta 2013a, b; Majeed et al. 2015; Karami et al. 2013; Setare and Mubasher 2010; Sadjadi and Mubasher 2011; Yadav 2011; Yadav et al. 2011; Saha 2012; Sheykhi and Mubasher 2013)

Recently, Saha (2014) investigated a number of cosmological models, namely Bianchi type I, III, V, \(VI_0\), VI, and FRW space–time, for the anisotropic models. He used proportionality condition as an additional constraint and found that the matter distribution remains anisotropic in the Bianchi type \(VI_0\), V, III, and I models. In addition, he observed that at the early stage, the EoS parameter is positive, i.e., the universe was matter dominated at the early stage, but at later time, the universe is evolving with negative values, i.e., the present epoch. Moreover, in this work, he has studied a system of two fluids within the scope of spatially flat and isotropic FRW model. To investigate this, three different scale factors were used that give rise to a variable deceleration parameter.

Therefore, it will be interesting to study the evolution of holographic DE in an anisotropic model like Bianchi type-III space–time. In this paper, we considered the generalized holographic DE cosmological model in anisotropic Bianchi type-III space–time to investigate the correspondence with quintessence models of the universe. We obtained the EoS parameter for the holographic DE model in Bianchi type-III space–time in Sect. 2. In Sect.3, we solved the Einstein field equations by considering deceleration parameter to be constant proposed by Berman (1983) and obtained the solution. The correspondence between the holographic DE with quintessence is shown in Sect. 4. Some concluding remarks are given in Sect. 5.

2 Dark energy model in Bianchi type-III universe

In observational cosmology and dark energy model, Bianchi type cosmological models are playing an important role, because they seem to require an addition to the standard cosmological model with positive cosmological constant. Bianchi type models are spatially homogeneous and anisotropic universe models. The Bianchi type-III space–time is generally defined by the metric

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^{2}-a_1^2\mathrm{d}x^2-a_2^2e^{-2mx}\mathrm{d}y^2-a_3^2\mathrm{d}z^2. \end{aligned}$$
(1)

To study the mathematical model of the universe, the required Einstein’s field equation can be described as

$$\begin{aligned} R_{ij}-\frac{1}{2}g_{ij}R=-(T_{ij}+\bar{T_{ij}}), \end{aligned}$$
(2)

where, \(R_{ij}\) is the Ricci tensor and R is the Ricci scalar.

For the physical interpretation of the model, the energy momentum tensor for matter and holographic dark energy can be defined as

$$\begin{aligned} T_{ij}=\rho _mu_iu_j ; \bar{T}_{ij}=(\rho _\wedge +p_{\wedge })u_iu_j-g_{ij}p_\wedge \end{aligned}$$
(3)

where \(\rho _m\) and \(\rho _{\wedge }\) are the energy densities of matter and holographic dark energy, respectively, and \(p_{\wedge }\) is the pressure of the holographic dark energy. Now, the field equations for Bianchi type-III space–time in Einstein general theory of relativity in the presence of dark energy can be obtained as

$$\begin{aligned} \frac{\dot{a}_1\dot{a}_2}{a_1a_2}+\frac{\dot{a}_1\dot{a}_3}{a_1a_3}+\frac{\dot{a}_2\dot{a}_3}{a_2a_3}-\frac{m^2}{a_1^2}=\rho _m+\rho _{\wedge } \end{aligned}$$
(4)
$$\begin{aligned} \frac{\ddot{a}_2}{a_2}+\frac{\ddot{a}_3}{a_3}+\frac{\dot{a}_2\dot{a}_3}{a_2a_3}=-p_{\wedge } \end{aligned}$$
(5)
$$\begin{aligned} \frac{\ddot{a}_1}{a_1}+\frac{\ddot{a}_3}{a_3}+\frac{\dot{a}_1\dot{a}_3}{a_1a_3}=-p_{\wedge } \end{aligned}$$
(6)
$$\begin{aligned} \frac{\ddot{a}_1}{a_1}+\frac{\ddot{a}_2}{a_2}+\frac{\dot{a}_1\dot{a}_2}{a_1a_2}-\frac{m^2}{a_1^2}=-p_{\wedge } \end{aligned}$$
(7)
$$\begin{aligned} \frac{\dot{a}_1}{a_1}-\frac{\dot{a}_2}{a_2}=0. \end{aligned}$$
(8)

The general formulation of the average scale factor a and the average Hubble’s parameter H can be defined as

$$\begin{aligned} a=(a_1a_2a_3)^\frac{1}{3} \end{aligned}$$
(9)
$$\begin{aligned} H=\frac{1}{3}\bigl (\frac{\dot{a}_1}{a_1}+\frac{\dot{a}_2}{a_2}+\frac{\dot{a}_3}{a_3}\bigr ). \end{aligned}$$
(10)

The scalar expansion \(\theta\), of the model becomes

$$\begin{aligned} \theta = 3H=\bigl (\frac{\dot{a}_1}{a_1}+\frac{\dot{a}_2}{a_2}+\frac{\dot{a}_3}{a_3}\bigr ). \end{aligned}$$
(11)

The deceleration parameter q that describes the rate of expansion can be obtained as

$$\begin{aligned} q = -\frac{a\ddot{a}}{\dot{a}^2} = -1-\frac{\dot{H}}{H^2}. \end{aligned}$$
(12)

The shear scalar \(\sigma ^2\) and the average anisotropy parameter \(\triangle\) are, respectively, defined as

$$\begin{aligned} \sigma ^2=\frac{1}{2}\bigl (H_1^2+H_2^2+H_3^2-\frac{1}{3}\theta ^2\bigr ) \end{aligned}$$
(13)
$$\begin{aligned} \triangle =\frac{1}{3}\Sigma \bigl (\frac{\triangle H_i}{H}\bigr )^2; i=1,2,3. \end{aligned}$$
(14)

Here, \(\triangle H_i= H_i-H; i=1,2,3.\)

Now, the holographic dark energy density is given by

$$\begin{aligned} \rho _{\wedge }=3(\alpha H^2+\beta \dot{H}) \end{aligned}$$
(15)

with \(M_p^{-2}=8\pi G=1.\)

The continuity equation can be obtained as

$$\begin{aligned} \dot{\rho }_m + \dot{\rho _{\wedge }}+3H(\rho _m+\rho _{\wedge }+p_{\wedge })=0. \end{aligned}$$
(16)

The continuity equation of the matter and dark energy are, respectively, represented as

$$\begin{aligned} \dot{\rho }_m +3H \rho _m =0 \end{aligned}$$
(17)
$$\begin{aligned} \dot{\rho }_{\wedge } + 3H(\rho _{\wedge }+p_{\wedge })=0. \end{aligned}$$
(18)

The barotropic equation of state is

$$\begin{aligned} p_{\wedge }= w_{\wedge } \rho _{\wedge }. \end{aligned}$$
(19)

Using Eqs. (15) and (19) in Eq. (18), we obtained

$$\begin{aligned} w_{\wedge }=-1-\frac{2\alpha H \dot{H}+\beta \ddot{H} }{3H(\alpha H^2+\beta \dot{H})}. \end{aligned}$$
(20)

3 Solutions

From Eq. (8), we obtained

$$\begin{aligned} a_1=ka_2 \end{aligned}$$
(21)

where k is any non-zero constant of integration. The volume scale factor V can be defined as

$$\begin{aligned} V=a^3=a_1a_2a_3. \end{aligned}$$
(22)

The directional Hubble parameter in the direction of x, y, and z for the Bianchi type-III metric can be defined as follows:

$$\begin{aligned} H_x=\frac{\dot{a}_1}{a};H_y=\frac{\dot{a}_2}{a}; H_z=\frac{\dot{a}_3}{a}. \end{aligned}$$
(23)

Now, using Eqs. (21) and (23) in Eqs. (11) and (13), we obtained

$$\begin{aligned} \theta =u_{;i}^i=3H= 2\frac{\dot{a}_1}{a_1}+\frac{\dot{a}_3}{a_3} \end{aligned}$$
(24)
$$\begin{aligned} \sigma ^2=\frac{1}{2} \bigl (\sum H_i^2-\frac{\theta ^2}{3}\bigr )= \frac{1}{3}\bigl ( H_1-H_3\bigr )^2, \end{aligned}$$
(25)

The shear scalar may be taken to be proportional to the expansion scalar which envisages a linear relationship between the Hubble parameters \(H_1\) and \(H_3\),

$$\begin{aligned} H_3=\alpha _1 H_1 \end{aligned}$$
(26)

which leads to a relation between \(a_1\) and \(a_3\) as

$$\begin{aligned} a_3=a_1^{\alpha _1} \end{aligned}$$
(27)

where \(\alpha _1\) is a constant and is usually assumed to be positive. \(\alpha _1\) takes care of the anisotropic nature of the model. The expansion scalar and the shear scalar now be expressed in terms of the single time varying parameter \(H_1\) as

$$\begin{aligned} \theta =(\alpha _1+2)H_1 \end{aligned}$$
(28)
$$\begin{aligned} \sigma ^2=\frac{1}{3}(1-\alpha _1)^2 H_1^2. \end{aligned}$$
(29)

The field equations (4–8) are highly non-linear. Hence, to obtain determinate solution of the system, we can take the help of special law of variation proposed by Berman (1983) for Hubble’s parameter that yields constant deceleration parameter models of the universe. It may be noted here that most of the well-known models of the Einstein’s theory and alternative theories including inflationary models are models with constant deceleration parameter. Therefore, we can assume the average Hubble parameter H to be related to the average scale factor a, by the relation as follows:

$$\begin{aligned} H=na^{-\frac{1}{n}} \end{aligned}$$
(30)

where n is a non-zero constant. On solving Eq. (30), we obtained

$$\begin{aligned} a(t)= (t+c)^n. \end{aligned}$$
(31)

Using Eqs. (21), (22), and (27) and with the help of Eq. (31), one can obtain

$$\begin{aligned} a_1(t)=k^\frac{1}{\alpha _1+2}(t+c)^\frac{3n}{\alpha _1+2} \end{aligned}$$
(32)
$$\begin{aligned} a_2(t)=k^\frac{-(\alpha _1+1)}{\alpha _1+2}(t+c)^\frac{3n}{\alpha _1+2} \end{aligned}$$
(33)
$$\begin{aligned} a_3(t)=k^\frac{\alpha _1}{\alpha _1+2}(t+c)^\frac{3n\alpha _1}{\alpha _1+2}. \end{aligned}$$
(34)

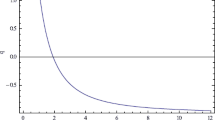
The deceleration parameter

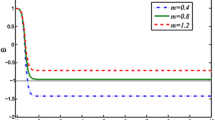
$$\begin{aligned} q=-1+\frac{1}{n} \end{aligned}$$
(35)

Since recent observational data indicate that the universe is accelerating and the value of deceleration parameter lies somewhere in the range \(-1<q<0\), and therefore, we have \(n>1\) for the accelerating universe.

The metric (1) with the help of Eqs. (32), (33), and (34) can now be written as:

$$\begin{aligned} \mathrm{d}s^2= \mathrm{d}t^2-k^\frac{1}{\alpha _1+2}(t+c)^\frac{3n}{\alpha _1+2}[\mathrm{d}x^2-k^{-1}e^{-2mx}\mathrm{d}y^2]-k^\frac{\alpha _1}{\alpha _1+2}(t+c)^\frac{3n\alpha _1}{\alpha _1+2}\mathrm{d}z^2. \end{aligned}$$
(36)

The directional Hubble’s parameter \(H_x\), \(H_y,\) and \(H_z\) have values given as:

$$\begin{aligned} H_x=\frac{3n}{(\alpha _1+2)(t+c)} \end{aligned}$$
(37)
$$\begin{aligned} H_y=\frac{3n}{(\alpha _1+2)(t+c)} \end{aligned}$$
(38)
$$\begin{aligned} H_z=\frac{3n\alpha _1}{(\alpha _1+2)(t+c)}. \end{aligned}$$
(39)

From Eq. (10), the mean Hubble’s parameter H has the value given by

$$\begin{aligned} H=\frac{n}{t+c} \end{aligned}$$
(40)

Using the directional and mean Hubble’s parameter, we obtained

$$\begin{aligned} \triangle =3\frac{(\alpha _1 -1)^2}{(\alpha _1+2)^2} .\end{aligned}$$
(41)

The dynamical scalars are given by

$$\begin{aligned} \theta =\frac{3n}{t+c} \end{aligned}$$
(42)
$$\begin{aligned} \sigma ^2=\frac{1}{3}(1-\alpha _1)^2\frac{9n^2}{[(\alpha _1+2)(t+c)]^2}. \end{aligned}$$
(43)

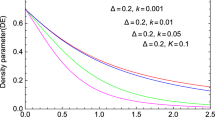
The matter density parameter \(\Omega _m\) and holographic dark energy parameter \(\Omega _{\wedge }\) are given by

$$\begin{aligned} \Omega _m =\frac{\rho _m}{3H^2} ; \Omega _{\wedge } =\frac{\rho _{\wedge }}{3H^2}. \end{aligned}$$
(44)

Using Eqs. (32)–(34), (40), and (44), we got

$$\begin{aligned} \Omega _m + \Omega _{\wedge } =3\frac{(2\alpha _1+1)}{(\alpha _1+2)^2}-\frac{m^2}{3n^2 k^\frac{2}{\alpha _1+2}(t+c)^{\frac{6n}{\alpha _1+2}-2}}. \end{aligned}$$
(45)

From Eq. (45), one can observe that the sum of the energy density parameters approaches to \(3\frac{2\alpha _1+1}{(\alpha _1+2)^2}\) as \(t\rightarrow \infty\). Therefore, at late times, the universe becomes flat. Therefore, for sufficiently large time, this model predicts that the anisotropy of the universe will damp out and universe will become isotropic. This result also shows that in the early universe, i.e., during the radiation and matter dominated era, the universe was anisotropic and the universe approaches to isotropy as dark energy starts to dominate the energy density of the universe. It is interesting to note that for \(\alpha _1=1,\) the universe becomes isotropic and the sum of the energy density parameters approaches to 1. This result is quite different from the result obtained by Pradhan et al. (2011), where they found in their model that the universe does not approach isotropy throughout the evolution.

Using Eq. (40) in Eqs. (15), (17), and (20), we found

$$\begin{aligned} \rho _{\wedge }=3\frac{\alpha _1(n\alpha _1-\beta )}{(t+c)^2} \end{aligned}$$
(46)
$$\begin{aligned} \rho _m=\frac{c_t}{(t+c)^{3n}} \end{aligned}$$
(47)
$$\begin{aligned} w_{\wedge }=-1+\frac{2}{3n}. \end{aligned}$$
(48)

Since recent observational data indicate that the universe is accelerating and the value of the deceleration parameter lies in the range \(-1<q<0\), so we have \(n>1\) for the accelerating universe. It is interesting to note that, from equation (48), one can observe that \(-1<w_{\wedge }<-\frac{1}{3}\), for \(n>1\). In this case, the holographic dark energy EoS parameter behaves like quintessence.

To get an idea about the geometric nature of the model, we calculate the state finder diagnostic pair r, s as

$$\begin{aligned} r=\frac{\dddot{a}}{aH^3}=\bigl (1-\frac{1}{n}\bigr )\bigl (1-\frac{1}{n}\bigr ) \end{aligned}$$
(49)
$$\begin{aligned} s=\frac{r-1}{3(q-\frac{1}{2})}=\frac{2}{3}\frac{\bigl (1-\frac{1}{n}\bigr )\bigl (1-\frac{1}{n}\bigr )}{\bigl (3-\frac{2}{n}\bigr )}. \end{aligned}$$
(50)

It is interesting to note here that the values of the state finder pair completely depend upon the value of the constant n, which are ultimately give constant values.

4 Holographic and quintessence scalar field model of dark energy

In this section, we have compared the EoS and the dark energy density for the corresponding models to establish the correspondence between the holographic dark energy and quintessence dark energy models.

The general formulation of action for the quintessence scalar \(\phi\) is given as

$$\begin{aligned} S=\int d^4x\sqrt{-g}\biggl [-\frac{1}{2}g^{ij}\partial _i\phi \partial _j\phi -V(\phi )\biggr ]. \end{aligned}$$
(51)

We have represented, respectively, the energy density and pressure for the quintessence scalar field represented as:

$$\begin{aligned} \rho _{\phi }=\frac{1}{2}\dot{\phi }^2+ V(\phi ) \end{aligned}$$
(52)
$$\begin{aligned} p_{\phi }=\frac{1}{2}\dot{\phi }^2-V(\phi ) \end{aligned}$$
(53)

where \(V(\phi )\) is denoting the quintessence potential.

The equation of state (EoS) for the scalar field is given by

$$\begin{aligned} \omega _{\phi }=\frac{{\dot{\phi }^2}-2V(\phi )}{{\dot{\phi }^2}+2V(\phi )}. \end{aligned}$$
(54)

From observations, we know that for the accelerated expansion of the universe, the equation of state parameter for quintessence must be less than \(-\frac{1}{3}\).

From Eqs. (48) and (54), we obtained

$$\begin{aligned} -1+\frac{2}{3n}=\frac{{\dot{\phi }^2}-2V(\phi )}{{\dot{\phi }^2}+2V(\phi )}. \end{aligned}$$
(55)

Again, comparing Eqs. (15) and (52), we conclude that

$$\begin{aligned} \rho _{\wedge }=3(\alpha H^2+\beta \dot{H})=\frac{1}{2}\dot{\phi }^2+V(\phi ). \end{aligned}$$
(56)

From Eqs. (54) and (55), the kinetic energy term and the quintessence potential in power-law form can be obtained as follows:

$$\begin{aligned} \phi -\phi _0=(2(n\alpha -\beta ))^\frac{1}{2} ln\biggl (\frac{t+c}{t_0+c}\biggr ) \end{aligned}$$
(57)
$$\begin{aligned} V(\phi )=(3n-1)(n\alpha -\beta )(t+c{-2}). \end{aligned}$$
(58)

Using Eq. (57) in Eq. (58), the potential in the exponential form can be obtained as

$$\begin{aligned} V(\phi )=(3n-1)(n\alpha -\beta ) t_0^{-2} exp\biggl (-\frac{1}{(2(n\alpha -\beta ))^\frac{1}{2}} (\phi -\phi _0)\biggr ) \end{aligned}.$$
(59)

Again, from observational point of view, this type of exponential potential can produce an accelerated expansion of the universe for \(n>1\). Hence, we have established a correspondence between the holographic dark energy and quintessence scalar field, and describe holographic dark energy by making use of quintessence.

5 Conclusions

Bianchi type models are nine in number, but according to the classification, it splits in two classes. There are six models in class A (I, II, \(VI_1\), VII, VIII, and IX) and five in class B (III, IV, V, \(VI_h,\) and \(VII_h\)). Spatially homogeneous cosmological models play an important role to understand the structure and properties of the space of all cosmological solutions of Einstein field equations. These spatially homogeneous and anisotropic models are the exact solutions of Einstein Field equations and are more general than the Friedman models in the sense that they can provide interesting results pertaining to the anisotropy of the universe. Moreover, the problem of global anisotropy has gained a lot of research interest. The standard cosmological model (\(\Lambda\)CDM) based upon the spatial isotropy and flatness of the universe is consistent with the data from precise measurements of the CMB temperature anisotropy from Wilkinson Microwave Anisotropy Probe(WMAP). However, the \(\Lambda\)CDM model suffers from some anomalous features at large scale and signals a deviation from the usual geometry of the universe. In addition, precise measurements from WMAP predict asymmetric expansion with one direction expanding differently from the other two transverse directions at equatorial plane which signals a non trivial topology of the large scale geometry of the universe.

It is well known that the holographic dark energy cosmological model with quintessence in general relativity plays a vital role in the discussion of the accelerated expansion of the universe which is the crux of the problem in the present scenario. Evolution of Bianchi type-III cosmological model is studied in the presence of holographic dark energy and quintessence with negative constant deceleration parameter. Though the present day universe appears to be isotropic, there is no evidence that the early universe was also of the same type. There is a cosmological view that the universe might be inhomogeneous and anisotropic in the very early era, and that in the course of its evolution, their characteristics have been wiped out under the action of some process or mechanism, and finally, an isotropic and homogeneous universe had resulted. Observational data also suggest that dark energy is responsible for gearing up the universe some five billion years ago. However, at that time, the universe need not to be isotropic. Therefore, in this paper, we assume the universe to be anisotropic and consider a homogeneous Bianchi type-III universe filled with matter and holographic dark energy. Our solution describes the accelerated expansion of the universe under certain conditions. The EoS parameter of the holographic dark energy behaves like quintessence EoS. For \(\alpha _1=1\), we obtained that the universe is isotropic throughout the evolution; the universes approaches to isotropy as \(t\rightarrow \infty\) for \(\alpha _1\ne 1\). We also established a correspondence between the holographic dark energy models with the quintessence scalar field dark energy models in Bianchi type-III universe.

Quintessence potential and the dynamics of the quintessence scalar field are reconstructed for this anisotropic accelerating model of the universe. Our result shows that the universe has anisotropic in the early stage, and at the late time, dynamics anisotropy of the universe dams out, and the present day, universe becomes isotropy as suggested by different observational data (Collins and Hawking 1973). Results and solutions of our model are quite different from the result and solutions obtained by Saha (2014), viz.; here, we obtained a isotropic model for \(\alpha _1=1\) throughout the evolution, whereas they observed that the model is anisotropic throughout the evolution. Moreover, Saha (2014) results on the LRS Bianchi type-I space–time filled with perfect fluid and anisotropic dark energy possessing dynamical energy density is remarkable which is in consistent with Bianchi type-III model also.