1 Introduction

Our universe is experiencing accelerated expansion that has been validated by many cosmological observations such as Type 1a Supernova [1, 2] and cosmic microwave background radiation [3, 4]. Two theories potentially explain the universe’s rapid expansion: (i) a mysterious force called Dark Energy (DE) (see [5,6,7,8] and references therein), and (ii) a modification of the General Theory of Relativity [9,10,11,12,13,14,15]. Moreover, WMAP estimates that nearly 73, 23, and 4% of our universe filled up with dark energy, dark matter and normal matter, respectively [16]. There are other types of dark energy models, including quintessence [17], k-essence [18], Chaplygin gas [19], holographic dark energy [20, 21], new agegraphic dark energy [22], and others. Existing measurements, in accordance with [23], point to a cosmic constant, i.e. \(\omega \approx - 1\). A useful tool for explaining the cosmic expansion at this time is the study of the holographic dark energy model [24] in the context of the holographic principle (HP) [20, 21]. There are other reading materials accessible (check references for illustration [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]). Assuming c is an arithmetic constant, the energy density of the HDE is written as \(\rho_{{\rm d}e} = 3c^{2} M_{p}^{2} L^{ - 2}\). System entropy (S), the IR (L), and UV cutoffs are correlated in \(L^{3} \Lambda^{3} \le S^{\frac{3}{4}}\) [24]. Following their work in [43], the authors have presented \(S_{\delta } = \gamma A^{\delta }\) (the horizon entropy of a black hole), where (i) A denotes the area of the horizon, (ii) δ denotes the non-additivity parameter, and (iii) γ deflects an unspecified constant. The consequence of this is \(\Lambda^{4} \le \left( {\gamma \left( {4\pi } \right)^{\delta } } \right)L^{2\delta - 4}\) [24]. Many dark energy models have been developed to represent or comprehend the accelerated phase of the universe; however, the challenge of distinguishing the numerous contenders is now required. To be able to discern between various conflicting cosmological scenarios, including dark energy, a sensitive and detailed analysis of dark energy ideas is needed. The long-range nature of gravity, the enigmatic character of space–time, and the fact that the Bekenstein entropy is a non-extensive entropy measure have all recently contributed to this. To examine cosmological and gravitational phenomena, the generalized entropies, or Tsallis and Rényi entropies, have been assigned to the horizons. Many extended entropy formalisms have been used to explore cosmological and gravitational events, but Tsallis and Rényi entropies produce the most accurate universe model. The horizon is given Tsallis and Rényi entropies in order to study the cosmic repercussions. Tsallis HDE, Renyi HDE, and Sharma Mitall Holographic Dark Energy (SMHDE) believe that the universe is made up of both interacting dark energy and cold dark matter in order to understand the accelerated expansion of our universe.

The dynamics of the Tsallis HDE and the increase in energy density are governed by its free parameters, which is what makes Tsallis HDE so intriguing because it exhibits good agreement with the expansion of the universe and exhibits a certain form of cosmological stability. The non-extensive Tsallis entropy within the context of cosmology has recently sparked a lot of curiosity. It has been proposed that the Tsallis parameter modifies the gravitational constant's strength and, consequently, the energy density of the universe's dark matter and dark energy, requiring less (more) dark energy to produce the late-time acceleration. The Tsallis cosmology/entropy experiments were also expanded to include the situation with a changeable Tsallis parameter [44]. It was shown that the additional terms from the Tsallis non-extensive entropy can serve as an efficient dark energy for explaining how the cosmos evolved from the early epoch to late-time acceleration [45]. The literature describes the construction of the Tsallis HDE [46, 47], Sharma-Mittal HDE (SMHDE) [48], and Renyi HDE model [49]. The Renyi HDE model was investigated in [50], with the IR cutoff serving as the Hubble horizon. The authors of Ref. [51] explored Tsallis, Renyi, and Sharma-Mittal entropies in the context of Chern-Simons modified gravity, whereas Ghaffari et al. [52] considered Tsallis HDE in various brane worlds. Jawad et al. investigated the Tsallis HDE, Renyi HDE, and Sharma-Mittal HDE models in loop quantum cosmology in [53]. Ghaffari et al. [54] investigated the implications of using the Tsallis HDE model to model dark energy in the Brans-Dicke cosmology. The authors of [55] investigated whether interacting Tsallis HDE can have a significant impact on the universe’s intergalactic progress. The energy conservation law for Tsallis HDE does not hold in Brans-Dicke gravity, according to Yadav [56].

Numerous attempts have been made by many cosmologists to modify the geometrical action and explain the late-time accelerated expansion phase of the universe. Modified gravity is mostly used as a substitute of dark energy and exotic matters with the introduction of higher order Ricci scalar modification. According to \(f(R)\) [57,58,59], and \(f(G)\) [60], “Modified theories of gravity are desired to detect faster expansion and give a substitute for the DE.” The authors of Refs. [61,62,63,64]. state that the torsion term T in the teleparallel scenario is modified by an arbitrary function with a changing action known as \(f(T)\) gravity, which is adjusted from the curvature term R in general relativity. Bamba and Geng examined the thermodynamics of the apparent horizon in [65]. In Ref. [66], Sharif and Rani looked into two subjects: the dynamic instability of a collapsing spherically symmetric star and charged wormhole solutions gravity with non-commutative background. Numerous scientists have recently explored \(f(T)\) gravity in relation to numerous cosmological features [67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84]. Inciting with above discussion, in this work, the author was interested in investigating an interacting scenario between two fluids, pressureless dark matter and dark energy in \(f(T)\) gravity toward FRW Universe. In light of the aforementioned discussion, the author investigates the Renyi HDE and Tsallis HDE \(f(T)\) gravity models.

2 Review of \(f(T)\) gravity

The action for \(f(T)\) theory of gravity is given by [65].

$$S = \int {\left[ {T + f(T) + L_{{{\text{matter}}}} } \right]} e{\kern 1pt} {\kern 1pt} d^{4} x.$$
(1)

Here \(f(T)\) represents an algebraic function of the torsion scalar \(T\). Making the functional variation of the action (1) with respect to the tetrads, one can get the following equations of motion [85, 86]

$$\begin{aligned} & S_{\mu }^{\nu \rho } \partial_{\rho } Tf_{TT} + \left[ {e^{ - 1} e_{\mu }^{i} \partial_{\rho } (ee_{i}^{\alpha } S_{\alpha }^{\nu \rho } ) + T_{\lambda \mu }^{\alpha } S_{\alpha }^{\nu \lambda } } \right](1 + f_{T} ) \\ & \quad + \frac{1}{4}\delta_{\mu }^{\nu } (T + f) = T_{\mu }^{\nu } ,\end{aligned}$$
(2)

where the energy momentum tensor is \(T_{\mu }^{\nu }\), \(f_{T} = \frac{{{\text{d}}f(T)}}{{{\text{d}}T}}\). Now, the energy momentum tensor for the obtained model of two fluids is defined as \(T_{\mu }^{\nu } = T_{\mu v}^{m} + T_{\mu v}^{{\rm d}e}\), where \(T_{\mu \nu }^{m} = \rho_{m} u_{\mu } u_{\nu }\); \(T^{{\rm d}e}_{\mu \nu } = (\rho_{{\rm d}e} + p_{{\rm d}e} )u_{\mu } u_{\nu } - g_{\mu \nu } p_{{\rm d}e} ,\) whereas \(\rho_{m}\) and \(\rho_{{\rm d}e}\) represent the energy density of matter and DE density.\(p_{{\rm d}e}\) is the pressure of the DE while equation of state (EoS) is defined as \(\omega_{{\rm d}e} = \frac{{p_{{\rm d}e} }}{{\rho_{{\rm d}e} }}\).The energy–momentum tensor of DE can be parameterized as

$$T_{\mu v}^{{\rm d}e} = ( - \omega_{{\rm d}e}, - \omega_{{\rm d}e} , - \omega_{{\rm d}e} ,1)\rho_{{\rm d}e} .$$
(3)

3 Metric and field equations

Assume that the universe is described by the homogeneous, isotropic and spatially FLRW metric given

$${\text{d}}s^{2} = {\text{d}}t^{2} - a^{2} (t)\left\{ {\frac{{{\text{d}}r^{2} }}{{1 - kr^{2} }} + r^{2} ({\text{d}}\theta^{2} + \sin^{2} \theta {\text{d}}\varphi^{2} )} \right\}.$$
(4)

The spherical coordinate system is azimuthal and polar angles are \(0 \le \theta \le \pi\) and \(0 \le \varphi \le \pi\), respectively. The following considerations can be made in light of the space’s curvature indicated by \(k\). It is related to the closed universe \(k = 1\), the flat universe \(k = 0\), and the open universe \(k = - 1\), respectively. In this work, the flat universe is purposefully taken into account. We obtain the torsion scalar as \(T = - 6H^{2}\). The Hubble parameter is defined as \(H = \frac{{\dot{a}}}{a}\). The field Eqs. (2) for the line element (4) take on the following form using Eq. (3)

$$\frac{{\dot{a}}}{a}\dot{T}f_{TT} + \left[ {\frac{{\ddot{a}}}{a} + 2\frac{{\dot{a}^{2} }}{{a^{2} }}} \right]\left( {1 + f_{T} } \right) + \frac{1}{4}\left( {T + f} \right) = - \omega_{{{\text{d}}e}} \rho_{{{\text{d}}e}} ,$$
(5)
$$3\left( {1 + f_{T} } \right)\frac{{\dot{a}^{2} }}{{a^{2} }} + \frac{1}{4}\left( {T + f} \right) = (\rho_{m} + \rho_{{{\text{d}}e}} ),$$
(6)

where dot stands for differentiation with respect to time.

4 Power law expansion solution

Equations (5) and (6) are two independent equations in six unknowns. Therefore, to obtain explicit solutions of the system, additional constraints relating these parameters are required. We consider in the following the power-law mode of the scalar factor in terms of cosmic time \(a = t^{n}\) [87,88,89], where \(n > 0\) is a constant, to describe the evolution of cosmological parameters. The choice of such a scale factor was motivated by the fact that the universe is expanding at a faster rate currently and has slowed in the past. For various numbers of n, different stages of the cosmos are expected. The model describes the universe's decelerating phase for \(0 < n < 1\) while it accelerates for \(n > 1\). The model displays singularity at an early stage. The big-bang at the first epoch will now cause the model to jerk. According to the following relationship, the scale factor \(a(t)\) and redshift z are related: \((1 + z) = \frac{{a_{0} }}{a}\), where \(a_{0}\) represents the current value of the scale factor. The deceleration parameter represents \(q = \frac{d}{{{\text{d}}t}}\left( \frac{1}{H} \right) - 1 = \frac{1}{n} - 1\). The deceleration parameter exhibits signature flipping on the constraints of n. The universe accelerates for \(q < 0\) and inflates for \(q > 0\). The deceleration parameter \(q \cong - 0.733\) is achieved after choosing \(n = 3.75\). If the observational data from the ΛCDM are used, the current value of DP might be \(q_{0} = - 0.6\).

5 Renyi Holographic dark energy model with Hubble’s horizon cutoff

The energy density of Renyi HDE is characterized as follows \(\rho_{{{\text{d}}e}} = \frac{{3\beta^{2} }}{{8\pi L^{2} }}\left( {1 + \pi \delta L^{2} } \right)^{ - 1}\), where \(\beta\) and \(\delta\) are constants. By considering the Hubble horizon as a candidate for the IR-cutoff, i.e.

$$L = H^{ - 1} \, {\text{as}}\,\rho_{{{\text{d}}e}} = \frac{{3\beta^{2} n^{2} }}{{8\pi t^{2} }}\left( {1 + \frac{{\pi \delta t^{2} }}{{n^{2} }}} \right)^{ - 1}$$
(7)
$${\text{The}}\,{\text{energy}}\,{\text{density}}\,{\text{of}}\,{\text{matter}}\,{\text{is}}\,{\text{obtained as}}\,\rho_{m} = \frac{{3n^{2} }}{{2t^{2} }} - \frac{{3\beta^{2} n^{2} }}{{8\pi t^{2} }}\left( {1 + \frac{{\pi \delta t^{2} }}{{n^{2} }}} \right)^{ - 1} .$$
(8)

The equation of state (EoS) parameter, which describes the relationship between pressure \(p_{{{\text{d}}e}}\) and dark energy density \(\rho_{{{\text{d}}e}}\), is frequently used to categorize the many parts of the expanding cosmos. EoS parameter is used to categorize decelerated and accelerated phases of the universe. The DE dominated phase has following eras:

  • Stiff fluid for \(\omega = 1\).

  • Radiation era for \(0 < \omega < {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}\).

  • Cold Dark Matter or dust fluid for \(\omega = 0\).

  • The cosmological constant, or \(\Lambda\) CDM model for \(\omega =-1\)

  • Phantom era (\(\omega < - 1\)).

    $${\text{The}}\,{\text{EoS}}\,{\text{parameter}}\,{\text{of}}\,{\text{Renyi}}\,{\text{HDE}}\,{\text{is}}\,{\text{obtained as}}\,\omega_{{{\text{d}}e}} = \frac{{\frac{{ - n^{2} }}{{t^{2} }}}}{{\frac{{3\beta^{2} n^{2} }}{{8\pi t^{2} }}\left( {1 + \frac{{\pi \delta t^{2} }}{{n^{2} }}} \right)^{ - 1} }}.$$
    (9)

Quintom period is a combination of phantom and quintessence. The Renyi HDE density parameter and the matter energy density parameter are described by

$$\Omega_{{{\text{d}}e}} = \frac{{\rho_{{{\text{d}}e}} }}{{3H^{2} }} = \frac{{\left\{ {\frac{{3\beta^{2} n^{2} }}{{8\pi t^{2} }}\left( {1 + \frac{{\pi \delta t^{2} }}{{n^{2} }}} \right)^{ - 1} } \right\}}}{{\frac{{3n^{2} }}{{t^{2} }}}},\;\Omega_{m} = \frac{{\rho_{m} }}{{3H^{2} }} = \frac{{\left\{ {\frac{{3n^{2} }}{{2t^{2} }} - \frac{{3\beta^{2} n^{2} }}{{8\pi t^{2} }}\left( {1 + \frac{{\pi \delta t^{2} }}{{n^{2} }}} \right)^{ - 1} } \right\}}}{{\frac{{3n^{2} }}{{t^{2} }}}}.$$
(10)
$${\text{Hence}}\,\Omega = \Omega_{m} + \Omega_{{{\text{d}}e}} = 1.$$
(11)

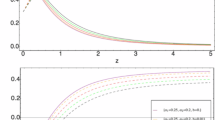
The behavior of Renyi HDE density versus z for various values \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt}\) and \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt}\) is shown in Fig. 1.It is observed that as the Universe expands, the energy density of Renyi HDE \(\rho_{{{\text{d}}e}}\) stays positive and decreasing function of cosmic time (or increasing function of redshift). The results indicate that “the energy density of matter falls from a high red-shift zone to a low red-shift region, i.e. from past to future.” Also they tend to zero in the future. The behavior of the Renyi HDE EoS parameter as a function of z for various values \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt}\) and \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt}\) is depicted in Fig. 2. In conclusion \(- 1 \le z \le 0\), it is observed that the model has crossed the quintessence phase (\(- 1 < \omega_{{{\text{d}}e}} < - 0.33\)), or Cosmological constant, i.e. finally, the model approaches the quintessence area for the value \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt}\), whereas for the value of \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt}\), the \(\Lambda\) CDM model leans toward the phantom region \(\left( {\omega_{{{\text{d}}e}} < - 1} \right)\). Also, the EoS parameter corresponding to the Observational Hubble datasets (OHD) + Pantheon is \({\omega }_{0}= - 0.7161\). Furthermore for \(z > 0\), the Renyi HDE EoS parameter leans toward the quintessence model which indicate the cosmic acceleration of the universe. Therefore, it is concluded that the dark energy EoS parameter shows a rich behavior; it can be quintessence-like, crossing the phantom-divide line, or phantom-like depending on the value of δ. The total energy density parameters (Ω) i.e. the sum of the matter energy density parameter and the Renyi HDE density parameter is one indicated by Eq. (11), which gives the affirmation that as the dark energy dominates the universe energy density, the universe shows the isotropic nature.

Fig. 1
figure 1

Renyi HDE density shown against z for \(\beta = 1.2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (blue) and \(\beta = 1.2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (green) (color figure online)

Full size image
Fig. 2
figure 2

Renyi HDE EoS parameter shown against z for \(\beta = 1.2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (red) and \(\beta = 1.2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (green) (color figure online)

Full size image

6 Tsallis holographic dark energy model with Hubble’s horizon cutoff

Tsallis and Citro [43] suggested that the Tsallis generalized entropy-area relation is independent of the gravitational theory used to describe the system. Hence the energy density of THDE is defined as

$$\rho_{{{\text{d}}e}} = L^{2\delta - 4} ,$$
(12)

where \(\delta\) is identical. For the value of \(\delta = 1\), the energy density of the Tsallis holographic dark energy is moderated by the energy density of the HDE model. By choosing the simplest IR-cutoff as Hubble horizon (\(L = H^{ - 1}\)), the corresponding energy density becomes \(\rho_{{\rm d}e} = \frac{1}{{H^{2\delta - 4} }}\)

$${\text{The}}\,{\text{density}}\,{\text{of}}\,{\text{Tsallis}}\,{\text{HDE}}\,{\text{is}}\,{\text{obtained}}\,{\text{as}}\,\rho_{{{\text{d}}e}} = \left( \frac{t}{n} \right)^{2\delta - 4} .$$
(13)
$${\text{The}}\,{\text{energy}}\,{\text{density}}\,{\text{of}}\,{\text{matter}}\,{\text{is}}\,{\text{found}}\,{\text{out}}\,{\text{to}}\,{\text{be}}\,\rho_{m} = \frac{{3n^{2} }}{{2t^{2} }} - \left( \frac{t}{n} \right)^{2\delta - 4} .$$
(14)
$${\text{The}}\,{\text{Tsallis}}\,{\text{HDE}}\,{\text{EoS}}\,{\text{parameter}}\,{\text{is}}\,{\text{characterized}}\,{\text{as}}\, \omega_{{{\text{d}}e}} = \frac{{\frac{{ - n^{2} }}{{t^{2} }}}}{{\left( \frac{t}{n} \right)^{2\delta - 4} }}.$$
(15)

The parameter for matter energy density and the Tsallis HDE are both written as

$$\Omega_{{{\text{d}}e}} = \frac{{\rho_{{{\text{d}}e}} }}{{3H^{2} }} = \frac{{\left\{ {\left( \frac{t}{n} \right)^{2\delta - 4} } \right\}}}{{\frac{{3n^{2} }}{{t^{2} }}}},\;\Omega_{m} = \frac{{\rho_{m} }}{{3H^{2} }} = \frac{{\left\{ {\frac{{3n^{2} }}{{2t^{2} }} - \left( \frac{t}{n} \right)^{2\delta - 4} } \right\}}}{{\frac{{3n^{2} }}{{t^{2} }}}}.$$
(16)
$${\text{Hence}}\,\Omega = \Omega_{m} + \Omega_{{{\text{d}}e}} = 1.$$
(17)

There is a correlation between the running behavior of δ and the EoS, which is an intriguing cosmological phenomenon shown by the Tsallis HDE, or the modified cosmological scenario with varying exponent [90,91,92]. The entropy relates to physical degrees of freedom, whereas the renormalization of quantum theory indicates that degrees of freedom depend on scale. Figure 3 shows the behavior of Tsallis HDE density against z for the values \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt}\) and \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt}\). The Tsallis energy density \(\rho_{{{\text{d}}e}}\) is positive and diminishing as the universe changes. The behavior of the Tsallis HDE EoS parameter against z for various values \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt}\) and \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt}\) is shown in Fig. 4. In Eq. (15), the EoS is explained in terms of n and δ. The values of δ must justify the restrictions followed from Eq. (15), to get the accelerated expansion. Overall \(- 1 \le z \le 0\), the model is found to cross the quintessence phase (\(- 1 < \omega_{{\rm d}e} < - 0.33\)), Cosmological constant, i.e. for the value of \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt}\) the \(\Lambda\) CDM model slants to \(\left( {\omega_{{\rm d}e} < - 1} \right)\), whereas for the value of \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt}\) the model approaches the region of the quintessence. Additionally \(z > 0\), the Tsallis HDE EoS parameter favors the Quintessence model. The dark energy sector can therefore be quintessence-like, phantom-like, or experience the phantom-divide crossing before or after the current time, depending on the values of δ. The resulting model’s findings are in strong accord with the available observational data. We have compared the derived results with the most recent Planck collaboration data [93], where the limitations on the EoS parameter are stated.

$$\left\{ \begin{array}{*{20}l} \omega_{{{\text{d}}e}} = - 1.56_{ - 0.48}^{ + 0.60} ({\text{Plank}} + TT + {\text{lowE}}) \hfill \\ \omega_{{{\text{d}}e}} = - 1.58_{ - 0.41}^{ + 0.52} ({\text{Plank}} + TT,TE,EE + {\text{lowE}}) \hfill \\ \omega_{{{\text{d}}e}} = - 1.57_{ - 0.40}^{ + 0.50} ({\text{Plank}} + TT,TE,EE + {\text{lowE}} + {\text{lensing}}) \hfill \\ \omega_{{{\text{d}}e}} = - 1.04_{ - 0.10}^{ + 0.10} ({\text{Plank}} + TT,TE,EE + {\text{lowE}} + {\text{lensing}} + {\text{BAO}}) \hfill \\ \end{array} \right\}$$
Fig. 3
figure 3

Density of THDE against z for \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (brown) and \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (pink) (color figure online)

Full size image
Fig. 4
figure 4

Plot of the THDE EoS parameter against z for \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (green) and \({\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = 4.5{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} n = {\kern 1pt} 1.5\) (purple) (color figure online)

Full size image

It can be seen that the results for the EoS parameter of both Renyi HDE and Tsallis HDE are consistent with the Planck Collaboration data [93]. The derived model predicts a flat universe because the overall energy density tends to unity.

7 Statefinder diagnostics

The accurate explanation of expansion of the universe can be done by using Hubble and deceleration parameters. The values of these parameters, however, are the same in many dynamical dark energy models at the moment. The best suited model among the numerous dynamical dark energy models cannot be found using these parameters. In 2003, Sahni et al. introduced the cosmological diagnostic pair, where r and s are defined as

$$r = \frac{\dddot a}{{aH^{3} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} s = \frac{(r - 1)}{{3\left( {q - \frac{1}{2}} \right)}}$$
(18)

The correlation between the parameters is given by

$$r = \frac{{9s^{2} - 9s + 2}}{2}.$$
(19)

The following is a description of the statefinder parameters:

  • \((r,s) = (1,0)\)\(\leftrightarrow\) \(\Lambda\) CDM model.

  • \((r,s) = (1,1)\)\(\leftrightarrow\) SCDM model.

  • \(s > 0\) and \(r < 1\)\(\leftrightarrow\) Quintessence.

  • \(s < 0\) and \(r > 1\)\(\leftrightarrow\) Chaplygin gas, and

  • \((r,s) = \left( {1,\frac{2}{3}} \right)\)\(\leftrightarrow\) HDE.

The major goal is to analyze how the trajectory of the r−s parametric curve corresponds to the \(\Lambda\) CDM model in terms of convergence and divergence. The deviation from indicates a departure from the \(\Lambda\) CDM model. Hence, in the near future, it will be important to describe the dark energy models. Figure 5 depicts the model's predicted behavior [94]. The parameter trajectories \(\left\{ {r,s} \right\}\) are given in Fig. 5. The parameter s is seen to remain negative for all values of r. This suggests that the HDE models and the Chaplygin gas model corresponded. Moreover, at late times, the r−s plane coincides to \(\Lambda\) CDM limit. Figure 5 suggests that the model will take place concurrently with the \(\Lambda\) CDM flat model. The conduct fits with accepted cosmology.

Fig. 5
figure 5

The graph shows the relationship between r and s

Full size image

8 Observational constraints

8.1 Distance modulus, luminosity distance, and redshift

Given the scale factor a and the redshift z, \(1 + z = \left( {\frac{{t_{0} }}{t}} \right)^{n}\), one can arrive at the following equation, which results through mathematical manipulation \(t = t_{0} \left( {1 + z} \right)^{{ - \frac{1}{n}}}\). An alternative form of above equation is \(H_{0} \left( {t_{0} - t} \right) = n\left[ {1 - \left( {1 + z} \right)^{{ - \frac{1}{n}}} } \right]\), where \(H_{0}\) is the current value of the Hubble’s parameter. In the event of a smallest redshift z, \(H_{0} \left( {t_{0} - t} \right) = n\left[ {\frac{z}{n} - \frac{{\frac{1}{n}\left( {\frac{1}{n} - 1} \right)}}{2}z^{2} + \cdots } \right]\). Hence,\(H_{0} \left( {t_{0} - t} \right) = \left[ {z - \frac{q}{2n}z^{2} + \cdots } \right]\). The expression for the distance modulus is

$$\mu (z) = 5\log d_{{\text{L}}} (z) + 25,$$
(20)

where \(d_{\rm L} (z)\) is the luminance distance and is written as \(d_{{\text{L}}} = r_{1} (1 + z)a_{0}\). For the purpose of determining \(r_{1}\), assume that a photon is emitted by a source with coordinates at \(r = r_{0}\) to \(t = t_{0}\) and received at a time t by an observer placed at \(r = 0\),

$$r_{1} = \int\limits_{t}^{{t_{0} }} {\frac{{{\text{d}}t}}{a}} = \int\limits_{t}^{{t_{0} }} {t^{ - n} {\text{d}}t} .$$
(21)

The luminosity distance expression can be expressed as

$$d_{{\text{L}}} = \tfrac{{(1 + z)H_{0}^{ - 1} \left[ {1 - (1 + z)^{{^{{1 - \frac{1}{n}}} }} } \right]}}{(1 - n)}.$$
(22)

Red shift causes the luminosity distance to increase more quickly, as expected from supernova data. Using Eqs. (20) and (22) yields

$$\mu (z) = 5\log \left\{ {\tfrac{{(1 + z)H_{0}^{ - 1} \left[ {1 - (1 + z)^{{^{{1 - \frac{1}{n}}} }} } \right]}}{(1 - n)}} \right\} + 25.$$
(23)

The distance modulus shows some potential with SN Ia statistics.

The distance modulus of the proposed model is in good agreement with SN Ia data, and the theoretical values generated from the derived model have been compared with SNe Ia related 581 data’s from Pantheon compilation [95]. Figure 6 in this analysis shows the contrast between the distance modulus of the derived model and the observational \(\mu (z)\) SN Ia data from Amanullah et al.[96], Yadav et al. [97], and Katore and Kapse [98]. Also, a comparison between the distance modulus of the calculated model and the range’s observational \(\mu (z)\) SN Ia data has been shown in (Table 1). It has been found that the developed model closely matches the physically plausible observed values for SN Ia.

Fig. 6
figure 6

The distance modulus as a function of z

Full size image
Table 1 Comparison between the results of observed data and present power law model
Full size table

9 Conclusions

In this paper, the main interest is to know the reason behind the universe’s rapid expansion. The Renyi HDE and Tsallis HDE models for \(f(T)\) gravity were used in this investigation. The Renyi HDE and Tsallis HDE energy densities are increasing functions of z, as shown by the Hubble horizon cutoff, supporting the universe’s ascending behavior. For example \(- 1 \le z \le 0\), Renyi HDE's EoS value is getting close to the phantom area, yet Tsallis HDE approves Quintessence. Since \(0 < z\) the Tsallis HDE settles in the Quintessence zone, the Renyi HDE EoS parameter tends to favor the \(\Lambda\) CDM model. In order to guarantee model consistency, the EoS parameters of Renyi HDE and Tsallis HDE are in the accelerated stage dominated by the dark energy era. Exact information about the EoS of DE at the present epoch and its evolution will provide valuable insights into cosmic evolution leading to the late-time cosmic acceleration. The developed models perform similar to the \(\Lambda\) CDM model [99,100,101,102]. As a result, both current evidence of cosmic expansion and well-known theoretical findings support the derived models.