1 Introduction

In the last few decades, there has been considerable interest in studying alternative theories of gravitation, the most important among them being the scalar–tensor theories proposed by Lyra (1951), Brans and Dicke (1961), Nordverdt (1970), Wagoner (1970), Ross (1972), Dunn (1974), Barber (1985), Saez and Ballester (1986), La and Steinhardt (1991). Saez and Ballester (1986) have put forward a scalar-tensor theory of gravity in which the metric is coupled to a scalar field. This modification helped to solve the ‘missing mass problem’. The study of cosmological models in the framework of scalar–tensor theories has been an active area of research in the last few decades. Cosmological models within the framework of the Sáez–Ballester scalar–tensor theory of gravitation have been studied by several relativists and they obtained solutions in the Sáez–Ballester scalar–tensor theory of gravitation in different contexts (Singh & Agrawal 1991, 1992; Ram & Tiwari 1998; Singh & Ram 2003; Mohanty & Sahu 2003, 2004; Reddy et al. 2006, 2008; Katore et al. 2010; Rao et al. 2011; Jamil et al. 2012; Samanta et al. 2013; Ghate & Sontakke 2014; Katore & Shaikh 2014b, 2015a, b).

The expansion of the universe is accelerating and are presented by two groups (the Supernova Cosmology Project and the High-Z team) (Garnavich et al. 1998a, b; Perlmutter et al. 1997, 1998, 1999; Riess et al. 1998, 2000, 2004; Schmidt et al. 1998; Tonry et al. 2003). A mysterious energy form called the dark energy (DE) may be responsible for the expansion and acceleration of the universe. DE obeys a simple EoS in the form \(p=w\rho \), where \(\rho \) is the energy density, p is the isotropic pressure and w is the EoS parameter, which is not necessarily constant. The Wilkinson Microwave Anisotropy Probe (WMAP) measures that dark energy, dark matter and baryonic matter occupies 73%, 23% and 4% respectively, of the energy-mass content of the universe. Also, \(w=-1\) is the simplest candidate of dark energy, i.e. cosmological constant with time-dependent equation of state. The quintessence, phantom, quintom, tachyon, dilaton with interacting dark energy models like holographic and agegraphic models are the other dynamical dark energy models with time-dependent equation of state that are studied to explain the accelerated expansion of the universe.

In recent years, holographic dark energy (HDE) models have received considerable attention by describing dark energy cosmological models. Several properties of the holographic Ricci DE have been investigated by Cohen et al. (1999), Huang and Li (2004), Zhang and Wu (2005), Gao et al. (2009), Hsu (2014). Granda and Oliveros (2008) proposed a new cutoff based on purely dimensional grounds, by adding a term involving the first derivative of the Hubble parameter. The proposed form of the holographic density is \(\rho _{\mathrm{DE}} \approx \;(\alpha _1 H^{2}+\beta _1 \dot{H})\), where H is the Hubble parameter and \(\alpha _1\), \(\beta _1 \) are constants which must satisfy the restrictions imposed by the current observational data. Chen and Jing (2009) modified this model by assuming that the density of dark energy contain the Hubble parameter H, the first-order and the second-order derivatives.

The expression of the energy density of dark energy is given by

$$\begin{aligned} \rho _\lambda =(3\eta _1 \ddot{H}H^{-1}+3\eta _2 \dot{H}+3\eta _3 H^{2}), \end{aligned}$$
(1)

where \(\eta _1\), \(\eta _2\), \(\eta _3\) are the arbitrary dimensionless parameters.

Setare (2007) discussed the holographic dark energy model in the Brans–Dicke theory. The cosmological dynamics of the interacting holographic dark energy model are obtained by Setare and Vanegas (2009). The evolution of the holographic dark energy is studied by Sarkar and Mahanta (2013) for Bianchi Type-I space-time with constant deceleration parameter. Sarkar (2014) investigated the holographic dark energy model in Bianchi Type-I universe with linearly varying deceleration parameter. Kiran et al. (2014b) investigated Bianchi-V universe filled with two minimally interacting fluids: matter and holographic dark energy components in the scalar—tensor theory proposed by Saez and Ballester (1986). The minimally interacting HDE models using linearly varying deceleration parameter have been obtained by Kiran et al. (2014a) and Reddy et al. (2015). The Bianchi type modified holographic Ricci dark energy (MHRDE) models in general relativity and in scalar-tensor theories have been investigated by Santhi et al. (2016, 2017a, b). Reddy (2016, 2017) studied Bianchi Type-III and Type-II modified holographic Ricci dark energy models in Lyra manifold. The Kantowski–Sachs cosmological model has been discussed by Ghate and Patil (2016) in the scalar–tensor theory of gravitation proposed by Saez–Ballester. Raju et al. (2016) discussed the five-dimensional spherically symmetric minimally interacting holographic dark energy model in the Saez–Ballester scalar–tensor theory of gravitation. Raut et al. (2016) studied anisotropic and homogeneous Bianchi Type-I space-time for the interaction between dark matter and holographic dark energy under the assumption of the hybrid expansion law (HEL). Rao and Prasanthi (2017a, b) investigated Bianchi Type-I and Type-III MHRDE models in the Saez–Ballester theory and Bianchi Type-\(\hbox {VI}_{0}\) MHRDE model in the self-creation theory with varying deceleration parameters (Rao and Prasanthi 2017a, b). Reddy et al. (2018) investigated the modified holographic Ricci dark energy model in the modified theory of gravitation using the hybrid expansion law. The non-static plane symmetric universe filled with matter and anisotropic modified holographic Ricci dark energy components were discussed by Rao et al. (2018) within the framework of the scalar–tensor theory formulated by Saez and Ballester (1986).

The main objective of this paper is to study the hypersurface-homogeneous cosmological model when the universe is filled with matter and a modified holographic Ricci dark energy in the scalar tensor theory of gravitation proposed by Saez and Ballester.

2 Metric and field equations

The general solutions of Einstein’s field equations for a perfect fluid distribution satisfying a barotropic equation of state for the hypersurface-homogeneous space time are investigated by Stewart and Ellis (1968). The hypersurface-homogeneous space-time is of the form

$$\begin{aligned} \hbox {d}s^{2}= & {} \hbox {d}t^{2}-A^{2}(t)\hbox {d}x^{2}\nonumber \\&-B^{2}(t)\left( \hbox {d}y^{2}+\sum {^{2}} (y,K)\hbox {d}z^{2}\right) , \end{aligned}$$
(2)

where A and B are the cosmic scale functions and \(\sum {(y,K)=\sin y, y, \sinh y} \) for \(K = 1, 0, -1\) respectively.

Hajj-Boutros (1985) developed a method to find the exact solutions of field equations for the metric (2) in the presence of a perfect fluid. The exact solutions of the field equations for hypersurface-homogeneous space-time under the assumption on the anisotropy of the fluid (dark energy) which are obtained for exponential and power-law volumetric expansions in a scalar–tensor theory of gravitation are obtained by Katore & Shaikh (2015a, b). Shaikh & Katore (2016a) derived the exact solutions of the field equations with perfect fluid in the framework of f(R, T) theory. The hypersurface-homogeneous cosmological model in f(R, T) theory of gravity with a term \(\Lambda \) are discussed by Shaikh & Wankhade (2017a).

The field equations for the combined scalar and tensor fields in the Saez–Ballester theory are

$$\begin{aligned}&R_{ij} -\frac{1}{2}g_{ij} R-\omega \varphi ^{n}\left( {\varphi _{,i} \varphi _{,j} -\frac{1}{2}g_{ij} \varphi _{,k} \varphi ^{{\prime }k}} \right) \nonumber \\&\quad =(T_{ij} +{\bar{T}}_{ij} ), \end{aligned}$$
(3)

where \(R_{ij}\) is the Ricci tensor, R is the Ricci scalar, \(\omega \) and n are arbitrary dimensionless constants and \(8\pi G=c=1\) in the relativistic units.

The energy–momentum tensor for matter and holographic dark energy are defined as

$$\begin{aligned} T_{ij} =\rho _m u_i u_j \end{aligned}$$

and

$$\begin{aligned} {\bar{T}}_{ij} =(\rho _\lambda +p_\lambda )u_i u_j -g_{ij} p_\lambda , \end{aligned}$$
(4)

where \(\rho _m\), \(\rho _\lambda \) are the energy densities of matter and holographic dark energy, and \(p_\lambda \) is the pressure of the holographic dark energy.

The energy–momentum tensor of dark energy can be parametrized as

$$\begin{aligned} {\bar{T}}_{ij} =\hbox {diag}[1,-w_\lambda ,-(w_\lambda +\delta _y ),-(w_\lambda +\delta _z )]\rho _\lambda , \end{aligned}$$
(4a)

where \(w_\lambda =p_\lambda /\rho _\lambda \) is the equation of state (EoS) parameter of the dark energy and \(\rho _m\), \(\rho _\lambda \) are the energy densities of matter and dark energy, and p is the pressure of the dark energy. Here skewness parameters \(\delta _y\) and \(\delta _z\) are the deviations along the y and z directions, respectively.

The scalar field \(\phi \) satisfies the equation

$$\begin{aligned} 2\phi ^{n}\phi _{:i}^i +n\phi ^{n-1}\phi _{,k} \phi ^{{\prime }k}=0. \end{aligned}$$
(5)

Also, the energy conservation equation is

$$\begin{aligned} T_{:i}^{ij} +{\bar{T}}_{:i}^{ij} =0. \end{aligned}$$
(6)

In a co-moving coordinate system, the field equations (3) for the metric (2), using Equation (4) can be explicitly written as

$$\begin{aligned}&\frac{2\ddot{B}}{B}+\frac{\dot{B}^{2}}{B^{2}}+\frac{K}{B^{2}}-\frac{\omega }{2}\phi ^{n}\dot{\phi }^{2}=-w_\lambda \rho _\lambda , \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}}{A}\frac{\dot{B}}{B}-\frac{\omega }{2}\phi ^{n}\dot{\phi }^{2}=-(w_\lambda +\delta _y )\rho _\lambda ,\end{aligned}$$
(8)
$$\begin{aligned}&\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}}{A}\frac{\dot{B}}{B}-\frac{\omega }{2}\phi ^{n}\dot{\phi }^{2}=-(w_\lambda +\delta _z )\rho _\lambda ,\end{aligned}$$
(9)
$$\begin{aligned}&2\frac{\dot{A}}{A}\frac{\dot{B}}{B}+\frac{\dot{B}^{2}}{B^{2}}+\frac{K}{B^{2}}+\frac{\omega }{2}\phi ^{n}\dot{\phi }^{2}=\left( {\rho _m +\rho _\lambda } \right) ,\end{aligned}$$
(10)
$$\begin{aligned}&\ddot{\phi }+\dot{\phi }\left( {\frac{\dot{A}}{A}+2\frac{\dot{B}}{B}} \right) +\frac{n}{2}\frac{\dot{\phi }^{2}}{\phi }=0, \end{aligned}$$
(11)

where ‘dot’ denotes a derivative with respect to the cosmic time t. We can write the conservation equation (6) for the matter and dark energy as

$$\begin{aligned}&\dot{\rho }_\lambda +\dot{\rho }_m +(\rho _m +\rho _\lambda +p_\lambda )\left( {\frac{\dot{A}}{A}+2\frac{\dot{B}}{B}} \right) \nonumber \\&\quad +\left( {\frac{\dot{B}}{B}(\delta _y +\delta _z )} \right) \rho _\lambda =0. \end{aligned}$$
(12)

3 Solution and the models

Using Equations (8) and (9), we obtain

$$\begin{aligned} \delta _y =\delta _z. \end{aligned}$$
(13)

The field equations (7)–(11) are a system of five highly non-linear differential equations in eight unknowns A, B, \(\phi \), \(w_\lambda \), \(\delta _y\), \(\delta _z\), \(\rho _\lambda \), \(\rho _m\). The system is thus initially undetermined. Thus, there is a need of extra physical conditions to solve the field equations completely.

Let us assume that the component of the shear tensor is proportional to the expansion scalar. This condition leads to the following relation between the metric potentials:

$$\begin{aligned} A=B^{m}, \end{aligned}$$
(14)

where \(m\ne 1\) is a positive constant which takes care of the anisotropy of the space-time.

If \(m=1\), the model becomes an isotropic model otherwise it becomes anisotropic. The motivation for the consideration of Equation (14) is the work of Throne (1967). The red-shift studies place the limit \(\sigma /H\le 0.3\) on the ratio of the shear \(\sigma \) to the Hubble constant H in the neighborhood of our Galaxy today. Collins et al. (1980) discussed the physical significance of this condition for perfect fluid and barotropic EoS in a more general case. They have pointed out that for spatially homogeneous metric, the normal congruence to the homogeneous expansion satisfies that the condition \(\sigma /\theta \) is constant. Many researchers (Sharif & Zubair 2010; Yadav & Yadav 2010; Katore & Shaikh 2012a, b, 2014a, b; Shaikh & Katore 2016b; Agrawal & Pawar 2017; Shaikh 2017) use Equation (14) to find the exact solutions of the cosmological models.

The power-law and exponential-law cosmologies can only be used to describe an epoch-based evolution due to constancy of the deceleration parameter. For instance, these cosmologies do not exhibit a transition from deceleration to acceleration. Akarsu et al. (2014) have shown that all the cosmological parameters related with the present-day universe as well as with the onset of the cosmic acceleration for hybrid expansion law (HEL) and \(\Lambda \) CDM models are consistent within the \(1\sigma \) confidence level. Hence we consider then, as a solution for the scale factor, the HEL (Akarsu et al. 2014; Moraes & Sahoo 2017) in the form

$$\begin{aligned} a(t)=AB^{2}=a_1 t^{\alpha }\hbox {e}^{\beta t}, \end{aligned}$$
(15)

where \(\alpha \), \(\beta \) are the non-negative constants and \(a_1\) is the present value of the scale factor. Equation (15) is known as the hybrid expansion law, which is a combination of a power law and an exponential function. It can be seen that \(\alpha =0\) provides power-law cosmology while \(\beta =0\) gives the exponential law cosmology. Such an ansatz mimics the power-law and the de Sitter cosmologies as special cases, but, as it will be shown below, it also provides an elegant description of the transition from decelerated to accelerated cosmic expansion. Here, one can choose the constants in such a way that the power-law dominates over the exponential law in the early universe and the exponential law dominates over the power-law at late times, in order to account for the present acceleration of the universe expansion. Yadav et al. (2015) examined the existence of LRS Bianchi-I dark energy model in f(R, T) gravity with the hybrid expansion law and observed that it gives a time-dependent DP, representing a transitioning Universe from early decelerating phase to current accelerating phase. Ram and Chandel (2015) and Santhi et al. (2016) studied Bianchi dark energy cosmological models with hybrid expansion law. Das and Sultana (2015) considered the hybrid expansion law to find an exact solution of the Einstein’s field equations for LRS Bianchi Type-II space-time filled with dark matter and anisotropic modified Ricci dark energy. Mahanta and Sarma (2017) studied the anisotropic Bianchi Type-\(\hbox {VI}_{0}\) metric filled with dark matter and anisotropic ghost dark energy by considering hybrid expansion law (HEL) for the average scale factor.

Using Equations (14) and (15), the metric potentials are obtained as

$$\begin{aligned} A= & {} \alpha _2 t^{\frac{3m\alpha }{m+2}}\hbox {e}^{\frac{3m\beta t}{m+2}}, \end{aligned}$$
(16)
$$\begin{aligned} B= & {} \alpha _1 t^{\frac{3\alpha }{m+2}}\hbox {e}^{\frac{3\beta t}{m+2}}. \end{aligned}$$
(17)

This is a point type singularity since the directional scale factor A(t), B(t) vanish at the initial time, which is similar with the investigations of Pradhan & Amirhashchi (2011) and Shaikh (2017).

Using Equations (11), (16) and (17), we get the scalar field as

$$\begin{aligned} \varphi ^{\frac{n+2}{2}}=\frac{n+2}{2}\int {\varphi _0 (a_1 t^{\alpha }\hbox {e}^{\beta t})}^{-3}\hbox {d}t+\psi _0. \end{aligned}$$
(18)

It may also be noted that the Saez–Ballester scalar field \(\phi \) goes to infinity as \(t\rightarrow \infty \) whereas it becomes zero when \(t=0\).

Using equations (16) and (17), the metric (2) takes the form

$$\begin{aligned} \hbox {d}s^{2}= & {} \hbox {d}t^{2}-\left[ {\alpha _2^2 t^{\frac{6m\alpha }{m+2}}\hbox {e}^{\frac{6m\beta t}{m+2}}} \right] \hbox {d}x^{2}\nonumber \\&-\left[ {\alpha _1^2 t^{\frac{6\alpha }{m+2}}\hbox {e}^{\frac{6\beta t}{m+2}}} \right] \left( \hbox {d}y^{2}+\sum {^{2}} (y,K)\hbox {d}z^{2}\right) . \end{aligned}$$
(19)

Equation (19) represents the hypersurface-homogeneous modified holographic dark energy cosmological model with hybrid expansion law in the Saez–Ballester theory of gravitation.

4 Physical discussion of the model

It is well known that one can study the behavior of the physical and kinematical parameters either by observing the analytical expressions or by graphical representation. The physical quantities of observational interest in cosmology are the spatial volume V, mean Hubble parameter H, the expansion scalar \(\theta \), the mean anisotropy parameter \(A_m\), the shear scalar \(\sigma ^{2}\) and the deceleration parameter q.

The spatial volume V of the universe is given by

$$\begin{aligned} V=a(t)=(a_1 t^{\alpha }\hbox {e}^{\beta t})^{3}. \end{aligned}$$
(20)
Fig. 1
figure 1

Spatial volume vs. time.

Full size image

From Figure 1, it is observed that at \(t=0\), the spatial volume vanishes and hence the model starts with a big bang singularity at \(t=0\) which is similar with the investigations of Katore & Shaikh (2015a, b).

The mean Hubble parameter H is given by

$$\begin{aligned} H=\frac{1}{3}\left( {\frac{\dot{A}}{A}+2\frac{\dot{B}}{B}} \right) =\frac{\dot{a}}{a}=\left( {\beta +\frac{\alpha }{t}} \right) . \end{aligned}$$
(21)
Fig. 2
figure 2

Hubble parameter vs. time.

Full size image

It is evident from Figure 2 that for large t, the Hubble parameter approached towards zero, i.e. \(H\rightarrow 0\) when \(t\rightarrow \infty \). The Hubble parameter has a singularity at \(t = 0\). The Hubble rates evolve with time in between the big bang and the big rip, i.e. the intermediate phase between the beginning and end of the universe. The model of the universe starts with a big bang and ends with a big rip.

The expansion scalar is given by

$$\begin{aligned} \theta =3H=3\left( {\beta +\frac{\alpha }{t}} \right) . \end{aligned}$$
(22)
Fig. 3
figure 3

Scalar expansion vs. time.

Full size image
Fig. 4
figure 4

Shear scalar vs. time.

Full size image

It is observed that the expansion scalar is infinite at \(t=0\) as shown in Figure 3. For \(t\rightarrow \infty \), we obtain \(\theta \rightarrow 3\beta \), \(q=-1\), \(\mathrm{d}H/\mathrm{d}t=0\) which implies the greatest value of the Hubble’s parameter.

The average anisotropy parameter \(A_m \) of the expansion is crucial while deciding whether the model approaches isotropy or not (Kumar & Akarsu 2012). \(A_m \) is the measure of the deviation from isotropic expansion and the universe expands isotropically when \(A_m = 0\).

The mean anisotropic parameter is defined by

$$\begin{aligned} A_m =\frac{1}{3}\sum _{i=1}^3 {\left( {\frac{\Delta H_i }{H}} \right) }^{2}=\frac{2(m^{2}+2)}{(m+2)^{2}}, \end{aligned}$$
(23)

where \(H_{i}\) (\(i = 1, 2, 3\)) is along the x, y and z axes which are the directional Hubble parameters.

The exponent m takes care of the anisotropic nature of the model that is clearly indicated by Equation (23). The anisotropy in expansion rates is maintained throughout the cosmic evolution as implied by the average anisotropic parameter in Equation (23) which is time-independent.

The shear scalar is defined and given by

$$\begin{aligned} \sigma ^{2}=\frac{3}{2}A_m H^{2}=\frac{9(m^{2}+2)}{(m+2)^{2}}\left( {\beta +\frac{\alpha }{t}} \right) ^{2}. \end{aligned}$$
(24)

The shear scalar diverges at an initial epoch as depicted in Figure 4 and tends to zero as \(t\rightarrow \infty \). The cosmological model goes up homogeneity and matter is dynamically negligible near the origin as \(\lim \limits _{t\rightarrow 0} (\rho /\theta ^{2})\) spread out to be a constant, which is similar with the investigations of Collins (1977). The deceleration parameter is

$$\begin{aligned} q=\frac{\hbox {d}}{\hbox {d}t}\left( {\frac{1}{H}} \right) -1=\frac{\alpha }{(\alpha +\beta t)^{2}}-1. \end{aligned}$$
(25)
Fig. 5
figure 5

Deceleration parameter vs. time.

Full size image
Fig. 6
figure 6

Energy density HDE vs. time.

Full size image
Fig. 7
figure 7

Energy density matter vs. time.

Full size image

Figure 5 represents the deceleration parameter evolution in time, obtained above for the hybrid scale factor. With negative sign of deceleration parameter at late times gives the accelerated expansion of the universe at present epoch while positive sign of deceleration parameter indicates the deceleration. We observe that the HEL universe evolves with a variable deceleration parameter, and a transition from deceleration to acceleration takes place at \(t=\frac{\sqrt{\alpha }-\alpha }{\beta }\) which restricts \(\alpha \) in the range \(0<\alpha <1\) indicating an unphysical context of the big bang cosmology. Thus a suitable model for describing the present evolution of the universe is analysed in this manuscript which is similar with the results of Katore et al. (2011).

From (1) and (21), we have the energy density of modified holographic Ricci dark energy as

$$\begin{aligned} \rho _\lambda =3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] . \end{aligned}$$
(26)

From (10), (16), (17), (18) and (26), we have the energy density of matter as

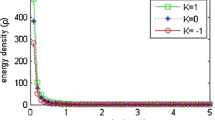
$$\begin{aligned} \rho _m= & {} \frac{9(2m+1)}{(m+2)^{2}}\left( {\beta +\frac{\alpha }{t}} \right) ^{2}\nonumber \\&+\frac{K}{\alpha _1^2 t^{\frac{6\alpha }{m+2}}\hbox {e}^{\frac{6\beta t}{m+2}}}+\frac{\omega \varphi _0 }{2(a_1 t^{\alpha }\hbox {e}^{\beta t})^{6}} \nonumber \\&-3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] . \end{aligned}$$
(27)

It is observed from Figures 6 and 7 that both the dark matter and the modified holographic Ricci dark energy densities decrease as the universe expands. At late times, the matter energy density and the modified holographic Ricci dark energy density tend to have a small value.

From (7), (16), (17), (18) and (26), the EoS parameter of the modified holographic Ricci dark energy can be found as

$$\begin{aligned} w_\lambda= & {} -\left\{ \frac{-3\alpha }{(m+2)^{2}t^{2}}+\frac{18}{(m+2)^{2}}\left( {\beta +\frac{\alpha }{t}} \right) ^{2}\right. \nonumber \\&\left. +\frac{K}{\alpha _1^2 t^{\frac{6\alpha }{m+2}}\hbox {e}^{\frac{6\beta t}{m+2}}}+\frac{\omega \varphi _0 }{2(a_1 t^{\alpha }\hbox {e}^{\beta t})^{6}} \right\} \nonumber \\&3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] ^{-1}. \end{aligned}$$
(28)
Fig. 8
figure 8

Equation of state parameter vs. time and k.

Full size image

Evolution of the EoS of dark energy transfer from \(w>-1\) in the near past (quintessence region) to \(w<-1\) at recent stage (phantom region) as specified by various relativists (Sahni & Shtanov 2003; Alam et al. 2004a, b; Feng et al. 2005; Huterer & Cooray 2005; Chang et al. 2006). The limits obtained are \(-1.67<w<-0.62\) and \(-1.33<w<-0.79\) for EoS parameter from SNe Ia data (Knop et al. 2003) and the combination of SNe Ia data with CMBR anisotropy and galaxy clustering statistics (Tegmark et al. 2004). The dark energy EoS are constrained to \(-1.44<w<-0.92\) (Hinshaw et al. 2009; Komatsu et al. 2009), with the combination of cosmological datasets from CMB anisotropies, luminosity distances of high redshift Type Ia supernovae and galaxy clustering. It is observed that the EoS parameter is a function of cosmic time as shown in Figure 8. It may be seen that the universe evolves through the dust \(w=0\) and radiating universes \(w=1/3\) and then crosses the phantom divided line \(w=-1\) to attain a constant value, ultimately, in the phantom region \(w<-1\). Figure 8 clearly shows that w evolves within a range, which is in good agreement with the SN Ia and CMB observations. The parameter EoS has also the same singularity as that of the Hubble parameter, i.e. at the initial phase and at the big rip which is similar with the investigations of Sahoo & Sivakumar (2015) and Sahoo et al. (2017).

The matter density parameter \(\Omega _\lambda \) and the holographic dark energy density parameter \(\Omega _\lambda \) are given by

$$\begin{aligned} \Omega _m= & {} \frac{\rho _m }{3H^{2}}=\frac{\frac{9(2m+1)}{(m+2)^{2}}\left( {\beta +\frac{\alpha }{t}} \right) ^{2}+\frac{K}{\alpha _1^2 t^{\frac{6\alpha }{m+2}}\hbox {e}^{\frac{6\beta t}{m+2}}}+\frac{\omega \varphi _0 }{2(a_1 t^{\alpha }\hbox {e}^{\beta t})^{6}}-3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] }{3\left( {\beta +\frac{\alpha }{t}} \right) ^{2}}, \end{aligned}$$
(29)
$$\begin{aligned} \Omega _\lambda= & {} \frac{\rho _\lambda }{3H^{2}}\nonumber \\= & {} \frac{\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] }{\left( {\beta +\frac{\alpha }{t}} \right) ^{2}}. \end{aligned}$$
(30)

The overall density parameter is

$$\begin{aligned} \Omega= & {} \Omega _m +\Omega _\lambda \nonumber \\= & {} \frac{{\begin{array}{l} \frac{9(2m+1)}{(m+2)^{2}}\left( {\beta +\frac{\alpha }{t}} \right) ^{2}+\frac{K}{\alpha _1^2 t^{\frac{6\alpha }{m+2}}\hbox {e}^{\frac{6\beta t}{m+2}}}+\frac{\omega \varphi _0 }{2(a_1 t^{\alpha }\hbox {e}^{\beta t})^{6}}\nonumber \\ \,\,-3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] \nonumber \\ \end{array}}}{3\left( {\beta +\frac{\alpha }{t}} \right) ^{2}}\nonumber \\&+\frac{\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] }{\left( {\beta +\frac{\alpha }{t}} \right) ^{2}}. \end{aligned}$$
(31)

The variation of the overall density parameter versus the cosmic time t is depicted in Figure 9. From a review of literature, it is found that for flat universe, \(\Omega =1\), for open universe, \(\Omega <1\) and for closed universe, \(\Omega >1\). From Figure 9, it can be seen that the total energy density tends to 1 for sufficiently large time. Thus the model predicts a flat universe for large times, as the present-day universe is very close to flat universe. Hence, with the observational results (Spergel et al. 2003, 2007; Bennett et al. 2013; Hinshaw et al. 2013), the derived model is compatible. Thus at late times, the universe becomes spatially homogeneous, isotropic and flat.

Fig. 9
figure 9

Overall density parameter vs. time.

Full size image
Fig. 10
figure 10

Skewness parameter vs. time.

Full size image

The coincidence parameter \({\bar{r}}=\rho _m /\rho _\lambda \), i.e. the ratio of energy densities of matter and holographic dark energy is given by

$$\begin{aligned} {\bar{r}}=\frac{{\begin{array}{l} \frac{9(2m+1)}{(m+2)^{2}}\left( {\beta +\frac{\alpha }{t}} \right) ^{2}+\frac{K}{\alpha _1^2 t^{\frac{6\alpha }{m+2}}\hbox {e}^{\frac{6\beta t}{m+2}}}+\frac{\omega \varphi _0 }{2(a_1 t^{\alpha }\hbox {e}^{\beta t})^{6}} \\ \quad -3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] \\ \end{array}}}{3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] }.\nonumber \\ \end{aligned}$$
(32)

It is observed that the coincidence parameter \({\bar{r}}\) at an initial epoch, i.e at a very early stage of evolution, varies, but after some finite time it converges to a constant value and remains constant throughout the evolution which is similar with Adhav et al. (2015).

From (8), (9), (16), (17), (26) and (28), we get the skewness parameter as

$$\begin{aligned} \delta _y= & {} \delta _z \nonumber \\= & {} -\left\{ \frac{3\alpha (m-1)}{(m+2)t^{2}}+\frac{(18-9m^{2}-9m)}{(m+2)^{2}}\left( {\beta +\frac{\alpha }{t}} \right) ^{2}\right. \nonumber \\&\left. +\frac{K}{\alpha _1^2 t^{\frac{6\alpha }{m+2}}\hbox {e}^{\frac{6\beta t}{m+2}}} \right\} \nonumber \\&3\left[ {\frac{2\eta _1 \alpha }{t^{2}(\alpha +\beta t)}-\frac{\eta _2 \alpha }{t^{2}}+\frac{\eta _3 (\alpha +\beta t)^{2}}{t^{2}}} \right] ^{-1}. \end{aligned}$$
(33)

At an early stage of evolution of the universe, the skewness parameter increases sharply and then decreases and tends to zero at late times as shown in Figure 10. Thus the anisotropy of the modified holographic Ricci dark energy becomes isotropic at a later age of the universe.

Jerk parameter

It is believed that the transition from the decelerating to the accelerating phase of the universe is due to a cosmic jerk. (Chiba & Nakamura 1998; Blandford et al. 2004; Visser 2004, 2005) defined by the jerk parameter j(t) in cosmology as

$$\begin{aligned} j(t)=\frac{\dddot{a}}{aH^{3}}, \end{aligned}$$
(34)

where a is the cosmic scale factor, H is the Hubble parameter and the dot denotes differentiation with respect to the cosmic time. It is the third derivative of the scale factor with respect to the cosmic time. Equation (34) can be written as

$$\begin{aligned} j(t)=q+2q^{2}-\frac{\dot{q}}{H}, \end{aligned}$$
(35)

where q is the deceleration parameter.

This is used to discuss the models close to \(\Lambda \) CDM. The complete sets of \(\Lambda \) CDM models characterized by \(j(t)=1\) (constant) are provided by Rapetti et al. (2007). It is said that the universe undergoes a smooth transition from deceleration to acceleration for models with negative values of deceleration parameter and positive value of jerk parameter. The cosmic jerk parameter is as follows:

$$\begin{aligned} j(t)=1-\frac{3\alpha }{(\alpha +\beta t)^{2}}+\frac{2\alpha }{(\alpha +\beta t)^{3}}. \end{aligned}$$
(36)
Fig. 11
figure 11

Jerk parameter vs. time.

Full size image

The value shows that the jerk parameter in Equation (36) changes significantly between the deceleration-to-acceleration transition and indicates the departure of the models from \(\Lambda \) CDM. Figure 11 shows that the cosmic jerk parameter is positive throughout the entire life of the universe and tends to 1 at late times which is similar with the investigations of Das and Sultana (2015).

Statefinder diagnostic pair

The viability of dark energy models can be detected with the help of the state finder diagnostic pair \(\{r,s\}\) which gives us an idea about the geometrical nature of the model. Sahni et al. (2003) introduced a diagnostic proposal that makes use of the parameter pair \(\{r,s\}\), the so-called ‘statefinder’. The expansion dynamics of the universe through higher derivatives of the expansion factor \(\ddot{a}\) is a natural companion to the deceleration parameter which depends upon \(\ddot{a}\) and this is probed by the statefinder.

The statefinder pair \(\{r,s\}\) is defined as (Akarsu et al. 2014)

$$\begin{aligned} r=\frac{{\dddot{a}}}{aH^{3}}, \quad s=\frac{r-1}{3\left( {q-\frac{1}{2}} \right) }. \end{aligned}$$
(37)

A wide variety of dark energy models including the cosmological constant, quintessence, the Chaplygin gas, braneworld models and interacting dark energy models can be differentiated by the statefinder as demonstrated by Vasilyev (2003), Alam et al. (2003) and Zhang (2005). Panotopoulos (2008) concluded that for the observational value of \(w\cong -1\), the values of \(\{r,s\}\) for the system under study is only slightly different from that of \(\Lambda \) CDM. Mishra and Tripathy (2015) constructed anisotropic dark energy model for spatially homogeneous diagonal Bianchi Type V space-time in general relativity with dynamic pressure anisotropies along different spatial directions. To simulate a cosmic transition from early deceleration to late time acceleration, a time varying deceleration parameter generating a hybrid scale factor is considered. The statefinder pair can be obtained as

$$\begin{aligned} r= & {} 1-\frac{3\alpha }{(\alpha +\beta t)^{2}}+\frac{2\alpha }{(\alpha +\beta t)^{3}}, \end{aligned}$$
(38)
$$\begin{aligned} s= & {} \frac{2\alpha [3(\alpha +\beta t)-2]}{3(\alpha +\beta t)[3(\alpha +\beta t)^{2}-2\alpha ]}. \end{aligned}$$
(39)
Fig. 12
figure 12

r vs. s.

Full size image

At an initial epoch, the statefinder pair for the present model is \(\{ {1+\frac{2-3\alpha }{\alpha ^{2}},\frac{2}{3\alpha }}\}\), whereas at late time cosmic evolution, the model behaves like \(\Lambda \) CDM with the statefinder pair having values \(\{1,0\}\). The pair \(\{1,1\}\) represents the standard cold dark matter model containing no radiation. The Einstein static universe corresponds to the pair \(\{ {\infty ,-\infty } \}\) (Debnath 2008). The spatially flat \(\Lambda \)CDM scenario corresponds to a fixed point \(\{r, s\} = \{1, 0\}\) in this model as shown in Figure 12 which corresponds with the investigations of Feng (2008). Figure 12 shows that the universe passes through a phase close to the \(\Lambda \) CDM model at the point (\(r = 1\), \(s = 0\)). This clearly implies that at late time cosmic evolution, the dark energy dominates and drives the cosmic acceleration.

5 Conclusion

In this paper, we have investigated hypersurface-homogeneous and anisotropic modified holographic Ricci dark energy cosmological model in the Saez–Ballester (1986) scalar–tensor theory of gravitation. We have obtained the cosmological model using hybrid expansion law of average scale factor. Akarsu et al. (2014) exhibited a smooth transition of the universe from the decelerated phase to the accelerating phase.

  • There is a point type singularity since directional scale factor A(t), B(t) vanish at the initial time which is similar with the investigations of Katore et al. (2011).

  • It may also be noted that the Saez–Ballester scalar field \(\phi \) goes to infinity as \(t\rightarrow \infty \), whereas it becomes zero when \(t=0\).

  • It is observed that at \(t=0\), the spatial volume vanishes and hence the model starts with a big bang singularity at \(t=0\) which is similar with Katore and Shaikh (2012c, 2012d, 2012e).

  • The Hubble’s parameter (H) starts off with an extremely large value and continues to decrease with time (Shaikh et al. 2017).

  • It is observed that the expansion scalar is infinite at \(t=0\). For \(t\rightarrow \infty \), we obtain \(\theta \rightarrow 3\beta \), \(q=-1\), \(\frac{\hbox {d}H}{\hbox {d}t}=0\) which implies the greatest value of Hubble’s parameter.

  • The anisotropy in expansion rates is maintained throughout the cosmic evolution as implied by the average anisotropic parameter (Katore & Shaikh 2015a, b).

  • The shear scalar diverges at an initial epoch and tends to zero as \(t\rightarrow \infty \). The cosmological model goes up homogeneity and matter is dynamically negligible near the origin as \(\lim \limits _{t\rightarrow 0} ( {\frac{\rho }{\theta ^{2}}})\) spread out to be a constant.

  • The present universe is accelerating is exposed by the recent observations of SNe Ia, and the value of deceleration parameter lies in some place in the range \(-1<q<0\) (Katore et al. 2014). The transition of universe from the decelerating phase to the accelerating phase takes place at \(t=\frac{\sqrt{\alpha }-\alpha }{\beta }\).

  • At late times, the matter energy density and the modified holographic Ricci dark energy density tends to a small value (Shaikh & Katore 2016a, b).

  • The Equation of State parameter (EoS) w evolves within a range, which is in good agreement with the SN Ia and CMB observations. Thus, our DE model is in good agreement with the well-established theoretical results as well as with the recent observations (Shaikh & Wankhade 2017a, b).

  • It can be seen that the total energy density tends to 1 for sufficiently large times. Thus the model predicts a flat universe for large times and hence the present-day universe is very close to the flat universe.

  • At an early stage of evolution of the universe, the skewness parameter increases sharply and then decreases and tends to zero at late times.

  • The cosmic jerk parameter is positive throughout the entire life of the universe and tends to 1 at late times.

  • At an initial epoch, the statefinder pair for the present model is \(\{ {1+\frac{2-3\alpha }{\alpha ^{2}},\frac{2}{3\alpha }}\}\), whereas at late times of cosmic evolution, the model behaves like \(\Lambda \)CDM with the statefinder pair having values \(\{1,0\}\) which is similar with the results of Katore and Shaikh (2012c, 2012d, 2012e).

  • The results obtained and the observed behavior of the model agrees with the recent observational facts of cosmology.