1 Introduction

Memristor (short for memory resistor) was first discovered by Chua in 1971, which was the fourth basic circuit element of the passive two-terminal and had full rights to use the other three classic circuits, such as existing inductors, resistors and capacitors [1]. In the following years, the concept of memristor had not been proved experimentally until 2008 when a memristor being constructed by the physical component was published by the authors in the Hewlett–Packard laboratory [2, 3]. The resistance value of the memristor depends on the magnitude and polarity of the voltage. Specifically, the current resistance will be remembered when the voltage is off. Because of memristor’s characteristics, its potential applications of the chaotic system with memristor have been discovered in quite a few fields such as cryptography [4], image encryption [5] and filters [6]. Therefore, the behaviors and properties of memristor arouse much attention from a number of researches.

As known to all, fractional calculus theory is an ancient and fresh concept extensively used in the nonlinear dynamical systems and in the fields of physics, ecology, machinery, engineering and biology [7,8,9]. Concerned by a number of researchers [10, 11], fractional differential equation is identified as the generalization of the integral-order differential equation and the form in which all physical phenomena are presented. Its practical applications have great correlation with the dynamical behaviors, especially the stability of models. As a result, the synchronization of fractional differential equation has become one of the most active areas of research. The dynamical behaviors of fractional-order systems can be revealed in lots of chaotic systems, such as fractional-order Lü system, fractional-order Lorenz system and fractional-order Chua system [12]. In addition, fractional-order systems are able to generate more accurate result than other integer-order systems, which arouses great interest of researchers [13,14,15].

Meanwhile, as investigated by many scholars [16,17,18], the chaotic synchronization of dynamic systems is applicable in many scientific fields such as bioengineering [19], electromagnetic field [20, 21], secure communication [22] and cryptography [23]. A variety of synchronization methods have been put forward for fractional-order chaotic systems, such as period intermittent control method [24], active control method [25], sliding mode control method [26] and impulsive control method [27,28,29,30,31]. Impulse as a frequently used method in chaotic system contributes to system stabilization. Some researchers investigated the impulsive synchronization of some complex dynamical systems [32, 33]; some reported that of the memristive chaotic system [34,35,36]. In addition, the synchronization of fractional chaotic systems via impulsive control scheme was proposed in some papers [37,38,39,40,41]. However, there is no study on the anti-synchronization problem of FMCC with time delay via impulsive control method.

Under this context, this paper attempts to study anti-synchronization strategy of FMCC with time delay via impulsive control, the criteria condition of which is proposed via Lyapunov stability theory and impulsive control principle. Meanwhile, some discussions about the stable region are given by numerical analysis and several feasible suggestions for improvement are put forward.

This paper is structured as follows. Section 2 describes the model formulation, fundamental definitions and lemmas. The anti-synchronization for FMCC with time delay via impulsive control scheme is realized in Sect. 3. The influential factors of the stable region are discussed in Sect. 4, followed by some numerical examples that illustrate the correctness of theoretical method. The results and suggestions are put forward in the last section.

2 Preliminaries

In this paper, let \(R^{n}\) denotes the n-dimensional Euclidean space, \(x = \left( {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right)^{T} \in R^{4}\), \(y = \left( {y_{1} ,y_{2} ,y_{3} ,y_{4} } \right)^{T} \in R^{4}\). In this section, some fundamental definitions and lemmas are recalled, and the mathematic model of FMCC with time delay is introduced.

2.1 Definitions and lemmas

Definition 1

[42] The Caputo fractional derivative of order q for function \(u\left( t \right)\) is defined by

$${}_{0}^{c} D_{t}^{q} u\left( t \right) = \frac{1}{{\varGamma \left( {m - q} \right)}}\mathop \int \limits_{0}^{t} \frac{{u^{m} \left( \tau \right)}}{{\left( {t - \tau } \right)^{q - m + 1} }}{\text{d}}\tau ,$$

where \(t \ge 0, m \in Z^{ + } , m - 1 < q < m,\) and \(\varGamma \left( \cdot \right)\) is the gamma function, that is, \(\varGamma \left( \tau \right) = \mathop \int \limits_{0}^{\infty } t^{\tau - 1} e^{ - t} {\text{d}}t\).

Moreover, when \(0 < q < 1\),

$${}_{0}^{c} D_{t}^{q} u\left( t \right) = \frac{1}{{\varGamma \left( {1 - q} \right)}}\mathop \int \limits_{0}^{t} \frac{{u^{\prime}\left( \tau \right)}}{{\left( {t - \tau } \right)^{q} }}{\text{d}}\tau .$$

For simplicity, we denote \(D^{q} u\left( t \right)\) as the \({}_{0}^{c} D_{t}^{q} u\left( t \right)\) and describe all of the following Caputo operators.

Definition 2

[42] The Mittag-Leffler function is defined by

$$E_{q} \left( t \right) = \mathop \sum \limits_{m = 0}^{\infty } \frac{{t^{m} }}{{\varGamma \left( {mq + 1} \right)}},$$

where \(q > 0\) and \(t \in C\).

Lemma 1

[43] For\(u\left( t \right) \in R^{n}\)is continuous and differentiable function, there is an inequality below

$$D^{q} u^{T} \left( t \right)u\left( t \right) \le 2u^{T} \left( t \right)D^{q} u\left( t \right),\quad 0 < q < 1.$$

Lemma 2

[44] For\(x \in R^{ + }\)and\(0 < q < 1\), \(E_{q} \left( x \right)\)is the monotone increasing function.

Lemma 3

[45] Suppose that\(x\left( t \right) = \left( {x_{1} \left( t \right),x_{2} \left( t \right), \ldots ,x_{n} \left( t \right)} \right)^{T} \in R^{n}\)and\(y\left( t \right) = (y_{1} \left( t \right),y_{2} \left( t \right), \ldots y_{n} \left( t \right))^{T} \in R^{n}\), for all\(D = \left( {r_{ij} } \right)_{n \times n}\), the following inequality holds:

$$y^{T} Dx \le s_{\hbox{max} } y^{T} y + \bar{s}_{\hbox{max} } x^{T} x,$$

where\(s_{\hbox{max} } = \frac{1}{2}\left\| D \right\|_{\infty } = \frac{1}{2}\max_{i = 1}^{n} \left( {\mathop \sum \nolimits_{j = 1}^{n} \left| {r_{ij} } \right|} \right)\), \(\bar{s}_{\hbox{max} } = \frac{1}{2}\left\| D \right\|_{1} = \frac{1}{2}\max_{j = 1}^{n} \left( {\mathop \sum \nolimits_{i = 1}^{n} \left| {r_{ij} } \right|} \right)\).

Lemma 4

[46] Suppose\(V\left( t \right)\)be a continuous nonnegative function on\(\left[ {t_{0} - \tau , t_{0} } \right]\)satisfying the following inequality:

$$D^{q} V\left( t \right) \le \vartheta \bar{V}\left( t \right)\;{\text{for}}\;t > t_{0} ,$$

where\(0 < q < 1\), \(\bar{V}\left( t \right) = \max_{t - \tau \le s \le t} \left\{ {V\left( s \right)} \right\}\)and\(\vartheta > 0\)is a constant. Then

$$V\left( t \right) \le V\left( {t_{0} } \right)E_{q} \left( {\vartheta \left( {t - t_{0} } \right)^{q} } \right).$$

2.2 Model description

Based on the chaotic circuit with one memristor of [47] shown in Fig. 1, let \(x_{1} = u_{1} , x_{2} = u_{2} , x_{3} = i_{3} , x_{4} = \phi , \alpha = \frac{1}{{C_{1} }}, \beta = \frac{1}{L}, C_{2} = 1, R = 1, \gamma = r/L, \xi = G\) and \(\tau\) is the time delay in the current transmission. The mathematic model of memristive chaotic system can be described by

$$\left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = \alpha \left( {\xi x_{1} - x_{1} + x_{2} - W\left( {x_{4} } \right)x_{1} } \right),} \hfill \\ {\dot{x}_{2} = x_{1} - x_{2} + x_{3} \left( {t - \tau } \right),} \hfill \\ {\dot{x}_{3} = - \beta x_{2} - \gamma x_{3} \left( {t - \tau } \right), } \hfill \\ {\dot{x}_{4} = x_{1} .} \hfill \\ \end{array} } \right.$$
(1)
Fig. 1
figure 1

Chua’s chaotic circuits with a flux-controlled memristor

Full size image

Similar to [47], the flux-controlled memristor is defined by

$$\omega \left( \phi \right) = a\phi + b\phi^{3} ,$$
(2)
$$W\left( \phi \right) = \frac{{{\text{d}}\omega \left( \phi \right)}}{{{\text{d}}\phi }} = a + 3b\phi^{2} ,$$
(3)

where \(W\left( \phi \right)\) is the memductance, \(\phi\) is flux, and \(a\) and \(b\) are constants.

Referring to the above model, the new fractional-order chaotic system with memristor according to (1) is described as

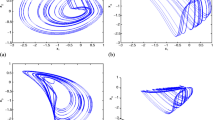
$$\left\{ {\begin{array}{*{20}l} {D^{q} x_{1} = \alpha \left( {\xi x_{1} - x_{1} + x_{2} - W\left( {x_{4} } \right)x_{1} } \right),} \hfill \\ {D^{q} x_{2} = x_{1} - x_{2} + x_{3} \left( {t - \tau } \right), } \hfill \\ {D^{q} x_{3} = - \beta x_{2} - \gamma x_{3} \left( {t - \tau } \right), } \hfill \\ {D^{q} x_{4} = x_{1} . } \hfill \\ \end{array} } \right.$$
(4)

Usually, in order to get the phenomenon of chaos, we set \(q = 0.985, a = 12/11, b = 1/11, \alpha = 10, \beta = 14, \gamma = 0.1, \xi = 2.2\) and \(\tau = 0.02\); then, the simulation is done with the initial value \(\left( {0, 0.1, 0, 0} \right)^{T}\) to system (4), and the simulation results are shown in Fig. 2.

Fig. 2
figure 2

Chaotic attractor of FMCC, (a)\(x_{1} \left( t \right), x_{2} \left( t \right)\); (b)\(x_{2} \left( t \right), x_{3} \left( t \right)\); (c)\(x_{2} \left( t \right), x_{4} \left( t \right)\) and (d)\(x_{1} \left( t \right), x_{4} \left( t \right)\)

Full size image

Let \(x = \left( {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right)^{T}\), system (4) can be written as

$$D^{q} x = Ax + Bx\left( {t - \tau } \right) + \phi \left( x \right),$$
(5)

where

$$A = \left[ {\begin{array}{*{20}c} {\alpha \left( {\xi - 1} \right)} & \alpha & 0 & 0 \\ 1 & { - 1} & 0 & 0 \\ 0 & { - \beta } & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & { - \gamma } & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad \phi \left( x \right) = \left[ {\begin{array}{*{20}c} { - \alpha W\left( {x_{4} } \right)x_{1} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$

and \(a,b,\gamma ,\xi ,\alpha ,\beta\) are positive constants.

To investigate the impulsive anti-synchronization of FMCC with time delay, the drive system can be rewritten as

$$\left\{ {\begin{array}{*{20}l} {D^{q} x\left( t \right) = Ax\left( t \right) + Bx\left( {t - \tau } \right) + \phi \left( {x\left( t \right)} \right),} \hfill \\ {x\left( t \right) = h\left( t \right), \quad - \tau \le t < 0. } \hfill \\ \end{array} } \right.$$
(6)

In order to achieve anti-synchronization, we construct the following response system with impulsive control

$$\left\{ {\begin{array}{*{20}l} D^{q} y\left( t \right) = Ay\left( t \right) + By\left( {t - \tau } \right) + \phi \left( {y\left( t \right)} \right),\quad t \ne t_{k} , \hfill \\ \Delta y|_{{t = t_{k} }} = C_{k} \left( {y\left( {t_{k} } \right) + x\left( {t_{k} } \right)} \right),\quad k = 1,2, \ldots , \hfill \\ y\left( t \right) = h\left( t \right), \quad - \tau \le t < 0, \hfill \\ y\left( {t_{0}^{ + } } \right) = y_{0} , \hfill \\ \end{array} } \right.$$
(7)

where \(C_{k} \in R^{4 \times 4}\) is the impulsive control matrix and \(t_{k}\) is the impulsive instants which satisfy \(t_{1} \le t_{2} \le \cdots \le t_{k}\).

For systems (6) and (7), let the error states \(e\left( t \right) = y\left( t \right) + x\left( t \right)\), where \(e\left( t \right) = \left( {x_{1} \left( t \right) + y_{1} \left( t \right),x_{2} \left( t \right) + y_{2} \left( t \right),x_{3} \left( t \right) + y_{3} \left( t \right),x_{4} \left( t \right) + y_{4} \left( t \right)} \right)^{T}\). Then, the error dynamical system between drive system (6) and response system (7) is described by

$$\left\{{\begin{array}{*{20}l} {D^{q} e\left(t \right) = Ae\left(t \right) + Be\left({t - \tau} \right) + \phi \left({e\left(t \right)} \right),\quad t \ne t_{k},} \\ {\Delta e|_{{t = t_{k}}} = C_{k} e\left({t_{k}} \right),\quad k = 1,2, \ldots,} \\ {e\left({t_{0}^{+}} \right) = e_{0},} \\ \end{array}} \right.$$
(8)

where

$$\begin{aligned} \phi \left( {e\left( t \right)} \right) & = \phi \left( {y\left( t \right)} \right) + \phi \left( {x\left( t \right)} \right) \\ & = \left[ { - \alpha W\left( {x_{4} \left( t \right)} \right)x_{1} \left( t \right) - \alpha W\left( {y_{4} \left( t \right)} \right)y_{1} \left( t \right),0,0,0} \right]^{T} . \\ \end{aligned}$$
(9)

3 Main result

In this section, the anti-synchronization problem of FMCC with time delay via an impulsive strategy is investigated.

Assumption 1

Because chaotic systems have bounded states regardless of the initial states, we assume that the following assumptions hold:

$$\left| {x_{1} \left( t \right)} \right| \le M_{1} ,\quad \left| {x_{2} \left( t \right)} \right| \le M_{2} ,\quad \left| {x_{3} \left( t \right)} \right| \le M_{3} ,\quad \left| {x_{4} \left( t \right)} \right| \le M_{4} ,$$

where \(M_{1} , M_{2} ,M_{3} ,M_{4}\) are real constants.

Remark 1

Based on the chaotic theory, the state of the chaotic system is bound, and many of the published articles use this assumption, such as [27, 31, 33].

Theorem 1

Let\(\rho\)is spectral radius, \(C_{k}\)is Hermite matrix, \(\hat{A} = \left\| A \right\|_{2} , d_{k}\)is the largest eigenvalue of matrix\(\left( {I + C_{k} } \right)^{T} \left( {I + C_{k} } \right).\)If there exists a constant\(\eta > 1\)such that the following conditions hold:

$$(H_{1} )\quad \rho \left( {I + C_{k} } \right) \le 1,$$
(10)
$$(H_{2} )\quad \eta d_{k} E_{q} \left( {\delta \tau_{k}^{q} } \right) < 1,$$
(11)

where\(\delta = 2\left( {\hat{A} + 3\alpha bM_{1} M_{4} + s_{\hbox{max} } + \bar{s}_{\hbox{max} } } \right)\), \(s_{\hbox{max} } = \frac{1}{2}\left\| B \right\|_{\infty }\), \(\bar{s}_{\hbox{max} } = \frac{1}{2}\left\| B \right\|_{1}\), and\(\tau_{k} = t_{k } - t_{k-1}\), \(k = 1,2, \ldots\), then the trivial solution of error dynamical system (8) is asymptotically stable, which implies that systems (6) and (7) achieve anti-synchronization.

Proof

Construct the following Lyapunov-like function

$$V\left( t \right) = \frac{1}{2}e^{T} \left( t \right)e\left( t \right).$$
(12)

Take a time derivative of \(V\left( t \right)\) along \(e\left( t \right)\) of system (12). From Lemma 1, for \(t \in \left( {t_{k} ,t_{k + 1} } \right]\), we get

$$\begin{aligned} D^{q} V\left( t \right) & \le e^{T} \left( t \right)D^{q} e\left( t \right) \\ & = e^{T} \left( t \right)\left( {Ae\left( t \right) + Be\left( {t - \tau } \right) + \phi \left( {e\left( t \right)} \right)} \right) \\ & = e^{T} \left( t \right)Ae\left( t \right) + e^{T} \left( t \right)Be\left( {t - \tau } \right) + e^{T} \left( t \right)\phi \left( {e\left( t \right)} \right) \\ & = e^{T} \left( t \right)Ae\left( t \right) + e^{T} \left( t \right)Be\left( {t - \tau } \right) - a\alpha e_{1}^{2} \left( t \right) - 3\alpha b(y_{4}^{2} \left( t \right)y_{1} \left( t \right) \\ & \quad + y_{4}^{2} \left( t \right)x_{1} \left( t \right) + x_{4}^{2} \left( t \right)x_{1} \left( t \right) - y_{4}^{2} \left( t \right)x_{1} \left( t \right))e_{1} \left( t \right) \\ & = e^{T} \left( t \right)Ae\left( t \right) + e^{T} \left( t \right)Be\left( {t - \tau } \right) - a\alpha e_{1}^{2} \left( t \right) - 3\alpha by_{4}^{2} \left( t \right)e_{1}^{2} \left( t \right) \\ & \quad + 3\alpha bx_{1} \left( t \right)\left( {y_{4} \left( t \right) - x_{4} \left( t \right)} \right)e_{4} \left( t \right)\,e_{1} \left( t \right) \\ & \le \hat{A}e^{T} \left( t \right)e\left( t \right) + e^{T} \left( t \right)Be\left( {t - \tau } \right) \\ & \quad + 3\alpha b\left| {x_{1} \left( t \right)} \right|\left( {\left| {y_{4} \left( t \right)} \right| + \left| {x_{4} \left( t \right)} \right|} \right)e_{4} \left( t \right)\,e_{1} \left( t \right)\, \\ & \le e^{T} \left( t \right)Ae\left( t \right) + e^{T} \left( t \right)Be\left( {t - \tau } \right) \\ & \quad + \frac{3}{2}\alpha b\left| {x_{1} \left( t \right)} \right|\left( {\left| {y_{4} \left( t \right)\left| + \right|x_{4} \left( t \right)} \right|} \right)(e_{4}^{2} \left( t \right) + e_{1}^{2} \left( t \right)) \\ & \le e^{T} \left( t \right)Ae\left( t \right) + e^{T} \left( t \right)Be\left( {t - \tau } \right) + 3\alpha bM_{1} M_{4} e^{T} \left( t \right)e\left( t \right). \\ \end{aligned}$$
(13)

From Lemma 3, we have

$$\begin{aligned} D^{q} V\left( t \right) & \le \left( {\hat{A} + 3\alpha bM_{1} M_{4} } \right)e^{T} \left( t \right)e\left( t \right) + s_{\hbox{max} } e^{T} \left( t \right)e\left( t \right) + \bar{s}_{\hbox{max} } e^{T} \left( {t - \tau } \right)e\left( {t - \tau } \right) \\ & \le 2\left( {\hat{A} + 3\alpha bM_{1} M_{4} + s_{\hbox{max} } } \right)V\left( t \right) + 2\bar{s}_{\hbox{max} } V\left( {t - \tau } \right) \\ & \le 2\left( {\hat{A} + 3\alpha bM_{1} M_{4} + s_{\hbox{max} } + \bar{s}_{\hbox{max} } } \right)\bar{V}\left( t \right), \\ \end{aligned}$$
(14)

where \(\bar{V}\left( t \right) = \max_{t - \tau \le s \le t} \left\{ {V\left( s \right)} \right\}\). From Lemma 4,

$$V\left( t \right) \le V\left( {t_{k}^{ + } } \right)E_{q} \left( {2\left( {\hat{A} + 3\alpha bM_{1} M_{4} + s_{\hbox{max} } + \bar{s}_{\hbox{max} } } \right)\left( {t - t_{k} } \right)^{q} } \right),{\text{for}}\;t \in \left( {t_{k} ,t_{k + 1} } \right].$$
(15)

Put \(\delta\) into Eq. (16), we have

$$V\left( t \right) \le V\left( {t_{k}^{ + } } \right)E_{q} \left( {\delta \left( {t - t_{k} } \right)^{q} } \right).$$
(16)

When \(t = t_{k},k \in N\), we have

$$\begin{aligned} V\left( {t_{k}^{ + } } \right) & = \frac{1}{2}e^{T} \left( {t_{k}^{ + } } \right)e\left( {t_{k}^{ + } } \right) \\ & = \frac{1}{2}e^{T} \left( {t_{k} } \right)\left( {I + B_{k} } \right)^{T} \left( {I + B_{k} } \right)e\left( {t_{k} } \right) \\ & \le d_{k} V\left( {t_{k} } \right). \\ \end{aligned}$$
(17)

Therefore, from inequalities (18) and (19), we have

$$V\left( t \right) \le d_{k} V\left( {t_{k} } \right)E_{q} \left( {\delta \left( {t - t_{k} } \right)^{q} } \right).$$
(18)

For \(t \in \left( {t_{0} ,t_{1} } \right]\), it follows from inequality (20) that

$$V\left( t \right) \le V\left( {t_{0}^{ + } } \right)E_{q} \left( {\delta \left( {t - t_{0} } \right)^{q} } \right).$$
(19)

When \(t = t_{1}\), we have

$$V\left( {t_{1}^{ + } } \right) \le d_{1} V\left( {t_{1} } \right) \le d_{1} V\left( {t_{0}^{ + } } \right)E_{q} \left( {\delta \left( {t_{1} - t_{0} } \right)^{q} } \right).$$
(20)

Similarly, for \(t \in \left( {t_{1} ,t_{2} } \right]\), we have

$$\begin{aligned} V\left( t \right) & \le V\left( {t_{1}^{ + } } \right)E_{q} \left( {\delta \left( {t - t_{1} } \right)^{q} } \right) \\ & \le d_{1} V\left( {t_{0}^{ + } } \right)E_{q} \left( {\delta \left( {t_{1} - t_{0} } \right)^{q} } \right)E_{q} \left( {\delta \left( {t - t_{1} } \right)^{q} } \right). \\ \end{aligned}$$
(21)

When \(t = t_{2}\), we have

$$V\left( {t_{2}^{ + } } \right) \le d_{2} V\left( {t_{2} } \right) \le d_{2} d_{1} V\left( {t_{0}^{ + } } \right)E_{q} \left( {\delta \left( {t_{1} - t_{0} } \right)^{q} } \right)E_{q} \left( {\delta \left( {t_{2} - t_{1} } \right)^{q} } \right).$$
(22)

In general, when \(t = t_{k}\), we have

$$V\left( {t_{k}^{ + } } \right) \le d_{k} V\left( {t_{k} } \right) \le d_{k} \ldots d_{1} V\left( {t_{0}^{ + } } \right)E_{q} \left( {\delta \left( {t_{1} - t_{0} } \right)^{q} } \right)E_{q} \left( {\delta \left( {t_{2} - t_{1} } \right)^{q} } \right) \cdots \times E_{q} \left( {\delta \left( {t_{k} - t_{k - 1} } \right)^{q} } \right),$$
(23)

and for \(t \in \left( {t_{k} ,t_{k + 1} } \right]\), we have

$$\begin{aligned} V\left( t \right) & \le d_{k} \ldots d_{1} V\left( {t_{0}^{ + } } \right)E_{q} \left( {\delta \left( {t_{1} - t_{0} } \right)^{q} } \right)E_{q} \left( {\delta \left( {t_{2} - t_{1} } \right)^{q} } \right) \ldots \\ & \quad \times E_{q} \left( {\delta \left( {t_{k} - t_{k - 1} } \right)^{q} } \right)E_{q} \left( {\delta \left( {t - t_{k} } \right)^{q} } \right) \\ & \le \frac{1}{{\eta^{k} }}V\left( {t_{0}^{ + } } \right)E_{q} \left( {\delta \left( {t - t_{k} } \right)^{q} } \right). \\ \end{aligned}$$
(24)

According to the condition (H2), when \(k \to \infty\), we have

$$V\left( t \right) \to 0.$$
(25)

Consequently, \(\left\| {e\left( t \right)} \right\| \to 0\) as \(k \to \infty\). It follows that the trivial solution of error dynamical system (8) is asymptotically stable, which implies that system (7) is anti-synchronized with system (6). This completes the proof.

Remark 2

Recently, there has been a small number of works about the impulsive anti-synchronization of the fractional-order chaotic circuit, but these research findings are without considering the effect of time delay and memristor. Compared with [34,35,36,37,38], we consider a fractional-order delayed chaotic circuit under with memristor. The condition of impulsive anti-synchronization between master–slave systems is achieved. Figures 3, 4 and 5 show that the control scheme is effective.

Fig. 3
figure 3

Dynamical behaviors of systems (6) and (7) without impulsive control matrix, \(q = 0.985\), (a)\(x_{1} \left( t \right), y_{1} \left( t \right)\); (b)\(x_{2} \left( t \right), y_{2} \left( t \right)\); (c)\(x_{3} \left( t \right), y_{3} \left( t \right)\); (d)\(x_{4} \left( t \right), y_{4} \left( t \right)\)

Full size image
Fig. 4
figure 4

Dynamical behaviors of systems (6) and (7) with impulsive control matrix, \(q = 0.985, k_{b} = 1.6, \tau_{k} = 0.01\), (a)\(x_{1} \left( t \right), y_{1} \left( t \right)\); (b)\(x_{2} \left( t \right), y_{2} \left( t \right)\); (c)\(x_{3} \left( t \right), y_{3} \left( t \right)\); (d)\(x_{4} \left( t \right), y_{4} \left( t \right)\)

Full size image
Fig. 5
figure 5

Synchronization errors between systems (6) and (7) with impulsive control matrix, \(q = 0.985, k_{b} = 1.6, \tau_{k} = 0.01\)

Full size image

4 Numerical simulations

In this section, some numerical simulations are presented to verify and demonstrate the proposed theoretical approach; and the connection of stable region is given later. The simulations are run on MATLAB program based on the predictor–corrector algorithm [48] for fractional-order differential equations.

4.1 Anti-synchronization of FMCC under impulsive control

To facilitate the description of impulsive property, the impulsive matrix is denoted as \(C_{k} = {\text{diag}}\left( { - k_{b} , - k_{b} , - k_{b} , - k_{b} } \right),\) which \(k_{b}\) refers to the impulsive coupling strength. On the basis of Fig. 2, when \(M_{1} = 3\), and \(M_{4} = 1.8\) are selected, \(\delta = 69.6\) is obtained. According to the condition (H1) of Theorem 1, the result of \(0 \le k_{b} \le 2\) is got. Moreover, after setting \(\tau_{k} = 0.01, q = 0.985, \eta = 1.1,\) and \(k_{b} = 1.6\), by MATLAB calculation program, we get

$$\eta d_{k} E_{q} \left( {\delta \tau_{k}^{q} } \right) = 1.1 \times 0.36 \times E_{0.985} \left( {69.6 \times 0.01^{0.985} } \right) = 0.84 < 1\,;$$

then, the condition (H2) of Theorem 1 holds. The initial values of system (6) and system (7) are set to be \(\left( {0,\,0.1,\,0,\,0} \right)^{T}\) and \(\left( { - 0.5,\,0,\,0.5,\, - 0.5} \right)^{T}\), respectively. It follows from Theorem 1 that system (7) is anti-synchronized with system (6) under the impulsive control matrix \(B_{k}\).

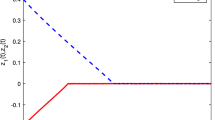
Figure 3 illustrates the time evolution curves between system (6) and system (7) without impulsive control matrix \(C_{k}\), indicating that both systems have different state trajectories over time. Figure 4 gives the state trajectories of systems (6) and (7) with impulsive control matrix \(C_{k}\). Figure 5 depicts the error dynamics of the two systems with impulsive control matrix \(C_{k}\), suggesting the feasibility of implementing impulsive anti-synchronization in limited time.

4.2 The analysis of stable region

Figure 6 displays the stable region about impulsive interval \(\tau_{k}\) and order \(q\) with different \(k_{b}\). Under the condition (H2) of Theorem 1 when \(\eta = 1.1\) and \(\delta = 69.6\), the stable region about \(\tau_{k}\) increases with order \(q\) from 0 to 1.

Fig. 6
figure 6

Estimation of the stable region about \(\tau_{k}\) and \(q\), when \(\eta = 1.1\), \(\delta = 69.6\)

Full size image

With different \(\tau_{k}\), the stable region of impulsive coupling strength \(k_{b}\) and order \(q\) is shown in Fig. 7. Obviously, a larger stable region can be obtained with a bigger \(q\).

Fig. 7
figure 7

Estimation of the stable region about \(k_{b}\) and \(q\), when \(\eta = 1.1\), \(\delta = 69.6\)

Full size image

Under some fixed values of \(\eta\) when \(q = 0.985\), the stable region with impulsive coupling strength \(k_{b}\) and impulsive interval \(\tau_{k}\) is displayed in Fig. 8. It shows that \(\tau_{k}\) goes infinity when \(k_{b} = 1\). This is because the condition (H2) of Theorem 1 is always satisfied if \(d_{k} = 0\).

Fig. 8
figure 8

Estimation of the stable region about \(k_{b}\) and \(\tau_{k}\), when \(q = 0.985\), \(\delta = 69.6\)

Full size image

5 Results and discussions

In this paper, the anti-synchronization of FMCC with time delay has been achieved in finite time based on Lyapunov stability theories and principle of impulsive control. The results are given not only by theoretical analysis, but also by numerical simulation. Under the conditions of Theorem 1, some discussions about the stable region have been obtained. With fixed impulsive coupling strength, a larger stable region for FMCC with time delay is obtained at smaller impulsive interval \(\tau_{k}\) and the bigger fractional order \(q\) where \(0 < q < 1\). Because the discussed chaotic system with memristor takes into account impulsive interval, impulsive coupling strength and fractional order, it is practical and attractive in understanding the chaotic system with memristor. This study will have potential applications to cryptography, filters and image encryption.