Sampled-Data $H_{\infty }$ Synchronization of Chaotic Lur’e Systems with Time Delay

Abstract

This paper deals with the problem of robust $H_{\infty }$ synchronization of chaotic Lur’e systems with time-varying delays via sampled-data control. In order to make full use of the information about sampling intervals, nonlinear functions and time-varying delays, an improved Lyapunov–Krasovskii (L–K) functional is introduced. Based on reciprocal convex combination technique, sufficient conditions are derived in terms of linear matrix inequalities (LMIs) to ensure the asymptotic synchronization of the considered Lur’e system with a guaranteed $H_{\infty }$ performance. By solving the obtained LMIs, the required sampled-data control gain matrix is obtained, which assures the asymptotic stability of the error system and reduces the effect of external disturbance according to $H_{\infty }$ norm. Finally, the effectiveness and less conservatism of the proposed method are verified through numerical simulations of the Chua’s circuit and neural networks.

1 Introduction

It is well known that chaotic systems are sensitive dependence on initial conditions, i.e., small change in initial conditions leads to very large differences in the system states. The concept of master–slave synchronization between two identical chaotic systems has been initially introduced by Pecora and Carroll in [27], in which particular chaotic system is called the master system and another chaotic system is called the slave system. Main thirsts along master–slave synchronization is that slave system is controlled by using the output of the master system, that is, output of the slave system tracks the output of other one asymptotically. In recent years, the problem of chaos control and synchronization have been paid much attention because of their a wide applications in secure communication, chemical reaction, biological systems, and information science [2, 5, 23–25, 46]. More precisely, in the field of secure communication, same chaotic systems have been used for both master (transmitter) system and slave (receiver) system. Firstly, to obtain the chaotified original message, the given message is added to the output of the chaotic system in transmitter based on encryption. Then, from the output of the chaotic system in the receiver, the transmitted message is subtracted by decryption, and the outcome is the message signal itself. However, to obtain successful communication message securely, the chaotic systems in the transmitter and receiver should be synchronized. So far, many synchronization schemes have been proposed such as complete synchronization [23], lag synchronization [24], projective synchronization [5, 25] and projective lag synchronization [5].

Lur’e system is one of the important classes of nonlinear system, and it can be represented as a linear system in the forward path and a nonlinear element in the feedback path, whose nonlinearity satisfies some sector bound constraints. The problem of chaos control and synchronization of Lur’e systems have been paid a lot of efforts in recent years [3, 11, 15, 17, 34, 42, 43, 45], because many nonlinear systems such as Chua’s circuit, n-scroll attractors and hyperchaotic attractors can be modeled in this form. Meanwhile, time delay is unavoidable in real situations, which leads the dynamical behavior of the system to be more complex. For this reason, Yalcin et al. [42] have introduced the effect of time delay in the problem of synchronization for chaotic Lur’e system and presented sufficient conditions for stability. Thus, synchronization of chaotic Lur’e system with time delay has been widely investigated by many researchers (see [9, 15, 40, 42, 45] and the references therein).

In order to achieve synchronization of chaotic Lur’e systems, a lot of control schemes have been proposed including feedback control [34], delayed output-feedback control [15, 34], observer-based control [11], adaptive control [17] and proportional derivative (PD) control [43]. In these control methods, feedback signals are updated continuously, and thus, it can be found in analog circuits. When working in an open communication networks, it may be difficult to obtain an accurate feedback signal in real time because of the noise corruption in these controllers. To overcome this difficulty, signals are updated at instant times, i.e., discrete-time controllers are used such as impulsive control [3] and sampled-data control [1, 6, 29, 38, 39, 41]. Because of the rapid growth of modern high-speed computers, communication networks and microelectronics, discrete (digital) controllers are more preferable than continuous controllers. Therefore, by using sampled-data control, synchronization of chaotic Lur’e system has become an important topic and it has attracted many researchers [4, 9, 18, 35, 37, 40, 44]. The main advantage of using sampled-data controller is to exploit the digital control techniques in real time. This digital controller allows synchronization of chaotic systems only by using the samples of the state variables of the master system and the slave system at discrete-time instants.

In sampled-data control problems, selecting proper sampling interval is very important for designing suitable controllers. It should be noted that a bigger sampling period will lead to lower communication channel occupation, fewer actuation of the controller and less signal transmission. Therefore, the main objective is to design a controller in such a way that leads to synchronization under bigger sampling period. In the problem of designing sampled-data controllers, an input delay approach has been proposed in [6], where sampling holder is modeled as a delayed control input and the stability conditions are derived based on L–K functional method. By introducing piecewise L–K functional, sampled-data synchronization criterion has been given in [4], where the results in [4] are less conservative than in [18]. In [40], exponential synchronization of chaotic Lur’e system with time delays has been investigated, where the proposed L–K functional is positive definite at sampling times but not necessarily positive definite during the sampling interval. Asymptotic synchronization of two identical chaotic Lur’e systems based on sampled-data control has been studied in [37, 44], where they have introduced novel L–K functional which includes the information about the slope of the nonlinear function.

In mathematical modeling problems, parameter uncertainties are unavoidable one due to environmental noise, uncertain or slowly varying parameters, variations of the operating point and aging of the devices. In this regard, the problem of synchronization for chaotic systems with uncertainties has been investigated. On the other hand, some noises or disturbances occur widely in the physical systems which may lead to difficulties in achieving synchronization. Therefore, to reduce the effect of noises or disturbances in synchronization of chaotic systems, $H_{\infty }$ control concept has been introduced by Hou et al. [8]. In [12, 28, 36], $H_{\infty }$ synchronization for delayed chaotic neural networks and mechanical systems with external disturbance have been presented, while $H_{\infty }$ synchronization for Lur’e system has been studied in [10]. The problem of $H_{\infty }$ filtering for time-delay systems has been investigated in [20, 22, 30–32], whereas stability and stabilization of time-delay systems with disturbances have given in [13, 16, 19, 21]. Recently, the problem of synchronization for identical chaotic Lur’e systems with external disturbance and uncertainties using sampled-data $H_{\infty }$ controller has been discussed in [7]. However, there are only very few works only having results on $H_{\infty }$ synchronization problem of Lur’e systems, and thus, there is enough room for extra improvement. This is the main motivation of this paper. To the best of the author’s knowledge, the problem of sampled-data $H_{\infty }$ synchronization for Lur’e systems with time delays has not been fully investigated and remains open.

Inspired by above discussions, this paper studies the problem of robust $H_{\infty }$ synchronization of chaotic Lur’e system with time delays via sampled-data control. By introducing an improved discontinuous L–K functional in Theorem 1 and by utilizing reciprocal convex technique, sufficient conditions for synchronization are derived in terms LMIs under $H_{\infty }$ performance index. Then, by solving the obtained LMIs, desired control gain matrices are obtained. Main contributions to this paper lie in the following facts: (1) in real situations, external disturbances and time-varying delays are unavoidable, and thus, they are taken into account. (2) With the ideas in [17], a sampled-data feedback control is designed, which utilizes both input sampling delay and signal transmission delay. (3) The aim is to derive new synchronization criteria to achieve less conservative result (i.e., finding larger sampling period). Different from the works [11, 15, 34], reciprocal convex approach is used to deal wit the derivative of L–K functional which may lead less conservative results. (4) Our considered L–K functional fully utilizes the information about sampling patterns and bounds of time-varying delays. Also, the information about the slope of the nonlinear function is used in this paper, whereas the L–K functional proposed in [11, 34] ignores this information. Finally, numerical simulations are performed by Chua’s circuit and neural networks, which shows that the proposed method is less conservative and more effective.

Notation: Throughout this paper, the superscripts T and $-1$ mean the transpose and the inverse of a matrix, respectively. ${\mathbb {R}}^n$ denotes the n-dimensional Euclidean space, ${\mathbb {R}}^{n \times m}$ is the set of all $n \times m$ real matrices, $\Vert \cdot \Vert$ refers to the Euclidean vector norm or the induced matrix 2-norm, $P >0\,(P\ge 0)$ means that P is a real symmetric and positive definite (semi-positive definite) matrix, I stands for an appropriately dimensioned identity matrix, ${\text{ diag }}\{\cdots \}$ denotes a block-diagonal matrix and symmetric term in a symmetric matrix is denoted by $\star$.

2 Problem Description

Consider the following master–slave-type synchronization scheme with sampled-data control

$$\begin{aligned} \begin{array}{ll} {\mathcal {M}}&{}:\left\{ \begin{array}{ll} \dot{x}(t)=&{} Ax(t)+Bx(t-d(t))+W\varphi (Dx(t))\\ p(t)=&{} Cx(t) \end{array}\right. \\ {\mathcal {S}}&{}:\left\{ \begin{array}{ll} \dot{z}(t)=&{} Az(t)+Bz(t-d(t))+W\varphi (Dz(t))+u(t)+H\omega (t)\\ q(t)=&{} Cz(t) \end{array}\right. \\ {\mathcal {C}}&{}: u(t)=K(p(t_k)-q(t_k)),\,\,\,t_k\le t \le t_{k+1} \end{array} \end{aligned}$$

(1)

with the master system (${\mathcal {M}}$), the slave system (${\mathcal {S}}$) and the controller (${\mathcal {C}}$). $x(t)\in {\mathbb {R}}^n$ and $z(t)\in {\mathbb {R}}^n$ are state vectors of ${\mathcal {M}}$ and ${\mathcal {S}}$, respectively, corresponding outputs are p(t) and $\,q(t)\in {\mathbb {R}}^l$, $u(t)\in {\mathbb {R}}^n$ is the slave system control input and $\omega (t) \in {\mathbb {R}}^{k}$ is the external disturbance which belongs to ${\mathcal {L}}_2[0,\infty ]$. $A\in {\mathbb {R}}^{n\times n},\,B\in {\mathbb {R}}^{n\times n},\,C\in {\mathbb {R}}^{l\times n},\,D\in {\mathbb {R}}^{n_h\times n}$, $H \in {\mathbb {R}}^{n \times k}$ and $W\in {\mathbb {R}}^{n\times n_h}$ are known constant matrices. The time-varying delay satisfies the following conditions

$$\begin{aligned} 0\le d(t) \le d,\,\,\, \dot{d}(t)\le d_{\mu }. \end{aligned}$$

(2)

Assume that $\varphi (\cdot ):{\mathbb {R}}^{n_h}\rightarrow {\mathbb {R}}^{n_h}$ is a diagonal nonlinearity with $\varphi _i(\cdot )$ belonging to the sector $\left[ k_i^- , k_i^+\right]$ and satisfies the following condition

$$\begin{aligned} \left[ \varphi _i(s)-k_i^+ s\right] \left[ \varphi _i(s)-k_i^- s\right] \le 0, \forall s,\quad i=1,\ldots , n_h. \end{aligned}$$

(3)

Denote the updating instant time of the ZOH by $t_k$. The control input to the system ${\mathcal {S}}$ is denoted by $u(t)\in {\mathbb {R}}^n$ under sampler time $t_k$, and $K\in {\mathrm {R}}^{n\times n_h}$ is the sampled-data controller gain matrix to be designed later. For sampled-data synchronization purpose, discrete measurements of p(t) and q(t) at the sampling instant $t_k$ are used, that is, $p(t_k)$ and $q(t_k)$, respectively. Suppose that the updating signal (successfully transmitted signal from the sampler to the controller and to the ZOH) at the instant $t_k$ has experienced a constant signal transmission delay $\rho$. It is assumed that the sampling intervals are bounded and satisfy

$$\begin{aligned}&0 = t_0 <t_1< \cdots < t_k <\cdots < \lim _{k \rightarrow +\infty }t_k=+\infty , \\&t_{k+1}-t_k \le \tau _m, \ \ \forall \ k \ge 0, \end{aligned}$$

where $\tau _m>0$ represents the largest sampling period. Thus, we have

$$\begin{aligned} t_{k+1}-t_k+\rho \le \tau _m+\rho \le \tau _M. \end{aligned}$$

(4)

Here, $\tau _M$ denotes the maximum time span between the time $t_k-\rho$ at which the state is sampled and the time $t_{k+1}$ at which the next update arrives at the destination. Let the synchronization error between ${\mathcal {M}}$ and ${\mathcal {S}}$ be $e(t)= x(t)-z(t)$. Our main aim of this study is to design sampled-data controller ${\mathcal {C}}$ to achieve synchronization between ${\mathcal {M}}$ and ${\mathcal {S}}$ in (1), which means e(t) is asymptotically stable. Moreover, based on the above sampled-data controller design formulation, the feedback controller takes the form

$$\begin{aligned} u(t)=Ke(t_k-\rho ), \ \ \ t_k \le t \le t_{k+1}, \ \ k=0,1,2,\ldots \end{aligned}$$

(5)

with $t_{k+1}$ being the next updating instant time of the ZOH after $t_k$. Then, we can written closed loop error dynamical system in the following form for $t_k\le t \le t_{k+1}$

$$\begin{aligned} \dot{e}(t)= Ae(t)+Be(t-d(t))+W\eta (De(t),z(t))-KCe(t_k-\rho )-H \omega (t), \end{aligned}$$

(6)

where $\eta (De(t),z(t))=\varphi (D(e(t)+z(t))-\varphi (Dz(t))$ and $\tau (t)=t-t_{k}+\rho$. It can be seen that $\rho \le \tau (t) < t_{k+1}-t_{k}+\rho \le \tau _M$ and $\dot{\tau }(t) = 1$ for $t \ne t_{k}$. It can be easily checked that $\eta _i(0)=0$ and the nonlinearity $\eta _i(\cdot )$ belongs to the sector $[k_i^-,k_i^+]$ for all $i=1,2,\ldots , n_h$ and $\forall s \in {\mathbb {R}}$

$$\begin{aligned} \left[ \varphi _i(s)-k_i^+ s\right] \left[ \varphi _i(s)-k_i^- s\right] \le 0. \end{aligned}$$

(7)

Also, we denote $K_1={\text{ diag }} \left\{ k_1^-,\ldots ,k_{n_h}^-\right\}$ and $K_2={\text{ diag }} \left\{ k_1^-,\ldots ,k_{n_h}^-\right\}$.

Suppose the matrices $A, \ B$ and W have parameter perturbation $\Delta A(t), \ \Delta B(t)$ and $\Delta W(t)$, which are in the form of

$$\begin{aligned} \left[ \begin{array}{ccc} \Delta A(t)&\Delta B(t)&\Delta W(t) \end{array}\right] =M\varLambda (t)\left[ \begin{array}{ccc} E_1&E_2&E_3 \end{array}\right] \end{aligned}$$

(8)

where $M,E_1,E_2$ and $E_3$ are given matrices. The class of parametric uncertainties $\varLambda (t)$ that satisfy

$$\begin{aligned} \varLambda (t)=\left[ I-F(t)J\right] ^{-1}F(t) \end{aligned}$$

(9)

is said be admissible, where J is also a known matrix satisfying

$$\begin{aligned} I-JJ^{-1}>0 \end{aligned}$$

(10)

and F(t) is an uncertain matrix satisfying

$$\begin{aligned} F^\mathrm{T}(t)F(t)\le I. \end{aligned}$$

(11)

Before proceeding further, the following essential lemmas and definitions are introduced.

Lemma 1

[33] For any constant matrix $X\in {\mathbf {R}}^{n\times n}$, $X=X^\mathrm{T}>0$, two scalars $h_{2}\ge h_{1}>0$, such that the integrations concerned are well defined, and then,

$$\begin{aligned} -(h_{2}-h_{1})\displaystyle \int _{t-h_{2}}^{t-h_{1}}\mathrm{e}^\mathrm{T}(s)Xe(s)\mathrm{d}s \le&-\Big (\displaystyle \int _{t-h_{2}}^{t-h_{1}} e(s)\mathrm{d}s\Big )^\mathrm{T}X \Big (\displaystyle \int _{t-h_{2}}^{t-h_{1}} e(s)\mathrm{d}s\Big ),\\ -\frac{(h_{2}^2-h_{1}^2)}{2}\displaystyle \int _{t-h_{2}}^{t-h_{1}} \int _{\theta }^{t}\mathrm{e}^\mathrm{T}(s)Xe(s)\mathrm{d}s\mathrm{d}\theta \le&-\Big (\displaystyle \int _{t-h_{2}}^{t-h_{1}}\int _{\theta }^{t} e(s)\mathrm{d}s\mathrm{d}\theta \Big )^\mathrm{T}X \\ {}&\times \Big (\displaystyle \int _{t-h_{2}}^{t-h_{1}}\int _{\theta }^{t} e(s)\mathrm{d}s\mathrm{d}\theta \Big ). \end{aligned}$$

Lemma 2

[26] For any vectors $\delta _{1}, \delta _{2}$, constant matrices R, S, and real scalars $\alpha \ge 0$, $\beta \ge 0$ satisfying that $\left[ \begin{array}{cc} R &{} S \\ *&{} R\end{array}\right] \ge 0$ and $\alpha +\beta =1$, then the following inequality holds:

$$\begin{aligned} -\frac{1}{\alpha }\delta _{1}^\mathrm{T}R\delta _{1}-\frac{1}{\beta } \delta _{2}^\mathrm{T}R\delta _{2}\le -\left[ \begin{array}{c}\delta _{1} \\ \delta _{2} \end{array}\right] ^\mathrm{T}\left[ \begin{array}{cc} R &{}\quad S \\ *&{}\quad R\end{array}\right] \left[ \begin{array}{c}\delta _{1} \\ \delta _{2} \end{array}\right] . \end{aligned}$$

Lemma 3

[14] Suppose $\varLambda (t)=\left[ I-F(t)J\right] ^{-1}F(t)$ and satisfying the conditions (10) and (11). Given matrices $\varPi =\varPi ^\mathrm{T}, \ \varTheta$ and $\varOmega$ of appropriate dimensions, the following inequality holds for F(t)

$$\begin{aligned} \varPi +\varTheta \varLambda (t)\varOmega +\varOmega ^\mathrm{T}\varLambda ^\mathrm{T}(t)\varTheta ^\mathrm{T} \end{aligned}$$

such that $F^\mathrm{T}(t)F(T)<I$, if and only if, for some $\sigma >0$

$$\begin{aligned} \left[ \begin{array}{ccc} \varPi &{}\quad \varTheta &{}\quad \sigma \varOmega ^\mathrm{T}\\ \star &{}\quad -\sigma I &{}\quad \sigma J^\mathrm{T} \\ \star &{} \star &{} -\sigma I \end{array}\right] <0. \end{aligned}$$

(12)

Definition 1

[10] The error system (6) is $H_{\infty }$ synchronized if the synchronization error e(t) satisfies

$$\begin{aligned} \int _{0}^{\infty } \mathrm{e}^\mathrm{T}(s)Se(s)\mathrm{d}s < \gamma ^2 \int _{0}^{\infty } \omega ^\mathrm{T}(s)\omega (s)\mathrm{d}s \end{aligned}$$

for a given level $\gamma >0$ under zero initial condition, where S is a positive symmetric matrix. The parameter $\gamma$ is called the $H_{\infty }$ norm bound or the disturbance attenuation level.

Our main objective of this paper is to find the maximum allowable sampling period (MASP) because a bigger sampling period leads to lower communication channel occupying and less transmission. Also, in order to achieve $H_{\infty }$ synchronization with the presence of external disturbances $\omega (t)$, suitable controller u(t) is designed which guarantees the asymptotical stability of the error system.

3 Main Results

In this section, we will derive the synchronization criteria for chaotic Lur’e system based on sampled-data control by introducing L–K functional. For the simplicity of matrix representation, $e_i(i=1,\ldots ,11) \in {\mathbb {R}}^{11n \times n}$ is defined a block entry matrix. For example, $e_3^\mathrm{T}=[0 \ 0 \ I \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0]$ and

$$\begin{aligned} \xi ^\mathrm{T}(t)&=\bigg [\mathrm{e}^\mathrm{T}(t) \ \ \mathrm{e}^\mathrm{T}(t_k-\rho ) \ \ \mathrm{e}^\mathrm{T}(t-\rho ) \ \ \mathrm{e}^\mathrm{T}(t-\tau _M) \ \ \int _{t_k-\rho }^{t-\rho } \mathrm{e}^\mathrm{T}(s)\mathrm{d}s \ \ \eta (De(t),z(t)) \\&\quad \quad \dot{e}(t) \ \ \mathrm{e}^\mathrm{T}(t-d(t)) \ \ \mathrm{e}^\mathrm{T}(t-d) \ \ \int _{t-d(t)}^{t}e(s)\mathrm{d}s \ \ \int _{t-d}^{t-d(t)} e(s)\mathrm{d}s \bigg ]. \\ \varUpsilon _1&= \left[ H^\mathrm{T} G^\mathrm{T} \ \ H^\mathrm{T} G^\mathrm{T} \ \ 0 \ \ 0 \ \ 0 \ \ 0 \ \ \epsilon H^\mathrm{T} G^\mathrm{T} \ \ 0 \ \ 0 \ \ 0 \ 0\right] , \ \ \varUpsilon _2=\left[ \varUpsilon _1 \ \ 0 \right] , \\ \bar{\mathcal {H}}&= {\text{ diag }}\{P, \ \ 0 ,\ \ 0\}+\tau _M{\mathcal {H}},\\ \varPhi _{11}&= S+Q_1\!+\!Q_2-\!R_1\!-d^2 R_2\!+\!S_1\!-\!S_2-\frac{X_1+X_1^\mathrm{T}}{2}+GA\!+\!A^\mathrm{T} G^\mathrm{T} \!+\!N_1\!+\!N_1^\mathrm{T}, \\ \varPhi _{12}&= X_1-X_2-LC+A^\mathrm{T} G^\mathrm{T}-N_1+N_2^\mathrm{T}, \ \ \varPhi _{13} = N_3^\mathrm{T}+S_2, \ \ \varPhi _{15} =N_5^\mathrm{T}-X_3, \\ \varPhi _{16}&= N_6^\mathrm{T}+GW, \ \ \varPhi _{17} = N_7^\mathrm{T}+P+D^\mathrm{T}K_1(\varLambda - \varDelta ) D - G +\epsilon A^\mathrm{T} G^\mathrm{T}, \\ \varPhi _{18}&= N_8^\mathrm{T}+R_1-V_1+GB, \ \ \varPhi _{110} = N_{10}^\mathrm{T}+2d R_2, \ \ \varPhi _{111} = N_{11}^\mathrm{T}+2d R_2,\\ \varPhi _{22}&= V_2-2 T_2 +X_2+X_2^\mathrm{T}-\frac{X_1+X_1^\mathrm{T}}{2}-LC- C^\mathrm{T} L^\mathrm{T}-N_2-N_2^\mathrm{T}, \\ \varPhi _{23}&=-N_3^\mathrm{T}+T_2-V_2^\mathrm{T}, \ \ \varPhi _{24} =-N_4^\mathrm{T}+T_2-V_2, \ \ \varPhi _{25} =-N_5^\mathrm{T}-X_4, \\ \varPhi _{26}&=-N_6^\mathrm{T}+GW, \ \ \varPhi _{27} = -N_7^\mathrm{T}-G-\epsilon L^\mathrm{T} G^\mathrm{T}, \ \ \varPhi _{28} =-N_8^\mathrm{T}+GB, \\ \varPhi _{33}&=-S_1-S_2+T_1-T_2, \ \ \varPhi _{44} =-T_1-T_2, \ \ \varPhi _{55} =-\frac{X_5+X_5^\mathrm{T}}{2}, \\ \varPhi _{67}&= -\varLambda D+ \varDelta D + \epsilon W^\mathrm{T} G^\mathrm{T}, \\ \varPhi _{77}&= d^2 R_1+\frac{d^4}{4}R_2+\rho ^2 S_2+(\tau _M-\rho )^2 T_2 -\epsilon G -\epsilon G^\mathrm{T}, \ \ \varPhi _{78} =\epsilon G B, \\ \varPhi _{88}&=-(1-d_{\mu })Q_1-2R_1+V_1+V_1^\mathrm{T}, \\ \varPhi _{11}^{'}&= \varPhi _{11}-2D^\mathrm{T}K_1U_2K_2D, \ \ \varPhi _{12}^{'} =\varPhi _{12}-\tau _M X_3, \ \ \varPhi _{13}^{'} =\varPhi _{13}+\tau _M X_3, \\ \varPhi _{16}^{'}&= \varPhi _{16}+D^\mathrm{T}(K_1+K_2)U_2,\ \ \varPhi _{17}^{'} = \varPhi _{17}+\tau _M(X_1+X_1^\mathrm{T}), \\ \varPhi _{22}^{'}&= \varPhi _{22}-\tau _M(X_4+X_4^\mathrm{T}-Z_1), \ \ \varPhi _{23}^{'} = \varPhi _{23}+\tau _M X_4, \\ \varPhi _{35}^{'}&= \tau _M \frac{X_5+X_5^\mathrm{T}}{2}, \ \ \varPhi _{11}^{''} = \varPhi _{11}-2D^\mathrm{T}K_1U_1K_2D, \\ \varPhi _{16}^{''}&= \varPhi _{16}+D^\mathrm{T}(K_1+K_2)U_1,\ \ \varPhi _{22}^{''} = \varPhi _{22}-\tau _M Z_1, \ \ \varXi =-\tau _M(Z_2+N_2). \end{aligned}$$

$$\begin{aligned} \varPi _1&=\left[ \begin{array}{ccccccccccc} \varPhi _{11}^{'}&{}\varPhi _{12}^{'}&{}\varPhi _{13}^{'}&{} -N_4^\mathrm{T}&{}\varPhi _{15}&{}\varPhi _{16}^{'}&{}\varPhi _{17}^{'}&{}\varPhi _{18}&{} N_9^\mathrm{T}+V_1&{}\varPhi _{110} &{} \varPhi _{111}\\ \star &{}\varPhi _{22}^{'}&{}\varPhi _{23}^{'}&{}\varPhi _{24} &{}\varPhi _{25}&{}\varPhi _{26}&{}\varPhi _{27}+\tau _M Z_2 &{}\varPhi _{28}&{} - N_9^\mathrm{T}&{}- N_{10}^\mathrm{T}&{} - N_{11}^\mathrm{T} \\ \star &{} \star &{} \varPhi _{33} &{} V_2 &{} \varPhi _{35}^{'} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{}\star &{}\star &{} \varPhi _{44} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{}\star &{}\star &{}\star &{} \varPhi _{55} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{}\star &{}\star &{}\star &{}\star &{} -2U_2 &{} \varPhi _{67} &{} 0 &{} 0 &{} 0 &{} 0 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \varPhi _{77}+\tau _M Z_3 &{} \epsilon GB &{} 0 &{} 0 &{} 0 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \varPhi _{88} &{} -V_1+R_1 &{} 0 &{} 0 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \star &{} -Q_2-R_1 &{} 0 &{} 0 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \star &{} \star &{} -R_2 &{} -2R_2 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \star &{} \star &{} \star &{} -R_2 \\ \end{array}\right] \end{aligned}$$

(13)

$$\begin{aligned} \varPi _2&=\left[ \begin{array}{cccccccccccc} \varPhi _{11}^{''}&{}\varPhi _{12}&{}\varPhi _{13}&{} -N_4^\mathrm{T}&{}\varPhi _{15}&{}\varPhi _{16}^{''}&{}\varPhi _{17}&{}\varPhi _{18}&{} N_9^\mathrm{T}+V_1&{}\varPhi _{110} &{} \varPhi _{111} &{} -\tau _MN_1 \\ \star &{}\varPhi _{22}^{''}&{}\varPhi _{23}&{}\varPhi _{24} &{}\varPhi _{25}&{}\varPhi _{26}&{}\varPhi _{27}&{}\varPhi _{28}&{} - N_9^\mathrm{T}&{}- N_{10}^\mathrm{T}&{} - N_{11}^\mathrm{T} &{} \varXi \\ \star &{} \star &{} \varPhi _{33} &{} V_2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\tau _MN_3\\ \star &{}\star &{}\star &{} \varPhi _{44} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\tau _MN_4\\ \star &{}\star &{}\star &{}\star &{} \varPhi _{55} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\tau _MN_5\\ \star &{}\star &{}\star &{}\star &{}\star &{} -2U_1 &{} \varPhi _{67} &{} 0 &{} 0 &{} 0 &{} 0 &{} -\tau _MN_6 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \varPhi _{77} &{} \epsilon GB &{} 0 &{} 0 &{} 0 &{} -\tau _MN_7 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \varPhi _{88} &{} -V_1+R_1 &{} 0 &{} 0 &{} -\tau _MN_8 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \star &{} -Q_2-R_1 &{} 0 &{} 0 &{} -\tau _MN_9 \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \star &{} \star &{} -R_2 &{} -2R_2 &{} -\tau _MN_{10} \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \star &{} \star &{} \star &{} -R_2 &{} -\tau _MN_{11} \\ \star &{}\star &{}\star &{}\star &{}\star &{}\star &{}\star &{} \star &{} \star &{} \star &{} \star &{} -\tau _M Z_3 \end{array}\right] \end{aligned}$$

(14)

Theorem 1

Given scalars $\epsilon$ and $\gamma$, the master system ${\mathcal {M}}$ and slave system ${\mathcal {S}}$ in (1) are synchronous if there exist matrices $P>0$, $Q_1 >0, \ Q_2 >0$, $R_1 >0, \ R_2 >0$, $S>0$, $S_1 >0$, $S_2 >0$, $T_1 >0, \ T_2 >0$, $\varLambda = diag\left\{ \lambda _1,\ldots , \lambda _{n_h}\right\} >0$, $\varDelta =diag \left\{ \delta _1,\ldots ,\delta _{n_h}\right\} >0$, $\left[ \begin{array}{cc}Z_1 &{} Z_2 \\ \star &{} Z_3\end{array}\right] >0$, $U_1 \ge 0, \ U_2 \ge 0$ and for any appropriately dimensioned matrices $X_i, \ i=1,\ldots ,5$, G, L, $V_1,V_2$ and $N=[N_1^\mathrm{T},N_2^\mathrm{T},N_3^\mathrm{T},N_4^\mathrm{T},N_5^\mathrm{T},N_6^\mathrm{T},N_7^\mathrm{T},N_8^\mathrm{T},N_9^\mathrm{T},N_{10}^\mathrm{T},N_{11}^\mathrm{T}]$ such that

$$\begin{aligned} \bar{\mathcal {H}}&>0 , \end{aligned}$$

(15)

$$\begin{aligned} \left[ \begin{array}{cc} R_1 &{} V_1 \\ \star &{} R_1 \end{array}\right]&> 0 , \end{aligned}$$

(16)

$$\begin{aligned} \left[ \begin{array}{cc} T_2 &{} V_2 \\ \star &{} T_2 \end{array}\right]&> 0 , \end{aligned}$$

(17)

$$\begin{aligned} \left[ \begin{array}{cc} \varPi _1 &{} \varUpsilon _1^\mathrm{T} \\ \star &{} - \gamma ^2 I\end{array}\right]&< 0, \end{aligned}$$

(18)

$$\begin{aligned} \left[ \begin{array}{cc} \varPi _2 &{} \varUpsilon _2^\mathrm{T} \\ \star &{} - \gamma ^2 I\end{array}\right]&< 0. \end{aligned}$$

(19)

Furthermore, the sampled-data controller gain matrix is given by

$$\begin{aligned} K=G^{-1}L. \end{aligned}$$

(20)

Proof

Consider the L–K functional candidate as follows:

$$\begin{aligned} V(t)=\sum _{i=1}^7V_i(t),\,\,t\in [t_k,t_{k+1}) \end{aligned}$$

(21)

where

$$\begin{aligned} V_1(t)&= \mathrm{e}^\mathrm{T}(t)Pe(t)+2 \sum _{i=1}^{n_h} \int _{0}^{d_i^\mathrm{T}e,z}\big [\varLambda _i \left( k_i^+ s - \eta _i(s)\right) +\varDelta _i \left( \eta _i(s)-k_i^- s\right) \big ]\mathrm{d}s,\\ V_2(t)&=\int _{t-d(t)}^{t}\mathrm{e}^\mathrm{T}(s)Q_1e(s)\mathrm{d}s+ \int _{t-d}^{t}\mathrm{e}^\mathrm{T}(s)Q_2e(s)\mathrm{d}s,\\ V_3(t)&= d \int _{t-d}^{t}\int _{\theta }^{t}\dot{e}^\mathrm{T}(s)R_1\dot{e}(s)\mathrm{d}s\mathrm{d}\theta + \frac{d^2}{2} \int _{t-d}^{t}\int _{\theta }^{t}\int _{\lambda }^{t}\dot{e}^\mathrm{T}(s) R_2\dot{e}(s)\mathrm{d}s \mathrm{d} \lambda \mathrm{d}\theta ,\\ V_4(t)&=\int _{t-\rho }^{t}\mathrm{e}^\mathrm{T}(s)S_1e(s)\mathrm{d}s +\rho \int _{t-\rho }^{t}\int _{\theta }^{t}\dot{e}^\mathrm{T}(s)S_2\dot{e}(s)\mathrm{d}s\mathrm{d}\theta ,\\ V_5(t)&=\int _{t-\tau _M}^{t-\rho }\mathrm{e}^\mathrm{T}(s)T_1e(s)\mathrm{d}s+(\tau _M-\rho ) \int _{t-\tau _M}^{t-\rho }\int _{\theta }^{t}\dot{e}^ T(s)T_2\dot{e}(s)\mathrm{d}s\mathrm{d}\theta ,\\ V_6(t)&=(\tau _M-\tau (t)) \xi _1^\mathrm{T}(t) {\mathcal {H}} \xi (t),\\ V_7(t)&=(\tau _M-\tau (t))\int _{t_k-\rho }^{t} \left[ \begin{array}{c}e(t_k - \rho )\\ \dot{e}(s)\end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} Z_1 &{} Z_2 \\ \star &{} Z_3 \end{array}\right] \left[ \begin{array} {c}e(t_k - \rho )\\ \dot{e}(s)\end{array}\right] \mathrm{d}s, \end{aligned}$$

with

$$\begin{aligned} \xi _1 (t)&=\left[ \mathrm{e}^\mathrm{T}(t)\mathrm{e}^\mathrm{T}(t_k) \int _{t_k-\rho }^{t-\rho }\mathrm{e}^\mathrm{T}(s)\mathrm{d}s\right] , \\ {\mathcal {H}}&=\left[ \begin{array}{ccc} \displaystyle \frac{X_1+X_1^\mathrm{T}}{2}&{}\quad -X_1+X_2&{}\quad X_3\\ \star &{}\quad -X_2-X_2^\mathrm{T}+\displaystyle \frac{X_1+X_1^\mathrm{T}}{2}&{}\quad X_4\\ \star &{}\quad \star &{}\quad \displaystyle \frac{X_5+X_5^\mathrm{T}}{2} \end{array}\right] . \end{aligned}$$

Note that from the assumptions, $V_i(t), \ i=1,2,3,4,5,7$ are positive definite. If $V_6(t)$ is positive definite, which implies V(t) is positive definite. It can seen that

$$\begin{aligned} V_6(t)&=\left( \frac{\tau (t)}{\tau _M} +\frac{\tau _M-\tau (t)}{\tau _M}\right) \mathrm{e}^\mathrm{T}(t) P e(t) + \frac{\tau _M-\tau (t)}{\tau _M} \xi _1^\mathrm{T}(t)\tau _M \bar{\mathcal {H}} \xi _1(t), \\&= \frac{\tau (t)}{\tau _M} \mathrm{e}^\mathrm{T}(t) P e(t) + \frac{\tau _M-\tau (t)}{\tau _M} \int _{t_k-\rho }^{t} \xi _1^\mathrm{T} (t) \frac{\bar{\mathcal {H}}}{t-t_k+\rho } \xi _1(t)\mathrm{d}s, \end{aligned}$$

If LMI (15) holds, then one has $V_6(t) \ge 0$, which gives L–K functional (21) is positive definite. It should be noted that V(t) is continuous on $[0,\infty )$ except the sampling instants $t_k, \ \forall k$. Calculating the time derivative of V(t) along the trajectories of (6), we have

$$\begin{aligned} \dot{V}(t)=\sum _{i=1}^7\dot{V}_i(t),\,\,t\in [t_k,t_{k+1}) \end{aligned}$$

(22)

where

$$\begin{aligned} \dot{V}_1(t)&= 2 \mathrm{e}^\mathrm{T}(t) P \dot{e}(t) + 2 \left[ \mathrm{e}^\mathrm{T}(t) D^\mathrm{T} K_1-\eta ^\mathrm{T}(D e(t),z(t))\right] \varLambda D \dot{e}(t) \nonumber \\&\quad + 2 \left[ \eta ^\mathrm{T}(D e(t),z(t))-\mathrm{e}^\mathrm{T}(t) D^\mathrm{T} K_2\right] \varDelta D\dot{e}(t), \end{aligned}$$

(23)

$$\begin{aligned} \dot{V}_2(t)&= \mathrm{e}^\mathrm{T}(t) \left( Q_1+Q_2\right) e(t)-(1-d_{\mu }) \mathrm{e}^\mathrm{T}(t-d(t))Q_1 e(t-d(t))\nonumber \\&\quad -\mathrm{e}^\mathrm{T}(t-d)Q_2e(t-d), \end{aligned}$$

(24)

$$\begin{aligned} \dot{V}_3(t)&= \dot{e}^\mathrm{T}(t) \left[ d^2 R_1+\frac{d^4}{4} R_2 \right] \dot{e}(t)-d \int _{t-d}^{t}\dot{e}^\mathrm{T}(s)R_1 \dot{e}(s)\mathrm{d}s \nonumber \\&\quad - \frac{d^2}{2} \int _{t-d}^{t}\int _{\theta }^{t}\dot{e}^\mathrm{T}(s)R_2\dot{e}(s)\mathrm{d}s \mathrm{d}\theta , \end{aligned}$$

(25)

$$\begin{aligned} \dot{V}_4(t)&= \mathrm{e}^\mathrm{T}(t)S_1e(t)-\mathrm{e}^\mathrm{T}(t-\rho )S_2 e(t-\rho ) +\rho ^2 \dot{e}^\mathrm{T}(t)S_2 \dot{e}(t)\nonumber \\&\quad -\rho \int _{t-\rho }^{t} \dot{e}^\mathrm{T}(s)S_2 \dot{e}(s)\mathrm{d}s, \end{aligned}$$

(26)

$$\begin{aligned} \dot{V}_5(t)&= \mathrm{e}^\mathrm{T}(t-\rho )T_1e(t-\rho )-\mathrm{e}^\mathrm{T}(t-\tau _M)T_1 e(t-\tau _M) +(\tau _M-\rho )^2 \dot{e}^\mathrm{T}(t)T_2 \dot{e}(t) \nonumber \\&\quad -(\tau _M-\rho ) \int _{t-\tau _M}^{t-\rho } \dot{e}^\mathrm{T}(s)T_2 \dot{e}(s)\mathrm{d}s, \end{aligned}$$

(27)

$$\begin{aligned} \dot{V}_6(t)&=-\left[ \begin{array}{c}e(t)\\ e(t_k)\\ \int _{t_k-\rho }^{t-\rho }e(s)\mathrm{d}s\end{array}\right] ^\mathrm{T} {\mathcal {H}} \left[ \begin{array}{c}e(t)\\ e(t_k)\\ \int _{t_k-\rho }^{t-\rho }e(s)\mathrm{d}s \end{array}\right] +2(\tau _M-\tau (t))\left[ \begin{array}{c}e(t)\\ e(t_k)\\ \int _{t_k-\rho }^{t-\rho }e(s)\mathrm{d}s\end{array}\right] ^\mathrm{T} \nonumber \\&\quad \times {\mathcal {H}} \left[ \begin{array}{c}\dot{e}(t)\\ 0\\ e(t-\rho )\end{array}\right] , \end{aligned}$$

(28)

$$\begin{aligned} \dot{V}_7(t)&=(\tau _M-\tau (t))\left[ \begin{array}{c}e(t_k - \rho )\\ \dot{e}(t)\end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} Z_1 &{} Z_2 \\ \star &{} Z_3 \end{array}\right] \left[ \begin{array}{c} e(t_k - \rho )\\ \dot{e}(t)\end{array}\right] \nonumber \\&\quad -\int _{t_k-\rho }^{t}\left[ \begin{array}{c}e(t_k - \rho )\\ \dot{e}(s)\end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} Z_1 &{} Z_2 \\ \star &{} Z_3 \end{array}\right] \left[ \begin{array}{c} e(t_k - \rho )\\ \dot{e}(s)\end{array}\right] \mathrm{d}s. \end{aligned}$$

(29)

By Lemma 1, we obtain

$$\begin{aligned} -&\rho \int _{t-\rho }^{t} \dot{e}^\mathrm{T}(s)S_2 \dot{e}(s)\mathrm{d}s \le - \left[ e(t)-e(t-\rho )\right] S_2 \left[ e(t)-e(t-\rho )\right] , \end{aligned}$$

(30)

$$\begin{aligned} -&\frac{d^2}{2} \int _{t-d}^{t}\int _{\theta }^{t}\dot{e}^\mathrm{T}(s)R_2\dot{e}(s)\mathrm{d}s \mathrm{d}\theta \nonumber \\&\le -\int _{t-d}^{t}\int _{\theta }^{t}\dot{e}^\mathrm{T}(s) \mathrm{d}s \mathrm{d}\theta R_2\dot{e}(s)\int _{t-d}^{t}\int _{\theta }^{t}\dot{e}(s) \mathrm{d}s \mathrm{d}\theta \nonumber \\&= -\left[ d e(t)-\int _{t-d(t)}^{t} e(s)\mathrm{d}s - \int _{t-d}^{t-d(t)}e(s)\mathrm{d}s\right] ^\mathrm{T} R_2 \nonumber \\&\quad \times \left[ d e(t)-\int _{t-d(t)}^{t} e(s)\mathrm{d}s - \int _{t-d}^{t-d(t)}e(s)\mathrm{d}s\right] . \end{aligned}$$

(31)

If the inequalities (16) and (17) are hold, according to Lemma 2, we conclude that

$$\begin{aligned}&-d \int _{t-d}^{t} \dot{e}^\mathrm{T}(s)R_1 \dot{e}(s)\mathrm{d}s = -d \int _{t-d(t)}^{t} \dot{e}^\mathrm{T}(s) R_1 \dot{e}(s) \mathrm{d}s - d \int _{t-d}^{t-d(t)} \dot{e}^\mathrm{T}(s) R_1 \dot{e}(s) \mathrm{d}s \nonumber \\&\quad \le - \frac{d}{d(t)} \int _{t-d(t)}^{t} \dot{e}^\mathrm{T}(s) \mathrm{d}s \ R_1 \ \int _{t-d(t)}^{t} \dot{e}(s) \mathrm{d}s \nonumber \\&\qquad -\frac{d}{d(t)-d} \int _{t-d}^{t-d(t)} \dot{e}^\mathrm{T}(s)\mathrm{d}s \ R_1 \ \int _{t-d}^{t-d(t)} \dot{e}^\mathrm{T}(s)\mathrm{d}s \nonumber \\&\quad \le -\left[ \begin{array}{c}\int _{t-d(t)}^{t} \dot{e}(s) \mathrm{d}s \\ \int _{t-d}^{t-d(t)} \dot{e}(s)\mathrm{d}s \end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc} R_1 &{} V_1 \\ \star &{} R_1 \end{array}\right] \left[ \begin{array}{c}\int _{t-d(t)}^{t} \dot{e}(s) \mathrm{d}s \\ \int _{t-d}^{t-d(t)} \dot{e}(s)\mathrm{d}s \end{array}\right] \end{aligned}$$

(32)

and

$$\begin{aligned} -(\tau _M&-\rho ) \int _{t-\tau _M}^{t-\rho } \dot{e}^\mathrm{T}(s)T_2 \dot{e}(s) \mathrm{d}s \nonumber \\&\le - \frac{\tau _M-\rho }{\rho -\tau (t)} \int _{t-\tau (t)}^{t-\rho } \dot{e}^\mathrm{T}(s) \mathrm{d}s \ T_2 \int _{t-\tau (t)}^{t-\rho } \dot{e}(s) \mathrm{d}s \nonumber \\&-\frac{(\tau _M-\rho )}{\tau _M-\tau (t)} \int _{t-\tau _M}^{t-\tau (t)} \dot{e}^\mathrm{T}(s)\mathrm{d}s \ T_2 \int _{t-\tau _M}^{t-\tau (t)} \dot{e}^\mathrm{T}(s)\mathrm{d}s \nonumber \\&\le - \left[ \begin{array}{c}\int _{t-\tau (t)}^{t-\rho } \dot{e}(s) \mathrm{d}s \\ \int _{t-\tau _M}^{t-\tau (t)} \dot{e}(s)\mathrm{d}s \end{array}\right] ^\mathrm{T} \left[ \begin{array}{cc}T_2 &{} V_2 \\ \star &{} T_2\end{array}\right] \left[ \begin{array}{c}\int _{t-\tau (t)}^{t-\rho } \dot{e}(s) \mathrm{d}s \\ \int _{t-\tau _M}^{t-\tau (t)} \dot{e}(s)\mathrm{d}s \end{array}\right] . \end{aligned}$$

(33)

For any appropriately dimensional matrix N, the following equation is considered

$$\begin{aligned} 0=2 \xi ^\mathrm{T} (t) N \left[ e(t)-e(t_k-\rho )-\int _{t_k-\rho }^{t}\dot{e}(s)\mathrm{d}s\right] . \end{aligned}$$

(34)

According to the error system (6), for any appropriately dimensioned matrix G and scalar $\epsilon$, the following equation holds:

$$\begin{aligned} 0&= 2 \left[ \mathrm{e}^\mathrm{T}(t)+ \mathrm{e}^\mathrm{T}(t_k-\rho )+\epsilon \dot{e}^\mathrm{T}(t)\right] G \nonumber \\&\quad \times \big [\!\!-\dot{e}(t)+\!Ae(t)\!+\!Be(t-d(t))\!+W\eta (De(t),z(t)) -KCe(t_k-\rho )-H \omega (t)\big ] \nonumber \\&= 2 \left[ \mathrm{e}^\mathrm{T}(t)+ \mathrm{e}^\mathrm{T}(t_k-\rho )+ \epsilon \dot{e}^\mathrm{T}(t)\right] G \big [-\dot{e}(t)+Ae(t)\nonumber \\ {}&\quad +Be(t-d(t))+W\eta (De(t),z(t)) -KCe(t_k-\rho )\big ] \nonumber \\&\quad -2 \left[ \mathrm{e}^\mathrm{T}(t)+ \mathrm{e}^\mathrm{T}(t_k-\rho ) + \epsilon \dot{e}^\mathrm{T}(t)\right] GH \omega (t). \end{aligned}$$

(35)

For any matrices $X \in {\mathbb {R}}^{n \times m}$, $Y \in {\mathbb {R}}^{n \times m}$, $\varTheta =\varTheta ^\mathrm{T} >0$, $\varTheta \in {\mathbb {R}}^{n \times n}$, the inequality $-2X^\mathrm{T}Y \le X^\mathrm{T} \varTheta X+Y^\mathrm{T} \varTheta ^{-1}Y$ is true. Then, the last term of (35) becomes

$$\begin{aligned} -2 \big [ \mathrm{e}^\mathrm{T}(t)&+ \mathrm{e}^\mathrm{T}(t_k-\rho )+\epsilon \dot{e}^\mathrm{T}(t)\big ]GH \omega (t) \le \gamma ^2 \omega ^\mathrm{T}(t) \omega (t)+\gamma ^{-2} \xi ^\mathrm{T}(t)\varUpsilon _1^\mathrm{T} \varUpsilon _1\xi (t). \end{aligned}$$

(36)

Moreover, for any $U_1={\text{ diag }}\{u_{11},\ldots , u_{1n_h}\} \ge 0$ and $U_2={\text{ diag }}\{u_{21},\ldots , u_{2n_h}\} \ge 0$, it follows from (7) that

$$\begin{aligned}&2\frac{\tau (t)}{\tau _M} \left[ \mathrm{e}^\mathrm{T}(t)D^\mathrm{T}K_1-\eta ^\mathrm{T}(D e(t),z(t))\right] U_1 \left[ \eta (D e(t),z(t))-K_2De(t)\right] \nonumber \\&+2 \frac{\tau _M-\tau (t)}{\tau _M} \left[ \mathrm{e}^\mathrm{T}(t)D^\mathrm{T}K_1-\eta ^\mathrm{T}(D e(t),z(t))\right] U_2 \left[ \eta (D e(t),z(t))-K_2De(t) \right] \ge 0. \end{aligned}$$

(37)

Applying expressions (23), (24), (28), (29), (31)–(34) into $\dot{V}(t)$ and adding the right-hand side of Eq. (35) and the left-hand side of inequality (37) and letting $L = GK$, we conclude that

$$\begin{aligned} \dot{V}(t)&\le \xi ^\mathrm{T}(t) \left[ \varSigma _0+\frac{\tau (t)}{\tau _M}\varSigma _1+\frac{\tau _M-\tau (t)}{\tau _M}(\varSigma _2+\tau _M \varSigma _3 )\right] \xi (t) \\ {}&-\int _{t_k-\rho }^{t} \left[ \begin{array}{c}\xi (t)\\ \dot{e}(s)\end{array}\right] ^\mathrm{T} \varSigma _4 \left[ \begin{array}{c}\xi (t)\\ \dot{e}(s)\end{array}\right] \mathrm{d}s -\mathrm{e}^\mathrm{T}(t)Se(t)+\gamma ^2 \omega ^\mathrm{T}(t)\omega (t) \nonumber \\&= \frac{\tau _M-\tau (t)}{\tau _M} \xi ^\mathrm{T}(t) \left( \varPi _1+\gamma ^{-2}\varUpsilon _1^\mathrm{T}\varUpsilon _1\right) \xi (t) -\frac{1}{\tau _M}\int _{t_k-\rho }^{t} \left[ \begin{array}{c}\xi (t)\\ \dot{e}(s)\end{array}\right] ^\mathrm{T} \\ {}&\quad \times \left( \varPi _2+\gamma ^{-2}\varUpsilon _2^\mathrm{T}\varUpsilon _2\right) \left[ \begin{array}{c}\xi (t)\\ \dot{e}(s)\end{array}\right] \mathrm{d}s-\mathrm{e}^\mathrm{T}(t)Se(t)+\gamma ^2 \omega ^\mathrm{T}(t)\omega (t), \end{aligned}$$

where

$$\begin{aligned} \varSigma _0&= \varSigma _{01}+\varSigma _{02}+\varSigma _{02}^\mathrm{T}, \\ \varSigma _{01}&= e_1 S e_1^\mathrm{T} + e_1 Q_1 e_1^\mathrm{T}+(1-d_{\mu })e_8 (Q_2-Q_1) e_8^\mathrm{T}-e_9 Q_2 e_9^\mathrm{T}\\&\quad +e_7 \left( d^2 R_1 + \frac{d^4}{4}R_2\right) e_7^\mathrm{T} -\left[ \begin{array}{c}e_1-e_8 \\ e_8-e_9\end{array}\right] \left[ \begin{array}{cc}R_1 &{} V_1 \\ \star &{} R_1\end{array}\right] \left[ \begin{array}{c}e_1-e_8 \\ e_8-e_9\end{array}\right] ^\mathrm{T}\\&\quad -[de_1-e_{10}-e_{11}] R_2 [de_1-e_{10}-e_{11}]^\mathrm{T} +e_1 S_1 e_1^\mathrm{T}-e_3 S_1 e_3^\mathrm{T} +\rho ^2 e_7 S_2 e_7^\mathrm{T}\\&\quad -[e_1-e_3]S_2 [e_1-e_3]^\mathrm{T}+e_3 T_1 e_3^\mathrm{T} -e_4 T_1 e_4^\mathrm{T} +(\tau _m-\rho )^2 e_7 T_2 e_7^\mathrm{T}\\&\quad -\left[ \begin{array}{c}e_1 \\ e_2 \\ e_5\end{array}\right] {\mathcal {H}} \left[ \begin{array}{c}e_1 \\ e_2 \\ e_5\end{array}\right] ^\mathrm{T} -\left[ \begin{array}{c}e_3-e_2 \\ e_2-e_4\end{array}\right] \left[ \begin{array}{cc}T_2 &{} V_2 \\ \star &{} T_2\end{array}\right] \left[ \begin{array}{c}e_3-e_2 \\ e_2-e_4\end{array}\right] ^\mathrm{T}, \\ \varSigma _{02}&= e_1 P e_7^\mathrm{T}+(e_1D^\mathrm{T} K_1-e_6) \varLambda D e_7^\mathrm{T} + (e_6-e_1D^\mathrm{T} K_2) \varDelta D e_7^\mathrm{T} \\&\quad + (e_1N_1+e_2 N_2+e_3N_3+e_4N_4+e_5N_5+e_6N_6+e_7N_7+e_8N_8+e_9N_9\\&\quad +e_{10}N_{10}+e_{11}N_{11}) (e_1-e_2)^\mathrm{T} +(e_1+e_2+\epsilon e_7)(-e_7+GAe_1+GBe_8\\&\quad +GHe_6-KCe_2), \\ \varSigma _i&= \left[ \begin{array}{c}e_1\\ e_6\end{array}\right] \left[ \begin{array}{cc}-2D^\mathrm{T} K_1 U_i K_2 D &{} D^\mathrm{T}(K_1+K_2)U_i \\ \star &{} 2 U_i\end{array}\right] \left[ \begin{array}{c}e_1\\ e_6\end{array}\right] ^\mathrm{T},\ \ i=1,2\\ \varSigma _3&= \left[ \begin{array}{c}e_2\\ e_7\end{array}\right] \left[ \begin{array}{cc} Z_1 &{} Z_2 \\ \star &{} Z_3 \end{array}\right] \left[ \begin{array}{c}e_2\\ e_7\end{array}\right] ^\mathrm{T} +2\left[ \begin{array}{c}e_1\\ e_2\\ e_5\end{array}\right] {\mathcal {H}} \left[ \begin{array}{c}e_1\\ 0\\ e_3\end{array}\right] ^\mathrm{T}, \\ \varSigma _4&= \left[ \begin{array}{cccccccccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_1 \\ \star &{}\quad Z_1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_2+Z_2 \\ \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_3 \\ \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_4 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_5 \\ \star &{}\quad \star &{} \quad \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_6 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_7 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_8 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_9 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad 0 &{}\quad N_{10} \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad 0 &{}\quad N_{11} \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad Z_3 \\ \end{array}\right] . \end{aligned}$$

If $\varPi _i+\gamma ^{-2}\varUpsilon _i^\mathrm{T}\varUpsilon _i < 0, \ i=1,2$, we have

$$\begin{aligned} \dot{V}(t) < - \mathrm{e}^\mathrm{T}(t)S e(t)+\gamma ^2 \omega ^\mathrm{T}(t) \omega (t). \end{aligned}$$

(38)

Integrating on both sides of (38) from 0 to $\infty$ gives

$$\begin{aligned} V(\infty )-V(0) <&- \int _{0}^{\infty } \mathrm{e}^\mathrm{T}(s)S e(s) \mathrm{d}s + \gamma ^2 \int _{0}^{\infty } \omega ^\mathrm{T}(s) \omega (s) \mathrm{d}s. \end{aligned}$$

(39)

From Schur complement, $<0$ is equivalent to the LMI (18) and 19, and since $V(\infty )>0$ and $V(0)=0$, then by definition 1, the error system (11) is $H_{\infty }$ synchronized. $\square$

Next theorem we consider robust $H_{\infty }$ synchronization of Lur’e system (1).

Theorem 2

Given scalar $\epsilon$, the master system ${\mathcal {M}}$ and slave system ${\mathcal {S}}$ in (1) are synchronous if there exist matrices $P>0$, $Q_1 >0, \ Q_2 >0$, $R_1 >0, \ R_2 >0$, $S_1 >0, \ S_2 >0$, $T_1 >0, \ T_2 >0$, $\varLambda = diag\left\{ \lambda _1,\ldots , \lambda _{n_h}\right\} >0$, $\varDelta =diag \left\{ \delta _1,\ldots ,\delta _{n_h}\right\} >0$, $\left[ \begin{array}{cc}Z_1 &{} Z_2 \\ \star &{} Z_3\end{array}\right] >0$, $U_1 \ge 0, \ U_2 \ge 0$ and for any appropriately dimensioned matrices $X_i, \ i=1,\ldots ,5$, G, L and $N=[N_1^\mathrm{T},N_2^\mathrm{T},N_3^\mathrm{T},N_4^\mathrm{T},N_5^\mathrm{T},N_6^\mathrm{T},N_7^\mathrm{T},N_8^\mathrm{T},N_9^\mathrm{T},N_{10}^\mathrm{T},N_{11}^\mathrm{T}]$ such that LMIs (15)–(17) hold and

$$\begin{aligned} \left[ \begin{array}{cccc} \varPi _1 &{}\quad \varUpsilon _1^\mathrm{T} &{}\quad \varTheta M &{}\quad \sigma \varOmega ^\mathrm{T} \\ \star &{}\quad - \gamma ^2 I &{}\quad 0 &{} \quad 0 \\ \star &{}\quad \star &{}\quad -\sigma I &{}\quad \sigma J^\mathrm{T} \\ \star &{}\quad \star &{}\quad \star &{}\quad -\sigma I \end{array}\right]&\quad < 0, \end{aligned}$$

(40)

$$\begin{aligned} \left[ \begin{array}{cccc} \varPi _2 &{}\quad \varUpsilon _2^\mathrm{T} &{}\quad \varTheta M &{}\quad \sigma \varOmega ^\mathrm{T} \\ \star &{}\quad - \gamma ^2 I &{}\quad 0 &{}\quad 0 \\ \star &{}\quad \star &{}\quad -\sigma I &{}\quad \sigma J^\mathrm{T} \\ \star &{}\quad \star &{}\quad \star &{}\quad -\sigma I \end{array}\right]&\quad < 0, \end{aligned}$$

(41)

Furthermore, the sampled-data controller gain matrix is given by

$$\begin{aligned} K=G^{-1}L. \end{aligned}$$

(42)

Proof

In the proof of Theorem 1, A, B and W can be replaced by $A + M\varLambda (t)E1$, $B + M\varLambda (t)E2$ and $W + M\varLambda (t)E3,$ respectively. The proof of this theorem follows the same steps as in Theorem 1. Finally, we obtain

$$\begin{aligned} \dot{\tilde{V}}(t)&= \frac{\tau _M-\tau (t)}{\tau _M} \xi ^\mathrm{T}(t) \bigg (\varPi _1+\gamma ^{-2}\varUpsilon _1^\mathrm{T}\varUpsilon _1+\varTheta \varLambda (t) \varOmega + \varOmega ^\mathrm{T} \varLambda (t) \varTheta ^\mathrm{T}\bigg )\xi (t) \\&\quad -\frac{1}{\tau _M}\int _{t_k-\rho }^{t} \left[ \begin{array}{c}\xi (t)\\ \dot{e}(s)\end{array}\right] ^\mathrm{T} \bigg (\varPi _2+\gamma ^{-2}\varUpsilon _2^\mathrm{T}\varUpsilon _2+\varTheta \varLambda (t) \varOmega + \varOmega ^\mathrm{T} \varLambda (t) \varTheta ^\mathrm{T}\bigg ) \left[ \begin{array}{c}\xi (t)\\ \dot{e}(s)\end{array}\right] \mathrm{d}s, \end{aligned}$$

where

$$\begin{aligned} \varTheta&= \left[ G^\mathrm{T} \ \ G^\mathrm{T} \ \ 0 \ \ 0 \ \ 0 \ \ 0 \ \ \epsilon G^\mathrm{T} \ \ 0 \ \ 0 \ \ 0 \ \ 0\right] ,\\ \varOmega&= \left[ E_1 \ \ 0 \ \ 0 \ \ 0 \ \ 0 \ \ E_2 \ \ 0 \ \ E_3 \ \ 0 \ \ 0 \ \ 0\right] . \end{aligned}$$

By using Lemma 3, LMIs (40) and (41) hold. This completes the proof. $\square$

The $H_{\infty }$ performance of $\gamma$ can be calculated by solving the following optimization problem

Theorem 3

For given scalar $\epsilon$, if the following optimization problem

$$\begin{aligned} \min \gamma ^2 =\gamma _{\min } \end{aligned}$$

(43)

subject to the LMIs (15)–(19), $P>0$, $Q_i >0$, $R_i >0$, $S_i >0$, $T_i >0$, $\varLambda >0$, $\varDelta >0$, $\left[ \begin{array}{cc}Z_1 &{} Z_2 \\ \star &{} Z_3\end{array}\right] >0$, $U_i \ge 0, i=1,2$, $X_j, \ j=1,\ldots ,5$, G, L and N.

Next, we consider the following sampled-data $H_{\infty }$ synchronization scheme of Lur’e system without time delays and uncertainties:

$$\begin{aligned} {\mathcal {M}}&:\left\{ \begin{array}{ll} \dot{x}(t)&{}=Ax(t)+W\varphi (Dx(t))\\ p(t)&{}=Cx(t) \end{array}\right. \nonumber \\ {\mathcal {S}}&:\left\{ \begin{array}{ll} \dot{z}(t)&{}=Az(t)+W\varphi (Dz(t))+u(t)+H\omega (t)\\ q(t)&{}=Cz(t) \end{array}\right. \nonumber \\ {\mathcal {C}}&: u(t)=K(p(t_k)-q(t_k)),\,\,\,t_k\le t \le t_{k+1}. \end{aligned}$$

(44)

Therefore, error system of the above equation can be written as follows

$$\begin{aligned} \dot{e}(t)&=Ae(t)+W\eta (De(t),z(t))-KCe(t_k-\rho )-H \omega (t),\,\,t_k\le t \le t_{k+1}, \end{aligned}$$

(45)

and corresponding L–K functional is constructed as

$$\begin{aligned} V(t)=V_1(t)+V_4(t)+V_5(t)+V_6(t)+V_7(t), \end{aligned}$$

(46)

where $V_1(t),V_4(t),V_5(t),V_6(t)$ and $V_7(t)$ are given in (21). From Theorem 1, we have the following corollary.

Corollary 1

For given scalar $\epsilon$, the master system ${\mathcal {M}}$ and slave system ${\mathcal {S}}$ in (44) are synchronous if there exist matrices $P>0$, $S_1 >0, \ S_2 >0$, $T_1 >0, \ T_2 >0$, $\varLambda = diag\left\{ \lambda _1,\ldots , \lambda _{n_h}\right\} >0$, $\varDelta =diag \left\{ \delta _1,\ldots ,\delta _{n_h}\right\} >0$, $\left[ \begin{array}{cc}Z_1 &{} Z_2 \\ \star &{} Z_3\end{array}\right] >0$, $U_1 \ge 0, \ U_2 \ge 0$ and for any appropriately dimensioned matrices $X_i, \ i=1,\ldots ,5$, G, L and $N=[N_1^\mathrm{T},N_2^\mathrm{T},N_3^\mathrm{T},N_4^\mathrm{T},N_5^\mathrm{T},N_6^\mathrm{T},N_7^\mathrm{T}]$ such that LMIs (15)–(17) hold and

$$\begin{aligned} \left[ \begin{array}{cccccccc} \hat{\varPhi }_{11}^{'}&{}\quad \varPhi _{12}^{'}&{}\quad \varPhi _{13}^{'}&{}\quad N_4^\mathrm{T}&{}\quad \varPhi _{15}&{}\quad \varPhi _{16}^{'}&{}\quad \varPhi _{17}&{}\quad H^\mathrm{T}G^T\\ \star &{}\quad \varPhi _{22}^{'}&{}\quad \varPhi _{23}^{'}&{}\quad \varPhi _{24} &{}\quad \varPhi _{25}&{}\quad \varPhi _{26}&{}\quad \varPhi _{27}+\tau _M Z_2 &{}\quad H^\mathrm{T}G^T\\ \star &{}\quad \star &{}\quad \varPhi _{33} &{}\quad V_2 &{}\quad \varPhi _{35}^{'} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \varPhi _{44} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \varPhi _{55} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -2U_2 &{}\quad \varPhi _{67} &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \varPhi _{77}+\tau _M Z_3 &{}\quad \epsilon H^\mathrm{T}G^T \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -\gamma ^2 I \end{array}\right] \!<\! 0 \quad \end{aligned}$$

(47)

$$\begin{aligned} \left[ \begin{array}{ccccccccc} \hat{\varPhi }_{11}^{''}&{}\quad \varPhi _{12}&{}\quad \varPhi _{13}&{}\quad -N_4^\mathrm{T}&{}\quad \varPhi _{15}&{}\quad \varPhi _{16}^{''}&{}\quad \varPhi _{17}&{}\quad -\tau _MN_1 &{}\quad H^\mathrm{T}G^T \\ \star &{}\quad \varPhi _{22}^{''}&{}\quad \varPhi _{23}&{}\quad \varPhi _{24} &{}\quad \varPhi _{25}&{}\quad \varPhi _{26}&{}\quad \varPhi _{27} &{}\quad \varXi &{}\quad H^\mathrm{T}G^T\\ \star &{}\quad \star &{}\quad \varPhi _{33} &{}\quad V_2 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\tau _MN_3&{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \varPhi _{44} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\tau _MN_4&{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \varPhi _{55} &{}\quad 0 &{}\quad 0 &{}\quad -\tau _MN_5&{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -2U_1 &{}\quad \varPhi _{67} &{}\quad -\tau _MN_6&{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \varPhi _{77} &{}\quad -\tau _MN_7&{}\quad 0 \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \varPhi _{88} &{}\quad \epsilon H^\mathrm{T}G^T \\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -\gamma ^2 I \end{array}\right] \!<\! 0\quad \end{aligned}$$

(48)

where

$$\begin{aligned} \hat{\varPhi }_{11}^{'}&= S+S_1-S_2-\frac{X_1+X_1^\mathrm{T}}{2}+GA+A^\mathrm{T} G^\mathrm{T} +N_1+N_1^\mathrm{T}-2D^\mathrm{T}K_1U_2K_2D, \\ \hat{\varPhi }_{11}^{''}&= S+S_1-S_2-\frac{X_1+X_1^\mathrm{T}}{2}+GA+A^\mathrm{T} G^\mathrm{T} +N_1+N_1^\mathrm{T}-2D^\mathrm{T}K_1U_1K_2D \end{aligned}$$

and other parameters are same as in Theorem 1. Furthermore, the sampled-data controller gain matrix is given by

$$\begin{aligned} K=G^{-1}L. \end{aligned}$$

To the end of this section, we derive master–slave synchronization scheme of system (44) without considering disturbance term, which has been studied in [7]. Then, letting $\rho =0$, by using Theorem 1 and Corollary 1, we have the following corollary.

Corollary 2

Given scalars $\epsilon$, the master system ${\mathcal {M}}$ and slave system ${\mathcal {S}}$ in (44) are synchronous if there exist matrices $P>0$, $T_1 >0, \ T_2 >0$, $\varLambda = diag\left\{ \lambda _1,\ldots , \lambda _{n_h}\right\} >0$, $\varDelta =diag \left\{ \delta _1,\ldots ,\delta _{n_h}\right\} >0$, $\left[ \begin{array}{cc}Z_1 &{} Z_2 \\ \star &{} Z_3\end{array}\right] >0$, $U_1 \ge 0, \ U_2 \ge 0$ and for any appropriately dimensioned matrices $X_i, \ i=1,\ldots ,5$, G, L and $N=[N_1^\mathrm{T},N_2^\mathrm{T},N_3^\mathrm{T},N_4^\mathrm{T},N_5^\mathrm{T},N_6^\mathrm{T}]$ such that LMIs (15)–(17) hold and

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \tilde{\varPhi }_{11}^{'}&{} \tilde{\varPhi }_{12}^{'} &{}\tilde{\varPhi }_{13}&{} \tilde{\varPhi }_{14}+\tau _M \frac{X_5+X_5^\mathrm{T}}{2} &{} \tilde{\varPhi }_{15}^{'}&{} \tilde{\varPhi }_{16}+\tau _M \frac{X_1+X_1^\mathrm{T}}{2}\\ \star &{}\tilde{\varPhi }_{22}^{'}&{}\tilde{\varPhi }_{23} &{} \tilde{\varPhi }_{24} &{} \tilde{\varPhi }_{25}&{} \tilde{\varPhi }_{26}+\tau _M Z_2\\ \star &{} \star &{} \tilde{\varPhi }_{33} &{} 0 &{} 0 &{} 0\\ \star &{}\star &{}\star &{} \tilde{\varPhi }_{44} &{} 0 &{} 0 \\ \star &{}\star &{}\star &{} \star &{} -2U_2 &{} 0\\ \star &{}\star &{}\star &{} \star &{} \star &{} \tilde{\varPhi }_{66} +\tau _M Z_3 \end{array}\right] < 0, \end{aligned}$$

(49)

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \tilde{\varPhi }_{11}^{''} &{}\tilde{\varPhi }_{12} &{} \tilde{\varPhi }_{13} &{} \tilde{\varPhi }_{14} &{} \tilde{\varPhi }_{15}^{''}&{} \tilde{\varPhi }_{16} &{} -\tau _M N_1\\ \star &{}\tilde{\varPhi }_{22}-\tau _M Z_1&{}\tilde{\varPhi }_{23}&{}\tilde{\varPhi }_{24} &{}\tilde{\varPhi }_{25}&{}\tilde{\varPhi }_{26} &{} \varXi \\ \star &{} \star &{} \tilde{\varPhi }_{33} &{} 0 &{} 0 &{} 0 &{}-\tau _M N_3 \\ \star &{}\star &{}\star &{} \tilde{\varPhi }_{44} &{} 0 &{} 0 &{} -\tau _M N_4\\ \star &{}\star &{}\star &{}\star &{} -2U_1 &{} 0 &{} -\tau _M N_5\\ \star &{}\star &{}\star &{}\star &{}\star &{} \tilde{\varPhi }_{66} &{}-\tau _M N_6 \\ \star &{}\star &{}\star &{}\star &{}\star &{} \star &{}-\tau _M Z_3 \end{array}\right] < 0, \end{aligned}$$

(50)

where

$$\begin{aligned} \tilde{\varPhi }_{11}&=T_1-T_2-\frac{X_1+X_1^\mathrm{T}}{2}+GA+A^\mathrm{T} G^\mathrm{T} +N_1+N_1^\mathrm{T}, \\ \tilde{\varPhi }_{12}&=T_2-V_2+X_1-X_2-LC+A^G-N_1+N_2, \\ \tilde{\varPhi }_{13}&=V_2+N_3, \ \ \tilde{\varPhi }_{14}=-X_3+N_4, \ \ \tilde{\varPhi }_{15}=GH+N_5, \ \ \tilde{\varPhi }_{22}=\varPhi _{22}, \\ \tilde{\varPhi }_{23}&=-V_2+T_2-N_3, \ \ \tilde{\varPhi }_{24}=-X_4-N_4, \ \ \tilde{\varPhi }_{25}=GH-N_5, \\ \tilde{\varPhi }_{26}&=-G-\epsilon L^\mathrm{T} G^\mathrm{T}-N_6, \ \tilde{\varPhi }_{33}=\varPhi _{44}, \ \ \tilde{\varPhi }_{44}=\varPhi _{55}, \ \ \tilde{\varPhi }_{56}=\varPhi _{67}, \\ \tilde{\varPhi }_{66}&=\tau _M^2 T_2- \epsilon G-\epsilon G^\mathrm{T}, \ \ \tilde{\varPhi }_{11}^{'}=\tilde{\varPhi }_{11}-D^\mathrm{T} K_1 U_2 K_2 D, \\ \tilde{\varPhi }_{12}^{'}&=\tilde{\varPhi }_{12}-\tau _M (X_3-X_4^\mathrm{T}), \ \ \tilde{\varPhi }_{15}^{'}=\tilde{\varPhi }_{15}+D^\mathrm{T} (K_1+K_2)U_2,\\ \tilde{\varPhi }_{22}^{'}&=\tilde{\varPhi }_{22}-\tau _M(X_4+X_4^\mathrm{T}-Z_1),\ \ \tilde{\varPhi }_{11}^{''}=\tilde{\varPhi }_{11}-D^\mathrm{T} K_1 U_1 K_2 D, \\ \tilde{\varPhi }_{15}^{''}&=\tilde{\varPhi }_{15}+D^\mathrm{T} (K_1+K_2)U_1. \end{aligned}$$

Furthermore, the sampled-data controller gain matrix is given by

$$\begin{aligned} K=G^{-1}L. \end{aligned}$$

Remark 1

Theorem 1 ensures the $H_{\infty }$ synchronization between Lur’e system with time delays under a sampled-data controller. It should be pointed out that the information of sampling instants and time delays has been considered for the construction of L–K functional which includes available information about the actual sampling pattern and upper bound of the time delay. Most of the authors in the literature have considered the problem of synchronization between identical Lur’e system without time delays. Synchronization for identical Lur’e system with constant time delays has been studied by authors in [9] and [40]. However, in real-life applications, time delays are unavoidable and the existence of delays is not always constant. Therefore, time-varying delays are considered to take the fact into account.

Remark 2

Noted that the term $V_6(t)$ in L–K functional (21) was newly proposed in Theorem 1 compared with the L–K functional used in [7, 9, 44]. By introducing the ${\mathcal {H}}$-dependent term $V_6(t)$, the constraint conditions of the matrices in the L–K functional have been relaxed. To make $V_6(t)$ positive, this constraint is replaced by a more relaxable condition (15).

Remark 3

The information about the slope of the nonlinear function has been used, where the slopes $k_i^-,k_i^+$ are used to construct the term $V_1(t)$ in the L–K functional (21). Noted that bigger sampling period leads to lower communication channel occupying and less transmission, so we need to find the maximum allowable sampling period. In order to increase the bound of sampling period, reciprocal convex technique has been utilized in this paper. Also, the proposed synchronization criterion is less conservative than other related studies.

Remark 4

In [40], the author investigates the exponential synchronization of chaotic Lure system with constant time delays based on sampled-data control. Asymptotical synchronization of two identical chaotic Lure systems via sampled-data control has been considered in [9, 44]. However, in sampled-data problems, updating signals (successfully transmitted signal from the sampler to the controller and to the ZOH) at the instant $t_k$ may experience a constant signal transmission delay $\rho$, which also may break stability of the system. But, most of the authors in existing works [4, 18, 40, 44] have not considered these signal transmission delays in the synchronization problem, and thus, it has been taken into fact in this paper. On the other hand, to obtain an exact mathematical model is a very difficult task owing to the noises or disturbances followed by environmental noise, slowly varying parameters and modeling errors. Hence, the problem of $H_{\infty }$ synchronization of chaotic Lur’e system with disturbances has been considered in [10], where they have used continuous delayed feedback control. Recently, robust $H_{\infty }$ synchronization of chaotic Lur’e system based on the sampled-data controller has been given in [7]. Note that, main aim of the $H_{\infty }$ control performance is to reduce the effect of external disturbances, that is, disturbance attenuation level is optimized by solving the convex optimization algorithm, which is not given in [7]. Moreover, by taking time-varying delays, external disturbances and signal transmission delay into Lur’e system, our sampled-data synchronization problem becomes more and more general than others. Also, convex optimization problem for disturbance attenuation level $\gamma$ is optimized in this paper, which is given in Theorem 3.

Remark 5

In [13], the robust $H_{\infty }$ filtering problem for singular systems with time-varying parameters and time delays has been investigated. A delay-dependent sufficient condition is derived by using bounded real lemma and delay-partitioning method. In this method, time-varying delays are divided into finite number of sub- intervals (l), which is an effective method to deal with time-delay systems. The obtained results in this paper confirmed that less conservative result occurs as l increases. However, when l increases, stability conditions become more complex and computational burden will increase. The distributed fuzzy filtering problem for a class of sensor networks described by discrete-time T–S fuzzy systems with time-varying delays and multiple packet losses has been dealt in [32]. An effective method, so called input–output approach, has been used to deal with time-varying delays in which the given stability problem of time delay systems is reduced to the stability problem for a class of systems with the same nominal part but with additional inputs and outputs. Based on this approach and small-scale gain theorem, delay-dependent stability conditions are derived under $H_{\infty }$ performance in [32]. Also, slack variable methods are used to get relaxation conditions for LMI-based optimization problems.

Table 1 Maximum allowable sampling period of $\tau _M$

4 Numerical Examples

In this section, we shall present numerical examples to demonstrate the effectiveness of the proposed method.

Example 1

Consider the following Chua’s circuit system with time-varying delay

$$\begin{aligned} \left\{ \begin{array}{cl} \dot{x}_1(t)=&{} a (x_2(t)-m_1x_1(t)-g(x_1(t)))-cx_1(t-d(t))\\ \dot{x}_2(t)=&{}x_1(t)-x_2(t)+x_3(t)-cx_1(t-d(t))\\ \dot{x}_3(t)=&{}-bx_2(t)+c(2x_1(t-d(t))-x_3(t-d(t))) \end{array} \right. \end{aligned}$$

(51)

with the nonlinear characteristics

$$\begin{aligned} g(x_1(t))=\frac{1}{2}(m_1-m_0)(|x_1(t)+1|-|x_1(t)-1|) \end{aligned}$$

and the parameters $m_0=-1/7,\,m_1=2/7,\,a=9,\,b=14.28,\,c=0.1$ and the time-varying delay $d(t)=1.0|\sin t|$. The above system can be expressed in the Lur’e form (1) with following matrices

$$\begin{aligned} A&=\!\left[ \begin{array}{ccc} -am_1&{}a&{}0\\ 1&{}-1&{}1\\ 0&{}-b&{}0\\ \end{array}\right] , B\!=\!\left[ \begin{array}{ccc} -c&{}0&{}0\\ -c&{}0&{}0\\ 2c&{}0&{}-c\\ \end{array}\right] , W\!=\!\left[ \begin{array}{c} -a(m_1-m_0) \\ 0 \\ 0\\ \end{array}\right] , D\!=\!\left[ \begin{array}{ccc} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1\\ \end{array}\right] , \end{aligned}$$

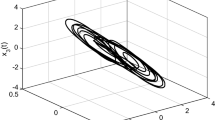
and $\varphi (x_1(t))=\frac{1}{2}(|x_1(t)+1|-|x_1(t)-1|)$ belonging to the sector [0, 1] and $\varphi _2(x_2(t))=\varphi _3(x_3(t))=0$. In this example, we choose $C=[\begin{array}{ccc}1&0&0\end{array}]$ and $\epsilon =2$. Solving LMIs (15)–(19) in Theorem 1 by using MATLAB LMI toolbox, we obtain maximum allowable sampling period (MASP) of $\tau _M$ and the results are listed in Table 1. The authors in [9] and [40], constant delay $d = 1$ was taken, but our results are presented for an upper bound of the time-varying delay as 1 (i.e., $d = 1$). From Table 1, it is clear that Theorem 1 is less conservative than results in [40] and [9]. Choosing $\tau _M=0.4395$, we can get the following gain matrix $K =\left[ \begin{array}{ccc} 4.0304&0.7769&-0.9536\end{array}\right] ^\mathrm{T}$. During the simulations, initial conditions of master and slave systems are taken as $x(0)=(0.2,0.2,0.2)$ and $z(0)=(0.2,-0.2,0.33)$, respectively. The chaotic attractors of master and slave systems of (51) are shown Fig. 1. Figure 2 displays the synchronization errors of Chua’s circuit (51). The number of decision variables used in this example is 267 based on Theorem 1.

Fig. 1

Chaotic attractors of master and slave systems of (51)

Fig. 2

Synchronization errors of Chua’s circuit (51)

Example 2

Consider following Chua’s circuit with noise disturbance is given by

$$\begin{aligned} \left\{ \begin{array}{cl} \dot{x}(t)&{}=a(y(t)-h(x(t)))+w(t), \\ \dot{y}(t)&{}=x(t)-y(t)+z(t)+2w(t), \\ \dot{z}(t)&{}=-by(t)-w(t) \end{array} \right. \end{aligned}$$

(52)

with the nonlinear function

$$\begin{aligned} h(x(t))=m_1x(t)+\frac{1}{2}(m_0-m_1)\left( \left| x(t)+1\right| -\left| x(t)-1\right| \right) \end{aligned}$$

belonging to the sector [0, 1] and the other parameters are taken as those in Example 1. The noise disturbance is chosen as

$$\begin{aligned} w(t)=\frac{1}{1+2t}, \ \ \ t \ge 0. \end{aligned}$$

Then, the system (52) can be represented in Lur’e form (44) with noise disturbance by

$$\begin{aligned} A&=\left[ \begin{array}{ccc}-am_1&{}a&{}0\\ 1&{}-1&{}1\\ 0&{}-b&{}0\end{array}\right] , W=\left[ \begin{array}{c}-a(m_1-m_0) \\ 0 \\ 0\end{array}\right] \\ H&=\left[ \begin{array}{c}1\\ 2 \\ -1\end{array}\right] , C=D=\left[ \begin{array}{ccc}1&0&0\end{array}\right] . \end{aligned}$$

By choosing $\tau _M=0.2$ and using LMIs in Corollary 1, we can get the following $H_{\infty }$ performance $\gamma _{\min }=0.936$ and control gain matrix $K =\left[ \begin{array}{ccc}3.2889&0.5781&-4.9260 \end{array}\right] .$ The initial conditions are taken $x(0)=(0.25, 0.11, 0.22)$ and $z(0)=(0.32, 0.18, 0.21)$ for the master and slave systems of (52), respectively. The time response of the master system and the slave system (52) is shown Fig. 3. Figure 4 displays the synchronization errors of system (52). The number of decision variables used in this example is 201 based on Corollary 1.

Fig. 3

Time response of the master system and the slave systems of (52)

Fig. 4

Synchronization errors of Chua’s circuit (52)

Table 2 Maximum allowable sampling period of $\tau _M$

Example 3

Consider the following chaotic neural networks in the form of Lur’e system 44 with following matrices

$$\begin{aligned} A&=\left[ \begin{array}{ccc}-1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1\end{array}\right] , W=\left[ \begin{array}{ccc}1.2 &{}\quad -1.6 &{}\quad 0 \\ 1.24 &{}\quad 1 &{}\quad 0.9 \\ 0 &{}\quad 2.2 &{}\quad 1.5 \end{array}\right] , C=D=\left[ \begin{array}{ccc}1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1\end{array}\right] . \end{aligned}$$

(53)

Moreover, neuron activation functions are given by

$$\begin{aligned} \varphi _i(x_i(t))=\frac{1}{2}(|x_i(t)+1|-|x_i(t)-1|), \ \ i =1,2,3. \end{aligned}$$

By solving LMIs in Corollary 2, MASP is calculated and listed in Table 2. When $\tau _M=0.4234$, the controller gain matrix is calculated as

$$\begin{aligned} K =\left[ \begin{array}{ccc} 0.5437 &{} 1.0369 &{} -0.7906 \\ -0.4719 &{} 0.5481 &{} 1.4796 \\ -0.6565 &{} 0.5406 &{} 2.1155 \\ \end{array}\right] . \end{aligned}$$

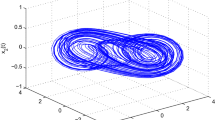
For the numerical simulations, the initial conditions of master and slave scheme of (53) are, respectively, taken as $x(0)=(0.7,-0.3,0.4)$ and $z(0)=(0.2,0.4,0.9 )$. Figures 5 and 6 show the chaotic attractors of master and slave systems of system (53) and the synchronization errors of system (53), respectively. The number of decision variables used in this example is 186 based on Corollary 2.

Fig. 5

Chaotic attractor of master and slave system of (53)

Fig. 6

Synchronization errors of neural networks (53)

5 Conclusion

In this paper, sampled-data robust $H_{\infty }$ synchronization problem for chaotic Lur’e systems with time-varying delays has been proposed. A novel L–K functional has been introduced, which includes the information about sampling intervals, interval time delays and nonlinear function. A new delay-dependent synchronization criteria has been derived in terms of LMIs by utilizing reciprocal convex method. Finally, numerical examples such as Chua’s circuit and neural networks have been provided to demonstrate the less conservatism and effectiveness of the proposed results.