1 Introduction

In 1971, the existence of memristor, as the fourth fundamental circuit element included along with the resistor, capacitor and inductor, was theoretically postulated by Chua [1] and experimentally confirmed by the researchers of Hewlett-Packard (HP) who reported on the first memristor device in 2008 [2]. From then on, memristor has attracted a lot of attention, because of its potential applications in programmable logic, signal processing, neural networks, control systems, reconfigurable computing, brain-computer interfaces, RFID and so on [3–6].

At present, research on the memristor has become popular, and it mainly focusses on two aspects. First, according to the HP laboratory study some scientists are making attempts to find the most economical materials to produce devices with the memristor properties. Second, based on Chua’s ideas, the dynamical behaviour and application of a system constructed by the memristor have been highlighted [1]. Recently, in electrical and electronic engineering communities, the physical realization of various memristors, the modelling, the analysis of basic memristor circuit and the design of memsistor-based application circuit have attracted much attention. Due to the nonlinearity of the memristor element, the memristor-based circuits can easily generate a chaotic signal and display a complex and unpredictable behaviour [7]. For example, several nonlinear oscillators are made from Chua’s oscillators by replacing Chua’s diodes with memristors [8]. A simple circuit composed of a linear passive inductor, a linear passive capacitor and a nonlinear active memristor has been proposed in [9]. Complex nonlinear behaviours including chaos were considered in a simple network of memristor oscillators [10]. In 2010, Muthuswamy provided a practical implementation of a memristor-based chaotic circuit with cubic nonlinearities [11] by using discrete-component circuits mimicking ideal memristor features. Circuital implementations of memristor-based oscillators are given in refs [12–14].

On the other hand, fractional calculus, an old mathematical topic, is now attracting intensive research in nearly all kinds of fields, particularly in the field of information [15–17]. The major merit of fractional calculus, different from integer calculus, lies in the fact that it has memory and has proven to be a very suitable tool for describing memory and hereditary properties of various materials and processes. Recently, study on the dynamics of fractional-order differential systems has greatly attracted the interest of many researchers. Numerous fractional-order chaotic systems have already been introduced and their chaotic behaviours have been investigated in detail, such as the fractional-order Chua’s circuit [18], fractional-order Duffing system [19], fractional-order Chen system [20], fractional-order Lü system [21], fractional-order Liu system [22], fractional-order financial system [23], fractional-order neural network [24] and so on. As we know, the main feature of the memristor lies in its memory characteristic and nanometer dimensions. Thus, introducing a fractional-order derivative into the memristor circuit is an important advancement. Recently, Ivo Petrás̆ proposed fractional-order memristor- based Chua’s circuit and investigated its numerical solution, simulation and stability [25].

However, contrary tointeger-order systems, there exist less theoretical tools to study dynamics of fractional systems. The Hopf bifurcation in integer-order systems can be investigated in detail using normal form theory and centre manifold theorem, while similar tools have not yet been developed for fractional systems. So, detailed results about the fractional Hopf bifurcation are few. Only through stability theory of equilibrium points and numerical simulations, fractional Hopf bifurcation can be analysed.

In this paper, the fractional-order simple memristor circuit system is proposed. The dynamics of the system including the stability of equilibrium points, chaos, bifurcations with a variation of system parameters are studied. Besides, two new stability and stabilization theorems for a class of fractional-order semilinear systems are proposed, based on which, the control problem of the system is examined by using the feedback control technique, and simulation results show that the system can be controlled by designing an appropriate controller.

The rest of the paper is organized as follows. Some necessary definitions, lemmas and models are given in §2. Main results are discussed in §3. Simulation results are presented in §4.

2 Preliminaries and model description

Fractional calculus is a generalization of integration and differentiation to a noninteger-order integro-differential operator. It is being used progressively in various fields, such as biophysics, non-linear dynamics, informatics, control engineering and so on. Some definitions are available for fractional derivatives. The commonly used definitions are: Grunwald–Letnikov (GL), Riemann–Liouville (RL) and Caputo (C). Caputo derivatives have well-understood physical meanings, for it takes on the same form as those for integer-order ones and Caputo derivative of a constant is equal to zero. Here definition of Caputo derivative is adopted, which is described below.

DEFINITION 1

[26] The fractional integral (RL integral) \(D_{t_{0}, t}^{-\alpha }\) with fractional-order α ∈ R + of function x(t) is defined as

$$\begin{array}{@{}rcl@{}} D_{t_{0},t}^{-\alpha}x(t)=\frac{1}{\Gamma(\alpha)}{\int}_{t_{0}}^{t}(t-\tau)^{\alpha-1}x(\tau)\mathrm{d}\tau, \end{array} $$
(1)

where Γ(⋅) is the gamma function, \({\Gamma }(\tau )={\int }_{0}^{\infty } t^{\tau -1}\mathrm {e}^{-t}\mathrm {d}t\).

DEFINITION 2

[26] The Caputo derivative of fractional-order α of function x(t) is defined as follows:

$$\begin{array}{@{}rcl@{}} {~}_{C}D_{t_{0},t}^{\alpha} x(t)&=&D_{t_{0},t}^{-(n-\alpha)}\frac{\mathrm{d}^{n}}{\mathrm{d}t^{n}}x(t)\\ &=&\frac{1}{\Gamma(n-\alpha)}{\int}_{t_{0}}^{t}(t-\tau)^{(n-\alpha-1)}x^{(n)}(\tau)\mathrm{d}\tau, \end{array} $$
(2)

where n−1 ≤ α < n ∈ Z +.

In order to obtain the main results, the following lemma is presented first.

Let us consider the following three-dimensional fractional-order commensurate system

$$\begin{array}{@{}rcl@{}} \left\{\begin{array}{c} D^{\alpha} x_{1}=f(x_{1},x_{2},x_{3}),\\ D^{\alpha} x_{2}=g(x_{1},x_{2},x_{3}),\\ D^{\alpha} x_{3}=h(x_{1},x_{2},x_{3}). \end{array} \right. \end{array} $$
(3)

Lemma 1 [22]. System (3) is asymptotically stable at the equilibrium points O if \(|\arg (\lambda _{i}(J))|>\alpha \pi /2\), i = 1,2,3, for all eigenvalues λ i of the Jacobian matrix J,

$$\begin{array}{@{}rcl@{}}J=\left( \begin{array}{ccc} \partial f/\partial x_{1} &\; \partial f/\partial x_{2} &\;\partial f/\partial x_{3} \\ \partial g/\partial x_{1} &\; \partial g/\partial x_{2} &\; \partial g/\partial x_{3} \\ \partial h/\partial x_{1} &\; \partial h/\partial x_{2} &\; \partial h/\partial x_{3} \\ \end{array} \right). \end{array} $$

Remark 1.

The equilibrium point O of system (3) is unstable if fractional-order α satisfies the following condition for at least one eigenvalue:

$$\begin{array}{@{}rcl@{}} \alpha>\frac{2}{\pi}\arctan\frac{|\text{Im}(\lambda)|}{|\text{Re}(\lambda)|}. \end{array} $$
(4)

By using the stability theory of fractional-order system and by choosing a proper bifurcation parameter, Hopf bifurcation of the system can be investigated. For this objective, we first present the integer-order case.

Consider a three-dimensional ordinary differential equations as

$$\begin{array}{@{}rcl@{}} \dot{x}(t)=f(x,\mu), \end{array} $$
(5)

where x ∈ R 3 is the stationary point and the critical value of the bifurcation parameter μ is μ ∗. The Hopf bifurcation conditions for integer-order system are described as follows:

  1. (1)

    J(μ) = D x f(0, μ) has one negative real root and a pair of complex conjugate eigenvalues λ(μ) = β(μ)+i γ(μ), where β(μ) > 0;

  2. (2)

    β(μ ∗)=0 and (dγ/dμ)| μ = μ∗≠0 (transversality condition).

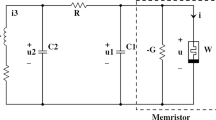
An autonomous circuit with two energy storage elements (a linear passive inductor and linear passive capacitor) and a nonlinear active memristor has been proposed in [9]. Here, fractional-order memristor-based system derived from [9] is considered.

$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{l} D^{\alpha} x_{1}=x_{2},\\ D^{\alpha} x_{2}=-bx_{1}+cx_{2}-d{{x_{3}^{2}}}x_{2},\\ D^{\alpha} x_{3}=-x_{2}-ax_{3}+x_{2}x_{3}, \end{array} \right. \end{array} $$
(6)

where x 1 is the voltage across the capacitor C, x 2 is the current through the inductor L and x 3 is the internal state of our memristive system. Real parameters a, b, c, d > 0. When a = 3/5, b = 1/3, c = 1/2 and d = 1/2 chaotic behaviour of system (6) is shown in figure 1.

Figure 1
figure 1

Phase portraits of chaotic attractors for system (6) with order α = 0.9: (a) x 1– x 2 plane, (b) x 1– x 3 plane, (c) x 2– x 3 plane and (d) three-dimensional space.

Full size image
Figure 2
figure 2

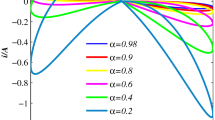
The maximum Lyapunov exponent of fractional-order chaotic system (6) with respect to the varying parameter α.

Full size image

3 Chaotic behaviours

3.1 Stability analysis

By simple computation, it is easy to obtain that system (6) admits one equilibrium point O(0,0,0,0) and the Jacobian matrix J at the equilibrium point O(0, 0, 0, 0) is given by

$$\begin{array}{@{}rcl@{}}J=\left( \begin{array}{ccc} 0 &\; 1 &\; 0 \\ -b &\; c &\; 0 \\ 0 &\; -1 &\; -a \\ \end{array} \right). \end{array} $$

Thus, the corresponding characteristic equation can be obtained:

$$\begin{array}{@{}rcl@{}} f(\lambda)=(\lambda+a)(\lambda^{2}-c\lambda+b)=0. \end{array} $$
(7)

If 4b−c 2 < 0, the corresponding characteristic roots are

$$\begin{array}{@{}rcl@{}} \lambda_{1}=-a<0, \quad\lambda_{2}=\frac{c}{2}+\frac{1}{2}\sqrt{c^{2}-4b},\quad \lambda_{3}=\frac{c}{2}+\frac{1}{2}\sqrt{c^{2}-4b}. \end{array} $$

It follows from Lemma 1 that equilibrium point O is unstable for order α > 0. If 4b − c 2>0, the corresponding characteristic roots are

$$\begin{array}{@{}rcl@{}} \lambda_{1}=-a<0, \quad\lambda_{2}=\frac{c}{2}+\frac{1}{2}\sqrt{4b-c^{2}}i,\quad\lambda_{3}=\frac{c}{2}-\frac{1}{2}\sqrt{4b-c^{2}}i. \end{array} $$

According to Remark 1, equilibrium point O is unstable when fractional-order α > (2/π)\(\arctan {(\sqrt {4b-c^{2}}}/{c})\); it means that when α >\(({2}/{\pi })\arctan {(\sqrt {4b-c^{2}}}/{c})\), system (6) with the above parameters has the necessary conditions for exhibiting a chaotic attractor. When a = 3/5, b = 1/3, c = 1/2, d = 1/2, and initial conditions are chosen as (0.09,0.1,0.1), as can be seen from the largest Lyapunov exponent spectrum with respect to the varying parameter α, shown in figure 2, it can be found that system (6) exhibits chaotic behaviours if fractional-order α is greater than 0.71. Further, the bifurcation diagrams of state variable x vs. the fractional-order α is shown in figure 3. When α = 0.8, a = 3/5, b = 1/3, d = 1/2, the largest Lyapunov exponent spectrum with respect to the varying parameter c is shown in figure 4. The bifurcation diagrams of state variable x vs. the parameter c is described in figure 5. From figures 3 and 5, we see that the system evolves into chaotic state by varying α and c.

Figure 3
figure 3

Bifurcation diagram of fractional-order chaotic system (6) vs. order α.

Full size image
Figure 4
figure 4

The maximum Lyapunov exponent of fractional-order chaotic system (6) with respect to the varying parameter c.

Full size image
Figure 5
figure 5

Bifurcation diagram of fractional-order chaotic system (6) vs. parameter c.

Full size image

3.2 Hopf bifurcation analysis vs. the fractional-order α

According to Remark 1, the fractional-order α has remarkable influence on the stability of fractional-order system. The fractional-order α can be chosen as the bifurcation parameter in fractional-order chaotic systems, which is different from integer-order systems. Here, by selecting the fractional-order α as the bifurcation parameter, Hopf bifurcation in system (6) will be considered.

Theorem 1 (Existence of Hopf bifurcation).

When bifurcation parameter α passes through the critical value α ∗∈(0,1), fractional-order system (6) undergoes a Hopf bifurcation at the equilibrium point O(0,0,0,0), if the following conditions hold:

  1. (1)

    4b−c 2>0;

  2. (2)

    \(m(\alpha ^{*})=\alpha ^{*}\pi /2-\min \!|\!\arg (\lambda _{i})|~(i=1,2,3)\);

  3. (3)

    (dm(α)/dα| α = α ∗) ≠ 0 (transversality condition).

Proof.

Define a function \(m(\alpha )=\alpha \pi /2-\min \!|\!\arg (\lambda _{i})|(i=1,2,3)\) with respect to α. Evidently, the equilibrium point is locally asymptotically stable if m(α) < 0 and the equilibrium point is unstable if m(α) > 0. It follows from Remark 1 that the solution of function m(α) is \(({2}/{\pi })\arctan ({\sqrt {4b-c^{2}}}/{c})\). Condition (1) implies that the corresponding characteristic eq. (7) of system (6) has one negative real root λ1 = −a and a pair of complex conjugate root \(\lambda _{2,3}=({c}/{2})\pm ({1}/{2})\sqrt {4b-c^{2}}i \). Condition (c) ensures that the sign of m(α) can change when the bifurcation parameter α passes through the critical value α ∗, i.e., the equilibrium point O(0,0,0,0) is asymptotically stable for α∈(0, α ∗) and is unstable when α∈(α ∗,1). Hence, one can assert that Hopf bifurcation in system (6) occurs at α = α ∗.

Remark 2.

It follows from the proof of Theorem 1 that the critical value of bifurcation parameter

$$\begin{array}{@{}rcl@{}} \alpha^{*}=\frac{2}{\pi}\arctan\frac{\sqrt{4b-c^{2}}}{c}. \end{array} $$

Next, the fractional-order α is fixed and the parameter c is considered as a control parameter. A similar method is adopted to analyse the occurrence of Hopf bifurcation in system (6). Hence, the following Theorem 2 is presented without proof.

3.3 Hopf bifurcation analysis vs. the parameter c

Theorem 2 (Existence of Hopf bifurcation). When bifurcation parameter c passes through the critical value c ∗, fractional-order system (6) undergoes the Hopf bifurcation at the equilibrium point O(0,0,0,0), if the following conditions hold:

  1. (1)

    4b−c 2>0;

  2. (2)

    \(m(c^{*})=\alpha \pi /2-\min \!|\!\arg (\lambda _{i}(c^{*}))|~(i=1,2,3)\);

  3. (3)

    (dm(c)/dc)| c = c ∗ ≠ 0 (transversality condition).

Remark 3.

From the proof, one can obtain the critical value of bifurcation parameter c ∗ by \(\alpha \pi /2=\arctan \frac {\pi \sqrt {4b-{c^{*}}^{2}}}{2c^{*}}\), in this case transversality condition \(({\mathrm {d}m(c)}/{\mathrm {d}c})|_{c=c^{*}}={1}/{\sqrt {4b-c^{2}}}\) is satisfied.

4 Chaos control

In this section, chaos control in system (3) will be discussed. First, two new stability and stabilization theorems for a class of nonlinear fractional-order systems are proposed. Consider the following fractional-order nonlinear system:

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}^{\alpha} x(t)}{\mathrm{d}t^{\alpha}}=F(x(t))=Ax(t)+s(x(t)), \end{array} $$
(8)

where x(t) = (x 1(t), x 2(t),…, x n (t))T ∈ R n denote the state vector of the state system, \(f\text {:}~R^{n}\rightarrow R^{n}\) define a nonlinear vector field in the n-dimensional vector space, fractional-order α belongs to 0<α < 1. A ∈ R n × n is a constant matrix, A x(t) and h(x(t)) denote linear and nonlinear parts of F(x(t)).

In [27], we have discussed stability and stabilization of a fractional-order nonlinear system (8) with order α:1<α < 2 and new sufficient conditions ensuring local asymptotic stability and stabilization are proposed. In fact, the results obtained are also established for the order 0<α < 1.

Theorem 3.

System (8) is locally asymptotically stable, if

  1. (i)

    s(x(t))satisfies s(0)=0and \(\lim _{x\rightarrow 0}\frac {\|s(x(t))\|}{\|x(t)\|}=0\);

  2. (ii)

    Re λ(A) < 0and \(\omega =-\max \{\text {Re}~{\lambda (A)}\}>({\Gamma }(\alpha ))^{1/\alpha }\).

Proof. The process of the proof is the same as in [24] and is therefore omitted here.

The fractional-order nonlinear system (8) with control input u(t) = K x(t) is said to be asymptotically stable if there exists a control gain matrix K with suitable dimension such that the closed-loop system

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}^{\alpha} x(t)}{\mathrm{d}t^{\alpha}}=Ax(t)+s(x(t))+Kx(t)=(A+K)x(t)+s(x(t)), \end{array} $$
(9)

is asymptotically stable.

It follows from Theorem 3 that the following stabilization results are established clearly.

Theorem 4.

If feedback gain K is chosen such that the following conditions hold:

  1. (i)

    s(x(t)) satisfies s(0)=0 and \(\lim _{x\rightarrow 0}\frac {\|s(x(t))\|}{\|x(t)\|}=0\);

  2. (ii)

    Re λ(A + K) < 0 and \(\omega =-\max \{\text {Re}~{\lambda (A+K)}\}>({\Gamma }(\alpha ))^{1/\alpha }\),

then the controlled system (9) is locally asymptotically stable.

System (6) can be written in the form of (8), where

$$\begin{array}{@{}rcl@{}}A&=\left( \begin{array}{ccc} 0 &\; 1 &\; 0 \\ -b &\; c &\; 0 \\ 0 &\; -1 &\; -a \\ \end{array} \right),\quad s(x(t))=\left( \begin{array}{ccc} 0 \\ -\mathrm{d}x_{2} {{x_{3}^{2}}} \\ x_{2}x_{3} \\ \end{array} \right). \end{array} $$

It is obvious that s(x(t)) satisfies

$$\begin{array}{@{}rcl@{}} \lim\limits_{x\rightarrow 0}\frac{\|s(x(t))\|}{\|x(t)\|}&=&\lim\limits_{x\rightarrow 0}\frac{\sqrt{(\mathrm{d}{{x_{3}^{2}}}x_{2})^{2}+(x_{3}x_{2})^{2}}}{\sqrt{{{x_{1}^{2}}}+{{x_{2}^{2}}}+{{x_{3}^{2}}}}}\\ &\leq&\lim\limits_{x\rightarrow 0}\frac{\sqrt{(\mathrm{d}{{x_{3}^{2}}}x_{2})^{2}+(x_{3}x_{2})^{2}}}{\sqrt{{{x_{2}^{2}}}}}\\ &=&\lim\limits_{x\rightarrow 0}\sqrt{\mathrm{d}^{2}{{x_{3}^{4}}}+{{x_{3}^{2}}}}=0. \end{array} $$
(10)

Based on Theorem 4, the following theorem is presented to control chaos in system (6).

Theorem 5.

If these exist linear feedback gains K such that

  1. (i)

    Re λ(A + K) < 0;

  2. (ii)

    \( \omega = -\max \{\text {Re}~{\lambda (A+K)}\} >({\Gamma }(\alpha ))^{1/\alpha }\), then the controlled system (10) is locally asymptotically stable.

Remark 4. Linear feedback control is especially attractive and has been successfully applied to practical implementation, which was adopted to realize control and synchronization of integer-order chaotic systems. Compared to sliding mode control and nonlinear feedback control used for discussing fractional-order chaotic systems in the existing literature, the linear control is economic and easy to implement.

5 Numerical simulations

In this section, to verify and demonstrate the effectiveness of the obtained results, some numerical simulations are presented which are carried out by virtue of the Adams–Bashforth–Moulton scheme in [28]. In the following simulations, parameters a = 3/5, b = 1/3, d = 1/2.

Case 1.

Fractional-order α is selected as the bifurcation parameter.

By using Matlab software, one can obtain the roots of the characteristic eq. (7) of system (6), λ1 = −0.6, λ2 = 0.2500+0.5204i, λ3 = 0.2500+0.5204i. It follows from Remark 1 that the critical value of the bifurcation parameter

$$\begin{array}{@{}rcl@{}} \alpha^{*}=\frac{2}{\pi}\arctan\frac{\sqrt{4b-c^{2}}}{c}=0.7149. \end{array} $$

Apparently, the transversality condition is established for

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}m(\alpha)}{\mathrm{d}\alpha}\left|\underset{\alpha=\alpha^{*}}\quad=\frac{\pi}{2}\neq 0.\right. \end{array} $$

Based on Theorem 1, Hopf bifurcation occurs in system (6), when bifurcation parameter α passes through the critical value 0.7149. The largest Lyapunov exponents (LE) close to the critical value α ∗ = 0.7149 are calculated (figure 2). When α ∗ = 0.71, according to Lemma 1, the equilibrium point O(0,0,0,0) of system (6) is locally asymptotically stable as shown in figures 6a and 6b. The equilibrium point losses its stability and Hopf bifurcation occurs when α increases above α ∗ = 0.7149. When α ∗ = 0.72, a limit cycle which attracts adjacent solutions appears as shown in figures 7a and 7b.

Figure 6
figure 6

Order α = 0.71: (a) phase portrait of fractional-order chaotic system (6); (b) state trajectories of fractional-order chaotic system (6).

Full size image
Figure 7
figure 7

Phase portrait of fractional-order chaotic system (6) with order α = 0.72: (a) phase portrait in the x 2– x 3 plane; (b) phase portrait in space.

Full size image

Case 2. c is selected as the bifurcation parameter.

Here, fractional-order α = 0.8 is fixed. Based on Remark 2, the critical bifurcation parameter c ∗ is determined by

$$\begin{array}{@{}rcl@{}} \alpha\pi/2=\arctan\frac{\sqrt{4b-{c^{*}}^{2}}}{c^{*}} \quad\text{and}\quad\frac{\mathrm{d}m(c)}{\mathrm{d}c}\left|\underset{c=c^{*}}\quad=\frac{1}{\sqrt{4b-c^{2}}}\neq 0\right. \end{array} $$

(i.e., the transversality condition holds). By some calculations, the critical value c ∗ is 0.3568. Figure 4 displays the largest Lyapunov exponents (LE) around the critical value c ∗ = 0.3568. When c = 0.33, the equilibrium O(0,0,0,0) of system (6) is locally asymptotically stable as shown in figures 8a and 8b. The equilibrium losses its stability and Hopf bifurcation occurs when c increases above 0.3568, and when c = 0.36, a limit cycle which attracts adjacent solutions appears as shown in figures 9a and 9b.

Figure 8
figure 8

Order c = 0.33: (a) phase portrait of fractional-order chaotic system (6); (b) state trajectories of fractional-order chaotic system (6).

Full size image
Figure 9
figure 9

Phase portrait of fractional-order chaotic system (6) with order c = 0.36: (a) phase portrait in the x 1– x 2 plane; (b) phase portrait in space.

Full size image

Chaos control

In the simulation, feedback gain is selected as K = diag(−1.5,−2,−2), which satisfies the conditions in Theorem 5, i.e.,

$$\begin{array}{@{}rcl@{}} \text{Re}~{\lambda(A+K)}&=&-2.5,\quad-1.5<0 \end{array} $$

and

$$\begin{array}{@{}rcl@{}}\omega=-\max \{\text{Re}~{\lambda(A+K)}\}=1.5>1.2093=({\Gamma}(0.8))^{1/0.8}. \end{array} $$

Simulation result is depicted in figure 10, which shows that the zero solution of the controlled system is asymptotically stable.

Figure 10
figure 10

Stabilization of fractional-order chaotic system (6) with feedback gain K = diag (−1.5,−2,−2).

Full size image

6 Conclusions

Chaos and stabilization of a new fractional-order simple chaotic memristor circuit system has been addressed in this paper. Some basic properties of the system have been investigated in terms of chaotic attractors, equilibria, Lyapunov exponent spectrum and bifurcation diagram. Two Hopf bifurcation conditions are presented with different bifurcation parameters. A new stabilization criterion for a class of nonlinear fractional-order system is given, based on which, linear feedback controller is designed to complete the stabilization of the new fractional-order memristor circuit system.