Quark star models with logarithmic anisotropy

Abstract

New models for the charged anisotropic stellar object were generated using the Einstein–Maxwell field equations. A new choice of pressure anisotropy in logarithmic form was used to generate a quark star model. Anisotropic and isotropic models were regained as a special case. We regained anisotropic models found by Maharaj, Sunzu and Ray; Abdalla, Sunzu and Mkenyeleye; and Sunzu and Danford. The isotropic models regained include the performance by Mak and Harko, and Maharaj and Komathiraj. Physical analysis showed that matter variables and the gravitational potentials are well behaved. Our model does satisfy the energy conditions and stability condition.

1 Introduction

The Einstein–Maxwell field equations are often used to describe the behaviour of the structure and properties of the stellar objects. Stellar objects such as dark energy stars, black holes, quark stars, gravastars, dwarf stars, compact stars and neutron stars have the highest densities which result in their collapse [1]. Schwarzshild [2] developed a model with the stress tensor energy–momentum for the perfect fluid. Stellar models generated using the field equations with astrophysical significance include the works performed in [3,4,5,6,7,8,9,10,11,12,13].

Pressure anisotropy is significant in modelling relativistic matter as it affects the stability, structure and physical property of relativistic bodies [14,15,16,17,18,19,20,21,22,23,24,25]. The electric field plays a great role in examining the gravitational behaviour of compact objects like quark stars [23, 26,27,28]. Models generated for stellar objects with both electric field and pressure anisotropy can be seen in [14, 17, 29, 30].

The equations of state in different forms such as linear, quadratic, Van der Waals, polytropic and Chaplygin, can be used in modelling the relativistic compact stellar objects. Recent charged anisotropic models with the linear equation of state include the studies conducted in [14, 23, 25, 31]. The exact models with quadratic equation of state are found in [14, 16, 17, 24, 27, 31, 32]. Models with Van der Waals equation of state are given in [33]. Models with the polytropic equation of state can be seen in [16,17,18, 27, 34]. Models that used the Chaplygin equation of state can be seen in [35,36,37,38,39].

Solutions for the field equations have been obtained using anisotropy in polynomial forms [3, 40]. Abdalla et al [25] generated charged anisotropic quark star models using anisotropy as a rational function. We generate new exact solutions of the field equations for charged anisotropic matter using a linear quark equation of state. In this work, we apply a new choice of anisotropy in logarithmic form. This form of anisotropy is missing in other choices made in the past. The generated model generalises several models found in the past.

2 Basic field equations

The static and spherically symmetric space–time is given by the interior line element

$$\begin{aligned} \mathrm {d}s^{2}&=-\mathrm {e}^{2\nu (r)}\mathrm {d}t^{2}+\mathrm {e}^{2\lambda (r)}\mathrm {d}r^{2} +r^{2}( \mathrm {d}\theta ^{2}+\sin ^{2}\theta \mathrm {d}\phi ^{2}), \end{aligned}$$

(1)

where $\lambda (r)$ and $\nu (r)$ are gravitational potentials. The energy–momentum tensor is defined as

$$\begin{aligned} \tau _{ij}\!\!=\!\!\text {diag}\!\left( \!\!-\!\rho \!-\!\frac{1}{2} E^{2}, p_{r}\!-\!\frac{1}{2} E^{2}, p_{t}\!\!+\!\!\frac{1}{2} E^{2}, p_{t}\!\!+\!\!\frac{1}{2} E^{2} \!\right) , \end{aligned}$$

(2)

where $p_t$ is the tangential pressure, $\rho$ is the energy density, E is the electric field and $p_r$ is the radial pressure. The system of field equations for a charged anisotropic stellar object is given as

$$\begin{aligned}&\frac{1}{r^{2}}(1-\mathrm {e}^{-2\lambda })+\frac{2\lambda '}{r}\mathrm {e}^{-2\lambda } = \rho +\frac{1}{2} E^{2}, \end{aligned}$$

(3a)

$$\begin{aligned}&\frac{-1}{r^{2}}(1-\mathrm {e}^{-2\lambda })+\frac{2\nu '}{r}\mathrm {e}^{-2\lambda } = p_{r}- \frac{1}{2} E^{2}, \end{aligned}$$

(3b)

$$\begin{aligned}&\mathrm {e}^{-2\lambda }\left( \nu ''+\nu '^{2}-\nu ' \lambda ' +\frac{\nu '}{r}- \frac{\lambda '}{r}\right) = p_{t}+ \frac{1}{2} E^{2}, \end{aligned}$$

(3c)

$$\begin{aligned}&\sigma =\frac{1}{r^{2}} \mathrm {e}^{-\lambda }(r^{2}E), \end{aligned}$$

(3d)

where $\sigma$ represents the proper charge density. The energy density and radial pressure are related with linear equation of state given by

$$\begin{aligned} p_{r}=\frac{1}{3}(\rho -4B), \end{aligned}$$

(4)

where B is the bag constant. The bag equation is consistent with the quark star model. Models for quark stars include the works by Komathiraj and Maharaj [26], Maharaj et al [41], Sunzu et al [3], Sunzu and Danford [23] and Abdalla et al [25].

We transform system (3) by

$$\begin{aligned} x=Cr^2,\quad A^{2}y^{2}(x)=\mathrm {e}^{2\nu (r)},\quad Z(x)=\mathrm {e}^{-2\lambda (r)}, \end{aligned}$$

(5)

as given by Durgapal and Bannerji [42]. The transformed system of field equations becomes

$$\begin{aligned}&\rho =3p_{r}+4B, \end{aligned}$$

(6a)

$$\begin{aligned}&\frac{p_{r}}{C}=Z\frac{{\dot{y}}}{y}-\frac{{\dot{Z}}}{2}-\frac{B}{C}, \end{aligned}$$

(6b)

$$\begin{aligned}&\Delta =4CxZ\frac{\ddot{y}}{y}+C\!\left( 6Z+2x{\dot{Z}}\right) \frac{{\dot{y}}}{y} \nonumber \\&\quad +C\!\left( 2\left( {\dot{Z}}+\frac{B}{C}\right) +\frac{(Z-1)}{x}\right) , \end{aligned}$$

(6c)

$$\begin{aligned}&p_{t}=p_{r}+\Delta , \end{aligned}$$

(6d)

$$\begin{aligned}&\frac{E^{2}}{2C}=\frac{(1-Z)}{x}-\frac{{\dot{Z}}}{2}-3Z\frac{{\dot{y}}}{y}-\frac{B}{C}, \end{aligned}$$

(6e)

$$\begin{aligned}&\sigma =2\sqrt{\frac{CZ}{x}}\left( x{\dot{E}}+E\right) . \end{aligned}$$

(6f)

System (6) is presented in six equations with eight variables ($\Delta$, $p_{t}$, Z, $p_{r}$, E, y, $\rho$, $\sigma$).

3 Model formulation

To solve the field of eqs (6), we specify two quantities namely, the metric function y and the measure of anisotropy $\Delta$. The metric potential is specified as

$$\begin{aligned} y=(a+x^{f})^{d}, \end{aligned}$$

(7)

where f, d and a are real constants. This metric function is continuous, regular and finite throughout the interior of the star. The same metric function was used by Komathiraj and Maharaj [26], Maharaj et al [41], Sunzu et al [3], Sunzu and Danford [23] and Abdalla et al [25]. We keep the same choice to regain models generated in the past.

We consider a new measure of anisotropy as

$$\begin{aligned}&\Delta =\frac{(\sum _{i=1}^{n} \beta _{i} x^{i}){\ln (\alpha +cx)}}{(1+qx)^{t}}, \nonumber \\&\quad n\in {\mathbb {N}}, \alpha \ge 1, c\ge 0, t\in {\mathbb {Z}}, \end{aligned}$$

(8)

where $\beta _{i}$ and q are arbitrary real constants. This choice is regular and continuous throughout the interior of the stellar objects under the given conditions. It is presented as an elementary function and can vanish at the centre, which is an important property for pressure anisotropy. Furthermore, it can be set to vanish within the stellar interior to give isotropic models. The nature of this anisotropy is missing in studies performed in the past. This work provides new insight for investigating the properties of charged anisotropic quark stars. Interestingly, we regain several models studied in the past. When $\alpha = \mathrm {e}$ and $c=0$, we regain the models performed by Abdalla et al [25]. For $\alpha = \mathrm {e}$, $c=0$, $t=0$ and $\beta _{1}=\beta _{2}=0$, we regain the models generated by Sunzu and Danford [23]. For $c=0$, $\alpha =\mathrm {e}$, $q=0$, we obtain the models studied by Sunzu et al [3] and Maharaj et al [41]. When $\alpha =1$ and $c=0$ or $\beta _{i}=0$, we regain several isotropic models studied by Komathiraj and Maharaj [26]. Therefore, our work is also a generalisation of other quark star models.

Using eqs (7) and (8) in (6c), we obtain

$$\begin{aligned}&{\dot{Z}}+\left[ \frac{1}{2x}+\frac{(4f(fd+1)-3f)x^{f-1}}{2(a+(1+fd)x^{f})}\right. \nonumber \\&\qquad \left. +\frac{2f(d-1)x^{f-1}}{a+x^{f}}\right] Z\nonumber \\&\quad =\frac{\left( 1-({2xB}/{C})+({x\Delta }/{C})\right) (a+x^{f})}{2x\left( fdx^{f}+x^{f}+a\right) }. \end{aligned}$$

(9)

Equation (9) is, in general, a nonlinear ordinary differential equation governing the model.

4 Non-singular model

The generalised non-singular model in our study is obtained by considering $f=1$, $d=2$, $n=3$ and $t=-1$. Equation (9) then becomes

$$\begin{aligned}&{\dot{Z}}+\left( \frac{1}{2x}+\frac{3}{a+3x}+\frac{2}{a+x}\right) Z\nonumber \\&\quad =\frac{\left( 1+({\Delta x}/{C})-({2xB}/{C})\right) \left( a +x\right) }{2x\left( 3x+a\right) }. \end{aligned}$$

(10)

Solving eq. (10), we obtain

$$\begin{aligned} Z&=\frac{35a^{3}+35a^{2}x+21ax^{2}+5x^{3}}{35\left( a+x\right) ^{2}\left( a+3x\right) }\nonumber \\&\quad +\frac{({K(x)}/{C})}{\left( a+x\right) ^{2}\left( a+3x\right) }\nonumber \\&\quad -\frac{2B}{C}\left( \frac{105a^{3}x+189a^{2}x^{2}+135ax^{3}+35x^{4}}{315\left( a+x\right) ^{2}\left( a+3x\right) }\right) \nonumber \\&\quad +\frac{h}{2\sqrt{x}\left( a+x\right) ^{2}\left( a+3x\right) }. \end{aligned}$$

(11)

The gravitational potentials and matter variables become

$$\begin{aligned} \mathrm {e}^{2\nu }&=A^{2}\left( a+x\right) ^{4}, \end{aligned}$$

(12a)

$$\begin{aligned} \mathrm {e}^{2\lambda }&=\left[ \frac{35a^{3}+35a^{2}x+21ax^{2}+5x^{3}}{35\left( a+x\right) ^{2}\left( a+3x\right) }\right. \nonumber \\&\left. \quad +\frac{({K(x)}/{C})}{\left( a+x\right) ^{2}\left( a+3x\right) }-\frac{2B}{C}\right. \nonumber \\&\quad \left. \times \left( \frac{105a^{3}x+189a^{2}x^{2}+135ax^{3}+35x^{4}}{315\left( a+x\right) ^{2}\left( a+3x\right) }\right) \right] ^{-1}, \end{aligned}$$

(12b)

$$\begin{aligned} \rho&=C\left[ \frac{420a^{4}+1302a^{3}x+954a^{2}x^{2}}{35\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad +C\left[ \frac{450ax^{3}+90x^{4}}{35\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad +B\left[ \frac{210a^{5}+798a^{4}x+1476a^{3}x^{2}}{105\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad +B\left[ \frac{+2540a^{2}x^{3}+2090ax^{4}+630x^{5}}{105\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -\left[ \frac{K(x)\left( 3a-9x\right) +{\dot{K}}(x)(3a^{2}+12ax+9x^{2})}{2\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] , \end{aligned}$$

(12c)

$$\begin{aligned} p_{r}&=C\left[ \frac{140a^{4}+434a^{3}x+318a^{2}x^{2}+150ax^{3}+30x^{4}}{35\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -B\left[ \frac{210a^{5}+2982a^{4}x+11124a^{3}x^{2}}{315\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -B\left[ \frac{16780a^{2}x^{3}+11770ax^{4}+3150x^{5}}{315\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -\left[ \frac{K(x)\left( a-3x\right) +{\dot{K}}(x)(a^{2}+4ax+3x^{2})}{2\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] , \end{aligned}$$

(12d)

$$\begin{aligned} p_{t}&=C\left[ \frac{140a^{4}+434a^{3}x+318a^{2}x^{2}+150ax^{3}+30x^{4}}{35\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -B\left[ \frac{210a^{5}+2982a^{4}x+11124a^{3}x^{2}}{315\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -B\left[ \frac{16780a^{2}x^{3}+11770ax^{4}+3150x^{5}}{315\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -\left[ \frac{K(x)\left( a-3x\right) +{\dot{K}}(x)(a^{2}+4ax+3x^{2})}{2\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad +[\beta _{1}(x+qx^{2})+\beta _{2}(x^{2}+qx^{3})]{\ln (\alpha +cx)}\nonumber \\&\quad +[\beta _{3}(x^{3}+qx^{4})]{\ln (\alpha +cx)}, \end{aligned}$$

(12e)

$$\begin{aligned} E^{2}&=C\left[ \frac{196a^{3}x^{2}+1452a^{2}x^{3}+1356ax^{4}+420x^{5}}{35x\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -B\left[ \frac{168a^{4}x^{2}+1296a^{3}x^{3}+6528a^{2}x^{4}}{315x\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad - B\left[ \frac{7280ax^{5}+2520x^{6}}{315x\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -\left[ \frac{K(x)(2a^{2}+25ax+51x^{2})}{x\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] \nonumber \\&\quad -\left[ \frac{{\dot{K}}(x)(a^{2}x+4ax^{2}+3x^{3})}{x\left( a+x\right) ^{3}\left( a+3x\right) ^{2}}\right] , \end{aligned}$$

(12f)

where ${\dot{K}}(x)$ is the derivative of K(x) with respect to x.

If we set $a=\mathrm {e}$, $c=0$ and $q=0$, we regain the anisotropic model found by Maharaj et al [41]. Moreover, if we set $\beta _{1}=\beta _{2}=\beta _{3}=0$, the isotropic models for quark stars generated by Komathiraj and Maharaj [26] are regained. If we set $c=0$, $\alpha =\mathrm {e}$ and $q=0$, we obtain the models generated by Sunzu et al [3] and Maharaj et al [41].

5 Physical analysis

A realistic stellar model should satisfy some physical properties including the energy conditions, regularity, casaulity and stability. In this section, we show that the generated non-singular model satisfies the physical properties.

5.1 Energy conditions

A physical stellar model should satisfy the following energy conditions:

• (i) Null energy conditions: $\rho \ge 0$

• (ii) Weak dominant energy conditions: $\rho -p_r\ge 0$ and $\rho -p_t\ge 0$

• (iii) Strong dominant energy conditions: $\rho -3p_r\ge 0$ and $\rho -3p_t\ge 0$

• (iv) Strong energy conditions: $\rho -p_r-2p_t\ge 0.$

All the energy conditions are satisfied by our model. This shows that the model is physically viable.

5.2 Regularity

The gravitational potential $\mathrm {e}^{2\nu }$ in eq. (12a) is a decreasing function while the gravitational potential in eq. (12b) is an increasing function with the radial distance r. They are finite, regular and continuous functions throughout the interior of the stellar object. It can be observed that the gravitational potential $\mathrm {e}^{2\nu }$ is minimum at the centre $(x=0)$ whereas the gravitational potential $\mathrm {e}^{2\lambda }$ is maximum at the centre. The radial pressure, tangential pressure and energy density are decreasing functions with the maximum values at the centre. We can also observe that $p_{r}=p_{t}$ at the centre, which is physically realistic.

5.3 Casuality

The speed of sound v for a compact star should be less than the speed of light c. The speed of sound for relativistic stellar object is given as $\displaystyle v={\mathrm {d} p_{r}}/{\mathrm {d} \rho }$. From eqs (12c) and (12d), we obtain $v=\frac{1}{3}<1$. This agrees with the equation of state given in eq. (4).

5.4 Stability

The adiabatic index $(\Gamma )$ is used for an anisotropic relativistic stellar object as the measure of stability. When $\Gamma \ge \frac{4}{3}$, an object is said to be stable from gravitational collapse. The adiabatic index $\Gamma$ is given by

$$\begin{aligned} \Gamma = v\left( 1 + \frac{\rho }{p_{r}}\right) . \end{aligned}$$

(13)

The minimum value of the adiabatic index at the centre ($x=0$) of the relativistic object is given as

$$\begin{aligned} \Gamma _{0}=\frac{1}{3}+\frac{6C+aB}{6C-aB}. \end{aligned}$$

(14)

From eq. (14), the adiabatic index at the centre of the star $\Gamma _{0}\ge \frac{4}{3}$ for $aB\ge 0$. Since the bag constant $B > 0$ for quark stars, $\Gamma _{0}\ge \frac{4}{3}$ for $aB\ge 0$, which shows that the model is stable from gravitational collapse.

Fig. 1

Weak dominant energy conditions ($\rho -p_r$, $\rho -p_t$).

Fig. 2

Strong dominant energy conditions ($\rho -3p_r$, $\rho -3p_t$, $\rho - p_r-2p_t$).

Fig. 3

Radial pressure ($p_{r}$).

Fig. 4

Tangential pressure ($p_{t}$).

Fig. 5

Energy density ($\rho$).

Fig. 6

Adiabatic index ($\Gamma$).

Fig. 7

Electric field ($E^{2}$).

Fig. 8

Measure of anisotropy ($\Delta$).

6 Discussion

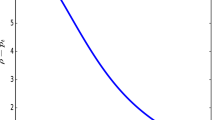
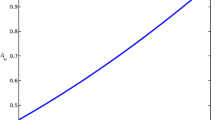
The model in system (12) is well behaved throughout the interior of the stellar object. The graphs are plotted by using Python programing language by specifying the values of the constants as $q=-0.5$, $\alpha =1$, $A=-0.5$, $B=0.05$, $C=0.5$, $c=0.3$, $\beta _{1}=0.01$, $\beta _{2}=0.02$, $\beta _{3}=0.03$ for the energy conditions, namely weak dominant energy conditions, $\rho - p_{r}$ and $\rho - p_{t}$ (figure 1), strong dominant energy conditions, $\rho - 3p_{r}$, $\rho - 3p_{t}$ and strong energy condition, $\rho - p_{r} - 2p_{t}$ (figure 2). We also plot the radial pressure $p_{r}$ (figure 3), the tangential pressure $p_{t}$ (figure 4), the energy density, $\rho$ (figure 5), the adiabatic index (figure 6), the electric field $E^{2}$ (figure 7) and the measure of anisotropy $\Delta$ (figure 8).

From figures 1 and 2, it is observed that the energy conditions $\rho -p_{r}\ge 0$, $\rho -p_{t}\ge 0$, $\rho -3p_{r}\ge 0$, $\rho -3p_{t}\ge 0$ and $\rho -p_{r}-2p_{t}\ge 0$. Thus, all the energy conditions are satisfied by our model. The radial pressure $p_{r}$, the tangential pressure $p_{t}$ and the energy density $\rho$ plotted in figures 3, 4 and 5, respectively, are decreasing functions from the core to the boundary of the stellar object. They are maximum at the centre of the star. This behaviour is physical as we expect these quantities to be maximum at the core of the star. We observe from figure 6 that the adiabatic index is greater than $\frac{4}{3}$ as required. This indicates that our model is stable.

The electric field $E^{2}$ is a decreasing function with the radial coordinate as shown in figure 7. In electrostatic, a charged sphere is neutral at the centre and the electric field increases with the increase in the radial distance. However, in stellar objects, the anisotropy may influence the electric field to decrease with the radial distance. This is also evident in models found by Feroze and Siddiqui [32] and Sunzu et al [40, 43]. The pressure anisotropy $\Delta$ in figure 8 is finite, regular and continuous. We note that $\Delta = 0$ at the centre and increases from the core to the surface of the stellar object. It indicates that anisotropy $\Delta \ge 0$ which indicates that $p_{t}\ge p_{r}$.

7 Conclusion

We have obtained new exact solutions by using Einstein–Maxwell field equations for a charged quark star. The model indicates that the matter variables are well behaved. We have regained several models studied in the past. We have also found that the model satisfies energy and stability conditions.