1 Introduction

The nonlinear Einstein-Maxwell field equations are necessary for the description of the behaviour of relativistic gravitating matter with or without electromagnetic field distributions, and they are tools for modeling relativistic compact objects such as dark energy stars, gravastars, quark stars, black holes and neutron stars. With the help of diverse solutions of the field equations and different matter configurations, the structure and properties of relativistic stellar bodies have been investigated. This is reflected in several investigations over the recent past. Models of neutral compact spheres with isotropic pressures have been studied by Murad and Pant (2014), Mak and Harko (2005), and Sharma et al. (2006). The case of neutral anisotropic matter was investigated by Paul et al. (2011), Harko and Mak (2002) and Kalam et al. (2012, 2013). Charged isotropic compact models are highlighted by Gupta and Maurya (2011a, 2011b), Negreiros et al. (2009), Murad and Fatema (2013), and Bijalwan (2011). The general model with charge and anisotropy was analysed by Esculpi and Aloma (2010), Mafa Takisa and Maharaj (2013a) and Rahaman et al. (2012). Several interesting features of exact solutions to the Einstein-Maxwell system for charged anisotropic quark stars were highlighted in the treatments of Maharaj et al. (2014) and Sunzu et al. (2014).

The effect of the electromagnetic distribution and pressure anisotropy are important ingredients to be considered when undertaking studies of relativistic stellar objects. Ivanov (2002) highlighted the fact that the presence of charge in a compact stellar matter contributes to changes in the mass, redshift and luminosity. It was shown by Sharma et al. (2001) that charged models could allow causal signals in the stellar interior over a wide range of parameters. On the other hand, Dev and Gleiser (2002) demonstrated that pressure anisotropy affects the physical properties, stability and structure of stellar matter. The stability of stellar bodies is improved for positive measure of anisotropy when compared to configurations of isotropic stellar objects. Furthermore the maximum mass and the redshift depend on the magnitude of the pressure anisotropy as illustrated by Dev and Gleiser (2003) and Gleiser and Dev (2004). They also showed that the presence of anisotropic pressures in charged matter enhances the stability of the configuration under radial adiabatic perturbations when compared to isotropic matter. There have been many recent investigations which include the presence of charge and anisotropy in the stellar interior. For example, Maharaj and Mafa Takisa (2012) presented regular models for charged anisotropic stellar bodies, generalized isothermal models were found by Maharaj and Thirukkanesh (2009), and superdense models were investigated by Maurya and Gupta (2012). Other new exact solutions for charged anisotropic stars are contained in the treatment of Mafa Takisa and Maharaj (2013b). Some other models describing anisotropic static spheres with variable energy density include the works of Cosenza et al. (1981), Gokhroo and Mehra (1994) and Herrera and Santos (1997).

On physical grounds for a stellar model we should include a barotropic equation of state so that the radial pressure is a function of the energy density. Exact models of charged anisotropic matter with a quadratic equation of state were found by Feroze and Siddiqui (2011). Using the same equation of state, Maharaj and Mafa Takisa (2012) generated regular models for charged anisotropic stars. A strange star model with a quadratic equation of state was recently generated by Malaver (2014). Polytropic models were analysed by Mafa Takisa and Maharaj (2013b) for charged matter with anisotropic stresses. Malaver (2013a, 2013b) found charged stellar models with a Van der Waals and generalized Van der Waals equation of state respectively. Anisotropic models with a modified Van der Waals equations of state are contained in the paper by Thirukkanesh and Ragel (2014). Other relativistic stellar models with a Van der Waals equation of state are studied in the treatment of Lobo (2007). However for a quark star we require a linear equation of state. The first treatment of quark stars was undertaken by Itoh (1970) for hydrostatic matter in equilibrium. Since then there have been many investigations on the study of structure and properties of quark matter by adopting a linear equation of state. It has been shown by Witten (1984), Chodos et al. (1974), Farhi and Jaffe (1984) that quark matter could be studied with the aid of the phenomenology of the MIT bag model; these studies indicate that a linear quark matter equation of state with a nonzero bag constant can be used. The review by Weber (2005) described the astrophysical phenomenology of compact quark stars. The study of nonradial oscillations of quark stars was performed by Sotani et al. (2004) and Sotani and Harada (2003). Charged isotropic models for quark stars are described by Mak and Harko (2004) and Komathiraj and Maharaj (2007). Particular models have been analysed to study the effect of both the electric field and the anisotropy in quark stars are those generated by Rahaman et al. (2012), Kalam et al. (2013), Varela et al. (2010), Thirukkanesh and Maharaj (2008), Maharaj and Thirukkanesh (2009) and Esculpi and Aloma (2010). However most charged anisotropic models of quark stars have anisotropy always present and do not regain isotropic pressures as a special case. Charged anisotropic models for quark stars that allow anisotropy to vanish have been found in the papers by Maharaj et al. (2014) and Sunzu et al. (2014).

The objective of this paper is to find new exact solutions to the Einstein-Maxwell system of equations with a linear quark matter equation of state for charged anisotropic stars. We build new models by specifying a particular form for one of the gravitational potentials and the measure of anisotropy. The model allows us to regain isotropic pressures as a special case. To achieve this objective we structure this paper accordingly. In Sect. 2 we give the fundamental equations and transformation of the field equations according to Durgapal and Bannerji (1983) and incorporate the linear quark matter equation of state. We then specify a new form for one of the gravitational potential and the measure of anisotropy which are physically viable and reasonable. This helps to deduce the master differential equation governing the behaviour of our model. In Sect. 3 we generate a regular model and regain the Einstein model with isotropic pressures. We show that this class produces objects with finite mass. In Sect. 4 we find a second class of solutions. This class has variable potentials and singularity at the centre. In Sect. 5 we give graphical analysis and make concluding remarks.

2 Fundamental equations

We intend to describe stellar structure with quark matter in a general relativistic setting. The spacetime manifold must be static and spherically symmetric. The interior spacetime is given by the metric

$$ ds^{2}=-e^{2\nu(r)}dt^{2}+e^{2\lambda(r)}dr^{2}+r^{2} \bigl(d\theta^{2}+\sin ^{2}\theta d\phi^{2}\bigr), $$
(1)

where ν(r) and λ(r) are arbitrary functions. The Reissner-Nordstrom line element describes the exterior spacetime

$$\begin{aligned} ds^{2} =& - \biggl(1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}} \biggr)dt^{2} \\ &{}+ \biggl(1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}} \biggr)^{-1}dr^{2} \\ &{}+r^{2}\bigl(d\theta^{2}+\sin^{2}\theta d \phi^{2}\bigr), \end{aligned}$$
(2)

where M and Q represent total mass and charge as measured by an observer at infinity. The energy momentum tensor

$$\begin{aligned} T_{ij} =&\mbox{diag} \biggl(-\rho-\frac{1}{2}E^{2},p_{r}-\frac{1}{2}E^{2},p_{t}+\frac{1}{2}E^{2}, \\ &{}p_{t}+\frac{1}{2}E^{2} \biggr), \end{aligned}$$
(3)

describes anisotropic charged matter. The energy density ρ, the radial pressure p r , the tangential pressure p t , and the electric field intensity E are measured relative to a vector u. The vector ua is comoving, unit and timelike.

The Einstein-Maxwell equations with matter and charge can be written as

$$\begin{aligned} &{\dfrac{1}{r^{2}} \bigl( 1-e^{-2\lambda} \bigr)+\dfrac{2\lambda^\prime}{r}e^{-2\lambda}=\rho+ \frac{1}{2}E^{2},} \end{aligned}$$
(4a)
$$\begin{aligned} &{-\dfrac{1}{r^{2}} \bigl( 1-e^{-2\lambda} \bigr)+\dfrac{2\nu^{\prime}}{r}e^{-2\lambda}=p_{r} - \frac{1}{2}E^{2},} \end{aligned}$$
(4b)
$$\begin{aligned} &{e^{-2\lambda} \biggl( \nu^{\prime\prime}+\nu^{\prime^{2}}-\nu^{\prime}\lambda^{\prime} +\dfrac{\nu^{\prime}}{r}-\dfrac{\lambda^{\prime}}{r}\biggr) = p_{t}+ \frac{1}{2}E^{2},} \end{aligned}$$
(4c)
$$\begin{aligned} &{\sigma=\frac{1}{r^{2}}e^{-\lambda} \bigl(r^{2}E \bigr)^{\prime},} \end{aligned}$$
(4d)

where primes indicate differentiation with respect to the radial coordinate r. The quantity σ denotes the proper charge density. Note that we are using units where the coupling constant \(\frac{8\pi G}{c^{4}}=1\) and the speed of light c=1. The mass contained within the charged sphere is defined by

$$ m(r)=\frac{1}{2}\int_{0}^{r} \omega^{2} \bigl( \rho_{*}+E^{2} \bigr) d\omega, $$
(5)

where ρ∗ is the energy density when the electric field E=0. For a quark star we have a linear relationship between the radial pressure and the energy density

$$ p_{r}=\frac{1}{3} (\rho-4B ), $$
(6)

where B is the bag constant.

We transform the field equations to an equivalent form by introducing a new independent variable x and defining metric functions Z(x) and y(x) as

$$ x=Cr^{2},\qquad Z(x)=e^{-2\lambda(r)},\qquad A^{2}y^{2}(x)=e^{2\nu(r)}, $$
(7)

where A and C are arbitrary constants. With this transformation the line element in (1) becomes

$$ ds^{2}=-A^{2}y^{2}dt^{2}+ \frac{1}{4xCZ}dx^{2}+\frac{x}{C}\bigl(d\theta ^{2}+ \sin^{2}\theta d\phi^{2}\bigr). $$
(8)

The mass function (5) becomes

$$ m(x)=\frac{1}{4C^{\frac{3}{2}}}\int_{0}^{x}\sqrt{\omega} \bigl( \rho _{*}+E^{2} \bigr) d\omega, $$
(9)

where

$$ \rho_{*}= \biggl( \frac{1-Z}{x}-2\dot{Z} \biggr)C, $$
(10)

and a dot represents differentiation with respect to the variable x.

Then we can write the Einstein-Maxwell field equations (4a)–(4d), with the quark equation of state (6), in the following form

$$\begin{aligned} &{\rho=3p_{r}+4B, } \end{aligned}$$
(11a)
$$\begin{aligned} &{\frac{p_{r}}{C}=Z\frac{\dot{y}}{y}-\frac{\dot{Z}}{2}-\frac{B}{C},} \end{aligned}$$
(11b)
$$\begin{aligned} &{p_{t}=p_{r}+\varDelta ,} \end{aligned}$$
(11c)
$$\begin{aligned} &{\varDelta =\frac{4xCZ\ddot{y}}{y}+C (2x\dot{Z}+6Z )\frac{\dot {y}}{y}} \\ &{\phantom{\varDelta =} +C \biggl(2 \biggl(\dot{Z}+\frac{B}{C} \biggr)+\frac{Z-1}{x}\biggr),} \end{aligned}$$
(11d)
$$\begin{aligned} &{\frac{E^{2}}{2C}=\frac{1-Z}{x}-3Z\frac{\dot{y}}{y}-\frac{\dot {Z}}{2}- \frac{B}{C},} \end{aligned}$$
(11e)
$$\begin{aligned} &{\sigma= 2\sqrt{\frac{ZC}{x}} (x\dot{E}+E ).} \end{aligned}$$
(11f)

The gravitational behaviour of the anisotropic charged quark star is governed by the system (11a)–(11f). The quantity Δ=p t −p r is called the measure of anisotropy. The system of equations (11a)–(11f) consists of eight variables (ρ,p r ,p t ,E,Z,y,σ,Δ) in six equations. The advantage of the Einstein-Maxwell system (11a)–(11f) is that it has a simple representation: it is given in terms of the matter variables (ρ,p r ,p t ,Δ), the charged quantities (E,σ) and the gravitational potentials Z and y. We rewrite (11d) in a more simplified form as

$$ \dot{Z}+ \dfrac{ (4x^{2}\ddot{y}+6x\dot{y}+y )}{2x (x\dot {y}+y )}Z= \dfrac{ ( \frac{x \varDelta }{C}+1-\frac{2xB}{C} )y}{2x (x\dot{y}+y )}. $$
(12)

This is a highly nonlinear equation in general. However if y and Δ are given functions then the form (12) of the field equation is linear in the variable Z. In order to find exact solutions to this model we will specify the two quantities y and Δ.

We choose the metric function as

$$ y=\frac{1-ax^{m}}{1+bx^{n}}, $$
(13)

where a, b, m and n are constants. This choice guarantees that the metric function y is continuous and well behaved within the interior of the star for a range of values of m and n. The metric function y is also finite at the centre of the star. We specify the measure of anisotropy in the form

$$ \varDelta =A_{1}x+A_{2}x^{2}+A_{3}x^{3}, $$
(14)

where A1, A2, and A3 are arbitrary constants. A similar choice of anisotropy was made by Maharaj et al. (2014). This choice is physically reasonable as it is continuous and well behaved throughout the interior of the star. It is finite at the centre of the star. It is possible to regain isotropic pressures when A1=A2=A3=0. We then have Δ=0 and the anisotropy vanishes. Substituting (13) and (14) in (12) we obtain the first order differential equation

$$\begin{aligned} &\dot{Z}+\dfrac{ [g(x)-1+ax^{m} (1-g(x)+k(x) ) ]}{ (1+bx^{n})h(x)}Z \\ &\quad =-\dfrac{ (\frac{(A_{1}x+A_{2}x^{2}+A_{3}x^{3}) x}{C}+1-\frac {2xB}{C} )l(x)}{h(x)}, \end{aligned}$$
(15)

where we have set

$$\begin{aligned} g(x) =&2b\bigl(-1+n+2n^{2}\bigr)x^{n}-b^{2}\bigl(1-2n+4n^{2}\bigr)x^{2n}, \\ k(x) =&4\bigl(m+bmx^{n}\bigr)^{2}-2m\bigl(1+bx^{n}\bigr) \bigl(b(4n-1)x^{n}-1\bigr), \\ h(x) =&2x \bigl[ b(n-1)x^{n}-1 \\ &{} +ax^{m}\bigl(1+m+bmx^{n}-b(n-1)x^{n} \bigr) \bigr], \\ l(x) =&\bigl(1-ax^{m}\bigr) \bigl(1+bx^{n}\bigr), \end{aligned}$$

for convenience.

3 A regular model

As solution to (15) is desirable. We can find a nonsingular exact model for the choice of values of the parameters

$$m=1,\qquad n=\frac{1}{2}, \quad \mbox{and} \quad a=b=0. $$

With these values the potential y=1 and (15) becomes

$$ \dot{Z}+\frac{1}{2x}Z=\frac{A_{1}x+A_{2}x^{2}+A_{3}x^{3}}{2C}+\frac {1}{2x}- \frac{B}{C}. $$
(16)

Solving the above differential equation we obtain

$$ Z=1+\frac{x}{C} \biggl(-\frac{2B}{3}+\frac{A_{1}x}{5}+ \frac {A_{2}x^{2}}{7}+\frac{A_{3}x^{3}}{9} \biggr). $$
(17)

Using the system (11a)–(11f) we obtain the exact solution describing the potentials and matter variables as

$$\begin{aligned} &e^{2\nu} = A^{2}, \end{aligned}$$
(18a)
$$\begin{aligned} &e^{2\lambda} = \dfrac{315}{315+\phi(x)}, \end{aligned}$$
(18b)
$$\begin{aligned} &\rho = 2B- \biggl(\frac{3A_{1}x}{5}+\frac{9A_{2}x^{2}}{14}+\frac{2A_{3}x^{3}}{3}\biggr), \end{aligned}$$
(18c)
$$\begin{aligned} &p_{r} = - \biggl(\frac{2B}{3}+\frac{A_{1}x}{5}+\frac{3A_{2}x^{2}}{14}+\frac{2A_{3}x^{3}}{9} \biggr), \end{aligned}$$
(18d)
$$\begin{aligned} &p_{t} = -\frac{2B}{3}+\frac{4A_{1}x}{5}+\frac{11A_{2}x^{2}}{14}+\frac{7A_{3}x^{3}}{9}, \end{aligned}$$
(18e)
$$\begin{aligned} &\varDelta = A_{1}x+A_{2}x^{2}+A_{3}x^{3}, \end{aligned}$$
(18f)
$$\begin{aligned} &E^{2} = - \biggl(\frac{4A_{1}x}{5}+\frac{5A_{2}x^{2}}{7}+\frac{2A_{3}x^{3}}{3} \biggr), \end{aligned}$$
(18g)

where

$$ \phi(x)=\frac{x}{C} \bigl(-210B+63A_{1}x+45A_{2}x^{2}+35A_{3}x^{3} \bigr). $$

This model admits no singularity in the interior in the potentials and in the matter variables. In addition Δ=0 and E2=0 at the stellar centre.

With this model the line element (8) becomes

$$\begin{aligned} ds^{2} =&-A^{2}dt^{2}+\frac{1}{4xC} \biggl( \dfrac{315}{315+\phi(x)} \biggr)dx^{2} \\ &{} +\frac{x}{C}\bigl(d\theta^{2}+\sin^{2}\theta d\phi ^{2}\bigr). \end{aligned}$$
(19)

Using the system (18a)–(18g), the mass function (9) becomes

$$ m(x)= \biggl(\dfrac{x}{C} \biggr)^{\frac{3}{2}} \biggl( \dfrac{1}{3}B-\frac {9}{50}A_{1}x-\frac{6}{49}A_{2}x^{2}- \frac{5}{54}A_{3}x^{3} \biggr). $$
(20)

In this exact solution we regain the special case of vanishing anisotropy and charge: Δ=0 and E2=0. Then the potentials and matter variables become

$$\begin{aligned} \begin{aligned} &e^{2\nu}=A^{2},\qquad e^{2\lambda}=\frac{315C}{315C-210Bx}, \\ &\rho=2B, \qquad p_{r}=p_{t}=-\frac{2B}{3}, \end{aligned} \end{aligned}$$
(21)

with the line element

$$\begin{aligned} ds^{2} =&-A^{2}dt^{2}+ \biggl(\frac{315}{4x(315C-210Bx)} \biggr)dx^{2} \\ &{} +\frac{x}{C}\bigl(d\theta^{2}+\sin^{2}\theta d \phi^{2}\bigr), \end{aligned}$$
(22)

in terms of the variable x.

Note that we can write (22) in the equivalent form

$$\begin{aligned} ds^{2} =&-A^{2}dt^{2}+ \biggl(1-\dfrac{r^{2}}{{\varGamma}^{2}} \biggr)^{-1}dr^{2} \\ &{} +r^{2}\bigl(d\theta^{2}+\sin^{2}\theta d \phi^{2}\bigr), \end{aligned}$$
(23)

where \(\varGamma^{2}=\frac{315}{210B}\). We observe that (23) is the familiar uncharged Einstein model with isotropic pressure and the equation of state \(p_{r}=p_{t}=-\frac{1}{3}\rho\). We can therefore interpret the exact solution (18a)–(18g) as a generalized Einstein model with charge and anisotropy. This possibility arises only because the energy density at the boundary is a nonzero constant in a quark star.

The solutions found in this section do represent finite masses that can be related to observed objects. To show this we introduce the transformations

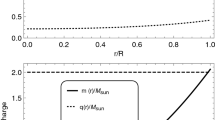
$$\begin{aligned} &\tilde{A}_{1}=A_{1}R^{2}, \qquad \tilde{A}_{2}=A_{2}R^{2}, \\ &\tilde{A}_{3}=A_{3}R^{2}, \qquad \tilde{B}=BR^{2}, \qquad \tilde{C}=CR^{2}. \end{aligned}$$

Based on these transformations we choose values of parameters to generate stellar masses and radii in Table 1. For computation purposes we have set R=43.245. Therefore we generate masses in the range 0.94–2.86M⊙ contained in the investigations of Mak and Harko (2004), Negreiros et al. (2009), Freire et al. (2011), Sunzu et al. (2014), Dey et al. (1998) and Thirukkanesh and Maharaj (2008). Therefore the exact solutions of this section do in fact produce finite masses consistent with masses of physically reasonable astronomical objects.

Table 1 Particular stellar objects obtained for various parameter values using a regular model
Full size table

4 Generalized models

It is possible that other exact solutions exist, in addition to those found above, and which may be obtained using the approach of this paper. Clearly these new solutions will correspond to different matter distributions, and consequently have different energy density profiles to the Einstein-Maxwell model considered in Sect. 3. The choice of parameters we made in Sect. 3 led to constant y. Here we again choose m=1, \(n=\frac{1}{2}\) but we take a=b2. Then the gravitational potential y is no longer constant. Consequently (15) can be written in the form

$$ \frac{ (1-3b\sqrt{x} )Z}{x(2-3b\sqrt{x})}= \dfrac{(b\sqrt{x}-1) (C+x (\varDelta -2B ) )}{Cx(3b\sqrt {x}-2 )}. $$
(24)

Equation (24) is more complicated than (16) but it can be integrated. Solving (24) we obtain the function

$$ Z=\dfrac{2-b\sqrt{x}+\frac{x}{C} (B (b\sqrt{x}-\frac{4}{3} )+f(x) )}{ {2- 3b\sqrt{x} }}, $$
(25)

where

$$\begin{aligned} f(x) =& A_{1}x \biggl( \frac{2}{5}-\frac{b\sqrt{x}}{3} \biggr) + A_{2}x^{2} \biggl(\frac{2}{7}-\frac{b\sqrt{x}}{4}\biggr) \\ &{} +A_{3}x^{3} \biggl( \frac{2}{9}-\frac{b\sqrt{x}}{5} \biggr). \end{aligned}$$

Note that when f(x)=0 then we have isotropic pressures. The function (25) demonstrates that there are other exact solutions to the differential equation (12) in terms of elementary functions.

Using the field equations indicated in the system (11a)–(11f) we obtain the following exact solution

$$\begin{aligned} &e^{2\nu} = A^{2} \biggl(\frac{1-b^{2}x}{1+b\sqrt{x}}\biggr)^{2}, \end{aligned}$$
(26a)
$$\begin{aligned} &e^{2\lambda} = \dfrac{2- 3b\sqrt{x}}{2-b\sqrt{x}+\frac{x}{C}[B (b\sqrt{x}-\frac{4}{3} )+f(x) ]}, \end{aligned}$$
(26b)
$$\begin{aligned} &\rho = \dfrac{3C (\frac{6b}{\sqrt{x}}-10b^{2}+3b^{3}\sqrt{x})}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)} \\ &\phantom{\rho =} +\dfrac{B (-16+47b\sqrt{x}-48b^{2}x+18b^{3}x^{\frac{3}{2}} )}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)} \\ &\phantom{\rho =} +\dfrac{3f_{r}(x)}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26c)
$$\begin{aligned} &p_{r} = \dfrac{C (\frac{6b}{\sqrt{x}}-10b^{2}+3b^{3}\sqrt{x})}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)} \\ &\phantom{p_{r} =} +\dfrac{B ( \frac{16}{3}-27b\sqrt{x}+40b^{2}x-18b^{3}x^{\frac{3}{2}} )}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)} \\ &\phantom{p_{r} =} +\dfrac{f_{r}(x)}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26d)
$$\begin{aligned} &p_{t} = \dfrac{C (\frac{6b}{\sqrt{x}}-10b^{2}+3b^{3}\sqrt{x})}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)} \\ &\phantom{p_{t} =} +\dfrac{B ( \frac{16}{3}-27b\sqrt{x}+40b^{2}x-18b^{3}x^{\frac{3}{2}} ) }{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)} \\ &\phantom{p_{t} =} +\dfrac{f_{t}(x)}{2(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26e)
$$\begin{aligned} &\varDelta = A_{1}x+A_{2}x^{2}+A_{3}x^{3}, \end{aligned}$$
(26f)
$$\begin{aligned} &E^{2} = \dfrac{C ( 2b^{2}+3b^{3}\sqrt{x}-\frac{2b}{\sqrt{x}})+B ( b\sqrt{x}-2b^{2}x )}{(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)} \\ &\phantom{E^{2} =} +\dfrac{f_{e}(x)}{(2-3b\sqrt{x})^{2}(b\sqrt{x}-1)}, \end{aligned}$$
(26g)

where we have set

$$\begin{aligned} &f_{r}(x) = A_{1}x \biggl( \frac{8}{5}- \frac{64}{15}b\sqrt{x}+\frac {18}{5}b^{2}x-b^{3}x^{\frac{3}{2}} \biggr) \\ &\phantom{f_{r}(x) =} +A_{2}x^{2} \biggl(\frac{12}{7}-\frac{141}{28}b\sqrt{x}+\frac{67}{14}b^{2}x-\frac{3}{2}b^{3}x^{\frac{3}{2}}\biggr) \\ &\phantom{f_{r}(x) =} +A_{3}x^{3} \biggl(\frac{16}{9}-\frac{82}{15}b\sqrt{x}+\frac{82}{15}b^{2}x-\frac{9}{5}b^{3}x^{\frac{3}{2}} \biggr), \\ &f_{t}(x) = A_{1}x \biggl(-\frac{32}{5}+\frac{416}{15}b\sqrt{x}-\frac{192}{5}b^{2}x+17b^{3}x^{\frac{3}{2}}\biggr) \\ &\phantom{f_{t}(x) =} +A_{2}x^{2} \biggl(-\frac{44}{7}+\frac{755}{28}b\sqrt{x}-\frac{521}{14}b^{2}x+\frac{33}{2}b^{3}x^{\frac{3}{2}} \biggr) \\ &\phantom{f_{t}(x) =} +A_{3}x^{3} \biggl(-\frac{56}{9}+\frac{398}{15}b\sqrt{x}-\frac{548}{15}b^{2}x+\frac{81}{5}b^{3}x^{\frac{3}{2}} \biggr), \\ &f_{e}(x) = A_{1}x \biggl( \frac{16}{5}-\frac{64}{5}b\sqrt{x}+\frac{84}{5}b^{2}x-7b^{3}x^{\frac{3}{2}}\biggr) \\ &\phantom{f_{e}(x) =} +A_{2}x^{2} \biggl( \frac{20}{7}-\frac{313}{28}b\sqrt{x}+\frac{101}{7}b^{2}x-6b^{3}x^{\frac{3}{2}}\biggr) \\ &\phantom{f_{e}(x) =} +A_{3}x^{3} \biggl(\frac{8}{3}-\frac{154}{15}b\sqrt{x}+\frac{196}{15}b^{2}x-\frac{27}{5}b^{3}x^{\frac{3}{2}} \biggr), \end{aligned}$$

for convenience.

Based on our exact solution in the system (26a)–(26g), the line element in (8) becomes

$$\begin{aligned} ds^{2} =&-A^{2} \biggl(\frac{1-b^{2}x}{1+b\sqrt{x}}\biggr)^{2}dt^{2} \\ &{} + \dfrac{1}{4xC} \biggl(\dfrac{2- 3b\sqrt{x}}{2-b\sqrt{x}+\frac{x}{C}(B (b\sqrt{x}-\frac{4}{3} )+f(x) )} \biggr)dx^{2} \\ &{} +\dfrac{x}{C}\bigl(d\theta^{2}+\sin^{2}\theta d\phi^{2}\bigr). \end{aligned}$$
(27)

The mass function has the form

$$\begin{aligned} m(x) =&\frac{x^{\frac{5}{2}}}{b^{4}C^{\frac{3}{2}}} \biggl(-\frac {2b^{4}A_{1}}{15}+\frac{47b^{2}A_{2}}{2520}+ \frac{113A_{3}}{12150} \biggr) \\ &{} -\frac{x^{\frac{7}{2}}}{b^{2}C^{\frac{3}{2}}} \biggl(\frac {5b^{2}A_{2}}{56}-\frac{5A_{3}}{378} \biggr) \\ &{} +\frac{x^{3}}{b^{6}C^{\frac{3}{2}}} \biggl(\frac{b^{6}B}{6}+\frac {b^{4}A_{1}}{30}+ \frac{b^{2}A_{2}}{56}+\frac{A_{3}}{90} \biggr) \\ &{} + \biggl( \frac{3b^{8}C}{2}-\frac{b^{6}B}{2}+\frac {b^{4}A_{1}}{10}+ \frac{3b^{2}A_{2}}{56} \\ &{} +\frac{A_{3}}{30} \biggr) \biggl( \frac{\ln(1-b\sqrt {x})}{b^{9}C^{\frac{3}{2}}} \biggr) \\ &{} + \biggl(\frac{2b^{8}C}{3}-\frac{4b^{6}B}{27}+\frac{64b^{4}A_{1}}{3645}+\frac{80b^{2}A_{2}}{15309} \\ &{} +\frac{512A_{3}}{295245} \biggr) \biggl(\frac{1}{2b^{9}C^{\frac{3}{2}}} \biggl( \frac{2}{3b\sqrt {x}-2}+1 \biggr) \biggr) \\ &{} +\frac{x^{3}}{3b^{3}C^{\frac{3}{2}}} \biggl(\frac{13b^{2}A_{3}}{240}x-\frac{b^{3}}{5}x^{\frac{3}{2}}+\frac{b^{2}A_{2}}{14}+\frac{17A_{3}}{540} \biggr) \\ &{} + \biggl(b^{8}C-\frac{2b^{6}B}{9}+\frac{32b^{4}A_{1}}{1215}+\frac{40b^{2}A_{2}}{5103} \\ &{} +\frac{256A_{3}}{98415} \biggr) \biggl(\frac{1}{b^{9}C^{\frac {3}{2}}} \ln \biggl( \frac{2}{2-3b\sqrt{x}} \biggr) \biggr) \\ &{}+\frac{x^{2}}{b^{5}C^{\frac{3}{2}}} \biggl(\frac {13b^{4}A_{1}}{360}+\frac{101b^{2}A_{2}}{6048}+ \frac {55A_{3}}{5832} \biggr) \\ &{} +\frac{x}{b^{7}C^{\frac{3}{2}}} \biggl(-\frac{b^{6}B}{6}+\frac {13b^{4}A_{1}}{324} \\ &{} +\frac{649b^{2}A_{2}}{27216} +\frac{2059A_{3}}{131220} \biggr) \\ &{} +\frac{\sqrt{x}}{b^{8}C^{\frac{3}{2}}} \biggl(\frac{b^{8}C}{2}-\frac {5b^{6}B}{18}+ \frac{179b^{4}A_{1}}{2430} \\ &{} +\frac{1867b^{2}A_{2}}{40824}+\frac{6049A_{3}}{196830} \biggr). \end{aligned}$$
(28)

Therefore we have obtained another exact solution to the Einstein-Maxwell system of equations (11a)–(11f) with a quark equation of state. Other solutions to (15) are possible for different choices of parameters m, n, a and b. It is not clear that other choices are likely to easily produce tractable forms for gravitational potential Z. The advantage of the exact solutions (18a)–(18g) and (26a)–(26g) is that they have a simple form. They are expressed in terms of elementary functions. The model (26a)–(26g) is singular at the centre. This is a feature that is shared with the quark star model of Mak and Harko (2004) but the stellar mass and electric field remain finite.

5 Discussion

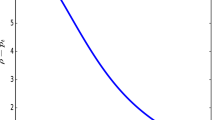
In this section we indicate that the exact solution of the field equations (26a)–(26g) is well behaved away from the centre. To do this we consider the behaviour of the gravitational potentials, matter variables and the electric field. We note that ρ′<0, \(p_{r} '<0\) and \(p_{t}' <0\), so that the energy density, the radial pressure and the tangential pressure are decreasing functions. The gradients are greatest in the central core regions. This happens because the profiles for ρ, p r and p t are dominated by the presence of the term containing the factor x−1/2. Other choices for the parameters m, n, a and b in (15) could lead to models with gradients where the rate of change is more gradual. The Python programming language was used to generate graphical plots for the remaining quantities of physical interest for the particular choices b=±0.5, A=0.664, B=0.198, C=1, A1=−0.6, A2=−0.15, and A3=0.2. The graphical plots generated are for the potential e2ν (Fig. 1), potential e2λ (Fig. 2), measure of anisotropy Δ (Fig. 3), the electric field E2 (Fig. 4) and the mass m (Fig. 5). All figures are plotted against the radial coordinate r. Most of these quantities are regular and well behaved in the stellar interior except for the electric field which is divergent at the centre. In this case our exact solutions may describe the outer regions, away from the centre, in a core envelope model. However, note that the gravitational potentials, the measure of anisotropy and the mass remain finite, regular and well behaved throughout the interior of the stellar structure. In general the measure of anisotropy Δ is finite and a continuous decreasing function as shown in Fig. 3. A similar profile of the anisotropy was obtained by Kalam et al. (2013) and Karmakar et al. (2007). The mass is an increasing function of the radial distance as indicated in Fig. 5.

Fig. 1
figure 1

The potential e2ν against radial distance

Full size image
Fig. 2
figure 2

The potential e2λ against radial distance

Full size image
Fig. 3
figure 3

Anisotropy against radial distance

Full size image
Fig. 4
figure 4

Electric field against radial distance

Full size image
Fig. 5
figure 5

Mass against radial distance

Full size image

We have found exact solutions for the Einstein-Maxwell equations for anisotropic charged quark matter. We have considered the spacetime geometry of the stellar interior to be static and spherically symmetric. The linear equation of state, consistent with quark matter, has been incorporated in our models. The solutions to the field equations are found after making a reasonable physical choice for the measure of anisotropy and one of the gravitational potentials. We have analysed two models: the first is regular throughout the interior in the matter variables and gravitational potentials, and the second is a generalized model that admits a singularity in some of the matter variables at the centre of the stellar object. We have regained masses and radii consistent with the Mak and Harko (2004), Negreiros et al. (2009), Freire et al. (2011), Sunzu et al. (2014), Dey et al. (1998) and Thirukkanesh and Maharaj (2008) models. We believe that our toy models may facilitate studies of anisotropic quark stars with an electromagnetic field distribution and provide room for further studies of other relativistic matter distributions. This may be achieved with a specific equation of state, spacetime geometry and metric functions different from what we have considered in this paper.