1 Introduction

In relativistic astrophysics, the impact of charge on the gross physical properties of stellar bodies has been a major area of research for many decades. In GR, it is well known that the collapse of a star to a point singularity can be avoided by incorporating a charge distribution since the gravitational attraction will then be counter-balanced by the Coulomb repulsion. Even though stellar systems are expected to be charge neutral, presence of a net charge at certain evolutionary stages of an astrophysical body cannot be ruled out. For example, in a binary pulsar system, a star may acquire a net charge by accretion from the surrounding medium to form a charged sphere (Treves and Turolla 1999; Mak et al. 2001). Analysis of the effect of charge is also relevant for ultra-compact stars like ‘strange stars’ composed of \(u\), \(d\) and \(s\) quarks. Investigations reveal that on the surface of a strange star, a thin electron layer may exist. Consequently, one associates a strong radially directed electric field at the interior of such stars which can be as high as \(\sim 10^{19}~\mbox{eV}/\mbox{cm}\) at the surface as pointed out by Usov (2004). Effects of electric field on the gross physical behavior of such systems can be studied by solving the relevant Einstein-Maxwell system. The exterior gravitational field of a static charged spherically symmetric distribution of matter is uniquely described by the Riessner-Nordström metric. The interior solution to a relativistic charged fluid sphere is, however, not unique and a large class of analytic solutions are available in the literature (Ivanov 2002).

Realistic models of charged fluid spheres have been developed and analyzed by many researchers in the past. Physical behavior and stability of charged dust have been carried out by Papapetrou (1947), Majumdar (1947), Bonner (1960, 1965), to name a few. Stettner (1973) has shown that a homogeneous fluid sphere with a considerable amount of net surface charge is more stable than that of an uncharged sphere. Bekenstein (1971) studied the dynamics and stability of spherically symmetric systems by generalizing the Oppenheimer-Volkoff equations of hydrostatic equilibrium (Oppenheimer and Volkoff 1939) and obtained a maximum limit on the electric field that a charged sphere might sustain. Cooperstock and de la Cruz (1978) found new class of solutions for uniformly distributed charged dust in equilibrium. Bonner and Wickramasuriya (1975) proposed a charged stellar model which shows a radially increasing matter density. Analytic solutions to Einstein-Maxwell systems for spherically symmetric objects with a variety of charge distributions have been studied by Wyman (1949), Adler (1974), Kuchowicz (1975) and Adams and Cohen (1975). Relativistic compact stars in equilibrium in the presence of charge have been studied by Ray et al. (2003), Ghezzi (2005), Ghezzi and Letelier (2007). By proposing specific analytic solutions to charged fluid objects, Whitman and Burch (1981) have discussed the stability of such objects. Pant and Sah (1971) obtained exact solutions to the Einstein-Maxwell system for a charged fluid distribution which allowed them to regain the Tolman IV solution as a particular case by switching off the charge contribution. Later, Pant and Sah (1971) solution was generalized by Tikekar (1984) who analyzed the physical viability of the new class of solutions. By assuming a particular charge distribution, Patel and Mehta (1995) proposed new exact solutions for charged fluid spheres. Rao and Trivedi (1998) developed a formalism to generate solutions to the Einstein-Maxwell system. Maartens and Maharaj (1990) have provided the necessary conditions for a solution of the Einstein-Maxwell system to be regular at the interior of a star. Chang (1983) generated new class of conformally flat solutions for charged fluid as well as dust distributions. In the recent past, analytic solutions to the Einstein-Maxwell system have been developed and analyzed by many researchers which include the works of Maharaj and Thirukkanesh (2009), Thirukkanesh and Maharaj (2009), Komathiraj and Maharaj (2007a), Maharaj and Komathiraj (2007), Hansraj and Maharaj (2006), Patel and Koppar (1987), Tikekar and Singh (1998), Sharma et al. (2001), Gupta and Kumar (2005), Komathiraj and Maharaj (2007b), Maurya and Gupta (2011a,b,c), Pant and Maurya (2012), Maurya et al. (2015), Murad and Fatema (2015a,b), Murad (2013), Murad and Fatema (2013), Fatema and Murad (2013), Pant et al. (2013), Ratanpal et al. (2015), Thomas and Pandya (2015), Durgapal (1982), Mak and Fung (1995), Mak et al. (1996), Lake (2003), Pant and Rajasekhara (2011), Pant and Negi (2012), among many others.

The aim of the current investigation is to provide new class of exact solutions to the Einstein-Maxwell system which are well behaved and can be used as viable models for stellar objects. Note that, in the absence of any reliable information about the equation of state (EOS) at extreme densities, the assumption of one of the metric potentials has been found to be a reasonable technique to construct both charged and uncharged spherical stellar models. A large class of solutions (Sharma et al. 2006; Sharma and Mukherjee 2001, 2002; Tikekar 1990; Tikekar and Thomas 1998, 1999, 2005; Thomas et al. 2005; Thomas and Ratanpal 2007; Paul et al. 2011; Chattopadhyay and Paul 2010; Chattopadhyay et al. 2012) for charged as well as uncharged fluid spheres have been developed making use of the ansatz put forward by Vaidya and Tikekar (1982). Similarly, the Finch and Skea (1989) ansatz has also been utilized by many authors (see, for example, Tikekar and Thomas 2005, Sharma and Ratanpal 2013, Pandya et al. 2015) to develop realistic stellar models. In this work, making use of the Finch and Skea (1989) ansatz, we present a new class solutions to the Einstein-Maxwell system for a spherically symmetric charged fluid distribution. In addition to studying the plausibility of the new class of solutions for the description of realistic compact stars, we intend to analyze the influence of electromagnetic field on the \(M-R\) relationship of relativistic compact stars.

The paper has been organized as follows: In Sect. 2 the field equations governing the spherically symmetric static charged fluid distribution have been laid down. By assuming a particular electric field intensity profile, the field equations have been solved. The exterior region of the charged fluid distribution is described by the Riessner-Nordström metric and consequently, the junction conditions have been laid down in Sect. 3. In Sect. 4, by imposing necessary regularity conditions, we have studied physical features of the system and analyzed the impact of the electromagnetic field on the gross features of the star. Finally, we have concluded by discussing our results in Sect. 5.

2 The Einstein-Maxwell system and its solution

We assume that the interior spacetime of a static spherically symmetric star is described by the metric

$$ ds^{2}=e^{\nu(r)}dt^{2}-e^{\lambda(r)}dr^{2}-r^{2} \bigl(d\theta^{2}+\sin^{2}\theta d\phi^{2} \bigr). $$
(1)

The physical behavior of the star can be understood by solving the Einstein-Maxwell field equations

$$ R_{i}^{j}-\frac{1}{2} R \delta_{i}^{j}=8\pi G \bigl(T_{i}^{j}+E_{i}^{j} \bigr), $$
(2)

where, the energy-momentum tensor corresponding to matter and electromagnetic fields are respectively given by

$$ T_{i}^{j}= (\rho+p )u_{i}u^{j}-p \delta_{i}^{j}, $$
(3)

and

$$ E_{i}^{j}=\frac{1}{4\pi} \biggl(-F_{ik}F^{jk}+\frac{1}{4}F_{mn}F^{mn} \delta_{i}^{j} \biggr). $$
(4)

In Eqs. (3) and (4), \(\rho\) and \(p\) denote the energy-density and pressure, respectively and \(u^{i}\) is the 4-velocity of the fluid. The electromagnetic field strength tensor can be derived from the 4-potential \(A_{i}= (\phi(r), 0, 0, 0 )\) so that

$$ F_{ij}=\frac{\partial A_{j}}{\partial x_{i}}-\frac{\partial A_{i}}{\partial x_{j}}. $$
(5)

The EM field strength tensor satisfies the Maxwell equations

$$ F_{ij,k}+F_{jk,i}+F_{ki,j}=0, $$
(6)

and

$$ \frac{\partial}{\partial x^{k}} \bigl(F^{ik}\sqrt{-g} \bigr)=4\pi \sqrt{-g}J^{i}. $$
(7)

The 4-current vector can be obtained in terms of the charge density \(\sigma\) using the relation

$$ J^{i}=\sigma u^{i}. $$
(8)

Due to spherical symmetry, the only non-vanishing components of \(F_{ij}\) are

$$ F_{01}= -F_{10} = -\frac{e^{\frac{\nu+\lambda}{2}}}{r^{2}} \int_{0}^{r} 4\pi r^{2}\sigma e^{\lambda/2}dr. $$
(9)

The total charge inside a radius \(r\) is given by

$$ q(r)=4\pi \int_{0}^{r} \sigma r^{2}e^{\lambda/2}dr. $$
(10)

Note that \(E^{2}=-F_{01}F^{01}\) so that the electric field intensity \(E\) is given by

$$ E=\frac{q(r)}{r^{2}}. $$
(11)

The field equations given by (2) for the spacetime described by the metric (1) are then equivalent to the following set of non-linear ODE’s

$$\begin{aligned} & 8\pi G \biggl(\rho+\frac{E^{2}}{2} \biggr) = \frac{1}{r^{2}}-e^{-\lambda} \biggl(\frac{1}{r^{2}}-\frac{\lambda'}{r} \biggr), \end{aligned}$$
(12)
$$\begin{aligned} & 8\pi G \biggl(p-\frac{E^{2}}{2} \biggr) = e^{-\lambda} \biggl( \frac{1}{r^{2}}+\frac{\nu'}{r} \biggr)-\frac{1}{r^{2}}, \end{aligned}$$
(13)
$$\begin{aligned} & 8\pi G \biggl(p+\frac{E^{2}}{2} \biggr) \\ &\quad{}= \frac{e^{-\lambda}}{4} \biggl[2\nu''+ \bigl( \nu'-\lambda' \bigr) \biggl(\nu'+ \frac{2}{r} \biggr) \biggr], \end{aligned}$$
(14)
$$\begin{aligned} & 4 \pi \sigma = \frac{e^{-\lambda/2}}{r^{2}} \frac{d}{dr}\bigl(r^{2} E \bigr), \end{aligned}$$
(15)

where, we have set \(c = 1\). Note that a prime (′) denote differentiation with respect to \(r\). We, therefore, have a system of five unknowns, namely \(\rho\), \(p\), \(E\), \(\nu\) and \(\lambda\). To solve the system, we use the Finch and Skea (1989) ansatz

$$ e^{\lambda}=1+\frac{r^{2}}{L^{2}}, $$
(16)

where \(L\) is the curvature parameter having dimension of length. The Finch and Skea (1989) ansatz is physically well motivated and has been used by many in the past to construct viable stellar models. Substituting (16) in (12), we get

$$ 8\pi G \biggl(\rho+\frac{E^{2}}{2} \biggr)=\frac{3+\frac{r^{2}}{L^{2}}}{L^{2} (1+\frac{r^{2}}{L^{2}} )^{2}}. $$
(17)

Combining (13) and (14) and using (16) we get,

$$\begin{aligned} &-\frac{\frac{r^{2}}{L^{2}}}{L^{2} (1+\frac{r^{2}}{L^{2}} )^{2}} -\frac{1}{ (1+\frac{r^{2}}{L^{2}} )} \biggl( \frac{\nu{''}}{2}+\frac{\nu{'}^{2}}{4}-\frac{\nu'}{2r} \biggr) \\ &\quad{}+\frac{r}{L^{2} (1+\frac{r^{2}}{L^{2}} )^{2}}\frac{\nu'}{2}+8 \pi G E^{2}=0. \end{aligned}$$
(18)

By making a coordinate transformation \(z=\sqrt{1+\frac{r^{2}}{L^{2}}}\) and introducing \(X=e^{\nu/2}\), equation (18) takes the form

$$ \frac{d^{2}X}{dz^{2}}-\frac{2}{z}\frac{dX}{dz}+ \biggl[ \frac{(z^{2}-1)-E^{2}L^{2}z^{4}}{z^{2}-1} \biggr]X=0. $$
(19)

To solve Eq. (19), we choose the electric field intensity as

$$ E^{2}=\frac{\alpha^{2}(z^{2}-1)}{L^{2}z^{6}}, $$
(20)

so that Eq. (19) reduces to

$$ z^{2}\frac{d^{2}X}{dz^{2}}-2z\frac{dX}{dz}+ \bigl(z^{2}-\alpha^{2} \bigr)X=0. $$
(21)

Our choice (20) ensures that \(E=0\) at \(r=0\). This particular choice also makes Eq. (21) tractable and its solutions is obtained as

$$ X=z^{3/2} \bigl[C_{1}J_{\beta}(z)+C_{2}Y_{\beta}(z) \bigr], $$
(22)

where \(\beta=\frac{\sqrt{9+4\alpha^{2}}}{2}\), \(C_{1}\), \(C_{2}\) are constants of integration, and \(J\) and \(Y\) are Bessel’s functions of first and second kind, respectively. The interior spacetime of the spherically symmetric charged fluid sphere finally takes the form

$$\begin{aligned} ds^{2} =&z^{3} \bigl[C_{1}J_{\beta}(z)+C_{2}Y_{\beta}(z) \bigr]^{2}dt^{2} - \biggl(1+\frac{r^{2}}{L^{2}} \biggr)dr^{2} \\ &{}-r^{2} \bigl(d\theta^{2}+\sin^{2}\theta d \phi^{2} \bigr). \end{aligned}$$
(23)

Subsequently, the energy density, pressure and charge density are obtained in the form

$$\begin{aligned} & 8\pi G \rho = \frac{2z^{2}(2+z^{2})-\alpha^{2}(z^{2}-1)}{2L^{2}z^{6}}, \end{aligned}$$
(24)
$$\begin{aligned} & 8\pi G p = \bigl\{ \bigl[3J_{\beta}(z)-z^{2}J_{\beta}(z)+2z \dot{J}_{\beta}(z) \bigr]C_{1} \\ &\phantom{8\pi G p =\,}+ \bigl[3Y_{\beta}(z)-z^{2}Y_{\beta}(z)+2z \dot{Y}_{\beta}(z) \bigr]C_{2}\bigr\} \\ &\phantom{8\pi G p =\,}\times\bigl\{ L^{2}z^{4} \bigl[C_{1}J_{\beta}(z)+C_{2}Y_{\beta}(z) \bigr]\bigr\} ^{-1} \\ &\phantom{8\pi G p =\,}+\frac{\alpha^{2} (z^{2}-1 )}{2L^{2}z^{6}}, \end{aligned}$$
(25)
$$\begin{aligned} &4\pi \sigma = \frac{3\alpha}{L^{2} z^{6}}, \end{aligned}$$
(26)

where an overhead dot (.) denotes differentiation with respect to \(z\). We note that for \(\alpha=0\), charge density vanishes.

3 Junction conditions

The spacetime metric (23) must be matched to the exterior Riessner-Nordström metric

$$\begin{aligned} ds^{2} =& \biggl(1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}} \biggr)dt^{2} - \biggl(1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}} \biggr)^{-1}dr^{2} \\ &{}-r^{2} \bigl(d\theta^{2}+\sin^{2}\theta d \phi^{2} \bigr), \end{aligned}$$
(27)

at the boundary of the star \(r=R\). The radius of the star can be obtained by utilizing the condition \(p(r=R)=0\). The boundary conditions determine the constants as

$$\begin{aligned} &C_{1}=\frac{1}{B}\bigl\{ 6z_{R}^{2}Y_{\beta}(z_{R})-2z_{R}^{4}Y_{\beta}(z_{R})+4z_{R}^{3} \dot{Y}_{\beta}(z_{R}) \\ &\phantom{C_{1}=\,}+\alpha^{2} \bigl(z_{R}^{2}-1 \bigr)Y_{\beta}(z_{R})\bigr\} , \end{aligned}$$
(28)
$$\begin{aligned} &C_{2}=-\frac{1}{B}\bigl\{ 6z_{R}^{2}J_{\beta}(z_{R})-2z_{R}^{4}J_{\beta}(z_{R})+4z_{R}^{3} \dot{J}_{\beta}(z_{R}) \\ &\phantom{C_{2}=\,}+\alpha^{2} \bigl(z_{R}^{2}-1 \bigr)J_{\beta}(z_{R})\bigr\} , \end{aligned}$$
(29)

where,

$$\begin{aligned} B =& z_{R}^{5/2}\bigl\{ J_{\beta}(z_{R}) \bigl[6z_{R}^{2}Y_{\beta}(z_{R}) -2z_{R}^{4}Y_{\beta}(z_{R})+4z_{R}^{3} \dot{Y}_{\beta}(z_{R}) \\ &{}+\alpha^{2} \bigl(z_{R}^{2}-1 \bigr)Y_{\beta}(z_{R}) \bigr] \\ &{} -Y_{\beta}(z_{R})\bigl[6z_{R}^{2}J_{\beta}(z_{R})-2z_{R}^{4}J_{\beta} (z_{R})+4z_{R}^{3}\dot{J}_{\beta}(z_{R}) \\ &{}+\alpha^{2} \bigl(z_{R}^{2}-1 \bigr)J_{\beta}(z_{R}) \bigr] \bigr\} . \end{aligned}$$
(30)

The total mass \(M\) is obtained as

$$ M=\frac{L (z_{R}^{2}-1 )^{3/2} [z_{R}^{4}+\alpha^{2} (z_{R}^{2}-1 ) ]}{2z_{R}^{6}}, $$
(31)

where \(z_{R}=\sqrt{1+\frac{R^{2}}{L^{2}}}\).

4 Physical analysis

A physically viable stellar model should satisfy the following conditions throughout the stellar configuration:

  1. (i)

    \(\rho \geq 0\), \(p \geq 0 \);

  2. (ii)

    \(\rho - 3 p \geq 0 \);

  3. (iii)

    \(\frac{d\rho}{dr} < 0 \), \(\frac{dp}{dr} < 0 \);

  4. (iv)

    \(0 \leq \frac{dp}{d\rho} \leq 1 \).

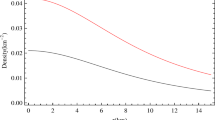
To examine the physical plausibility of the model, we have considered the data available from of the pulsar \(4U 1820-30\) whose mass and radius have been estimated to be \(M = 1.58~M_{\odot}\) and \(R = 9.1~\mbox{km}\), respectively (Gangopadhyay et al. 2013). Using these values as input parameters, we have determined the values of the other model parameters \(C_{1}\), \(C_{2}\) and \(L\). The values (\(C_{1} = 0.3910\) for \(\alpha=0\) and 0.3715 for \(\alpha=0.6\); \(C_{2} = -0.3633\) for \(\alpha=0\) and −0.4079 for \(\alpha=0.6\)) have been used to show graphically that all the requirements of a realistic star are satisfied in our model both for charged as well as uncharged cases (Figs. 1, 2, 3 and 4). From the figures, it is interesting to note that both density and pressure take lower values in the presence of an electric field. Figure 5 shows the thermodynamic relationship between the energy-density and pressure (\(p=p(\rho)\)) which indicates that the equation of state (EOS) of the relevant matter distribution remains almost linear in the presence or absence of the electric field.

Fig. 1
figure 1

Radial variation of density

Full size image
Fig. 2
figure 2

Radial variation of pressure

Full size image
Fig. 3
figure 3

Variation of sound speed at the stellar interior

Full size image
Fig. 4
figure 4

Fulfillment of the strong energy condition within the stellar interior

Full size image
Fig. 5
figure 5

Behavior of pressure against density (EOS)

Full size image

We have also calculated the adiabatic index in our model by using the relation

$$ \varGamma=\frac{\rho+p}{p}\frac{dp}{d\rho}. $$
(32)

Note that for the developed stellar configuration to be stable it is expected that \(\varGamma\) should be greater than \(4/3\) (Heintzmann and Hillebrandt 1975). In our model, this condition puts a restriction on \(\alpha\) such that \(0 \leq \alpha \leq 0.62\). Variation of the adiabatic index for charged as well as uncharged cases has been shown in Fig. 6. We observe a marginal decrease in the values of \(\varGamma\) near the center of a charged sphere as compared to its neutral counterpart.

Fig. 6
figure 6

Radial variation of adiabatic index

Full size image

The surface redshift

$$ z= \biggl(1-\frac{2 M}{R} \biggr)^{-\frac{1}{2}}-1, $$
(33)

also decreases when charge is incorporated into the system as shown in Fig. 7. Radial variation of charge \(Q\) has been shown in Fig. 8 which shows that the maximum deposition of charge occurs near the boundary of the star. Radial variation of the corresponding electric field has been shown in Fig. 9. We have also shown radial variation of the charge density for a given value of \(\alpha=0.6\) in Fig. 10.

Fig. 7
figure 7

Radial variation of gravitational redshift

Full size image
Fig. 8
figure 8

Distribution of charge at the stellar interior

Full size image
Fig. 9
figure 9

Radial variation of the electric field

Full size image
Fig. 10
figure 10

Radial variation of the charge density

Full size image

To show that the model can accommodate highly compact stars, we have also analyzed the viability of our model for some well known pulsars such as RX J 1856-37 (Pons et al. 2002), SAX J1808.4-3658 (Elebert et al. 2009), EXO 1785-248 (Ozel et al. 2009) and Her X-1 (Abubekerov et al. 2008). For the estimated masses and radii of these pulsars, we have determined the corresponding model parameters as given in Table 1. Making use of these values, in Table 2, we have evaluated values of the physically interesting quantities which have been shown to satisfy the requirements of a physically realistic star. Note that we have used \(()|_{0}\) and \(()|_{R}\) to denote the evaluated values of the physical parameters at the center and surface of the star, respectively.

Table 1 Values of model parameters
Full size table
Table 2 Values of physical quantities
Full size table

For a given value of the surface density (\(\rho(r=R) = 1.5\times 10^{15}~\mbox{gm}\,\mbox{cm}^{-3}\)), we have also obtained the mass-radius (\(M-R\)) relationship in our model for \(\alpha=0\) and \(\alpha \neq 0\) in Fig. 11 which clearly shows the significance of charge on the compactness of a star. It is interesting to note that inclusion of charge can accommodate more mass within a stellar configuration. In other words, compactness of a star increases in the presence of charge.

Fig. 11
figure 11

Mass-radius relationship for assumed surface density \(\rho_{R} = 1.5\times 10^{15}~\mbox{gm}\,\mbox{cm}^{-3}\)

Full size image

5 Discussion

Making use of the Finch and Skea (1989) ansatz, together with a particular choice of electric field intensity, we have found a non-singular solution of the Einstein-Maxwell system satisfying all regularity conditions. In the context of models of gravitationally collapsing systems, a similar class of solutions have earlier been found by Sharma and Das (2013) who utilized the Finch and Skea ansatz to describe the initial static stage of a gravitationally collapsing object which is anisotropic in nature but possesses zero charges. Earlier, Hansraj and Maharaj (2006) developed a charged analogue of the Finch-Skea stellar model for the charge parameter \(\alpha\) within some specified range of values. The work was further extended by Maharaj et al. (2017) who provided a more general class of solutions by incorporating anisotropy into the charged stellar system. The assumed forms of the electric field in the above formulations are such that in both cases the electric field attains a maximum value at a particular radial distance and gradually decreases towards the surface. Even though our class of solutions are obtained in terms of Bessel’s functions as in the previous studies, the choice of the electric field in our model is different which is evident from the fall-off behavior of the electric field shown in Fig. 9. Another distinguishing feature of our construction is that the class of solutions have been generated without specifying any restriction on \(\alpha\). However, physical requirements (stability condition) puts a bound on the electric field intensity parameter so that \(\alpha = [0, 0.62 ]\). Most interestingly, the electric field can be switched off simply by setting \(\alpha = 0 \). Another noticeable feature of our model is that in the presence of charge, both density \(\rho\) and pressure \(p\) take lower values as compared to uncharged configurations. The surface redshift in the charged case appears to be less than that of the uncharged case.

In our study, we have analyzed of the mass-radius (\(M-R\)) relationship of the model which, in general, is obtained by integrating the TOV equations for a given EOS. In the present study, even though we have not specified any EOS of the matter composition, we have successfully generated the \(M-R \) relationship for a given surface density. We note that, in the presence of an electric field, stellar configurations can accommodate more mass. It should be stressed here that even though most of the observed pulsar masses are clustered around \(1.4~M_{\odot}\), a wide range of values of masses and radii for a large class of pulsars have been predicted for which we still do not have any clue about their internal compositions. The current study shows that in classical gravity, the electromagnetic field can be used as a tool to fine-tune the mass vis-a-vis compactness of observed pulsars.