1 Introduction

Quantum communication is a field of applied quantum physics relates to quantum information processing. These two fields, i.e., quantum communication and quantum information, give us deeper insights into the application of the quantum physics. One of the most pure quantum mechanical phenomena widely used in quantum information is quantum entanglement [1]. Quantum entanglement plays a key role in different quantum information processing scenarios such as quantum secret sharing [2, 3], quantum cryptography [4] and quantum teleportation [5].

One valuable example of the power of quantum information transfer and exciting implications of the ’weirdness’ of quantum mechanics, is quantum teleportation that discovers from over two decades. Quantum teleportation is a unique quantum method that a quantum state sends from one party to another, without physically transmitting of the state by the combination of classical communication and quantum entanglement resources. Quantum teleportation as an elementary operation serves in quantum computers and such quantum communication protocols. Experimentally, it has been used in some quantum systems [6,7,8,9], for transferring quantum information in long distance for inside [10] and outside [11] laboratory conditions.

In a simple quantum teleportation, the procedure begins by preparing a pair of entangled particles as a quantum transmission channel. The first particle A is held by Alice (the sender), and the second particle B is sent to Bob (the receiver). Due to the entanglement of the particles, any physical operation on the particle A by Alice can be reflected in the Bob’s particle. Alice also has another particle C: wants to teleport onto B. For the aim of quantum teleportation, Alice makes a Bell measurement, on her particles A and C. Although Alice’s measurement doesn’t tell give any information about the quantum state of C, but due to the entanglement between A and B, it changes the quantum state of B in a new quantum state can be simply turned into initial quantum state of C by operating a unitary operation in Bob’s side. The required unitary operation can be deduce by using the outcome of Alice’s Bell measurement, i.e., Alice has to communicate her outcome to Bob by a classical means such as e-mail, phone, carrier pigeon, whatever works. Finally, having Alice’s outcomes, Bob knows what would be the proper operator to turn B into the original C. Since the proposing of the first quantum teleportation, it has been widely employed as an elementary operation for designing quantum communication protocols. In a recent couple of decade, considerable progress has been made in the field of quantum teleportation. Bennet and et al for the first time proposed a teleportation protocol of an arbitrary single qubit \( |\psi>_a = \alpha |0> + \beta |1>\) (with \(|\alpha |^2 + |\beta |^2 = 1\)) by using an entanglement EPR pair as quantum channel between the sender and receiver [5] and it was experimentally demonstrated four years later [12] .

By increasing the number of transmitted qubits in a quantum teleportation protocol, the complexity of the protocol increases in association with manifold multi-partite entanglement. A quantum teleportation protocol for transfer of two-qubit state using Bell state is presented in [13]. Moreover, a number of more protocols for teleporting two-qubit states are presented [14,15,16]. Also, in recent years multi-qubits quantum teleportation protocols have attracted several huge attention [17,18,19,20,21,22,23,24].

Furthermore, in a generalized quantum teleportation, a N-qubit system can be efficiently transferred from one party to another. The efficient scheme for perfect quantum teleportation of N-qubit by using Bell states as a quantum channel has been proposed in [25]. A nontrivial scheme for teleportation of an unknown N-qubit W-like state by costing only (\(N-1\)) shared bits and 2(\(N-1\)) bits of classical communication and employing only controlled-NOT gates and single-qubit measurements/operations was proposed in (2007) [26]. Moreover, a quantum teleportation protocol for teleporting of N-qubit through the composite GHZ-Bell channel was reported in (2012) [27]. Furthermore, a number of schemes for quantum teleportation of N-qubit state via n-pairs of EPR state and GHZ-like state as quantum channels were also studied [28,29,30].

In 2001, a new multi-particle entangled state proposed that called Cluster state [31]. It has been made clear that the cluster state ( with \(n>3\)) has maximally connected, robust against decoherence and better persistency compared to the GHZ states. So, the teleportation protocols prosper by using cluster states. In 2005, a 4-qubit cluster state is prepared by Walther et al. [32]. The 6-qubit cluster state was generated by Lu et al. in 2007 [33]. In 2010, teleportation of an arbitrary two-particle state via a 5-qubit cluster state is suggested by Liu et al. [34]. In 2013, Zha proposed a bidirectional quantum controlled teleportation via 5-qubit cluster state [35]. Then, in 2014, transporting a 3-qubit state using a five-particle cluster state is investigated by Liu et al. [36]. Later, several quantum teleportation protocols based on 5-qubit, 6-qubit, 9-qubit cluster states were proposed [37,38,39,40,41,42].

In this paper, a new quantum teleportation of a N-qubit entangled state by using a (\(N+1\))-qubit cluster state is investigated. A simple example is the proposed protocol is examined by teleportation of a 6-qubit entangled state via a 7-qubit cluster state as a quantum channel.

This paper is structured as follows: In Sect. 2, the teleportation of a N-qubit entangled state via a (\(N+1\))-qubit cluster state is proposed. In Sect. 3, we then examined the proposed scheme for teleportation of a 6-qubit entangled state via a 7-qubit cluster state. In Sect. 4, the efficiency of proposed scheme is calculated. Finally, the conclusion is given in Sect. 5.

2 Teleportation of a N-qubit entangled state via (\(N+1\))-qubit cluster state

A scheme for teleportation of 5-qubit entanglement quantum state by using a 7-qubit quantum channel was proposed by Binayak et al., in (2018) [24]. Inspired by this scheme, we present a new protocol in which a N-qubit entangled state can be transmitted between a sender called Alice and a receiver called Bob by using a cluster (\(N+1\))-qubit state. Suppose that, Alice wants to transfer the following N-qubit entangled state to Bob:

$$\begin{aligned} |\Psi \rangle _{A_{1} \ldots A_{N}}=x \left( \sum _{i=1}^2|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}\rangle \right) _{A_{1} \ldots A_{N}}+y \left( \sum _{i=1}^2|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}\rangle \right) _{A_{1} \ldots A_{N}},\nonumber \\ \end{aligned}$$
(1)

where \( 2(|x|^2+|y|^2)=1\) , \(b^{i}_{j}, C^{i}_{j}\in \lbrace 0,1\rbrace ; j=1,2,3, \ldots ,N\). In the above state, the \(\sum _{i=1}^2\) shows that there exist two terms contain N-qubit in each braces x and y. Alice and Bob share the entanglement (\(N+1\))-qubit cluster state \(|\rho \rangle \) is given by:

$$\begin{aligned}&|\rho \rangle _{A_{N+1}B_{1}B_{2} \ldots B_{N}}\nonumber \\&\quad =\frac{1}{2}\left( \sum _{i=1}^2|b_{N+1}^{i}b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}\rangle +\sum _{i=1}^2|C_{N+1}^{i}C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}\rangle )\right) _{A_{N+1}B_{1}B_{2} \ldots B_{N}},\nonumber \\ \end{aligned}$$
(2)

as well \(b^{i}_{j}, C^{i}_{j}\in \lbrace 0,1\rbrace \) but \( j=1,2,3, \ldots ,N+1\). So, the complete state can be written as:

$$\begin{aligned} |\Gamma \rangle&=|\Psi \rangle _{A_{1} \ldots A_{N}}\otimes |\rho \rangle _{A_{N+1}B_{1}B_{2} \ldots B_{N}}\nonumber \\&=\left( x \left( \sum _{i=1}^2|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}\rangle \right) +y \left( \sum _{i=1}^2|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}\rangle \right) \right) _{A_{1} \ldots A_{N}} \nonumber \\&\quad \otimes \frac{1}{2}\left( \sum _{i=1}^2|b_{N+1}^{i}b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}\rangle +\sum _{i=1}^2|C_{N+1}^{i}C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}\rangle )\right) _{A_{N+1}B_{1}B_{2} \ldots B_{N}} \nonumber \\&=\frac{1}{2} \left[ \left( \sum _{i=1}^2|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}b_{N+1}^{i}\rangle \right) _{A_{1} \ldots A_{N}A_{N+1}} \left( x\sum _{i=1}^2|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}\rangle \right) _{B_{1}B_{2} \ldots B_{N}} \right. \nonumber \\&\qquad + \left( \sum _{i=1}^2|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}C_{N+1}^{i}\rangle \right) _{A_{1} \ldots A_{N}A_{N+1}} \left( x\sum _{i=1}^2|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}\rangle \right) _{B_{1}B_{2} \ldots B_{N}} \nonumber \\&\quad \qquad \left( \sum _{i=1}^2|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}b_{N+1}^{i}\rangle \right) _{A_{1} \ldots A_{N}A_{N+1}} \left( y\sum _{i=1}^2|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}\rangle \right) _{B_{1}B_{2} \ldots B_{N}} \nonumber \\&\qquad + \left( \sum _{i=1}^2|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}C_{N+1}^{i}\rangle \right) _{A_{1} \ldots A_{N}A_{N+1}} \left( y\sum _{i=1}^2|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}\rangle \right) _{B_{1}B_{2} \ldots B_{N}}. \end{aligned}$$
(3)

We can write this state in terms of 4 orthogonal (\(N+1\))-qubit cluster states as follows:

$$\begin{aligned} |\Gamma \rangle&=\sum _{i=0}^3|\eta _i\rangle _{A_{1} \ldots A_{N+1}}\otimes |\Psi _i\rangle _{B_{1} \ldots B_{N}}\nonumber \\&=\sum _{i=0}^3|\eta _i\rangle _{A_{1} \ldots A_{N+1}}\otimes U_{i}|\Psi \rangle _{B_{1} \ldots B_{N}}, \end{aligned}$$
(4)

where

$$\begin{aligned}&|\eta _1\rangle =\frac{1}{2}[(|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}b_{N+1}^{i}\rangle )+(|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}C_{N+1}^{i}\rangle )] \\&|\eta _2\rangle =\frac{1}{2}[(|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}b_{N+1}^{i}\rangle )-(|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}C_{N+1}^{i}\rangle )] \\&|\eta _3\rangle =\frac{1}{2}[(|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}C_{N+1}^{i}\rangle )+(|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}b_{N+1}^{i}\rangle )] \\&|\eta _4\rangle =\frac{1}{2}[(|b_{N}^{i}b_{N-1}^{i} \ldots b_{1}^{i}C_{N+1}^{i}\rangle )-(|C_{N}^{i}C_{N-1}^{i} \ldots C_{1}^{i}b_{N+1}^{i}\rangle )]. \end{aligned}$$

Obviously, there are 4 orthogonal states for teleporting N-qubit state that transmitted by using 2 bits in classical channel. Alice makes measurement on her states \(|\eta _i\rangle ; i=0,1,2,3\), and sends outcome measurement to Bob through the classical channel. After that, Bob by affecting suitable unitary operator \(U_i\) corresponding to Alice’s measurement can recover the original state \(|\Psi \rangle \). The states \(|\Psi _i\rangle _{B_{1} \ldots B_{N}} \) are given by:

$$\begin{aligned}&|\Psi _1\rangle =U_1|\Psi \rangle \nonumber \\&|\Psi _2\rangle =U_2|\Psi \rangle \nonumber \\&|\Psi _3\rangle =U_3|\Psi \rangle \nonumber \\&|\Psi _4\rangle =U_4|\Psi \rangle , \end{aligned}$$
(5)

where the unitary operators \(U_i\) are combination of N Pauli operators. So, the process of teleportation is thereby completed. This scheme is a definitive scheme by the successful probability 1.

3 Teleportation of a 6-qubit entangled state via a 7-qubit cluster state

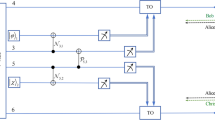
In this section, for the sake of more clarification, we examine the proposed protocol for a case of teleporting a 6-qubit state. Suppose, Alice as a sender intends to transfer a 6-qubit entangled state to receiver Bob, as follows:

$$\begin{aligned} |\kappa \rangle _{A_{1}A_{2}A_{3}A_{4}A_{5}A_{6}}=x(|000000\rangle +|101100\rangle )_{A_{1} \ldots A_{6}}+y(|001111\rangle +|100011\rangle )_{A_{1} \ldots A_{6}},\nonumber \\ \end{aligned}$$
(6)

where x and y are complex coefficients that satisfy \( 2(|x|^2+|y|^2)=1\) and subscripts \( A_{1},A_{2},A_{3},A_{4},A_{5},A_{6}\) refer to the Alice’s qubits. For the aim of completing the task, Alice and Bob share a 7-qubit entangled cluster state as quantum channel which is given by:

$$\begin{aligned} |\chi \rangle _{A_{7}B_{1}B_{2}B_{3}B_{4}B_{5}B_{6}}=\frac{1}{2}(|0000000 \rangle +|1001111 \rangle +|0101100 \rangle +|1100011\rangle )_{A_{7}B_{1} \ldots B_{6}},\nonumber \\ \end{aligned}$$
(7)

in which Alice takes the first qubit \(A_{7}\) and the remaining six qubits \(B_{1},B_{2},B_{3},B_{4},B_{5},B_{6}\) are with Bob. Therefore, the whole system can be written as:

$$\begin{aligned} |\Theta \rangle&=|\kappa \rangle _{A_{1}A_{2}A_{3}A_{4}A_{5}A_{6}}\otimes |\chi \rangle _{A_{7}B_{1}B_{2}B_{3}B_{4}B_{5}B_{6}} \nonumber \\&=x(|000000\rangle +|101100\rangle )_{A_{1} \ldots A_{6}}\nonumber \\&\quad +y(|001111\rangle +|100011\rangle )_{A_{1} \ldots A_{6}}\otimes \frac{1}{2}(|0000000 \rangle \nonumber \\&\quad +|1001111 \rangle +|0101100 \rangle +|1100011\rangle )_{A_{7}B_{1} \ldots B_{6}} \nonumber \\&=\frac{1}{2}[(|0000000\rangle +|1011000\rangle )_{A_{1} \ldots A_{7}}(x(|000000\rangle +|101100 \rangle )_{B_{1} \ldots B_{6}}) \nonumber \\&\quad +(|0000001\rangle +|1011001\rangle )_{A_{1} \ldots A_{7}}(x(|001111\rangle +|100011\rangle )_{B_{1} \ldots B_{6}}) \nonumber \\&\quad +(|0011110\rangle +|1000110\rangle )_{A_{1} \ldots A_{7}}(y(|000000\rangle +|101100\rangle )_{B_{1} \ldots B_{6}}) \nonumber \\&\quad +(|0011111\rangle +|1000111\rangle )_{A_{1} \ldots A_{7}}(y(|001111\rangle +|100011\rangle )_{B_{1} \ldots B_{6}})]. \end{aligned}$$
(8)

We can denote the above state as:

$$\begin{aligned} |\Theta \rangle= & {} |\epsilon _1\rangle _{A_{1} \ldots A_{7}}\otimes [x(|000000\rangle +|101100 \rangle )+y(|001111\rangle +|100011\rangle )]_{B_{1} \ldots B_{6}} \nonumber \\&+|\epsilon _2\rangle _{A_{1} \ldots A_{7}}\otimes [x(|000000\rangle +|101100 \rangle )-y(|001111\rangle +|100011\rangle )]_{B_{1} \ldots B_{6}} \nonumber \\&+|\epsilon _3\rangle _{A_{1} \ldots A_{7}}\otimes [x(|001111\rangle +|100011 \rangle )+y(|000000\rangle +|101100\rangle )]_{B_{1} \ldots B_{6}} \nonumber \\&+|\epsilon _4\rangle _{A_{1} \ldots A_{7}}\otimes [x(|001111\rangle +|100011 \rangle )-y(|000000\rangle +|101100\rangle )]_{B_{1} \ldots B_{6}},\nonumber \\ \end{aligned}$$
(9)

where the four orthogonal seven-qubit states write as:

$$\begin{aligned}&|\epsilon _1\rangle _{A_{1} \ldots A_{7}}=\frac{1}{2}(|0000000\rangle +|0011111\rangle +|1011000\rangle +|1000111\rangle )_{A_{1} \ldots A_{7}} \nonumber \\&|\epsilon _2\rangle _{A_{1} \ldots A_{7}}=\frac{1}{2}(|0000000\rangle -|0011111\rangle +|1011000\rangle -|1000111\rangle )_{A_{1} \ldots A_{7}} \nonumber \\&|\epsilon _3\rangle _{A_{1} \ldots A_{7}}=\frac{1}{2}(|0000001 \rangle +|0011110\rangle +|1011001\rangle +|1000110\rangle )_{A_{1} \ldots A_{7}} \nonumber \\&|\epsilon _4\rangle _{A_{1} \ldots A_{7}}=\frac{1}{2}(|0000001 \rangle -|0011110\rangle +|1011001\rangle -|1000110\rangle )_{A_{1} \ldots A_{7}}.\nonumber \\ \end{aligned}$$
(10)

So, we can write:

$$\begin{aligned} |\Theta \rangle&=\sum _{i=0}^3|\epsilon _i\rangle _{A_{1} \ldots A_{7}}\otimes |\kappa _i\rangle _{B_{1} \ldots B_{6}}\nonumber \\&=\sum _{i=0}^3|\epsilon _i\rangle _{A_{1} \ldots A_{7}}\otimes U_i|\kappa _0\rangle _{B_{1} \ldots B_{6}}, \end{aligned}$$
(11)

where the states \(|\kappa _i\rangle _{B_{1} \ldots B_{6}}\) built by affecting the unitary operators \(U_i\) on the state \(|\kappa \rangle \) in (6) are as follows:

$$\begin{aligned}&|\kappa _{1}\rangle =U_{1}|\kappa \rangle = x(|000000\rangle +|101100\rangle )+y(|001111\rangle +|100011\rangle ), \nonumber \\&U_1=IIIIII \nonumber \\&|\kappa _{2}\rangle =U_{2}|\kappa \rangle = x(|000000\rangle +|101100\rangle )-y(|001111\rangle +|100011\rangle ), \nonumber \\&U_2=IIIII\sigma _z \nonumber \\&|\kappa _{3}\rangle =U_{3}|\kappa \rangle = x(|001111\rangle +|100011\rangle )+y(|000000\rangle +|101100\rangle ), \nonumber \\&U_3=II\sigma _x\sigma _x\sigma _x\sigma _x \nonumber \\&|\kappa _{4}\rangle =U_{4}|\kappa \rangle = x(|001111\rangle +|100011\rangle )-y(|000000\rangle +|101100\rangle ), \nonumber \\&U_4=II\sigma _x\sigma _x\sigma _x\sigma _y, \end{aligned}$$
(12)

where \(I,\sigma _x,\sigma _y\) and \(\sigma _z\) are the Pauli operators as:

$$\begin{aligned} I=\left( \begin{array}{clcr} 1 &{} 0 \\ 0 &{}1 \\ \end{array} \right) \,\,,\,\, \sigma _x=\left( \begin{array}{clcr} 0 &{} 1 \\ 1 &{}0 \\ \end{array} \right) \,\,,\,\, \sigma _y=i\left( \begin{array}{clcr} 0 &{} -1 \\ 1 &{}0 \\ \end{array} \right) \,\,,\,\, \sigma _z=\left( \begin{array}{clcr} 1 &{} 0 \\ 0 &{}-1 \\ \end{array} \right) . \end{aligned}$$
(13)

Therefore, Alice performs a measurement on her states \(|\epsilon _i\rangle _{A_{1} \ldots A_{7}}; i=0,1,2,3\) and announces the outcome of her measurement to Bob by sending proper two classical bits through a classical channel. At last, by having Alice’s measurement outcome, Bob would be able to selects the proper unitary operator \(U_i\) and he can simply recover the original state by applying the proper operator to his states \(|\kappa _i\rangle _{B_{1} \ldots B_{6}}\). Thereby, the teleportation of 6-qubit entangled state by using 7-qubit cluster state is completed and Bob recovers the original state.

4 The efficiency

In this section, we calculate the efficiency of the proposed scheme. The intrinsic efficiency of the communication scheme is defined [43] as:

$$\begin{aligned} \eta =\frac{q_s}{q_u+b_t}, \end{aligned}$$
(14)

where \(q_s\) is the number of qubits of a state to be teleported, \(q_u\) is the number of the qubits which is used as the quantum channel and \(b_t\) is the number of classical bits transmitted. According to the above formula, the efficiency of teleportation of a N-qubit state via (\(N+1\))-qubit cluster state is:

$$\begin{aligned} \eta =\frac{N}{(N+1)+2}=\frac{N}{N+3}. \end{aligned}$$
(15)

It should be noted that the number of measurements in our scheme is always 4 and only 2 classical bits needed for transferring information in classical channel. For example, the efficiency of teleportation of 6-qubit entangled state via 7-qubit state is:

$$\begin{aligned} \eta =\frac{6}{9}=0.66 , \end{aligned}$$

where this value is significant. You can see, by increasing N the efficiency increases. In order to the underscore the advantage of proposed scheme, the efficiency of some previous related works is listed in Table 1.

Table 1 Efficiency of some previous protocols
Full size table

5 Conclusion

In summary, we proposed a new general protocol for the transfer of a N-qubit entangled state by using a (\(N+1\)) cluster state as a quantum channel. In this protocol, Alice makes measurement on her (\(N+1\))-qubit states including the N message qubits and one qubit of the (\(N+1\)) shared cluster states and announces outcome measurement to Bob by using 2 classical bits, after that by affecting suitable unitary operator corresponding to Alice’s measurement, the original state recovers by Bob. Comparing with the previously schemes, the high maximally connected, robust against decoherence and better persistency properties of cluster states suggests the proposed scheme as a definitive scheme by the successful probability 1 which exhibits a good efficiency.