1 Introduction

Quantum entanglement is a worth noting phenomena in quantum information science because of its correlation between two (or many) particles [1]. Quantum entanglement is a key element behind quantum information processing such as quantum teleportation [2], quantum dense coding [3], quantum secret sharing [4, 5], quantum cryptography [6], etc. Quantum teleportation is an important topic in quantum communication as it allows the transfer of information from a sender to a receiver at a large distance through a quantum channel though he sends a classical bit. Quantum teleportation was first proposed by Bennett et al. [2] and later experimentally demonstrated by Boschi et al. [7] and by Bouwmeester et al. [8]. Simply, we can explain the teleportation as a sender sends an unknown qubit to a receiver at a distance location via a quantum channel using some classical channel. GHZ and W states are commonly known as the three-qubit entangled states. Different schemes for teleportation were proposed by using the above mention entangled states [9].

Joo et al. [10] proposed two schemes of teleportation by using W state; out of those two schemes, in a scheme he considered as one qubit as a sender and the rest of the two qubits as receiver, and in the another scheme he considered two qubits as sender and teleported a state to the receiver. Ghosh et al. [11] have generalized a teleportation scheme of an entangle state using a GHZ-class state. Still, various new schemes are proposed in teleportation using W state and GHZ state or GHZ like state [12]. Li and Cao [13] proposed a theoretical scheme to teleport arbitrary two states using a four-qubit cluster state [14,15,16]. In quantum teleportation, different researchers use different entangled channels and different schemes. Here, we designed a new scheme by which we can teleport a two-qubit state using a four-qubit cluster state.

Since 2016, IBM quantum experience has given open access to the prototypes of quantum computers for testing and simulating quantum algorithms. IBM Q offers a cloud-based quantum computing platform, allowing the users to design quantum circuits using a interactive graphical user interface and test those circuits, both on a classical computer and on actual quantum processors. Several researchers have been benefited from this unique quantum experience provided by IBM. IBM provides the composer on their own website, which is a cloud-based quantum computing platform [17]. Any user can create a quantum circuit on the five-qubit, and fourteen-qubit devices for a real run or simulation. IBM Q Experience has now been used to perform many real experiments on the quantum chips. The real experiments include quantum simulation [18,19,20,21,22,23,24,25,26], developing quantum algorithms [27,28,29,30,31,32,33,34,35,36], testing of quantum information theoretical tasks [37,38,39], quantum cryptography [40,41,42,43], quantum error correction [44,45,46,47], quantum applications [47,48,49,50,51] to name a few.

The composition of the paper is as follows. Section 2 discusses the proposed scheme for quantum teleportation. Then the experimental realization of the scheme is demonstrated in Sect. 3. In Sect. 4, the experimental results are illustrated in detail. Finally, we conclude in Sect. 6 with discussions on future research works along this direction.

2 Scheme for quantum teleportation of an arbitrary two-qubit state using a four-qubit cluster state

In general an N-qubit linear cluster state is written as,

$$\begin{aligned} |{C_N}\rangle = {\frac{1}{2^\frac{N}{2}} \bigotimes _{a=1}^{N} (|{0}\rangle _a\sigma _{z}^{a+1} +|{1}\rangle _a )} \end{aligned}$$
(1)

A four-qubit cluster state used as quantum channel between Alice and Bob is in the state

$$\begin{aligned} |{C_4}\rangle _{3456}={\frac{1}{2}(|{0000}\rangle _{3456} + |{0011}\rangle _{3456} + |{1100}\rangle _{3456} - |{1111}\rangle _{3456})} \end{aligned}$$
(2)

A four-qubit cluster state from \(|{0000}\rangle _{2345}\) is generated from the following circuit (Fig. 1),

Fig. 1
figure 1

Quantum circuit generating the four-qubit cluster state, \(|C_4\rangle _{2345}\)

Full size image

A cluster state is a highly entangled state, and the following four-qubit cluster state can be used in the teleportation of any arbitrary single-qubit and two-qubit quantum state. In this scheme, we can teleport any two-qubit state \(|{\psi _{ab}}\rangle _{01} =\alpha |{00}\rangle _{01}+\beta |{01}\rangle _{01}+\gamma |{10}\rangle _{01} +\delta |{11}\rangle _{01}\) where \(|\alpha |^2+|\beta |^2+|\gamma |^2 +|\delta |^2=1\). We let Alice possess the qubit 2 and 3 along with \(\psi _{ab}\) and let Bob possess the qubit 4 and 5. In this process of teleportation, Alice makes a Bell state measurements on qubits (0,2) and (1,3). After then Alice tells Bob her measurement results via a classical channel. Finally, Bob can obtain the unknown state by performing appropriate unitary transformations on the particles 4 and 5.

3 Experimental realization in IBM QE

To perform quantum teleportation in IBM quantum processor, we use the given quantum circuit in Fig. 2.

Fig. 2
figure 2

A generalized circuit for quantum teleportation using four-qubit cluster state

Full size image

Figure 2 shows an actual quantum circuit used for the teleportation of an arbitrary two-qubit state in IBM QE processor. We have picked necessary gates from the toolbox and arranged to design the above circuit. First two-qubits which are to be teleported represent \(\Psi _{ab}\), and the last four qubits represent the cluster state which is distributed between Alice and Bob. The first four qubit belongs to Alice, and last two qubit belongs to Bob. The quantum circuit for generating cluster state is given in Fig. 1. A combination of CNOT and Hadamard gates is used for Bell-state measurement. Alice makes a Bell-state measurement on her qubits. After then, using two CNOT gates and two controlled-Z gate, Alice informs her measurement results to Bob. Finally, using unitary operation on Bob’s qubit, \(\psi _{ab}\) is obtained. In IBM quantum experience, the real experiments have been carried out using the fourteen-qubit quantum processor, where we can choose different number of shots, e.g., 1024, 4096 and 8192. Here, shots represent the number of times a given experiment is executed in a quantum processor. With single run, we will not get any sensible result compared to large number of run. The maximum number of times we can run an experiment in the quantum processor is 8192, and therefore, it gives almost accurate result of an experiment.

4 Results

As a part of our result, first, we verify our results in “IBM qasm simulator.” From Fig. 3, where Alice has a Bell state, and Alice wants to share the Bell state to Bob. From Table 2, we notice the probability distribution in case of the qasm simulator; Bob has got the exact Bell state that Alice had with probability distribution of 0.46 and 0.54 for \(\frac{1}{\sqrt{2}}|{00}\rangle +|{11}\rangle \) and \(\frac{1}{\sqrt{2}}|{01}\rangle +|{10}\rangle \) states. Again in the same table, we have shown the results for different states \(|{00}\rangle \), \(|{01}\rangle \), \(|{10}\rangle \) and \(|{11}\rangle \). Then we have run the results in the device “IBM 16 Melbourne.” Then, we compare the results in “IBM qasm simulator” and “IBM-16-Melbourne” for the above states. We see some error in the “IBM Q 16 Melbourne;” it is due to decoherence effect, state preparation error, gate errors, readout error etc. The single qubit and CNOT gate error rate and the measurement error (readout error) along with frequency, and coherence time are given in Table 3.

Fig. 3
figure 3

Quantum circuit illustrating the teleportation of Bell state

Full size image

In Table 1, we have shown the outcome of 9 run for the state \(|{\psi }\rangle =\frac{1}{\sqrt{2}}(|{00}\rangle +|{11}\rangle )\) each run having 8192 shots (Fig. 4).

Table 1 Results of teleportation for the state \(|{\psi }\rangle =\frac{1}{\sqrt{2}}(|{00}\rangle +|{11}\rangle )\)
Full size table
Fig. 4
figure 4

Histogram. This histogram shows the mean probabilities for \(|{00}\rangle \), \(|{01}\rangle \), \(|{10}\rangle \) and \(|{11}\rangle \) states and their percentage error

Full size image

We have performed the experiment of teleportation scheme for various state in both “IBM qasm Simulator” and “IBM 16 Melbourne” (real device) and the obtained probability shown in Table 2 (Table 3).

Table 2 Probability of states (in percentage) for “qasm simulator” (second column) and for “IBM melbourne 16”(third column)
Full size table
Table 3 The table shows the device calibration parameters of “IBM Melbourne 16”
Full size table

5 Quantum state tomography

Now we analyze state tomography [21] to know how well the unknown states are teleported from sender to receiver in our experiment. By comparing both theoretical and experimental density matrices of a quantum state, one can obtain the accuracy of the teleportation scheme. The theoretical and experimental density matrices of the unknown state are as follows

$$\begin{aligned} \rho ^T=|\psi \rangle \langle \psi | \end{aligned}$$
(3)

The experimental density matrix for two qubit unknown state is given by

$$\begin{aligned} \rho ^E= & {} \frac{1}{4}\big [ T_{II}(I \otimes I) +T_{IX}(I \otimes \sigma _X) +T_{IY}(I \otimes \sigma _Y)+T_{IZ}(I \otimes \sigma _Z)\nonumber \\&+\,T_{XI}(\sigma _X \otimes I)+T_{XX}(\sigma _X \otimes \sigma _X) +T_{XY}(\sigma _X \otimes \sigma _Y)+T_{XZ}(\sigma _X \otimes \sigma _Z)\nonumber \\&+\,T_{YI}(\sigma _Y \otimes I)+T_{YX}(\sigma _Y \otimes \sigma _X) +T_{YY}(\sigma _Y \otimes \sigma _Y)+T_{YZ}(\sigma _Y \otimes \sigma _Z)\nonumber \\&+\,T_{ZI}(\sigma _Z \otimes I)+T_{ZX}(\sigma _Z \otimes \sigma _X) +T_{ZY}(\sigma _Z \otimes \sigma _Y)+T_{ZZ}(\sigma _Z \otimes \sigma _Z)\big ] \end{aligned}$$
(4)

For the two-qubit entangled state \(|{\psi }\rangle =\frac{1}{\sqrt{2}}(|{00}\rangle +|{11}\rangle )\), theoretical and experimental density matrices are calculated as follows,

$$\begin{aligned} \rho ^T= & {} \frac{1}{2}\begin{pmatrix} 1 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 1 \\ \end{pmatrix} \end{aligned}$$
(5)
$$\begin{aligned} \rho ^E= & {} \begin{pmatrix} 0.255 &{} 0.013 &{} 0.065 &{} 0.005 \\ 0.013 &{} 0.224 &{} 0.009 &{} 0.054 \\ 0.065 &{} 0.009 &{} 0.264 &{} 0.022 \\ 0.005 &{} 0.054 &{} 0.022 &{} 0.255 \\ \end{pmatrix} +i \begin{pmatrix} 0 &{} -0.017 &{} -0.049 &{} 0.013 \\ 0.017 &{} 0 &{} -0.003 &{} -0.041 \\ 0.049 &{} 0.003 &{} 0 &{} 0.022 \\ -0.013 &{} 0.0410 &{} 0.009 &{} 0 \\ \end{pmatrix} \end{aligned}$$
(6)
Fig. 5
figure 5

Real and imaginary parts of theoretical and experimental density matrices for two-qubit quantum teleportation of \(|{\psi }\rangle =\frac{1}{\sqrt{2}}(|{00}\rangle +|{11}\rangle )\). a Real part of the theoretical density matrix, b imaginary part of the theoretical density matrix, c real part of experimental density matrix, d imaginary part of experimental density matrix. All experiments are performed on “IBM 16 Melbourne”

Full size image

For the following two-qubit entangled state \(|{\psi }\rangle =\frac{1}{\sqrt{2}}(|{01}\rangle +|{10}\rangle )\) theoretical and experimental density matrices are calculated as follows (Fig. 5)

$$\begin{aligned} \rho ^T&=\frac{1}{2}\begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{pmatrix} \end{aligned}$$
(7)
$$\begin{aligned} \rho ^E&=\begin{pmatrix} 0.2968 &{} 0.0115 &{} 0.0265 &{} 0.0005\\ 0.0115 &{} 0.2553 &{} -0.0045 &{} 0.0265\\ \ 0.0265 &{} -0.0045 &{} 0.2423 &{} 0.0075\\ 0.0005 &{} 0.0265 &{} 0.0075 &{} 0.2057\\ \end{pmatrix} +i \begin{pmatrix} 0 &{} -0.018 &{} 0.0075 &{} -0.0085\\ 0.018 &{} 0 &{} -0.0045 &{} 0.0005\\ -0.0075 &{} 0.0045 &{} 0 &{} -0.011\\ 0.0085 &{} -0.0005 &{} 0.0110 &{} 0 \\ \end{pmatrix} \end{aligned}$$
(8)
Fig. 6
figure 6

Real and imaginary parts of theoretical and experimental density matrices for two-qubit quantum teleportation of \(|{\psi }\rangle =\frac{1}{\sqrt{2}}(|{01}\rangle +|{10}\rangle )\). a Real part of the theoretical density matrix, b imaginary part of the theoretical density matrix, c real part of experimental density matrix, d imaginary part of experimental density matrix. Experiment is performed on “IBM 16 Melbourne”

Full size image

For the two-qubit entangled state \(|{\psi }\rangle =\frac{1}{2}(|{00}\rangle +|{01}\rangle +|{10}\rangle +|{11}\rangle )\) theoretical and experimental density matrices are calculated as follows (Fig. 6)

$$\begin{aligned} \rho ^T&=\frac{1}{2}\begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{pmatrix} \end{aligned}$$
(9)
$$\begin{aligned} \rho ^E&=\begin{pmatrix} 0.3025 &{} 0.016 &{} 0.0350 &{} 0.0095\\ 0.0160 &{} 0.2365 &{} -0.0015 &{} 0.0220\\ 0.0350 &{} -0.0015 &{} 0.2555 &{} 0.0150\\ 0.0095 &{} 0.022 &{} 0.0150 &{} 0.2055\\ \end{pmatrix} +i \begin{pmatrix} 0 &{} -0.0133 &{} 0.0072 &{} -0.011\\ 0.0133 &{} 0 &{} -0.0040 &{} -0.0083\\ -0.0072 &{} 0.0040 &{} 0 &{} -0.0197\\ 0.0110 &{} 0.0083 &{} 0.0197 &{} 0\\ \end{pmatrix} \end{aligned}$$
(10)
Fig. 7
figure 7

Real and imaginary parts of theoretical and experimental density matrices for two-qubit quantum teleportation of \(|{\psi }\rangle =\frac{1}{\sqrt{2}} (|{00}\rangle +|{01}\rangle +|{10}\rangle +|{11}\rangle )\). a Real part of the theoretical density matrix, b Imaginary part of the theoretical density matrix, c real part of experimental density matrix, d imaginary part of experimental density matrix. Experiment is performed on “IBM 16 Melbourne”

Full size image

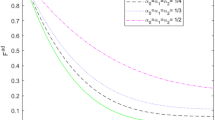
Fidelity is the measurement of the overlap between two density matrices of theoretical and experimental quantum states obtained as output. It can be calculated from the following formula (Eq. 11),

$$\begin{aligned} F(\rho ^T,\rho ^E)=\bigg [Tr\Bigg (\sqrt{\sqrt{\rho ^T} \rho ^E \sqrt{\rho ^T}}\Bigg )\Bigg ]^2 \end{aligned}$$
(11)

In Table 4, we have derived the fidelity for these states which is obtained from Eq. 11. This fidelity compares the closeness between the theoretical density matrix and experimental density matrix performed in “IBM Melbourne 16” (Fig. 7).

Table 4 Fidelity calculation in percentage between theoretical density matrix and density matrix obtained for “IBM melbourne 16”
Full size table

6 Conclusion

Four-qubit cluster states are created through appropriate circuit diagrams involving only quantum gates which have been shown here experimentally. We have successfully implemented quantum teleportation circuit in the IBM quantum computer. Teleportation of any arbitrary two-qubit quantum state has been verified in quantum simulator and QISKit (IBM quantum processor) taking 8192 number of shots. The probability distribution of each state has been observed. Here, the results for the two-qubit states and Bell state are shown. In the qasm simulator, Alice can teleport all the two-qubit states to Bob without any error, but in the real device, we get errors due to decoherence effect, state preparation error, gate errors, readout error, etc. We have calculated fidelity for three states shown in Table 4 and obtained a good fidelity above 70% for all the cases. The scheme can be utilized for practical application of teleportation of two-qubit state.